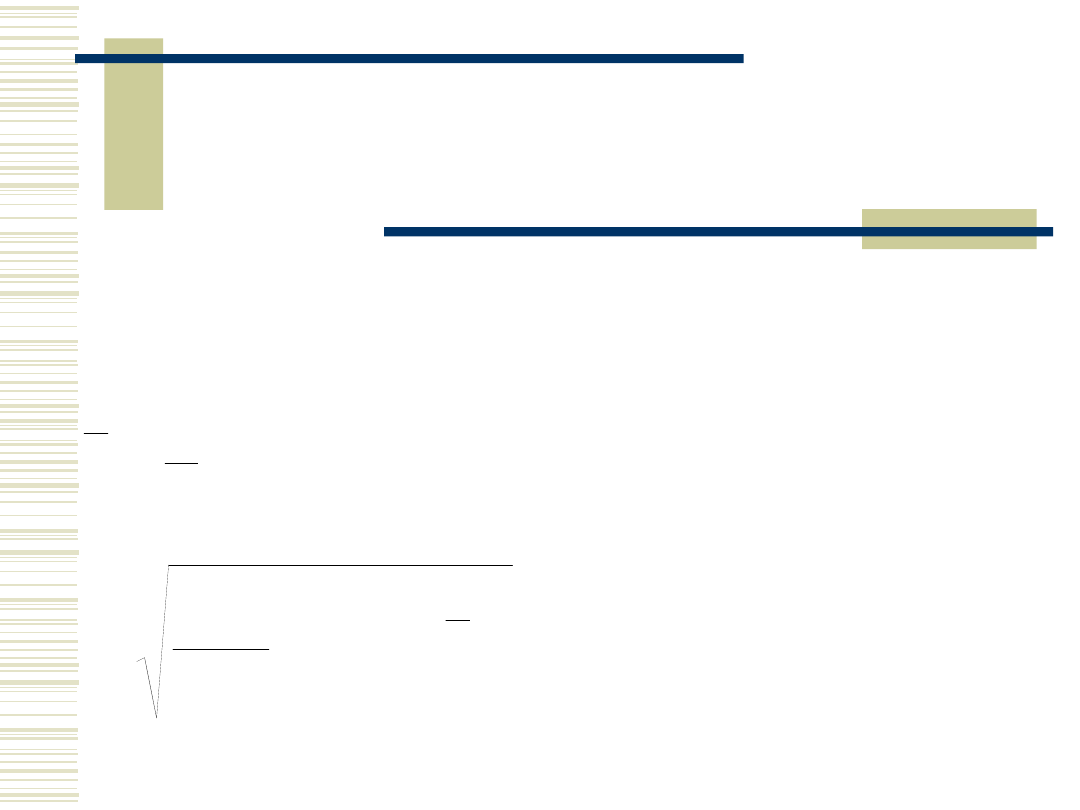
Estymacja parametrów
Parametry rozkładu normalnego zwykle
nie są znane. Na podstawie serii
pomiarów możemy je oszacować:
jest oszacowaniem dla wartości
oczekiwanej
jest oszacowaniem
odchylenia
standardowego
n
i
i
x
n
x
1
1
2
1
1
1
n
i
i
x
x
n
s
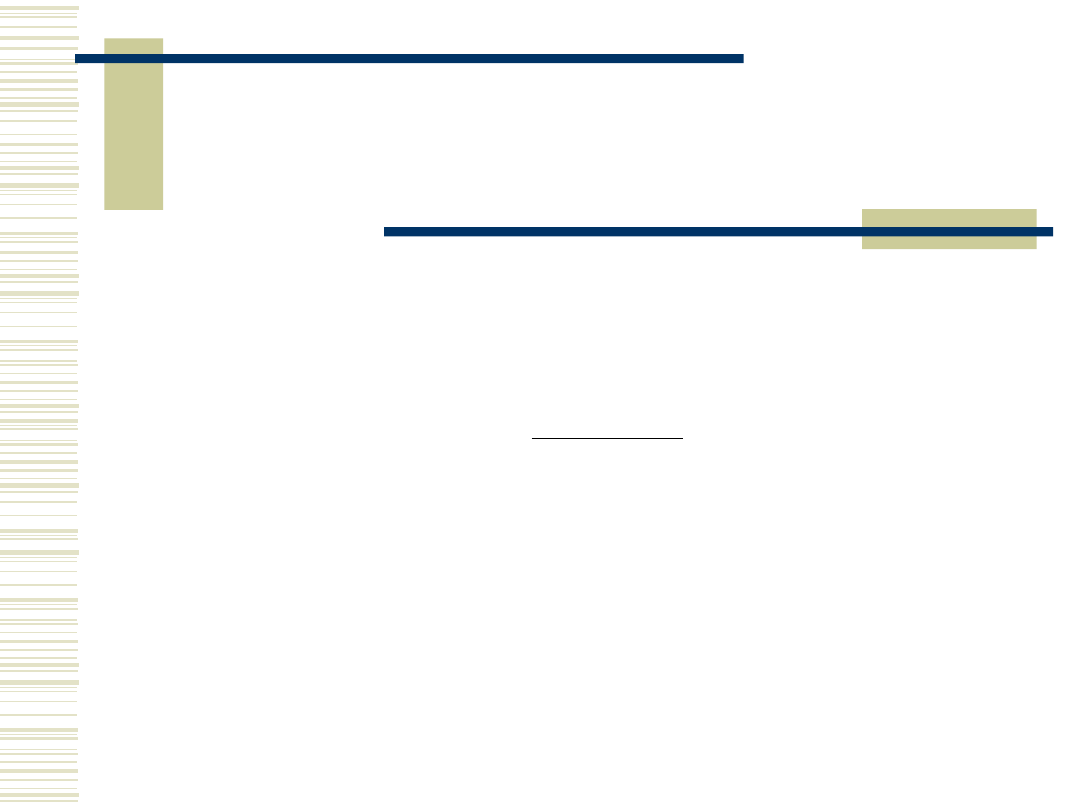
Standardowy rozkład
normalny
Jeśli X ma rozkład normalny o parametrach
i to:
ma rozkład normalny o parametrach
zwany standardowym rozkładem normalnym.
X
u
0
1
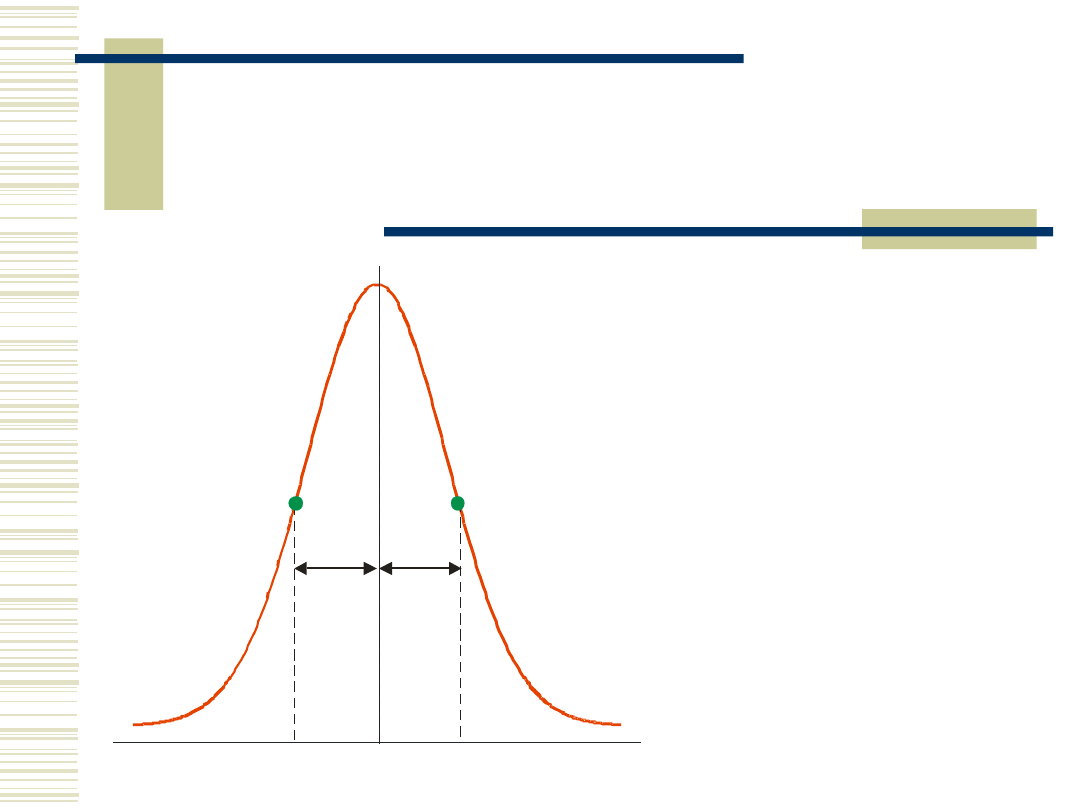
Standardowy rozkład
normalny
x
f(x)
stndardowy
rozkład Gaussa
punkt przegięcia
0
1 1
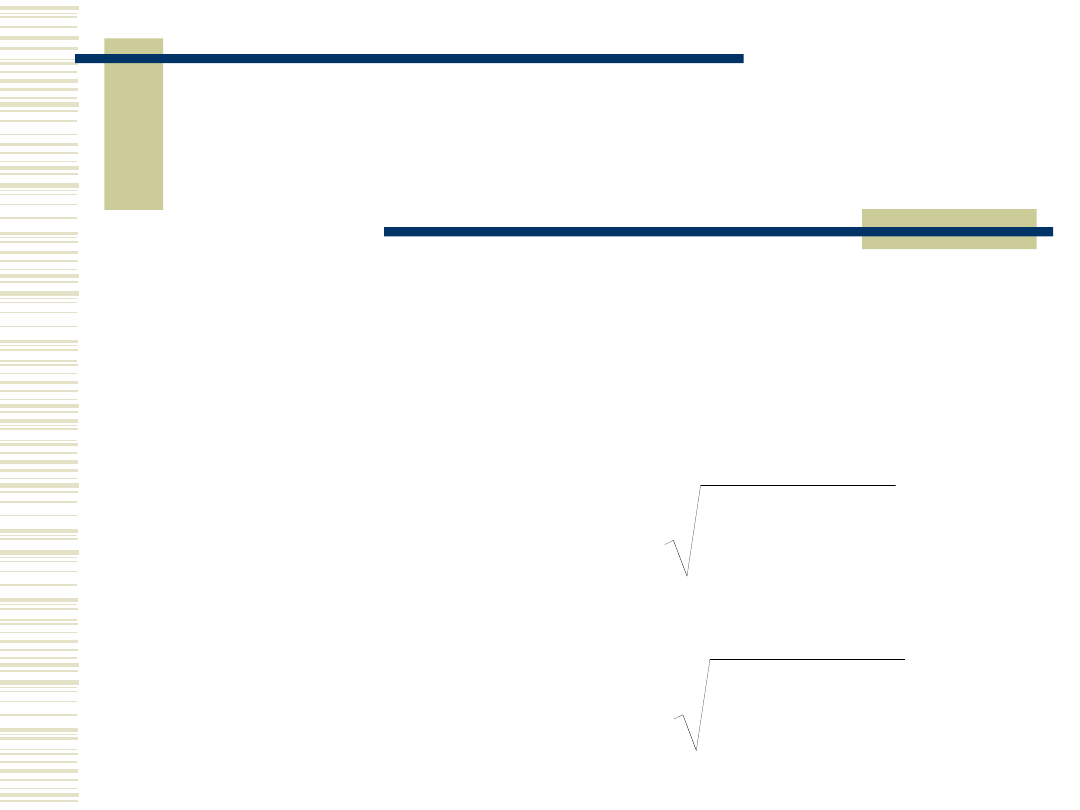
Suma i różnica
rozkładów
Jeżeli X ma rozkład o parametrach
i oraz Y ma rozkład o
parametrach i to parametry
rozkładu ich sumy są następujące:
Podobnie, dla różnicy X-Y:
x
x
y
y
2
2
y
x
y
x
2
2
y
x
y
x
Suma i różnica
rozkładów
Kształt rozkładu sumy lub różnicy
jest zwykle inny od kształtu
składników. Są jednak wyjątki, np.
rozkład normalny lub
Suma lub różnica dwóch zmiennych
o rozkładzie normalnym też ma
rozkład normalny.
2
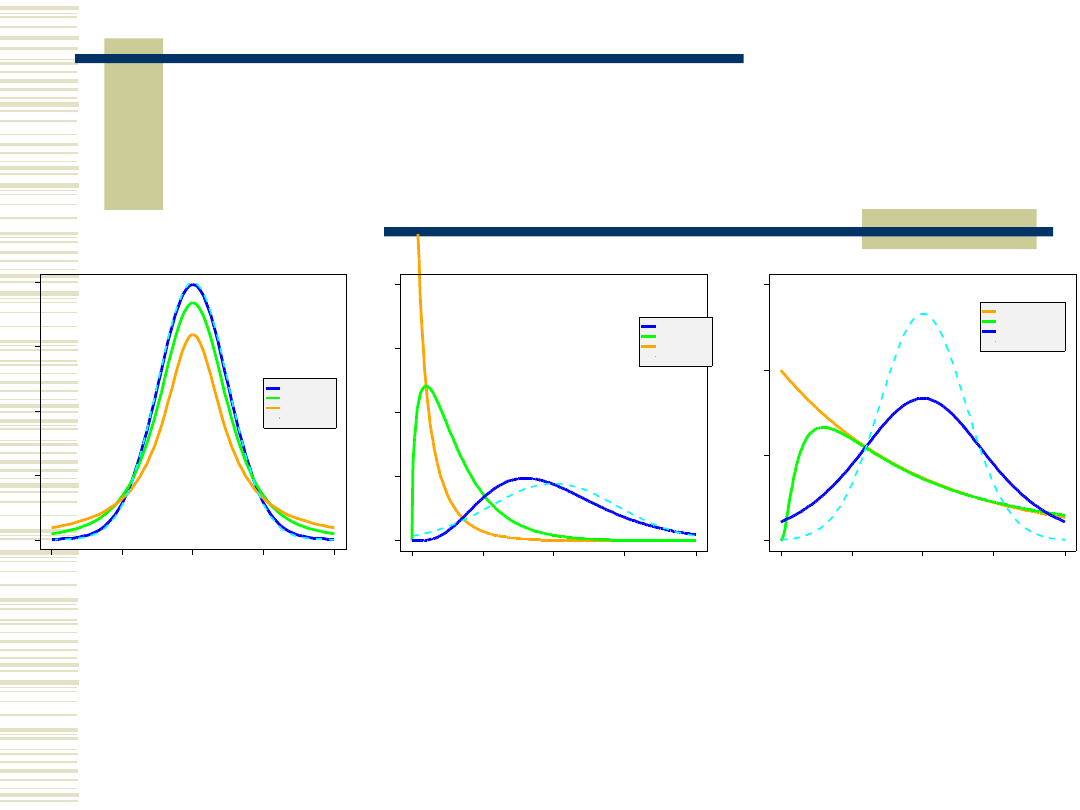
Galeria rozkładów
ciągłych
-4
-2
0
2
4
0.
0
0.
1
0.
2
0.
3
0.
4
Rozklad t-Studenta
t
f(t
)
30 st. swob.
3 st. swob.
1 st. swob
normalny
0
5
10
15
20
0.
0
0.
1
0.
2
0.
3
0.
4
Rozklad chi-kwadrat
chi^2
f(c
hi
^2
)
10 st. swob.
3 st. swob.
1 st. swob
normalny
0
5
10
15
20
0.
00
0.
05
0.
10
0.
15
x
f(x
)
eksponencjalny
log-normalny
logistyczny
normalny
Estymacja. Przedziały
ufności.
Umiemy, korzystając z funkcji gęstości
rozkładu, obliczać prawdopodobieństwo
znalezienia zmiennej losowej w
zadanym przedziale:
Często musimy rozwiązywać zadanie
odwrotne: Mamy z góry zadane
prawdopodobieństwo P, a szukamy
odpowiednich a i b.
b
a
dx
x
f
b
X
a
P
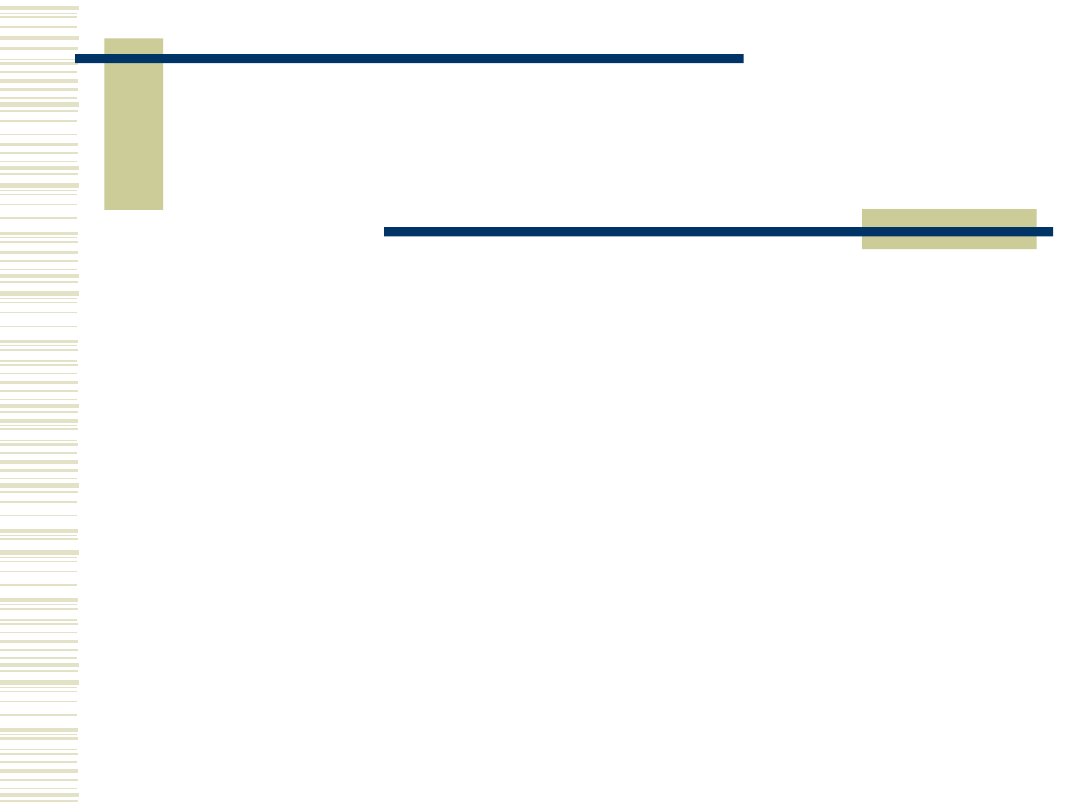
Zadanie to nie jest jednoznaczne.
Przykład: P=0,9=90%. a,b - ?
P nazywamy poziomem ufności i
często zapisujemy w postaci ,
gdyż zwykle jest nieco mniejsze od
100% (najczęściej 95%, wtedy
)
1
%
5
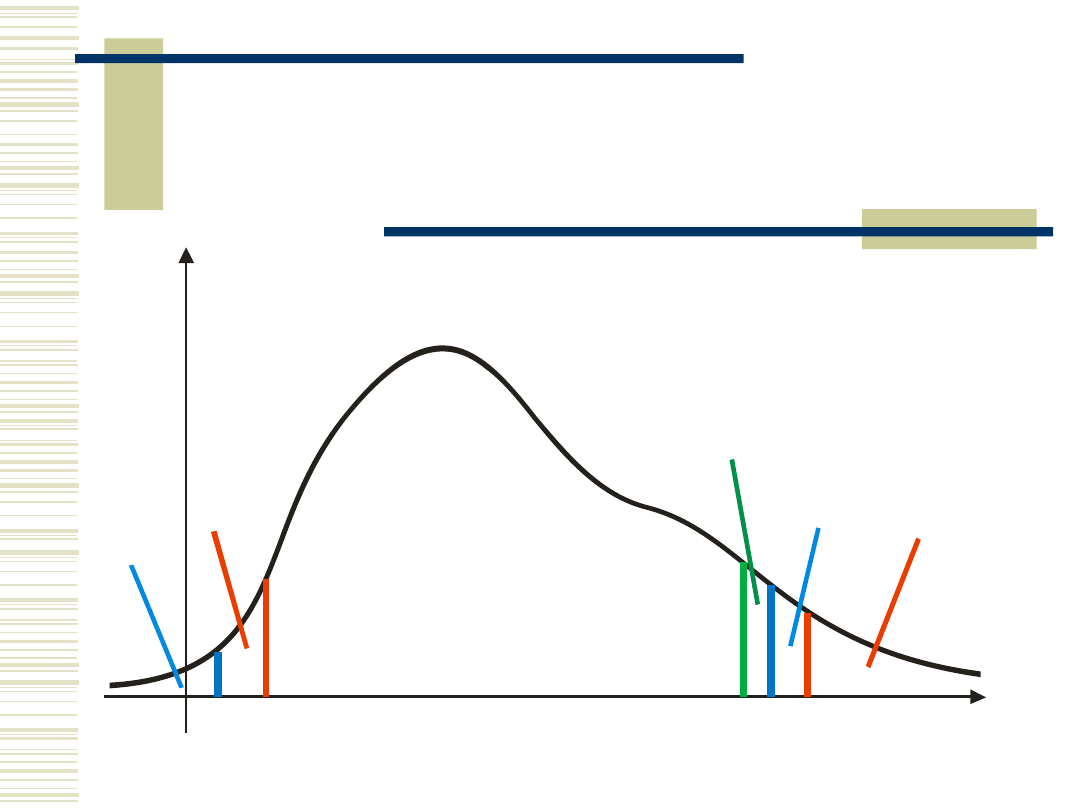
Wybór przedziału ufności
x
f x
( )
b
b
b
a
a
( =- )
a Ą
5%
5%
8%
10%
2%
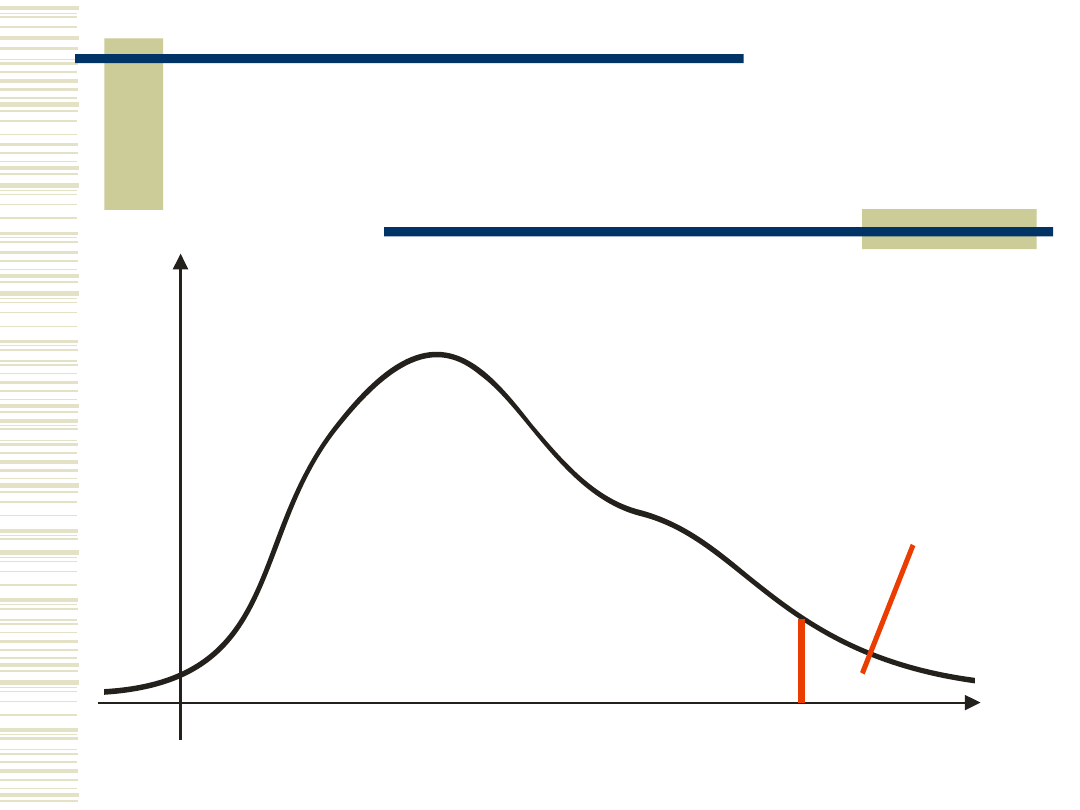
Wybór przedziału ufności
W praktyce stosujemy:
symetryczny (dwustronny) wybór
przedziału (równe
prawdopodobieństwa po obu stronach)
jednostronny wybór granicy przedziału
prawostronny
lewostronny
)
(
a
)
(
b
Fraktyle
x
f x
( )
1
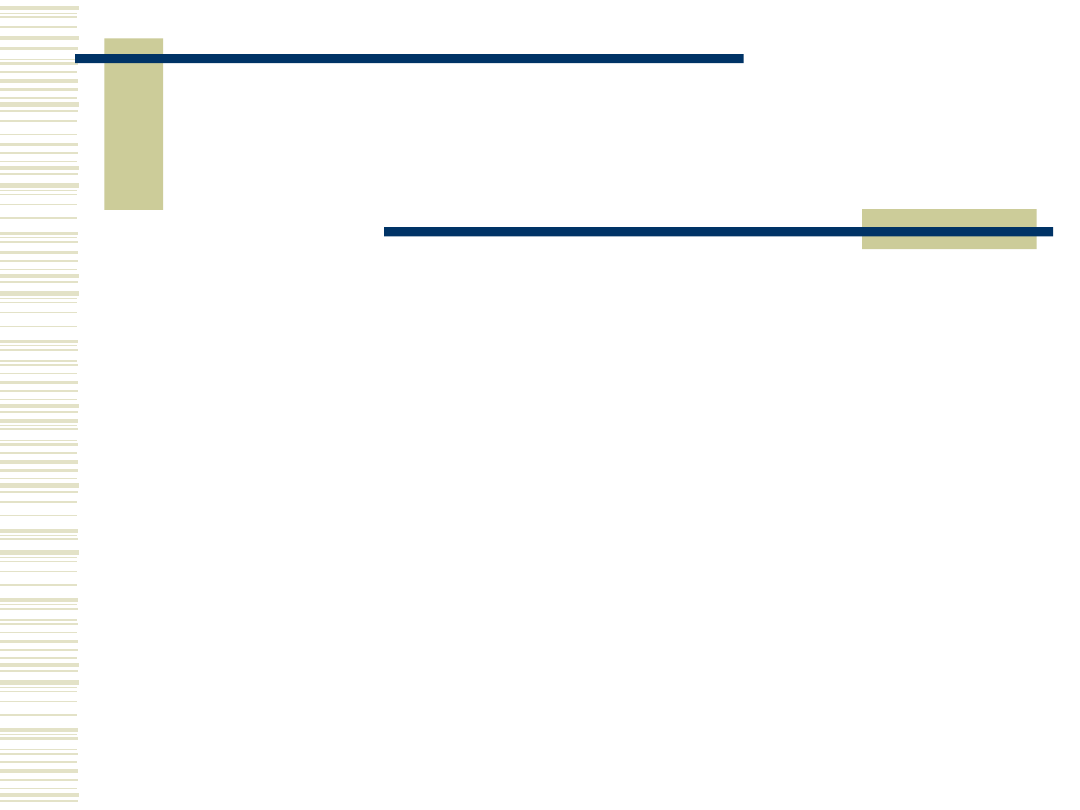
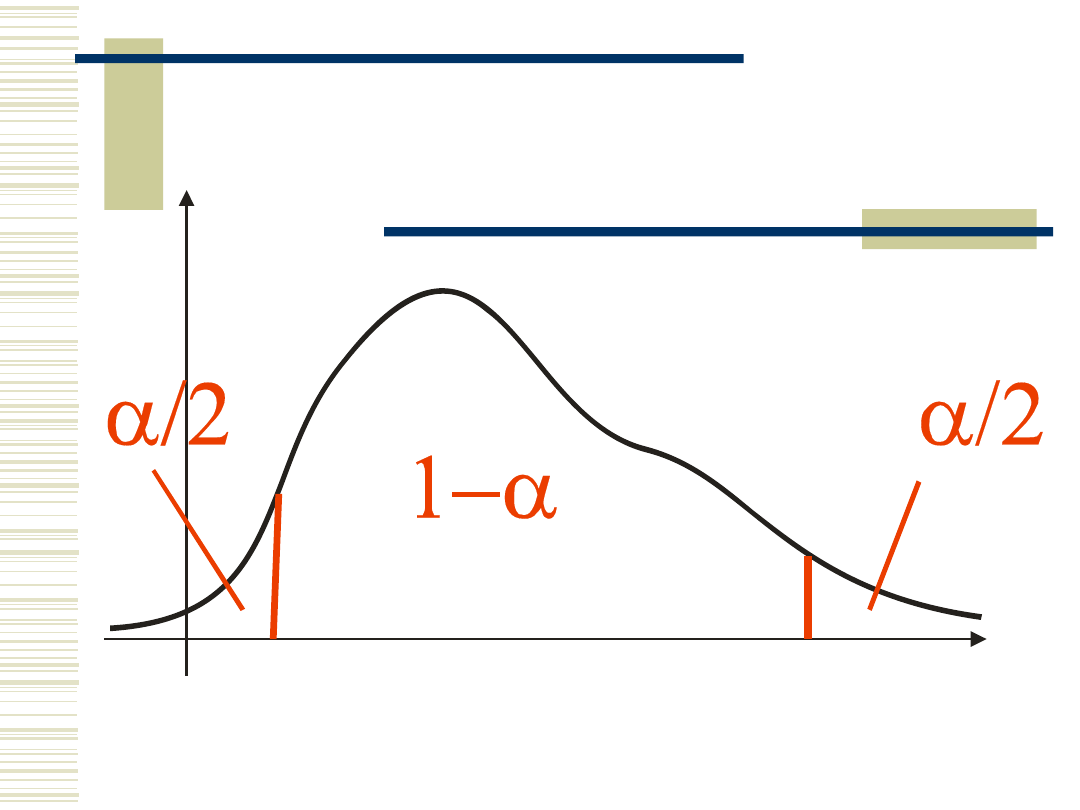
Fraktyle (percentyle)
Liczbę , taką że
nazywamy fraktylem rozkładu
prawdopodobieństwa zmiennej X.
x
0,5
nazywamy medianą, x
0,75
pierwszym, a x
0,25
– trzecim
kwartylem.
x
x
X
P
Fraktyle i wybór
przedziału.
x
/2
x
1 - /2
f x
( )
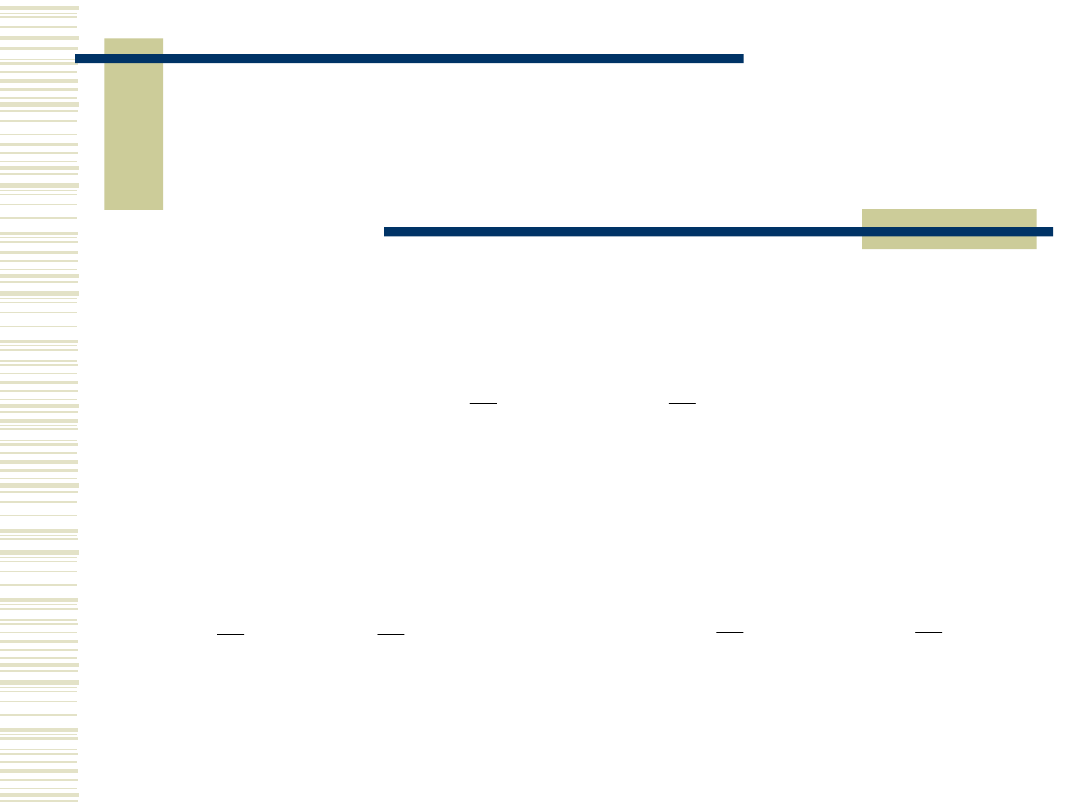
Symetryczny wybór
przedziału
Przy symetrycznym wyborze
przedziału mamy .
Jeśli funkcja gęstości jest parzysta
(symetryczna względem zera) to:
więc
Rozkłady: standardowy normalny i t-
Studenta są parzyste.
2
2
1
,
x
b
x
a
2
2
,
x
b
x
a
2
2
1
x
x
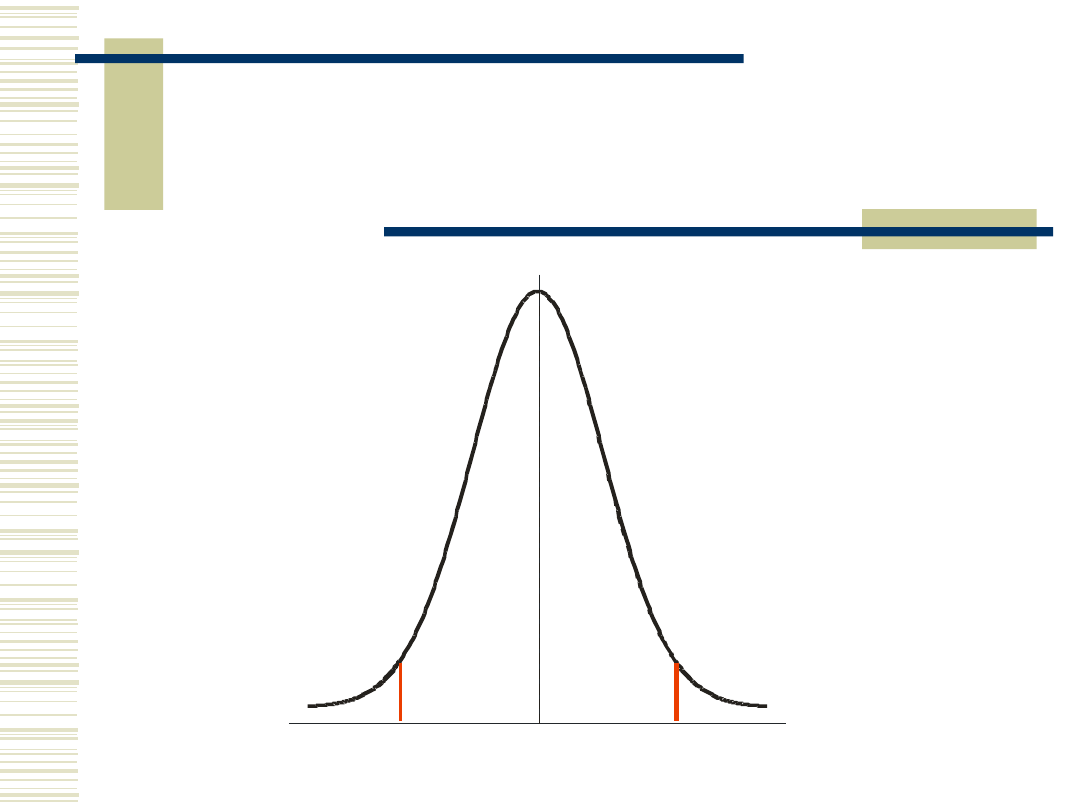
Symetryczny przedział
dla stand. rozkładu
normalnego.
u
u
2,5%
-u
2,5%
f( )
u
0
95%
Przedziały ufności
Załóżmy, że X podlega rozkładowi
normalnemu.
Wiemy, że
W takim razie
n
N
X
,
~
1
,
0
~N
n
X
u
Przedziały ufności
1
2
2
u
u
u
P
1
2
2
u
n
X
u
P
Przedziały ufności
Rozwiązując te nierówności tak, aby w
środku pozostało otrzymamy:
Z prawdopodobieństwem
(zwanym poziomem ufności)
wyznaczony prze-dział zawiera
wartość oczekiwaną .
1
2
2
u
n
X
u
n
X
P
1
Przedziały ufności
Na przeszkodzie praktycznemu
stosowaniu tego wzoru stoi
nieznajomość .
Czy popełnimy duży błąd zastępując
jego estymatą s ?
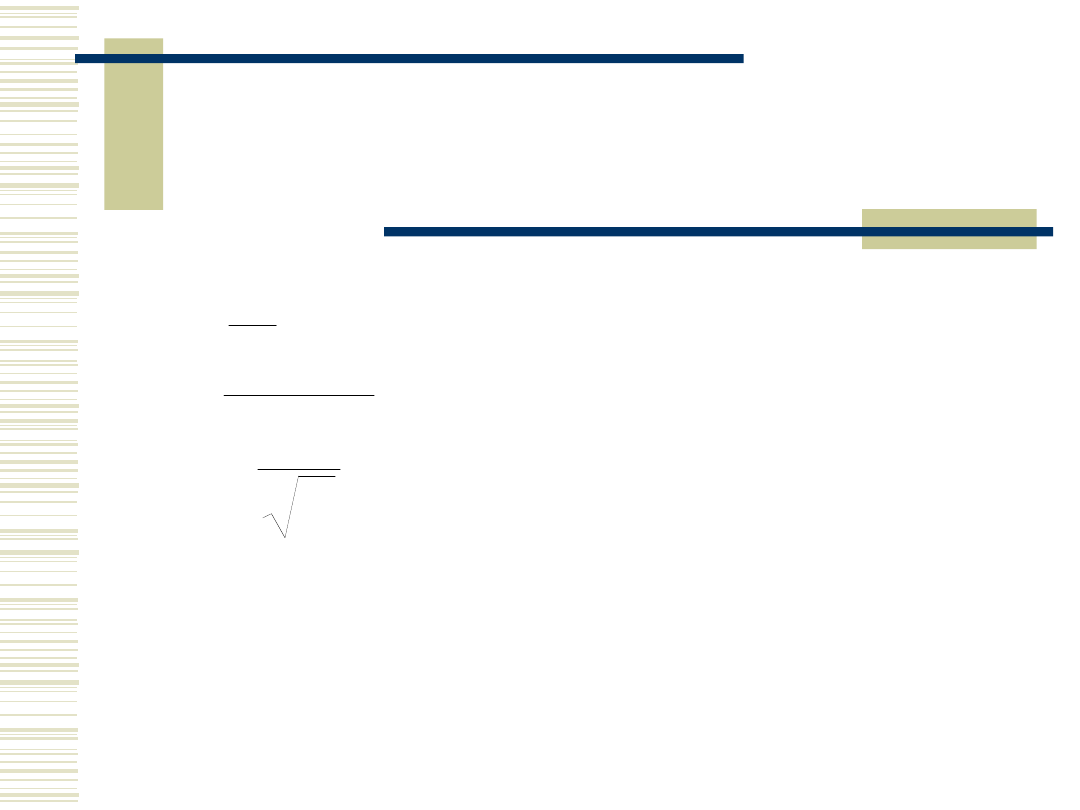
Przedziały ufności
Gosset badał rozkład zmiennej losowej
Rozkład ten różni się trochę od rozkładu
normalnego. Nazywa się rozkładem t-Stu-
denta. Dokładny jego kształt określa liczba
r = n-1, zwana liczbą stopni swobody.
n
s
X
t
Przedziały ufności
Rozumowanie bardzo podobne do
poprzedniego, prowadzi do wzoru:
dla r > 30 różnica między t i u jest
znikoma
1
2
2
t
n
s
X
t
n
s
X
P
Rozkład estymatora s
2
Jeśli X ma rozkład normalny, to
ma rozkład zwany rozkładem
(chi-kwadrat).
Kształt tego rozkładu zależy do
liczby stopni swobody r = n – 1.
1
2
2
n
s
2
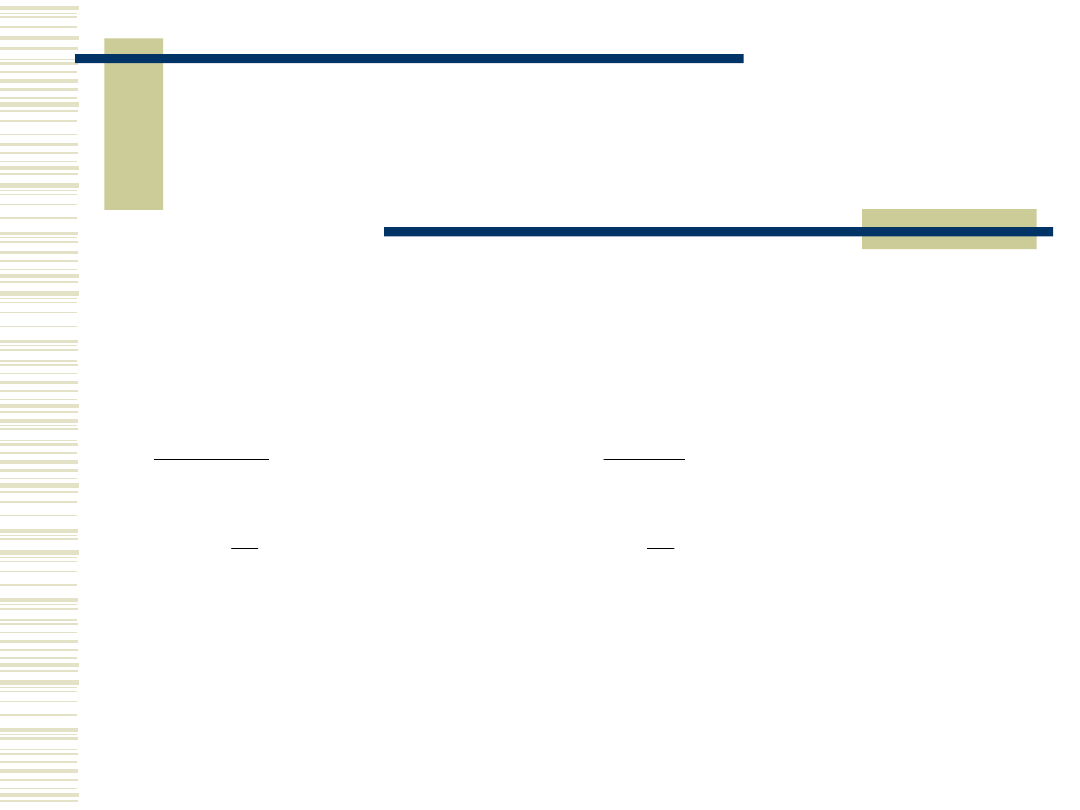
Przedział ufności
wariancji.
Z powyższego wynika, że przedział
ufności wariancji dany jest wzorem:
Przedział ufności dla odchylenia
standar-dowego otrzymamy
pierwiastkując strony tej nierówności.
1
1
2
2
2
2
2
2
1
2
n
s
n
s
Statystyka opisowa
Statystyka opisowa
Pełna wiedza o ciągłym rozkładzie
prawdopodobieństwa zawarta jest w
jego funkcji gęstości.
Często jednak chcemy wyodrębnić
pewne cechy rozkładu, jak np. jego
symetrię. Podajemy wtedy
parametry charakterystyczne, takie
jak lub .
Momenty
Momenty zwykłe rzędu k:
Momenty centralne rzędu k:
dx
x
f
x
a
k
k
dx
x
f
x
m
k
k
Momenty
Wartość oczekiwana to pierwszy
moment zwykły:
Wariancja to drugi moment centralny:
Inne parametry rozkładu definiowane
przy pomocy momentów to skośność i
kurtoza.
1
a
2
2
m
Skośność i kurtoza
nazywamy skośnością lub współ-
czynnikiem asymetrii.
nazywamy kurtozą. Kurtoza
rozkładu normalnego jest
równa 3.
Nazwa ‘kurtoza’ często stosowana jest
do nadwyżki kurtozy ponad 3, tj.
4
4
2
2
4
m
m
m
3
2
2
4
m
m
3
3
m
Kurtoza
Kurtoza większa od 3 (0) wskazuje,
że rozkład jest bardziej płaski
(platykurtyczny) od normalnego.
Rozkład o mniejszej kurtozie niż
normalny (ostrzejszy) nazywa się
leptokurtycznym.
Moda
Moda (lub modalna), to wartość x dla
której funkcja gęstości f(x) osiąga
maksimum.
Jeśli jest kilka maksimów lokalnych
rozkład nazywamy wielomodalnym.
Dla rozkładu normalnego moda, mediana
i watość oczekiwana są sobie równe.
Estymacja parametrów
opisowych
Należy pamiętać, że prawdziwe
wartości wymienionych parametrów
pozostają zazwyczaj nieznane
(podobnie jak sama funkcja gęstości
rozkładu).
Wielkości wyznaczane na podstawie
próby są tylko ich oszacowaniami
(estymatami).