T10. Hipotezy wytężenia

materiału



Istota hipotezy wytężenia materiału.



Hipoteza Coulomba-Tresci.



Hipoteza Hubera-Mizesa.



Przykłady wytrzymałości złożonej.

Istota hipotezy wytężenia
materiału

Problem:

W jaki sposób dla przestrzennego stanu
naprężenia, scharakteryzowanego za pomocą
tensora naprężenia, ocenić, czy wartości
naprężeń

nie

przekroczyły

wartości

dopuszczalnych ?

Rozwiązanie - hipoteza wytężenia materiału:

Stopień

obciążenia

materiału

siłami

wewnętrznymi (

wytężenia materiału

) można

scharakteryzować za pomocą jednej wielkości
liczbowej,

nazywanej

naprężeniem

zredukowanym



zr

. Warunek wytrzymałości dla

przestrzennego stanu naprężenia ma postać:

zr

r

k

s �

Hipoteza Coulomba-
Tresci

Problem:

W

jaki

sposób

wyznaczyć

naprężenie

zredukowane na postawie znanych wartości
składowych tensora naprężenia?

Rozwiązanie I - hipoteza największego
naprężenia stycznego (hipoteza Coulomba-
Tresci):

Naprężenie

zredukowane

obliczamy

na

podstawie równości maksymalnych wartości
naprężenia stycznego dla przestrzennego i
jednoosiowego stanu naprężenia

max

max

2

2

xx

zr

s

t

s

t

=

�

=

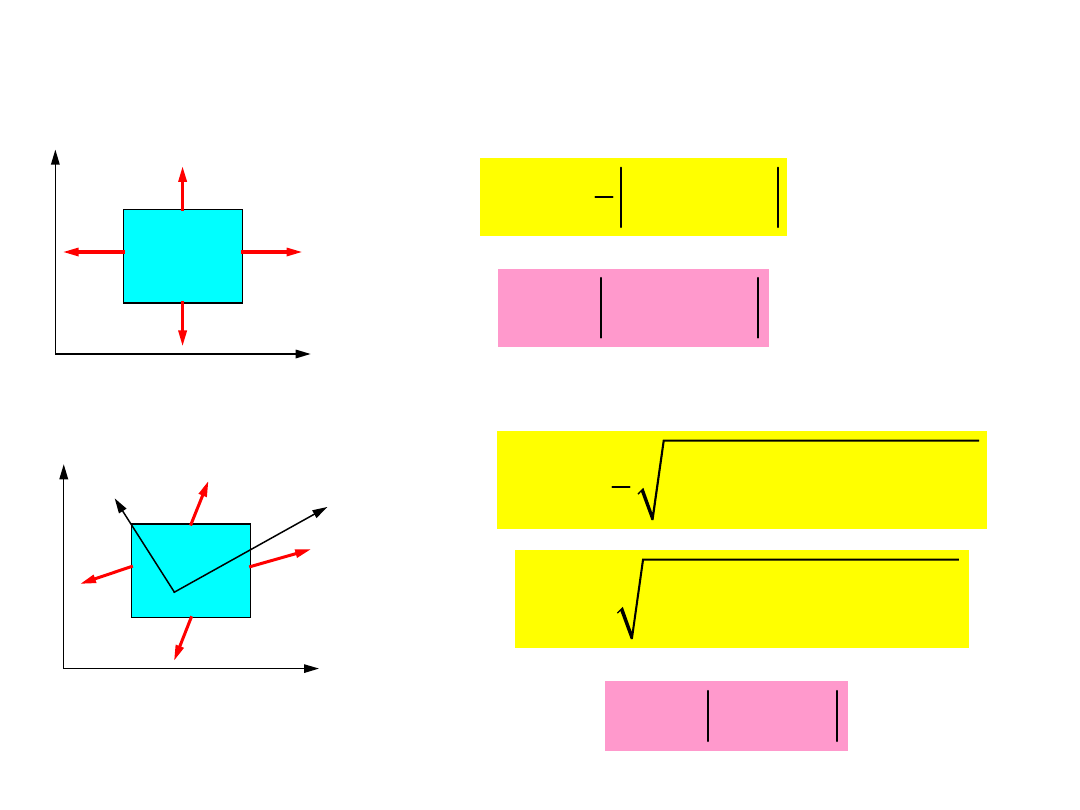
Hipoteza Coulomba-
Tresci

Dwuosiowy

stan

naprężenia:

x

y

1

max

2

yy

xx

t

s

s

=

-

Płaski stan naprężenia:

x

y

(

)

2

2

1

max

2

4

yy

xx

xy

t

s

s

s

=

-

+

zr

yy

xx

s

s

s

=

-

(

)

2

2

4

zr

yy

xx

xy

s

s

s

s

=

-

+



1



2

1

2

zr

s

s

s

=

-

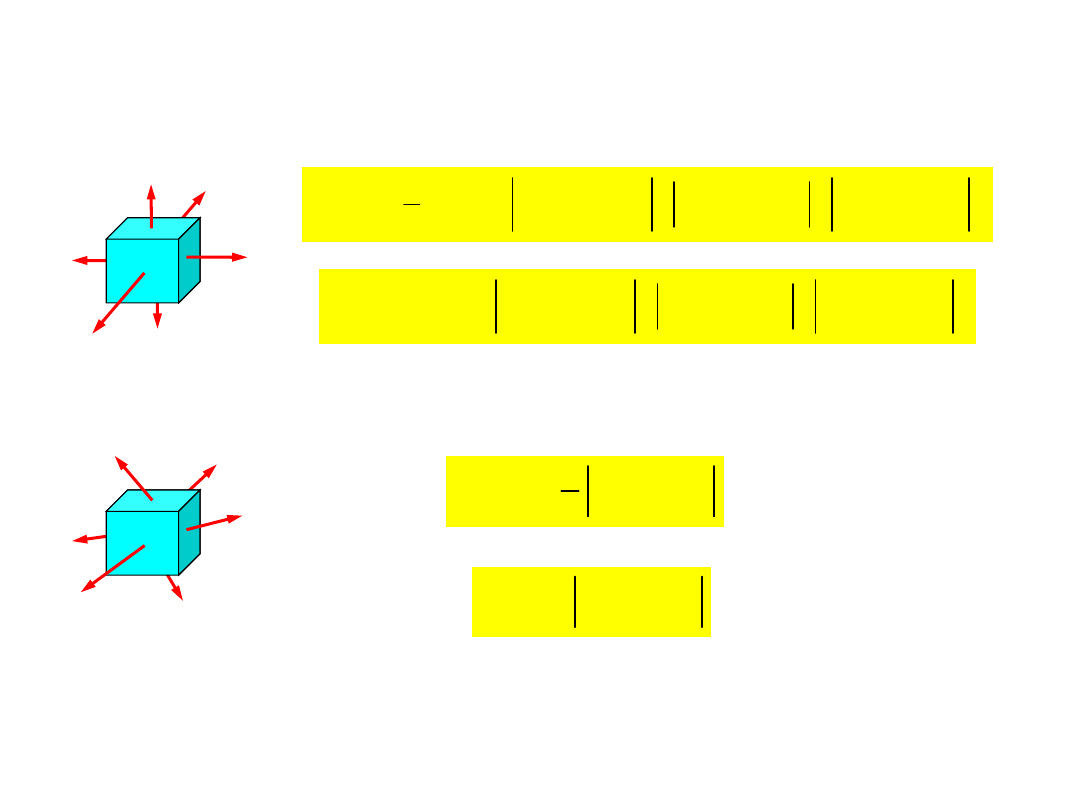
Hipoteza Coulomba-
Tresci

Trójosiowy

stan

naprężenia:

{

}

1

max

2

max

,

,

yy

xx

xx

zz

zz

yy

t

s

s

s

s

s

s

=

-

-

-

{

}

max

,

,

zr

yy

xx

xx

zz

zz

yy

s

s

s

s

s

s

s

=

-

-

-

Przestrzenny

stan

naprężenia:

1

3

zr

s

s

s

=

-

1

max

1

3

2

t

s

s

=

-

Hipoteza Coulomba-
Tresci

Hipoteza Coulomba-Tresci ma zastosowanie w
odniesieniu do materiałów sprężysto-plastycznych
(stal konstrukcyjna, metale kolorowe i ich stopy).
Nie może być stosowana w odniesieniu do
materiałów kruchych (żeliwo, beton, ceramika,
szkło).

Hipoteza Hubera-
Mizesa

Hipoteza Hubera-
Mizesa

Problem:

W

jaki

sposób

wyznaczyć

naprężenie

zredukowane na postawie znanych wartości
składowych tensora naprężenia?

Rozwiązanie II - hipoteza krytycznej wartości
energii odkształcenia postaciowego (hipoteza
Hubera-Mizesa):

Naprężenie zredukowane obliczamy na podstawie
równości wartości gęstości energii odkształcenia
postaciowego

dla

przestrzennego

i

jednoosiowego stanu naprężenia

( )

( )

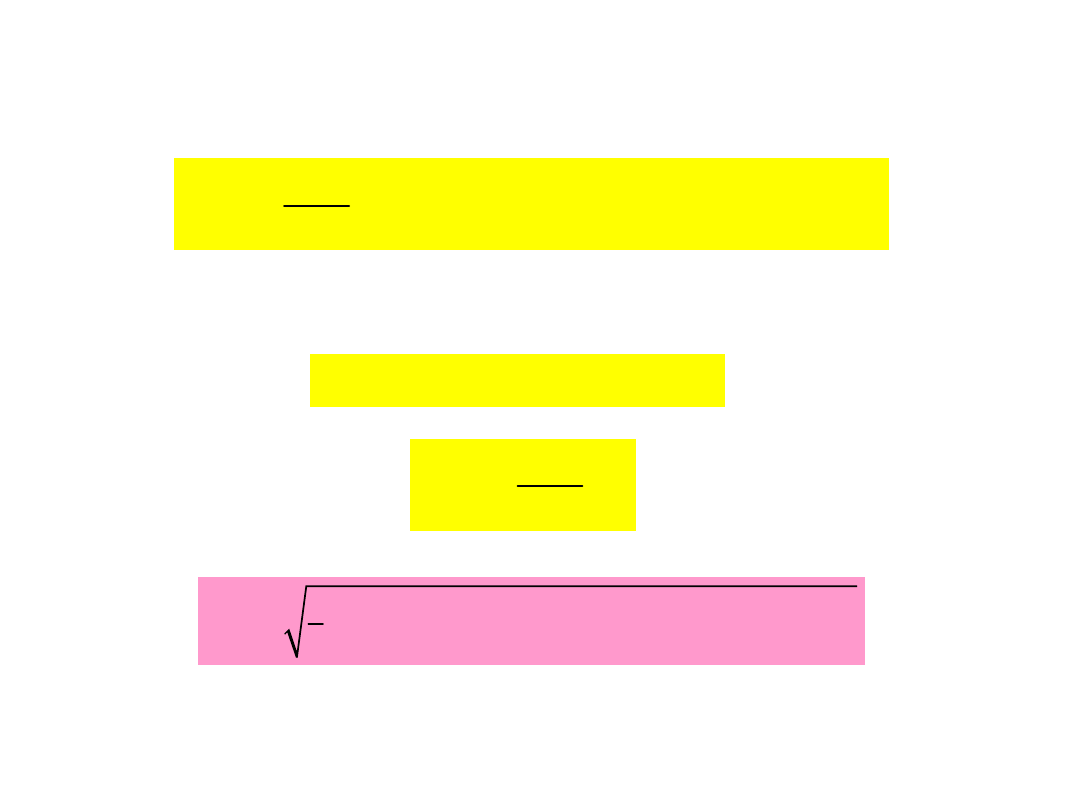
3

1

p D

p D

zr

E

E

s

=

σ

Hipoteza Hubera-
Mizesa

(

) (

) (

)

2

2

2

3

1

2

2

3

3

1

1

6

p D

E

E

n

s

s

s

s

s

s

+ �

�

=

-

+

-

+

-

�

�

Przestrzenny

stan

naprężenia:

Jednoosiowy

stan

naprężenia:

1

2

3

,

0,

0

xx

zr

s

s

s

s

s

=

=

=

=

2

1

1

3

p D

zr

E

E

n

s

+

=

(

) (

) (

)

2

2

2

1

1

2

2

3

3

1

2

zr

s

s

s

s

s

s

s

�

�

=

-

+

-

+

-

�

�

Hipoteza Hubera-
Mizesa

Dla płaskiego stanu naprężenia:

(

) (

)

(

)

1

1

1,2

2

2

1

2

cos2

sin2

sin2

cos2

0

yy

xx

xx

yy

m

xy

m

yy

xx

m

xy

m

s

s

s

s

s

a

s

a

t

s

s

a

s

a

=

+

+

-

+

=

-

+

=

(

)

(

)

2

2

1

1

2

2

2

1

2

2

4

4

xx

yy

xx

yy

xy

xx

yy

xx

yy

xy

s

s

s

s

s

s

s

s

s

s

s

s

�

�

=

+

+

-

+

�

�

�

�

�

�

=

+

-

-

+

�

�

�

�

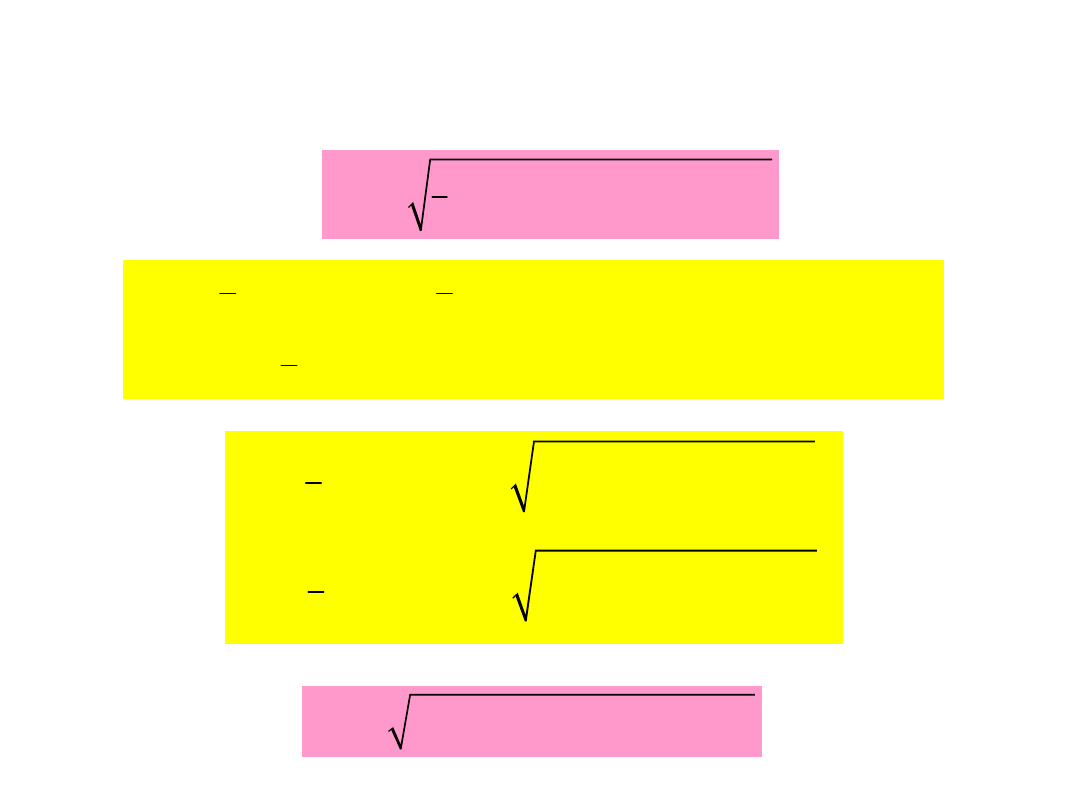
2

2

2

3

zr

xx

yy

xx

yy

xy

s

s

s

s s

s

=

+

-

+

(

)

2

2

2

1

1

2

1

2

2

zr

s

s

s

s

s

�

�

=

-

+ +

�

�

Hipoteza Hubera-
Mizesa

Maksymilian Tytus Huber

(ur. 4 stycznia 1872, zm. 9

grudnia 1950) – polski

naukowiec, inżynier mechanik



Rektor Politechniki Lwowskiej w latach

1922-
1923.



Kierownik Katedry Mechaniki Politechniki

Warszawskiej w latach 1928-1939



Organizował Politechnikę Gdańską w latach

1945-1949



Kierownik Katedry Wyższych Zagadnień

Mechaniki w AGH w latach 1949-1950



Położył wielkie zasługi dla rozwoju polskiej

nauki i
kultury, pracując społecznie w Zarządzie
Kasy
im. Józefa Mianowskiego, która odegrała
doniosłą rolę w życiu społeczeństwa
polskiego na
przełomie XIX i XX wieku.

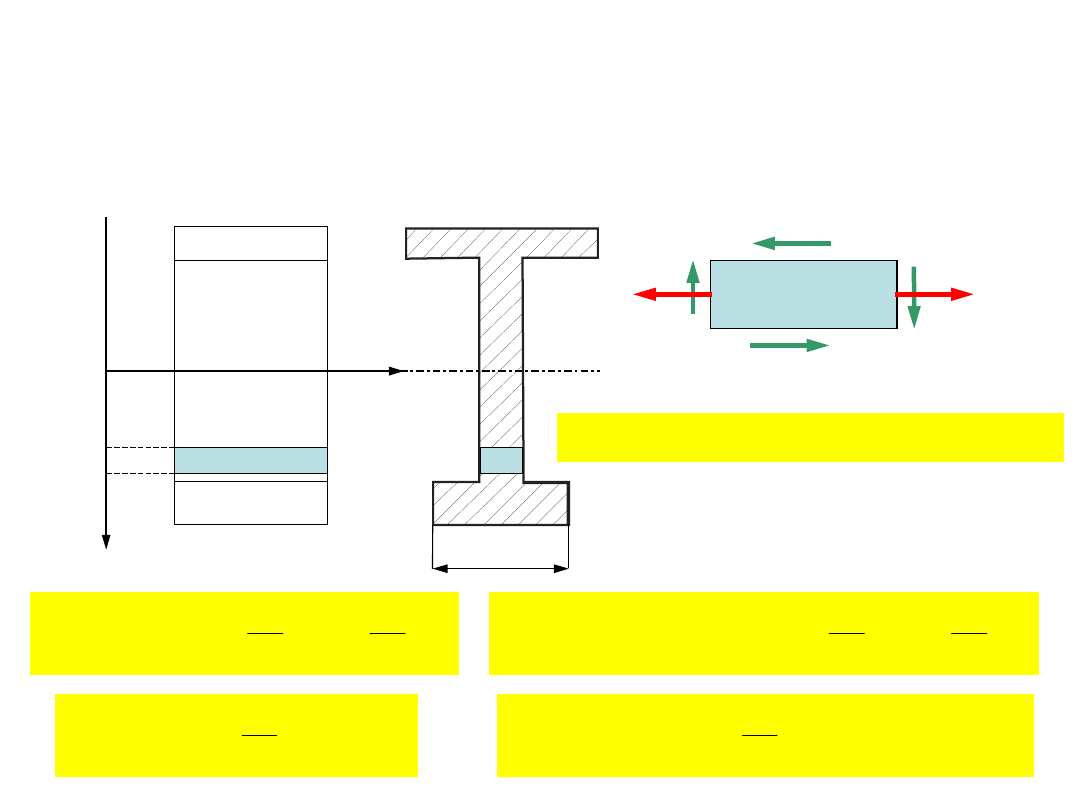
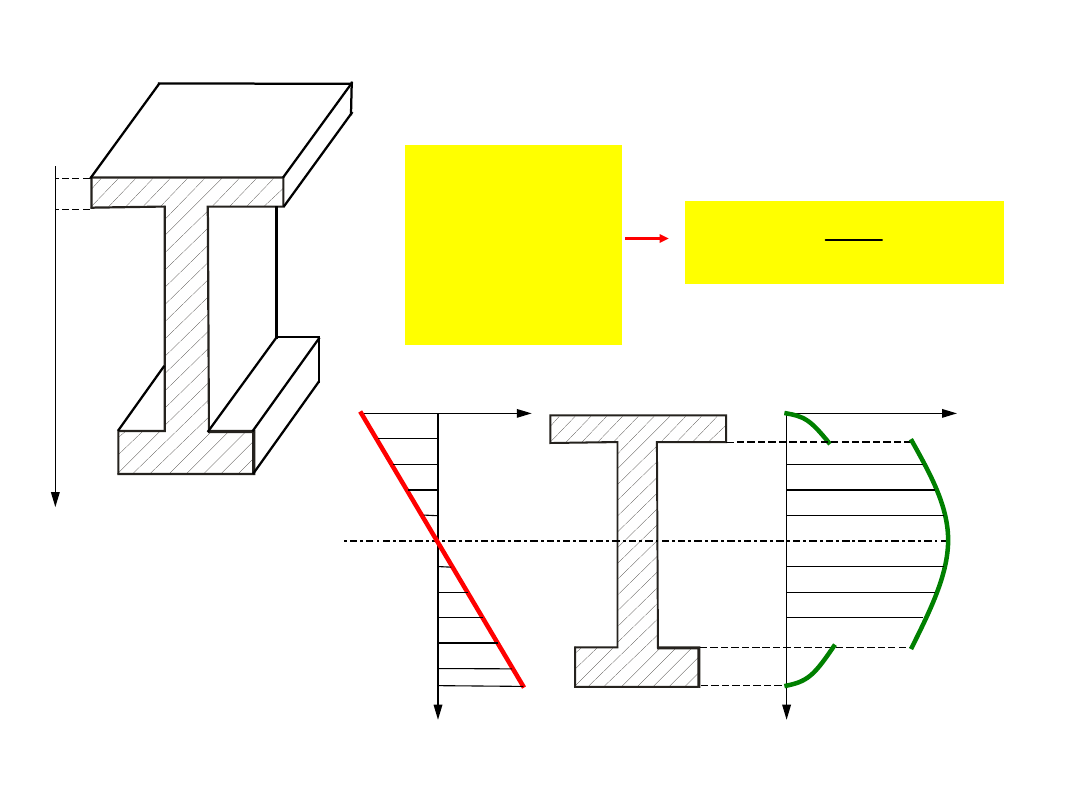
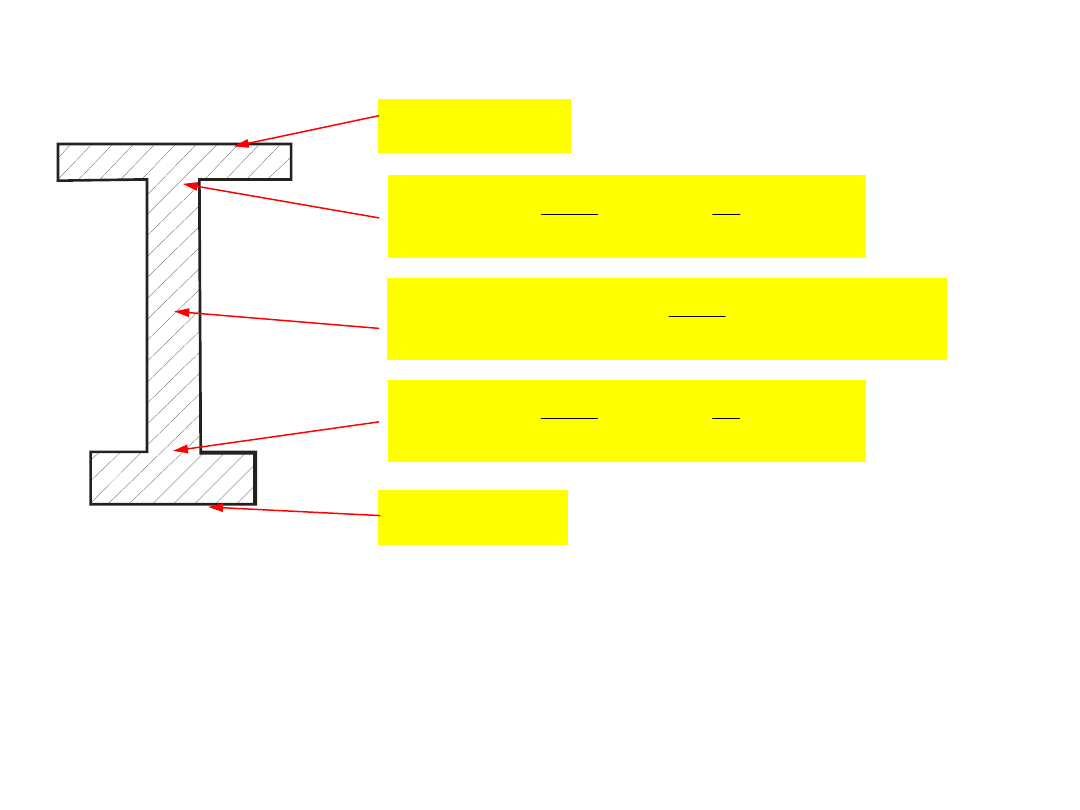
Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

Obliczenia wytrzymałościowe belki zginanej
przy uwzględnieniu siły tnącej

y

x

x+x

y+y

N(x+x)

N(x)

T(y)

T(y+y)

b(y)

( )

,

(

)

2

2

xx

y

y

N x

x y

b y

y

s

D

D

�

�

=

+

+

D

�

�

�

�

(

)

,

(

)

2

2

xx

y

y

N x

x

x

x y

b y

y

s

D

D

�

�

+D =

+D

+

+

D

�

�

�

�

( )

,

( )

2

xy

x

T y

x

y b y x

s

D

�

�

=

+

D

�

�

�

�

(

)

,

(

)

2

xy

x

T y

y

x

y

y b y

y x

s

D

�

�

+D =

+

+D

+D D

�

�

�

�

(

)

( )

(

)

( )

0

N x

N x

x T y T y

y

-

+

+D -

+

+D =

,

(

)

,

(

)

2

2

2

2

,

( )

,

(

)

0

2

2

xx

xx

xy

xy

y

y

y

y

x y

b y

y

x

x y

b y

y

x

x

x

y b y x

x

y

y b y

y x

s

s

s

s

D

D

D

D

�

�

�

�

-

+

+

D +

+D

+

+

D +

�

�

�

�

�

�

�

�

D

D

�

�

�

�

-

+

D +

+

+D

+D D =

�

�

�

�

�

�

�

�

,

,

2

2

(

)

2

,

(

)

,

( )

2

2

xx

xx

xy

xy

y

y

x

x y

x y

y

b y

x

x

x

x

y

y b y

y

x

y b y

y

s

s

s

s

D

D

�

�

�

�

+D

+

-

+

�

�

�

�

D

�

�

�

� +

=

D

D

D

�

�

�

�

+

+D

+D -

+

�

�

�

�

�

�

�

�

-

D

( )

(

)

dla ,

0

xy

xx

y x

b

b y

x

y

s

s

D D �

�

�

=-

�

�

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

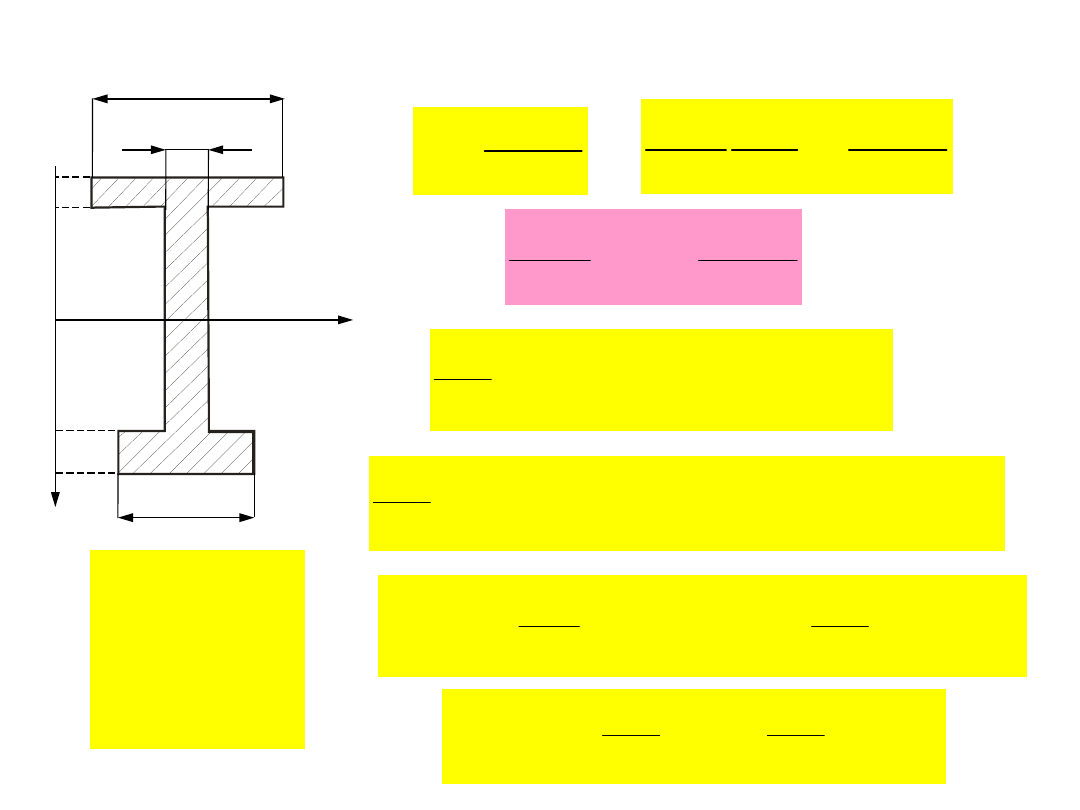
b

1

b

2

b

3

y

1

y

2

y

3

y

4

( )

g

xx

z

M x y

J

s =

( )

(

)

xy

g

z

b

dM

b y y

J

d x

y

s

�

=-

�

( )

(

)

( )

xy

z

b

b y y

T x

J

y

s

�

=-

�

( )

(

)

( )

(

)

( )

(

)

0

0

0

,

,

( )

xy

xy

b y

x y

y

xy

z

y

b y

x y

T x

b

d

d b

J

s

s

h h h

s

=-

�

�

( )

( )

(

)

( )

(

)

0

0

0

( )

,

,

y

xy

xy

z

y

T x

b

d

b y

x y b y

x y

J

h h h

s

s

=-

+

�

(

)

( )

( )

(

)

( )

0

0

0

1

( )

,

,

y

xy

xy

z

y

T x

x y

b y

x y

b

d

b y

J

s

s

h h h

�

�

=

-

�

�

�

�

�

�

�

( )

(

)

1

2

1

0

1

0

dla

,

,

,

,

0

xy

y

y y

b y

b

y

y

x y

s

+

�

�

��

�

=

=

=

(

)

(

)

1

2

2

1

( )

( )

,

2

y

xy

z

z

y

T x

T x

x y

d

y

y

J

J

s

h h

=-

=

-

�

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

( )

( )

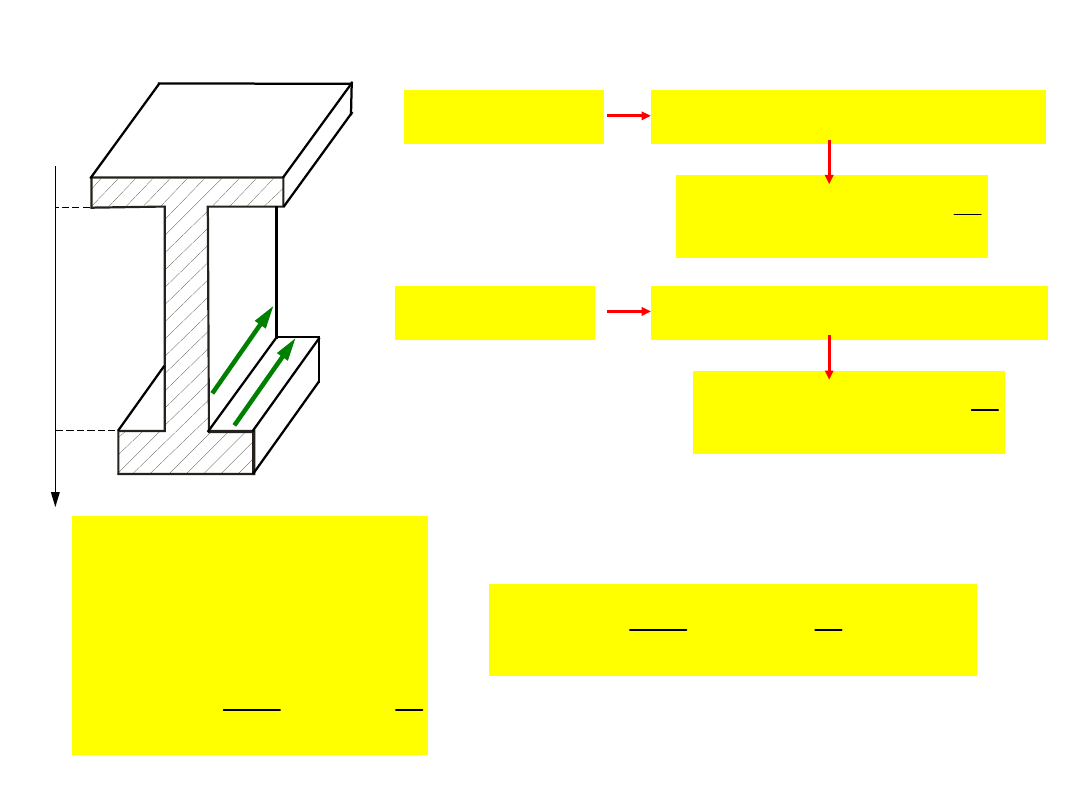
2

2

x

x

T y

T y

+

-

=

(

)

(

)

2

1

2

2

,

,

xy

xy

x y b x

x y b x

s

s

+

-

D =

D

(

)

(

)

1

2

2

2

,

,

xy

xy

b

x y

x y

b

s

s

-

+

=

y

2

y

3

( )

( )

3

3

x

x

T y

T y

+

-

=

(

)

(

)

3

3

3

2

,

,

xy

xy

x y b x

x y b x

s

s

+

-

D =

D

(

)

(

)

_

2

3

3

3

,

,

xy

xy

b

x y

x y

b

s

s

+

=

( )

(

)

(

)

2

3

2

0

2

2

2

1

0

1

2

2

dla

,

,

,

( )

,

2

xy

z

y

y y

b y

b

y

y

T x

b

x y

y

y

J

b

s

-

+

-

�

�

��

�

=

=

=

-

+

+

-

-

(

)

(

)

2

2

2

2

1

1

1

2

2

( )

,

2

xy

z

T x

b

x y

y

y

y

y

J

b

s

�

�

=

-

+ -

�

�

�

�

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

Przykłady wytrzymałości
złożonej

y

3

( )

(

)

3

4

3

0

4

0

dla

,

,

,

,

0

xy

y

y y

b y

b

y

y

x y

s

-

�

�

��

�

=

=

=

(

)

(

)

2

2

4

( )

,

2

xy

z

T x

x y

y

y

J

s

=

-

y

4

y



x

x

y



x

y

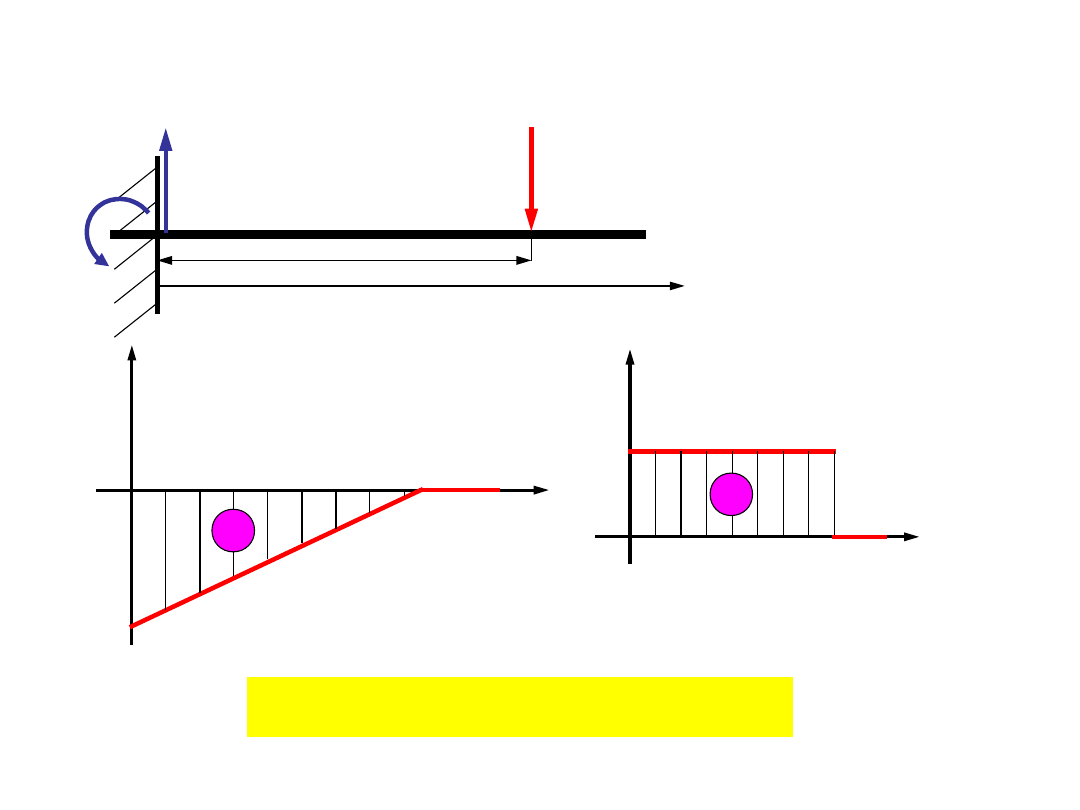
F

R

a

M

100 kN,

300 kNm

T

M

=

=-

x

M

g

x

x=a

-

T

x

x=a

+

F

-Fa

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

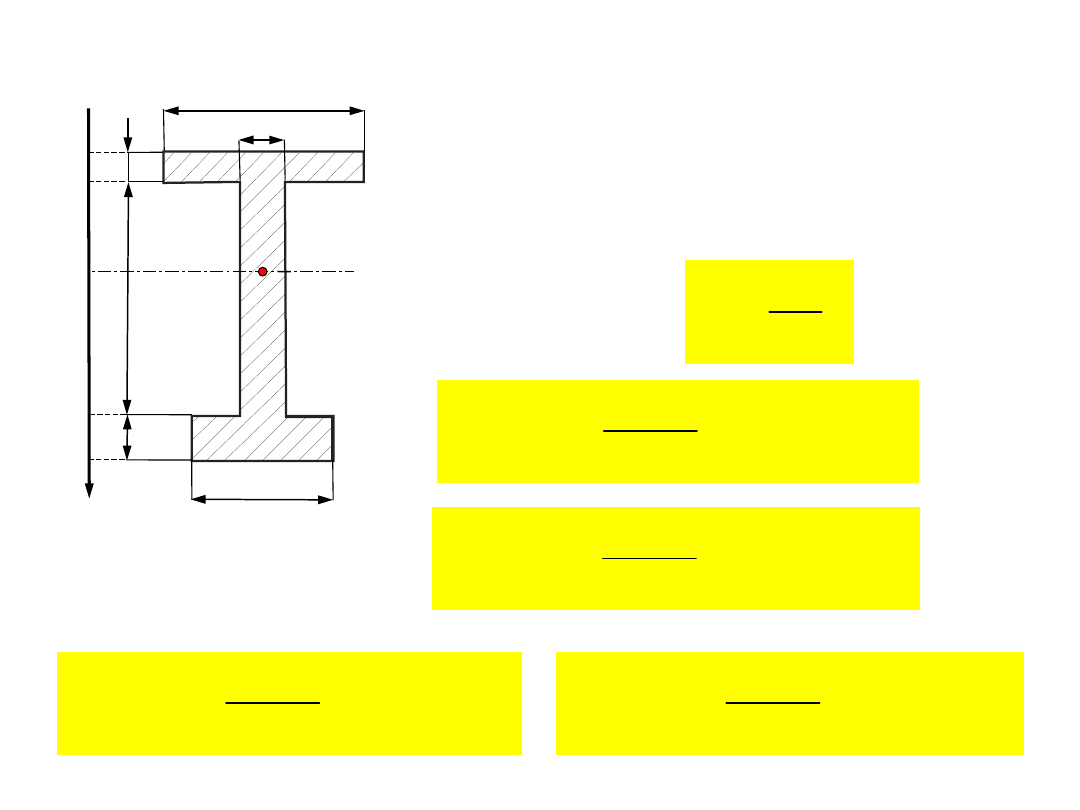
b

c

d

e

f

a

a

= 0,2 m, b = 0,03 m, c = 0,03 m,

d = 0,2 m, e = 0,05 m, f = 0,14 m

y

1

= 0,14 m, y

2

= 0,09 m, y

3

= -0,11 m, y

4

=

-0,14 m

J

z

= 0,0002665 m

4

g

xx

z

M

y

J

s =

y

1

y

2

y

3

y

4

1

1

(0)

(0, )

158 MPa

g

xx

z

M

y

y

J

s

=

=-

3

3

(0)

(0, )

124 MPa

g

xx

z

M

y

y

J

s

=

=

2

2

(0)

(0, )

101 MPa

g

xx

z

M

y

y

J

s

=

=-

4

4

(0)

(0, )

158 MPa

g

xx

z

M

y

y

J

s

=

=

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

4

(0, ) 0

xy

y

s

=

(

)

(

)

2

2

1

2

1

2

2

(0)

0,

10 MPa

2

xy

z

T

b

y

y

y

J

b

s

-

=

-

=

(

)

(

)

2

2

3

3

4

3

2

(0)

0,

10 MPa

2

xy

z

b

T

y

y

y

J

b

s

+

=

-

=

(

)

(

)

(

)

2

2

2

(0)

0,0

0,

0 12 MPa

2

xy

xy

z

T

y

y

J

s

s

-

=

+

-

=

1

(0, ) 0

xy

y

s

=

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

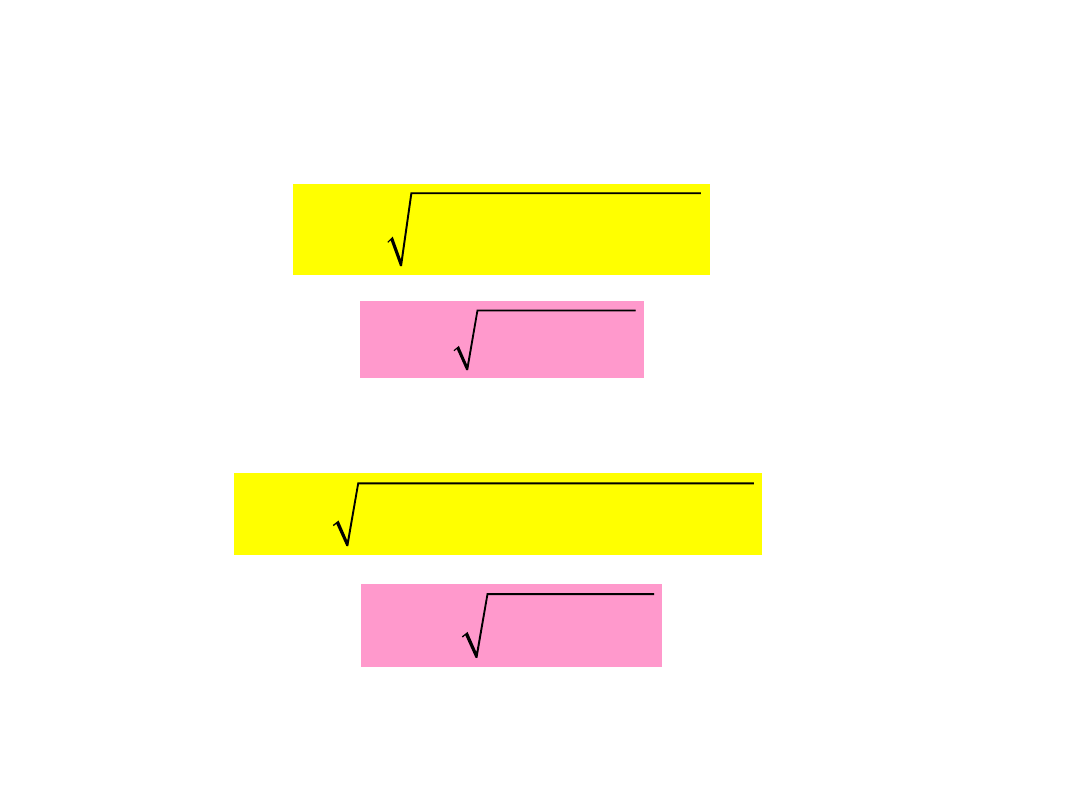
Na podstawie hipotezy Hubera –
Mizesa:

Na podstawie hipotezy Coulomba-
Tresci:

(

)

2

2

4

zr

yy

xx

xy

s

s

s

s

=

-

+

2

2

4

zr

xx

xy

s

s

s

=

+

2

2

3

3

zr

xx

yy

xx

yy

xy

s

s

s

s s

s

=

+

-

+

2

2

3

zr

xx

xy

s

s

s

=

+

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

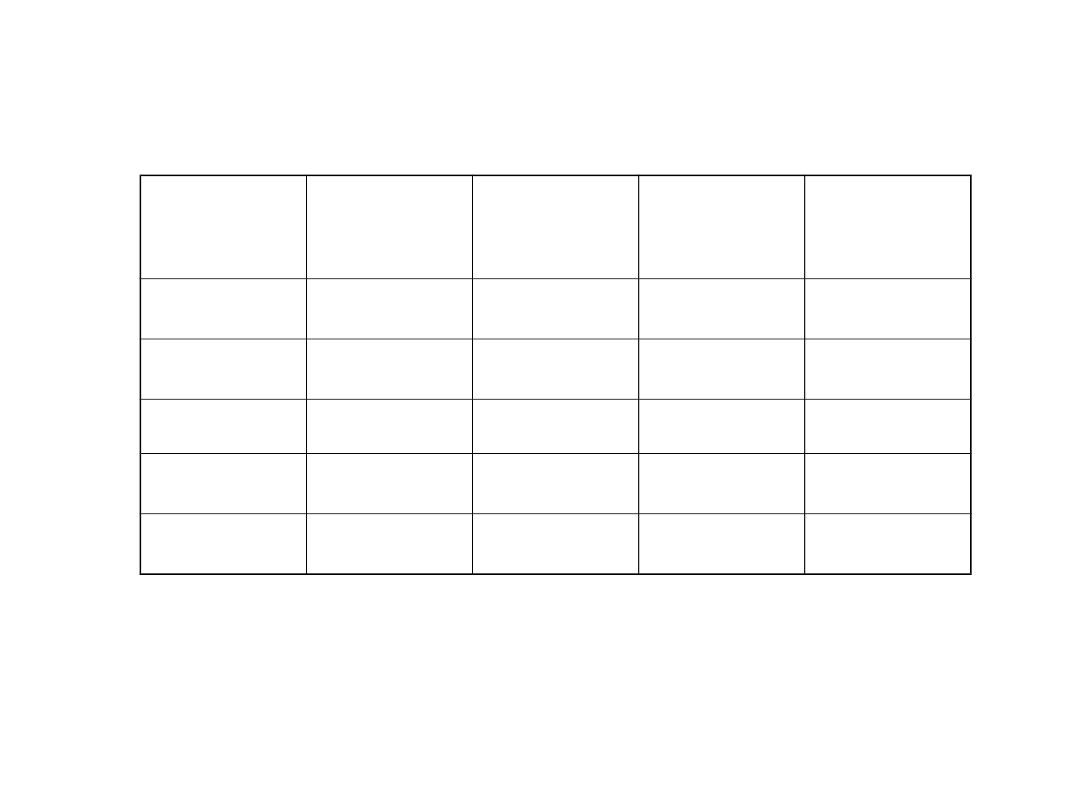
y



xx



xy



zr

(C-T)



zr

(H-

M)

y

1

-158

0

158

158

y

2

-101

10

103

102

0

0

12

23

20

y

3

124

10

125

125

y

4

158

0

158

158

Przykłady wytrzymałości złożonej (zginanie ze
ścinaniem)

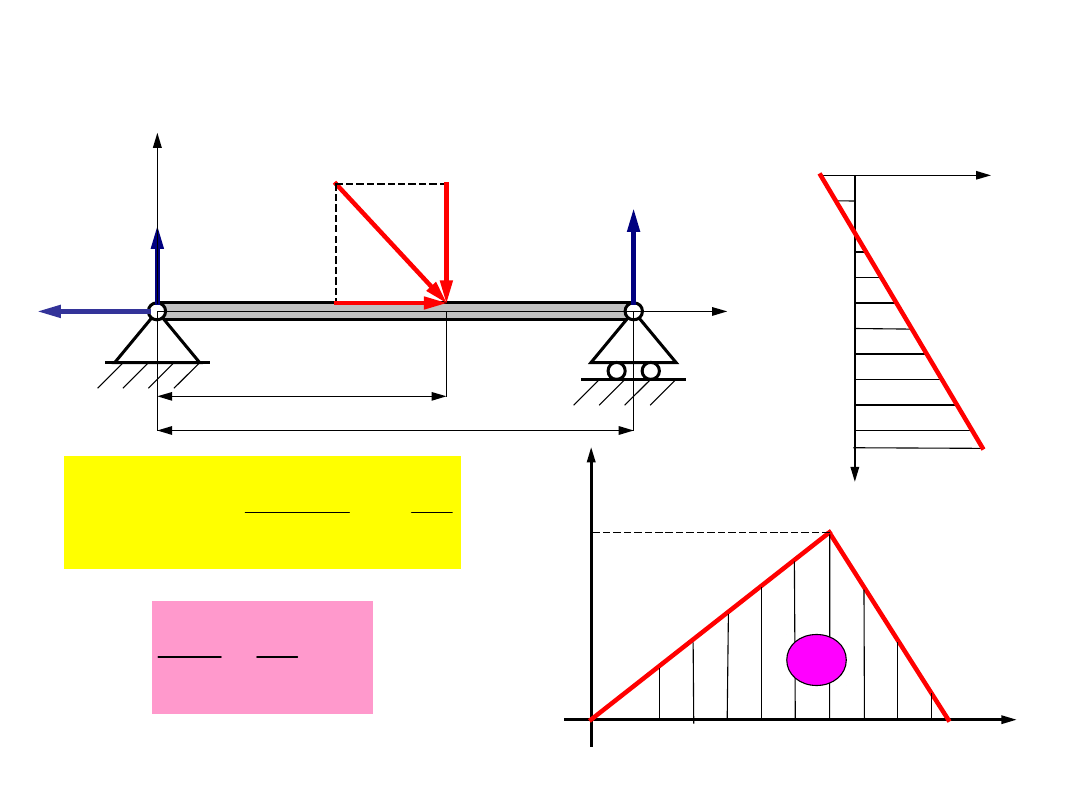
Przykłady wytrzymałości złożonej

(zginanie z rozciąganiem lub

ściskaniem)

F

R

Ay

R

B

A

B

x

y

a

l

F

y

F

x

R

Ax

(

)

( )

,

g

x

xx

z

M x

F

x y

y

J

S

s

=

+

M

g

x

+

aF

y

y

x

g

z

aF

F

k

W

S

+

�

y



xx

Przykłady wytrzymałości złożonej

(zginanie z rozciąganiem lub

ściskaniem)

F

F

-F

e

(

)

,

xx

z

Fe

F

x y

y

J

S

s

=

-

R

M

( )

g

M x

Fe

=

F

F

-F

e

R

M

M

M

y

M

z

M

z

( )

( )

gz

y

gy

z

M x

Fe

M x

Fe

=

=

(

)

, ,

y

z

xx

z

y

Fe

Fe

F

x y z

y

z

J

J

S

s

=

+

-

max

y

z

g

z

y

Fe

Fe

F

y

z

k

J

J

S

�

�

+

-

�

�

�

�

�

�

�

Przykłady wytrzymałości złożonej

(zginanie z rozciąganiem lub

ściskaniem)

(

)

, ,

0

y

z

xx

z

y

Fe

Fe

F

x y z

y

z

J

J

S

s

=

+

-

�

Można tak dobrać wartości e

y

i e

z

, że naprężenie w

całym przekroju słupa jest ściskające:

Miejsce geometryczne punktów przyłożenia siły, dla
których naprężenie w całym przekroju słupa jest
ściskające, nazywane jest

rdzeniem przekroju

.

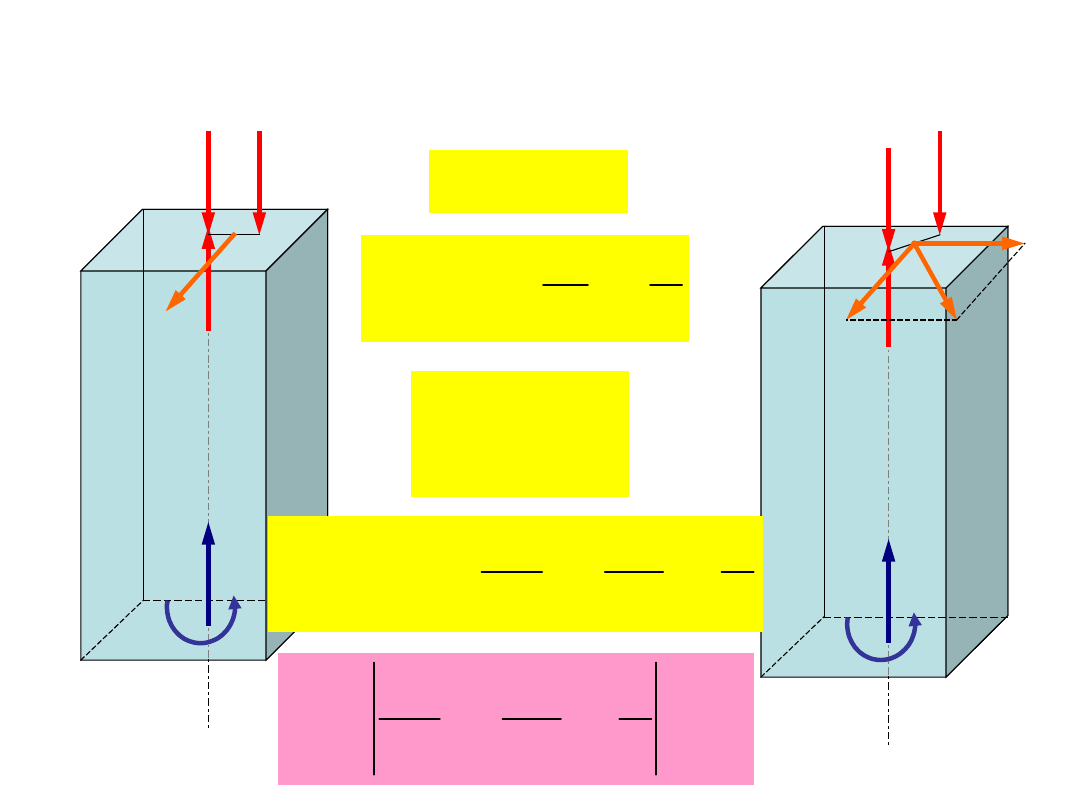
Przykłady wytrzymałości złożonej

(zginanie ze skręcaniem)

F

4 x F

1

2 x T

2

4 x M

1

G

2 x T

1

2 x R

1

2 x R

2

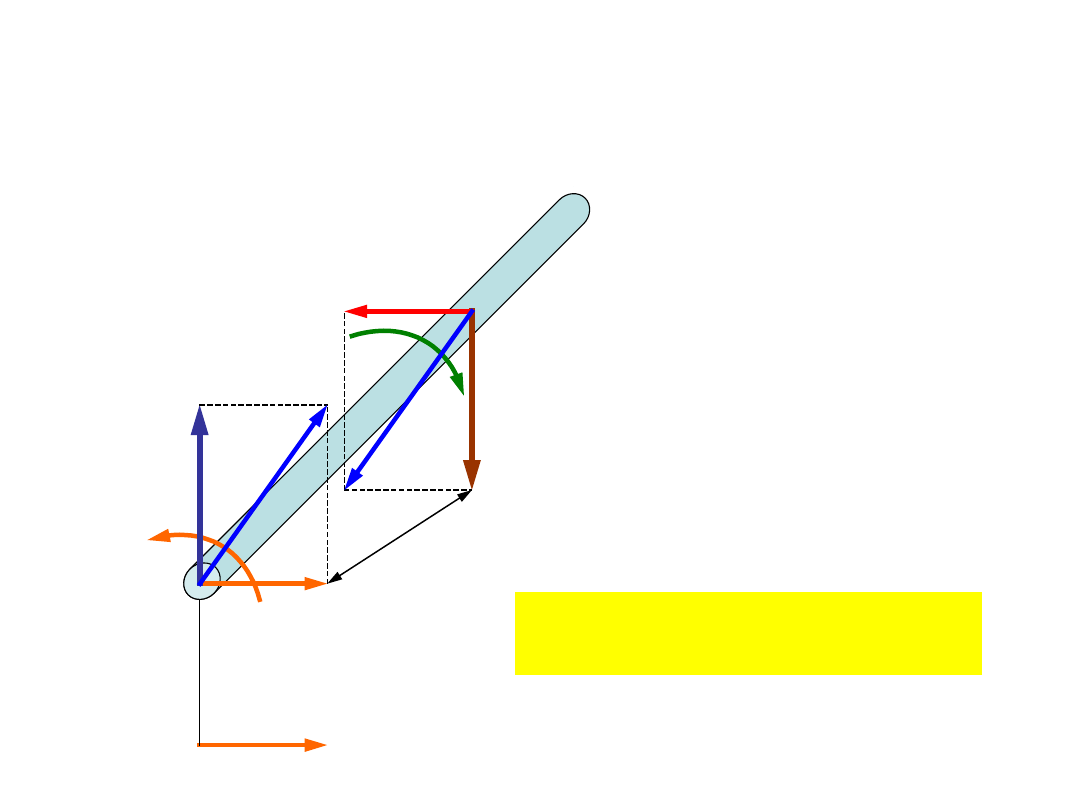
Przykłady wytrzymałości złożonej

(zginanie ze skręcaniem)

R

1

T

1

M

T1

G

1

F

1

-M

T1

Para sił (P,-P)
powoduje zginanie osi
wózka

Momenty M

T1

oraz -M

T1

powodują skręcanie
osi wózka

P

-P

1

,

g

s

T

M

Pa M

M

=

=

a

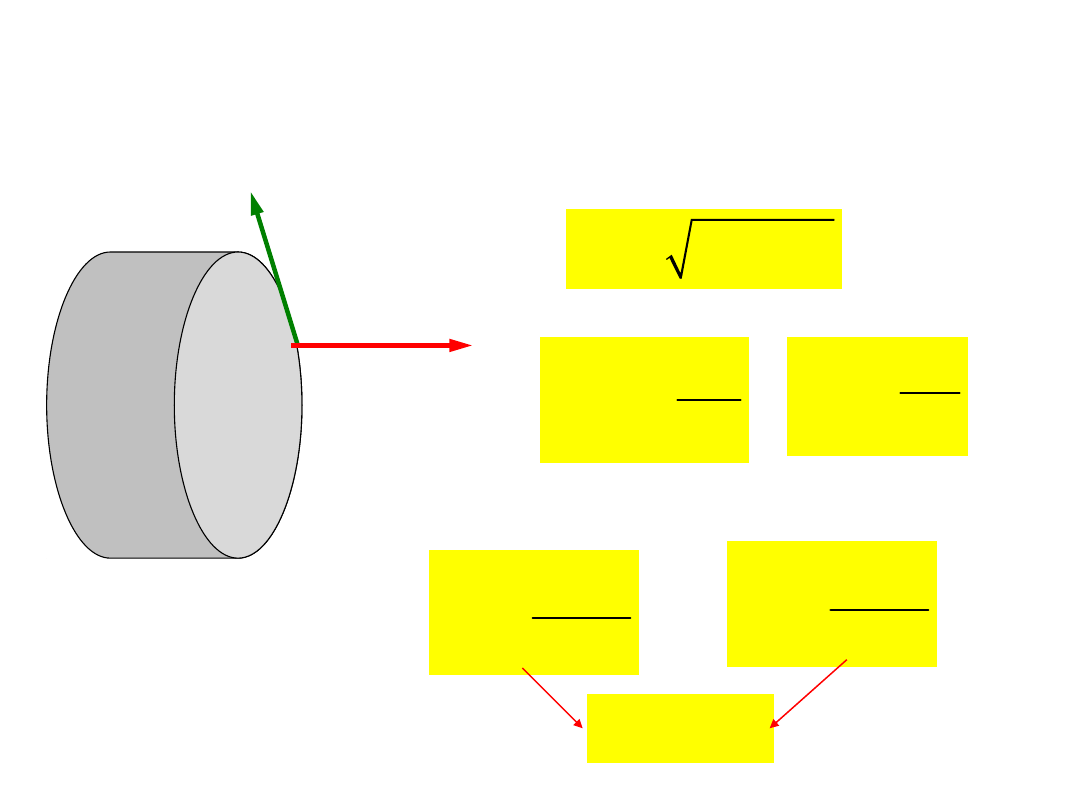
Przykłady wytrzymałości złożonej

(zginanie ze skręcaniem)





n

2

2

3

zr

n

s

s

t

=

+

Na podstawie hipotezy Hubera –
Mizesa:

max

0

s

M
W

t

=

max

g

n

z

M

W

s

=

Dla przekroju
kołowego:

3

max

0

2

r

W

p

=

3

max

4

z

r

W

p

=

0

2

z

W

W

=

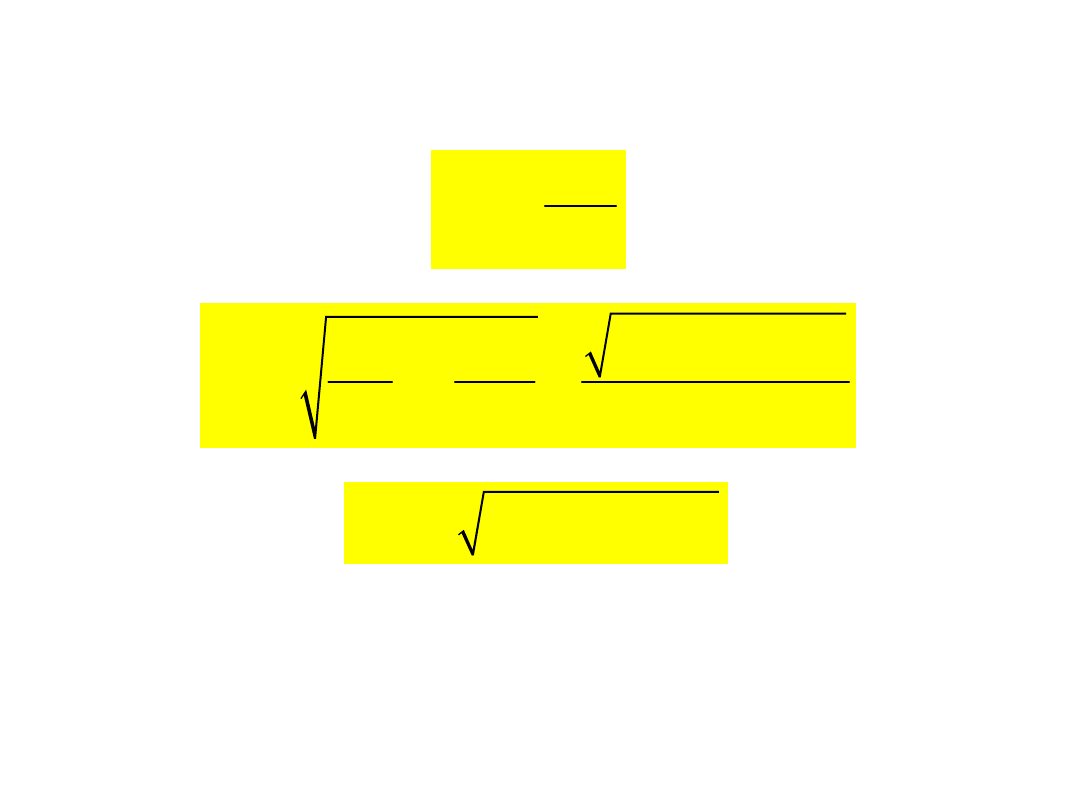
Przykłady wytrzymałości złożonej

(zginanie ze skręcaniem)

max

2

s

z

M

W

t

=

2

2

2

2

2

2

0,75

3

4

g

s

g

s

zr

z

z

z

M

M

M

M

W

W

W

s

+

=

+

=

2

2

0,75

zr

g

s

M

M

M

=

+

Przykłady wytrzymałości złożonej

(ścinanie ze skręcaniem)

Jeżeli odległość

a

jest mała, moment zginający

będzie mały i w obliczeniach wytrzymałościowych
powinniśmy uwzględnić ścinanie siłą P.

max

0

s

M

P

W

S

t

=

+

max

0

n

s

@

2

2

0

3

3

s

zr

n

M

P

W

S

s

s

t

�

�

=

+

=

+

�

�

�

�