T13. Dynamika punktu

materialnego



Zasady dynamiki Newtona.



Zasada d’Alemberta.



Równania ruchu punktu

materialnego.



Pęd i impuls.



Moment pędu.



Praca i energia mechaniczna.

I zasada dynamiki Newtona:

Punkt materialny, na który nie działa żadna siła,
lub siły działające równoważą się, pozostaje w
spoczynku lub porusza się ruchem jednostajnym
prostoliniowym

II zasada dynamiki Newtona:

Przyspieszenie

punktu

materialnego

jest

proporcjonalne do siły wypadkowej działającej na
ten punkt i ma kierunek oraz zwrot tej siły.

( )

( )

F t

a t

m

=

r

r

Zasady dynamiki
Newtona

Jeżeli przyspieszenie punktu materialnego równe
jest zeru, prędkość ma stałą wartość (ruch
jednostajny lub spoczynek) i nie zmienia kierunku
ruchu (ruch prostoliniowy).

( ) 0

( ) 0

F t

a t

=

�

=

r

r

Zasady dynamiki
Newtona

Pierwsza zasada dynamiki jest szczególnym
przypadkiem drugiej zasady.

Uwzględniając, że siła F jest wypadkową sił,
mamy:

( )

( )

( )

( ) 0

F t

ma t

F t ma t

=

�

-

=

r

r

r

r

Zasada
d’Alemberta

1

( )

( ) 0

n

i

i

F t ma t

=

-

=

�

r

r

Powyższe równanie przybierze postać równania
równowagi

układu

sił

zbieżnych,

jeżeli

wprowadzimy

siłę

zdefiniowaną

w

sposób

następujący:

( )

( )

B

F t

ma t

=-

r

r

Siłę F

B

nazywamy

siłą bezwładności

.

Zasada
d’Alemberta

1

( )

( ) 0

n

i

B

i

F t

F t

=

+

=

�

r

r

Zasada d’Alemberta

:

Układ sił rzeczywistych i siły bezwładności
pozostaje w każdej chwili czasu w równowadze.

Zasada d’Alemberta pozwala zastosować metody
statyki do wyznaczania siły bezwładności, a co za
tym idzie wektora przyspieszenia.

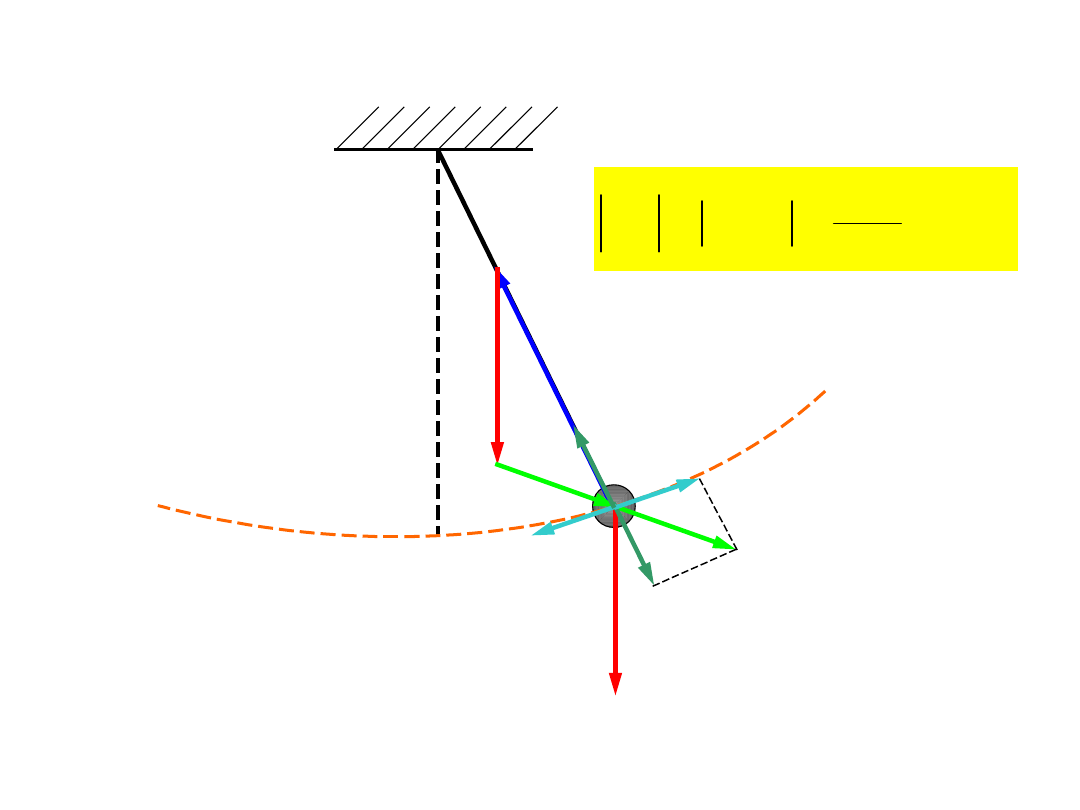
Zasada
d’Alemberta

G

R

F

B

F

Bs

F

Bn

F

Bn

–

siła odśrodkowa

a

s

a

n

2

Bn

n

mu

F

ma

mu

r

w

=-

=

=

r

r

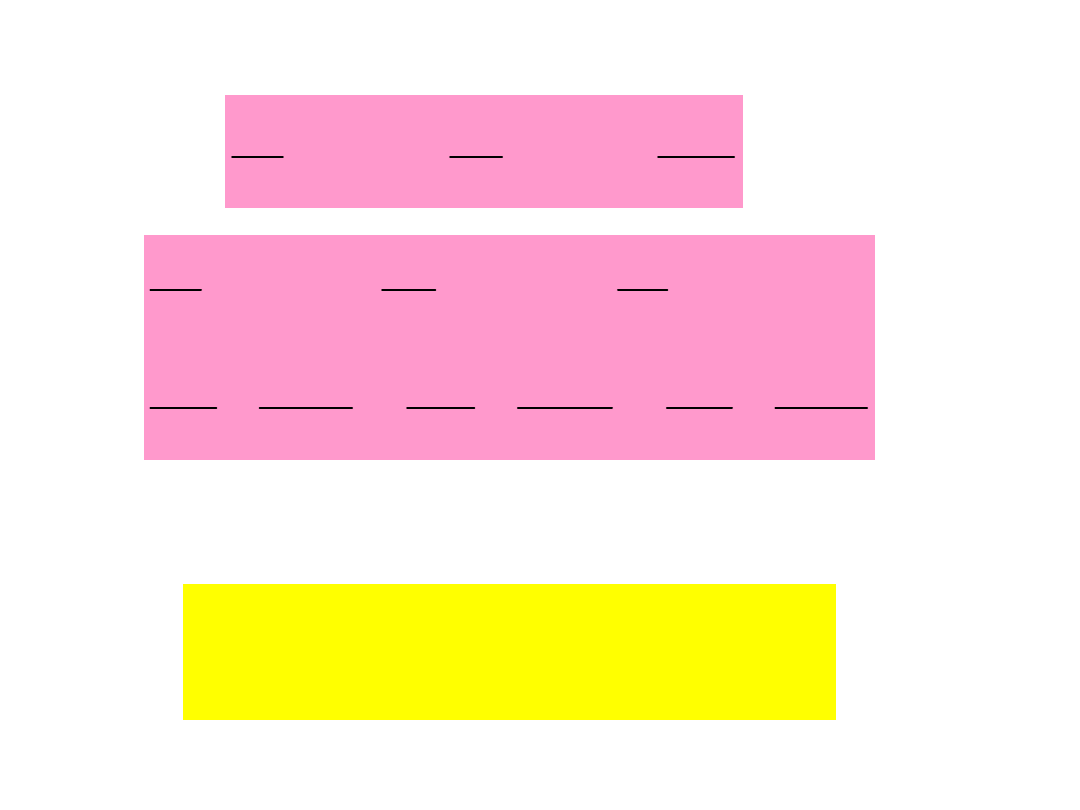
Równania ruchu punktu
materialnego

( )

( )

( )

,

dr

du

F t

u t

a t

dt

dt

m

=

=

=

r

r

r

r

r

( )

( )

( )

( )

( )

( )

,

,

,

,

x

y

z

y

y

x

z

x

z

dx

dy

dz

u t

u t

u t

dt

dt

dt

du

F t

F t

F t

du

du

dt

m

dt

m

dt

m

=

=

=

=

=

=

( )

( )

( )

( )

( )

( )

0

0

0

0

0

0

0

,

0

,

0

0

,

0

,

0

x

x

y

y

z

z

x

x

y

y

z

z

u

u

u

u

u

u

=

=

=

=

=

=

Warunek początkowy:

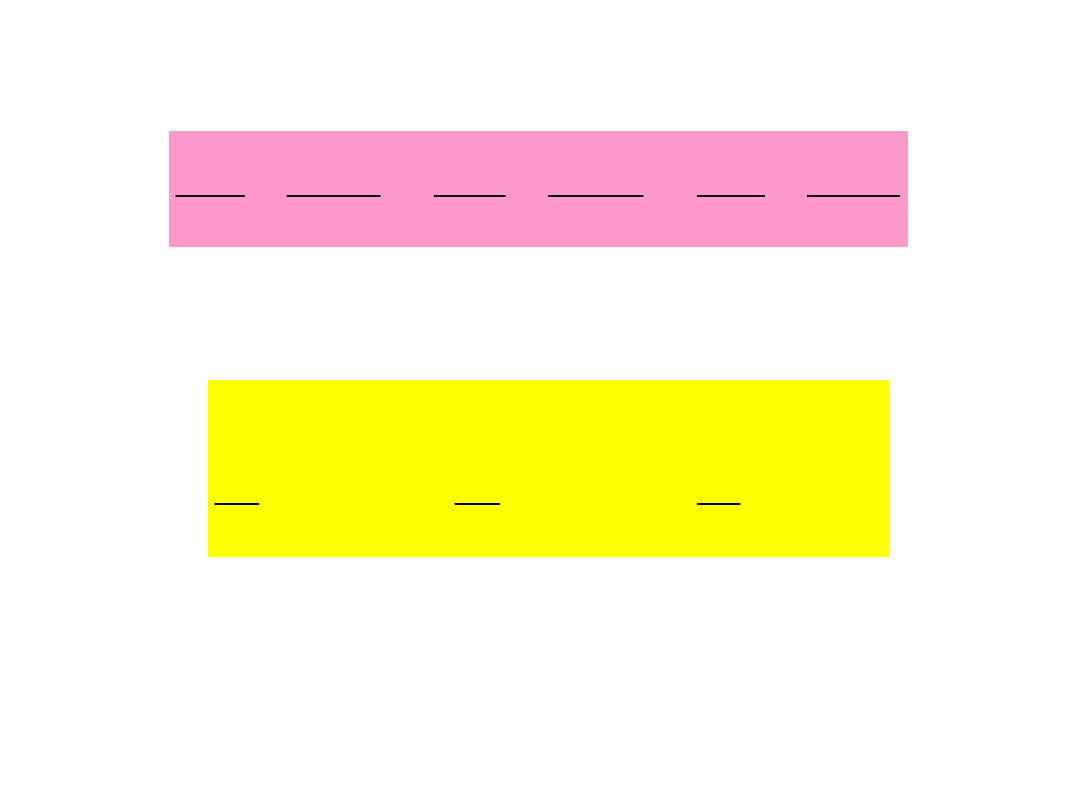
Równania ruchu punktu
materialnego

( )

( )

( )

2

2

2

2

2

2

,

,

y

x

z

F t

F t

F t

d x

d y

d z

dt

m

dt

m

dt

m

=

=

=

( )

( )

( )

( )

( )

( )

0

0

0

0

0

0

0

,

0

,

0

0

,

0

,

0

x

y

z

x

x

y

y

z

z

dx

dy

dz

u

u

u

dt

dt

dt

=

=

=

=

=

=

Warunek początkowy:

Równania ruchu punktu
materialnego

( )

( )

( , , )

,

dr

du

F t r u

u t

a t

dt

dt

m

=

=

=

r

r

r

r r

r

r

( )

( )

( )

(

)

(

)

(

)

,

,

, , , , , ,

,

, , , , , ,

,

, , , , , ,

x

y

z

x

x

y

z

x

y

x

y

z

y

z

x

y

z

z

dx

dy

dz

u t

u t

u t

dt

dt

dt

F t x y z u u u

du

dt

m

F t x y z u u u

du

dt

m

F t x y z u u u

du

dt

m

=

=

=

=

=

=

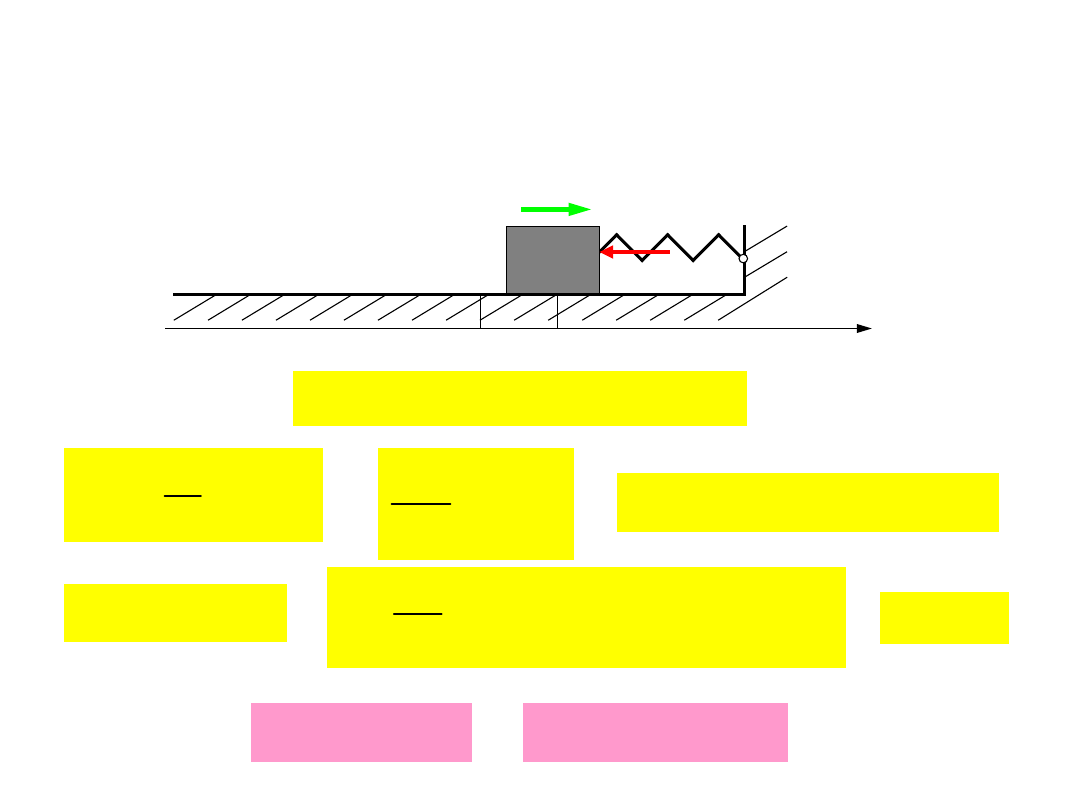
Równania ruchu punktu
materialnego

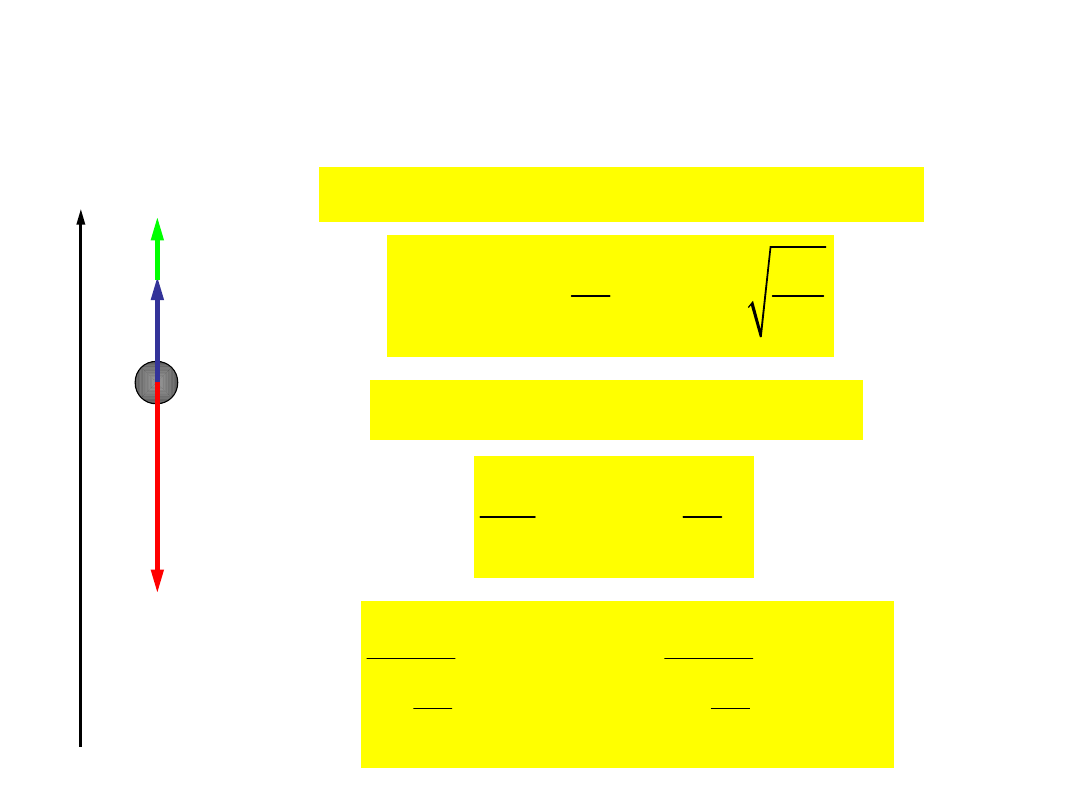
Przykład 1: Ruch harmoniczny po
prostej

x

0

x

0

2

x

kx

a

w x

m

=-

=-

2

2

2

d x

w x

dt

=-

( )

( )

sin

cos

x A

wt

B

wt

=

+

0

(0)

x

x

B

= =

( )

( )

cos

sin

d x

u

Aw

wt

Bw

wt

dt

=

=

-

0 Aw

=

( )

0

cos

x x

wt

=

( )

0

cos

u

wx

wt

=-

F

F

B

0

0

B

x

F

F

ma

kx

-

= � -

-

=

Równania ruchu punktu
materialnego

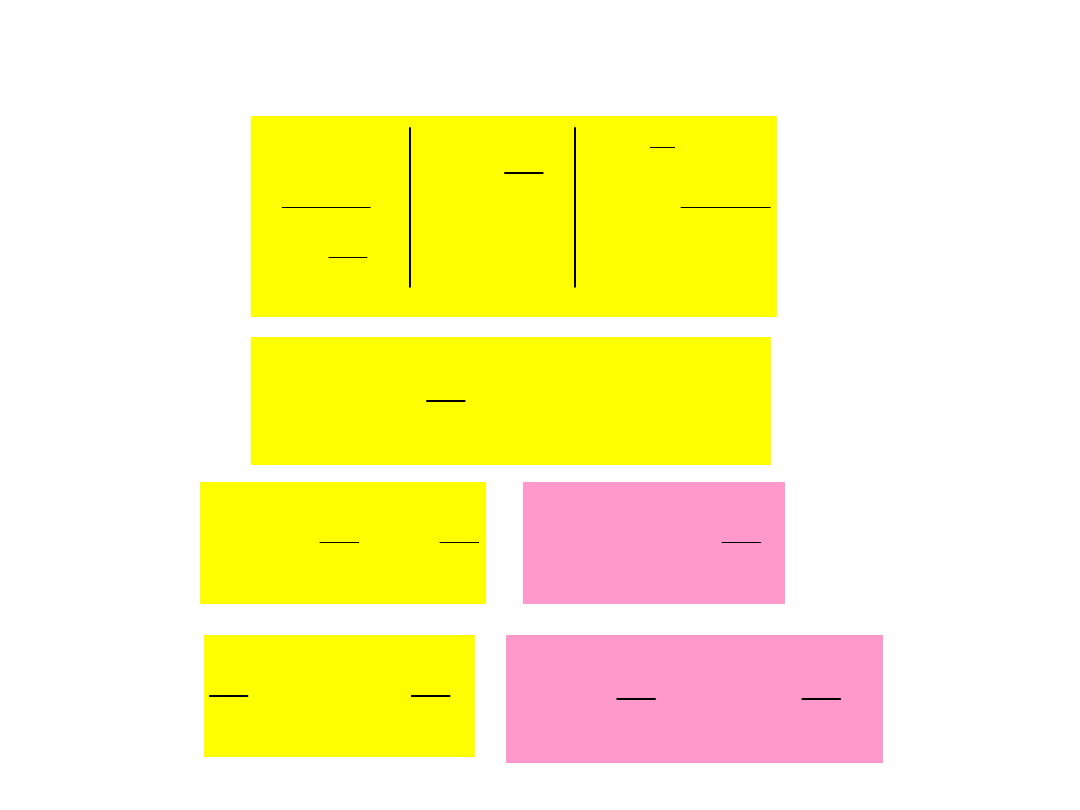
Przykład 2: Spadek swobodny z oporem
powietrza

2

0

0

B

z

z

F

R G

ma cu

mg

+ -

= � -

+

-

=

z

G

R

F

B

2

2

1

,

z

z

g

g

u

mg

a

g

u

u

c

�

�

=-

-

=

�

�

�

�

�

�

2

2

1

z

z

g

du

u

g

dt

u

�

�

=-

-

�

�

�

�

�

�

2

2

0

0

2

2

1

1

z

u

t

z

z

g

g

du

d

gdt

g dt

u
u

u

n

n

=-

�

=-

-

-

�

�

(

)

0,

0,

( )

x

y

z

z

z

F

F

F

F u t

=

=

=

Równania ruchu punktu
materialnego

2

2

0

0

2

1

1

z

g

z

u

u

u

g

g

g

g

d

d

u

u

d

u d

u

n

y

n

y

n

y

n

y

=

=

=

-

-

=

�

�

( )

arctgh

arctgh 0

z

g

g

u

u

gt

u

�

�

� �

-

=-

�

�

� �

� �

�

�

� �

�

�

arctgh

z

g

g

u

gt

u

u

� �

=-

� �

� �

� �

tgh

z

g

g

gt

u

u

u

� �

=-

� �

� �

� �

tgh

g

g

dz

gt

u

dt

u

� �

=-

� �

� �

� �

2

ln cosh

g

g

u

gt

z h

g

u

�

�

� �

= -

�

�

� �

� �

�

�

� �

�

�

Równania ruchu punktu
materialnego

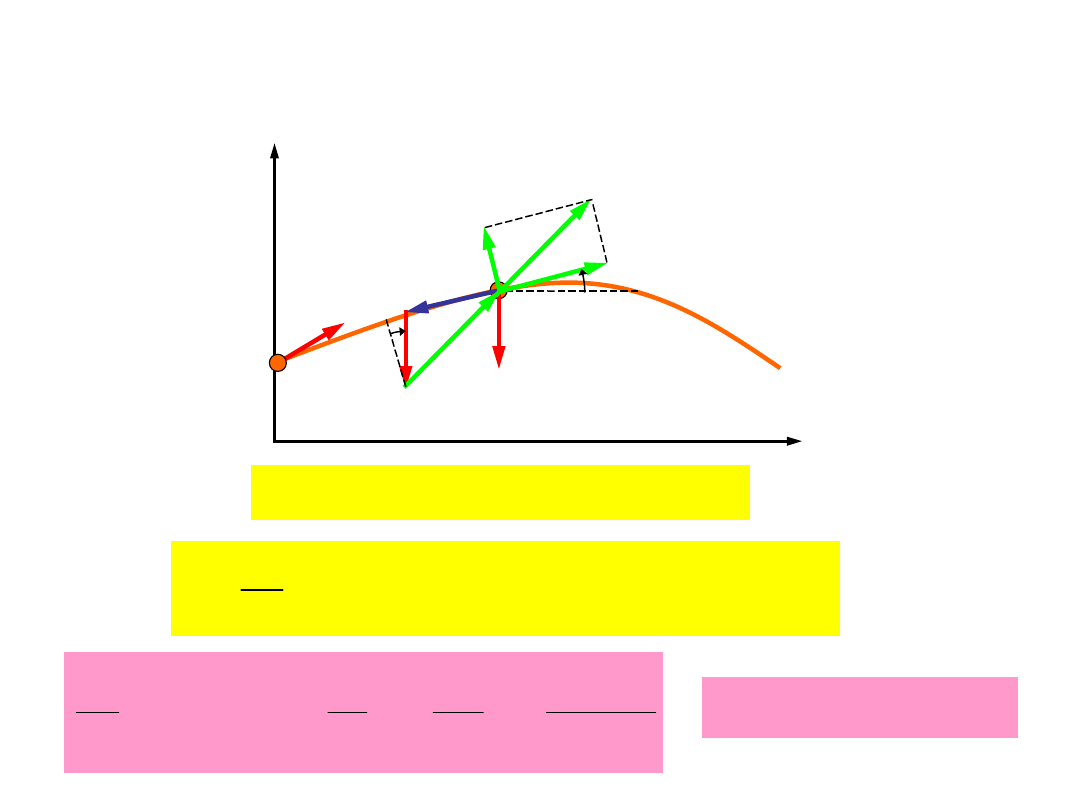
Przykład 3: Rzut ukośny z oporem
powietrza

G

y

0

u

r

R

F

B

F

Bs

F

Bn

a

x

sin ,

cos

Bs

Bn

F

R G

F

G

a

a

= +

=

2

sin ,

cos

du

m

cu

mg

mu

mg

dt

a

w

a

-

=

+

-

=

2

2

cos

sin

,

g

du

u

d

g

g

dt

u

dt

u

a

a

a

�

�

=-

+

=-

�

�

�

�

�

�

( )

( )

0

0

0

,

0

u

u a

a

=

=

a

a

Równania ruchu punktu
materialnego

2

2

cos

sin

,

g

du

u

d

g

g

dt

u

dt

u

a

a

a

�

�

=-

+

=-

�

�

�

�

�

�

( )

( )

0

0

0

0

0

,

0

, (0)

, (0)

u

u

x

x y

y

a

a

=

=

=

=

cos ,

sin

dx

dy

u

u

dt

dt

a

a

=

=

Równania ruchu punktu
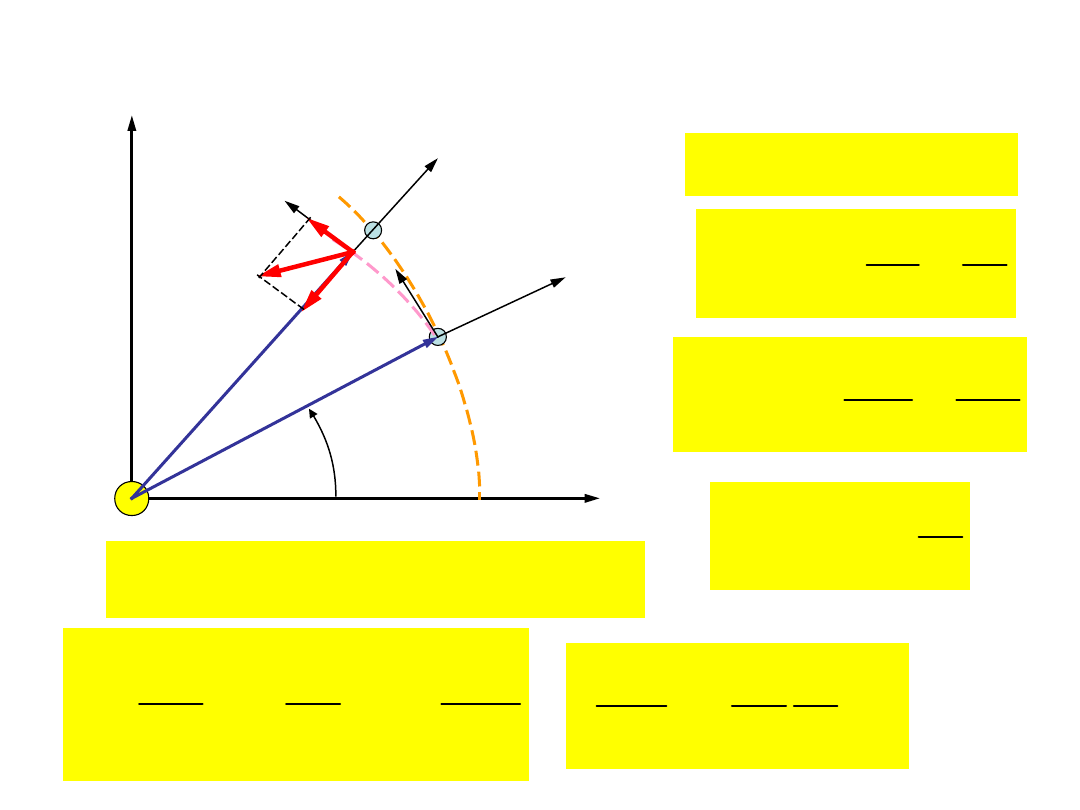
materialnego

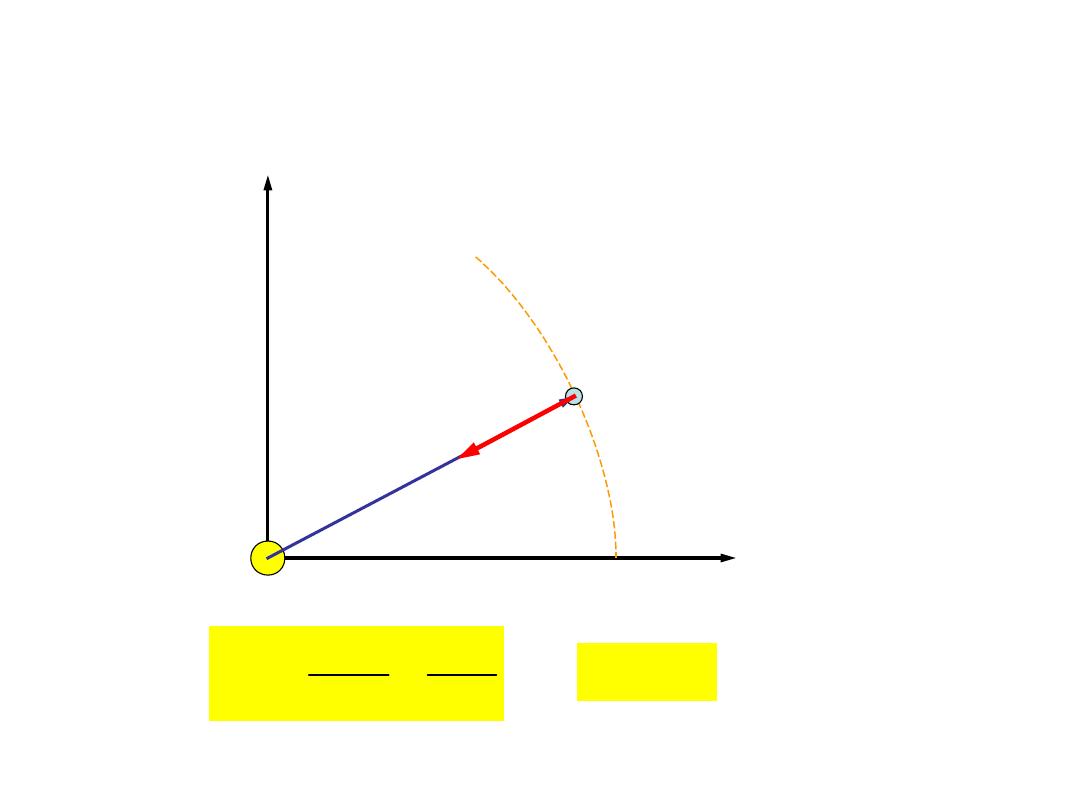
Przykład 4: Ruch planet wokół
słońca

x

y

G

2

2

z

s

z

mm

Km

G k

r

r

=

=

( )

r t

r

z

ma G

=

r

r

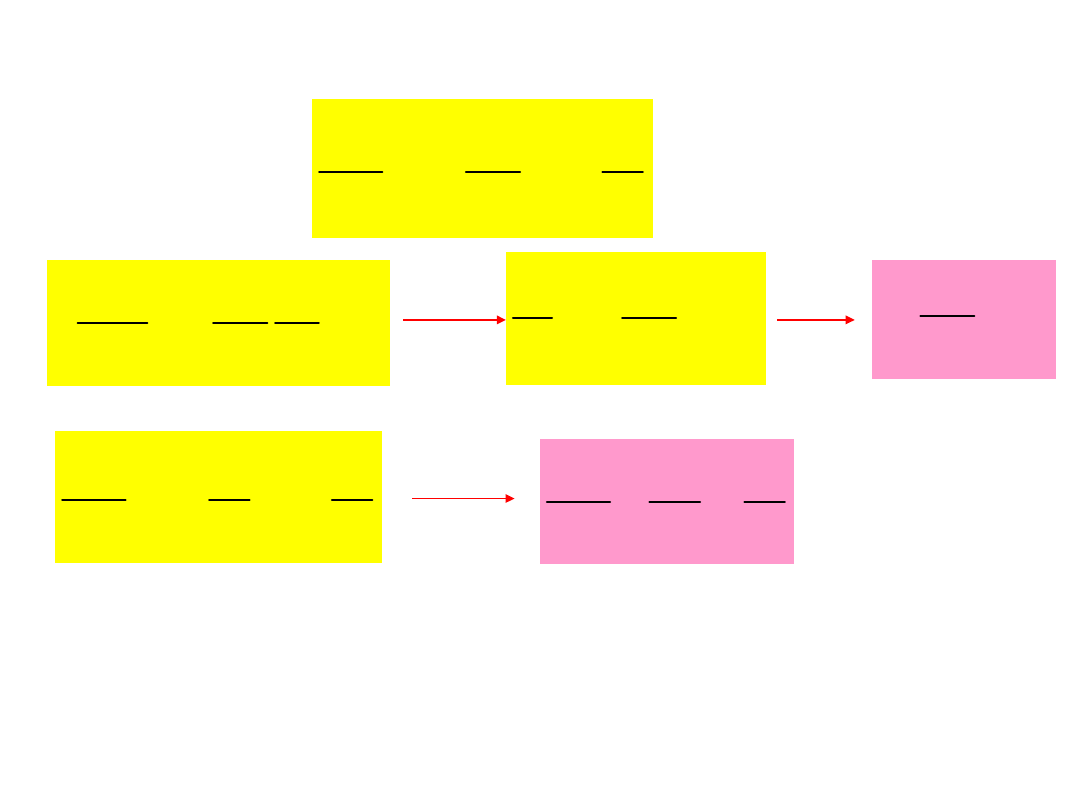
Równania ruchu punktu
materialnego

x

y

x

x

h

h

1

1

2

e

a a a

u

w

= + +

�

r

r r

r

r

1

1

d

dr

u u

dt

dt

x

x

=

=

=

2

2

1

1

2

2

d

d r

a

a

dt

dt

x

x

=

=

=

1

dr

u i

dt

h

w

w

� =

r

r r

(

)

( )

2

e

n

s

a

a

a

i

r

i

r

x

h

w

e

= + = -

+

r

r

r

r

r

e

a

r

n

a

r

s

a

r

j

2

2

2

2

z

z

d r

d

Km

m

r

dt

dt

r

j

�

�

� �

-

=

�

�

� �

�

�

� �

�

�

2

2

2

0

d

d dr

r

dt

dt dt

j

j

+

=

Równania ruchu punktu
materialnego

2

2

2

2

d r

d

K

r

dt

dt

r

j

� �

-

=

� �

� �

2

2

2

0

d

d dr

r

dt

dt dt

j

j

+

=

2

0

d

d

r

dt

dt

j

�

�

=

�

�

�

�

2

d

r

C

dt

j

=

2

2

2

2

2

d r

C

K

r

dt

r

r

� �

-

=

� �

� �

2

2

2

3

2

d r C

K

dt

r

r

-

=

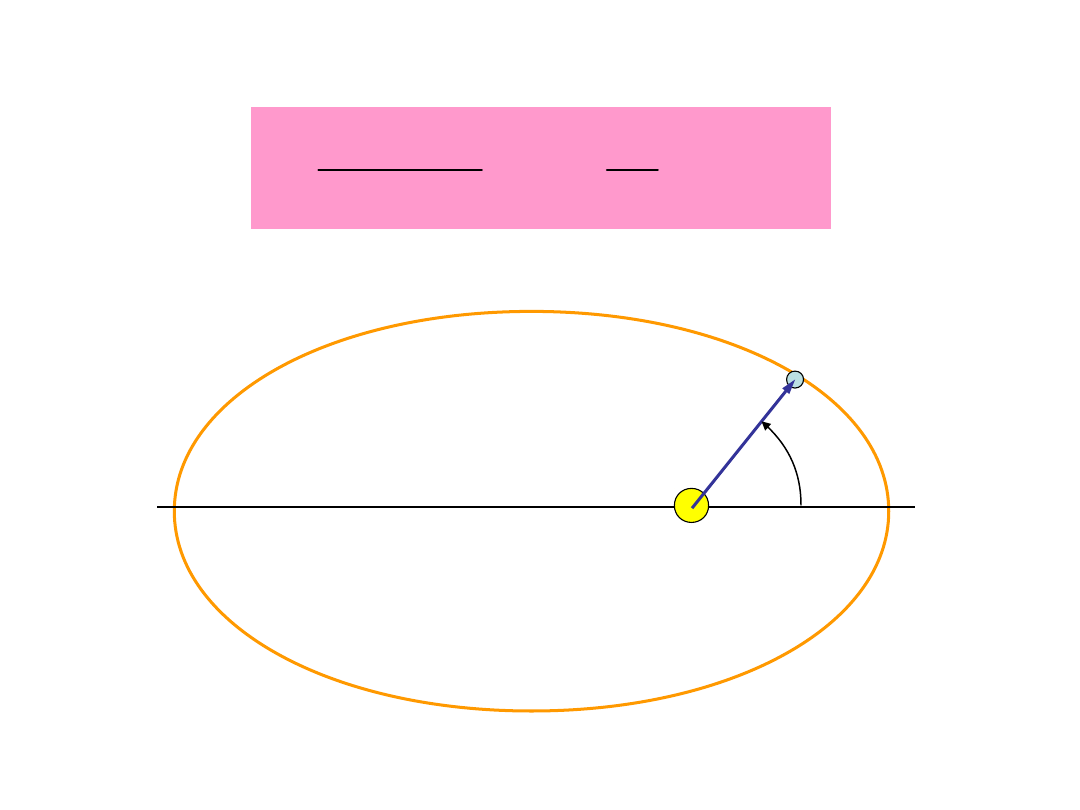
Równania ruchu punktu
materialnego

2

,

,

1

cos

p

C

r

p

e Ap

e

K

j

=

=

=

+

j

Pęd i
impuls

du

ma m

F

dt

=

=

r

r

r

(

)

d mu

dP

F

dt

dt

=

=

r

r

r

Wielkość wektorową o wartości równej iloczynowi
masy i wartości wektora prędkości oraz kierunku
i zwrocie
wektora prędkości nazywamy

pędem

.

dP Fdt

=

r

r

t

t

t

P

Fdt S

+D

D =

=

�

r

r

r

Całkę z siły po czasie nazywamy

impulsem siły

(popędem siły)

(

)

t

t

t

t

t

t

t

t

x

y

z

x

y

z

t

t

t

t

S

iF

jF

kF dt i

F dt j

F dt k

F dt

+D

+D

+D

+D

=

+

+

=

+

+

�

�

�

�

r

r

r

r

r

r

r

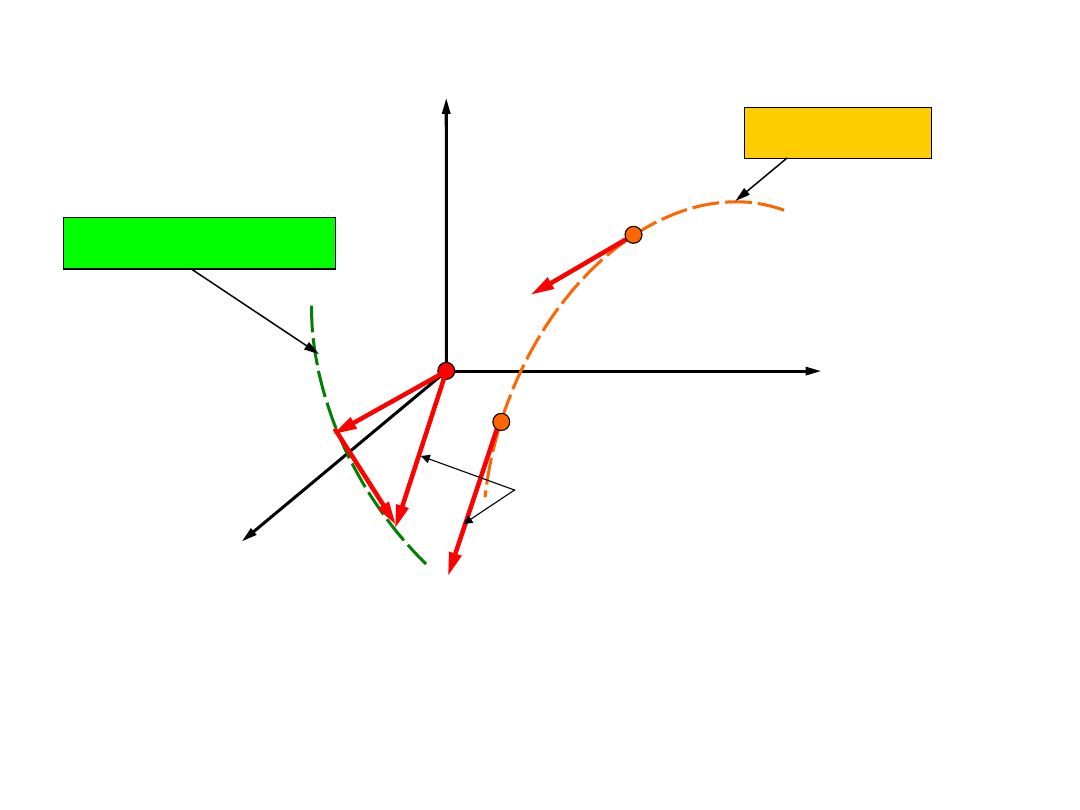
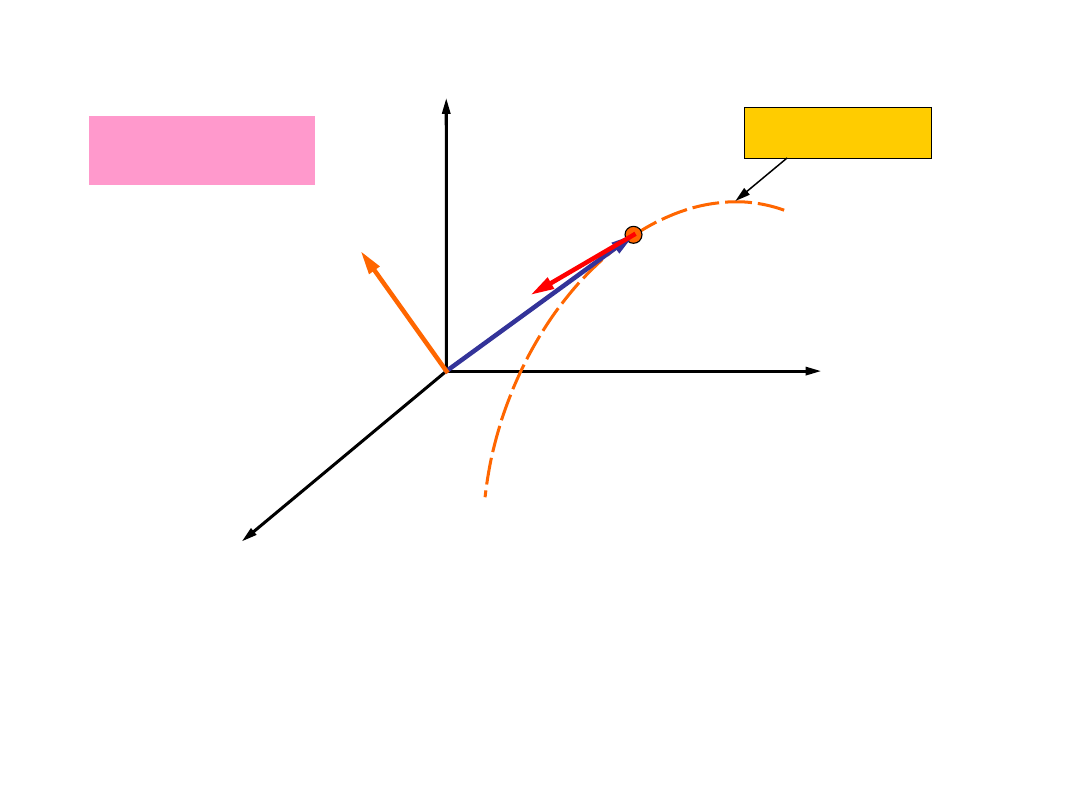
Pęd i
impuls

0

( )

P t

r

x

y

z

(

)

P t

t

+D

r

A

B

hodograf pędu

tor punktu

S

r

( )

P t

r

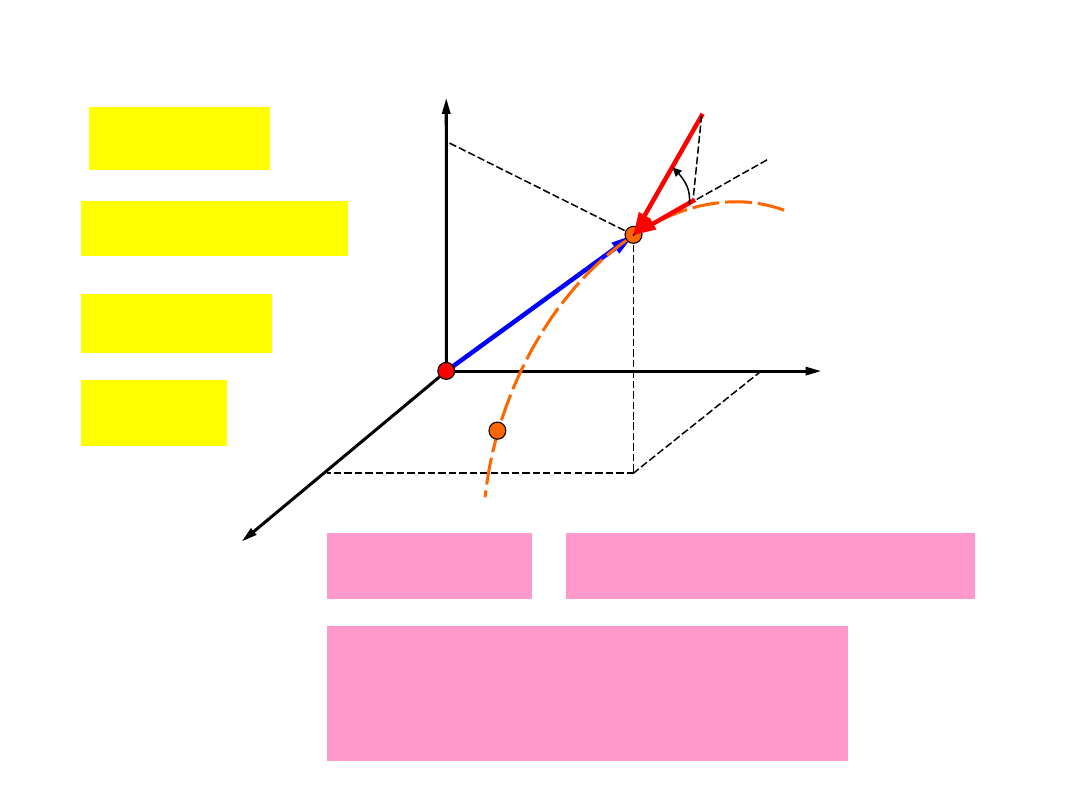
Moment pędu
(kręt)

0

( )

P t

r

x

y

z

A

tor punktu

( )

r t

r

0

( )

K

r P t

= �

r

r

r

0

( )

K t

r

Momentem pędu

(krętem)

względem bieguna 0

nazywamy wektor wyrażony iloczynem wektorowym
promienia wodzącego i wektora pędu.

Moment pędu
(kręt)

(

)

0

( )

dK

d

dr

dP

r P

P t

r

dt

dt

dt

dt

=

� =

�

+ �

r

r

r

r

r

r

r

0

( )

dK

u P t

r F

dt

= �

+ �

r

r

r

r

r

( )

( ) 0

u P t

u P t

=

޴

r

r

r

r

0

0

dK

r F M

dt

= � =

r

r

r

r

Pochodna momentu pędu punktu materialnego
względem bieguna 0 równa jest momentowi
wypadkowej siły działającej na ten punkt względem
bieguna 0.

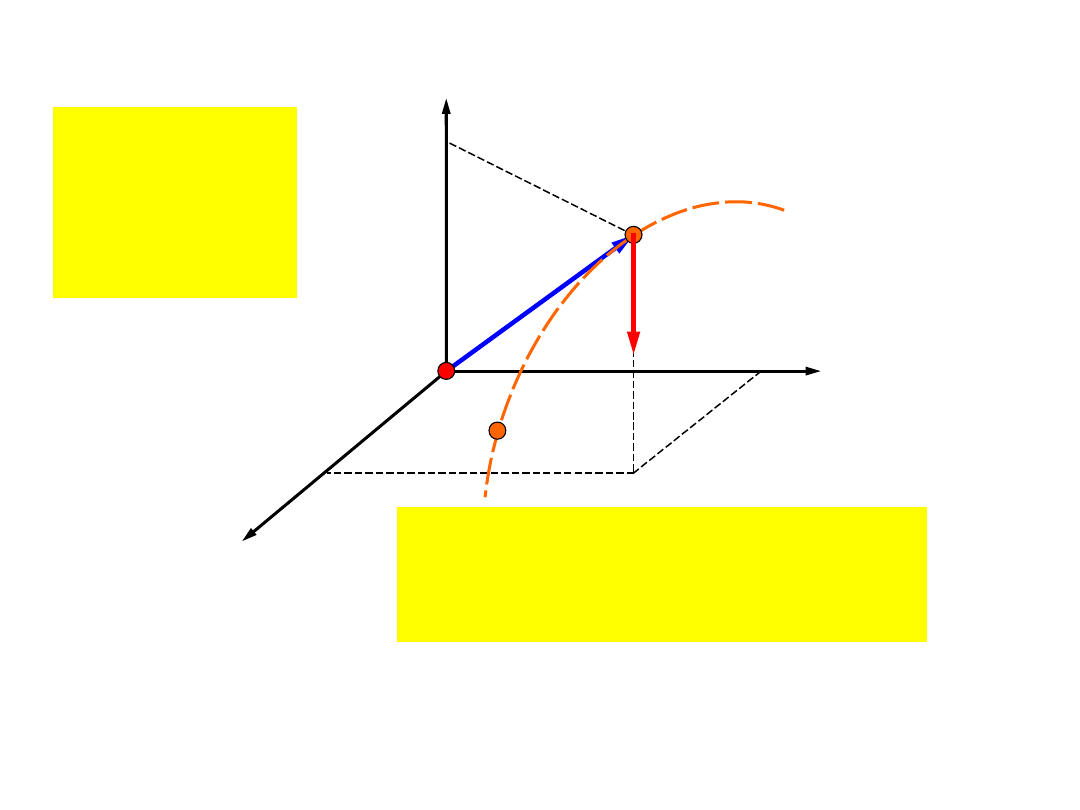
Praca i energia
mechaniczna

0

( )

r t

r

A

y

A

x

A

z

x

y

z

F

r

s

F

r

s

dL F ds

=

a

cos

dL F

ds

a

=

dL F ds

= �

r

r

ds dr

=

r

r

dL F dr

= �

r

r

x

y

z

dL F dx F dy F dz

=

+

+

B

B

B

A

A

A

x

y

z

AB

x

y

z

x

y

z

L

F dx

F dy

F dx

=

+

+

�

�

�

A

B

Praca i energia
mechaniczna

0

( )

r t

r

A

y

A

x

A

z

x

y

z

G

r

(

)

B

A

z

AB

B

A

z

L

mgdz

mg z

z

=-

=-

-

�

A

B

0

0

x

y

z

F
F
F

G

mg

=

=

= =-

Praca siły ciężkości nie zależy od drogi, a jedynie od
różnicy wysokości początkowego i końcowego punktu
ruchu punktu materialnego.

Praca i energia
mechaniczna

AB

B

A

pA

pB

L

mgz

mgz

E

E

=-

+

=

-

Praca siły ciężkości równa jest różnicy

energii

potencjalnej

punktu materialnego w początkowym i

końcowym punkcie drogi punktu.

Praca i energia
mechaniczna

cos

cos

dL F

ds F

udt

a

a

=

=

dL F udt

= �

r r

(

)

x x

y y

z z

dL

F u

F u

F u dt

=

+

+

(

)

B

A

t

AB

x x

y y

z z

t

L

F u

F u

F u dt

=

+

+

�

dL

N

F u

dt

=

= �

r r

Moc:

Praca i energia
mechaniczna

s

s

dL Fudt ma udt

=

=

(

)

2

1

2

k

du

dL m

udt d mu

dE

dt

=

=

=

AB

kB

kA

L

E

E

=

-

Zmiana energii kinetycznej punktu materialnego
równa jest pracy wykonanej na tym punkcie przez
siły działające na ten punkt.
Gdy punkt materialny porusza się jedynie pod
wpływem siły ciężkości:

kB

kA

pA

pB

E

E

E

E

-

=

-

kB

pB

kA

pA

E

E

E

E

+

=

+

const

k

p

E E

E

= +

=

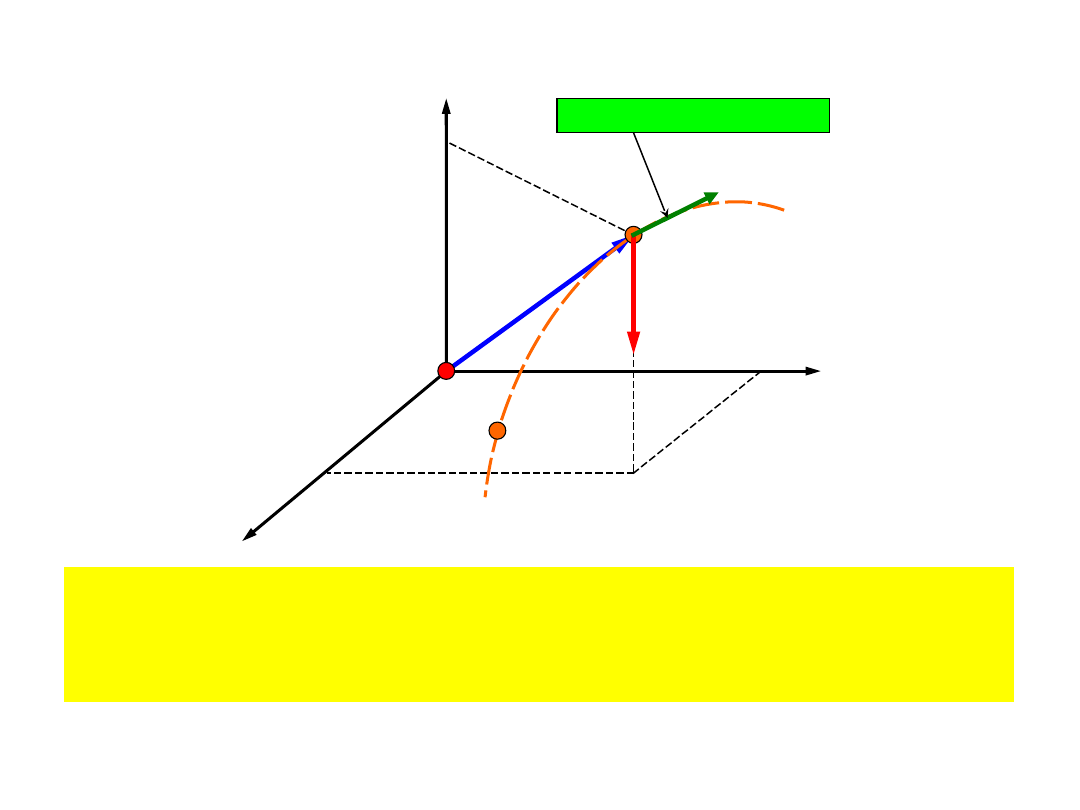
Praca i energia
mechaniczna

0

( )

r t

r

A

y

A

x

A

z

x

y

z

G

r

B

A

z

kB

kA

AB

pA

pB

z

AB

AB

E

E

L

mgdz

R ds E

E

Rds

-

=

=-

+

� =

-

-

�

�

�

r

r

A

B

R

r

siła oporu powietrza