
Właściwości
przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
•Liniowość
•Sprzężenie
•Charakterystyki a-cz i f-cz
•Zmiana skali
•Symetria
•Przesunięcie w czasie
•Przesunięcie w częstotliwości
•Modulacja
•Splot w czasie
•„Pole” sygnału

Właściwości
przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
•Różniczkowanie w dziedzinie czasu
•Całkowanie w dziedzinie czasu
•Część rzeczywista i urojona sygnału
•Sygnał parzysty i nieparzysty
•Składowa parzysta i nieparzysta
sygnału
•Właściwości graniczne transformaty
Fouriera
•Twierdzenie Parsevala i Rayleigha
•Widmo gęstości energii; energia
ułamkowa

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
Założenia podstawowe
Y
t
y
X
t
x
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
LINIOWOŚĆ
Y
X
t
y
t
x
t
y
t
x
t
y
t
x
F
F
F
F
F
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SPRZĘŻENIE
*
*
X
t
x
Dla sygnału rzeczywistego zachodzi związek:
*
*
,
X
X
t
x
t
x
t
x
R

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
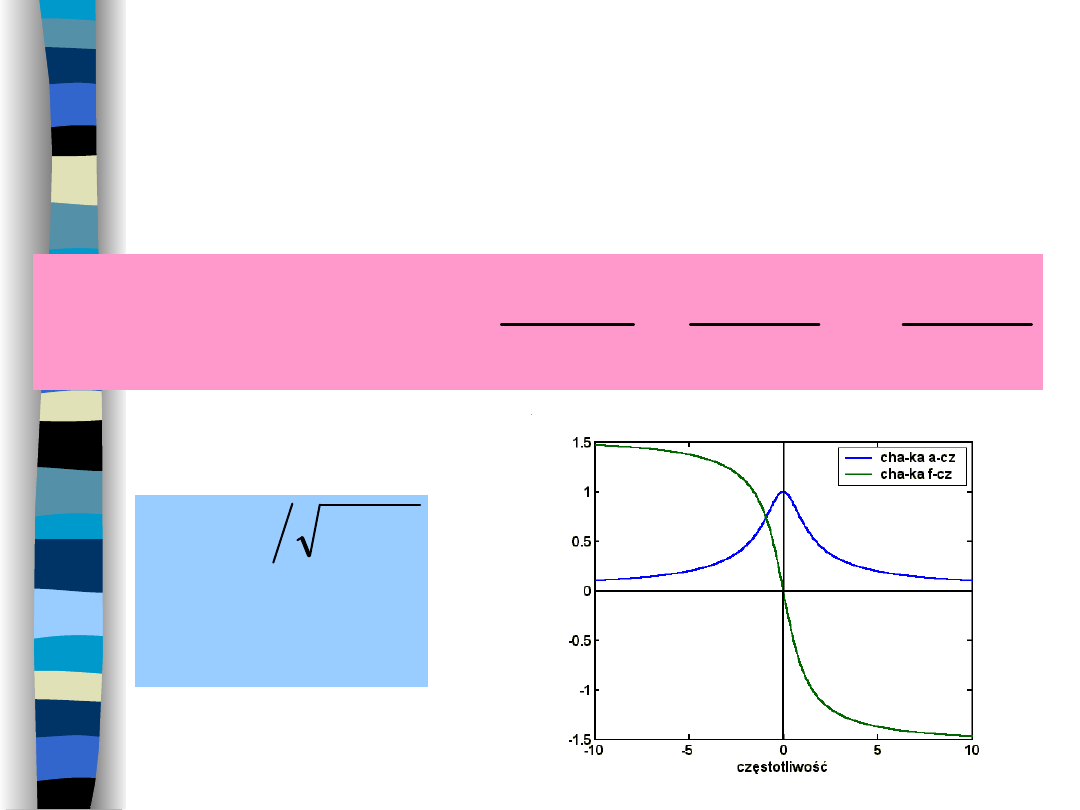
CHARAKTERYSTYKI A-CZ i F-CZ
cz
-
f
ka
-
cha
-
cz
-
a
ka
-
cha
-
e
A
A
X
t
x
j
Dla sygnału rzeczywistego zachodzi związek:
a
nieparzyst
ka
-
cha
-
parzysta
ka
-
cha
-
A
A
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
CHARAKTERYSTYKI A-CZ i F-CZ
2
2
2
1
1
1
1
1
1
1
j
j
j
e
t
t
1
arctg
1
1
2
A
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
ZMIANA SKALI
0
,
1
1
e
1
j
j
t
t
1
X
t
x
1
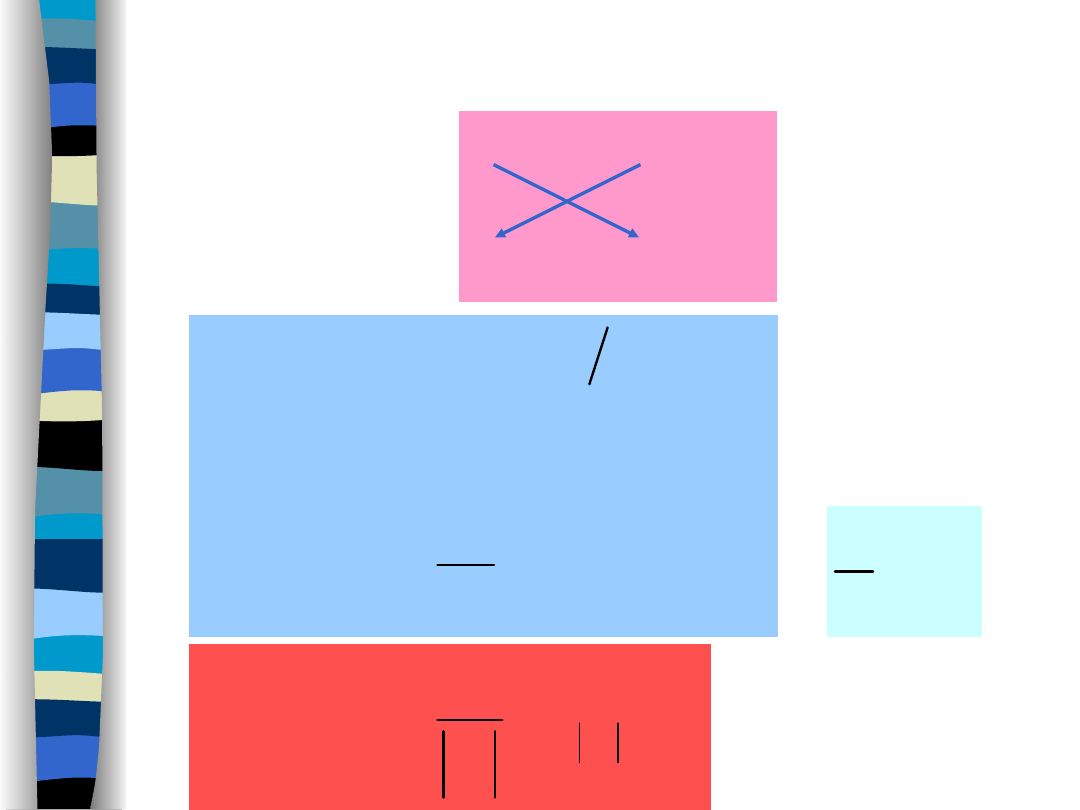
•„Ścieśnianie” sygnału w dziedzinie czasu powoduje
rozszerzanie jego widma; „rozciąganie” sygnału skutkuje
zawężaniem widma.
•Im krócej trwa sygnał, tym szersze jest jego widmo.
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SYMETRIA
x
t
X
X
t
x
2
W
T
T
W
Wt
tT
T
T
T
t
2
Sa
2
2
/
Sa
2
Sa
W
T
2
W
W
Wt
2
Sa

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SYMETRIA
x
t
X
X
t
x
2
x
t
X
d
e
x
d
e
x
t
X
d
e
x
t
X
t
dt
e
t
x
X
t
j
t
j
t
j
t
j
2
2
2
1

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
PRZESUNIĘCIE W CZASIE
Wpływ na charakterystykę f-cz
j
j
j
j
A
A
X
e
e
e
e
j
e
X
t
x
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
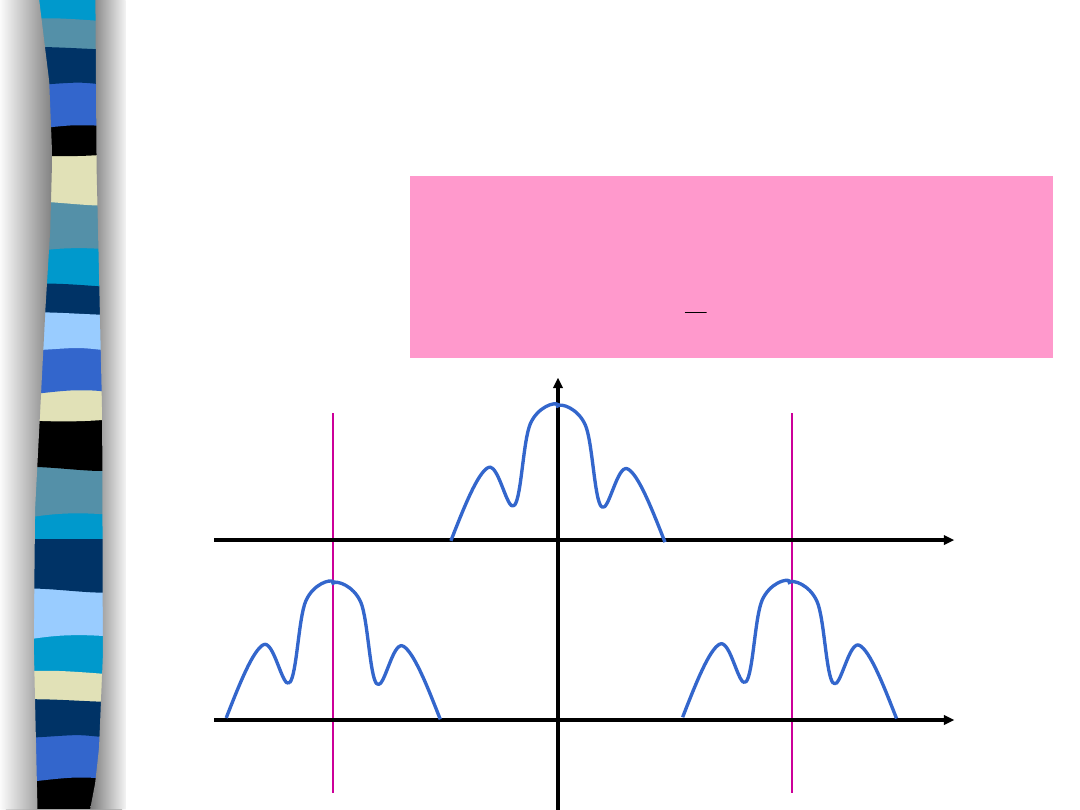
PRZESUNIĘCIE W CZĘSTOTLIWOŚCI
o
o
e
X
t
x
t
j
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
MODULACJA
o
o
o
o
o
o
o
2
1
cos
exp
exp
X
X
t
t
x
X
t
j
t
x
X
t
j
t
x
X(
)
X(
-
o
)/2
X(
+
o
)/2
-
o
+
o
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SPLOT W CZASIE
d
t
y
x
t
y
t
x
WŁAŚCIWOŚCI
Przemienność
t
x
t
y
t
y
t
x
Łączność
t
z
t
y
t
x
t
z
t
y
t
x
Rozdzielność względem
dodawania
t
z
t
x
t
y
t
x
t
z
t
y
t
x
Przemienność splotu
„Teoria sygnałów” Zdzisław Papir
d
t
y
x
t
y
t
x
t
x
t
y
t
y
t
x
)
(
)
(
t
y
t
x
d
t
y
x
)
(
)
(
dz
d
z
t
t
x
t
y
dz
z
y
z
t
x
)
(
)
(

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SPLOT W CZASIE
d
t
y
x
t
y
t
x
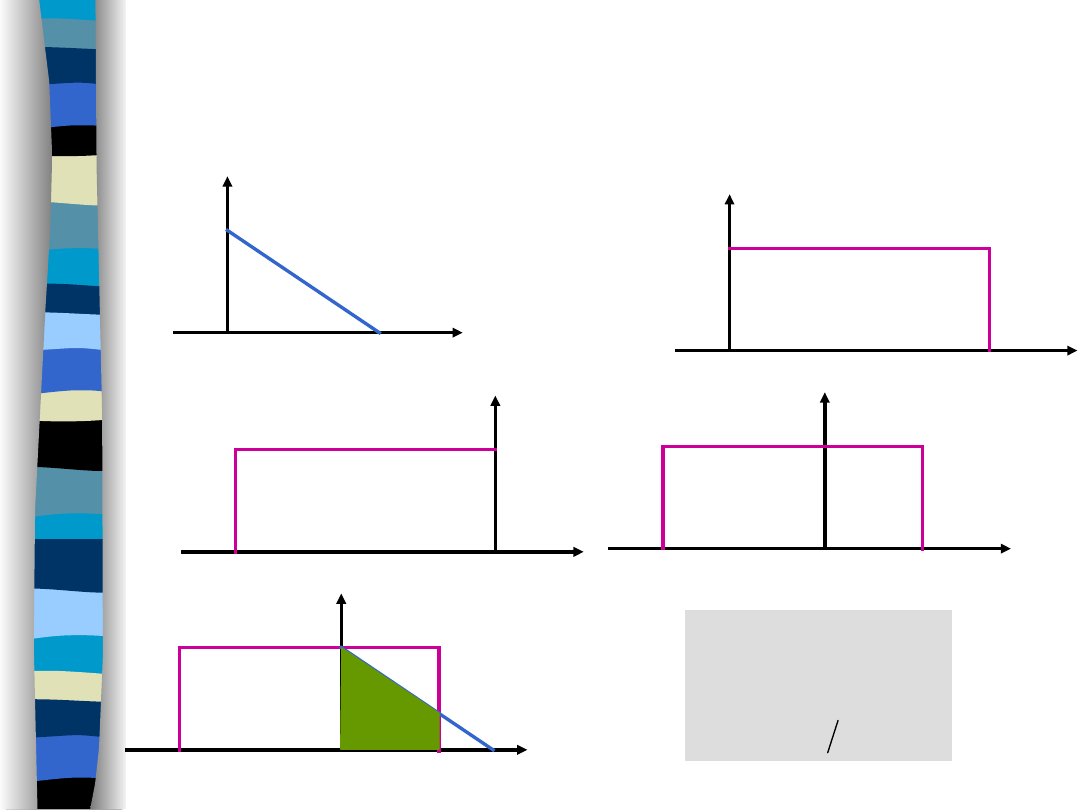
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SPLOT w CZASIE
określa stopień „pokrywania” się
wykresów funkcji w zależności od ich przesunięcia.
0
1
x
1
0
2
y
1
0
-2
y
1
t
y
1
t
1
t
y
1
2
t
2
2
t
t
S
d
t
y
x
S
t - 2
t
0
S

Splot w czasie
„Teoria sygnałów” Zdzisław Papir
dt
d
y
t
x
t
j
e
)
(
)
(
)
(
)
(
t
y
t
x
d
y
dt
e
t
x
t
j
)
(
)
(
dz
dt
z
t
d
y
dz
e
z
x
z
j
)
(
)
(
)
(

Splot w czasie
d
y
dz
e
z
x
z
j
)
(
)
(
)
(
d
y
dz
e
z
x
j
z
j
e
)
(
)
(
d
y
X
j
e
)
(
)
(
)
(
)
(
Y
X
)
(
)
(
t
y
t
x
„Teoria sygnałów” Zdzisław Papir

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SPLOT W CZĘSTOTLIWOŚCI
d
Y
X
t
y
t
x
Y
X
t
y
t
x
2
1
2
1
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
„POLE” SYGNAŁU (składowa stała sygnału)
0
0
0
X
X
dt
e
t
x
dt
t
x
t
j
W
W
dt
Wt
Wt
W
Wt
Wt
Wt
W
W
0
sin
sin
Sa
2
2
„Teoria sygnałów” Zdzisław Papir
W
W
W
W
W
W
W
dt
Wt
Wt
sgn
0
,
0
,
sin
sgn
0
,
0
,
1
sin
sin
1
j
j
j
j
t
dt
t
t
j
dt
t
t
j
dt
t
e
t
t
j
F
F
j
t
j
t
2
sgn
sgn
1

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
RÓŻNICZKOWANIE W DZIEDZINIE CZASU
0
lim
,
t
x
X
j
dt
t
dx
X
t
x
t
X
j
dt
e
t
x
j
e
x
e
x
dt
e
t
x
j
e
t
x
dt
e
t
x
dt
t
dx
t
j
j
j
t
j
t
j
t
j
lim
lim
F
Różniczkowanie w dziedzinie czasu uwypukla szybkie
zmiany sygnału, a więc uwypukla również wyższe
częstotliwości.
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
CAŁKOWANIE W DZIEDZINIE CZASU
j
X
X
d
x
X
t
x
t
0
Całkowanie w dziedzinie czasu wygładza szybkie
zmiany sygnału, a więc uwypukla również niższe
częstotliwości.
Jeżeli sygnał nie zawiera składowej stałej, X(
= 0) = 0,
wtedy:
j
X
d
x
X
t
x
t

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
CAŁKOWANIE W DZIEDZINIE CZASU
t
X
d
x
t
t
t
d
t
x
t
t
x
d
x
t
t
1
1
1
1
F
,
0
,
1
Dowód właściwości „całkowanie w dziedzinie czasu”
opiera się na przedstawieniu
całki w postaci splotu.
0
,
1
0
,
0
t
t
t
1

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
CZĘŚĆ RZECZYWISTA I UROJONA SYGNAŁU
j
X
X
t
x
X
X
t
x
2
2
*
*
Im
Re
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SYGNAŁY PARZYSTE i NIEPARZYSTE
R
R
dt
t
t
x
X
t
x
t
x
t
x
0
cos
2
,
sygnał parzysty transformata Fouriera rzeczywista
dt
t
t
x
j
X
t
x
t
x
t
x
0
sin
2
,
R
sygnał nieparzysty urojona transformata Fouriera

Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
SKŁADOWA PARZYSTA i NIEPARZYSTA SYGNAŁU
2
2
n
p
p
n
t
x
t
x
t
x
t
x
t
x
t
x
t
x
t
x
t
x
X
j
t
x
X
t
x
Im
Re
n
p
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
WŁAŚCIWOŚCI GRANICZNE
TRANSFORMATY FOURIERA (Riemann)
0
lim
X
W miarę wzrostu częstotliwości „wartość”
transformaty Fouriera maleje do zera:
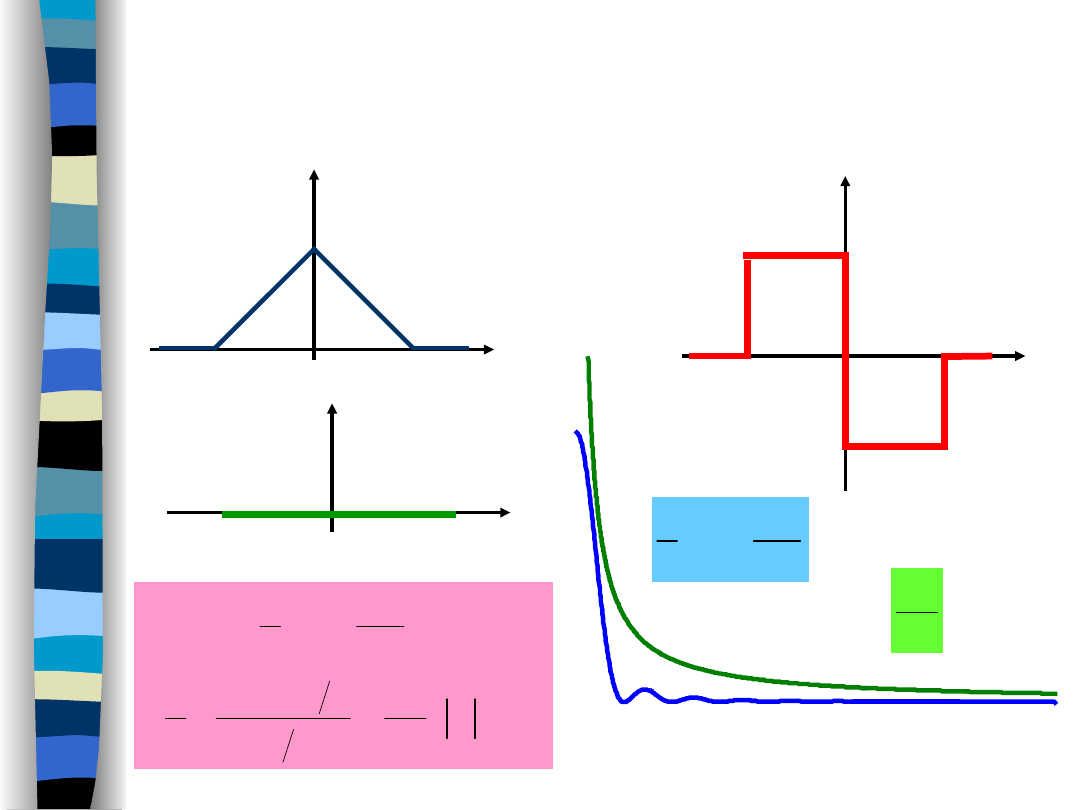
Transformata Fouriera (dla impulsów o czasie trwania T)
zanika, X(ω) 0, z szybkością:
jeżeli tylko istnieją ciągłe pochodne
2
2
T
x
T
x
n
const
X
X
n
n
n
2
2
2
lim
1
lim
0
1
lim
„Teoria sygnałów” Zdzisław Papir
WŁAŚCIWOŚCI GRANICZNE
TRANSFORMATY FOURIERA
,
1
4
4
sin
2
1
4
Sa
2
1
2
2
2
2
T
T
T
T
T
t
T
T/2
-T/2
t
T
T/2
-T/2
t
T
1
t
T
2
4
Sa
2
1
2
T
T
2
1
„Teoria sygnałów” Zdzisław Papir
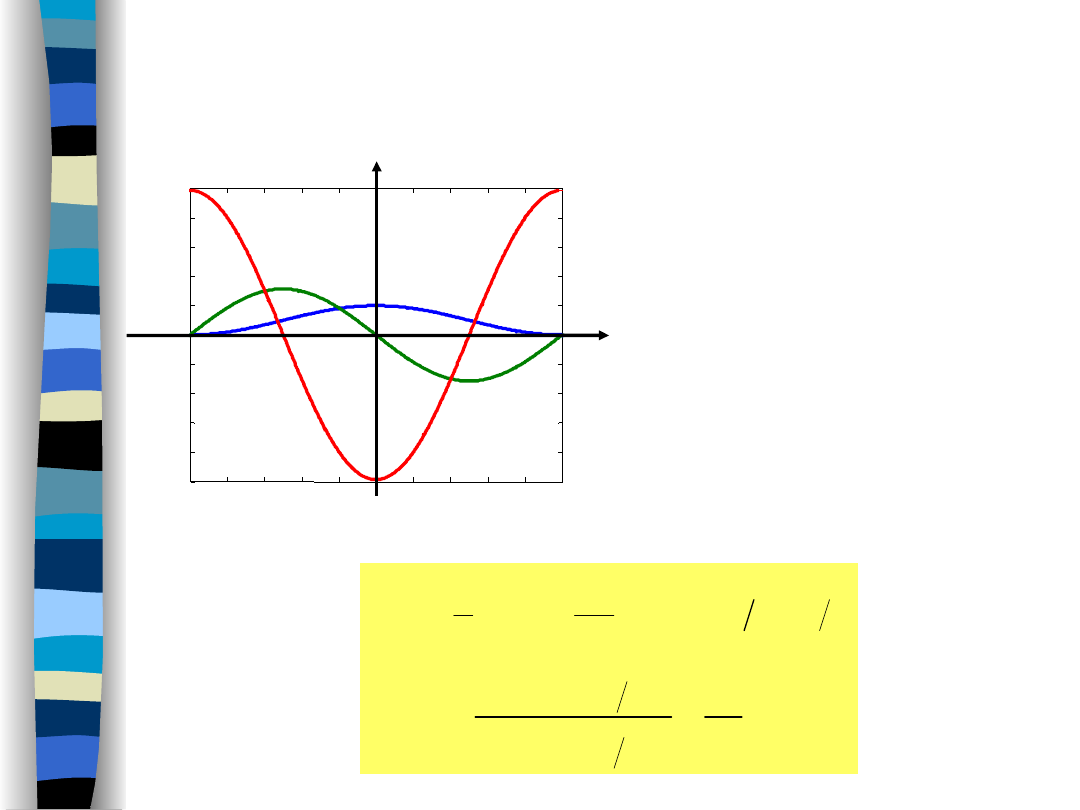
WŁAŚCIWOŚCI GRANICZNE
TRANSFORMATY FOURIERA
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
+T/2
-T/2
Impuls „podniesiony kosinus”
(raised cosine)
3
2
2
2
1
~
2
2
sin
2
,
2
,
2
cos
1
2
1
T
T
X
T
T
t
t
T
t
x
T
T
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
TWIERDZENIE PARSEVALA
0
2
2
2
1
2
1
d
X
d
X
dt
t
x
E
t
x
R
i(t) = x(t)
u(t) = x(t)
E
dt
t
x
dt
t
i
t
u
E
2
R = 1
TWIERDZENIE PARSEVALA
„Teoria sygnałów” Zdzisław Papir
dt
t
x
2
)
(
dt
t
x
t
x
)
(
)
(
*
dt
d
e
X
t
x
t
j
)
(
2
1
)
(
*
d
dt
e
t
x
X
t
j
)
(
)
(
2
1
*
d
X
X
)
(
)
(
2
1
*
d
X
2
)
(
2
1

Marc-Antoine PARSEVAL (1755 - †1836)
Very little is known of Antoine Parseval's life.
Parseval had only
five publications, all presented to the Académie des
Sciences.
The second was Mémoire sur les séries et sur
l'intégration complète
d'une équation aux differences partielle linéaires du
second ordre,
à coefficiens constans dated 5 April 1799, contains the
result known
today as Parseval's theorem.
Parseval's result was not published until his five
papers were all
published by the Académie des Sciences in 1806.
Before that it was
known by members of the Academy and appeared in
works by Lacroix
and Poisson before Parseval's papers were printed.
Parseval was never honoured with election to
the Académie
des Sciences. He remains a somewhat shadowy figure
and it is hoped
that research will one day provide a better
understanding of his life
and achievements.
„Teoria sygnałów” Zdzisław Papir
d
X
dt
t
x
2
2
2
1
(no picture available)
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
TWIERDZENIE RAYLEIGHA
d
Y
X
dt
t
y
t
x
t
y
t
x
*
*
2
1
,
C
Twierdzenie Rayleigha stanowi
uogólnienie twierdzenia Parsevala
dla dwóch różnych sygnałów.
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
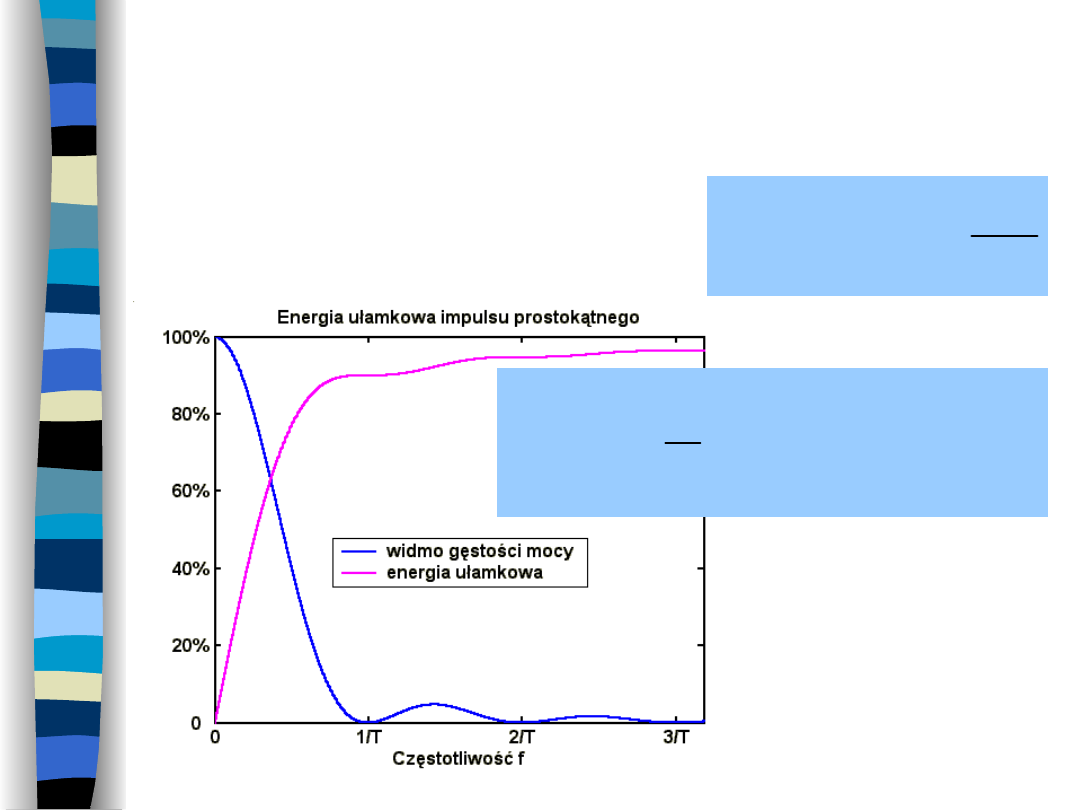
ENERGIA UŁAMKOWA
WIDMOWA GĘSTOŚĆ ENERGII
2
2
2
1
1
,
X
S
X
dv
v
X
E
E
E
E
E
dv
v
X
E
dv
v
X
E
E
u
o
2
o
2
1
0
,
1
,
0
Właściwości przekształcenia
Fouriera
„Teoria sygnałów” Zdzisław Papir
2
Sa
T
T
t
T
0
,
Sa
2
o
2
u
f
dv
v
f
E
fT
ENERGIA UŁAMKOWA

Podsumowanie
•
W większości przypadków transformaty Fouriera
wyznaczamy korzystając z udowodnionych właściwości
przekształcenia Fouriera oraz wyliczonych wcześniej
par transformat.
Nie korzystamy z definicji przekształcenia Fouriera.
•
Twierdzenie o splocie oraz twierdzenie Parsevala są
właściwościami przekształcenia Fouriera
o najbardziej doniosłym znaczeniu.
•
Splot jest wykorzystywany do opisu filtracji sygnałów.
•
Twierdzenie Parsevala jest punktem wyjściowym dla
analizy spektralnej procesów losowych.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
Wyszukiwarka
Podobne podstrony:
5 Przekształcenie Fouriera
Przekształcenie Fouriera narzedzie nie tylko analizy przebiegów schodkowych
Dyskretne przekształcenie Fouriera
Dyskretne Przekształcenie Fouriera, WAT, SEMESTR V, Cfrowe przetwarzanie sygnałów, Cps, od borysa, C
Przekształcenie Fouriera obrazów
5 Przekształcenie Fouriera
Dyskretne przekształcenie Fouriera, cz 1
Dyskretne przekształcenie Fouriera, cz 4
Dyskretne przekształcenie Fouriera, cz 2
Dyskretne przekształcenie Fouriera, cz 3
Dyskretne przeksztaĹ'cenie Fouriera
Dyskretne przeksztaĹ'cenie Fouriera
Zarządzanie w Administracji Publicznej Rzeszów właściwe
Przeksztalcanie wzorow
Szeregi Fouriera
więcej podobnych podstron