Mechanika

Mechanika

Ogólna

Ogólna

Statyka IV

Statyka IV

Adam F.

Adam F.

Bolt

Bolt

Wykład IV

Wykład IV



Redukcja płaskiego uładu sił



Redukcja płaskiego uładu sił do jednej
siły wypadkowej



Równowaga dowolnego płaskiego układu
sił



Równowaga płaskich układu sił
równoległych



Równowaga układów złożonych z ciał
sztywnych



Zaganienia statycznie wyznaczalne i
niewyznaczalne

Płaskie układy sił bez tarcia

Płaskie układy sił bez tarcia

Redukcja płaskiego układu
sił

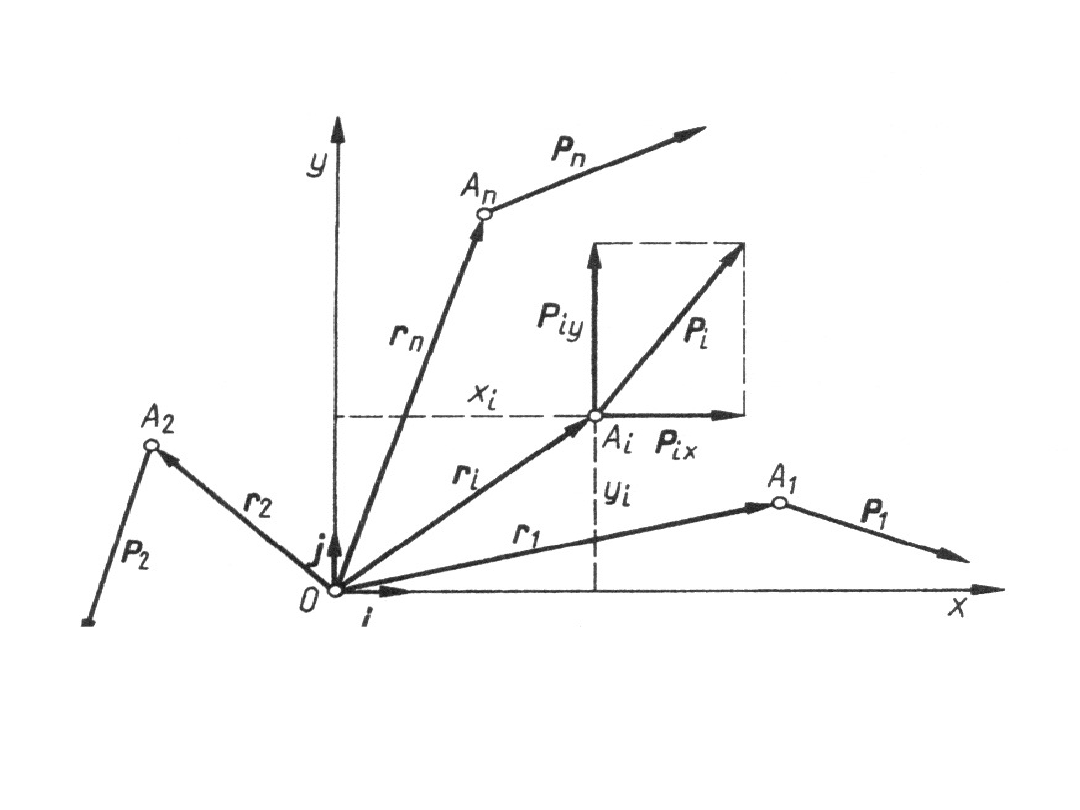
Płaski układ sił - siły leżą w jednej
płaszczyźnie

Przesuwając równolegle wszystkie siły danego

Przesuwając równolegle wszystkie siły danego

układu do jednego punktu

układu do jednego punktu

O

O

otrzymamy jedną siłę

otrzymamy jedną siłę

R

R

równą ich sumie geometrycznej i jedną parę sił o

równą ich sumie geometrycznej i jedną parę sił o

momencie

momencie

M

M

o

o

równym sumie momentów tych par sił

równym sumie momentów tych par sił

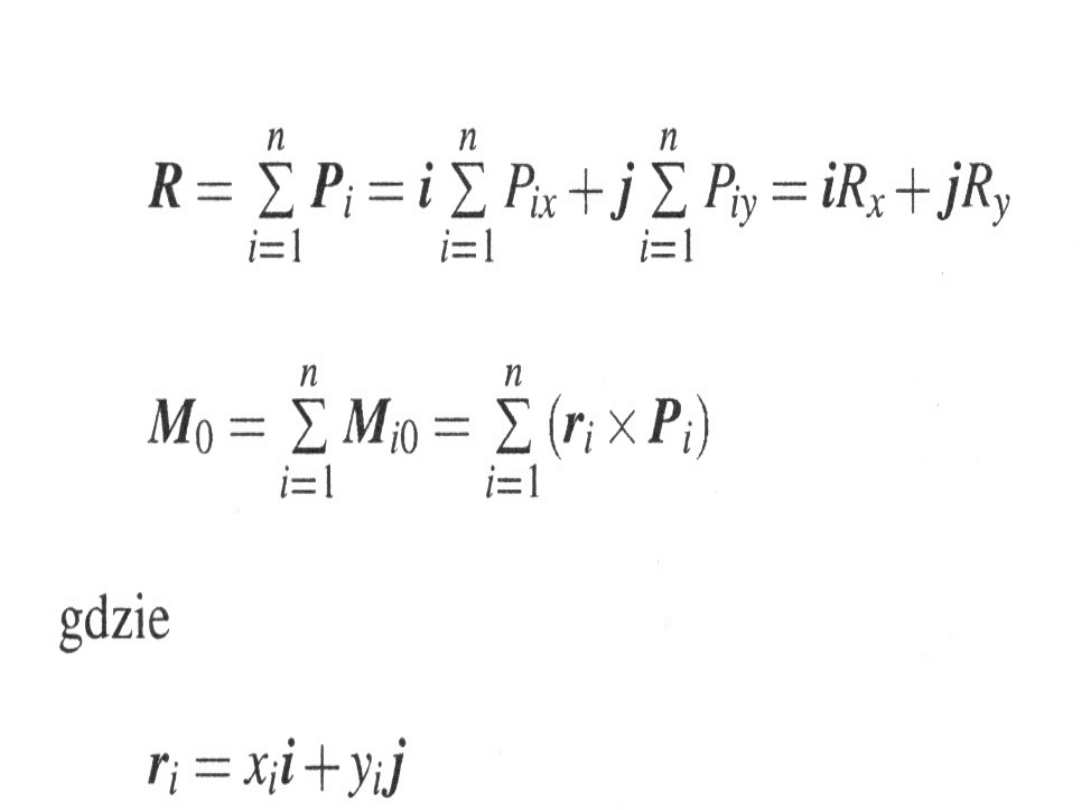
Redukcja płaskiego uładu sił

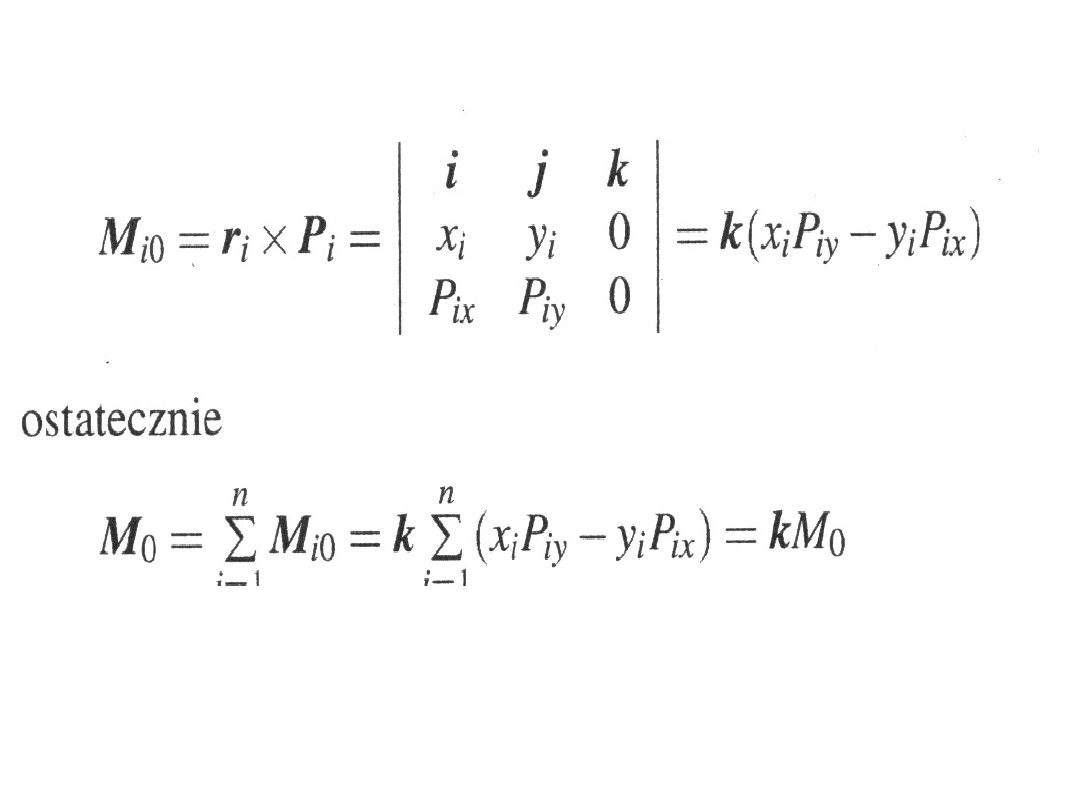
Redukcja płaskiego uładu sił - cd.

Wzór ten pozwala stwierdzić, że wektor momentu

Wzór ten pozwala stwierdzić, że wektor momentu

głównego

głównego

M

M

0

0

jest wektorem o jednej składowej w

jest wektorem o jednej składowej w

kierunku wersora

kierunku wersora

k,

k,

czyli jest prostopadły do

czyli jest prostopadły do

płaszczyzny

płaszczyzny

Oxy

Oxy

i

i

wektora głównego

wektora głównego

R

R

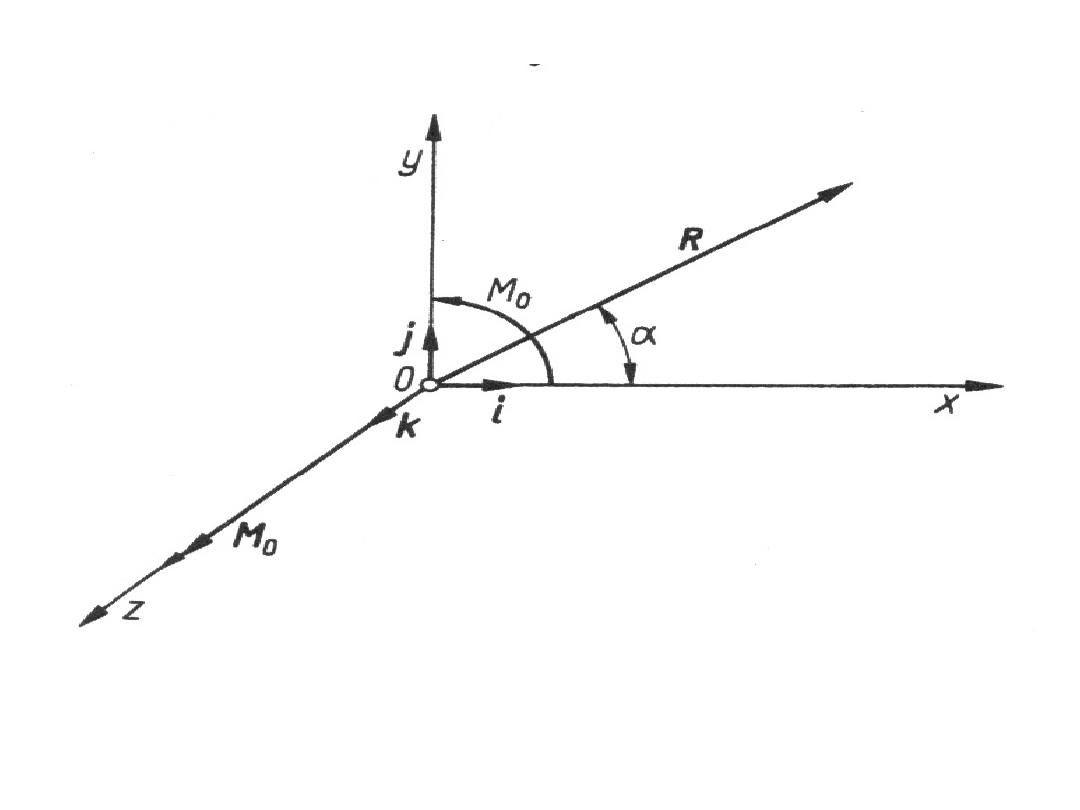
Wektor główny

Wektor główny

R

R

i wektor momentu

i wektor momentu

głównego

głównego

M

M

0

0

Siłę R nazywamy wektorem głównym, a
moment M

0

momentem głównym płaskiego

układu sił względem środka redukcji 0

Wyznaczenie wartośći wektora

Wyznaczenie wartośći wektora

głównego

głównego

R

R

oraz kąta

oraz kąta

a

a

jaki wektor

jaki wektor

tworzy z osią

tworzy z osią

Ox

Ox

Redukcja płaskiego układu
sił do jednej siły
wypadkowej

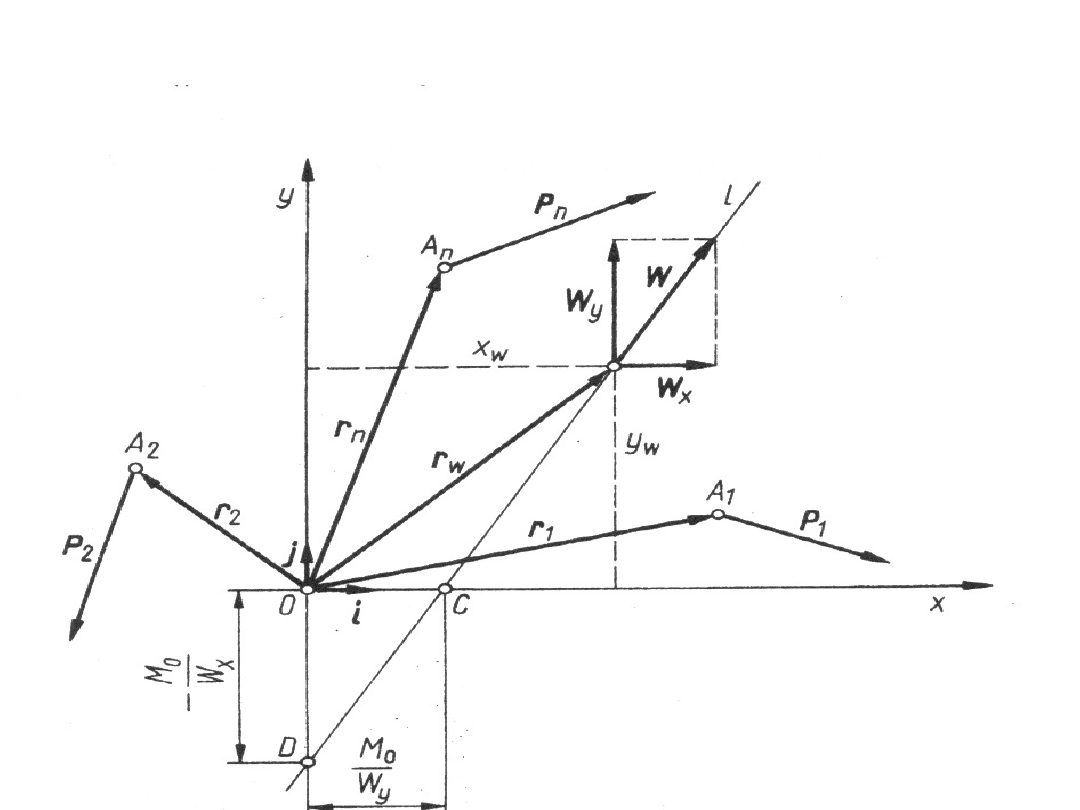
Wypadkowa płaskiego układu sił

Mo

Mo

Redukcja płaskiego układu sił do
jednej siły wypadkowej

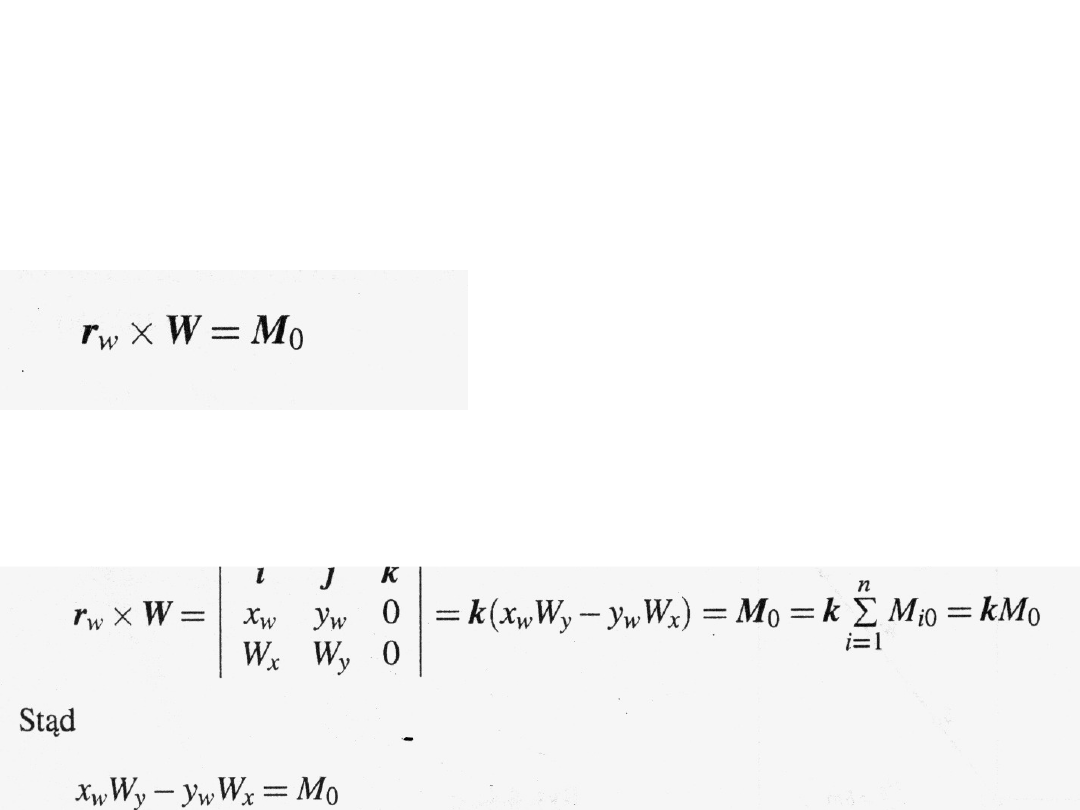
Równanie linii działania wypadkowej

• wyznacza się z warunku, że moment wypadkowej
względem początku układu równa się momentowi
głównemu M

o

równemu sumie momentów danych sił

względem początku układu współrzędnych

Po rozpisaniu tego równania z uwzględnieniem
składowych wektora r

w

=i x

w

+ jy

w

i siły wypadkowej W =

iW

x

+jW

y

otrzymamy:

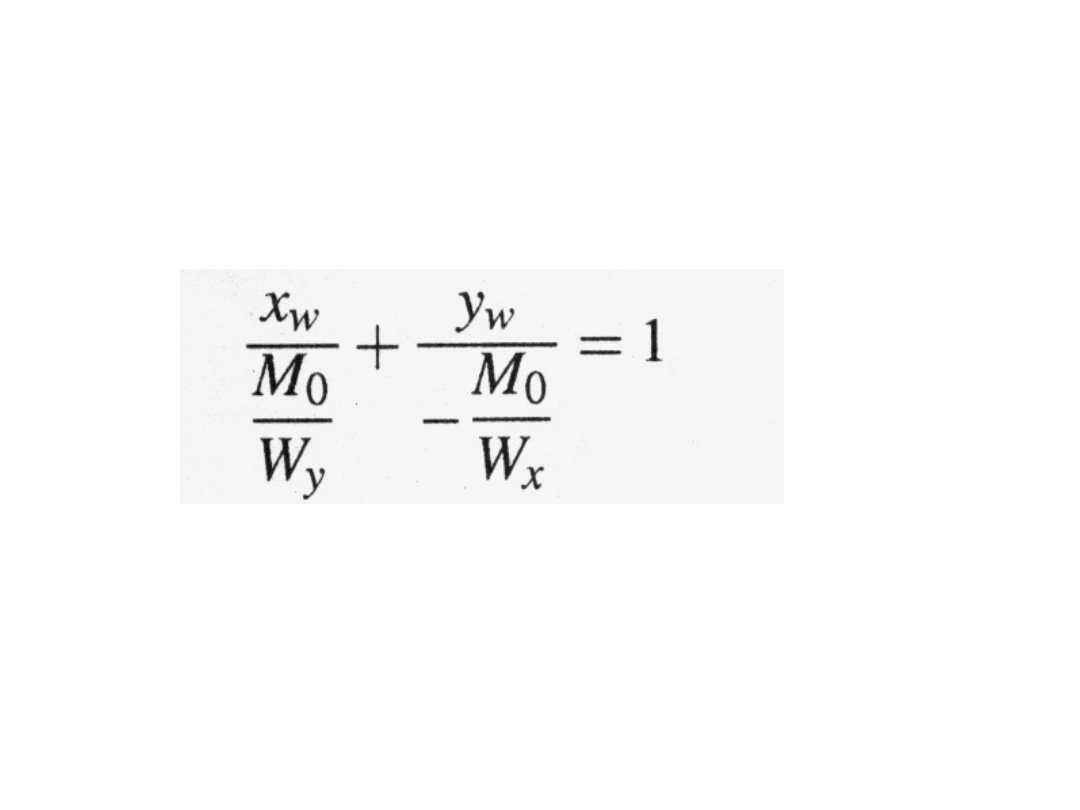
Po przekształceniu otrzymamy postać

odcinkową linii działania wypadkowej

Gdzie: wyrażenia w mianownikach M

o

/W

y

,

—M

o

/W

x

odpowiadają odcinkom OC i OD,

jakie linia działania wypadkowej odcina na
osiach x i y

R = O i M

0

= 0— układ jest w

równowadze.

W układzie płaskim mogą zachodzić
cztery przypadki:





0

0

0





M

,

R

1
)

— układ sprowadza się do wypadkowej o
linii działania wg powyższego wzoru

0

0

0



 M

,

R

2
)

— układ sprowadza się do wypadkowej
przechodzącej przez środek redukcji 0,

3)

0

0

0



 M

,

R

układ sprowadza się do pary sił leżących w
płaszczyźnie Oxy,

4)

Równowaga dowolnego
płaskiego układu sił

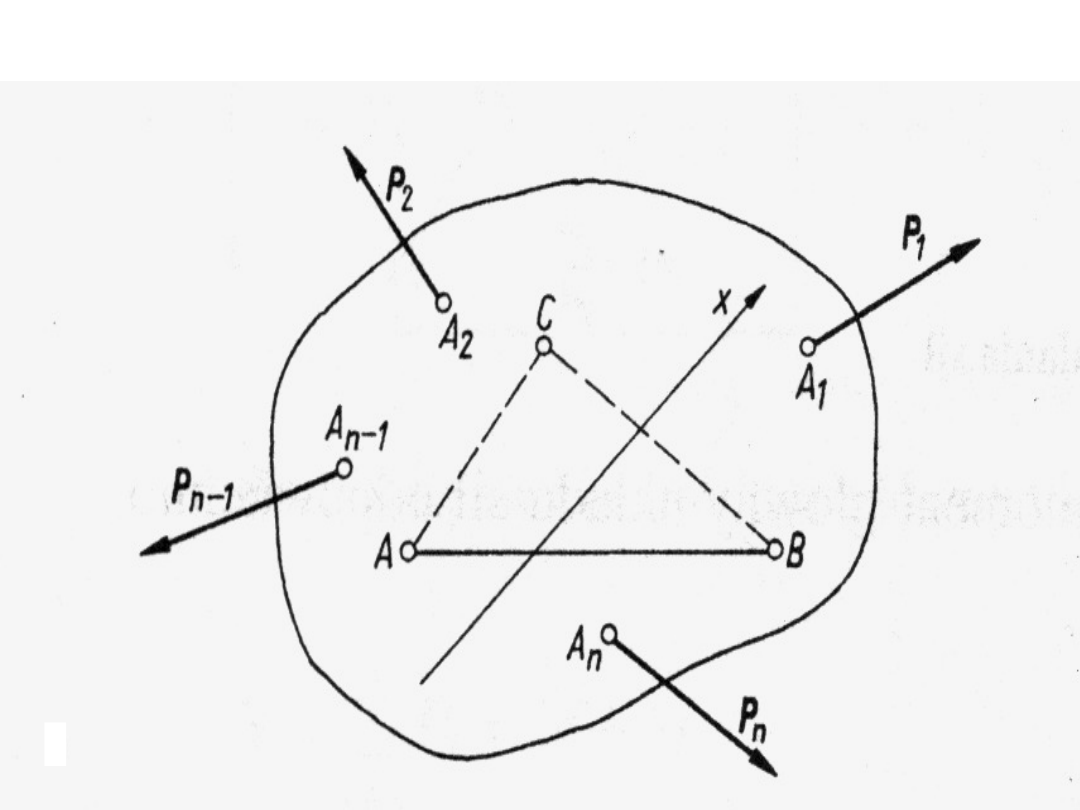
Równowaga płaskiego dowolnego
układu sił

Równowaga dowolnego płaskiego
układu sił

Warunki równowagi dowolnego płaskiego
układu sił otrzymuje się, przyrównując do
zera wektor główny układu R i moment
główny M względem środka redukcji O
R = 0,

M

0

= 0

Dwa równania wektorowe (można zastąpić
trzema równaniami skalarnymi:

Należy dodać, że punkt 0, względem
którego oblicza się sumę momentów danych
sił, może być obrany zupełnie dowolnie i nie
musi pokrywać się z początkiem przyjętego
układu współrzędnych.

Równowaga dowolnego płaskiego
układu sił

Płaski dowolny układ sił znajduje się w
równowadze, jeśli sumy rzutów
wszystkich sił na osie układu są równe
zeru i moment wszystkich sił
względem dowolnego punktu
płaszczyzny działania sił jest równy
zeru.

Pierwsze dwa równania nazywamy:
- równaniami rzutów sił,
a ostatnie
- równaniem momentów.

Równania te nie stanowią jedynej postaci
równań równowagi.

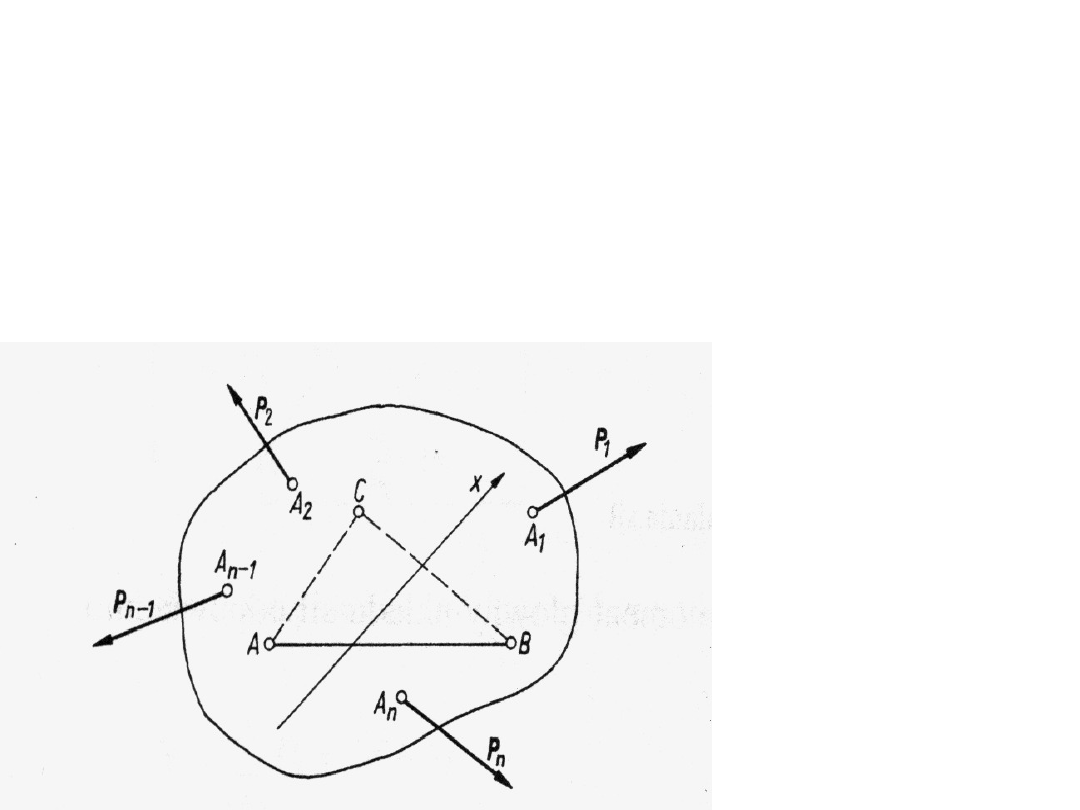
Inne sposoby układania równań
równowagi.

Wykażemy, że sumy momentów względem
dowolnych dwóch punktów A i B są równe
zeru oraz suma rzutów sił na dowolną oś x,
nieprostopadłą do odcinka AB łączącego
dwa punkty, jest także równa zeru (rys.)

Równowaga
płaskiego
dowolnego
układu sił

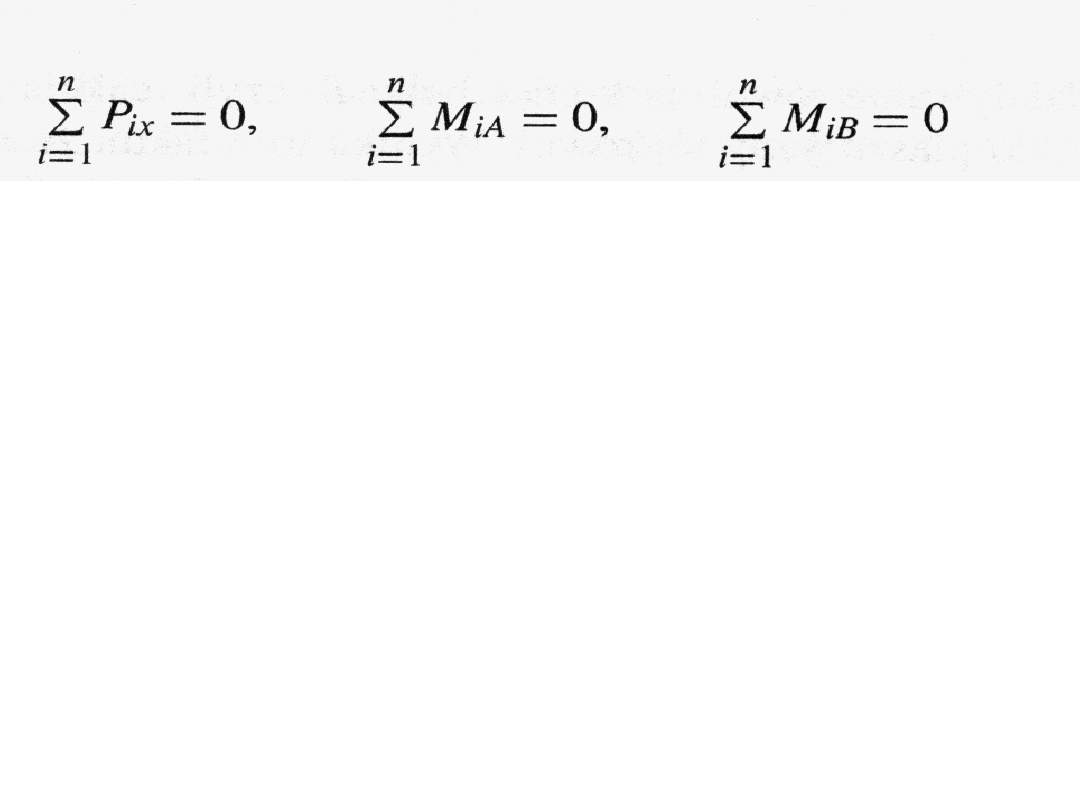
Pierwsze równanie momentów oznacza, że
układ jest w równowadze lub ma
wypadkową przechodzącą przez punkt A.

Jeżeli ponadto jest spełnione drugie
równanie

momentów, to układ sił jest

w równowadze lub

ma wypadkową

działającą wzdłuż odcinka AB.

Natomiast, jeżeli jeszcze jest spełnione
równanie rzutów sił, to układ sił jest w
równowadze.

Gdyby istniała wypadkowa, działająca
wzdłuż odcinka AB, wtedy jej rzut na oś x,
nieprostopadły do AB, nie byłby równy
zeru.

Jeżeli moment układu sił względem
dwóch punktów jest równy zeru oraz
rzut sił na oś nieprostopadłą do
odcinka łączącego te punkty jest
równy zeru, to płaski układ sił jest w
równowadze.

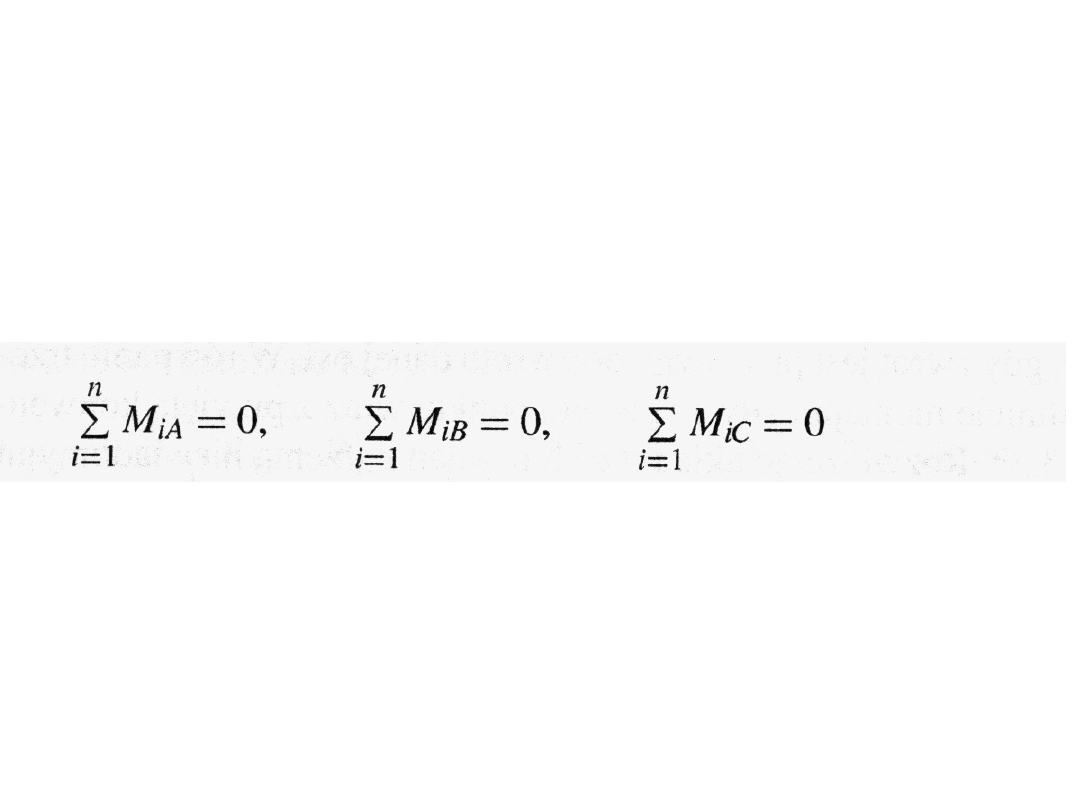
otrzymamy, pisząc równania momentów
względem trzech punktów A, B, C, nie
leżących na jednej prostej

Trzeci sposób układania równań równowagi
dowolnego płaskiego układu sił.

Prowadząc rozumowanie tak, jak dla równań
drugiego przypadku można stwierdzić, że i
te równania stanowią konieczny i
wystarczający warunek równowagi
dowolnego płaskiego układu sił, pod
warunkiem, że punkty A, B i C nie leżą na
jednej prostej.

Trzeci sposób układania równań równowagi
dowolnego płaskiego układu sił.

Gdyby punkty te leżały na jednej prostej,
mogłaby wzdłuż niej działać wy padkowa
układu sił (układ sił nie znajdowałby się w
równowadze, mimo spełnienia równań
momentów względem trzech punktów).

Jeżeli moment układu sił względem
trzech punktów nie leżących na
jednej prostej jest równy zeru, to
płaski układ sił jest w równowadze.

Równowaga płaskiego
układu sił równoległych

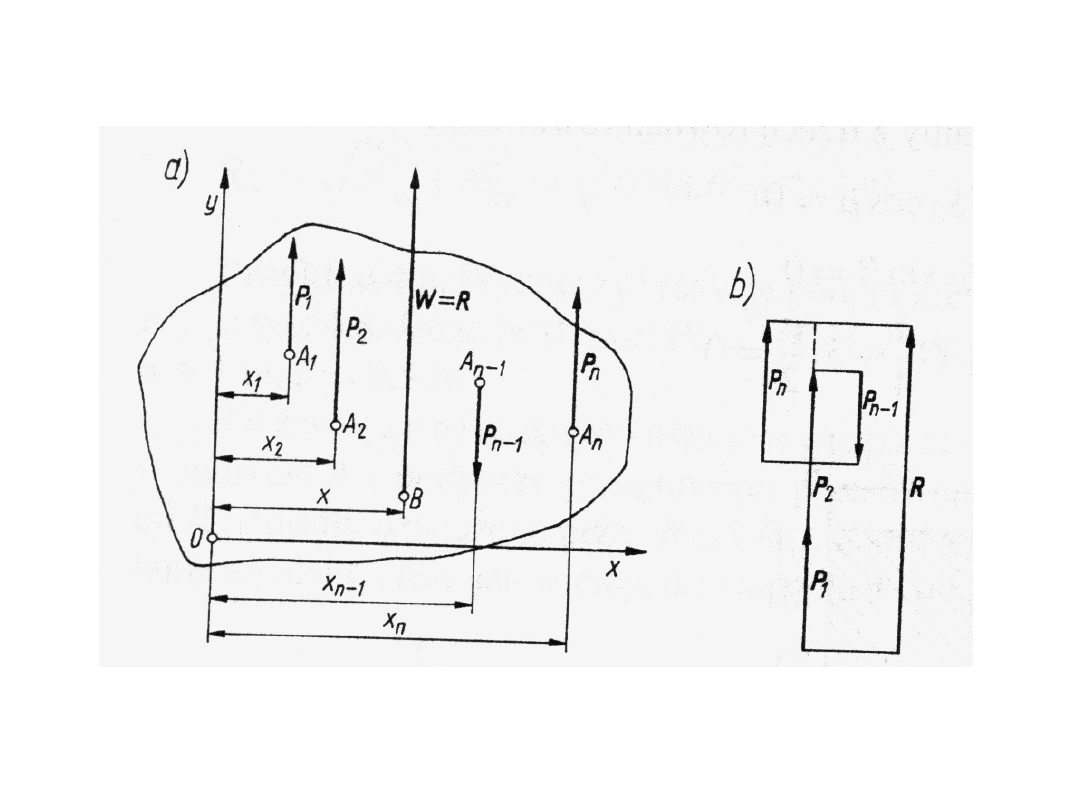
Płaski układ sił równoległych

Plaski układ sił równoległych( rys a) jest szczególnym
przypadkiem dowolnego płaskiego układu sił. Wielobok sił
(rys. b) staje się odcinkiem prostej.

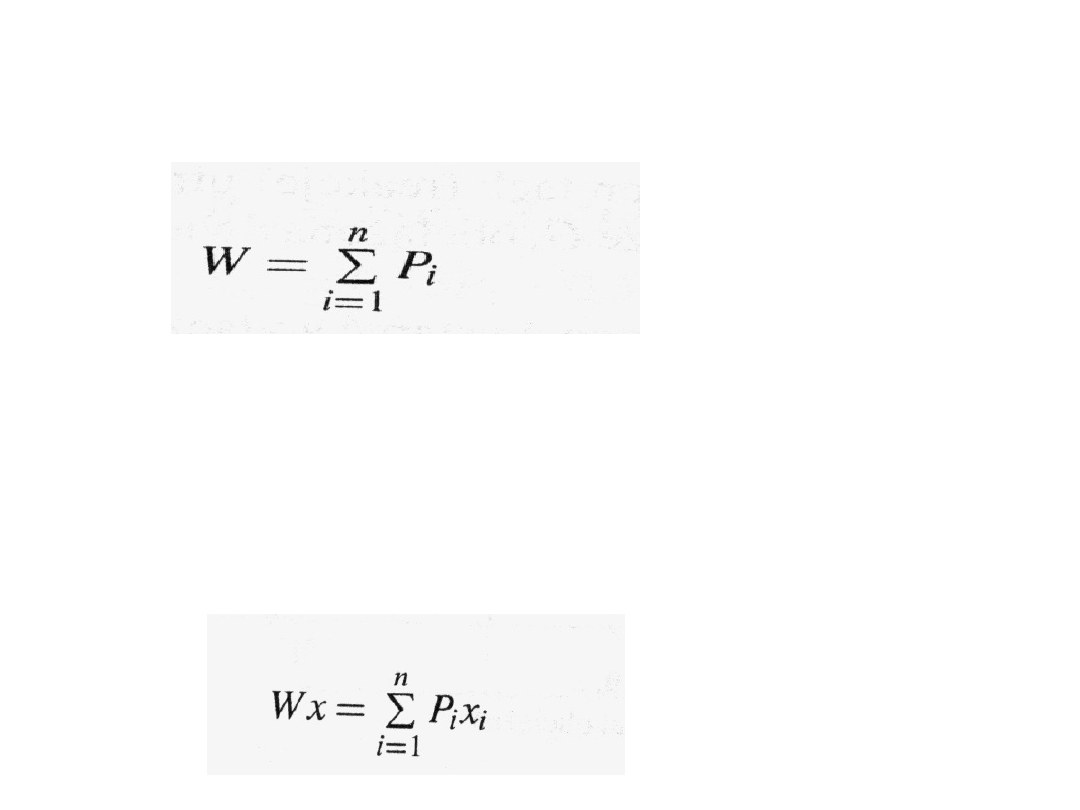
Wartość wypadkowej jest równa sumie wartości sił
P

1

, P

2

... P

n

Równowaga płaskiego układu sił
równoległych

Gdy siły są skierowane zgodnie z osią Oy, Wartości
Pi > 0

Gdy siły są skierowane przeciwnie osią Oy,
Wartości Pi < 0

Na podstawie twierdzenia, że moment siły wypadkowej jest
równy sumie momentów sił ddających tę wypadkową,
otrzymamy:

Odległość x linii działania wypadkowej od początku
układu współrzędnych O

Równowaga płaskiego układu sił
równoległych

Przyjmując osie układu jak na rys a, stwierdzamy że pierwsze
z równań równowagi jest spełnione tożsamościowo i powstają
dwa równania równowagi

Dla płaskiego równoległego układu sił mamy tylko dwa równania
równowagi

Pierwsze równanie rzutów sił na oś równoległą do linii
działania sił możemy zastąpić równaniem momentów.

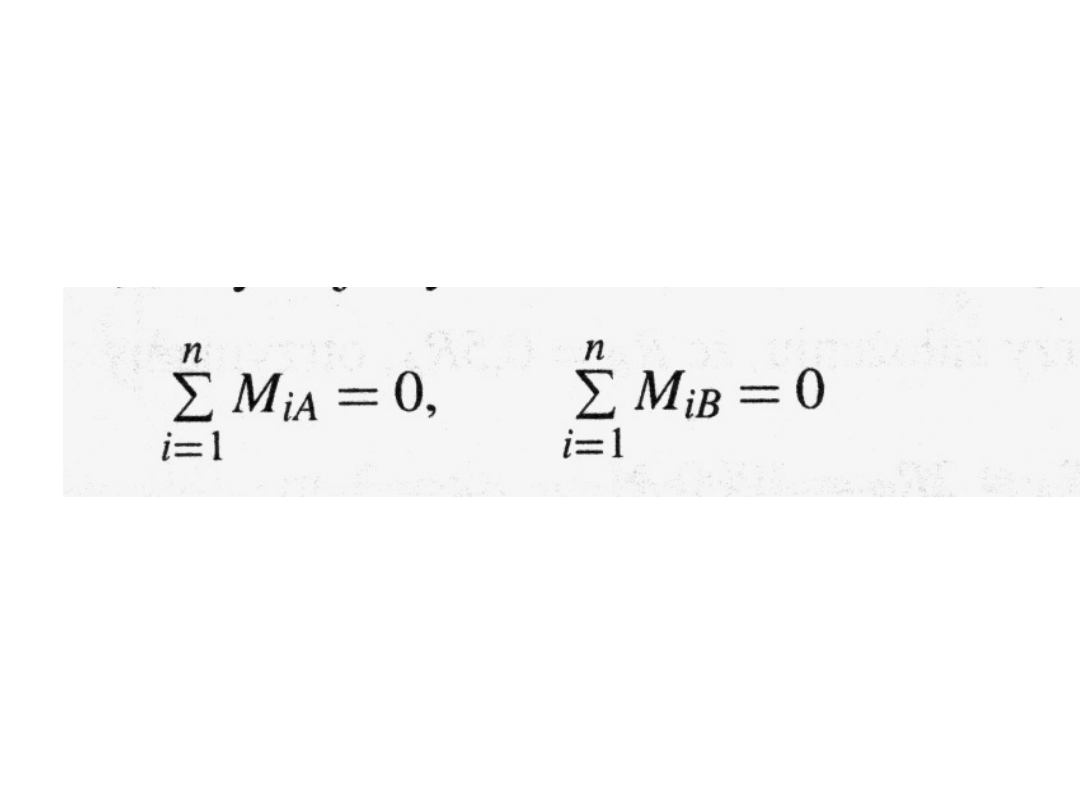
Przyjmując dowolne dwa punkty A i B, nie leżące na

Przyjmując dowolne dwa punkty A i B, nie leżące na

jednej prostej równoległej do linii działąnia układu sił,

jednej prostej równoległej do linii działąnia układu sił,

otrzymujemy dwa równania równowagi wyrażone przez

otrzymujemy dwa równania równowagi wyrażone przez

momenty

momenty

Równowaga układów
złożonych z ciał sztywnych

Równowaga układów złożonych z ciał
sztywnych

Zagadnienie równowagi dwóch lub
większej liczby ciał sztywnych,
stykających się ze sobą lub
połączonych odpo wiednimi więzami
(przegubami, prętami, cięgnami itp.).

Przykłady układów ciał sztywnych,
spotykanych w konstrukcjach
inżynierskich:

•belki przegubowe,

•ramy trójprzegubowe i bardziej
złożone konstrukcje.

Typowy tok postępo wania przy
wyznaczaniu reakcji podpór i sił
wzajemnego oddziaływania między
częściami układu złożonego

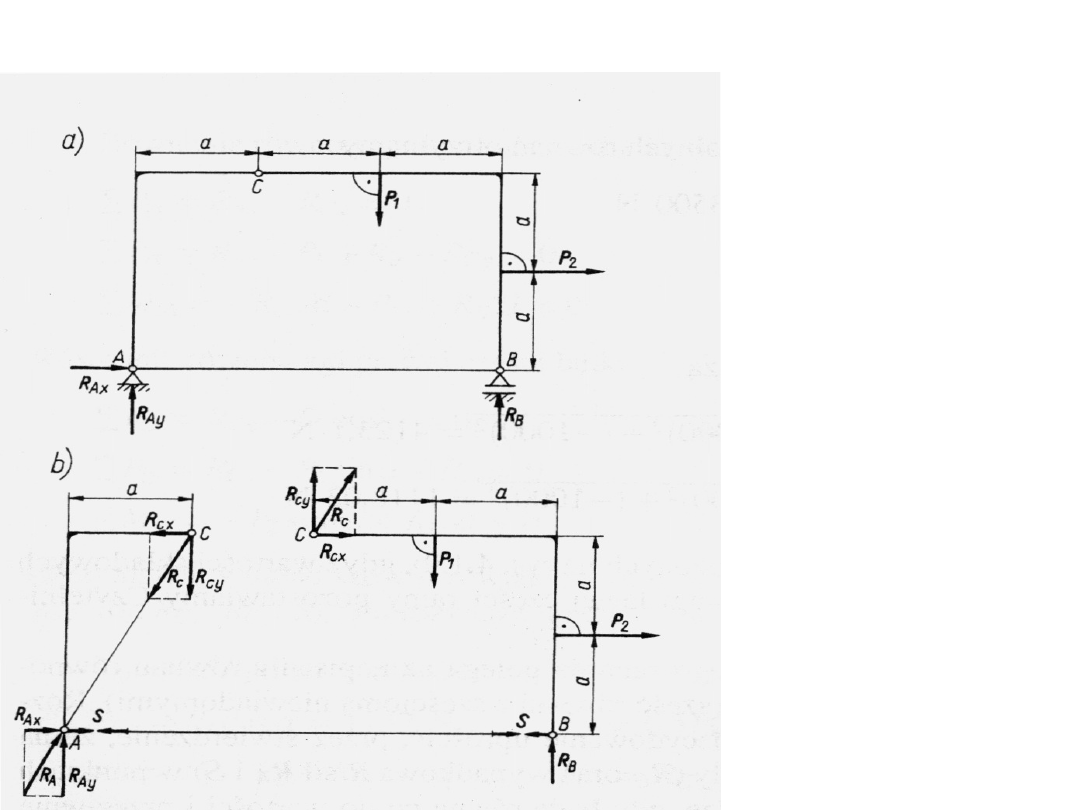
Przykład - rama trójprzegubowa

Ciężar własny
konstrukcji
oraz tarcie w
przegubach
można pominąć

Dane
liczbowe:

P

1

= 1 000 N

P

2

= 4 000 N

a=1 m

Zadanie:
Wyznaczyć reakcje podpór A i B, reakcje
wzajemnego oddziaływaniaobydwu części
układu w przegubie C i siłę rozciągającą lub
ściskającą pręt AB

Rozwiązaniee:

Rozważamy równowagę całej ramy ACB.

Działaja na nią dwie siły zewnętrzne P

1

i P

2

oraz reakcje podporze przegubowej stałej A
i podporze przesuwnej B.
Ponieważ kierunek reakcji R

A

w punkcie a

jest nieznany, rozkładamy ją na dwie
składowe R

Ax i

R

Ay

Trzy niewiadome wyznaczamy z trzech
równań równowagi całej ramy

W celu wyznaczenia reakcji wzajemnego
oddziaływania obydwu części R

C

i siły S w

pręcie AB możemy rozważyć równowagę lewej
lub prawej części tej samej ramy

Z równowagi prawej części ramy otrzymamy trzy
równania

A ich zwroty są przeciwne do założonych na rysunku bo ich
wartości są ujemne

Zagadnienia statycznie wyznaczalne i
niewyznaczalne

Zagadnienia statycznie wyznaczalne

m

m

m

m

•W przy padku układu statycznie
wyznaczalnego liczba reakcji zastępujących
działanie wię zów (równa liczbie więzów
potrzebnych do unieruchomienia danego
układu) jest równa liczbie równań równowagi.

•Jeżeli więzów jest za mało,
to dany układ mechaniczny jest niesztywny.

•Równowaga takiego układu może być
zapewniona w przypadku spełnienia
dodatkowych warunków, które zapewniają
układowi od powiednią postać geometryczną.

Zagadnienia statycznie wyznaczalne

m

m

m

m

•Zagadnieniami statycznie wyznaczalnymi
nazywamy takie zagadnienia, które
dotyczą równowagi układu sił
działających w jednej płaszczyźnie na
jedno lub kilka ciał sztywnych (układ
mechaniczny), w których istnieje
możliwość wyznaczenia niewiadomych sił.

• Niewiadome siły stanowią zwykle
reakcje podpór albo siły wza jemnego
oddziaływania wewnątrz rozważanego
układu mechanicznego.

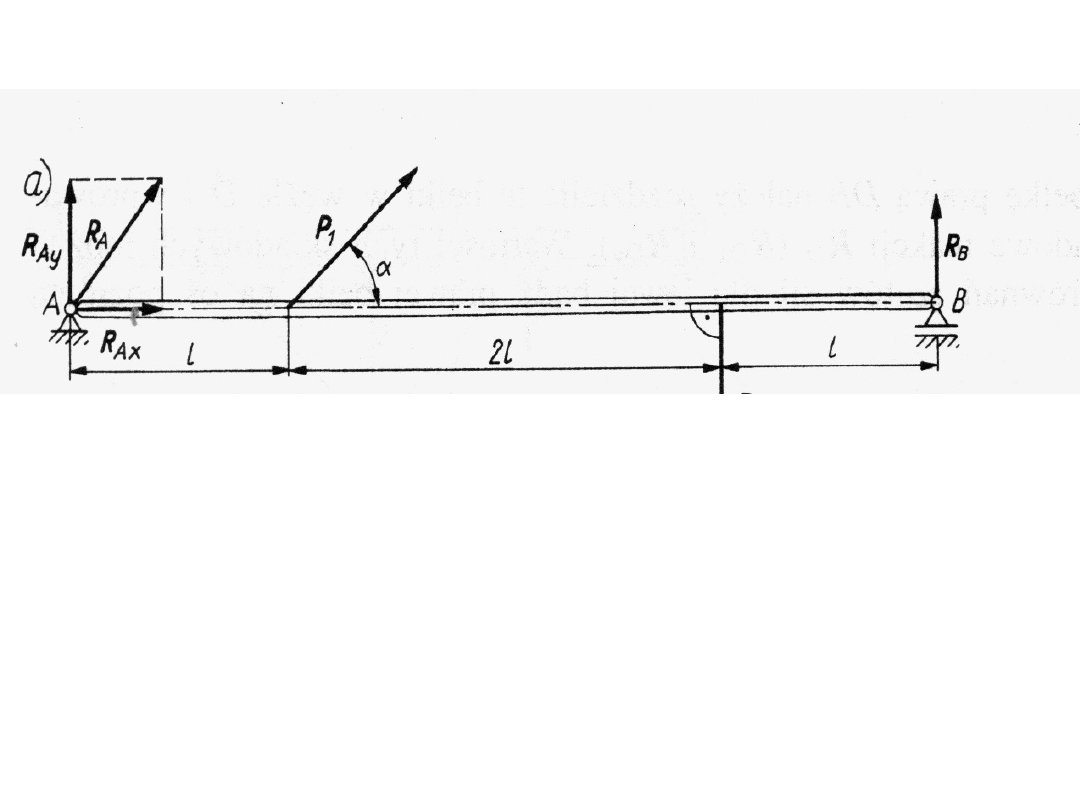
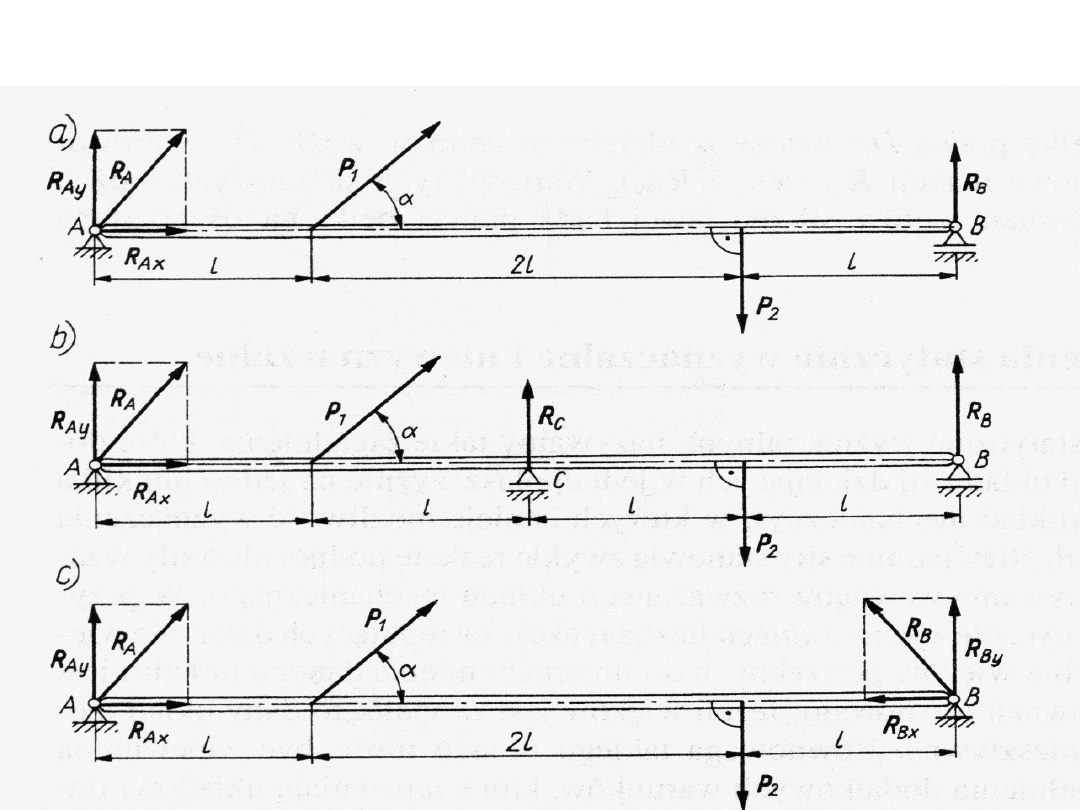
Przykłady

a)

belka statycznie wyznaczalna, nieznane są tylko

reakcje podpór.

•na podporze przegubowej przesuwnej B znany
jest kierunek reakcji R

B

,

•należy wyznaczyć tylko jej wartość R

B

.

•kierunek reakcji RA w podporze przegubowej
stałej A jest nieznany, dlatego trzeba ją rozłożyć
na dwie składowe R

Ax

i R

Ay

Łącznie mamy trzy niewiadome i taką samą
liczbę równań do ich wyznaczenia.

Zagadnienia statycznie
niewyznaczalne.

•gdy więzów jest więcej niż potrzeba do
unieruchomienia danego układu
mechanicznego, dany układ jest
przesztywniony,

•wówczas niewiadomych reakcji jest
więcej niż mamy równań równowagi i
dlatego niektórych reakcji nie można
wyznaczyć metodami stosowanymi w
statyce,

•jeżeli liczba zbytecznych więzów
wynosi n, to układ jest n-krotnie
statycznie niewyznaczalny.

Zagadnienia statycznie
niewyznaczalne

Statyczna niewyznaczalność może być:

•

zewnętrzna (gdy niewyznaczalnymi są

reakcje podpór nie należących do danego
układu)

•wewnętrzna (gdy nie można wyznaczyć
sił stykowych między elementami układu
lub sił wewnętrznych przenoszonych
przez jakiekolwiek elementy tego układu).

Przykłady

Przykłady

b) w przypadku dodatkowego podparcia
omawianej belki w punkcie C na pod porze
przegubowej przesuwnej

lub

c) oparciu jej w punkcie B na podpo rze
przegubowej stałej liczba niewiadomych
wzrośnie do czterech.

Belki jednokrotnie stycznie
niewyznaczalne

Belki jednokrotnie stycznie niewyznaczalne

Ponieważ liczba równań równowagi

pozostaje nie zmieniona (trzy równania),
zadań tych nie można już rozwiązać,
posługując się jedynie równaniami
wyprowadzonymi dla ciała sztywnego.

Aby określić reakcje w podporach belek
pokazanych na rys. b i c, należy rozważyć
ich odkształcenia pod wpływem sił na nie
działajacych.

Zadaniami takimi zajmuje się wytrzymałość
materiałów

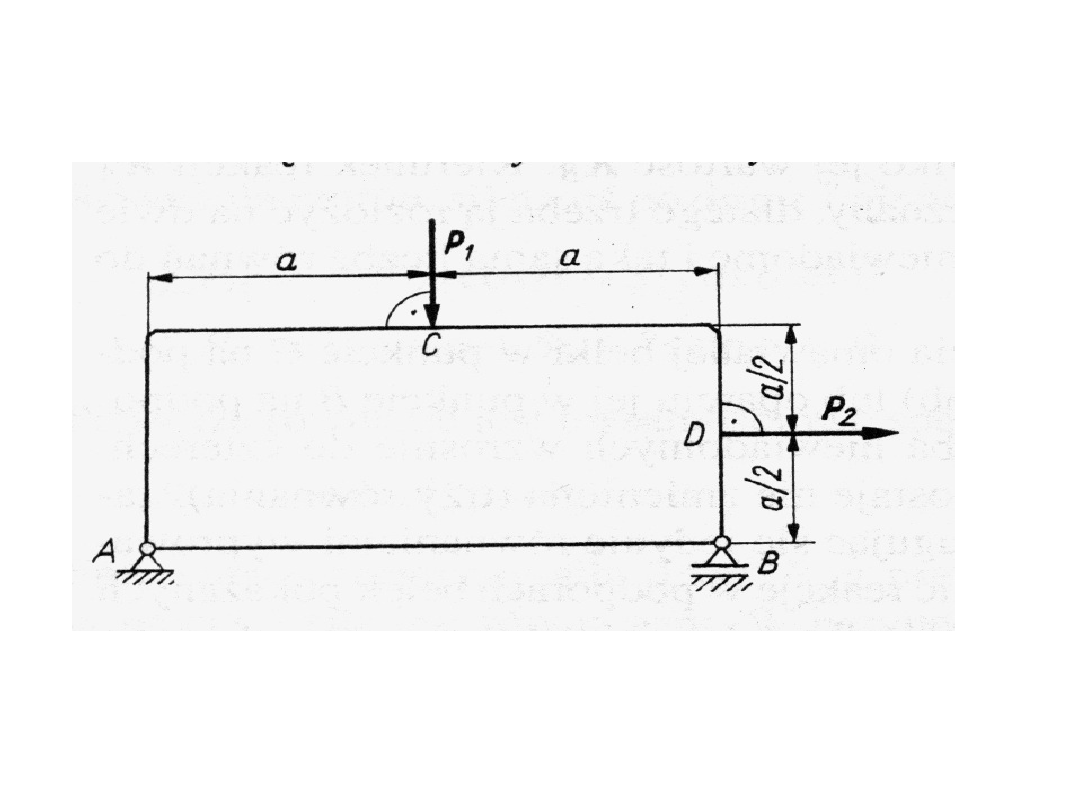
Przykład układu jednokrotnie
wewnętrznie statycznie
niewyznaczalnego

Przesztywnieniem jest pręt AB, albowiem po
usunięciu jego rama jest sztywna i ma zapewnioną
równowagę

Dziekuje:D