STATYSTYKA

Wnioskowanie statystyczne to proces myślowy polegający na formułowaniu sądów o całości przy dysponowaniu o niej ograniczoną liczbą informacji.

Zmienna losowa skokowa i jej rozkład

Zmienną losową X jest wielkość, która przy zajściu każdego zdarzenia losowego ω przyjmuje konkretną wartość
, co można zapisać w sposób następujący:

Innymi słowy zmienna losowa X jest liczbową prezentacją wyniku doświadczenia losowego, a więc jej wartość zależna jest od przypadku.

Jeśli doświadczenie polega na kontroli jakości 20 komputerów wyprodukowanych przez producenta tych wyrobów, to zmienną losową X będzie liczba wadliwych komputerów, która może przyjąć wartości: od 0 do 20.

Jeśli poszczególnym wartościom
przyporządkujemy prawdopodobieństwa realizacji tej zmiennej losowej oznaczonej przez
, wówczas otrzymamy rozkład prawdopodobieństwa zmiennej losowej skokowej, przy czym:

Znać rozkład zmiennej losowej skokowej X to znać realizacje tej zmiennej, czyli
, oraz odpowiadające im prawdopodobieństwa
.

Rozkład zmiennej losowej skokowej można przedstawić za pomocą funkcji prawdopodobieństwa zmiennej losowej skokowej lub tablicy.

Przykładem zmiennej losowej skokowej jest wielkość popytu na określone dobro. Popyt zależy bowiem od wielu czynników, takich jak: ceny dobra, ceny innych dóbr (substytucyjnych), dochód do dyspozycji gospodarstwa domowego zgłaszającego popyt na to dobro itp. Jest zatem, przynajmniej częściowo, zależny od przypadku.

Przykład 1

Rozkład prawdopodobieństwa liczby oczek przy rzucie kostką do gry.

	1	2	3	4	5	6
lub

To jest rozkład jednostajny (prawdopodobieństwa są równe).

Wartość oczekiwana (nadzieja matematyczna) zmiennej losowej skokowej

Wartość oczekiwana jest zatem średnią arytmetyczną ważoną realizacji
zmiennej losowej X, a wagami są odpowiadające im prawdopodobieństwa
.

Wariancja zmiennej losowej skokowej

Odchylenie standardowej zmiennej losowej skokowej

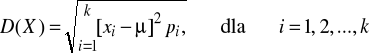
Przykład 2

Rozkład zmiennej losowej

Nieobecność studentów na zajęciach ze statystyki. Grupa liczyła 10 osób

Liczba nieobecnych osób	Prawdopodobieństwo lub	lub
1	2	3	4	5	6
0 1 2 3 4 5 6 7 8 9 10	0,1 0,2 0,4 0,1 0,1 0,1 0,0 0,0 0,0 0,0 0,0	0,0 0,2 0,3 0,3 0,4 0,5 0,0 0,0 0,0 0,0 0,0	-2,2 -1,2 -0,2 0,8 1,8 2,8 3,8 4,8 5,8 6,8 7,8	4,84 1,44 0,04 0,64 3,24 7,84 . . . . .	0,484 0,288 0,016 0,064 0,324 0,784 0,0 0,0 0,0 0,0 0,0
X	1,0	2,2	X	X	1,960

Obliczenia:

Wartość oczekiwana:

Wariancja dla zmiennych losowych skokowych:

Odchylenie standardowe: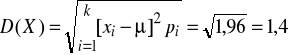

Dystrybuanta zmiennej losowej
nazywa się prawdopodobieństwem tego, że zmienna losowa przyjmie wartości mniejsze lub równe określonej wartości
(czyli jest równa sumie prawdopodobieństw realizacji wartości zmiennej, mniejszych bądź równych
).

Jest to funkcja określana wzorem:

Dystrybuanta zmiennej losowej skokowej (dyskretnej)

W naszym przykładzie:

Odp.: Prawdopodobieństwo, że na zajęciach nie będą obecne najwyżej 2 osoby wynosi 0,7.

Ważniejsze teoretyczne rozkłady zmiennej losowej skokowej

Zmienna losowa X ma rozkład zero-jedynkowy, jeżeli jej funkcja prawdopodobieństwa (rozkład) jest następująca:

Wartość oczekiwana i wariancja w tym rozkładzie wynoszą:

Przykład 3

Klientami sklepu spożywczego są kobiety i mężczyźni. Na podstawie wcześniejszych badań stwierdzono, że prawdopodobieństwo zakupu żywności przez kobietę w tym sklepie wynosi 0,6.

1. Co jest zmienną losową w powyższym przykładzie?

2. Wyznacz wartość oczekiwaną i wariancję badanej zmiennej losowej.

Odpowiedzi:

1. Zmienną losową jest płeć klienta. Przyjmuje ona wartość 1 w powyższym przypadku kobiety (sukces) oraz 0, gdy do sklepu wchodzi mężczyzna. Jest to przykład zmiennej zero-jedynkowej.

2. 
   

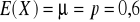
oraz

Zmienna losowa X ma rozkład dwumianowy (Bernoulliego)
, jeśli jej funkcja prawdopodobieństwa określona jest wzorem:

,

gdzie:

- liczba wariantów zmiennej losowej,

- liczba realizacji zdarzenia
,

- prawdopodobieństwo realizacji zdarzeń
w każdej z niezależnych realizacji.

Wartość oczekiwana w tym rozkładzie wynosi:

a wariancja:

Schemat Bernoulliego:

Z takim rozkładem mamy do czynienia w przypadku wyznaczania prawdopodobieństwa kolejnych wartości
w
doświadczeniach. Aby rozkład dwumianowy mógł znaleźć zastosowanie, muszą być spełnione następujące warunki:

• przeprowadza się
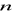
  jednakowych doświadczeń,

• dla każdego doświadczenia możliwe są dwa wyniki: jeden - zwany sukcesem, a drugi porażką,

• prawdopodobieństwo sukcesu
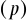
  czy porażki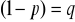
  w kolejnych doświadczeniach jest stałe,

• doświadczenia są od siebie niezależne.

Przykład 4

Sprzedawca pewnego dobra trwałego użytku kontaktuje się z 8 potencjalnymi klientami dziennie. Z wcześniejszych doświadczeń wiadomo, że prawdopodobieństwo zakupu tego dobra przez potencjalnego klienta wynosi 0,10.

1. Jakie jest prawdopodobieństwo tego, że sprzedawca przeprowadzi dokładniej 2 transakcje dziennie

2. Jakie jest prawdopodobieństwo tego, że sprzedawca przeprowadzi co najmniej 2 transakcje dziennie

3. Jaki odsetek stanowić będą dni, w których sprzedawca nie dokona żadnej transakcji sprzedaży?

4. Jakiej średniej liczby sprzedanych dóbr trwałego użytku dziennie może się spodziewać sprzedawca?

Odpowiedzi:

1. Korzystając ze wzoru na prawdopodobieństwo w rozkładzie dwumianowym, otrzymujemy:

Zamiast przeprowadzania dość skomplikowanych obliczeń można również skorzystać z tablic rozkładu dwumianowego odczytując
dla
(por. tablica 1 na końcu książki).

Odp.: Prawdopodobieństwo, że sprzedawca przeprowadzi dokładnie 2 transakcje sprzedaży dziennie wynosi 0,1488.

b)

Zamiast przeprowadzania dość skomplikowanych obliczeń to samo można odczytać z tablic rozkładu dwumianowego:

czyli

Odp.: Prawdopodobieństwo, że sprzedawca przeprowadzi co najmniej 2 transakcje sprzedaży dziennie wynosi 0,19.

c)

Uwaga: przyjmuje się, że 0! = 1.

Odp.: 43% ogółu dni roboczych stanowią takie dni, kiedy nie zostanie dokonana żadna transakcja sprzedaży.

d)

Odp.: Sprzedawca może spodziewać się, że sprzeda dziennie 0,8 dóbr trwałego użytku.

Rozkład Poissona (rozkład rzadkich zdarzeń) dotyczy zmiennej losowej skokowej. Znajduje on zastosowanie w sytuacjach, gdy próba jest liczna
oraz gdy prawdopodobieństwo zajścia sukcesu jest małe (co najwyżej kilkuprocentowe). Jego przydatność jest duża, np. w ustalaniu prawdopodobieństwa wadliwości produkcji czy awaryjności maszyn.

Prawdopodobieństwo w rozkładzie Poissona

gdzie:

- średnia liczba zdarzeń,

Rozkładem Poissona można przybliżyć rozkład dwumianowy, gdy spełnione są następujące warunki:

• duża liczba doświadczeń
  

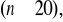
• stały iloczyn
  
  

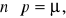
• prawdopodobieństwo
  

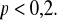
Przykład 5

Wadliwość produkcji pewnego przedsiębiorstwa wynosi 3%. Z gotowych wyrobów znajdujących się w magazynie sprzedano 40 sztuk.

1. Jakiej średniej liczby braków można się spodziewać w sprzedanej partii towarów?

2. Jakie jest prawdopodobieństwo, że dokładnie 5 sztuk wadliwych znajdzie się w sprzedanej partii towarów?

3. Jakie jest prawdopodobieństwo, że w sprzedanej partii towarów znajdą się więcej niż 3 braki?

4. Jakie jest prawdopodobieństwo, że w tej partii towarów znajdują się mniej niż 4 braki?

Odpowiedzi:

a)

b)
(por. tablicę prawdopodobieństwa w rozkładzie Poissona, czyli tablicę 2 na końcu książki, dla
).

Inne podejście opiera się na rachunku dystrybuant. Korzystamy z tablic dystrybuanty w tym rozkładzie (por. tablicę 3 na końcu książki).

c)

Wyznaczenie tego prawdopodobieństwa jest rachunkowo dość skomplikowane. Warto więc skorzystać z tablic dystrybuanty rozkładu Poissona.

lub z tablic prawdopodobieństwa w tym rozkładzie (por. tablicę 2 na końcu książki):

d)

Rozkład normalny i inne rozkłady zmiennej losowej ciągłej

Zmienna losowa ciągła jest to taka zmienna, która przyjmuje wszystkie wartości z pewnego określonego przedziału liczbowego.

Zmienną losową ciągłą jest czas pracy przeznaczony na wyprodukowanie sztuki wyrobu przez pracowników pewnej fabryki, waha się on np. w przedziale od 3 do 5 godzin. Może zatem przyjąć dowolne wartości z tego przedziału, np. 3, 1; 4,23 itp.

Rozkład normalny to najważniejszy rozkład zmiennej losowej ciągłej. Odgrywa on w zastosowaniach statystyki ogromną rolę.

Zmienna losowa standaryzowana

Przykład 6

Zbadano wzrost 100 wylosowanych do próby studentów jednej ze szkół wyższych w Polsce i stwierdzono, że średni wzrost wynosi 183 cm, a odchylenie standardowe wzrostu wynosi 7 cm. Znajdź prawdopodobieństwo, że losowo wybrany student:

1. Będzie niższy niż 169 cm,

2. Będzie miał wzrost z przedziału pomiędzy 176 a 190 cm,

3. Będzie wyższy niż 200,5cm.

Zakładamy, że rozkład wzrostu studentów jest rozkładem normalnym z wartością oczekiwaną
i odchyleniem standardowym
.

Należy znaleźć prawdopodobieństwo, że:

a)

(z tablicy na końcu książki)

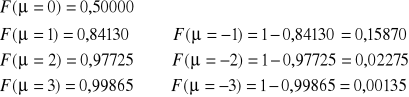
Odp.: Prawdopodobieństwo, że losowo wybrany student będzie niższy niż 169 cm wynosi 0,027.

b)

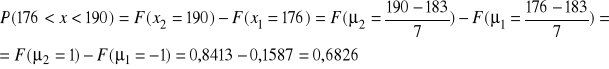
Odp.: Prawdopodobieństwo, że losowo wybrany student będzie miał wzrost pomiędzy 176 a 190 cm wynosi 0,6826.

c)

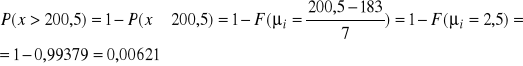
Odp.: Prawdopodobieństwo spotkania studentów niższych od 200,5 cm wynosi 0,00621.

Przykład 7

W pewnym teście psychologicznym przeprowadzonym na 50 wybranych uczniach szkoły podstawowej stwierdzono, że średnia liczba zapamiętanych przez dzieci elementów wyniosła 25 z odchyleniem standardowym równym 5. chcemy znaleźć prawdopodobieństwo, że losowo wybrany uczeń zapamięta:

1. mniej niż 15 z zadanych elementów,

2. od 25 do 30 z zadanych elementów

Zakładamy jednocześnie, że rozkład liczby zapamiętanych elementów jest rozkładem normalnym.

Odpowiedzi

a)

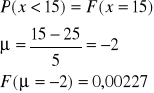
b)

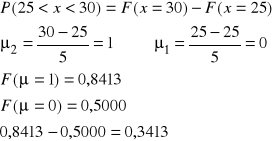
Rozkład chi-kwadrat

Zakładając, że
są niezależnymi zmiennymi losowymi o rozkładzie normalnym o parametrach
zmienna losowa
określona jest w sposób następujący:

ma rozkład
z
„liczbą stopni swobody”.

Zmienna losowa o rozkładzie chi-kwadrat przyjmuje wartości dodatnie, a jej rozkład zależy od liczby stopni swobody
. Dla małych wartości
jest to rozkład silnie asymetryczny, w miarę wzrostu
asymetria jest coraz mniejsza:
wyznaczamy najczęściej jako:

gdzie:

- liczebność próby,

- liczba szacowanych parametrów z próby.

Wartość oczekiwana w rozkładzie

Wariancja w rozkładzie

Odchylenie standardowe w rozkładzie

Przykład 8

Zmienna
ma rozkład o
stopni swobody. Wyznaczyć
wiedząc, że

Korzystamy z tablicy dystrybuanty rozkładu
(por. tablicę 6 na końcu książki)

, dla
oraz

Otrzymujemy wartość dla 0,05

Wykres graficzny:

0,95

0

37,65

Rozkład t-Studenta

Wartość oczekiwana w rozkładzie t-Studenta

Wariancja w rozkładzie t-Studenta

Odchylenie standardowe w rozkładzie t-Studenta

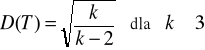
Przykład 9

Zmienna losowa
ma rozkład t-Studenta z
stopniami swobody. Wyznaczyć
wiedząc, że:

Odpowiedź:

(por. tablicę 5 na końcu książki dla wartości 0,1)

---