Modele systemów ciągłych
W MATLABie istnieją trzy sposoby modelowania liniowych, ciągłych, stacjonarnych układów dynamicznych: poprzez transmitancję, opis w przestrzeni stanów oraz opis przy pomocy zer, biegunów i wzmocnienia transmitancji.
Opis w przestrzeni stanów
Dowolny ciągły system liniowy można opisać w przestrzeni stanów w następujący sposób:
![]()
gdzie: x jest wektorem stanu, u jest wektorem sterowań, a y jest wektorem wyjściowym. Macierze A, B, C, D o wymiarach stosownych do wymiarów u, x, y opisują jednoznacznie system.
Opis przy pomocy transmitancji
Wielowymiarowe systemy dynamiczne można opisywać przy pomocy macierzy transmitancji G(s). W MATLABie przy tego rodzaju opisie występują pewne ograniczenia:
transmitancją możemy opisywać jedynie systemy o jednym wejściu i wielu wyjściach (SIMO).
w macierzy kolumnowej transmitancji takiego systemu mianowniki wszystkich transmitancji muszą być identyczne.
Przykład transmitancji spełniającej powyższe warunki:
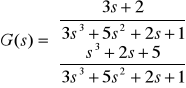
Powyższą macierz transmitancji wprowadzamy podając dwie zmienne: macierz o wierszach zawierających współczynniki wielomianów w licznikach i wektor-wiersz ze współczynnikami wielomianu mianownika.
num = [ 0 0 3 2
1 0 2 5 ]
den = [ 3 5 2 1 ]
Obowiązuje następująca konwencja dla wielomianów - pierwszy element wektora-wiersza odpowiada współczynnikowi wielomianu przy najwyższej potędze. W naszym przykładzie den reprezentuje wielomian z mianownika transmitancji, natomiast wiersze macierzy num wielomiany liczników transmitancji składowych wektora G(s).
Opis w postaci zera - bieguny - wzmocnienie
Jeśli znamy zera i bieguny transmitancji, to możemy przedstawić ją zapisując wielomiany jako iloczyny czynników liniowych, na przykład:
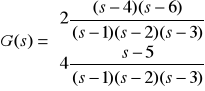
I w tym przypadku ograniczamy się do transmitancji spełniających poprzednie warunki. Transmitancję tak zapisaną wprowadzamy podając trzy macierze:
macierz, w kolumnach której wyszczególniamy zera kolejnych liczników
z = [ 4 5
6 inf ]
wektor-kolumnę z biegunami transmitancji:
p = [ 1 2 3 ]'
wektor-kolumnę ze wzmocnieniami na poszczególnych wyjściach:
k = [ 2 4 ]'
Przypomnijmy również tutaj że funkcja roots oblicza pierwiastki wielomianu: r = roots( p ) zwraca wektor-kolumnę z pierwiastkami dla p wektora-wiersza ze współczynnikami wielomianu. Na odwrót, mając dany wektor-kolumnę r funkcja poly: p = poly( r ) zwraca wektor wiersz ze współczynnikami wielomianu o pierwiastkach zadanych w wektorze r. Funkcje poly można również wywoływać z argumentem - macierzą kwadratową: p = poly( A ) zwraca wektor-wiersz ze współczynnikami wielomianu charakterystycznego macierzy A: det( λI - A ). Do obliczania wartości wielomianu służy funkcja polyval: polyval( V, s ) jest wartością wielomianu reprezentowanego przez wektor-wiersz V dla zmiennej s (może to być skalar, wektor lub macierz ). Przydatna może być również funkcja conv: conv( a, b ): jeśli a, b - wektory-wiersze, to conv( a, b ) jest wektorem-wierszem reprezentującym wielomian będący iloczynem wielomianów reprezentowanych przez a i b.
Konwersja opisów
ss2tf-przestrzeń stanów→transmitancja
[ num, den ] = ss2tf( A, B, C, D, iu ),
gdzie: A, B, C, D - macierze z opisu w przestrzeni stanów,
num, den - macierze z opisu przy pomocy transmitancji,
iu - współrzędna wektora sterowania u, dla której liczona jest transmitancja. Transmitancją można bowiem opisywać jedynie systemy jednowejściowe. Funkcja ss2tf zwraca więc transmitancję przejścia między wejściem ui ( i-ta współrzędna wektora u ) i wyjściem y.
ss2zp - przestrzeń stanów→zera-bieguny-wzmocnienie.
[ z, p, k ] = ss2zp( A, B, C, D, iu )
tf2ss - transmitancja→przestrzeń stanów
[ A, B, C, D ] = tf2ss( num, den )
zp2ss - zera-bieguny-wzmocnienie→przestrzeń stanów
[ A, B, C, D ] = zp2ss( z, p, k )
zp2tf - zera-bieguny-wzmocnienie→transmitancja
[ num, den ] = zp2tf( z, p, k )
Uwagi o wyborze opisu:
MATLAB najdokładniej pracuje na modelach opisanych w przestrzeni stanów. Konieczność używania opisu w przestrzeni stanów jest ponadto wymuszona tym, że wymaga go większość funkcji do analizy systemu. Należy unikać niepotrzebnego przechodzenia z opisu na opis.
Analiza systemu w dziedzinie czasu
impulse - odpowiedź impulsowa systemu
[ y, x ] = impulse( A, B, C, D, iu, t )
A, B, C, D - macierze opisujące system w przestrzeni stanów
iu - numer wejścia, na które podawany jest impuls ( i-ta składowa wektora u )
y - macierz wyjść. Kolumna i-ta tej macierzy zawiera wartości i-tego wyjścia w chwilach czasu wskazywanych przez wektor t.
x -macierz zawierająca wartości wektora stanu x w chwilach czasu wskazywanych przez wektor t.
Przykład wyznaczania odpowiedzi systemu drugiego rzędu o pulsacji wn = 1 i tłumieniu z = 0.2 w przedziale 0 - 10 sekund:
[ A, B, C, D ] = ord2(1, 0.2);
t = 0:0.1:10;
y = impulse( A, B, C, D, 1, t );
plot( t, y )
Można również wywoływać funkcję impulse dla opisu przy pomocy transmitancji:
[ y, x ] = impulse( num, den, t )
Przykład wyznaczania odpowiedzi impulsowej systemu o transmitancji
![]()
num = [ 2, 5, 1 ];
den = [ 1, 2, 3 ];
t = 0:0.1:10;
plot( t, impulse( num, den, t ))
step - odpowiedź skokowa systemu.
Wywołanie tej funkcji jest identyczne jak wywołanie funkcji impulse:
[ y, x ] = step( A, B, C, D, iu, t )
[ y, x ] = step( num, den, t )
lsim - dpowiedź systemu na dowolne wymuszenie
[ y, x ] = lsim( A, B, C, D, u, t )
[ y, x ] = lsim( num, den, u, t , x0 )
gdzie A, B, C, D - macierze opisujące system w przestrzeni stanów,
t - wektor-wiersz dyskretnych chwil czasu, w których obliczane są wyjścia
u - macierz wejść w chwilach czasu wskazywanych przez wektor t. Macierz u ma tyle kolumn ile jest wejść; w i-tej kolumnie są wartości i-tego wejścia w chwilach czasu z wektora t
x0 - wektor-kolumna warunków początkowych x(0). Jeśli nie podajemy tego argumentu, to domyślnie przyjmuje się zerowe warunki początkowe
y - macierz wyjść. Kolumna i-ta tej macierzy zawiera wartości i-tego wyjścia w chwilach czasu wskazywanych przez wektor t.
Można również wywoływać funkcję lsim dla opisu za pomocą transmitancji:
[ y, x ] = lsim( num, den, u, t )
Przykład obliczenia odpowiedzi systemu o transmitancji
![]()
na wymuszenie sinusoidalne zakłócone szumem w przedziale 0-10 sekund:
num = [ 2 5 1 ];
den = [ 1 2 3 ];
t = 0:0.1:10;
u = sin( t ) + rand( t );
y = lsim( num, den, u, t );
plot( t, y )
Budowanie modeli systemów złożonych
Złożone systemy można modelować przy pomocy połączeń równoległych, szeregowych oraz sprzężeń zwrotnych. Do tworzenia modeli systemów złożonych służą następujące funkcje:
parallel: połączenie równoległe elementów opisanych w przestrzeni stanów przy pomocy macierzy A1, B1, C1, D1 (pierwszy człon) oraz A2, B2, C2, D2 (drugi człon). Wynikiem jest czwórka macierzy A, B, C, D będąca opisem w przestrzeni stanów systemu złożonego.
[ A, B, C, D ] = parallel( A1, B1, C1, D1, A2, B2, C2, D2 )
series: połączenie szeregowe
[ A, B, C, D ] = series( A1, B1, C1, D1, A2, B2, C2, D2 )
Wejściem systemu złożonego jest wejście pierwszego członu, a wyjściem - wyjście drugiego członu.
feedback: połączenie przy pomocy ujemnego sprzężenia zwrotnego
[ A, B, C, D ] = feedback( A1, B1, C1, D1, A2, B2, C2, D2 )
append: połączenie dynamiki dwóch niezależnych systemów
[ A, B, C, D ] = append( A1, B1, C1, D1, A2, B2, C2, D2 )
Nowy wektor stanu: x = [ x1; x2 ], u = [ u1, u2 ], y = [ y1, y2 ].
ord2: opis w przestrzeni stanów systemu drugiego rzędu
[ A, B, C, D ] = ord2( wn, z )
wn - pulsacja drgań własnych nie tłumionych.
z - współczynnik tłumienia.
Analiza systemu w dziedzinie częstotliwości
bode - funkcja przygotowująca dane do rysowania charakterystyk częstotliwościowych
[ mag, phase ] = bode( A, B, C, D, iu, w )
[ mag, phase ] = bode( num, den, w )
A, B, C, D - macierze opisujące system w przestrzeni stanów.
iu - numer wejścia, dla którego tworzona będzie charakterystyka.
num, den - wektory reprezentujące odpowiednio licznik i mianownik transmitancji systemu.
w - wektor-wiersz z wartościami pulsacji (w radianach), w których obliczana będzie charakterystyka.
mag, phase - macierze modułów i faz transmitancji systemu. Jeśli G(s) transmitancja, to: mag( w ) = abs( G( jw ) ), phase( w ) = angle( G( jw ) ). Moduł może być zamieniony na decybele: 20*log10( mag ). Faza podawana jest w stopniach. Macierze mag i phase mają tyle kolumn ile jest wyjść systemu, długość każdej kolumny jest taka jak długość wektora w.
logspace - tworzenie wektora w skali logarytmicznej.
y = logspace( d1, d2 ) - generuje wektor o długości 50 z wartościami między dekadami 10d1 i 10d2.
y = logspace( d1, d2, n ) - generuje taki sam wektor lecz o zadanej długości n.
nyquist - funkcja przygotowująca dane do charakterystyki amplitudowo - fazowej (Nyquista).
[ re, im ] = nyquist( A, B, C, D, iu, w ) [ re, im ] = nyquist( num, den, w )
Argumenty funkcji nyquist są takie same jak argumenty funkcji bode. Funkcja nyquist zwraca macierze re oraz im według zasady re ( w ) = real( G(s) ), im( w ) = imag( G(s) ). Macierze te mają tyle kolumn ile jest wyjść systemu. Długość każdej kolumny równa jest długości wektora w.
Przykład rysowania charakterystyk dla systemu drugiego rzędu o pulsacji drgań własnych wn = 1 i tłumieniu z = 0.2.
z = 0.2.
[ A, B, C, D ] = ord2( 1, 0.2 );
w = logspace( -1, 1 );
[ mag, phase ] = bode( A, B, C, D, 1, w );
loglog( w, mag );
title(`Logarytmiczna charakterystyka amplitudowa') semilogx( w, phase );
title(`Logarytmiczna charakterystyka fazowa')
semilogy( mag, phase );
title(`Wykres Nicholsa')
[ re, im ] = nyquist( A, B, C, D, 1, w );
loglog( re, im );
title(`Charakterystyka amplitudowo-fazowa')
Symulacja:
Równania stanu są formą opisu sytemów dynamicznych nadającą się dobrze do symulacji komputerowej w dziedzinie czasu. Prostą metodą numeryczną stosowaną do symulacji komputerowej jest metoda Eulera. Zakładamy, że dysponujemy opisem systemu w postaci równań stanu:
![]()
,
gdzie x(t) jest n-wymiarowym wektorem stanu, u(t) jest wektorem sterowań, a A i B są macierzami liczbowymi.
Stosujemy następujące przybliżenie pochodnej:
![]()
,
T jest niewielką liczbą zwaną krokiem symulacji. Wstawiając przybliżenie pochodnej do równań stanu otrzymujemy:
![]()
Oznaczmy Ψ(T) = In + TA, gdzie In oznacza macierz jednostkową rzędu n. Dostajemy ostatecznie wzór dogodny do symulacji:
![]()
.
Przyjmujemy, że czas zmienia się w sposób dyskretny z krokiem T, tzn. t = 0, T, 2T, ... i wyznaczamy wartości wektora stanu w kolejnych momentach czasu
![]()
dla t = 0,
![]()
dla t = T,
..................................................................................
![]()
dla t = kT.
Krok symulacji T powinien być dobrany tak aby nie stracić informacji o elementach systemu o najszybszej dynamice. W praktyce wartość T powinna być o rząd mniejsza niż najmniejsza stała czasowa systemu, tzn. T = 0,1τmin, gdzie τmin jest najmniejszą stałą czasową systemu.
Ogólna idea przedstawionej powyżej metody symulacji może być stosowana zarówno do systemów liniowych jak i nieliniowych oraz do systemów stacjonarnych jak i niestacjonarnych. Jej wadą dla bardziej złożonych systemów może być mała dokładność.
Zadania:
Dla systemów przedstawionych na rysunkach należy
wyznaczyć równania ruchu
wyznaczyć reprezentację systemu w formie równań stanu
obliczyć transmitancje
napisać funkcję do symulacji systemu za pomocą metody Eulera
przeprowadzić symulację za pomocą SIMULINKa opierając się na równaniach stanu
wyznaczyć odpowiedzi impulsowe i skokowe systemów
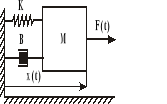
Zad. 1
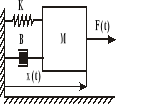
Dany jest system składający się z masy, dołączonej do sprężyny i tłumika. Wartości i znaczenie parametrów:
M = 1kg - masa ciężarka
B = 7 Ns/m - współczynnik tarcia lepkiego
K = 12.5 N/m - współczynnik sprężystości
x(t) - bieżące położenie
F(t) - siła (wymuszenie) działająca na ciężarek.
Przy symulacji za pomocą pakietu SIMULINK zastosuj różne rodzaje pobudzeń np. F(t) = 2 N, pobudzenie przebiegiem prostokątnym o okresie 2s i amplitudzie 2 N.
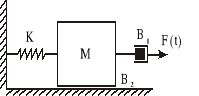
Zad. 2.
Na rysunku przedstawiono system składający się z masy sprężyny i tłumika.
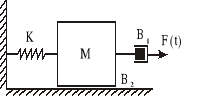
Wartości i znaczenie parametrów:
M = 2 kg - masa ciężarka
B1 = 3 Ns/m - współczynnik tarcia lepkiego tłumika
B2 = 2 Ns/m - współczynnik tarcia lepkiego masy o podłoże
K = 18 N/m - współczynnik sprężystości
Przy symulacji za pomocą pakietu SIMULINK zastosuj różne rodzaje pobudzeń np. F(t) = 5 N, pobudzenie przebiegiem prostokątnym o okresie 20 i amplitudzie 5.
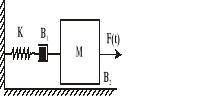
Zad. 3.
Na rysunku dany jest system ze sprężyną i tłumikiem dołączonymi do masy.
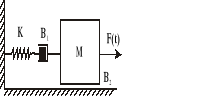
Wartości i znaczenie parametrów:
M = 1 kg - masa ciężarka
B1 = 2 Ns/m - współczynnik tarcia lepkiego tłumika
B2 = 8 Ns/m - współczynnik tarcia lepkiego masy o podłoże
K = 20 N/m - współczynnik sprężystości
Przy symulacji za pomocą SIMULINKA zastosuj różne rodzaje pobudzeń np. F(t) = 5 N, pobudzenie falą prostokątną o okresie 8s i amplitudzie 5 N.
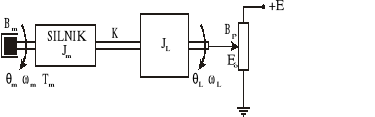
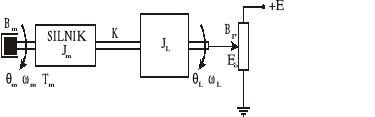
Zad. 4.
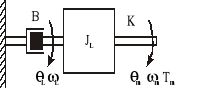
Na rysunku pokazano system złożony z silnika połączonego za pomocą wału o sprężystości K z potencjometrem obrotowym. Zmienną wejściową jest moment napędowy silnika Tm, natomiast zmienną wyjściową napięcie Eo na suwaku potencjometru. Maksymalny zakres potencjometru wynosi 10 obrotów ( 20π radianów ).
Wartości i znaczenie parametrów:
Jm = 4 kgm2 - moment bezwładności silnika
JL = 6 kgm2 - moment bezwładności obciążenia
K = 20 N/m - współczynnik sprężystości wału
Bm = 0.5 Ns/m - współczynnik tarcia lepkiego w łożyskach silnika
BP = 3 Ns/m - współczynnik tarcia lepkiego potencjometru
E = 12 V - napięcie zasilające potencjometr
EO - napięcie na suwaku potencjometru
Θm - przemieszczenie kątowe wału silnika
ΘL - przemieszczenie kątowe osi potencjometru
ωm - prędkość kątowa osi silnika
ωL - prędkość kątowa osi potencjometru
Tm - moment napędowy silnika
Wyznacz równania ruchu systemu, równania stanu oraz transmitancję EO(s)/Tm(s).
Zad. 5.
Na rysunku przedstawiono układ obrotowy. Wielkością sterującą jest moment napędowy Tm, a wielkościami wyjściowymi θL i ωL.
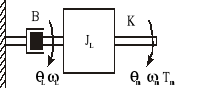
Znaczenie i wartości parametrów systemu:
B = 2 Ns/m - współczynnik tarcia lepkiego łożyska
K = 20 N/m - współczynnik sprężystości wału
JL = 5 kgm2 moment bezwładności obciążenia
Tm moment napędowy
Θm - przemieszczenie kątowe wału silnika
ΘL - przemieszczenie kątowe osi po stronie napędu
ωm - prędkość kątowa wału po stronie napędu
ωL - prędkość kątowa osi po stronie obciążenia
Wyznacz równania ruchu, równania stanu oraz transmitancje ΘL(s)/ Tm(s) i ωL(s)/ Tm(s).
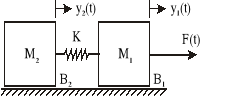
Zad. 6.
Na rysunku przedstawiono system złożony z dwóch mas połączonych sprężyną. Zmienną wejściową jest siła F(t) działająca na układ. Zmiennymi wyjściowymi są prędkości i położenia ciał.
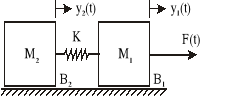
Znaczenie i wartości parametrów:
M1 = 2 kg
M2 = 3 kg
K = 20 N/m - współczynnik sprężystości
B1 = 0.5 Ns/m - współczynnik tarcia lepkiego o podłoże
B2 = 1 Ns/m - współczynnik tarcia lepkiego o podłoże
Wyznaczyć równania ruchu, równania stanu, transmitancje Y1(s)/F(s), Y2(s)/ F(s) oraz V1(s)/ F(s) i V2(s)/ F(s). Wykonaj symulacje systemu badając jego zachowanie w pierwszych kilku sekundach ruchu.
Wyszukiwarka
Podobne podstrony:
Matlab-kurs, Systemy sterowania, Systemy sterowania
Matlab-kurs, MATLAB, MATLAB
Wyklad2 Modele systemów informatycznych zarządzania
ANALITYCZNE MODELE SYSTEMÓW KOLEJKOWYCH 2 ppt
06 MODELE-SYSTEMOW-FINANSOWYCH-NA-SWIECIE, UEP lata 2014-2019, Bankowość inwestycyjna
17(45) Modele systemów informatycznychid 17383 ppt
ANALITYCZNE MODELE SYSTEMÓW KOLEJKOWYCH ppt
kurs matlaba, Lab4 KURS MATLABa, KURS MATLABa
kurs 1, BUKMACHERSKIE SYSTEMY, systemy bukmacherskie w wordzie
kolokwium rok II 20070117, Prywatne, 1 SUM, infa, Matlab kurs pl (bd4ty3), matlab
Pomoc do MATLABA (PG Katedra Systemow Geoinformatycznych)
07 Modele systemuid 7061 ppt
3. Modele systemów ochrony zdrowia, licencjat(1)
Matlab kurs SIMULINK
Świadczenia medyczne i modele systemu zdrowia, Pedagogika
3 mecze kurs 2, BUKMACHERSKIE SYSTEMY, systemy bukmacherskie w wordzie
Wyciąg z poleceń MATLABA, kurs Matlaba PL
1 Modele systemów fizjologicznych
więcej podobnych podstron