Podstawy Szczególnej Teorii Względności

Podstawy Szczególnej Teorii Względności (STW)

##################################################################################
Autor : R. Waligóra ; data powstania dokumentu : 2009-09-12
; ostatnie poprawki z dnia: 2010-12-10
##################################################################################

I. Wprowadzenie.

Szczególna teoria względności jest jedną z podstawowych teorii fizyki. Całokształt idei, zasad i metod skupionych wokół
tej teorii tworzy paradygmat relatywistycznego ujmowania praw przyrody, w tym sensie możemy również mówić o
filozofii relatywistycznej ( relatywizm fizyczny ) podobnie jak wcześniej mówiono o filozofii mechanicystycznej ( zobacz
12 –literatury dodatkowej ). Każda współczesna teoria fizyczna musi uwzględniać rolę STW tj. musi być relatywistycznie
niezmiennicza. Relatywizm zmienia zasadniczo koncepcje (nabywane wraz z codziennym doświadczeniem lub intuicyjnie)
sposobu postrzegania czasu, przestrzeni, jednoczesności czasowej i przestrzennej zdarzeń.
Należy mocno podkreślić iż współcześnie, w związku z bogatym materiałem empirycznym
( zobacz np. tekst „Eksperymentalna baza STW” ) właściwie nie ma już odwrotu od relatywizmu, możliwe jest jedynie
jego ewoluowanie ale nie porzucenie. (podobnie jak w raz z pojawieniem się STW nie porzucono mechaniki
newtonowskiej, a jedynie wyznaczono granice jej stosowalności. Przykładem teorii odrzuconej jest teoria cieplika lub
teoria geocentryczna ). Obecnie wskazuje się kilka punktów które mogłyby stanowić przyczółki dalszego rozwoju STW,
do takich punktów należy np. teoria tachionów – obiektów szczególnego typu, poruszających się z prędkością większą niż
prędkość światła w próżni, oraz dualny jej problem nielokalności w mechanice kwantowej.
Na pytanie czy STW jest ostatecznym słowem fizyki teoretycznej w temacie czasu i przestrzeni, czy też będzie zastąpiona
inną teorią można odpowiedzieć tak : „...każda teoria fizyczna powstała w oparciu o skończoną liczbę znanych faktów
doświadczalnych i potwierdzona w pewnym skończonym zakresie zmienności występujących w niej wielkości jest zawsze
konstrukcja przejściową. Mówiąc o teorii względności i to zarówno szczególnej jak i ogólnej, należy jeszcze dodać iż jest
ona teorią klasyczną , nie opisującą zjawisk kwantowych , a więc jest szczególnego rodzaju rozdziałem zamykającym
fizykę Newtona i Maxwella” [ 22 – literatury dodatkowej ]

Historia powstania STW związana jest głównie z takimi naukowcami jak : A. Einstein, H. Poincare, H. Lorentz,
H. Minkowski, nie będę wnikał w zagadnienia historyczne omawiające szczegółowy wkład poszczególnych fizyków
teoretyków i eksperymentatorów do omawianej teorii, zainteresowanego odsyłam do [ 9, od str. 434 , 16 – dodatki ;
2, 3, 4, 6, 8, 22 – literatury dodatkowej ; 3 –literatury w języku angielskim ; 5, 6 –literatury w języku rosyjskim ].
Dla naszych celów wystarczające będzie, krótkie przypomnienie.
Historia STW organicznie związana jest z rozwojem eksperymentalnej bazy elektrodynamiki klasycznej. Empiryczne
potwierdzenie istnienia fal elektromagnetycznych skierowało większa uwagę teoretyków na zagadnienie hipotetycznego
ośrodka w którym rozchodziłoby się zaburzenie falowe związane z falami elektromagnetycznymi. Kilka cytatów powinno
naświetlić problem :
„Od kiedy stało się wiadome, że światło ma własności falowe, fizykom wydawało się, naturalną koniecznością
zaproponowanie ośrodka, który ten ruch falowy mógłby przenosić tj. czegoś w czym fale mogłyby wędrować. Ośrodek ten
był powszechnie znany jako „eter świetlny”. Aby eter mógłby nośnikiem fal świetlnych, musiałby mieć szereg bardzo
dziwnych własności. Postulowano, że jest on substancją lżejszą niż jakikolwiek znany gaz czy para i że równocześnie jego
sztywność jest porównywalna ze sztywnością stali.” [ 7 –literatury dodatkowej, str. 49 ]

„Eter umożliwiał wyobrażenie sobie tego, że fala świetlna rozchodzi się w pustce, a jednocześnie konkretyzował
wprowadzone przez Newtona pojęcie pustej przestrzeni, która stanowi arenę dla ruchu ciał wyznaczając absolutnie
spoczywający układ odniesienia od ciał niezależny”. [ 12 str. 79 ]

( Koncepcja eteru zmieniała się z czasem i zgodnie z panującymi dominującymi „prądami” w fizyce. Pojęcie „eteru
świetlnego” zostało najpełniej wyrażone w niezwykle skrupulatnych ( zobacz [ 9 –literatury w języku rosyjskim ]) pracach
H. Lorentza. „Eter Lorentza jest eterem elektromagnetycznym, który trwa w spoczynku w przestrzeni absolutnej i
właściwie niczym nie różni się od tej przestrzeni, z tym jednak, że ma własność przepuszczania fal elektromagnetycznych i
strumieni elektronów. Stan eteru można opisać równaniami pól elektrycznych i magnetycznych; o jego strukturze Lorentz
nie wypowiada się”.[ cytat z 17 str. 219 ]. Inną koncepcją jest teoria „eteru relatywistycznego” której autorem jest
A. Einstein [ zobacz 26-literatury dodatkowej ] )

W miarę utrwalania się ideii eteru w fizyce XIX wieku, pojawiła się kwestia ruchu eteru względem ciał materialnych.
Wysuwano szereg koncepcji dotyczących sposobu zachowania się eteru wobec poruszających się ciał materialnych, w
konsekwencji czego odwołano się do nieubłaganego werdyktu eksperymentalnego faktu.
Eksperyment ten znany jest jako „Doświadczenie Michelsona-Morleya” (M-M ). Był to eksperyment trudny do wykonania
w roku 1887, wymagał bowiem użycia całkiem nowych przyrządów ( interferometr ). ( Badano zjawiska optyczne z
dokładnością do co najmniej drugiej potęgi stosunku szybkości Ziemi w jej ruchu orbitalnym do szybkości światła c )
[ 12 str. 80 ; 7-literatury dodatkowej , od str. 50 , 9-literatury dodatkowej od str. 135 ; zobacz również ciekawe omówienie
„analogu z pływakami” dla doświadczenia M-M w 5 , rozdział III „Eter” ]

„Zerowy” wynik tego doświadczenia skomentuje cytatem :
„Próby wykrycia własności eteru doprowadziły nas do trudności i sprzeczności. Po tak przykrych doświadczeniach
nadeszła chwila , by o eterze zupełnie zapomnieć i postarać się nigdy go nie wspominać. Powiemy po prostu , że nasza
przestrzeń ma fizyczną własność przenoszenia fal i w ten sposób unikniemy użycia słowa którego postanowiliśmy nie
używać. Oczywiście skreślenie słowa ze słownika nie jest ratunkiem.”
[ 8-literatury dodatkowej, str. 157 ; warto przeczytać całość wywodu ]

( Należy zdawać sobie sprawę, że „zerowy” wynik eksperymentu M-M nie wystarcza aby wyprowadzić na drodze
indukcyjnej wzory transformacyjne Lorentza, do tego celu potrzebne są wyniki innych eksperymentów, które zostały
oczywiście przeprowadzone w latach trzydziestych XX wieku, były to doświadczenie Kennedy’ego – Thordnike’a ( 1932)
( interferometr o różnej długości ramion ), doświadczenie Ivesa-Stilwella (1938) ( pomiar przesunięcia dopplerowskiego
światła emitowanego przez szybko poruszające się cząstki ). Pierwsze z tych doświadczeń, łącznie z doświadczeniem
M-M, pozwoliło ustalić słuszność wzorów Lorentza w drugim rzędzie wielkości względem v/c z dokładnością do pewnego
czynnika zależnego od prędkości względnej, drugie pokazało, że czynnik ten jest równy jedności
[ 25-literatury dodatkowej, str. 535 ] )

Zatem, przychylając się do autorytetu autorów tego cytatu, przyjmuje ( co jest dosyć powszechne ) iż dla STW koncepcja
eteru nie odgrywa żadnej, twórczej z fizycznego punktu widzenia roli. Przyjmuje, jako podstawę dla dalszego tekstu
jedynie konkluzje wynikająca z doświadczenia M-M : prędkość światła jest stała i niezależna od wyboru IUO.
Należy podkreślić jednak, że hipoteza eteru nie kończy się definitywnie na takim „gładkim” stwierdzeniu.
( powrócę do niej w rozdziale XIII )
( Zobacz również np. „Pisma z filozofii nauk empirycznych” – I. Lakatos WN-PWN 1995, od str. 118 )

Obecnie sprawę eteru zakończę jeszcze jednym cytatem :
„Eter we współczesnym wykładzie STW stwarza dość dziwną sytuacje. Należy długo wyjaśniać przyczyny wprowadzania
pojęcia eteru , żeby potem, po jego wprowadzeniu , stwierdzić, że eteru niema. Czy takie ujęcie jest uzasadnione
dydaktycznie ? Niekiedy twierdzi się , że „niezależnie od wszystkiego” od eteru nie ma ucieczki gdyż wymaga tego
analogia z dźwiękiem i falami na wodzie. Potrzeba dużych umiejętności, by w odpowiednim czasie wskazać na różnicę w
sposobie rozchodzenia się fal grawitacyjnych i elektromagnetycznych z jednej strony oraz fal sprężystych z drugiej ; tym
samym do rozchodzenia się fal pierwszego typu ośrodek nie jest potrzebny. Światło może rozchodzić się tam, gdzie materii
w zwykłym tego słowa znaczeniu ( o niezerowej masie spoczynkowej) nie ma. Zatem „niezależnie od wszystkiego” z eteru
trzeba zrezygnować.” [ 16, str. 293 ]
Przyjmuje zatem, że z punktu widzenia elektrodynamiki klasycznej jak i kwantowej światło nie potrzebuje ośrodka w
którym rozpatrujemy zaburzenie falowe. Nie biorę również pod uwagę koncepcji „eteru niematerialnego” Lorentza.
( równanie falowe omówię w dalszym rozdziale )

Dla przedstawionego tekstu kluczowym będzie wprowadzenie wzorów transformacyjnych Lorentza, a w dalszej kolejności
uwypuklenie roli grupy Poincarego jako grupy symetrii ( izometrii ) przestrzeni Minkowskiego. Jeśli chodzi o własności
tej przestrzeni ( z matematycznego punktu widzenia jest to czterowymiarowa przestrzeń pseudoeuklidesowa ), to
dokładniej zobacz tekst pt. „Matematyczne podstawy szczególnej teorii względności”.
Spróbuje również pokazać pewne związki ogólno fizyczne STW z innymi działami fizyki teoretycznej.
Przed lekturą prezentowanego tekstu warto również zaznajomić się wcześniej z pozycjami i/lub [ 1, 2, 3, 4 ]

II. „Postulaty Einsteina”.

Einstein zbudował STW opierając się na dwóch postulatach, pierwszy z nich to postulat rozszerzający na zjawiska
elektromagnetyczne zasadę względności Galileusza ( Galileusz postulował ją dla układów mechanicznych, stwierdzając, że
wszystkie zjawiska mechaniczne przebiegają tak samo w dowolnym IUO ) - nazywa się go „szczególną zasadą
względności”. Głosi ona, że wszystkie układy inercjalne są równoważne i żadnego z nich nie da się wyróżnić za pomocą
jakiegokolwiek doświadczenia wykorzystującego dowolne zjawiska np. mechaniczne, elektromagnetyczne lub jądrowe.
( oczywiście zachowując te same warunki fizyczne, co matematycznie oznacza przyjęcie tych samych warunków
brzegowych dla rrc opisujących te zjawiska ). Inaczej mówiąc, nie można stwierdzić bezwzględnego spoczynku
jakiegokolwiek układu lub nie istnieje wyróżniony IUO, lub wszystkie zjawiska zarówno mechaniczne jak i
elektrodynamiczne przebiegają tak samo w dowolnym IUO.
Treścią drugiego postulatu jest stwierdzenie, że maksymalną możliwą prędkością rozchodzenia się sygnałów fizycznych
( właściwie chodzi tu o prędkość przenoszenia energii-masy-informacji. Podstawową cechą sygnału fizycznego jest jego
energia - mówimy, że sygnał fizyczny np. fala, przenosi energię. Dołączenie pojęcia informacji uzasadnić można
następującym cytatem : „Przede wszystkim trzeba zgodzić się z twierdzeniem, że informację należy traktować jako pojęcie
nierozerwalnie związane z wszelką postacią masy i energii, które to byty fizyczne uzyskują określone cechy w miarę jak
ustala się w nich porządek lub organizacja” – „O istocie informacji” – E. Kowalczyk, WkiŁ 1981, str. 60 ) w przyrodzie
jest prędkość światła w próżni, której wartość jest stała i jest to uniwersalna stała przyrody oznaczana zazwyczaj literką „c”

c = ( 2,99792458

0,00000012 )

108 [m/s ]. Wartość stałej c wyznaczana jest doświadczalnie, wartości tej nie możemy

wyprowadzić teoretyczne z STW. Postulat istnienia uniwersalnej stałej przyrody c uzasadniono licznymi doświadczeniami
( oprócz doświadczenia M-M znane jest wspomniane już doświadczenie Kennedy’ego – Thordnike’a ).

Wartość stałej c możemy obliczyć ze wzoru znanego z elektrodynamiki : c = 1/ sqrt(ε0µ0 )
Gdzie : ε0- stałe przenikalności elektrycznej próżni , µ0 – stała przenikalności magnetycznej próżni

Jak zobaczymy dalej wzory transformacyjne Lorentza mogą być wyprowadzone bez wprowadzenia tego postulatu.
Istnienie pewnej prędkości granicznej, której nie może przekroczyć żadne ciało o niezerowej masie spoczynkowej tj. dla
którego istnieje IUO względem którego może ono spoczywać, jest matematyczną konsekwencją przyjętego modelu tj.
uznania przestrzeni Minkowskiego jako „areny” dla zdarzeń fizyki relatywistycznej. Matematyka oczywiście nie narzuca
konkretnej wartości tej prędkości granicznej ani nie pokazuje zależności STW z korpuskularno-falową naturą światła.
To fizyczne doświadczenie pozwala nam utożsamić stałą wynikająca z rozważań teoretycznych ze stałą c – jako wartość
szybkości światła w próżni. ( gdyby jakieś subtelne hipotetyczne doświadczenie pokazało, że prędkość światła w próżni nie
jest stałą przyrody to z logicznego punktu widzenia nie obalałoby to STW, podobnie odkrycie obiektów nadświetlnych nie
unieważniałoby jej wyników a jedynie wyznaczałoby jej granice stosowalności – wiadomo bowiem, że obiekty takie
charakteryzują się specyficznymi własnościami jak na razie wywodzonymi teoretycznie )

Należy podkreślić, że to dopiero STW postawiła problem istnienia prędkości maksymalnej ( jak i własności ciał
poruszających się w granicy tej prędkości ), wcześniejsze teorię zakładały milcząco, że sygnały fizyczne mogą rozchodzić
się z prędkościami dowolnymi – zatem i nieskończonymi. Postawienie zagadnienia ograniczającego teorię fizyczne od tego
momentu stawało się bardzo płodną regułą heurystyczną. Pytania o granice narzucane przez przyrodę na wartości
wielkości fizycznych zawsze są niebanalne. Jak wiemy zagadnienie ograniczenia od dołu wielkości energii ( konkretnie
działania ) prowadzą do MK i m.in. zasad nieoznaczoności , pytanie dotyczące maksymalnej gęstości energii-masy
prowadzi do teorii czarnych dziur.

Nazwa „szczególna teoria względności”, jak zauważono we wczesnych latach jej rozwoju nie jest nazwą zbyt udaną.
Jednak ze względów tradycyjnych i historycznych uwarunkowań , nazwa tak jest przyjęta jako powszechnie obowiązująca
( ang.

“The special theory of relativity”

STR lub prosto “special

relativity” ;

ros. Специалная Теория

Относительности – СТО lub również stosowana nazwa : Частная Теория Относительности. )

Problem nazewnictwa wywodzi się z prac teoretycznych dotyczących elektromagnetycznej natury światła. Pod koniec XIX
wieku wprowadzono koncepcje „eteru świetlnego”. W pewnym momencie teoretycznych rozważań założono, że istnieje
absolutny układ odniesienia i jest to układ w którym ten hipotetyczny eter spoczywa. Przeciw takiemu wyróżnionemu
układowi wystąpił Einstein oraz Poincare, uczeni ci swoje koncepcje oparli na „postulacie względności” – czyli postulacie
odrzucającym istnienia układu absolutnego spoczynku. W ten sposób zaczęła funkcjonować „teoria względności” , nazwa
ta została ugruntowana przez wybitnych i uznanych fizyków m.in. przez Plancka.
„Szczególna” ponieważ dotyczy układów odniesienia w których pomija się wpływ pola grawitacyjnego ( przymiotnik ten
pojawił się w sposób „naturalny” po zbudowaniu OTW ).
Spotyka się również nazwy : specjalna, cząstkowa – teoria względności.
Niefortunność nazwy teoria względności ( z podkreśleniem słowa względność ) staje się widoczna, kiedy uświadomimy
sobie fakt, że u jej podstaw leżą pewne wielkości niezmiennicze – inwarianty np. niezmienniczy interwał
czasoprzestrzenny, których obecność konstytuuje tą teorię.
[ 16 str. 32 ; 2-literatury dodatkowej str. 102 ; 1-literatury w języku rosyjskim , str. 32 ]

III. Układy odniesienia w mechanice klasycznej i relatywistycznej.

Matematycznym modelem przestrzeni mechaniki newtonowskiej (MN) jest jak wiadomo trójwymiarowa przestrzeń
Euklidesa. Układ odniesienia w mechanice newtonowskiej zgodnie z przyjętymi zasadami związany jest z zegarem
( układem zegarów ) oraz układem sztywnych prętów pomiarowych. ( zobacz tekst pt. „Kinematyka punktu materialnego
w mechanice klasycznej” ). W mechanice newtonowskiej nie występował problem synchronizacji zegarów lub problem
sztywności prętów pomiarowych. Dlatego też zagadnienie arytmetyzacji tj. koordynacji przestrzenno-czasowej punktów
modelu matematycznego, jest właściwie problemem trywialnym. Absolutny czas i absolutna przestrzeń niejako implikuje
istnienie idealnego zegara i idealnego pręta pomiarowego, ponadto dopuszczone istnienie sygnału o nieskończonej
prędkości rozchodzenia gwarantuje dowolnie szybkie przenoszenie zmian wprowadzonych arytmetyzacji.
( nie bez znaczenia jest również „płaskość” wykorzystywanej przestrzeni ).
Matematycznym modelem przestrzeni mechaniki relatywistycznej jest czterowymiarowa przestrzeń Minkowskiego (M)
- nazwana ogólnie „czasoprzestrzenią”. Układ odniesienia w STW podobnie jak w MN wyposażamy w układ zegarów i
układ sztab pomiarowych. Arytmetyzacja nie jest jednak w tym przypadku problemem trywialnym.
W dalszym rozwinięciu teorii przydatne będzie zdefiniowanie pojęcia „zdarzenia”. Z matematycznego punktu widzenia
zdarzenia to wektory należące do przestrzeni M ( a zatem punkty czasoprzestrzeni wskazywane przez te wektory ), z
fizycznego punktu widzenia pod pojęciem „zdarzenia” będziemy rozumieli zaistnienie dowolnego zjawiska (procesu)
fizycznego np. wyemitowanie fotonu, elektronu, uderzenie lub zderzenie dwóch piłek ; wystrzał pocisku itp.
Ważnym jest, aby zjawisko to zachodziło w dostatecznie małym obszarze przestrzennym ( w granicy będzie to punkt ) oraz
trwały dostatecznie krótko ( w granicy będzie to tzw. moment, chwila )
Takie warunki pozwalają w miarę jednoznacznie przyporządkować zdarzeniu fizycznemu pewien punkt (wektor) należący
do M. Układem odniesienia ( układem laboratorium ) nazwiemy pewien wyróżniony punkt ( punkt odniesienia , punkt
zerowy ) w którym umieszczono zespół urządzeń pomiarowych ( zegar, sztabę pomiarową, źródło światła, lustro,

fotodetektor itp. ). Ten makroskopowy układ urządzeń nazwiemy „obserwatorem”. Z określenia tego wynika, że dla
zapewnienia stabilności i jednoznaczności pomiarów układ laboratorium jest ciałem materialnym dla którego efekty
kwantowe są pomijalne. Układu odniesienia który byłby czuły na wszelkie efekty kwantowe np. doznawałby odrzutu
podczas emisji lub absorpcji kwantu promieniowania nie spełniałby wymogu jednoznacznego określenia np. pomiaru
długości. Warto zastanowić się nad takim określeniem obserwatora i jego roli w procesie pomiarowym ( kwestię tę
podejmę w końcowych rozdziałach ).
Do podstawowych zadań mechaniki w tym i relatywistycznej należy badanie ruchu ciała materialnego ( punktu
materialnego). Opisanie ruchu polega na wyznaczeniu trajektorii w przestrzeni M. Do tego celu potrzebujemy zegara oraz
sztaby pomiarowej. Zegar jest przyrządem fizycznym ( mechanicznym ,elektronicznym, atomowym ) który z określoną
dokładnością odmierza i zlicza jednakowe odcinki czasu ( interwały czasowe ). „Dobry” zegar powinien jednakowym
odcinkom czasu przypisać jednakowe wartości liczbowe, bez względu na warunki fizyczne ( chemiczne, atmosferyczne lub
biologiczne ) w jakich pracuje.
W MK ze względu na założenie absolutności upływu czasu wystarczał jeden zegar, wspólny dla wszystkich obserwatorów
związanych zarówno z IUO jak i NIUO. Ten wspólny zegar mógł być umieszczony w dowolnym miejscu przestrzeni
( zazwyczaj jednak był to punkt związany z układem laboratorium, który jednocześnie był początkiem układu
współrzędnych ). Istnienie nieskończenie szybkiego sygnału gwarantowało dostępność odczytu tego zegara dla każdego
innego obserwatora związanego z innym IUO. Zakładano, że zegar ten można przemieszczać ruchem dowolnym bez
wpływu na jego wskazania. Ponadto przyjmowano, że dowolną ilość „kopii” takich zegarów można ustawić jednocześnie
według dowolnego wskazania dowolnie wybranego zegara ( nie istniał więc problem synchronizacji zegarów ).
W mechanice relatywistycznej musimy zrewidować te właściwie naiwne założenia. Ponieważ upływ czasu nie jest już
wielkością absolutną ale związana z konkretnym IUO musimy przyjąć że każdy układ odniesienia dysponuje własnym
lokalnym zegarem spoczywającym w tym układzie. W dalszej kolejności zostanie omówiony związek między
wskazaniami zegarów poszczególnych IUO, jak również zagadnienie synchronizacji dwóch lub wielu zegarów.
Obecnie powiem tylko, że możliwe jest zsynchronizowanie wielu zegarów spoczywających w danym IUO, można również
zsynchronizować dwa zegary poruszające się względem siebie, nie możliwe jest jednak zsynchronizowanie trzech lub
więcej zegarów poruszających się dowolnym ruchem względnym. [ 4, str. 27 ]

Niech będą dane dwa identycznie zegary spoczywające w jednym IUO ( np. opierające się na emisji fotonów w atomie
cezu ). Ponieważ przenoszenie zegarów wiąże się z niezerowymi przyspieszeniami, nie możemy przyjąć procedury
synchronizacji, która opierałaby się na nastawieniu wszystkich zegarów w jednym miejscu, a następnie umieszczeniu ich w
wybranych punktach M. Pierwsze musimy rozmieścić zegary w odpowiednich miejscach, a następnie dokonać kolejno
procedury ich synchronizacji. Według Einsteina taką synchronizacje możemy przeprowadzić za pomocą sygnałów
świetlnych wysyłanych ze zegara „wzorcowego” do każdego zegara mającego być z nim zsynchronizowanym.
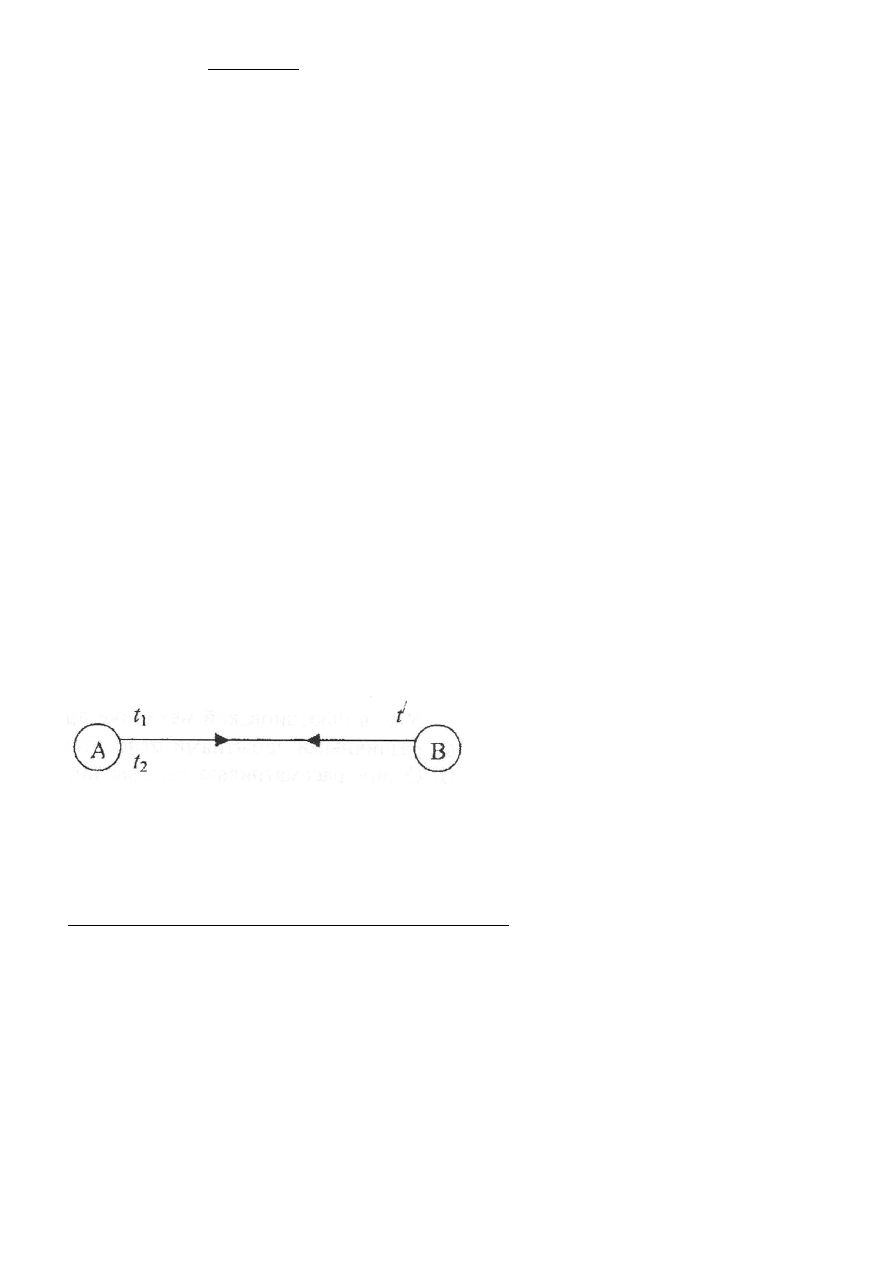
Mówimy, że zegary A, B rozmieszczone w różnych punktach M, jednego i tego samego IUO, będą zsynchronizowane,
jeśli w chwili przyjścia sygnału do zegara B będą one wskazywały czas :
t’ = ½ ( t1 + t2 ) , gdzie : t1 – chwila wysłania sygnału według zegara A , t2 – chwila powrotu tego sygnału ( po
natychmiastowym jego odbiciu w punkcie umieszczenia zegara B ). ( rys. 1 )

Rys. 1 Synchronizacja zegarów A, B

Oczywiście milcząco przyjmujemy, że sygnał porusza się z jednakową szybkością „tam i z powrotem” , oraz to, że
możliwe jest „natychmiastowe” odbicie sygnału świetlnego ( co na pewno nie wynika z elektrodynamiki kwantowej )
Dwa zdarzenia zachodzące w różnych punktach danego i jednego IUO, nazwiemy „jednoczesnymi”, jeśli wskazania
dwóch wcześniej zsynchronizowanych zegarów umieszczonych w tych punktach, będą jednakowe.

Transformacja Lorentza. ( Lorentz transformations )

IV. Wzory transformacyjne Lorentza jako konsekwencja postulatu stałości prędkości światła.

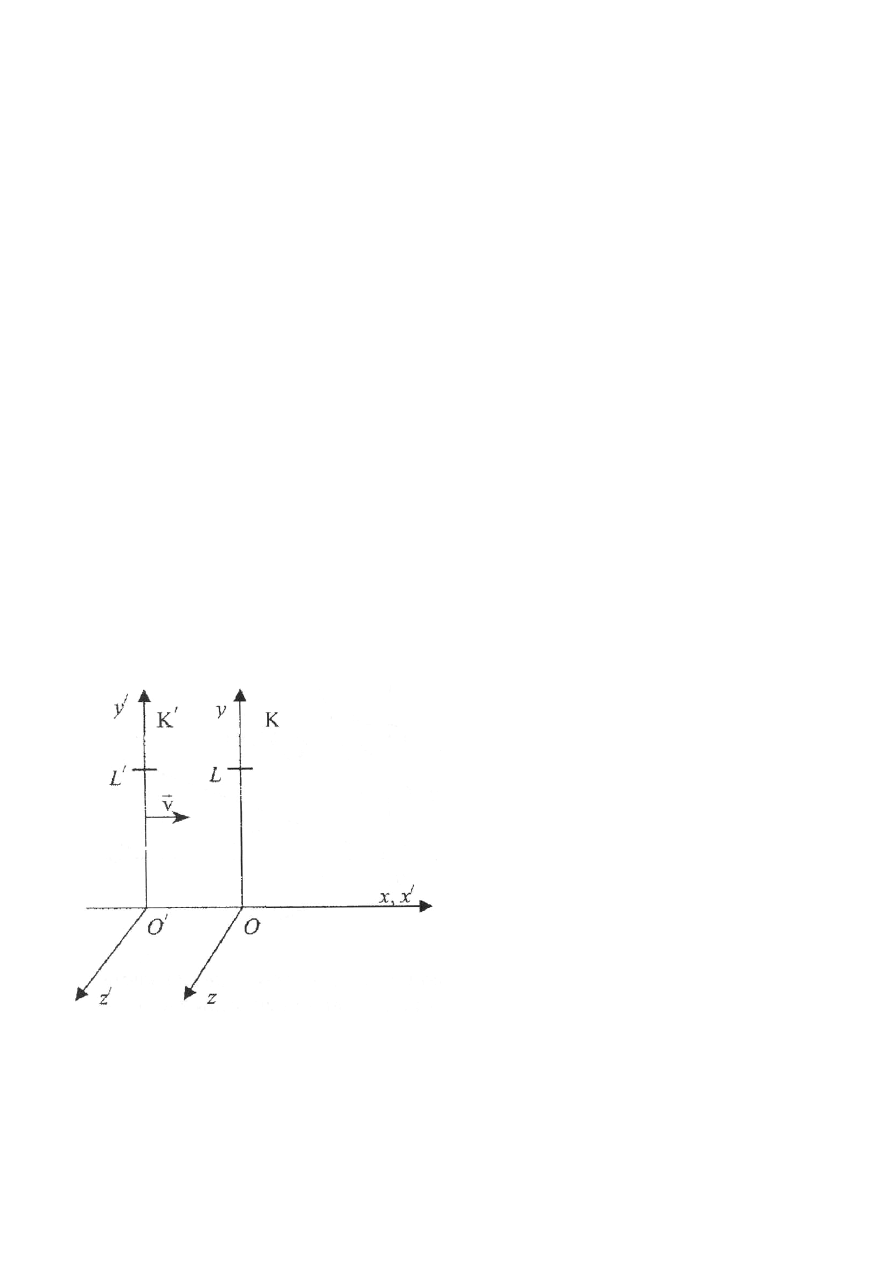
Rozważmy dwa IUO : U oraz U’ , niech U’ porusza się względem U ze prędkością v , dla prostoty rachunków
( nie ujmując jednak walorów ogólności ) załóżmy, że ruch odbywa się zgodnie z kierunkiem wyznaczonym przez oś Ox
kartezjańskiego układu współrzędnych Oxyz stowarzyszonego z IUO U, nadto założymy, że oś O’x’ kartezjańskiego
układu współrzędnych O’x’y’z’ stowarzyszonego z IUO U’ jest równoległa do osi Ox. Dobre zegary Z i Z’ zostały
wcześniej zsynchronizowane. Niech w momencie t = t’ = 0 środki układów współrzędnych primowanego i
nieprimowanego pokrywają się, w tej również chwili spoczywające w układzie U źródło światła np. lampa błyskowa
wysyła krótki impuls światła. Zgodnie z drugim postulatem Einsteina obserwatorzy związani, odpowiednio z układem U
oraz U’ obserwować będą rozchodzącą się kuliście „warstwę” promieniowania rozchodzącą się względem nich z
prędkością c. Równanie kulistego czoła fali w układzie U będzie miało postać :

x2 + y2 + z2 = c2 t2 (4.1)

Jest to równanie sfery o środku w punkcie (0, 0), której promień rośnie w czasie z prędkością c.
W układzie U’ odpowiednie równanie czoła fali będzie miało postać :

x’2 + y’2 + z’2 = c2 t’2 (4.2)
Przyjmując hipotezę absolutnego czasu tj. zakładając ,że czas płynie tak samo w U i U’ ( t = t’ ) musielibyśmy przyjąć, że
czoło fali w pierwszym układzie było by sferą o środku O a w drugim inna sferą o środku O’, oczywiście jest tylko jedno
czoło fali i jedna sfera, zatem musimy przyjąć, że : t

≠

t’. Zastanówmy się teraz nad możliwą postacią wzorów

transformacyjnych, które pozwalałyby „przetłumaczyć” opis zbioru zdarzeń widzianych w jednym IUO, w naszym
przypadku niech będzie to układ U, na opis tych samych zdarzeń widzianych z innego IUO – dla nas układu U’.
Tradycyjnie w STW zajmujemy się opisem układów inercjalnych tj. poruszających się względem siebie ruchem
jednostajnym prostoliniowym, ruch NIUO i transformacje takich układów - w szczególności ruchy w polu grawitacyjnym
stanowią przedmiot zainteresowania Ogólnej Teorii Względności ( OTW ).
Zakładamy, że równania które wiążą odpowiednie współrzędne układów U i U’ są równaniami liniowymi. Wynika to z
faktu, że pojedynczemu zdarzeniu w jednym układzie odniesienia musi odpowiada jedno i tylko jedno zdarzenie w drugim
układzie, transformacja w postaci kwadratowej mogłaby dawać dwa rozwiązania co nie zapewniałoby jednoznaczności
zdarzeń. Ponadto zasada względności wymaga, aby ruch jednostajny prostoliniowy zachowywał swój charakter,
niezależnie od wyboru układu odniesienia. Przyjmijmy następująca postać liniowych wzorów transformacyjnych :
x’ = k1x + k0t (4.3)
y’ = y - ruch odbywa się zgodnie z kierunkiem osi Ox || O’x’
z’ = z
t’ = k2x + k3t (4.4)
k0, k1 , k2 , k3 - szukane współczynniki.
Początek układu U’ porusza się ze stała prędkością v, względem układu U, dla tego punktu tj. dla x’ = 0 równanie (4.3)
zapisać możemy następująco :
k1x = - k0t ⇒ x/t = - k0/ k1 (4.5)
ale x/t = v zatem
- k0/ k1 = v ⇒ k0 = - k1 v (4.6)
czyli :
x’= - k1 ( x - vt ) (4.7)
Zgodnie z postulatem o stałości c, czoło fali świetlnej musi by sferą o jednakowym promieniu zarówno w układzie U jak i
U’ , zatem musi by spełniona zależność :

x2 + y2 + z2 - c2 t2

≡

x’2 + y’2 + z’2 - c2 t’2 (4.8)

Dla uproszczenia rachunków rozważmy wariant jednowymiarowy tożsamości (4.8) :

x2 - c2 t2

≡

x’2 - c2 t’2 (4.9)

Podstawmy teraz wzory (4.7) i (4.4) do (4.9) :

[ - k1 ( x - vt ) ]

2 - c2 ( k

2x + k3t )

≡

x2 - c2 t2 (4.10)

( k1vt - k1x )

2 - c2 ( k

2x + k3t )

≡

x2 - c2 t2

I dalej :

x2 ( k1

2 - c2 k

2 ) – 2xt ( k

2 v + c2 k

2k3 ) + t

2 ( k

2 v2 - c2 k

2 ) v2

≡

x2 - c2 t2 (4.11)

Porównując odpowiednie współczynniki otrzymujemy :

2 - c2 k

2 = 1 ⇒ k

2 – 1 = c2 k

2 (4.12)

2 v + c2 k

2k3 = 0 ⇒ k1

2 v = c2 k

2k3 (4.13)

2 v2 - c2 k

2 = - c2 ⇒ k

2 v2 + c2 = - c2k

2 (4.14)

Rozwiązując ten układ równań otrzymujemy :

k1 = 1/ sqrt [ 1 – (v/ c)

2 ] (4.15)

k2 =

(v/c2) / sqrt [ 1 – (v/ c)2 ] (4.16)

k3 =

1 / sqrt [ 1 – (v/ c)2 ] (4.17)

Z równania (4.13) wynika, że k2 i k3 muszą mieć znaki przeciwne, ale k3 musi być dodatnie co wynika z założenia
jednakowego kierunku upływu czasu w układach U i U’ , zatem k2 musi by ujemne.
Oznaczmy : γ = k1 ( czynnik Lorentza ) wtedy :
k2 = γ (v/c

2) (4.18)

k4 = γ (4.19)
Podstawiając te zależności do wzorów (4.3) i (4.4), otrzymujemy :
x’ = γ (x - vt )

(4.20)

t’ = γ [ t - (v/ c2 ) x ]

(4.21)

y’ = y
z’ = z
Są to wzory na transformacje Lorentza. Wzory te możemy „odwrócić” tj. wyrazić współrzędne układu U przez
współrzędne U’ :
x = γ (x’+ vt’ ) (4.22)

t = γ [ t’ + (v/ c2 ) x’ ] (4.23)
y = y’
z = z’
[ 13, str. 17 ]
Jak widać wzory transformacyjne Lorentza ( nazwa nadana przez Poincarego ) różnią się od klasycznych wzorów
transformacyjnych Galileusza. Obecnie w skład przekształcenia współrzędnych przestrzennych wchodzi zmienna czasowa,
a w skład wzorów przekształcających współrzędną czasową wchodzi współrzędna przestrzenna, takie wymieszanie
współrzędnych przestrzennych i czasowych nieobecne w transformacji Galileusza jest charakterystyczne dla transformacji
relatywistycznej. Związek ten wskazuje na wzajemne powiązania obu rodzajów współrzędnych. Jak przekonamy się w
dalszej kolejności wzory te wymuszają na nas przemyślenie a następnie sformułowanie nowych poglądów dotyczących
natury czasu i przestrzeni a w szczególności pojęcia jednoczesności oraz przyczynowości.
Wzory (4.20) i (4.21) oraz dualne do nich wzory (4.22) i (4.23) ukazują symetrię przejścia U

→

U’ oraz U

→

Symetria ta odzwierciedla zasadę względności ruchu IUO.
W dalszej kolejności wygodnie będzie wprowadzić wielkość :
β = v/ c

γ = 1/sqrt ( 1 – β2 ) (4.24)
Widać ,że jeżeli β

→

0 ⇒ γ

→

1 ( co tradycyjnie oznacza, że stała c dąży do nieskończoności c

→

∞

, można oczywiście

zapytać czy jest sensownie fizycznie mówić, że uniwersalna stała przyrody zmierza do jakieś granicy ),
to wzory (4.20) i (4.21) redukują się do znanych wzorów szczególnej transformacji Galileusza :
x’ = x - vt

(4.25)

t’ = t

(4.26)

W praktyce przyjmuje się, że jeśli rozpatrywane prędkości IUO są dużo, dużo mniejsze od prędkości c tj. v <<< c
( co ze względu na olbrzymią wartość stałej c jest w praktyce dnia codziennego spełnione w większości rozpatrywanych
przypadków ), to możemy w granicach rozsądnego i niewielkiego błędu przyjąć za obowiązujące wzory klasyczne.
Wielkości β i γ przyjmują odpowiednio następujące wartości : β

∈

< 0, 1 ) ; γ

∈

< 1 , +

∞

)

Wzór (4.24) zgodnie ze wzorem na rozkład dwumianu :

( 1- x )p = 1 - px + [ p(p –1)x2 / 2! ] - ….

Możemy przedstawić w postaci często stosowanego rozwinięcia ( p = - ½ , x = v2/ c2 ) :

γ = 1 + ½ (v2/ c2 ) + ....
Jest to tzw. rozwinięcie z dokładnością do wyrazów drugiego rzędu. Jest ono dla większości przypadków wystarczającym

Jak łatwo sprawdzi następnym składnikiem sumy będzie wyrażenie 3/8 (v4/ c4 )
( a odpowiednie rozwinięcie będzie rozwinięciem z dokładnością do wyrazów trzeciego rzędu )

V. Wzory transformacyjne Lorentza wyprowadzane bez postulatu o stałości prędkości światła.

( Wzory Lorentza jako konsekwencja transformacji liniowej uwzględniającej zasadę względności )

Wzory transformacyjne Lorentza można wyprowadzić konsekwentnie i jednoznacznie bez opierania się o postulat istnienia
stałej c. ( istnieje kilka wariantów takiego wyprowadzenia )
Wprowadźmy następujące „klasyczne” założenia :

przestrzeń jest izotropowa tj. wszystkie kierunki przestrzenne są równouprawnione, nie ma kierunku
wyróżnionego.

Przestrzeń jest jednorodna tzn. wszystkie punkty przestrzeni są równouprawnione, nie ma punktów
wyróżnionych, w szczególności każdy punkt przestrzeni może by wybrany jako punkt z którym możemy związać
IUO.

Czas jest jednorodny tzn. każda chwila jest jednakowo dobra aby mogła być wybrana jako chwila początku
odliczania czasu ( chwila zero )

Spełniona jest zasada względności Einsteina : „Jeżeli K jest układem inercjalnym, to każdy układ K’ poruszający
się ruchem jednostajnym i postępowym względem K jest także układem inercjalnym ; prawa przyrody wyglądają
jednakowo we wszystkich układach inercjalnych. Twierdzenie to będziemy nazywali „szczególną zasadą
względności” [ cytat z 15-literatury dodatkowej , str. 33 ]. Warto zauważyć, że oryginalna zasada Einsteina jest
równoważna wprowadzonemu już postulatowi mówiącemu o równoważności IUO lub stwierdzeniu że wszystkie
prawa fizyki są niezmiennicze względem transformacji Lorentza.

Naszym celem będzie znalezienie postaci funkcji transformujących współrzędne przestrzenne (x,y,z ) oraz współrzędną
czasową t, z jednego IUO U do drugiego IUO U’ . Ogólnie funkcje te możemy zapisać następująco :
x’ = f1 (x,y,z, t)
y’ = f2 (x,y,z, t)

z’ = f3 (x,y,z, t)
t’ = f4 (x,y,z, t)
W pierwszej kolejności należy zauważyć, że założenia jednorodności czasu i przestrzeni nakładają warunek liniowości na
funkcje fi . Ogólna postać transformacji liniowych dana jest wzorami :
x’ = axx + bxy + cxz + dxt + mx
y’ = ayx + byy + cyz + dyt + my
x’ = azx + bzy + czz + dzt + mz
x’ = atx + bty + ctz + dtt + mt
Współczynniki a, b, c ,d są pewnymi stałymi lub funkcjami prędkości względnej IUO ; współczynniki m – to pewne stałe.
Z założenia jednorodności i izotropowości przestrzeni i czasu wynika, że wzory transformacyjne powinny mieć postać :
x’ = axx + dxt + mx

(5.1)

y’ = byy + dyt + my
z’ = czz + dzt + mz
t’ = atx + bty + ctz + dtt + mt
Aby dokładnie określić postać tych wzorów wybierzmy dwa dowolne IUO U i U’ niech w chwili zero początki O i O’ tych
układów pokrywają się. Niech układ U’ porusza się w kierunku wyznaczonym przez oś Ox || O’x’ z prędkością v
względem U. Dla takiego określenia ruchu wzory (5.1) przepiszemy następująco :
t’ = at + bx + n
x’ = ct + dx + m
y’ = y
z’ = z
Dla chwili zero mamy x’ = x = 0 zatem współczynniki m, n muszą by równe zeru. Współczynniki a, b, c, d mogą a nawet
muszą zależeć jedynie od prędkości względnej v. Zasada względności wymaga ponadto aby :
t’ = at + bx

⇔

t = at’ + bx’

(5.2)

x’ = ct + dx

⇔

x = ct’ + dx’

(5.3)

( znaki zależne są od przyjętej orientacji osi Ox i O’x’ )
Podstawiając otrzymamy :

t = a (at + bx) + b(ct + dx) = ( a2 + bc)t + b (a + d)x

x = c ( at + bx) + d(ct + dx ) = c(a + d) t + (d2 + bc)x
Zatem :

( a2 + bc) = 1 ; b (a + d) = 0 ; c(a + d) = 0 ; (d2 + bc) = 1
Równania te nie są niezależne i prowadzą do pary równań :

a2 + bc = 1
a = - d
Ponieważ v = x/t = c/a ; a

≠

Mamy zatem trzy równania i cztery współczynniki. Wobec tego przyjmijmy, że a = γ(v) – będzie pewną funkcją czasu.

a = γ(v) ⇒ c = γ(v) v ⇒ d = - γ(v) ⇒ b = [ 1 – γ2 (v) ] / γ(v) v
Podstawiając te zależności do funkcji (5.2) i (5.3) otrzymamy :

t = γ { t’ + [ ( 1 – γ2 )x’ / γ2 v ] }

(5.4)

x = γ ( vt’ – x’ )

(5.5)

Naszym celem jest teraz wyznaczenie postaci funkcji γ = γ(v). W tym celu rozważymy trzeci IUO U’’ ( o zwrocie osi
O’’x’’ || O’x’ || Ox ) poruszający się z prędkością V względem IUO U’ , ponieważ układ U’’ spełnia wszystkie analogiczne
wyprowadzone wcześniej warunki to wzory transformacyjne U’

→

U’’ będą miały postać :

t’ = γ { t’’ + [ ( 1 – γ2 )x’’ / γ2 V ] }

(5.6)

x’ = γ ( Vt’’ – x’’ )

(5.7)

Podstawiając x’ i t’ określone powyższymi wzorami do wzorów (5.4) i (5.5) otrzymamy wzory transformacyjne U

→

U’’

Analizując te wzory ( koniecznie zobacz [ 5, str. 36 ] ) stwierdzamy , że :

(1/V2) [ 1 – (1/γ2 (V) ) ] = (1/v2) [ 1 – (1/γ2 (v) ) ] = const. = C
( równość ta wynika z następującego rozumowania : po prawej stronie równości mamy pewną funkcje f = f(v) , po lewej
funkcje f = f(V) , równość dwóch funkcji , dwóch zmiennych zachodzi tylko w przypadku kiedy są one stałe i równe sobie)
Otrzymujemy zatem :

γ = 1/ sqrt ( 1 – cv2 )
Podstawiając tak otrzymane wyrażenie dla γ, do wzorów (5.4) I (5.5) otrzymamy :
t = γ ( Cvx, + t’ )

(5.8)

x = γ (x’ + vt’ )

(5.9)

Stała C ma wymiar odwrotności kwadratu prędkości ; Jej wartość powinna być wyznaczona doświadczalnie – teoria

wskazuje jedynie na istnienie takiej stałej. Z doświadczenia możemy otrzymać wartość : C = 1.11

10-17 [ s2 / m2 ].

Zatem C = 1/c2
Jak można się przekonać otrzymane wzory (5.8) i (5.9) przedstawiają wzory transformacyjne Lorentza.
[ 5, 17 –literatury dodatkowej ; troszkę inny wariant podanego wyprowadzenia pokazano w 1-literatury w języku rosyjskim
od str. 23 ]

VI. Konsekwencje wzorów transformacyjnych Lorentza.

Wzory Lorentza implikują szereg na pozór niezgodnych ze „zdrowym rozsądkiem” własności przestrzeni i czasu.
Są one niejako rewolucją, która burzy nasze codzienne poglądy dotyczące natury czasu i przestrzeni, oczywiście ich
charakterystyczne własności najpełniej przejawiają się gdy rozpatrujemy ruchy o prędkościach zbliżonych do c.
W tym kontekście zazwyczaj mówi się o „paradoksalnych własnościach” wynikających z STW. W istocie konsekwentne
stosowanie zasad STW w żadnym przypadku nie prowadzi do zjawisk lub następstw, które istotnie można było by nazwać
paradoksalnymi. Lekcja jakiej udziela STW naszym „zdrowym zmysłom” pokazuje pewną ograniczoność i stereotypowość
ludzkiej perspektywy poznawczej. Nasze poglądy ukształtowane na zwykłej, codziennej mechanice okazują się nie
prawdziwe, a dokładniej ograniczone do pewnego zakresu wielkości fizycznych.

1) Dodawanie prędkości. Wzór na relatywistyczne składanie prędkości.
Zapiszmy wzory transformacyjne Lorentza w postaci :

x’ = (x

−

vt) / sqrt( 1

−

v2/c2 ) = γ(x

−

vt)

t’ = [ t – ( v/c2 )x ] / sqrt( 1

−

v2/c2 ) = γ[ t – ( v/c2 )x ]

y’ = y ; z’ = z
Niech punkt materialny P porusza się z prędkością u względem układu U, oraz z prędkością u’ względem układu U’. Niech
układ U’ porusza się z prędkością v względem układu U ( kierunek wektora prędkości v zgodny jest z osiami O’x’ || Ox )

Rys 1a. Zależność u’ od u według wzoru relatywistycznego i klasycznego.
( wyróżniamy następujące obszary wartości szybkości : obszar klasyczny v << c, obszar relatywistyczny v < c ,
obszar ultrarelatywistyczny v

≈

c )

Zbadajmy zależność między u i u’.
Mamy oczywiście :
u = dx/dt ; u’ = dx’/dt’
Obliczając odpowiednie różniczki otrzymamy :

dx’ = (dx – vdt ) / sqrt ( 1

−

v2/c2 ) = γ (dx – v dt) ; dt’ = [ dt – ( v/c2 )dx ]/ (sqrt ( 1

−

v2/c2 ) = γ[ dt – ( v/c2 )dx ]

zatem :

u’ = (dx – v dt) /[ dt – ( v/c2 )dx ] = [ (dx/dt) – v ] / [ 1– (v/c2 )(dx/dt) ] = (u – v) / [ 1– (u v/c2 ) ]

u’ = dx’/dt’ = ( u – v ) / [ 1 – u v/c2 ] - dla wektorów u ,v o tym samym zwrocie. (6.1)

u’ = dx’/dt’ = ( u + v ) / [ 1 + u v/c2 ] - dla wektorów u ,v o zwrocie przeciwnym. (6.2)

Dla przypadku granicznego c

→

∞

wzory (6.1), (6.2) przechodzą w klasyczne wzory na dodawanie prędkości w mechanice

newtonowskiej ( wzory Galileusza ), jest tak również dla przypadku kiedy uv/c2 << 1

Przykład 6.1 Z rakiety kosmicznej zbliżającej się do Ziemi z prędkością v = 200000[ km/s ]

≈

2/3 c wystrzelono w

kierunku jej ruchu pocisk którego prędkość względem rakiety wynosi u’ = ½ c.

dko

ść

relatywistyczna

dko

ść

klasyczna

Przedział mechaniki klasycznej

Pytanie z jaka prędkością ten pocisk będzie zbliżał się do obserwatora na Ziemi ?
Stosując wzór klasyczny, otrzymamy : u = u’ + v = 7/6c - wynik ten nie jest zgodny z postulatem stałości c.
( przypominam, że postulat ten ma poparcie doświadczenia ). Stosujemy zatem wzór relatywistyczny :

u = ( u’ + v ) / [ 1 – u’v/c2 ] = 21/24 c [ km/s ]

Przykład 6.2 Niech w układzie U punkt materialny P porusza się z prędkością c ( lub bliską c ). Obliczyć prędkość punktu
P w układzie U’ poruszającym się względem U z prędkością v ( wektory v, c mają ten sam zwrot )
Stosując wzór (6.1) otrzymujemy :
u’ = ( c – v ) / [ 1 – ( v/c ) ] = c

Przykład 6.3 Wzory (6.1), (6.2) możemy wyprowadzi bez odwoływania się do różniczek dzieląc po prostu x /t oraz
zauważając, że :
u’ = x’/t’ .

u’ = ( x’+ vt’ ) / [ t’ + ( vx’/c2 ) ] = [ (x’/t’) + v ] / [ 1 + (vx’’/t’c2 ) ] = u + v / [ 1 + (uv/c2 ) ]

Obliczmy teraz pozostałe składowe wektora prędkości. W kolejności otrzymamy :

ux’ = dx’/dt’ = ( ux – v ) / [ 1 – ux v /c

2 ] (6.3)

uy’ = dy’/dt’ = uy sqrt [ 1 – (v/c)

2 ] / [ 1 – ( v /c2 )] u

x (6.4)

uz’ = dz’/dt’ = uz sqrt [ 1 – (v/c)

2 ] / [ 1 – ( v /c2 )] u

x (6.5)

Zauważmy, że chociaż prędkość v jest skierowana wzdłuż osi Ox , to składowe uy’ , uz’ zależą od ux.
Czasami wygodnie jest zastosować wektorowy zapis powyższych wzorów :

u = ( 1 + u’v /c2 )-1 [ γ -1 u’ + v + ( 1 – γ -1 ) (u’v) v /v2 ) ]

Kinematyka relatywistyczna różni się od nierelatywistycznej wtedy gdy dodajemy prędkości mierzone w różnych IUO.
Wzór na dodawanie prędkości dotyczy dwóch takich układów. Gdy mamy do czynienia z prędkościami dwu punktów w
jednym układzie to odpowiedź na pytanie jaka jest ich względna prędkość jest taka sama w kinematyce relatywistycznej
jak i klasycznej.
Przykładowo niech związany z pewnym IUO obserwator przygląda się ruchowi dwóch pociągów poruszających się
względem niego z prędkościami +0,9c i – 0.9c. (wektory ich prędkości są równoległe i oczywiście przeciwnie skierowane )
Pytanie brzmi z jaka prędkością z jego punktu widzenia pociągi się zbliżają do siebie ?
Odpowiedź brzmi pociągi zbliżają się do siebie z prędkością 1,8c !! Z punktu widzenia naszego obserwatora nie mamy
podstaw zastosować relatywistyczny wzór na dodawanie prędkości. Z punktu widzenia maszynistów jak najbardziej.
Wynik 1,8c nie stoi oczywiście w sprzeczności z postulatami STW – prędkość zbliżania się pociągów nie jest prędkością
przenoszącą energie-masę–informację. [ zobacz dalsze przykłady 17-literatury dodatkowej str. 14 ; 12 str. 98 ]

2) Prędkość maksymalna.
Prędkość światła w próżni jest prędkością maksymalną – graniczną, dla ciał materialnych które mogą spoczywać w
pewnym układzie odniesienia. W związku z tym mówimy również, że dla fotonu nie istnieje układ odniesienia w którym
mógłby on spoczywać. Gdyby ciało o niezerowej masie spoczynkowej mogłoby się poruszać z prędkością c, to związany z
tym ciałem układ odniesienia również poruszałby się z prędkością c, względem każdego innego układu odniesienia, próba
zastosowania wzorów Lorentza dla takiego przypadku skończyłaby się tym, że we wspomnianych wzorach pojawiłoby się
zero w mianowniku, zatem całe wyrażenie stawałoby się nieokreślone. Zatem wniosek jest jeden - układ odniesienia nie
może być ( sensownie ) związany z ciałem o zerowej masie spoczynkowej.
Rozważmy punkt materialny o niezerowej masie spoczynkowej, który w pewnym IUO U’ doznaje stałego przyspieszenia a
Zbadajmy w jaki sposób będzie narastała prędkość tego punktu materialnego w układzie U.
a’ = du’/dt’ ⇒ du’ = a’dt’

du = [ 1

−

(v/c)2 ]a’dt’ / [ 1 + (u’v/c2 ) ] (6.6)

Przyjmijmy teraz, że u’ = 0 i du = dv tzn. punkt materialny utożsamiamy z układem U’ ( to cały układ U’ jest
przyspieszany ). Podstawiając do wzoru (6.6) otrzymamy :

dv = [ 1

−

(v/c)2 ] a’dt’ (6.7)

Następnie całkujemy to wyrażenie :
v t’

∫

dv / [ 1 - (v/c)2 ] =

∫

a’dt’ (6.8)

0 0
Ponieważ a’ = const. zatem :

∫

a’dt’ = a’t’

Następnie stosujemy zamianę zmiennych n = v/c , dv = dnc :

∫

dn / [ 1 - (n)2 ] = arctgh (n) = c arctgh (v/c)

Zatem

arctgh (v/c) = a’t’/ c ⇒ v/c = tgh (a’t’/ c ) ⇒ v = c tgh (a’t’/ c )
Jest to wzór na prędkość punktu ( układu U’ ) względem układu U w funkcji czasu t’. Prędkość ta zbliża się
asymptotycznie do prędkości światła. [ 12, str. 24 ]

Możemy zatem powiedzieć, że w przyrodzie istnieje jedna jedyna prędkość c – wspólna dla wszystkich cząstek (obiektów
fizycznych ), które posiadają zerową masę spoczynkową tj. dla których nie można wskazać spoczynkowego IUO.
( mówimy wtedy o prędkości c jako o prędkości absolutnej ). Prędkość c jest prędkością graniczną dla cząstek które
posiadają niezerową masę spoczynkową. Jakkolwiek nie próbować rozpędza takie obiekty ich prędkość będzie jedynie
dążyć do prędkości c ale nigdy jej nie osiągnie ( możliwe jest jedynie asymptotyczne zbliżenie do prędkości c ).
Widać więc, że w zależności od zachowania relatywistycznego cząstek fizycznych moglibyśmy je podzielić na :
- cząstki dla których jest sensowne określenie spoczynku ( poruszają się one z prędkościami zawartymi w zbiorze < 0, c )
możliwe jest związanie ich z układem odniesienia
- cząstki dla których pojęcie spoczynku traci sens ( poruszają się one tylko z prędkością c )
niemożliwe jest związanie ich z układem odniesienia
- cząstki dla których pojęcie prędkości związanej z układem odniesienia traci sens (lub sens traci klasyczne rozumienie
pojęcia cząstki ).

Efekty kinematyczne transformacji Lorentza

3 Dylatacja czasu – wydłużenie interwałów czasowych. Względność pojęcia jednoczesności.
Jednym z najważniejszych wniosków, wypływającym z konsekwentnie stosowanych wzorów transformacyjnych Lorentza
jest odrzucenie absolutności pojęcia czasu i wprowadzenie pojęcia „czasu własnego” przy czym jednocześnie stwierdzamy,
( co jest poparte bogatym materiałem empirycznym) względność upływu takiego czasu tj. interwał czasowy jest zależny od
IUO w którym dokonujemy pomiaru takiego interwału. Jest to efekt kinematyczny tj. związany z samą naturą określenia
przestrzeni i czasu a nie z fizyczną naturą samych przyrządów pomiarowych ( ciał materialnych). Należy podkreślić, że dla
rozpatrywanych przez nas głownie IUO jest to efekt całkowicie symetryczny - ponieważ zasada względności pozostaje w
mocy, za jego pomocą nie można wskazać układu absolutnie spoczywającego ( sens tych zdań by może stanie się
jaśniejszy po przeczytaniu całego punktu ).
W fizyce klasycznej uznawano jako sensowne stwierdzenie, że pewna określona klasa zdarzeń zachodzi w różnych
miejscach w tej samej chwili czasu tj. równocześnie. Postulowanie istnienia sygnałów rozchodzących się nieskończenie
szybko umożliwia zasadność tak sformułowanej jednoczesności a co za tym idzie czasu absolutnego.
Zasługą Einsteina było m.in. zwrócenie uwagi na to, że pojęcie równoczesności przyjmowane dotychczas, w związku z
postulatem istnienia stałej c (absolutnej) nie jest uzasadnione i jest niepoprawne. Czas w którym zaszło dowolne zdarzenie
mierzymy zegarem a co jest najważniejsze dla tego pomiaru, to bezpośrednia bliskość zegara i zachodzącego zjawiska.
Z instrumentalistycznego (operacyjnego ) punktu widzenia możemy wyposażyć IUO w układ zegarów tak aby w każdym
dostatecznie małym obszarze przestrzenny możliwy był „natychmiastowy” pomiar czasu zachodzącego w tym obszarze
zjawiska. W tym miejscu pojawia się nie znany w mechanice klasycznej problem synchronizacji takich zegarów. Poprzez
synchronizacje rozumiemy operacje ustawienia na nich jednej, wspólnej godziny np. godziny zero- zero.
Można pokazać, że dwa zegary spoczywające w IUO możemy zsynchronizować bez żadnych specjalnych kłopotów.
W tym celu wybieramy punkt środkowy (jednakowo odległy od obu zegarów), prostej łączącej te dwa zgary i wysyłamy z
niego równocześnie ( równoczesność jest zagwarantowana punktowością tego zdarzenia ) do każdego zegara sygnał np.
świetlny. Zegary uważamy za zsynchronizowane jeżeli w momencie dojścia do nich wysłanych sygnałów wskazują
jednakowy czas. ( lub po prostu w tej właśnie chwili włączamy te zegary ustawiając je wcześniej na jednakową godzinę )
Z jednorodności i izotropowości czasu wnioskujemy, że relacja synchronizacji jest relacją przechodnią , zatem tym
sposobem możemy zsynchronizować dowolną ilość zegarów spoczywających w danym i jednym IUO.
Możliwe jest również zsynchronizowanie dwóch i tylko dwóch zegarów poruszających się względem siebie ruchem
swobodnym. Cały „problem” STW polega właśnie na niemożliwości zsynchronizowania dwóch zbiorów zegarów
związanych z układami U i U’ ( poruszającymi się ruchem względnym ). Mówimy, że układ zsynchronizowanych zegarów
związany z układem U nie jest już układem zsynchronizowanych zegarów w układzie U’. ( zobacz określenie definicji
synchronizacji zegarów według Einsteina )
Mając do dyspozycji układ zsynchronizowanych zegarów w dowolnym IUO, możemy dokonać pomiaru czasu zdarzeń
zachodzących w dowolnie ( lub prawie dowolnych ) odległościach przestrzennych. Znając odległość od danego zdarzenia i
dysponując sygnałem świetlnym o stałej prędkości c, możemy obliczyć czas w jakim to zdarzenie zaszło.
Oczywistym problemem jest zagadnienie pomiaru stałej c. Pomiaru tego dokonujemy mierząc czas potrzebny na przebycie
zadanej odległości przez promień światła. Mamy dwa sposoby aby tego dokonać, w pierwszym z nich odejmujemy
wskazania dwóch zsynchronizowanych zegarów umieszczonych w punkcie początkowym i końcowym, ale cały problem
tej metody polega na pierwotnym braku zsynchronizowanych zegarów. Drugi sposób polega na pomiarze czasu, który
upłynął między wysłaniem a rejestracją sygnału świetlnego. Sygnał wysłany odbija się od lustra umieszczonego na zadanej
odległości od nadajnika. W metodzie tej korzystamy tylko z jednego zegara, odpada wiec problem synchronizacji.
Podwojona odległość między nadajnikiem a lustrem podzielona przez odmierzony czas wyznacza szybkość sygnału
świetlnego. ( utajoną hipotezą jest przyjęcie, że szybkość promienia świetlnego w kierunku lustra jest taka sama jak
szybkość promienia odbitego – w każdym bądź razie empiria nie przeczy tej hipotezie )
[ 12, str. 84 ; 7-literatury w języku rosyjskim , str. 30 ]

Wydawać by się mogło, że istnieje jeszcze jeden sposób synchronizacji zegarów : zbieramy zegary w jednym miejscu
nastawiamy wszystkie na jednakowe wskazanie a następnie przemieszczamy zegary, każdy do swojego położenia
pierwotnego. Problemem jest tylko to, że proces przemieszczania spowoduje rozsynchronizowanie tych zegarów – wynika
to z faktu przejścia zegara w momencie rozpoczęcia ruchu do NIUO a następnie do IUO poruszającego się względem
pierwotnego układu synchronizacyjnego. ( taki sposób nazywa się „synchronizacją zegarów w sensie Galileusza” )
Właściwa procedura polega zatem na ustawieniu w odpowiednich miejscach zegarów a później kolejnej ich synchronizacji
z zegarem odniesienia np. zegarem umieszczonym w początku układu odniesienia ( początku układu współrzędnych ).
Ten opis szczegółowy opis procedury synchronizacji jest kluczowym dla całej STW.
W przeciwieństwie do niego opis sposobu pomiaru odległości przestrzennych w STW właściwie sprowadza się do opisu
pomiaru klasycznego. Wzorcowy pręt mierniczy ( odpowiednio wyskalowany, absolutnie sztywny ) przykładamy wzdłuż
prostej ( ogólnie najkrótszej krzywej) łączącej dany punkt z początkiem układu współrzędnych, uważając aby za każdym
razem jego początek pokrywał się z punktem w którym był jego koniec. Powstaje naturalne pytanie : o ile mając pręt
mierniczy o postulowanych własnościach możemy ( w zasadzie ) dokonać takich pomiarów, to problemem pozostaje
zagadnienie wyznaczenia najkrótszej krzywej oraz problem „niefizycznych” własności pręta pomiarowego, w
szczególności pręty absolutnie sztywne nie istnieją. W STW możemy jednak dopuść taką idealizację, jednak powody dla
których jest to możliwe wykraczają poza ramy obecnie omawianych zagadnień.

Na szczególne podkreślenie zasługuje fakt, że do jednej z zasług jakie oddała STW fizyką , jest zwrócenie uwagi na
konieczność krytycznego podejścia do procedury pomiarowej. Procedura pomiarowa określa wielkości fizyczne tj.
istnienie „czegoś” w fizyce jest przede wszystkim określeniem (poprawnym i fizycznie sensownym) procedury pomiaru
tego „czegoś”.
„Pomiary w fizyce odgrywają decydującą rolę. Możliwość zmierzenia pewnej wielkości jest warunkiem koniecznym, aby
wielkość ta mogła stać się przedmiotem zainteresowania fizyka. Lord Kelvin mawiał : „Jeżeli potraficie zmierzyć to, o
czym mówicie oraz wyrazić to w liczbach, wówczas wiecie o czym mówicie; lecz jeżeli nie potraficie tego zmierzyć ,
jeżeli nie potraficie wyrazić tego w liczbach, to wasza wiedza jest niewystarczająca i jałowa” ”
( cytat z [ 20-literatury dodatkowej, str. 210 ] )

Oczywiście, konsekwentne trzymanie się tak określonego sposobu definicyjnego dla wszystkich pojęć fizycznych
prowadzi do „operacjonizmu”.
( Zainteresowanego odsyłam np. do hasła „operacjonizm” w „Filozofia a nauka” – zarys encyklopedyczny PWN 1987
lub do pewnych jego filozoficznych implikacji „Granice racjonalności – eseje z filozofii nauki” – J. Zyciński
WN-PWN 1993 )
Kończąc, te troszkę metodologiczne komentarze, należy jeszcze powiedzieć, że we współczesnej fizyce w związku z
bardzo intensywnym rozwojem metod pomiarowych czas ( właściwie częstotliwość ) jest wielkością , którą potrafimy
zmierzyć z bardzo dużą dokładnością ( rzędu femtosekund ), dlatego standardowymi wzorcem stał się właśnie zegar
( częstościomierz – zazwyczaj atomowy ), wzorzec długości ( pierwotnie była nim sztaba platynowo-irydowa ) został
zastąpiony przez ultra dokładny pomiar czasu ( przy postulacie istnienia stałej c, metoda ta jest równoważna pomiarowi
odległości przestrzennych ).
( zobacz definicje odpowiednich wzorców np. w „Legalne jednostki miar i stałe fizyczne” -- J. M. Massalski, J. Studnicki
PWN 1988 ; współczesne metody pomiaru czasu omówiono np. artykule pt. „Clocks for Length and Time Measurement” -
Fritz Riehle, dostępnym w książce “Gyros, Clocks, Interferometers...Testing Relativistic Gravity in Space” -
C. L¨ammerzahl C.W. F. Everitt F.W. Hehl (Eds.) Springer 2000 )

Rozważmy teraz dwa IUO U i U’ poruszające się względem siebie z prędkością v ( v || Ox || O’x’ ). Niech na osiach : Ox i
O’x’ rozmieszone będą zsynchronizowane w swoich układach spoczynkowych układy zegarów ( rys. 2 )

Rys. 2 Układy zegarów.

Zegary z punkcie x =x’ = 0 wskazują w chwili mijania się chwile zero. Zegary układu U’ mijają kolejno zegar
umieszczony w punkcie x = 0. Powstaje pytanie jakie jest wskazanie zegara układu U’, mijającego ten zegar ?
Zgodnie z wzorami transformacyjnymi otrzymujemy :

t’ = γ [ t – ( v/c2 )x ] ale x = 0 , zatem t’ = γt

Analogicznie do zagadnienia możemy podejść również tak :
Rozważmy dwa IUO U i U’ , poruszające się tak samo jak poprzednio. Obserwator związany z układem U dokonuje
pomiaru pewnych stałych, periodycznych odcinków czasu np. między dwoma błyskami światła. Oznaczmy taki
pojedynczy interwał czasowy, jak następuje :
t = tk – tk (6.9)
Pytanie, na jakie teraz musimy odpowiedzieć jest następujące : jaki będzie wynik pomiaru tego interwału w układzie U’ ?
( analogicznie zagadnienie to możemy postawić następująco : zegar spoczywający w układzie U odmierza stałe interwały

∆

t, interwały o jakich wartościach odmierza zegar umieszczony w układzie U’ ?

Wykorzystamy oczywiście wzór :

t’ = γ [ t – ( v/c2 )x ]

t’ = γ[ ( tk – tp ) - ( v/c

2 ) ( x

k – xp ) ] = γ t (6.10)

( bo xk – xp = 0 – zdarzenia zachodzą w jednym miejscu )
Ponieważ γ

∈

< 1 , +

∝

) t’

≥

Wniosek. Zegar poruszający się względem układu U idzie wolniej, niż zegar znajdujący się w spoczynku w tym
układzie U.
Efekt ten nazywamy „dylatacją czasu” ( wydłużeniem lub spowolnieniem czasu ). Obrazowo mówiąc powiemy, że
ruchomy zegar (zsynchronizowany w swoim układzie spoczynkowym) spóźnia się w stosunku do zegara spoczywającego.
Ponieważ mówimy o IUO efekt dylatacyjny jest efektem symetrycznym tj. obserwator związany z układem U porównując
odczyty swojego zegara z zegarem znajdującym się w układzie U’ stwierdzi, że to jego zegar spieszy.
Jest jeszcze jedne problem : możemy sensownie powiedzieć, że zegar ruchomy spóźnia się nie w stosunku do jednego
nieruchomego zegara ale w stosunku do kolejno mijanych nieruchomych zegarów.
„Stwierdzenie, że pojedynczy zegar U’ spóźnia się w stosunku do pojedynczego zegara U nie ma w rzeczywistości
żadnego obiektywnego sensu. Zegary są odległe od siebie i nie można bezpośrednio porównywać ich wskazań więcej niż
jeden raz w ich historii.” [ 4, str. 50 ].
Dla dwóch obserwatorów związanych z układami U i U’ możemy sensownie powiedzieć, że obaj mają rację mówiąc :
ponieważ ja „spoczywam” to moje zegary chodzą dobrze a zegary w układzie U’ chodzą wolniej
ponieważ to ja spoczywam to moje zegary chodzą dobrze a zegary w układzie U spóźniają.
Cały problem zasadza się na „rozsynchronizowaniu” się zegarów znajdujących się w ruchu.
Obserwator U sprawdza chód zegarów w U’ porównując odczyty jednego z nich z odczytem dwóch swoich zegarów
(zsynchronizowanych w U’ ), to samo robi obserwator U’, używając zegarów zsynchronizowanych w swoim IUO.
Jak wiemy jednak : zegary zsynchronizowane w układzie U nie są (na ogół ) zsynchronizowane kiedy „patrzeć” na nie z
innego IUO. Co oczywiście wynika z określenia pojęcia równoczesności.
Dlatego też podstawowy problem STW jakim jest pojęcie jednoczesności ( synchronizacji ) musi być uwzględniony przy
pomiarze długości. ( punkt następny ) ( zobacz również [18, str. 518 ] )

Względność pojęcia równoczesności.
Niech w pewnym IUO U obserwowane zdarzenia z1i z2 zachodzą w jednej chwili czasu t = t1= t2. O tych zjawiskach
powiemy, że w układzie U zaszły równocześnie ( jednocześnie ). Powstaje pytanie czy te dwa zdarzenia równoczesne w
układzie U są równoczesne w dowolnym innym IUO U’ ?
Możemy wyróżnić dwie odmienne sytuacje :
a) zdarzenia jednoczesne w układzie U zachodzą w różnych punktach przestrzennych ( w różnych miejscach przestrzeni )
b) zdarzenia jednoczesne w układzie U zachodzą w jednym miejscu w przestrzeni.
Zgodnie z wzorami transformacyjnymi Lorentza dla t1= t2 = 0 , otrzymujemy :
t’2 - t’1 = γ ( v/c

2 ) ( x

2 – x1)

Dla przypadku b) mamy x2 = x1 zatem t’2 - t’1 = 0 tj. zdarzenia z1i z2 równoczesne w układzie U będą również
jednoczesnymi w układzie U’.

Zanim rozpatrzymy przypadek a) wprowadzimy pewne oznaczenia
W układzie U zdarzenie z2 nazwiemy „zdarzeniem późniejszym” a zdarzenie z1, nazwiemy zdarzeniem „wcześniejszym”.
Ustaliliśmy w ten sposób pewną kolejność zdarzeń dla układu U.
Ogólny wzór wynikający z transformacji Lorentza ( dla zdarzeń niejednoczesnych ) ma oczywiście postać :

t’2 - t’1 = γ ( t2 – t1) - ( v/c

2 ) ( x

2 – x1)

Dla zdarzeń równoczesnych w układzie U ( t1= t2 = 0 ) i nie zachodzących w jednym miejscu x2

≠

x1 otrzymamy :

Jeżeli x1 > x2 to t’2 - t’1 > 0 tzn. w układzie U’ zdarzenia z2 i z1 mają taka samą kolejność jak w układzie U.
Jeżeli x1 < x2 to t’2 - t’1 < 0 tzn. w układzie U’ zdarzenia z2 i z1 mają taka samą odwrotną kolejność jak w układzie U.
tj. z punktu widzenia obserwatora U’ to zdarzenie z2 jest wcześniejsze a zdarzenie z1 jest późniejsze.
Dal zdarzeń nie jednoczesnych i zachodzących w różnych miejscach mamy przypadki :

( t2 – t1) - ( v/c

2 ) ( x

2 – x1) = 0 – zdarzenia równoczesne w U’

( t2 – t1) - ( v/c

2 ) ( x

2 – x1) > 0 – zachowana kolejność zdarzeń w U’

( t2 – t1) - ( v/c

2 ) ( x

2 – x1) < 0 – odwrócona kolejność zdarzeń w U’

Widzimy więc, że z punktu widzenia mechaniki relatywistycznej kolejność zdarzeń jest pojęciem względnym, zależy od
układu odniesienia.

Przypadek ( t2 – t1) - ( v/c

2 ) ( x

2 – x1) < 0 zachodzi wtedy gdy : ( c

2/v ) ( t

2 – t1) < ( x2 – x1)

tzn. gdy odległość dwóch zdarzeń jest tak duża , że promień światła wychodzący z x1 w chwili t1nie może osiągnąć punktu
x2 przed upływem czasu t2. Mówimy, że kolejność dwóch zdarzeń może być odwrócona tylko wtedy gdy nie może między
tymi zdarzeniami związek przyczynowy. [ 2, str. 34 ]
Mówimy, że między dwoma zdarzeniami występuje związek przyczynowy jeżeli możemy je połączyć sygnałem
świetlnym. Jeżeli wysłanie promienia świetlnego z jakiegoś punktu uznamy za przyczynę, natomiast odbiór tego sygnału w
innym punkcie za skutek to na terenie STW kolejność tych zdarzeń nie może być odwrócona.
Kolejność dwóch zdarzeń może być odwrócona jeżeli nie występuje między nimi związek przyczynowy.

Mówimy również, że względność pojęcia równoczesności dwóch zdarzeń nie kolokalnych świadczy o tym, że przestrzeń i
czas są ściśle powiązane ze sobą – przy przejściu U

→

U’ odcinki czasu między zdarzeniami, uzależniane są od ich

odległości przestrzennych.

4) Skrócenie Lorentza-Fitzgeralda. ( The Lorentz-Fitzgerald contraction )
Rozpatrzmy następujący problem : obserwator związany z pewnym IUO U zmierzył długość dowolnego przedmiotu np.
stalowego pręta. Pręt ten spoczywa w tym układzie odniesienia. Wynik tego pomiaru :
L = współrzędna początku pręta – współrzędna końca pręta
L = xp – xk (6.11)
Dla uproszczenia zakładamy, że nieruchomy pręt leży na osi Ox.
Pytanie jakim się teraz zajmiemy brzmi : jaki wynik pomiaru długości otrzyma obserwator związany z układem U’ ?
( Układ ten porusza się tak jak poprzednio tj. z prędkością v || Ox || O’x’ )

Długość pręta w układzie U’ będzie równa :
L’ = x’p – x’k (6.12)
W teorii klasycznej mieliśmy oczywistą odpowiedź na to pytanie : L = L’ tj. obie te długości były sobie równe.
Możemy zastanowić się teraz w jaki sposób dokonać pomiaru długości pręta gdy znajduje się on w ruchu. Oczywiste jest,
że zgodnie z powyższymi wzorami powinniśmy wyznaczy współrzędne końca i początku a co najważniejsze powinniśmy
wykonać te pomiary w jednej chwili tj. jednocześnie.
( Zobacz również wspomniany tekst pt. „Matematyczne podstawy szczególnej teorii względności” )
Aby uzyskać związek pomiędzy L a L’ należy wyrazić współrzędne początku i końca pręta w układzie U przez
współrzędne i czas początku i końca pręta w układzie U’ i przyjąć tę samą wartość czasu t dla obu tych współrzędnych w
układzie U’.
x’p = γ ( xp – vtp ) ; x’k = γ ( xk – vtk ) (6.13)
Zatem :
L’ = γ [ xk – xp – v ( tk – tp ) ] (6.14)
t’p = γ [ tp – (v/c

2)x

p ] ; t’k = γ [ tk – (v/c

2)x

k ] (6.15)

Zatem, ponieważ żądamy aby t’p = t’k :
tp - tk = (v/c

2) ( x

k - xp ) (6.16)

L’ = γ { xk – xp – v [ (v/c

2) ( x

k - xp ) ] } = γ [ ( xk – xp ) ( 1 – β

2 ) ] (6.17)

L’ = γ ( 1 – β2 ) L = L ( 1 – β2 ) / sqrt ( 1 – β2 ) = L sqrt ( 1 – β2 )

Ponieważ β

∈

< 0, 1) to sqrt ( 1 – β2 )

∈

< 1, 0 ) co oznacza , że L’ < L.

L’ = L sqrt ( 1 – β2 ) (6.18)
Wniosek. Przedmiot obserwowany z dowolnego IUO, poruszającego się względem IUO w którym ten przedmiot spoczywa
ma krótszy wymiar zgodny z kierunkiem ruchu względnego tych układów. Mówimy w tym przypadku o tzw. kontrakcji
długości podłużnej.
Długość pręta w układzie w którym on spoczywa ( w naszym przypadku L ) nazywamy „długością własną”.

Dla β = 10-8 , co w przybliżeniu odpowiada prędkości liniowej ruchu Ziemi względem układu związanego ze Słońcem,
zmniejszenie długości promienia ziemi w kierunku ruchu z punktu widzenia obserwatora związanego ze Słońcem wynosi

6,5

10-2 [m ]. [ 12, str. 91 ]

Omówmy pewien kontekst historyczny związany z kontrakcją długości.
W celu utrzymania hipotezy spoczywającego eteru Lorentz wysunął postulat, że jeżeli ciało porusza się z szybkością v

względem eteru, to jego długość w kierunku ruchu ulega skróceniu – miarą tego skrócenia jest czynnik sqrt ( 1 – β2 ).
Niezależnie od niego taki postulat wysunął Fitzgerald. Lorentz posługując się własną teorią elektronową uważał, że
zjawisko kontrakcji przedmiotów znajdujących się w ruchu jest spowodowane pewna siłą działająca na przedmioty
przechodzące podczas ruchu przez stacjonarny eter ( naturę tych sił upatrywano w siłach elektrodynamicznych ).
Na przełomie XIX i XX wieku tj. w okresie burzliwego naporu nowych ideii problem ten był bardzo szeroko dyskutowany.
Jak wiadomo przełomową dla tego zagadnienia okazała się praca A. Einsteina, który przyjąwszy zupełnie odmienny do
powszechnie przyjmowanego stanowiska, punkt widzenia kładzie fundament pod gmach STW.
( zobacz 2-literatury dodatkowej )
Einstein zaproponował, że omawiane skrócenie nie jest „własnością” poruszającego się ciała ale własnością samej
przestrzeni.

Dla małych wartości prędkości względnej v, otrzymujemy : L

≈

L’. Ponieważ kontrakcja dotyczy tylko wymiarów

podłużnych mamy : Lx’ = Lx sqrt ( 1 – β

2 ) , L

y’ = Ly , Lz’ = Lz

W związku z względnością pojęcia równoczesności możliwy jest jeszcze jeden sposób pomiaru długości pręta.
Można uznać również, że długością pręta ruchomego będzie odległość między współrzędnymi jego końców w układzie
U’, wyznaczonych w jednakowym czasie t. Wtedy :

L’ = γ ( xk – xp ) = L / sqrt ( 1 – β

2 )

Proszę porównać z wzorem poprzednio otrzymanym :

L’ = L sqrt ( 1 – β2 )
Przy tym sposobie pomiaru długości liniowe są najmniejsze w tym układzie względem którego ciało spoczywa. Wida więc
,że ruchomy pręt nie doznaje „rzeczywistego” skurczenia ,ale jego długość zależy od układu odniesienia, względem
którego ją mierzymy oraz od przyjętej zasady pomiaru długości. [ 13, str. 38 ]
Kontrakcja długości jest więc bezpośrednią konsekwencją względności pojęcia równoczesności , a ta z kolei jest
konsekwencją postulatu istnienia prędkości absolutnej c.
Można pokazać, że skróceniu nie ulegają wymiary poprzeczne – jeśli wystąpiłby taki efekt została by złamana zasada
względności [ 18 str. 524 ].
Dlaczego ?
Niech będą dane dwa IUO U, U’ poruszające się wzdłuż osi Ox || O’x’. Ustawmy równolegle do osi Oy, O’y’ dwa pręty
pomiarowe OL, O’L’. Niech na końcu tych prętów zamontowane będą pisaki – tak, że podczas ruchu rysowane są dwie
linie. Czy linie te pokrywają się ? Jeśli linie te nie pokrywałyby się to moglibyśmy określić, który z układów się porusza, a
to przeczyłoby zasadnie względności. Zatem musi zachodzić y’ = y i z’ = z

Rys. 2a Chcąc zachować zasadę względności wnioskujemy, że wymiary poprzeczne ciał poruszających się z pewną
prędkością względna są jednakowe.

Ponieważ poprzeczne rozmiary obiektów nie ulegają zmianie wzór na relatywistyczną zmianę objętości ma postać :

V’ = V sqrt ( 1 – β2 ) ; V – objętość spoczynkowa w układzie U , V’ – objętość w układzie U’

Należy zauważyć, że zarówno efekt dylatacji jak i kontrakcji są w istocie konsekwencją jednego efektu –
rozsynchronizowania się poruszających się zegarów. ( zatem i względności jednoczesności ).

A jak wiadomo problem ten jest wynikiem istnienia stałej c. Temat ten poruszam również w punkcie XIII.
Przykład 4.1 [ 7-literatury dodatkowej, str. 65 ]
Pręt pomiarowy o długości 1,5 [ m] spoczywa w układzie U. Jaka będzie jego długość w układzie U’ ( poruszającym się z
prędkością v || Ox || O’x’ = 0.98 c ) oraz jego orientacja jeżeli w układzie U tworzy on kąt φ = 45

z osią Ox.

Rozłóżmy długość pręta w układzie U, na dwie składowe :
Lx = L cos(φ) – składowa pozioma
Ly = L sin(φ) – składowa pionowa
Składowa pionowa jest prostopadła do v i zgodnie z wzorami transformacyjnymi Lorentza nie dozna żadnego skrócenia :
L’y = Ly = L sin(φ)
Składowa pozioma jest równoległa do v i dozna skrócenia zgodnie ze wzorem (6.18) :

L’x = Lx sqrt ( 1 – β

2 ) = L cos(φ)

sqrt ( 1 – β

2 )

Długość pręta L’ będzie zatem równa :

L’ = sqrt ( L’x

2 + L’

2 ) = L sqrt [ 1 - β2 cos2 (φ) ]

Orientacja pręta w układzie U’ będzie określona wzorem :
tg (φ’) = L’y / L’x = γ tg(φ)
Podstawiając wartości liczbowe otrzymujemy :
L’ = 1.08 [ m] , φ = 78, 7

Zatem pręt nie tylko doznał kontrakcji ale również zmienił kąt nachylenia.

Czasami bardzo pomocny jest następujący wzór ( wynika on ze wzorów (6.3), (6.4), (6.5) ) :

tg(

) = u’ sqrt [ 1 – (v2/ c2 ) ] sin(

’) / [u’ cos(

’) + v ]

Określa on zmianę kierunku wektora prędkości przy przejściu U

→

U’.

-kąt jaki prędkość u tworzy z osią Ox układu U ;

’ - kąt jaki prędkość u’ tworzy z osią Ox układu U’

Dla u’= u = c wzór ten ma postać :

tg(

) = sqrt [ 1 – (v2/ c2 ) ] sin(

’) / [ (v/c) cos(

’) ]

gdy v << c wzór ten możemy przybliżyć następująco :
tg(

) = tg(

’) [ 1 – v / c cos(

’) ]

możemy otrzymać znany wzór na aberracje światła :

∆θ

= (v /c) sin(

’)

Przykład 4.2 [ 12, str. 94 ]
W IUO U w punkcie xp = 0 w chwili tp = 0, został wyemitowany foton w kierunku osi Ox. Po czasie tk = xk /c ;
( L = xk - xp - długość drogi fotonu w układzie U ) został on zarejestrowany w punkcie.
Jaka jest długość drogi fotonu względem układu U’ ? ( poruszającym się z prędkością v || Ox || O’x’ )

Na pierwszy wzgląd wydawać by się mogło, że zadanie sprowadza się do prostego zastosowania wzoru (6.18)
Jednak należy pamiętać, że wzór na kontrakcję został wyprowadzony przy warunku jednoczesności tj. :

L’ = L sqrt ( 1 – β2 )
ale gdy : t’p = t’k – zdarzenia zachodzą w jednej chwili.
Podobnie wzór na dylatację został wyprowadzony przy warunku kolokalności tj. :
t’ = γt
ale gdy : xk = xp – zdarzenia zachodzą w jednym miejscu ( mówimy również, że zdarzenia są kolokalne,
przedrostek ko- zazwyczaj znaczy tyle co przymiotnik „współ” np. kolinearny ( współliniowy), koplanarny
(współpłaszczyznowy ) itp. )

W podanym zagadnieniu długość drogi, oczywiście L nie może by wyznaczona w jednej chwili, zatem wzór (6.18) nie
może by zastosowany.
W układzie U dowolna prędkość cząstki lub sygnału jest to, naturalnie stosunek drogi przebytej przez cząstkę do czasu w
jakim została przebyta ta droga tj. v = L/t. Dla naszego przykładu będziemy mieli : c = xk/tk . ( c = L/t ; t = tk -tp = tk )
W układzie U’ „przetransformowane” przeniesienie tego prostego wzoru prowadziłoby do sprzeczności tzn. :

c = L’/t’ = (L sqrt ( 1 – β2 )/ γt = ( L/t) ( 1 – β2 ) = c ( 1 – β2 ) ⇒ c = c ( 1 – β2 ) – co jest jawną sprzecznością z
postulatami STW.

Skorzystajmy zatem z wzorów (4.20) i (4.21) :
x’ = γ ( x – vt )

t’ = γ [ t – ( v/ c2 ) x ]
W chwili startu fotonu w układzie U mamy :

xp = 0 , tp = 0
w chwili rejestracji :
tk = L/c , xk = L
Przechodząc do układu U’ w chwili startu mamy :
x’p = 0 , t’p = 0
a w chwili rejestracji :

t’k = γ [ (L/c) + ( v/ c

2 ) L ] = γ (L/c) ( 1 + β)

x’k = γ [ L + (vL/c ) ] = γ L ( 1 + β)
Długość drogi przebytej przez foton, zmierzona w układzie U’ wynosi :
xk = L (1 + β) / sqrt [ (1 + β) (1 - β) ] = L sqrt [ (1 + β) (1 - β) ] / (1 - β)

Przykład 4.3 [ 12, str. 98 ]
W układzie U spoczywa pręt o długości L. Zwierciadła umocowane równolegle na jego końcach umożliwiają odbicie
promienia świetlnego i jego ruch wzdłuż pręta. W układzie tym czas potrzebny na przebycie przez promień świetlny drogi
„tam” i „z powrotem” wynosi : t = 2L/c.
Ile wynosi czas potrzebny do przebycia tej drogi z punktu widzenia ( „standardowo” poruszającego się ) układu U’ ?

W tym zadaniu możemy po prostu zastosować wzór : t’ = γ t ( zdarzenie emisji i odbioru są kolokalne )

Przykład 4.4 [ na podstawie 8, str. 166 oraz 19 str. 90 ]
Zadanie jest typowym zadaniem relatywistycznym pokazującym „namacalnie” pewne konsekwencje STW.
( do kręgu takich zagadnień należy często dyskutowany np. problem „drabiny w stodole” lub „klocka i dziury” )
Rozważmy następujący problem: w układzie U mamy podłużny pojemnik o długości własnej 1 [m] w kształcie prostokąta
otwartego na jednym z dłuższych boków. W układzie U’ poruszającym się z prędkością v || Ox || O’x’ = 0,6 c względem U
znajduje się wąż o długości własnej 1 [m] ustawiony równolegle do osi O’x’. Obserwator w układzie U pragnie schwytać
węża do pojemnika ustawionego równolegle do osi Ox w ten sposób aby poprzez otwartą jego część zamknąć w nim węża.
Pytanie czy mu się to uda ?
Obserwator U rozumuje następująco : wąż porusza się z parametrem prędkości 0.6 c , zatem jego długość zmniejszy się o
czynnik γ = 5/4 zatem w układzie U wąż będzie miał długość 0.8 [m] to znaczy, że wąż bez problemu zmieści się w
pojemniku.
Obserwator związany z U’ powie, że pojemnik ma długość 0.8 [m] zatem wąż na pewno nie zmieści się do niego.
Aby rozwiązać ten „paradoks” umieśćmy początek pojemnika w początku układu U tj. współrzędna początku pojemnika
xp = 0 a współrzędna jego końca xk = 1. Podobnie uczyńmy w układzie U’ z wężem tj. współrzędna jego „głowy” x’p = 0
a współrzędna „ogona” x’k = 1.
Dla całego tego zagadnienia kluczowym jest określenie gdzie i kiedy znajdą ścianki początkowa i końcowa i musimy to
określić zarówno dla układu U jak i U’.
W układzie U ścianki opadają oczywiście jednocześnie w chwili t = 0. W tym momencie koniec ogona węża znajduje się w
punkcie x = 0. Ponieważ jego długość jest równa 0.8 [m] to jego głowa znajduje się w punkcie x = 0.8 Zatem obserwator
złapie węża do pojemnika.
Na czym polega błąd rozumowania obserwatora U’ ?
Błąd polega na nieuzasadnionym przyjęciu równoczesnego „opadnięcia” ( i w konsekwencji zamknięcia ) ścianek
pojemnika.
Ścianka przednia opada w chwili tp= 0 i w punkcie xp = 0 zatem dla układu U’ zgodnie z wzorami transformacyjnymi
Lorentza otrzymamy :

t’p = γ [ tp – (vxp/ c

2 ) ] = 0

x’p = γ ( xp – vtp ) = 0
Ścianka tylna dla obserwatora U’ opada w chwili tk = 0 w punkcie xk = 1 zatem :
t’k = γ [ tk – (vxk/ c

2 ) ] = - 2,5 [ns]

x’k = γ ( xk – vtk ) = 1,25 [m]
Zatem ścianki nie opadają w tej samej chwili, ścianka tylna opada 2,5 [ns] wcześniej od ścianki przedniej, nadto z punktu
widzenia węża opada w punkcie oddalonym od środka jego układu o 1,25 [m] zatem wąż istotnie zostanie złapany.
( pozostaje jedynie problem co stanie się z wężem kiedy dotrze do tej ścianki )

W związku z wymienionymi konsekwencjami kinematycznymi przekształceń Lorentza powstaje naturalne pytanie
Na ile realne są to efekty ? W szczególności : Czy poruszający się pręt pomiarowy rzeczywiście ulega skróceniu w
kierunku ruchu ?
Odpowiedź na te pytania zależy od znaczenia jakie przypisujemy słowu „rzeczywiście”. W fizyce rzeczywiste jest to, co
jest zmierzone ( i to co podlega pomiarowi ). Obserwator przyglądający się zegarom i prętom w swoim układzie

odniesienia nie dostrzeże żadnych odchyleń od ich „zwyczajności”. Efekty te są jednak rzeczywiste w tym sensie, że
potwierdza je doświadczenie. [ 20-literatury dodatkowej, str. 217 ; 4 str. 51 ]
Na zakończenie charakterystyczny cytat :
„Można spotkać się jeszcze z pytaniem : jaka jest „rzeczywista” długość linijki ? Pytanie to jest pozbawione sensu, wtedy
gdy jest zadawane w znaczeniu „ogólnym”. Pytanie o długość linijki bez odniesienia do jakiegokolwiek układu
odniesienia nie ma sensu. W każdym układzie odniesienia linijka ma swoją długość ; jest to zawsze jej długość
„rzeczywista”. Wszystkie układy inercjalne są równoprawne, wszystkie określane w tych układach długości linijki są też
równoprawne” [ 16 str. 64 ]

Jeszcze tylko jedna uwaga dotycząca zadań związanych z STW. Generalnie możemy powiedzieć, że jeżeli postawione
zagadnienie wydaje się na pierwszy rzut oka „paradoksalne” to zazwyczaj związane jest to z „klasycznym” błędem ( który
oczywiście jest wynikiem usilnego stosowania „zdroworozsądkowej” intuicji do problemów relatywistycznych, w których
ta intuicja wielokrotnie prowadzi na manowce ) polegającym na uznawaniu zdarzeń jednoczesnych w jednym IUO U za
jednoczesne w układzie U’. I dualnie - zdarzeń kolokalnych w układzie U za zdarzenia kolokalne w U’.
( generalnie, mowa oczywiście o zdarzeniach które można połączyć krzywa czasopodobną )
A sprawa jest jasna : zdarzenie kolokalne i jednoczesne w U jest zdarzeniem kolokalnym i jednoczesnym w U’
Zdarzenie jednoczesne i nie kolokalne w U nie jest zdarzeniem jednoczesnym w U’. Zdarzenie kolokalne i nie jednoczesne
w U nie jest koloklane w U’. Wszystko to wynika naturalnie z własności przestrzeni M.
Sprawa druga : wszystko co do tej pory powiedziano odnosiło się do układów inercjalnych, układy inercjalne są
podstawowymi układami rozpatrywanymi w STW i chociaż nie ma przeszkód formalnych aby rozpatrywać układy
nieinercjalne w STW, zazwyczaj się tego nie czyni. Układu inercjalne mają ta przyjemna własność, że spełniona jest w
nich zasada bezwładności a tor światła jest geodezyjną zerową. Wszystko to sprawia, że sensowne jest symetryczne
potraktowanie wszystkich efektów kinematycznych wynikających ze wzorów Lorentza. Innymi słowy spełniona jest
zasada względności Einsteina. Problematyka przejścia do NIUO jak wiadomo zajmuje się OTW, dlatego też nie zadaje
sobie trudu ich rozważania. Generalnie można powiedzieć tak : ponieważ przyspieszenie jest wielkością absolutną tj.
zależną od układu odniesienia rozpatrywanie NIUO musi prowadzi do złamania zasady względności a w konsekwencji do
naruszenia warunków symetrii efektów kinematycznych ( patrz tzw. „paradoks zegarów” )

5) Relatywistyczna transformacja przyspieszenia.
Rozpatrzmy ponownie wzory (6.3) , (6.4), (6.5) zapisane w postaci :

ux = dx/dt = ( ux + v ) / ( 1 – v ux /c

2 )

uy = dy/dt = uy / γ ux [ 1 – ( v/c

2 ) ]

uz = dz/dt = uz / γ ux [ 1 + ( v/c

2 ) ]

Powtórne różniczkowanie względem czasu tych wzorów prowadzi do następujących zależności :

ax = dux /dt = d/dt [ ( ux + v ) / ( 1 – vux /c

2 ) ] = a’

x ( 1- β

2 )3/2 / ( 1 + vu’

x /c

2 )3 (6.19)

ay = [ ( 1 – β

2 ) / ( 1 – vu’

x /c

2 )2 ] [ a’

y – ( a’x vu’y /c

2 ) / ( 1 – vu’

y /c

2 ) ] (6.20)

az = [ ( 1 – β

2 ) / ( 1 – vu’

x /c

2 )2 ] [ a’

z – ( a’z vu’z /c

2 ) / ( 1 – vu’

z /c

2 ) ] (6.21)

Ze wzorów tych widać, że przyspieszenie zmienia się po przejściu od IUO U do U’ – co nie występowało w kinematyce
klasycznej. Inną różnicą jest również występowanie we wzorach prędkości punktu. [ 12, str. 100 ]

6) Ograniczenia zastosowania wzorów Lorentza.
Wzory transformacyjne :

x = (x’+ vt’ ) / sqrt [ 1 – ( v2/ c2 ) ]

t = [ t’ + (v/ c2 ) x’ ] / sqrt [ 1 – ( v2/ c2 ) ]
możemy bezkrytycznie stosować dla cząstek poruszających się z prędkościami v < c tj. dla cząstek o niezerowej masie
spoczynkowej.
Dla cząstek o zerowej masie spoczynkowej tj. cząstek poruszających się tylko z prędkością c wzory te tracą sens.
( ponieważ dzielimy przez zero )
Dla cząstek ( hipotetycznych ) mogących poruszać się z prędkościami większymi od c wzory przekształcają wartości
rzeczywiste ( można powiedzieć fizyczne ) czasu i przestrzeni na wartości zespolone ( konkretnie urojone, niektórzy
mówią, że nie fizyczne – zobacz jednak punkt X. Tachiony. ).

Nic nie stoi na przeszkodzie aby rozpatrywać ( matematycznie lub nawet fizycznie) zespolone przekształcenia Lorentza :
x =

(x’+ vt’ )

t =

[ t’ + (v/ c2 ) x’ ]

y = iy’
z = iz’

gdzie :

= sqrt [ ( v2/ c2 ) – 1 ] dla v > c

Geometryczna interpretacja wzorów transformacyjnych Lorentza.

VII. Czterowymiarowa przestrzeń Minkowskiego.

( Zobacz przedtem tekst pt. „Matematyczne podstawy szczególnej teorii względności” )
Jak już wiemy wzajemny stosunek przestrzeni i czasu w interpretacji Galileusza-Newtona tj. w mechanice klasycznej, jest
zupełnie różny od interpretacji Einsteina tj. w mechanice relatywistycznej. W mechanice klasycznej czas i przestrzeń są
kategoriami ( pojęciami fizycznymi ) zupełnie niezależnymi od siebie. Przejawia się to m.in. w osobnej „metryzowalności”
wprowadzanych dla rozmaitości przestrzennej ( trójwymiarowej ) i czasowej ( jednowymiarowej ).
Einstein, Poincare wykazali, że rozdzielne traktowanie pojęcia czasu i przestrzeni jest nieuzasadnione fizycznie.
W IUO poruszających się względem siebie czas i przestrzeń są ze sobą powiązane, powiązanie to wyraża się za pomocą
zależności liniowych ( równań transformacyjnych Lorentza ), które funkcyjnie ( dla standardowego pchnięcia ) mają postać
x’ = fx (x, t)

⇔

x = gx (x’, t’ )

t’ = fx’ (x, t)

⇔

t = gx’ (x’, t’ )

Wida więc, że wzory te „mieszają“ wzajemnie współrzędne czasowa i przestrzenną.
Fakty te doprowadziły H. Minkowskiego do koncepcji nadania jednolitej matematycznej struktury, odpowiadającej
strukturze wzorów Lorentza narzucanej na wielkości fizyczne czasu i przestrzeni.
Wprowadził on pojęcie „czasoprzestrzeni” jako czterowymiarowej przestrzeni pseudoeuklidesowej o metryce
lorentzowskiej, oznaczmy ją przez M. Czasoprzestrzeń nazywamy również „światem zdarzeń”.
Przypomnijmy pewne określenia.
Punkt należące do tej przestrzeni nazywamy „zdarzeniami”. Krzywe w M nazywamy linią światową ( cząstki materialnej
lub fotonu )
Metrykę w M określamy wzorem :

∆

s2 = c2

∆

t2 -

∆

x2 -

∆

y2 -

∆

z2 sygnatura ( - - - +) (7.1)

Wielkość :

sqrt(

∆

s2 ) = sqrt [ c2

∆

t2 – (

∆

y2 +

∆

z2 +

∆

z2 ) ] (7.2)

nazywa się „interwałem”.
Można pokazać że interwał jest niezmiennikiem przekształcenia Lorentza tj. nie ulega zmianie przy tych przekształceniach.
W zależności od znaku interwału możemy wyróżnić :

dla sqrt(

∆

s2 ) = 0 mówimy, że interwał jest „interwałem zerowym” ( świetlnym )

dla sqrt(

∆

s2 ) > 0 mówimy, że interwał jest „interwałem przestrzennym”

dla sqrt(

∆

s2 ) < 0 mówimy, że interwał jest „interwałem czasowym”

Warto zauważyć, że „przeskalowanie” ct =

„zamienia” zmienną czasową na zmienną przestrzenną. Czas mierzony jest

w jednostkach zwanych „metrami świetlnymi” Metr świetlny jest to czas w ciągu którego światło przebywa drogę 1 [m]

[mświetlny ] = c [m/s] t [s]

1 [ mświetlny ]

≈

3,3356

10-9 [ s ]

Diagramy Minkowskiego.

Jak wiadomo przestrzeń M to przestrzeń nie dosyć, że czterowymiarowa to jeszcze pseudoeuklidesowa. Poglądowe
przedstawienie wykresu krzywej w przestrzeni M jest oczywiście z przyczyn zasadniczych nie możliwe.
Na dwuwymiarowej przysłowiowej „kartce papieru” możemy jednak przedstawić dwuwymiarowe „cięcie” tej przestrzeni
Zazwyczaj jest to cięcie w płaszczyźnie Otx. Należy jednak pamiętać, że świat Minkowskiego narysowany jest na płaskiej
kartce papieru o metryce euklidesowej i tylko analiza stosunków miar daje poprawne rozwiązanie problemu a nie ocena
wizualna. W szczególności dla trójkątów prostokątnych na płaszczyźnie Minkowskiego obowiązuje pseudo-twierdzenie
Pitagorasa :

Podstawową własnością diagramów Minkowskiego jest stwierdzenie, że linia świata fotonu jest symetralną kąta pomiędzy
osiami t i x.

Rys. 3 Diagram Minkowskiego.

Dla sytuacji przedstawionej na rysunku 3 linię świata nachylone pod kątem φ = 45

należą do fotonów ( i innych cząstek

nie posiadających układu spoczynkowego ). Linię o kącie nachylenia 90

≥

φ > 45

( m.in. linia 1 na rys 3 ) należeć mogą

do cząstek materialnych ( tj. cząstek posiadających układ spoczynku )
Linię o kącie nachylenia φ < 45

( m.in. linia 2 na rys. 3 ) nie należą do „standardowo” określanych fizycznie cząstek.

Diagram Minkowskiego dwu wymiarowy ( zazwyczaj o cięciu Otxy ) przedstawia oczywiście odpowiedni stożek :
( mówimy wtedy o stożku świetlnym związanym z danym zdarzeniem )

Rys. 4 Diagram Minkowskiego w dwóch wymiarach.

Jak wiadomo stożek ten dokonuje kazualnego podziału M, względem zdarzenia O (wierzchołek stożka).
Jeżeli zdarzenie O może wpływać za pomocą sygnału o prędkości mniejszej niż c, na inne zdarzenie np. zdarzenie C to
zdarzenie to musi leżeć wewnątrz stożka świetlnego przyszłości zdarzenia O.
Jeżeli zdarzenie O może wpływać za pomocą sygnału o prędkości równej c ( np. grawitacyjnego ), na inne zdarzenie np.
zdarzenie B to zdarzenie to musi leżeć na powierzchni tworzącej stożka świetlnego zdarzenia O.
Jeżeli zdarzenie O nie może wpływać za pomocą żadnego sygnału o prędkości mniejszej lub równej niż c, na inne
zdarzenie np. zdarzenie D to zdarzenie to musi leżeć na zewnątrz stożka świetlnego zdarzenia O.
Jeżeli zdarzenie O jest skutkiem działania zdarzenia np. E , który to skutek został wywołany za pomocą sygnału o
prędkości mniejszej niż c to zdarzenie to musi leżeć wewnątrz stożka świetlnego przeszłości zdarzenia O.
Jeżeli zdarzenie O jest skutkiem działania zdarzenia np. F , który to skutek został wywołany za pomocą sygnału o
prędkości równej c, to zdarzenie to musi leżeć na powierzchni tworzącej stożka świetlnego przeszłości zdarzenia O.
( Zobacz również tekst pt. „Matematyczne podstawy STW” )

Hiperbola niezmiennicza.

W geometrii euklidesowej miejscem geometrycznym punktów jednakowo odległych od początku układu współrzędnych,

na płaszczyźnie Oxy jest okrąg o równaniu : x2 + y2 = r2. W przestrzeni Minkowskiego miejscem geometrycznym zdarzeń
mających jednakowy interwał od początku układu współrzędnych jest hiperbola określona równaniem :

s2 = c2 t2 - x2

Rys. 5 Hiperbole niezmiennicze. ct2 - x2

≡

2 - x2 =

Geometryczna interpretacja transformacji Lorentza.

Pchnięciem ( boost ) w kierunku x nazwiemy sytuacje kiedy jeden z IUO np. U’ porusza się z prędkością v || Ox || O’x’
względem IUO np. U ( czyli taką jaka była zakładana dla omówienia wszystkich konsekwencji kinematycznych STW )
Pchnięcie jak już wiemy możemy interpretować jako pewien obrót na płaszczyźnie Minkowskiego.

Rys. 6 Pchnięcie w kierunku x.

Parametr

( kąt ) taki, że tg (φ) = v/c nazywa się „pospiesznością” ( parametr pchnięcia )

Linie równoczesności w przestrzeni M.

Wykorzystując diagram Minkowskiego łatwo jest pokazać w sposób „geometryczny” względność pojęcia jednoczesności.
Z rysunku 7 widać, że dwa zdarzenia jednoczesne w U tj. leżące na jednej linii łączącej zdarzenia równoczesne w U ,
W ogólnym przypadku nie będą równoczesne w U’ tj. nie będą leżały na jednej linii zdarzeń równoczesnych określonych
w U’. ( zobacz również rysunek 12 w tekście pt. „Matematyczne podstawy STW” )

Rys. 7 a) Linia równoczesności w układzie U jako styczna do hiperboli niezmienniczej, b) linia jednoczesności w U’

Podział krzywych w przestrzeni M.

W przestrzeni M możemy wyróżnić następujące rodzaje krzywych :
a) krzywe czasowe – to krzywe do których każdy wektor styczny jest wektorem czasowym.
b) krzywe zerowe (izotropowe ) – to krzywe do których każdy wektor styczny jest wektorem zerowym.
a) krzywe przestrzenne – to krzywe do których każdy wektor styczny jest wektorem przestrzennym.

Krzywe czasowe to tory cząstek o zerowej masie spoczynkowej.

Rys 8. Linia czasopodobna i możliwe linie do niej styczne.

Podział krzywych jest lorentzowsko niezmienniczy tj. np. linia czasopodobna w U będzie linią czasopodobną w U’.

Zespolona przestrzeń Minkowskiego.

Przy sygnaturze ( + + + - ) element liniowy przestrzeni M ma postać :

∆

s2 =

∆

x2 +

∆

y2 +

∆

z2 – c2

∆

Często dla wygody i ujednolicenia zapisu ( wymiar czasowy wchodzi wtedy do wyrażenia na element liniowy na
„równych” prawach ze współrzędnymi przestrzennymi ) wprowadzamy urojoną współrzędną czasową tj. mnożymy

przez i. Przepis ten jest tylko wygodnym sposobem zapisu, bez żadnych „urojonych” konotacji.

Dla takiego zapisu otrzymujemy :

∆

s2 =

∆

x2 +

∆

y2 +

∆

z2 +

∆τ

Można pokazać, że w czasoprzestrzeni zespolonej przejściu U

→

U’ odpowiada obrót układu prostokątnego o kąt α taki ,

że : tg(α) = v/c
Dla sygnatury ( - - - + ) wprowadzenie współrzędnej urojonej będzie skutkowało następująco :

∆

s2 = -

∆

x2 -

∆

y2 -

∆

z2 -

∆τ

[ 13, str. 26 ; 12 str. 113 ]

Transformacje Lorentza jako „obroty” w czasoprzestrzeni.

Zapiszmy współrzędne w przestrzeni M w sposób ujednolicony wykorzystując zapis indeksowy :
x0 =

= ct , x1 = x , x2 = y , x3 = z

Otrzymujemy :
x’0 = γx0 – γβx1

(7.3)

x’1 = - γβx0 + γx1 (7.4)
x’2 = x2
x’3 = x3
Wprowadźmy teraz wektory kolumnowe postaci :
X = [ x0 ] ; X’ = [ x’0 ]
[ x1 ] [ x’1 ]
[ x2 ] [ x’2 ]
[ x3 ] [ x’3 ]
oraz macierz pchnięcia :
L = [ γ -γβ 0 0 ]
[ -γβ γ 0 0 ]
[ 0 0 1 0 ]
[ 0 0 0 1 ]
Wzory (7.3) i (7.5) możemy wtedy zapisać w postaci równania macierzowego :
X’ = LX (7.5)
Ponieważ γ

≥

1 możemy wprowadzić „kąt” φ spełniający relacje γ = cosh(φ) , wtedy γβ = sinh(φ)

Macierz pchnięcia będzie miała zatem postać :
L = [ cosh(φ) -sinh(φ) 0 0 ]
[ -sinh(φ) cosh(φ) 0 0 ]
[ 0 0 1 0 ]
[ 0 0 0 1 ]
Macierz ta przypomina macierz obrotu w przestrzeni euklidesowej, dlatego też mówimy o „obrocie” w przestrzeni
pseudoeuklidesowej Minkowskiego ( jest to obrót hiperboliczny )
( Zobacz również tekst pt. „Matematyczne podstawy STW” )
Oczywiście dla funkcji hiperbolicznych spełnione są następujące zależności :

cosh(x) = ½ ( ex

e-x ) = 1 + x2/ 2! + x4/ 4! + ...

sinh(x) = ½ ( ex

e-x ) = x + x3/ 3! + x5/ 5! + ...

cosh2 (x) - sinh2 (x) = 1 ; d/dx cosh (x) = sinh(x) ; d/dx sinh (x) = cosh(x) ; cosh (x) + sinh(x) = ex

Pojęcie czterowektora ( wektor w 4-wymiarowej przestrzeni Minkowskiego ).

Czterowektorem, ogólnie mówiąc nazywamy wektor należący do przestrzeni M.
Dowolny czterowektor x możemy zapisać poprzez jego składowe :
x = ( x0, x1, x2 , x3 ) = (

, r )

składowa czasowa czterowektora składowa przestrzenna czterowektora
( zwana również trójwektorem )
( temporal part , spatial part )

Jest to zapis z użyciem współrzędnych kowariantnych, możemy również skorzysta z zapisu czterowektora używając

jego składowych kontrawariantnych. ( zobacz tekst pt. „Podstawy rachunku wektorowego i tensorowego” )
Formalna definicja czterowektora może brzmieć następująco :
Czterowektorem w układzie U, x nazywamy zbiór czterech liczb ( x0, x1, x2 , x3 ) które przy przejściu do innego układu
U’ transformują się zgodnie z zależnością : x’ = Lx
Oprócz czterowektorów w przestrzeni M możemy definiować również czteroskalary ( skalary lorentzowskie ).
( Zobacz również punkt X )

Czas własny.

Czasem własnym pewnego określonego IUO związanym z ciałem materialnym, nazywamy czas, który wskazuje zegar
spoczywający w tym układzie.
Rozważmy dwa zdarzenia A, B które można połączyć krzywą czasopodobną. Dla takich zdarzeń jak wiadomo istnieje taki
IUO w którym zdarzenia A i B zachodzą w tym samym miejscu tzn. :

∆

s2 = c2

∆

t2 -

∆

x2 -

∆

y2 -

∆

z2 = c2

∆

lub

∆

s2 =

∆τ

2 ( lub w zapisie infinitezymalnym ds2 = d

2 )

Taki interwał nazywamy „czasem własnym” zdarzeń A, B określonym w IUO U, w którym te zdarzenia zaszły kolokalnie.
Możemy zapytać jaki odstęp czasu dt, wskazywać będzie zegar w innym IUO U’, poruszającym się względem U, zgodnie
z wzorami transformacyjnymi otrzymamy :
d

= (1/γ) dt

ds = cd

⇒ d

= (1/c) ds = sqrt [ ( c2

∆

t2 -

∆

x2 -

∆

y2 -

∆

z2 )/c2 ] = sqrt { dt2 – [ (

∆

x2 +

∆

y2 +

∆

z2 ) /c2 ] } =

= sqrt { 1 - [ (

∆

x2 +

∆

y2 +

∆

z2 ) /c2dt2 ] }dt = sqrt [ 1 – (1/c2 ) (dr /dt)2 ] dt = sqrt [ 1 – (v2/ c2 ) ]dt

Zatem :

= sqrt [ 1 – (v2/ c2 ) ]dt

Czas własny

, w odróżnieniu od czasu „zwykłego” jest relatywistycznie niezmienniczy. Mówimy, że jest on skalarem

lorentzowskim.

W ogólnym przypadku otrzymamy :
B t2

∫

dt / sqrt{ 1 – [ v2(t) / c2 ] } =

∫

γ(t) dt (7.6)

A t1
Dla dowolnej linii świata dla której wektor styczny nigdzie nie jest zerowy, można określić niezmiennik będący
odpowiednikiem długości łuku krzywej w geometrii euklidesowej.

Jeżeli funkcja λ = xα (λ) określa linie świata pomiędzy zdarzeniami A i B to niezmiennik ten definiujemy wzorem :
B

∫

sqrt [ ε ηαβ (dx

α/ dλ)(dxβ/ dλ) ]ds ; ε = + 1 dla linii czasopodobnych ; ε = -1 dla linii przestrzennopodobnych

A
Parametr

w zależności od rodzaju krzywej – dla krzywej czasopodobnej jest to czas własny, dla krzywej

przestrzennopodobnych jest to długość własna.

Rys. 9 Linia świata cząstki poruszającej się ze zmienną prędkością.

Rozważmy cząstkę poruszająca się ze zmienna prędkością v(t), jeśli porusza się ona od punktu A ( współrzędna czasowa
t1) do punktu B ( współrzędna czasowa t2 ) jej czas własny dany będzie przez wzór (7.6)

Czterowektor prędkości ( 4-prędkość )

Czterowektor prędkości określamy wzorem :
V = dR/d

= ( dx0 /d

, dr/d

) = ( γc, γvx, γvy, γvz ) = γ (c, v )

R – czterowektor wodzący punktu materialnego.
Gdy v << c mamy γ

≈

1, zatem V = ( c, vx, vy, vz )

Widać, że V

≠

0 ( zawsze ) tzn. w przestrzeni M „spoczynek” jest niemożliwy.

Ważnym jest zauważenie, że długość czterowektora prędkości jest równa

| V | = c2
tzn. jest stała.
Tak na marginesie, to należy pamiętać, że długość każdego czterowektora jest skalarem lorentzowskim.

Dla fotonu ( poruszającego się po liniach świetlnych ) pojęcie czteroprędkości nie może być określone.

Czterowektor przyspieszenia.

A = dV/d

Czterowektor przyspieszenia jest czterowektorem prostopadłym do czterowektora prędkości, a ponieważ czterowektor
prędkości jest wektorem czasopodobnym to czterowektor przyspieszenia jest wektorem przestrzennopodobnym.
Składowe czterowektora przyspieszenia są następujące :
A = ( γ d/dt (cγ) , γ d/dt (γv) )

VIII. Dynamika relatywistyczna.

Pojęcie masy w teorii względności – masa niezmiennicza.

Masą niezmienniczą m (skalar lorentzowski ), ciała materialnego, nazywamy jego masę spoczynkową tj. masę jaką ma
ciało w układzie w którym ono spoczywa.

Czteropęd (czterowektor energii-pędu ), Energia w STW.

Klasyczne określenie pędu : p = mv , nie jest wielkością relatywistycznie niezmienniczą. ( w jednym IUO pęd może być
zachowany, podczas gdy w innym IUO może by nie zachowany )
Wielkością relatywistycznie niezmienniczą jest 4-pęd określany wzorem :
P = mV = ( γmc , γmv ) = ( E/c , γmv ) = ( E/c, p ) = ( E/c, px , py, pz ) ; p – jest trójwektorem (8.1)
Analogicznie do mechaniki klasycznej w mechanice relatywistycznej obowiązuje zasada zachowania czteropędu.
Wielkość : γm, Einstein nazwał „masą relatywistyczną” mrel = γm , podczas gdy sama wielkość m została nazwana „masą
spoczynkową” ( oznaczaną jako m0 ). Jednak z pewnych względów ( masa relatywistyczna nie jest skalarem
lorentzowskim i jej wprowadzenie nie wnosi niczego pożytecznego a jedynie powoduje komplikacje pojęć ) obecnie
porzucono tę terminologię, wprowadzając pojęcie „energii relatywistycznej” ( jest to energia całkowita, swobodnie
poruszającego się ciała o czteropędzie P ) :

E = γmc2

(8.2)

Jak widać w teorii względności dwie klasycznie odrębne wielkości fizyczne jakimi są energia i pęd są powiązane razem
tworząc czterowektor energii-pędu.

Relatywistyczny wzór na energie kinetyczną jest następujący :

Ek = γmc

2 - mc2 = E - mc2 = mc2( γ –1)

(8.3)

Energia spoczynkowa tj. energia całkowita mierzona w IUO w którym ciało spoczywa, dana jest wzorem :

E0 = mc

(8.4)

Zatem :
Ek = E - E0

(8.5)

lub
E = Ek + E0
W obszarze nierelatywistycznym ( v << c ) możemy rozwinąć pierwiastek kwadratowy względem potęg parametru

v2/ c2 otrzymując :

γ = ( 1 - v2/ c2 )-1/2 = 1 + ½ (v/c)2 + ....
Zgodnie z tym rozwinięciem otrzymujemy :

Ek = ½ mv

2 + 3/8 mv4/ c2 + ...

Zatem :

≈

½ mv2 + mc2

(8.6)

Długość czterowektora czteropędu jest równa :

| P | = sqrt ( P

•

P ) = sqrt [ E2/c2 + (γmv)2 ] = sqrt( E2/c2 + p2 ) = mc

(8.7)

Jest to niezmiennik.

P 2 = m2c2

E = sqrt [ m2c4 + (γm vc )2 ] lub E = sqrt [ m2c4 + (pc)2 ] lub E2 = m2c4 + (γmvc )2 (8.8)

Pomiędzy parametrami m, v, P , E – charakteryzującymi ruch ciała możemy wskazać bardzo ważne związki :
β = v / c = γmvc / E lub β = v / c = pc / E

(8.9)

Zależność ta pozwala nam wyznaczyć trójprędkość v ciała materialnego jeśli znamy jego trój pęd p i energię całkowitą.

Pojęcie siły w STW – czterosiła.

Pojęcie siły w mechanice relatywistycznej odgrywa znacznie mniejszą rolę niż w mechanice klasycznej.
Klasyczny wzór na siłę :
F = dp/dt
Nie jest niezmienniczy wobec transformacji Lorentza. Jednak wprowadzając do niego zamiast pędu czteropęd, otrzymamy
relatywistyczną postać II prawa Newtona :
F = dP/dt = d /dt ( γmv )

Jednak równanie to prowadzi w konsekwencji do konieczności osobnego rozpatrywania zależności transformacyjnych
składowej podłużnej i poprzecznej siły :
F’

⊥

= (1/γ)F

⊥

; F’|| = F||

Chcąc uniknąć tej złożonej konsekwencji wprowadzamy wielkość zwaną „siłą Minkowskiego” lub po prostu czterosiłą,
jest ona określoną zależnością :
K = dP/d

Można pokazać, że składowe siły Minkowskiego mają postać :
K = γ ( dP/d

, 1/c dEc/d

)

Składowa czasowa tego czterowektora z dokładnością do czynnika 1/c jest mocą dostarczaną cząstce czyli ( własną )
szybkością wzrostu jej energii :
Składowa przestrzenna jest równa :
K = ( dt/d

) dP/dt = γ F

Trzecia zasada dynamiki nie jest ( na ogół ) spełniona w mechanice relatywistycznej. Ze względu na postulat istnienia
granicznej prędkości przenoszenia energii-pędu, trzecia zasada dynamiki jest spełniona tylko dla oddziaływań punktowych
i momentalnych ( kontaktowych )

Ruch hiperboliczny.

Rozważmy teraz ruch jednostajnie przyspieszony np. ruch cząstki materialnej poddanej działaniu stałej siły materialnej w
układzie U z punktu widzenia dynamiki relatywistycznej.
F = m d/dt γv = const. = G
Całkując to równanie otrzymujemy :

v(t) = Gt / sqrt [ 1 + ( Gt/c)2 ]
ponowne całkowanie pozwala otrzymać :

x(t) = (c2/G) sqrt [ 1 + ( Gt/c)2 ] + x0 – (c

2/G)

Równanie to pozwala napisać :

[ x - x0 + (c

2/G) ]2 - c2t2 = c4/g2

Rys. 10 Linia świata w ruchu hiperbolicznym o stałym przyspieszeniu W

Cząstki o zerowej masie spoczynkowej – foton.

W mechanice klasycznej pojęcie cząstek o zerowej masie ( bezmasowych) było pozbawione treści fizycznej, cząstka taka
nie mogłaby oddziaływać z innymi cząstkami przez co była by bytem „poza fizycznym”. Zaskakująca konsekwencją STW
jest możliwość istnienia cząstek o zerowej masie spoczynkowej.
Zastosujmy teraz wzór :
| P | = mc dla m = 0 otrzymujemy | P | = 0

sqrt [ E2/c2 + (γmv)2 ] = 0 ⇒ E2/c2 = (γmv)2 ⇒ (γmc2)2/ c2 = (γmv)2 ⇒ c2 = v2

Wtedy oczywiście ze wzoru :
v / c = pc / E ⇒ p = E/c

Innymi słowy jeśli cząstka bezmasowa istnieje to z ogólnych praw mechaniki relatywistycznej wynika, że musi poruszać
się z prędkością c. Dla fotonu czteropęd jest równy energii. Nie ma układu odniesienia w którym foton spoczywa , zatem
jego masa jest wielkością nie mierzalną, bez sensu jest zatem mówić o czasie w układzie związanym z fotonem ( ogólnie o
IUO związanym z fotonem lub inną cząstką o zerowej masie spoczynkowej).
Mechanika relatywistyczna już niczego nam nie podpowie, ale z mechaniki kwantowej wiemy, że energia fotonu jest
określona wzorem :
E = hν = hc/ λ ; ν - częstość fali , λ – długość fali
p =h/λ
Zatem :
E = pc

Relatywistyczny efekt Dopplera.

Faza fali jest wielkością niezmienniczą tj. taka samą we wszystkich IUO. ( wynika to z tego, że zmiana fazy fali jest
proporcjonalna do liczby grzbietów fali jakie minęły obserwatora . ponieważ jest to po prostu operacja liczenia , jej wynik
nie może zależeć od wyboru IUO ) [21 str. 490 ]
Czterowektor częstości-wektor falowy
( ν, k ) ( ω/c, k )
| k | = 2π / λ - wektor falowy ( liczba falowa )
ω = 2πν = c k
ν = c/λ
v = ω / | k | - prędkość fali , dla światła w próżni mamy : ω = c |k |

Wzór na relatywistyczny efekt Dopplera dla światła :
ω = ω0 / γ [ 1 – β cos (

) ]

ω0 – częstość światła w układzie spoczynkowym źródła , ω – częstość obserwowana w układzie względem którego źródło
porusza się z prędkością v ;

- kąt między v i linią obserwacji.

Gdy

= 0 tj. gdy źródło O’ zbliża się do obserwatora O wzdłuż osi Ox || v wtedy wzór ten przyjmuje postać :

ω = ω0 / γ ( 1- β ) = ω0 sqrt [( 1- β ) ( 1- β ) ] / ( 1- β ) = ω0 sqrt [( 1- β ) ( 1+ β ) / ( 1- β )( 1- β ) ] =
= ω0 sqrt [ ( 1+ β ) / ( 1- β ) ] = ω0 γ ( 1 + β)
Przypominam, że klasyczny efekt Dopplera określał wzór :
ω = ω0 / [ 1 - β cos (

) ]

i dla niego gdy

= 0 jest ω = ω0 / ( 1 - β )

Gdy

= π/2 tj. źródło zbliża się do O z kierunku w jego układzie prostopadłym do kierunku ruchu tj. wektora v.

Wtedy to , ze wzoru klasycznego mamy : ω = ω0 , a ze wzoru relatywistycznego : ω = ω0/γ.
Jest to tzw. poprzeczne zjawisko Dopplera, w odróżnieniu od podłużnego opisywanego wzorem :
ω = ω0 γ ( 1 + β)
Widać, że z obecność czynnika γ powoduje istnienie poprzecznego efektu Dopplera, efekt ten zaobserwowano
doświadczalnie metodami spektroskopowymi dla atomów w ruchu ( wspomniane już doświadczenie Ivesa –Stilwella 1938
r. ), jak również w precyzyjnych pomiarach mossbauerowskich absorpcji rezonansowej.

Rys.11 Schemat wyprowadzenia relatywistycznego efektu Dopplera.

( Dokładniejsze omówienie efektu Dopplera zainteresowany czytelnik znajdzie np. w „Fizyka fal” – J. Ginter WN-PWN
1993, od str. 207 lub w tekście pt. „Fale – ruch falowy” )

Ogólne uwagi dotyczące zależności pędu i energii.

W mechanice klasycznej, której podstawą jest grupa ( transformacj ) Galileusza, szczególna ich postać jest dana
zależnościami :

x’ = x - vt
y’ = y
z’ = z
t’ = t

zależności między pędem : p = mv a energią E = E(0) + ½ m v2 nie była zależnością jawną.
Energię spoczynkową E(0) jako wielkość addytywną na ogół zaniedbywano.

Stosowanie pojęcia „masy relatywistycznej ( masy zależnej od prędkości ): mrel = γm prowadzi do „dziwnych” pojęć typu
masa poprzeczna i podłużna. Skąd się bierze to całe zamieszanie pojęciowe ?
Jak łatwo zauważyć we wzorach na pęd i energię całkowita pojawia się wielkość : γm , istnieje pewna pokusa aby nadać tej
wielkości osobną nazwę – „masa relatywistyczna”. Wtedy odpowiednie wzory miały by postać :

E = mrel c

2 ⇒ m

rel = E/c

2 ( zatem masa relatywistyczna to po prostu energia – co łatwo zauważyć przyjmując c = 1 )

P = ( mrel c , mrel v )
Zatem twierdzenie jakoby masa rośnie w raz ze wzrostem prędkości jest jałowe.
Całkiem sensownym jest natomiast wprowadzenie pojęcia „energii spoczynkowej” :

E0 = mc

Wprowadzenie pojęcia masy relatywistycznej bywa usprawiedliwiane analogiami do wzoru Newtona :
d/dt ( mv) = F

→

d/dt ( mγv) = F

Problem polega jednak na tym iż jest to wzór słuszny gdy F

⊥

v (mówimy wtedy o masie relatywistycznej poprzecznej )

Przykładem takiego zachowania jest ruch cząstki naładowanej w stałym polu magnetycznym. Kierunek siły Lorentza :
F = e ( v

B ) jest taki , że Fv = 0

Ruch cząstki dla takiego przypadku dany jest wzorem quasiklasycznym :
mγ dv/dt = F

W przypadku kiedy F || v wzór ma masę relatywistyczna będzie miał postać :

mrel = m / ( 1 – β

2 )3/2

mówimy wówczas o masie relatywistycznej podłużnej.
A w sytuacji kiedy siła tworzy pewien dowolny kąt z wektorem prędkości zmuszeni bylibyśmy wprowadzić jeszcze
pojęcie „masy skośnej”. Przykład ten pokazuje nieprzydatność a nawet „zwodniczość” pojęcia masy relatywistycznej.
Nie ma jednej uniwersalnej zależności masy od prędkości.
We współczesnej fizyce używamy jedynie pojęć : masa - m , energia ( całkowita ) -E , energia spoczynkowa E0
( są to skalar lorentzowski ( niezmienniczy ) i skalary nielorentzwoskie )

Wzór E0 = mc

2 wskazuje na proporcjonalność masy ( oczywiście, że spoczynkowej ) do energii spoczynkowej, która

zachodzi w układzie własnym ciała materialnego. Ponieważ ( z czterowymiarowego punktu widzenia ) energia i masa mają
różne własności ze względu na przekształcenia Lorentza, mówienie o zamianie masy na energię nie ma po prostu sensu.
STW uściśla pojęcie „zamkniętości” układu mechanicznego – układ zamknięty to układ nie zmieniający czterowektora
pędu.
( zobacz [ 2, str. 130 , 4 str. 95, 16 str. 125 i dodatek ] jak również książeczkę pt.
„Teoria względności” – A. Szymacha , J. P. Lasota 1984 str. 48 )

IX. Tachiony

Zgodnie z wzorami transformacyjnymi Lorentza widać, że cząstki fizyczne możemy podzielić w zależności od ich
„sposobu” zachowania względem stałej c.
Mamy następujący podział :
a) Cząstki o niezerowej masie spoczynkowej – poruszają się z prędkościami mniejszymi od c ( lub co najwyżej ich
prędkość asymptotycznie dąży do c ). Cząstki te to cząstki materii zwykłej ( nie polowej ) w tym :
elektrony, protony, neutrony ; układy tych cząstek elementarnych ( w tym i ciała materialne ).
Ogólnie ( mając na względzie właśnie sposób zachowania względem stałej c ) cząstki te nazywamy : bradionami.
Dla bradionów spełniona jest zasada przyczynowości.
b) Cząstki o zerowej masie spoczynkowej – poruszają się tylko i wyłącznie z prędkością c.
Ogólnie cząstki te nazywamy „luksonami”. Do luksonów należy foton i grawiton (?).
c) Cząstki poruszające się z prędkością większą niż c ( superluminarnie ).
Cząstki te nazywamy „tachionami”.

Podział ten nie przeczy STW, a wzory Lorentza dla odpowiednich typów cząstek są nie sprzeczne i nieosobliwe (jeśli
przyjąć pewne założenia – jakie ? W pierwszej kolejności takie, że jeśli „coś” nie jest zabronione to jest możliwe w
przyrodzie, reszta - zobacz dalszy ciąg ).
Dla tachionów z punktu widzenia elektrodynamiki musimy założyć zasadę wymienności tj. zasadę mówiąca, że przy
Przejściu U

→

U’ emiter (tachionów) przechodzi w absorber a przy przejściu U’

→

U absorber przechodzi w emiter.

Wynika to z faktu iż dla bradionów i luksonów proces emisji zawsze ( tj. w każdym IUO ) jest wcześniejszy od procesu
absorbcji ( np. fotonu ). Dla tachionów porządek procesu emisji i absorbcji zależny jest od wyboru układu odniesienia.
Może się więc zdarzyć, że w pewnym IUO proces absorbcji wyprzedzać będzie proces emisji, łamiąc mikroskopową
zasadę przyczynowości. ( tachion poruszający się do przodu w czasie w jednym układzie może poruszać się wstecz w
czasie w innym układzie). Jeśli dla tachionów proces emisji i proces absorbcji rozpatrywać jako jeden proces emisji-
absorbcji tj. zakładać kolokalność i jednoczesność tych procesów to zasadę przyczynowości możemy zachować przyjmując
również zasadę wymienności.
Jeśli przyjąć, że tachion jest cząstką fizyczną tj. może oddziaływać z luksonami i bradionami to powinien mieć pęd oraz
energię ( „masę” ? ). Na podstawie wzorów (8.8), (8.9) mamy :

(E/c)2 – p2 = (mc)2 ; Ev/c2 = p

m2 = (E/c2)2 ( 1 – v2/c2 )

Z równania tego otrzymujemy dla tachionów bardzo ważną nierówność : m2 < 0
Oznacza to, że masa ( ciągle hipotetycznych ) tachionów jest wielkością urojoną. Widać o również z definicji 4-pędu
( wszystkie jego składowe są urojone ). W przypadku tachionów intuicje dotyczące pojęcia „masy własnej” nie są
odpowiednie. Zakładając dla tachionów : m = iµ
Otrzymamy następującą postać czteropędu :

P = ( E/c , p ) = ( µc/ sqrt [ ( v2/c2 ) – 1 ] , µv/ sqrt [ ( v2/c2 ) – 1 ] )
Dla v > c składowe będą rzeczywiste.
Dla takiego określenia czteropędu energia tachionu dąży do zera przy v

→

∞

i rośnie nieskończoności przy v

→

| P |

→

µc przy v

→

∞

oraz | P |

→

E/c przy v

→

Pęd tachionów zawsze jest większy od µc, a ich energia nie ma zwykłej najmniejszej wartości.
Dla tachionów istnieje układ odniesienia w którym ich prędkość jest nieskończona jednak w układzie tym tachionu nie
można wyobrażać sobie jako pewnej poruszającej się cząstki a jako natychmiastowo pojawiający się i znikający obiekt.
( W związku z tym niektórzy upatrywali obecności tachionów w procesach wirtualnej kreacji i anihilacji cząstek )

Można powiedzieć, że wyżej omówiony podział cząstek wynika również ze struktury stożkowej czasoprzestrzeni :
bradiony to cząstki poruszające się wewnątrz stożka świetlnego ( przy tej terminologii, raczej luksonowego ), luksony
poruszają się tylko po tworzących stożka a tachiony na zewnątrz stożka.
Urojona masa tachionów nie powinna sprawiać problemu fizycznego, ponieważ masa jest wielkością mierzalną tylko w
układzie spoczynkowym, w układach poruszających się możemy zmierzyć jedynie energię, co w przypadku tachionów
teoretycznie jest możliwe.
[ 23 –literatury dodatkowej, 8-literatury w języku rosyjskim, str. 302 ; 1-literatury w języku rosyjskim]

Dlaczego ruch w prędkością superluminarną prowadzi do złamania mikroskopowej zasady
przyczynowości ?

Rys.12 Proste (geometryczne wyjaśnienie ) dlaczego tachion łamie klasyczną zasadę przyczynowości.

Rozważmy dwa zdarzenia : zdarzenie A ( t1, x1) tj. zachodzące w czasie t1 i w punkcie x1układu U ;
zdarzenie B (t2, x2) zachodzące również w układzie U.
Niech w układzie U t2 > t1 tj. zdarzenie A poprzedza czasowo zdarzenie B.
Rozważmy teraz układ U’. Zgodnie z wzorami transformacyjnymi mamy :

t’2 – t’1 = γ [ ( t2 - t1) – ( v/c

2 )( x

2 - x1) ]

Rozważmy teraz sytuacje kiedy sygnał łączący zdarzenia A i B ma prędkość u > c. Ponieważ w układzie U prędkość u z
definicji jest równa :
u = ( x2 - x1) / ( t2 - t1) [ m/s]
Zatem :

t’2 – t’1 = γ ( t2 - t1) ( 1 - uv/c

2 )

dla u < c czynnik uv/c2 < 1 ( bo v < c zatem iloczyn vc < c2 ) zatem t’2 – t’1 > 0 tj. w układzie U’ ( jak i dowolnym
innym ) kolejność czasowa zdarzeń A, B jest zachowana.

Jeżeli u > c to możemy wskazać taki IUO U’’ poruszający się z prędkością v < c , względem U, w którym uv/c2 > 1

a wtedy czynnik ( 1 - uv/c2 ) < 0 , zatem t’2 – t’1 < 0 tj. zdarzenia A i B w układzie U’’ zachodzą w odwrotnej kolejności
czasowej. Widać więc, że dopuszczenie sygnałów superluminarnych może ( przy odpowiednim wyborze układów
względnych ) łamią zasadę przyczynowości.
[ 1-literatury w języku rosyjskim, str. 74 ]

X. Grupa Lorentza. Przekształcenia Poincarego.

Dotychczas rozpatrywaliśmy tylko szczególną postać transformacji współrzędnych w przestrzeni M. Z tą szczególną
postacią transformacji związane są wzory Lorentza o znanej i najczęściej, dotychczas wykorzystywanej postaci :
x’ = γ (x - vt )

t’ = γ [ t - (v/ c2 ) x ]

y’ = y
z’ = z
lub w zapisie „ujednoliconym” – indeksowym :
x’0 = γx0 – γβx1

x’1 = - γβx0 + γx1
x’2 = x2
x’3 = x3
Wzory te obrazują pewne szczególne pchnięcie ( boost ) – pchnięcie w kierunku osi Ox || O’x’ || v
Oczywiście ten szczególny przypadek nie wyczerpuje możliwych postaci transformacji izometrycznych w przestrzeni M.
Transformacje te zgodnie z definicją muszą zachowywać wartość elementu metrycznego ds tzn. :
ds = ds’ przy transformacji U

→

U’

Jak wiadomo w ogólności na izometrię mogą składać się : obroty, translacje i odbicia.
( zobacz tekst pt. „Przestrzenie metryczne” )
Macierzowo izometrię możemy zapisać następująco :
X’ = A X + B
A – jest pewną nieosobliwą macierzą ortogonalną.

Mamy zatem : det A =

1 oraz AT A = 1 ; AT – jest macierzą A – transponowaną.

Wzory te są liniowe – zapewniają więc spełnienie zasady względności Einsteina ( m.in. zasadę bezwładności )
A przy odpowiednim doborze macierzy A zapewnią spełnienie drugiego postulatu Einsteina tj. stałości prędkości światła w
próżni. Warto zauważyć, że najogólniejszą postacią transformacji spełniających oba postulaty są przekształcenia

konforemne postaci : gµν = J

1/2 gαβ ; gµν – macierz tensora metrycznego

Jednak w niniejszym tekście przekształcenia takiego rodzaju nie będą nas interesować. [ zobacz 14 str. 194 ]
Zajmiemy się teraz ogólnymi przekształceniami o postaci :

X’

= Λ

µν

Xν + B

(10.1)

Gdzie :

( Λ00 , Λ

1 , Λ

2 , Λ

3 )

(Λ10 , Λ

1 , Λ

2 , Λ

3 )

µν

= ( Λ20 , Λ

1 , Λ

2 , Λ

3 )

(Λ30 , Λ

1 , Λ

2 , Λ

3 )

jest znaną już macierzą Lorentza L. Macierz ta jest macierzą ortogonalną zatem :

( macierz Λ

µν

„odpowiada” za obroty czasoprzestrzenne i odbicia , macierz wyrazów wolnych B

odpowiada za translacje

– przesunięcia czasoprzestrzenne )

LT η L = η ; η – macierz : diag ( 1, -1, -1, -1 )
Wzór (10.1) określa ogólną postać transformacji przestrzeni M. Transformację o tej postaci nazywa się :
„Transformacją Poicarego”. Jednorodne przekształcenia Poincarego tj. przekształcenia o postaci :

X’

= Λ

µν

Xν (10.2)

Nazywamy „ogólnymi przekształceniami Lorentza”. Zbiór wszystkich transformacji Poincarego tworzy grupę ( grupa
transformacji Poincarego ), zbiór wszystkich jednorodnych transformacji Poincarego również tworzy grupę ( podgrupę
grupy Poincarego – nazywamy ją grupą Lorentza ).

Zbiór ogólnych transformacji Lorentza dla których det L = +1 nazywa się „zbiorem dodatnich transformacji Lorentza”
Zbiór te oznaczamy następująco :

L+(M) ( zbiór ten tworzy grupę )
Transformacje należące do tego zbioru zachowują orientacje czterowektorów.
Zbiór ogólnych transformacji Lorentza dla których det L = -1 nazywa się „zbiorem ujemnych transformacji Lorentza”
Zbiór te oznaczamy następująco :
L-(M) ( zbiór ten nie tworzy grupy )
Transformacje należące do tego zbioru nie zachowują orientacji czterowektorów ( zawierają odbicia czasoprzestrzenne ).
Oczywiście mamy : L(M) = L+(M)

∪

L-(M)

Można pokazać, że dla wszystkich transformacji Lorentza spełniony jest warunek : | Λ00 |

≥

W zależności od znaku elementu Λ00 , zbiór L(M) możemy podzielić na dwa podzbiory :

Jeśli : Λ00

≥

+ 1 mówimy o zbiorze ortochronicznych transformacji Lorentza, który oznaczamy : L

↑

(M)

Jeśli : Λ00

≤

- 1 mówimy o zbiorze antychronicznych transformacji Lorentza, który oznaczamy : L

↓

(M)

Pod wpływem transformacji ortochronicznych znak współrzędnej zerowej ( czasowej ) wektorów czasowych nie ulega
zmianie tj. transformacje te zachowują orientacje czasu – przeprowadzają wektory skierowane ku przyszłości ( czasowe i
zerowe ) na wektory skierowane ku przyszłości ( czasowe i zerowe )
Grupa Lorentza jest więc sumą czterech składowych :

↑

+ = L+

∩

↑

odpowiada : det Λ = +1 , Λ00

≥

+ 1 ; ( dodatnia ortochroniczna )

↓

+ = L+

∩

↓

odpowiada : det Λ = +1 , Λ00

≤

- 1 ; ( dodatnia antychroniczna )

↑

- = L-

∩

↑

odpowiada : det Λ = -1 , Λ00

≥

+ 1 ; ( ujemna ortochroniczna )

↓

- = L-

∩

↓

odpowiada : det Λ = -1 , Λ00

≤

- 1 ; ( ujemna antychroniczna )

Jak widać, tylko przekształcenie L

↑

+ zawiera w sobie przekształcenie jednostkowe , nazywamy je „przekształceniem

właściwym Lorentza”. Do tego zbioru przekształceń, jak łatwo zauważyć, należy również wprowadzone wcześniej
szczególne przekształcenie Lorentza, do którego odnoszą się również zwykłe trójwymiarowe ortogonalne obroty.

Zbiory przekształceń : L

↓

+ , L

↑

- , L

↓

- nie zawierają przekształcenia jednostkowego i stanowią przekształcenia tzw.

„niewłaściwe”. Dowolny element każdego z tych zbiorów nie może być w sposób ciągły przeprowadzony w inny z tych
zbiorów. ( zobacz tłumaczenie skryptu pt. „pola klasyczne” - D. W. Galcow, Ju. W. Grac, W. Cz. śukowskij ,
Wydawnictwo Uniwersytetu Moskiewskiego Moskwa 1991 )

Grupa Poincarego jest grupą 10-cio parametrową. Grupa Lorentza jest grupą 6-cio parametrową ( mamy 10 liniowo
niezależnych równań na 16 elementów macierzy L )
Jako parametry swobodne najczęściej wybieramy : trzy parametry określające położenie osi współrzędnych ( kąty Eulera )
Oraz trzy parametry określające wzajemną prędkość dwóch IUO ( współrzędne wektora β )
Jak wiadomo grupy transformacji zależne od skończonej liczby parametrów nazywają się grupami Liego, mówimy zatem
że grupa Poincarego jest 10-cio parametrową grupą Liego. Szczególne transformacje Lorentza, nie zawierające obrotów
przestrzennych tj. sparametryzowane jedynie wektorem prędkości v ( lub β ) nazywamy jak już powiedziano wcześniej
„pchnięciami lorentzowskimi” Dla „sztandarowego’ pchnięcia w kierunku osi Ox mamy następujące macierze :
X’ = [ x’0 ] ; X = [ x0 ] - macierze kolumnowe
[ x’1 ] [ x1 ]
[ x’2 ] [ x2 ]
[ x’3 ] [ x3 ]

( γ , -γβ , 0 , 0 )
( -γβ , γ , 0 , 0 )

µν

= ( 0 , 0 , 1 , 0 ) - macierz pchnięcia w kierunku osi Ox

( 0 , 0 , 0 , 1 )

( γ , -γβ , 0 , 0 )
( 0 , 1 , 0 , 0 )

µν

= ( -γβ , 0 , γ , 0 ) - przykładowa macierz pchnięcia w kierunku osi Oy

( 0 , 0 , 0 , 1 )
Można pokazać, że macierz przekształcenia Lorentza składającego się z pchnięcia w kierunku Ox z prędkością względną v,
a następnie z pchnięcia w kierunku osi Oy z prędkością względną u będzie macierzą powstałą w wyniku przemnożenia
( w kolejności pchnięć ) odpowiednich macierzy pierwszego i drugiego pchnięcia. Ponieważ mnożenie macierzowe nie jest
w ogólności mnożeniem przemiennym od razu widać, że odwrócenie kolejności pchnięć prowadzi do innych wzorów
transformacyjnych. [zobacz 12-literatury w języku angielskim , zadanie I.1 ].

Grupa Poincarego jest chyba najważniejszą z grup wykorzystywanych w fizyce teoretycznej. Mówiąc, że każda teoria
powinna być relatywistycznie niezmiennicza mamy na myśli niezmienniczość jej równań względem właśnie grupy
Poincarego.

Rys. 13 Różne hiperbole niezmiennicze dla różnych parametrów pchnięcia ( w dowolnym kierunku )

( 1, 0 , 0 , 0 )
( 0 , )

µν

= ( 0 ,

) - przykład macierzy „czystych” obrotów.

( 0 , )
( problemy teorio-grupowego podejścia do przekształceń Poincarego zostaną omówione w przygotowywanym tekście
pod roboczym tytułem „Wprowadzenie do teorii grup i jej zastosowań w fizyce” )

Definicja 10.1 Kontrawariantnymi składowymi 4-wektora A

nazywamy zbiór czterech wielkości (A0, A1, A2 , A3 ),

Które przy przekształceniu Lorentza przekształcają się według prawa :

’ = Λ

’

Aν

Definicja 10.2 Kontrawariantnymi składowymi 4-tensora rzędu n, nazywamy zbiór wielkości T

1 ... µn , które przy

przekształceniach Lorentza przekształcają się według prawa :

’1 ... µ’n = Λ

1’µ

2’µ

... Λ

n’µ

1... µ1

Tensor metryczny przestrzeni M ma jak wiemy postać : ηµν = diag( 1, -1, -1, -1 ) i oczywiście ( η

-1 )

≡

ηµν = η

µν

Za pomocą takiego tensora metrycznego dokonujemy operacji podnoszenia i opuszczania indeksów, tym samym możemy
wprowadzać wielkości zarówno ko- jak i kontrawariantne. Przykładowo określmy 4-wektor kowariantny :

Aµ = ηµν A

Ponieważ macierz Λ

ν jest nieosobliwa, to możemy określić macierz do niej odwrotną transponowaną Λ

~µ

ν , oczywiście :

Λ~αµ’ Λµ’β = δαβ
Naturalnie składowe tensora kowariantnego będą przekształcały się za pomocą macierzy Λ~µν.
Iloczyn skalarny dwóch 4-wektorów :

Aµ Bµ = A

0 B

0 + A

i B

i = A

0B0

−

A B

Jest inwariantem przekształcenia Lorentza. Taką sama własność posiada oczywiście kwadrat dowolnego 4-wektora.

Definicja 10.3 Składowe kowariantne tensora rzędu n określamy następująco :

Tµ

1... µn

= ηµ

1ν1

ηµ

2ν2

... ηµ

nνn

Tν1... νn

Czterowymiarowym analogiem operatora Hamiltona

∇

jest 4-gradient :

∂

µ =

∂

xµ = ( 1/c

∂

t ,

∇

)

XI. Relatywistyczna postać równań Lagrange’a i Hamiltona.

Wprowadzając działanie relatywistyczne musimy uwzględnić, że nie powinno być ono zależne od wyboru IUO, dlatego też
wyrażenie podcałkowe powinno być skalarem lorentzowskim. Działanie dla cząstki swobodnej powinno mieć postać :
b b

S = - mc

∫

ds = - mc2

∫

γ(t) dt

a a

( Działanie o tej postaci jest niezmiennicze względem przekształceń z grupy Poincarego. )
Relatywistyczna funkcja Lagrange’a ma więc postać :

L = - γmc2
Dla małych prędkości tj. w granicy nierelatywistycznej możemy rozwinąć funkcje L w szereg potęgowy względem v/c,
opuszczając wyrazy wyższych rzędów otrzymamy wówczas :

≈

- mc2 + ½mv2

Jak wiadomo wyraz stały w funkcji Lagrange’a nie ma wpływu na równanie ruchu i można go pominąć.
Pęd cząstki jest równy : p =

∂

v , zatem :

p = γmv
Hamiltonian relatywistyczny ma postać :

H = c sqrt ( p2 + m2 c2 )
Dla małych prędkości p << mc , otrzymujemy :

≈

mc2 + ½ p2/m

XII. STW a elektrodynamika klasyczna.

Jaku już powiedziałem geneza powstania STW w sposób organiczny związana jest z własnościami transformacyjnymi
wzorów Maxwella. Wzory te nie są niezmiennicze względem grupy transformacji Galileusza ( która jest podstawową
grupą transformacji mechaniki klasycznej. Przykładowo można pokazać, że równanie ruchu - jedno z podstawowych w
mechanice klasycznej - cząstki materialnej w polu siły potencjalnej :

•

= -

∇

U ; U – funkcja potencjalna.

jest niezmiennicze względem grupy transformacji Galileusza), są one niezmiennicze względem grupy Poincarego.
Powstało wobec tego pytanie : czy prawa elektrodynamiki nie łamią zasady względności Galileusza ?
( tj. czy nie wyróżniają one jednego układu odniesienia – układu w którym prędkość światła jest równa c )
Doświadczenie pokazało, że taki układ odniesienia jest niewykrywalny a prędkość c jest absolutna.
Konsekwencje tego doświadczalnego faktu ujmują w sposób prosty i klarowny postulaty Einsteina.

Jedną z najdonioślejszych konsekwencji równań Maxwella jest ( teoretyczne ) wskazanie na istnienie fal EM oraz
utożsamienie tych fal ze światłe.
( zobacz wcześniej tekst pt. „Podstawy elektrodynamiki klasycznej” )

Prawo rozchodzenia się czoła fali świetlnej ma postać :

(1/c2)

∂

2φ/

∂

t2 – [ (

∂

2φ/

∂

x2 ) + (

∂

2φ/

∂

y2 ) + (

∂

2φ/

∂

z2 ) ] = 0

( Ogólnie, można pokazać, że operator falowy : = (1/c2)

∂

t2 –

∂

x2 -

∂

y2 -

∂

jest niezmienniczy względem transformacji Lorentza.

Równanie falowe φ = 0 oraz równanie Kleina-Gordona ( - m2 )

= 0

nie jest niezmiennicze względem grupy Galileusza, ale względem grupy Lorentza – problemy symetrii grupowej równań
( relatywistycznych) teorii pól kwantowych pozostają jednak poza obecnym kręgiem naszych zainteresowań.
Zainteresowanego jak na razie odsyłam do : 15- literatury w języku angielskim ; 10, 11–literatury w języku rosyjskim )

Jak wiadomo : c = 1/ sqrt ( ε0 µ0 ) ( w tym miejscu możemy zapytać czy próżnia, może mieć własności fizyczne takie jak
przenikalność elektryczna lub magnetyczna, ale na razie musimy go pominąć ponieważ prowadziłoby to do zagadnień
elektrodynamiki kwantowej )
W związku z powyższym mówimy, że transformacje Lorentza zachowują stożkową strukturę czasoprzestrzeni ( czego
konsekwencja jest model czasoprzestrzeni jako właśnie przestrzeni M )
( W ogólności zachowane są wszystkie równania falowe cząstek o spinie równym zeru. )
Równanie falowe ulega modyfikacji w obecności pola grawitacyjnego widać zatem konieczność ( nie jedyną ) przejścia do
rozważania układów nieinercjalnych, co oznacza nieuchronne przejście do OTW.
[ 27- literatury dodatkowej, od str. 165 ]

******************** Komentarze i dodatki ********************

XII. Podsumowanie.

Zwyczajowo mówi się, że STW jest teorią która w pewnym stopniu łączy dwie klasyczne teorie tj. mechanikę klasyczną i
elektrodynamikę klasyczną stanowiąc ich „zwieńczenie”. Mówi się również w tym kontekście, że mechanika klasyczna
musi uznać prymat teorii polowej ( a taka jest elektrodynamika ) tj. fizycznie nieuzasadnionym jest hipoteza oddziaływań
natychmiastowych. Każde działanie przenosi się z określoną prędkością w czasie i przestrzeni ( mechanika kwantowa doda
jeszcze, że każde oddziaływanie wiąże się z pewnym polem o określonym nośniku ).

Fizyka jest nauką głównie doświadczalną, każdy model lub hipoteza musi mieć uzasadnienie w empirii tj. musi zgadzać się
z doświadczeniem ( lub w innym ujęciu nie może mu przeczyć ). Jak wiadomo STW jest taka teorią, żaden uzyskany w

niej teoretyczny wynik nie przeczy doświadczeniu ( np. hipoteza tachionów ), a bardzo wiele z nich doskonale zgadza się z
doświadczeniem ( np. w wielu eksperymentach z różną dokładnością potwierdzono efekt dylatacji czasu, stałość prędkości
światła czy też stwierdzono występowanie poprzecznego efektu Dopplera ).
Istnieje wiele możliwych teoretycznych podejść do sformułowania podstaw STW.
Można wyjść od zasady względności, można wyjść od stałości prędkości światła, można zapostulować, że czasoprzestrzeń
jest modelowana przestrzenia M, można wyjść od postulatu zachowania struktury przyczynowej,
można oprzeć się na kinematyce Lorentza, można wyjść od postulatu zachowania struktury stożkowej.
Wszystkie te podejścia wymagają wprowadzenia dodatkowo pewnych przedzałożeń ( sztucznych lub mniej sztucznych, o
naturze fizycznej lub niefizycznej , matematycznych lub metodologicznych ).
Wszystkie te wyprowadzenia suma sumarum powinny prowadzić do wyników uzasadnialnych doświadczalnie.
Trywialnym wydaje się stwierdzenie, że jeśli tak nie jest to dane wyprowadzenie jest niepoprawne.

Wyjdziemy teraz od zasady względności Galileusza. W IUO ( tj. układach w których spełniona jest zasada bezwładności ),
wszystkie zjawiska przebiegają jednakowo ( tj. za pomocą eksperymentów mechanicznych nie można wykryć absolutnego
spoczynku a to znaczy, że ruch swobodny jest ruchem względnym. Właściwie jest ot treść I zasady dynamiki ).
Stwierdzenie powyższe ma wartość podstawową dla mechaniki klasycznej. Skoro zjawiska mechaniczne przebiegają
jednakowo we wszystkich IUO to możemy wnioskować, że przestrzeń jest jednorodna i izotropowa ( zjawiska
mechaniczne nie zależą od kierunku wektora v – prędkości względnej). Najprostszym przykładem przestrzeni jednorodnej
jest przestrzeń o stałej krzywiźnie równej zeru. ( przestrzeń Euklidesa ).
Grupą przekształceń (ale nie izometrii ) przestrzeni Euklidesa są kinematyczne przekształcenia Galileusza ( g : E

→

αE’ ).

Szczególnymi przekształceniami Galileusza są przekształcenia o znanej postaci :
x’ = x – vt
t’ = t
Oczywiście, że w czasach kształtowania się pojęciowego mechaniki klasycznej nie było doświadczalnych powodów aby
nie przyjmować absolutności czasu. Stad też przyjęcie t’ = t wydawało się uzasadnione.
Warto zauważyć również, że pojęcie czasoprzestrzeni Galileusza o metryce diag ( + + + + ) prowadzi do przestrzeni
niemetrycznej. ( zobacz tekst pt. „Kinematyka punktu materialnego w mechanice klasycznej” )

Osobnym problemem jest problem postulowania w mechanice klasycznej istnienia sygnałów o prędkości nieskończonej.
Właściwie jest to postulat niespawdzalny w zakresie możliwości zarówno teoretycznych jak i praktycznych w czasach
Newtona i Galileusza. Wiadomo jednak, że był on szeroko dyskutowany w owych czasach.
Jeżeli istnieje taki sygnał (sygnały), to pojęcie czasu absolutnego ma sens.

Jak wiadomo konsekwentne zastosowanie zasady względności prowadzi do wniosku o istnieniu prędkości granicznej,
zatem jako tego konsekwencje otrzymujemy niemożliwość istnienia czasu absolutnego a co za tym, niemożliwość
ustalenia jednej synchronizacji dla wszystkich IUO, a co za tym, przyjęcie do wiadomości znanych efektów
kinematycznych.
Warto również zauważyć, że o ile w STW możliwe jest ustalenie jednoznaczne czasu globalnego, to w OTW już takiej
możliwości nie ma.

Powstanie elektrodynamiki klasycznej pozwoliło nadać fizycznego sensu prędkości granicznej oraz ustalić jej wartość.
Przy okazji pozwoliło rozszerzyć zasadę względności Galileusza o zjawiska elektromagnetyczne. Wiadomo zatem, że
zjawiska elektrodynamiczne nie preferują żadnego IUO. Skoro nie preferują zatem wspierają koncepcje jednorodności i
izotropowości czasoprzestrzeni.

Przestrzeń STW jest przestrzenią jednorodną i izotropową ( co jest warunkiem postawienia zasady względności ).
Jak wiadomo ogólnie przestrzeni o takich własnościach to przestrzenie o stałej krzywiźnie (dodatniej ujemnej lub zerowej )
Przestrzeń M jest przestrzenią o zerowej krzywiźnie.

***********************************************************************************************

Dodatek 1. Elementy analizy globalnej czasoprzestrzeni ( rozmaitości lorentzowskich ).

W dodatku tym prezentuje ( raczej w charakterze ogólnego zapoznania się ) pewne „standardowe” definicje związane z
pojęciem czasoprzestrzeni. Pojęcia stanowią podstawę dla dowodu znanych twierdzeń OTW, dotyczących osobliwości
czasoprzestrzeni. Dodatek ten w pewnym sensie łączy formalizm STW i OTW. Aby postawić poniższe definicje we
właściwej „scenerii” należy przypomnieć co następuje : naturalną przestrzenią OTW jest rozmaitość pseudoriemannowska,
zwana również rozmaitością Lorentza, przestrzeń M jest przestrzenią styczną do tej rozmaitości.

Definicja 1. Czasoprzestrzeń M, jest to gładka rozmaitość : rzeczywista, czterowymiarowa, spójna, Hauudsdorffowska, na
której w sposób globalny zdefiniowano pole tensora metrycznego g, walencji ( 0, 2) ( lorentzowskiego typu lub
hiperbolicznego typu )
Często też czasoprzestrzenią nazywamy parę ( M, g) ( ściślej mówiąc matematycznym modelem czasoprzestrzeni jako
ogółu zdarzeń fizycznych jest para ( M, g ) )

Dla przestrzeni M metrykę przyjęto oznaczać symbolem η ;
n-1

W „wyrafinowanej postaci” metrykę na M możemy zapisać następująco : η = -dx0 dx0 +

ΣΣΣΣ

dxi dxi ,

i=1
a w postaci mniej subtelnej jako : η = diag ( - + + +) ( proszę pamiętać o konwencji wyboru sygnatury )

Definicja 2. Przestrzeń Tx (M) nazywamy przestrzenią styczną do M w punkcie x

∈

Definicja 3. Niech M będzie czasoprzestrzenią i nich x

∈

M. Wtedy mówimy, że wektor styczny X

∈

Tx (M) jest:

czasopodobny, przestrzennopodobny lub zerowy w zależności od tego czy : forma g(X, X) ( = gab X

a Xb ) przyjmuje

wartość odpowiednio : dodatnią, ujemną lub zerową.

Definicja 4. Zbiór wszystkich wektorów zerowych w Tx (M) nazywamy „stożkiem świetlnym” ( light or null cone ) w
punkcie x. Stożek świetlny oddziela od siebie wszystkie wektory czasopodobne od wszystkich wektorów
przestrzennopodobnych. ( The null cone disconnects the timelike vector into two separate components )

Definicja 4. Zbiór

ℑ

x – wszystkich wektorów czasopodobnych ma dwie spójne składowe :

ℑ

x ,

ℑ

x , które nazywamy

odpowiednio „przyszłością” i „przeszłością” punktu x. Analogicznie stożek świetlny ma dwie spójne składowe

ℜ

x ,

ℜ

x , które nazywamy odpowiednio „stożkiem przyszłości” i „stożkiem przeszłości” punktu x.

Definicja 5. Mówimy , że M jest „czasowo orientowalna” ( time orientable )jeśli możliwe jest ciągłe, jednoznaczne i
globalne przyporządkowanie każdemu punktowi x

∈

M zbioru

ℑ

x - wektorów czasopodobnych. Jeżeli zbiór

ℑ

x ma tylko

jedną składową to mówimy, że M jest czasowo nieorientowalna. Wybór orientacji dla składowych

ℑ

x ,

ℑ

x sprawia że

M jest czasowo zorientowana ( time oriented ).

Definicja 6. Dwie czasoprzestrzenie (M, g ) i (M’, g’ ) uważamy za równoważne jeśli są one izometryczne tj. jeśli istnieje
dyfeomorfizm φ : M

→

M’ , który przeprowadza metrykę g w metrykę g’.

Zatem nie istnieje jeden model czasoprzestrzeni tylko cała ich klasa.

Definicja 7. Czasoprzestrzeń ( M’, g’ ) nazywamy przedłużeniem lub rozszerzeniem ( extension) czasoprzestrzeni (M, g)
jeżeli istnieje izometryczne włożenie f , rozmaitości M w rozmaitość M’ f : M

→

M’. Czasoprzestrzeń nazywamy

nieprzedłużalną ( inextendible ) jeżeli nie istnieje żadne jej przedłużenie.

Rys. D.1 Rozszerzenie rozmaitości M. Krzywą γ można przedłużyć do rozmaitości M’.

Można pokazać, że każdą rozmaitość Lorentza można przedłużać tak długo, aż stanie się ona nieprzedłużalną.
Nieprzedłużalność jest matematycznym odpowiednikiem pojęcia „całości” czasoprzestrzeni [warto przeczytać 1, od str.38]
Zazwyczaj zakłada się że wykorzystywane czasoprzestrzenie są nieprzedłużalne w odpowiedniej klasie gładkości.

Twierdzenie 1. Czasoprzestrzeń (M, g) jest czasowo orientowalna wtedy i tylko wtedy, gdy istnieje w niej nigdzie nie
zerujące się pole wektorowe czasopodobne X : M

→

T(M)

Zazwyczaj zakłada się, że wykorzystywane czasoprzestrzenie są czasowoorientowalne.
Oprócz orientacji czasowej czasoprzestrzen może by orientowalna w „klasycznie” rozumianym sensie orientacji bazy
wektorów przestrzennopodobnych. ( orientacja lewo i prawoskrętna )
Pokazuje się , że każda czasoprzestrzeń jednospójna jest orientowalna całkowicie tj. czasowo i przestrzennie.

Definicja 8. Czasoprzestrzeń (M, g)nazywa się czasoprzestrzenią geodezyjnie zupełną, jeżeli : Dp = Tp (M) dla każdego
p

∈

Definicja odgrywa zasadnicza rolę przy badaniu osobliwości czasoprzestrzeni.
W ogólności Dp

⊂

T(M) jest zbiorem wektorów v dla których istnieją geodezyjne nieprzedłużalne.

Literatura

1) „Teoretyczne podstawy kosmologii” – M. Heller PWN 1988
2) „Osobliwy wszechświat” - M. Heller PWN 1991
3) „Astrofizyka relatywistyczna” – M. Demiański PWN 1991
4) „Techniques of differential topology in relativity” – R. Penrose
5) “Global lorentzian geometry” - J. Beem, P. Ehrlich ( jest tłumaczenie rosyjskie )
6) “The large scale structure of space-time” S. Hawking, G. Ellis ( jest tłumaczenie rosyjskie )
7) “Semi-Riemannian geometry with applications to relativity” - Barrett O’Neill

Dodatek 2. Zagadnienie fizyczności przejścia „na druga stronę stożka”

Jak już powiedziano transformacja Lorentza dzieli cząstki na trzy rozłączne klasy. Odpowiednio stożek świetlny dzieli
( umownie ) czasoprzestrzeń na trzy obszary w których te cząstki mogą się poruszać. Wartym zastanowienia jest fakt, że
tworzące stożka tj. linie zerowe są niejako symetryczne dla bradionów jak i tachionów. śaden tachion ani bradion nie może
stać się luksonem tj. żaden realny proces fizyczny nie może zamienić bradionu na lukson.
Od strony matematycznej jest to uzasadnione odpowiednią postacią wzoru transformacyjnego. Ze strony bradionów świat
tachionów ma dziwne własności ( i jak należy się spodziewa i vice versa ). Powstaje pytanie czy oba te światy funkcjonują
na równych prawach i czy istnieje między nimi jakaś zależność tj. czy świat bradionów jest fizyczny ?
( czy świat bradionów jest niejako sprzężony ze światem tachionów, i jak należy traktować „wspólny” świat luksonów ?
Być może uda mi się kiedyś przedstawić „jakościowe” dywagacje na ten temat )

Dodatek 3. Krótki słowniczek polsko - angielski podstawowych terminów stosowanych w STW :

Inercjalny Układ Odniesienia – inertial frame of reference
Zasada względności – principle of relativity
Hipoteza wleczenia eteru – ether drag hypothesis
Skrócenie Lorentza-Fitzgeralda - the Lorentz-Fitzgerald contraction
Skrócenie długości - length contraction
Transformacja Lorentza - lorentz transformations
Jednoczesnosć - simultaneity
Interwał między zdarzeniami – interval between events
Interwał czasoprzestrzenny - spacetime interval
Zasada przyczynowości - principle of causality
Struktura przyczynowa - causal structure
Zdarzenie - event
Czas własny - proper time
Krzywa czasowa - timelike curve
Czteroprędkość - fourvelocity (4 –velocity )
Czteropęd - 4-momentum
Interwał niezmienniczy - the invariant interval
Sztywny pręt - rigid rod
Ruch hiperboliczny - hyperbolic motion
Tachiony - Tachyons
Eksperyment myślowy - thought experiment

The speed of light is the same in all frames of reference.
The spacetime interval between two events, defined by

∆

s2 = c2

∆

t2 -

∆

x2 -

∆

y2 -

∆

is invariant, i.e., the same in all frames of reference.

A point in spacetime, which is called an event, is indicated by four coor-
dinates: (ct, x, y, z). Spacetime is the totality of all events.

If a particle travels slower than light in some frame of reference, it
travels slower than light in every frame of reference.

A moving object appears contracted along the direction of its
motion by a factor γ. This effect is called length contraction.

Literatura.

( tekstem podkreślonym zaznaczono pozycje o szczególnym znaczeniu )

1) „Porozmawiajmy o teorii względności ” -- J. L. Synge
PWN 1974
2) „Elementy teorii względności” -- M. Sawicki
WSiP 1975
3) „Fizyka czasoprzestrzeni” -- E. F. Taylor, J. A. Wheeler
PWN 1972
4) „Szczególna teoria względności” -- A. Szymacha
Wydawnictwo Alfa 1985
5) „Teoria względności” -- G. B. Kuzniecow
PWN 1962
6) „Wstęp do szczególnej teorii względności” -- R. Katz
PWN 1967
7) „Mechanika teoretyczna” -- W. Rubinowicz, W. Królikowski
WN-PWN 1998
8) „Mechanika klasyczna” -- J. R. Taylor
tom 2 WN-PWN 2006
9) “Historia fizyki” -- A. K. Wróblewski
WN-PWN 2007
10) „Sześć trudniejszych kawałków – Teoria względności -- R. P. Feynman
Einsteina, symetria i czasoprzestrzeń” Prószyński i S-ka 1999
11) „Zrozumieć teorię względności „ -- J. Czerniawski
Wydawnictwo TASSO Kraków 1993
12) „Wstęp do fizyki współczesnej” -- J. Kociński
PWN 1977
13) „Podstawy fizyki relatywistycznej i mechaniki kwantowej” -- M. Kozielski
WPW Warszawa 1999
14) „Mechanika klasyczna” -- R. S. Ingarden, A. Jamiołkowski
PWN 1980
15) „Fizyka ruchu i czasoprzestrzeni” -- M. Heller
WN-PWN 1993
16) „Szczególna teoria względności” -- W. A. Ugarow
PWN 1985
17) „Elementy teorii względności, relatywistycznej mechaniki -- B. Konorski
i elektrodynamiki dla inżynierów” WNT 1976
18) „Podstawy elektrodynamiki” -- D. J. Griffiths
WN-PWN 2001
19) „Czasoprzestrzeń i grawitacja” -- W. Kopczyński, A. Trautman
PWN 1984
20) „Wstęp do ogólnej teorii względności” -- B. F. Schutz
WN-PWN 2002
21) „Elektrodynamika klasyczna” -- J. D. Jackson
PWN 1982

Literatura dodatkowa

1) „Czas” -- B. Muchotrzeb, M. Prószyński
WSiP 1983
2) „Albert Einstein – 5 prac, które zmieniły oblicze fizyki” -- A. Einstein
WUW Warszawa 1998
3) „Literatura źródłowa do kursu „Podstawy fizyki” -- red. W. Kruczek
na Politechnice Warszawskiej” tom I STW Warszawa 1983
4) „Filozofia czasoprzestrzeni” -- red. J. Miśek
Kraków 1988
5) „Zadania i problemy z fizyki” -- A.Hennel, W. Krzyżanowski
tom I W. Szuszkiewicz, K. Wódkiewicz
WN-PWN 1997
6) „Pan Bóg jest wyrafinowany ... Nauka i życie Alberta Einsteina” -- A. Pais
Prószynski i Ska 2001
7) „Podstawy fizyki współczesnej” -- V. Acosta, C. L. Cowan, B. J. Graham
PWN 1981
8) „Ewolucja fizyki – rozwój poglądów od najdawniejszych pojęć -- A. Einstein, L. Infeld
do teorii względności i kwantów” PWN 1962
9) „Wstęp do fizyki” tom I -- A. K. Wróblewski, J. A. Zakrzewski
PWN 1984

10) „Kwanty a relatywistyka” -- Z. Chyliński
UJ Kraków 1992
11) „Ontologia świata przyrody” -- M. Tempczyk
Universitas 2005
12) „Wszechświat maszyna czy myśl ? – filozofia mechanicyzmu : -- M. Heller, J. śyciński
powstanie – rozwój - upadek” PTT Kraków 1988
13) „Przestrzeń, czas, ruch” -- zbiór artykułów

PWN 1976

14) „Fizyka – spojrzenie na czas, przestrzeń i materię” -- zbiór artykułów
WN-PWN 2002
15) „Istota teorii względności” -- A. Einstein
PWN 1962
16) „Fizyka ruchu i czasoprzestrzeni” -- M. Heller
WN-PWN 1993
17) „Niezwykle szczególna teoria względności” -- A. Dragan
wersja elektroniczna pdf
18) „Fizyka a świat realny - elementy filozofii fizyki” -- M. Tempczyk

1986 PWN

19) „Ontologia świata przyrody” -- M. Tempczyk
Universitas Kraków 2005
20) „Zagadnienia filozoficzne współczesnej nauki” – M. Heller, M. Lubański S. Ślaga
ATK Kraków 1992
21) „ Jak powstawała teoria względności ?” -- Andrzej Krasinski
POSTEPY FIZYKI TOM 54 ZESZYT 3
22) „Czy teoria względności wymaga naprawy ?” -- Stanisław Bażański
POSTEPY FIZYKI TOM 38 ZESZYT 1
( + odpowiedź na ten artykuł pt.
„ Czy Lorentz nie rozumiał szczególnej teorii względności ?” -- J. Czerniawski, J. Kajfosz
POSTEPY FIZYKI TOM 41 ZESZYT 3-4 )
23) „Tachiony : cząstki szybsze niż światło” -- S. Mrówczyński
POSTEPY FIZYKI TOM 32 ZESZYT 4
24) „Powstawanie i wczesny odbiór Szczególnej Teorii Względności” -- Stanisław Bażański
POSTEPY FIZYKI TOM 56 ZESZYT 6
25) „Fizyka współczesna dla inżynierów” -- red. L. N. Ridenour, W.A. Nierenberg
artykuł pt. “zagadnienia względności a podstawy mechaniki” H. P. Robertson
PWN 1965
26) „Alberta Einsteina koncepcja eteru relatywistycznego” -- Ludwik Kostro
Wydawnictwo Uniwersytetu Gdańskiego
1992
27) „Zagadnienia filozoficzne mechaniki kwantowej i teorii -- D. Błochnicew, W. Fok, S. Frisz
względności” L. Infeld, E. Szpolski
artykuł : „Współczesna teoria przestrzeni i czasu” -- W. Fok PWN 1954

Literatura w języku angielskim.

1) „Special Relativity” -- N. M. Woodhouse
Springer-Verlag 1992
2) “Relativity and the nature of spacetime” -- V. Petkov
Springer 2005
3) “Henri Poincare and relativity theory” -- A. A. Logunov
dostępne w arXiv
4) „A primer of special relativity” -- P. L. Sardesai
New Age International 2004
5) “Introduction to special relativity” – R. Resnick
John Wiley & Sons Inc. 1968
6) “The special theory of relativity” -- D. Bohm
tłumaczenie rosyjskie Moskwa Mir 1967
7) „The geometry of Minkowski spacetime – An introduction -- G. L. Naber
to the mathemetics of the special theory of relativity” Springer-Verlag 1992
8) “Foundations of space-time theories – relativistic physics -- M. Friedman
and philosophy of science” Princeton University Press
9) “Introduction to spacetime – a first course on relativity” -- B. Laurent
World Scientific 1994
10) “Understanding space-time. The philosophical development -- R. Disalle

of physics from Newton to Einstein” Cambridge 2006
11) “The theory of relativity” -- C. Moller
tłumaczenie rosyjskie

Moskwa Atomizdat 1975

12) „Problem book in relativity and gravitation” -- A. P. Lightman, W. Press, R. Price
S. Teukolsky
tłumaczenie rosyjskie Moskwa Mir 1979
13) „Relativity. An introduction to special and -- H. Stephani
general relativity” Cambridge 2004
14) “Special relativity and motions faster than light” -- Moses Fayngold
Wiley VCH 2002

15) “Symmetry and Separation of Variables” --Willard Miller, Jr.
School of Mathematics University of
Minnesota 1977
Addfebn-Wesfey Publishing Company
Tłumaczenie rosyjskie Moskwa Mir 1981

Literatura w języku rosyjskim.

1) „Paradoksy teorii otnositielnosti” -- A. P. Terleckii
Moskwa Nauka 1966
2) „Klasiczeskaja elektrodinamika i teorja otnositielnosti” -- R. A. Szaripow
UFA 1997
3) „ O teorii otnositielnosti” -- W. L. Ginzburg
Moskwa Nauka 1979
4) „Specialnaja i obszaja teorja otnositielnosti – istoriczeskie oczerki” -- U. I. Frankfurt
Moskwa Nauka 1968
5) „Princip otnositielnosti – sbornik rabot po specialnoj -- red. A. A. Tjapkin
teorii otnositielnosti” Moskwa Atomizdat 1973
6) „Paradoksy wremieni w reljatibistskoj mechanikie” -- I. I. Goldenblat
Moskwa Nauka 1972
7) „Lekcii po teorii otnositielnosti i grawitacii” -- A. A. Logunow
sowremnienny analiz problemy Moskwa Nauka 1987
dostępne tłumaczenie własne.
8) „Elektrodinamika” -- Ja. P. Terleckij, Ju. P. Rybakow
Moskwa Wysszaja Szkoła 1990
9) „Teorija elektronow i jej primenenie k jawlenijam sweta -- H. A. Lorentz
i teplowogo izluczenija” Moskwa 1953
( jest to przekład z angielskiego, klasycznej pracy Lorentza )
10) „Gruppy preobrazowania w matematiczeskoj fizikie” -- N. H. Ibragimow

11) „Symetrija urawnienij kwantowoj mechaniki” -- W. I. Fuszicz, A. G. Nikitin
12) „Osnowy teorii otnositielnosti – kurs lekcij” -- E. A. Uszakow ; Minsk 2003

Literatura w języku niemieckim.

1) „Relativitatstheorie” -- W. Pauli
tłumaczenie rosyjskie Moskwa Nauka 1983

Wyszukiwarka

Podobne podstrony:

więcej podobnych podstron