6 [kN/m]

2

6

EI

2

1

2

x

y

2

4

4

=  

2

=

 =

2

[

/ ]

=



 =

2

= ⋅





2

=

[

/ ]

1/4

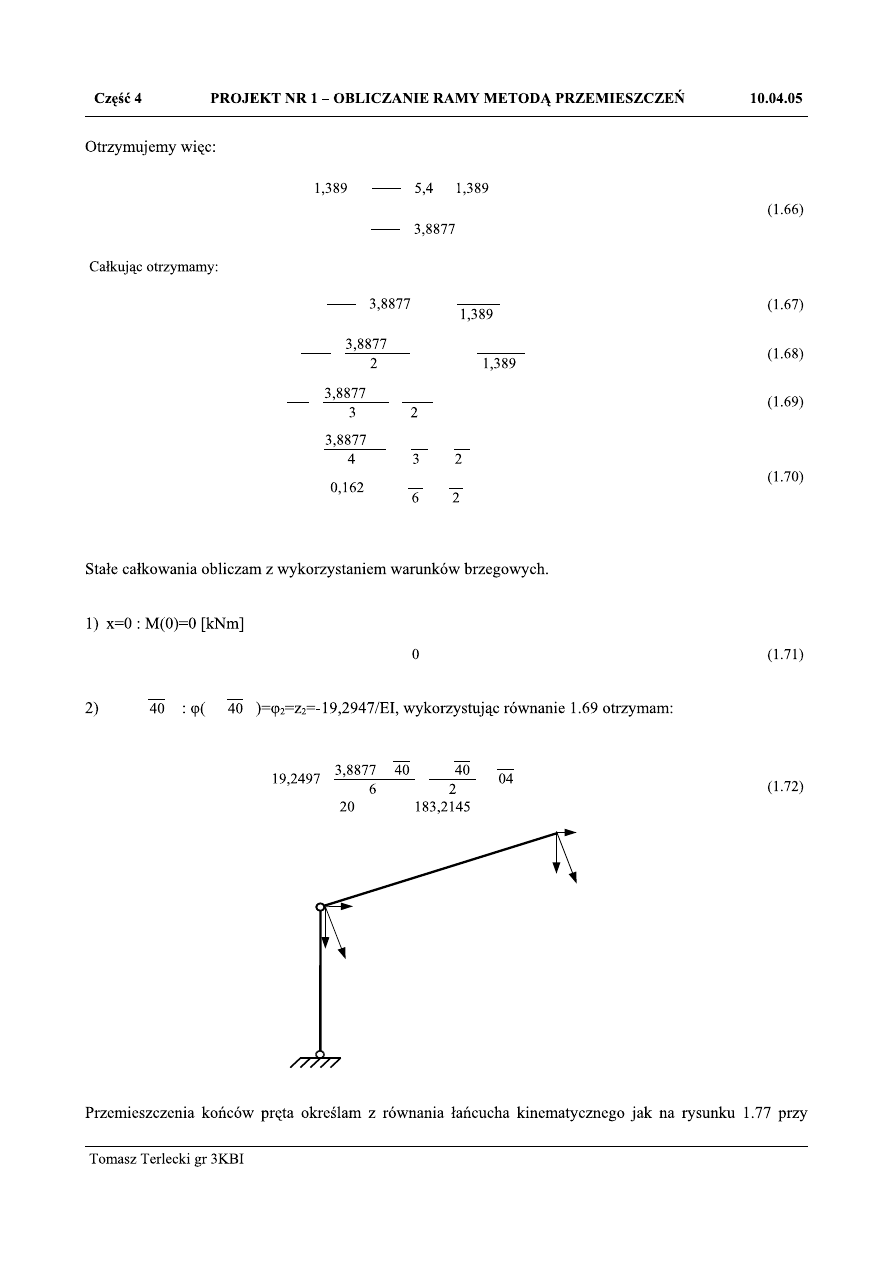
EI

d

4

y

dx

4

=

/:



EI

d

4

y

dx

4

=

EI

d

3

y

dx

3

=

x A=

−T  x

EI

d

2

y

dx

2

=

⋅x

2

!

 AxB=

−M  x

EI

d y

dx

=

⋅x

3

!



A⋅x

2

!

xBxC =EI 

EI y=

⋅x

4

!

 A

x

3

!

B

x

2

!

CxD

EI y=

x

4

 A

x

3

B

x

2

CxD

B=

x=





−

=

⋅



3



A⋅



2





BC

AC =−

ψ

01

ψ

12

=0

v

1

v

2

v

2

x

v

2

y

v

1

x

v

1

y

Rys.1.77. Łańcuch kinematyczny dla części ramy 012

2/4

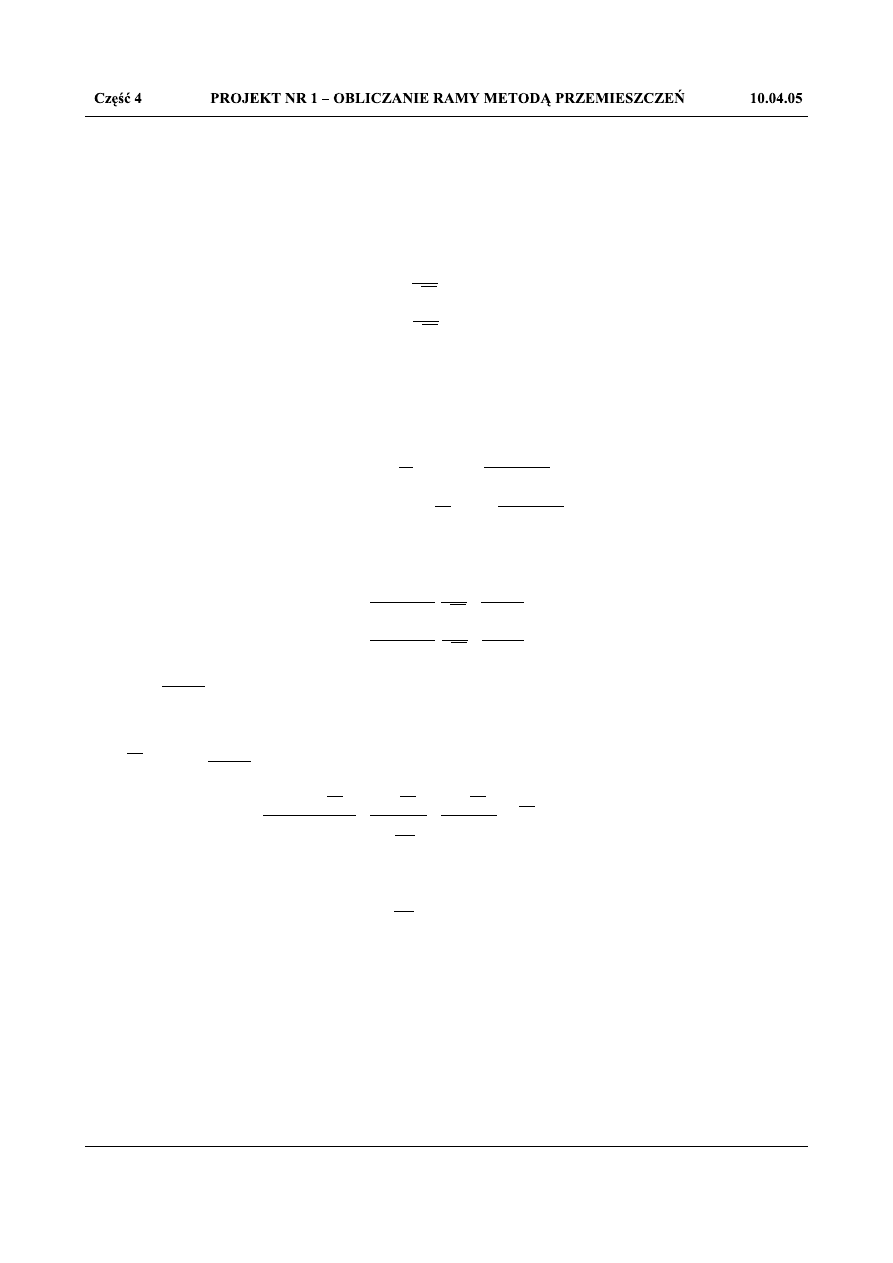
czym:

v

1

=v

1 y

cos v

1 x

sin 

v

2

=v

2 y

cos v

2 x

sin 

(1.73)

Dane:

sin =

1



10

cos =

3



10

(1.74)

Obliczając przemieszczenia końców pręta należy pamiętać, iż w zadaniu nie uwzględniamy zmian długości
pręta.

Z równania łańcucha kinematycznego na określonych niżej drogach otrzymam:

v

1 y

=0

01  4 

01

=v

1 x

, 

01

=

z

1

4

⇒ v

1 x

=z

1

=

−10,6897

EI

012  4 

01

2 

12

=v

2 x

, 

01

=

z

1

4

⇒ v

2 x

=

−10,6897

EI

012  6 

12

=v

2 y

, 

12

=0 ⇒ v

2 y

=0

(1.75)

Stąd:

v

1

=v

1 x

sin =

−10,6897

EI

⋅

1



10

=

−3,38

EI

v

2

=v

2 x

sin =

−10,6897

EI

⋅

1



10

=

−3,38

EI

(1.76)

x=0 :

v

1

=

−3,38

EI

, wykorzystując równanie 1.70 otrzymam:

D=−3,38

(1.77)

x=



40

:

v

2

=

−3,38

EI

, wykorzystując równanie 1.70 otrzymam:

−3,38=

3,8877 ⋅



40

4

24



A⋅



40

3

6



B⋅



40

2

2





40 C D=0

42,1637 A



40 ⋅C =−259,18

(1.78)

Rozwiązaniem układu równań:

20 AC =−183,2145

42,1637 A



40 ⋅C =−259,18

(1.79)

jest para liczb (stałe całkowania):

A=−10,6676

C =75,1375

(1.80)

Stąd otrzymujemy równania momentów zginających oraz sił tnących jak niżej:

T  x=−1,389⋅4,3197 x−6,812

M  x=−1,389 ⋅2,1599 x

2

−6,812

(1.81)

Sprawdzenie wartości przęsłowych przywęzłowych momentów zginających oraz sił tnących:

Tomasz Terlecki gr 3KBI

3/4

x=0 ⇒ T 0=10,6676⋅1,389=14,817 [ kN ] ,

x=0 ⇒ M 0=0 [ kNm]

x=



40 ⇒ T 



40=−3,8877



4010,6676⋅1,389=−19,335 [ kN ] ,

x=



40 ⇒ M 



40=−

3,8877 ⋅



40

2

2

−10,6676⋅



40⋅1,389=−14,287 [ kNm]

(1.82)

Uwaga: ujemne wartości momentów oznaczają rozciąganie włókien górnych pręta!!!

Wartości sił wewnętrznych obliczone metodą przemieszczeń:

T 0=14,817 [ kN ]

M 0=0 [ kNm]

T 



40=−19,335 [ kN ]

M 



40=−14,287 [ kNm]

(1.83)

Jak widać znalezione równania momentów zginających oraz sił poprzecznych potwierdzają poprawność
wyników otrzymanych w części 1.1. projektu obliczania ram metodą przemieszczeń.

=

M

max

I

y

⋅z

max

(1.84)

≤

dop

=20,5 [kN /cm

2

]

dla

I

1

=3060 [cm

4

] I 220  z

max

=11 cm M

max

=14,285 [kNm]

=

1428,5

3060

⋅11=5,14 [

kN

cm

2

]

5,14 [

kN

cm

2

]≤20,5 [

kN

cm

2

]

dla

I

2

=4250 [cm

4

] I 240  z

max

=12 cm M

max

=21,551 [kNm]

=

2155,1

4250

⋅12=6,08 [

kN

cm

2

]

6,08 [

kN

cm

2

]≤20,5 [

kN

cm

2

]

Naprężenia w obu przypadkach są znacznie mniejsze od dopuszczalnych dlatego dobrane przekroje mogłyby
być mniejsze.

Tomasz Terlecki gr 3KBI

4/4