Egzamin z Analizy 2, 12 IX 2008 godz. 9.00

1. Znaleźć różniczkę zupełną funkcji

f (x, y) =

x

2

+ 3y

xy

+ y cos(y − x)

w punkcie P (1, 1) . Znaleźć płaszczyznę styczną do powierzchni: z = f (x, y) w punkcie
leżącym nad punktem P .

Rozwiązanie:

Różniczka zupełna f jest równa

df =

∂f
∂x

dx +

∂f

∂y

dy

Obliczamy:

∂f
∂x

=

2x

2

y − (x

2

+ 3y)y

x

2

y

2

+ y sin(y − x)

∂f
∂x

(P ) = −2

∂f

∂y

=

3xy − (x

2

+ 3y)x

x

2

y

2

+ cos(y − x) − y sin(y − x)

∂f

∂y

(P ) = 0

Różniczka zupełna f w punkcie P jest równa

df = −2 dx + 0 dy

Szukamy równania płaszczyzny stycznej:

f (P ) = 5

z − 5 = −2(x − 1) + 0(y − 1)

po uproszczeniu:

2x + z − 7 = 0

2. Znaleźć ekstrema lokalne funkcji

f (x, y) = x

2

− x

2

y + 4y

2

+ 8y

Rozwiązanie

Dziedzina funkcji D : R

2

Rozwiązujemy układ równań :



























∂f
∂x

= 0

∂f

∂y

= 0

Obliczamy pochodne cząstkowe:

∂f
∂x

= 2x − 2xy

∂f

∂y

= −x

2

+ 8y + 8

Stąd:

(

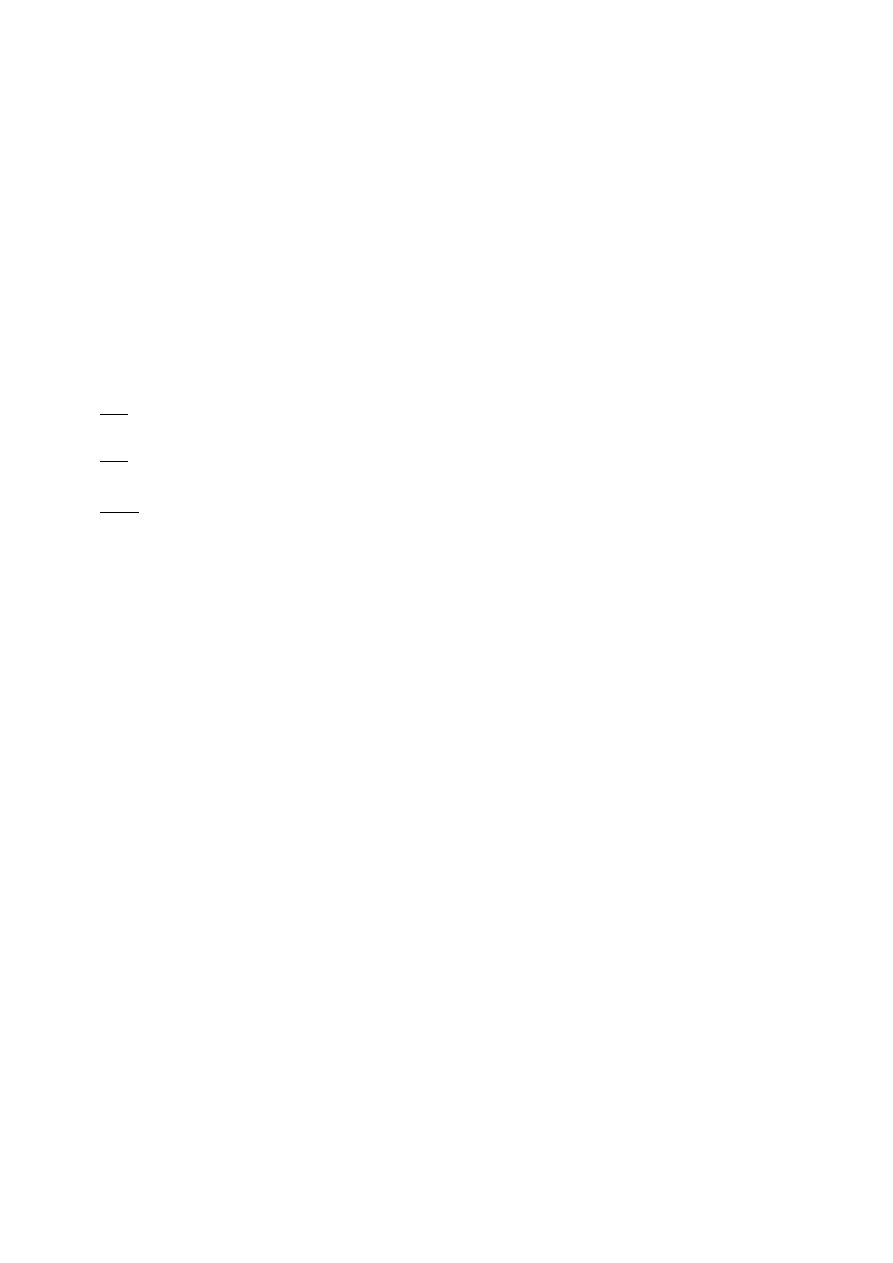
2x − 2xy = 0
−x

2

+ 8y + 8 = 0

Z pierwszego równania:

2x(1 − y) = 0

Czyli x = 0 lub y = 1

Dla x = 0 z drugiego równania y = −1

Dla y = 1 z drugiego równania x = ±4

Mamy więc trzy punkty stacjonarne:

P

1

(0, −1) , P

2

(−4, 1) , P

3

(4, 1)

Obliczamy pochodne cząstkowe drugiego rzędu:

∂

2

f

∂x

2

= 2 − 2y

∂

2

f

∂y

2

= 8

∂

2

f

∂x∂y

= −2x

Badamy macierz drugich pochodnych w punkcie P

1

:

"

4 0
0 8

#

Znaki wyznaczników:

W

1

= 4 > 0 , W

2

= 32 > 0

Funkcja f (x, y) ma więc w punkcie P

1

minimum lokalne.

Badamy macierz drugich pochodnych w punkcie P

2

:

"

0 8
8 8

#

Znaki wyznaczników:

W

1

= 0 , W

2

= −64 < 0

Funkcja f (x, y) nie ma w punkcie P

2

ekstremum.

Badamy macierz drugich pochodnych w punkcie P

3

:

"

0

8

8 −8

#

Znaki wyznaczników:

W

1

= 0 > 0 , W

2

= −64 < 0

Funkcja f (x, y) nie ma w punkcie P

3

ekstremum.

3. Obliczyć pole obszaru ograniczonego krzywymi 4y = x

2

, xy = 16 i y = 1 zawierającego

punkt P (4, 2).

Rozwiązanie:

Pole S obszaru D jest równe:

S =

Z

D

Z

dx dy

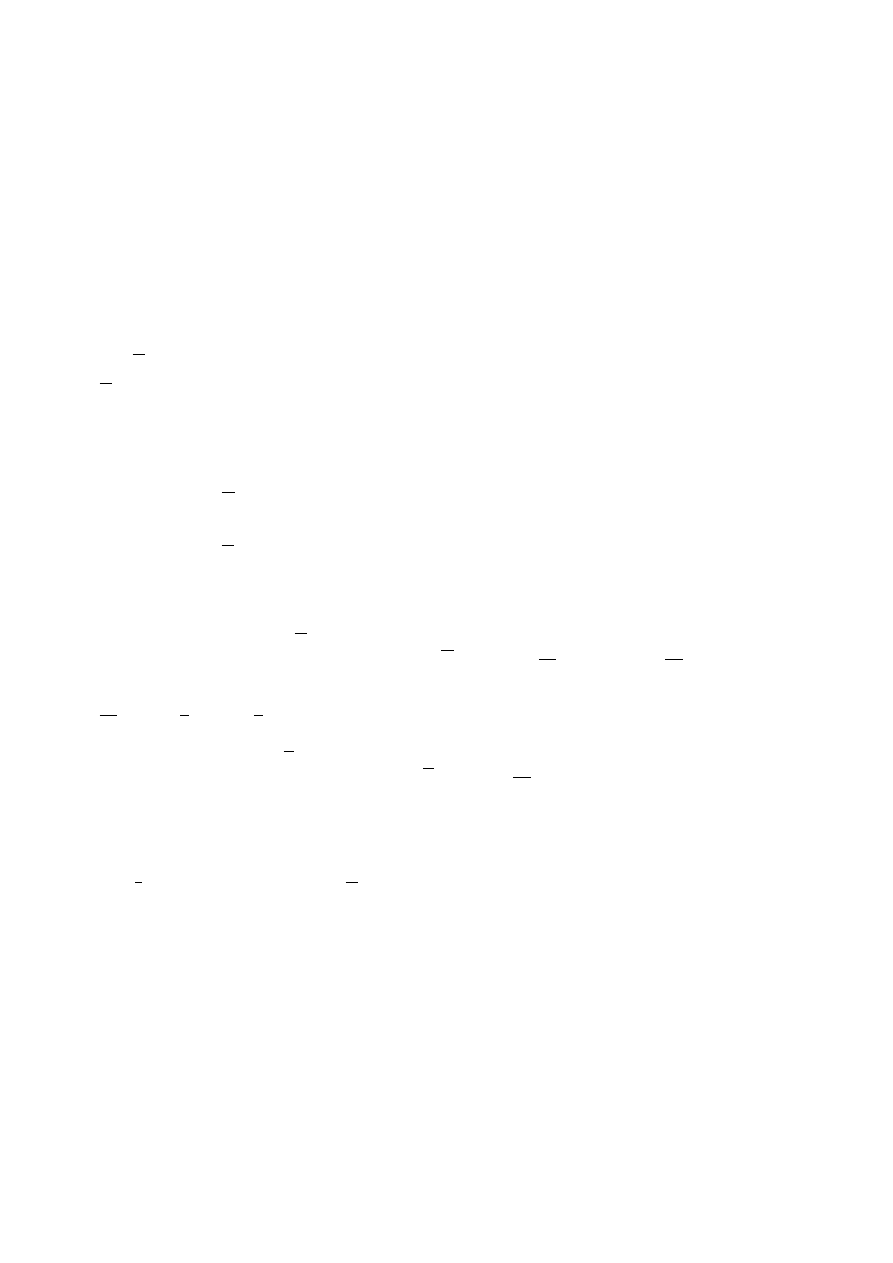
Szukamy punktów przecięcia krzywych:

(

4y = x

2

y = 1

x = ±2

(

xy = 16
y = 1

x = 16

(

4y = x

2

xy = 16

y =

16

x

64

x

= x

2

x = 4

Figurę D dzielimy na dwie części:

D

1

:

(

2 ¬ x ¬ 4
1 ¬ y ¬

x

2

4

D

2

:

(

4 ¬ x ¬ 16
1 ¬ y ¬

16

x

S = S

1

+ S

2

Obliczamy całki:

S

1

=

Z

D

1

Z

dx dy =

4

Z

2









x2

4

Z

1

dy









dx =

4

Z

2

[y]

x2

4

1

dx =

4

Z

2

(

x

2

4

− 1) dx =

"

x

3

12

− x

#

4

2

=

16

3

− 4 − (

2
3

− 2) =

8
3

S

2

=

Z

D

2

Z

dx dy =

16

Z

4









16

x

Z

1

dy









dx =

16

Z

4

[y]

16

x

1

dx =

16

Z

4

(

16

x

− 1) dx = [16 ln |x| − x]

16
4

=

16 ln 16 − 16 − (16 ln 4 − 4) = 32 ln 2 − 12

Stąd:

S =

8
3

+ 32 ln 2 − 12 = 32 ln 2 −

28

3

4. Obliczyć objętość bryły ograniczonej: walcami parabolicznymi y = x

2

− 1 , y = 1 − x

2

, oraz płaszczyznami z = x + 1 i z = 0

Rozwiązanie:

Szukamy rzutu krzywej przecięcia powierzchni z = x + 1 , z = 0 na płaszczyznę Oxy:

x + 1 = 0

x = −1

Rzut bryły A na płaszczyznę xy jest ograniczony krzywymi:

y = x

2

− 1 , y = 1 − x

2

oraz x = −1

Mamy więc bryłę A: x ∈< −1, 1 > ; y ∈< x

2

− 1, 1 − x

2

> ; z ∈< 0, x + 1 >

Objętość bryły jest równa:

V =

Z Z

A

Z

dx dy dz =

1

Z

−1







1−x

2

Z

x

2

−1





x+1

Z

0

dz





dy







dx =

1

Z

−1







1−x

2

Z

x

2

−1

[z]

x+1
0

dy







dx =

1

Z

−1







1−x

2

Z

x

2

−1

(x + 1) dy







dx =

1

Z

−1

[xy + y]

1−x

2

x

2

−1

dx =

1

Z

−1

(2x + 2 − 2x

3

− 2x

2

) dx =

−

1
2

x

4

−

2
3

x

3

+ x

2

+ 2x

1

−1

=

8
3

5. Znaleźć moment bezwładności względem osi Oz bryły o gęstości ρ(x, y, z) = y ogra-

niczonej: stożkiem z

2

= 4x

2

+ 4y

2

, paraboloidą obrotową z = x

2

+ y

2

oraz leżącej w

obszarze y ­ 0

Rozwiązanie:

I

z

=

Z Z

A

Z

(x

2

+ y

2

)ρ dx dy dz =

Z Z

A

Z

(x

2

+ y

2

)y dx dy dz

Stosujemy współrzędne walcowe:

I

z

=

Z Z

A

∗

r

2

· r sin ϕ · r dr dϕ dz =

Z Z

A

∗

Z

r

4

sin ϕ dr dϕ dz

Zbiór A

∗

jest ograniczony powierzchniami:

z

2

= 4r

2

, z = r

2

, zachodzić ma nierówność: r sin ϕ ­ 0 oraz standardowe ograniczenia

współrzędnych walcowych: r ­ 0 oraz ϕ należy do jednego okresu. Stąd mamy:

A

∗

: ϕ ∈< 0, π > ; r ∈< 0, 2 > ; z ∈< r

2

, 2r >

Obliczmy całkę:

Z Z

A

∗

Z

r

4

sin ϕ dr dϕ dz =

π

Z

0

sin ϕ dϕ ·

2

Z

0





2r

Z

r

2

r

4

dz





dr = [− cos ϕ]

π
0

·

2

Z

0

h

r

4

z

i

2r

r

2

dr =

2

2

Z

0

(2r

5

− r

6

) dr = 2

2
6

r

6

−

1
7

r

7

2

0

=

128

21

6. Sformułować warunek dostateczny istnienia potencjału pola wektorowego w R

3

. Znaleźć

potencjał pola wektorowego [P, Q, R] = [3x

2

yz

2

, x

3

z

2

+ cos(y − z) , 2x

3

yz − cos(y − z)]

i obliczyć całkę

B

Z

A

P dx + Q dy + R dz jeśli A = (0, 1, 1), B = (1, 2, 2).

Rozwiązanie

Szukamy potencjału ϕ

Rozwiązujemy układ równań:



















































∂ϕ

∂x

= 3x

2

yz

2

∂ϕ

∂y

= x

3

z

2

+ cos(y − z)

∂ϕ

∂z

= 2x

3

yz − cos(y − z)

Zaczynamy od pierwszego równania:

ϕ(x, y, z) =

Z

3x

2

yz

2

dx = x

3

yz

2

+ f (y, z)

Podstawiamy obliczone ϕ do drugiego równania:

x

3

z

2

+

∂f

∂y

= x

3

z

2

+ cos(y − z)

Stąd:

f (y, z) =

Z

cos(y − z) dy = sin(y − z) + g(z)

czyli

ϕ(x, y, z) = x

3

yz

2

+ sin(y − z) + g(z)

Podstawiamy obliczone ϕ do trzeciego równania:

2x

3

yz − cos(y − z) + g

0

= 2x

3

yz − cos(y − z)

Stąd:

g(z) =

Z

0 dz = C

czyli potancjał jest równy:

ϕ(x, y, z) = x

3

yz

2

+ sin(y − z) + C

B

Z

A

P dx + Q dy + R dz = ϕ(B) − ϕ(A) = 8 + 0 + C − (0 + 0 + C) = 8