GEODEZJA

WYKŁAD

Teoria błędów

Katedra Geodezji im. K. Weigla

ul. Poznańska 2/34

TEORIA BŁĘDÓW

Twórca teorii błędów

CARL FRIEDRICH GAUSS

niemiecki

matematyk i astronom Uniwersytetu Helmstedt. 

Wydał dwutomowe dzieło (1844 i 1847) z dziedziny geodezji. 
Pierwsze

prace z zakresu teorii błędów w geodezji

.

„Theoria combinationia observationum erroribus minimis

obnoxiae”

Gauss jako pierwszy zastosował rachunek

prawdopodobieństwa do oszacowania błędów (rozkład
Gaussa).

- hipotezy Hagena o rozkładzie błędów.
Adrien-Marie Legendre (1752-1833), matematyk francuski,

autor podstaw teorii pomiarów geodezyjnych, wydaje
"Elementy geometrii”

praca, która wyparła obowiązujące wcześniej "Elementy"

Euklidesa.

- postulat

Legendre’a

– metoda najmniejszych kwadratów,

Błędy pomiarów i ich charakterystyka

Błąd prawdziwy

obserwacji



- różnica między

nieznanym wymiarem

X

(prawdziwą wartością)

mierzonej

wielkości i wynikiem pomiaru

L

 



i

= X - L

Źródła błędów:
- niedoskonałość zmysłów obserwatora,
- narzędzia pomiarowe (dalmierz, teodolit, niwelator)
- warunki pracy, czyli środowisko (temperatura,

ciśnienie, wilgotność, wiatr, opady, promieniowanie

słoneczne).

Ogólna klasyfikacja błędów obserwacji:
-

błędy grube

(omyłki),

-

systematyczne

,

-

przypadkowe (losowe)

.

Błędy pomiarów i ich charakterystyka

Wyniki pomiarów (obserwacji) mają wartości przybliżone,
różniące się o pewną wielkość (błąd pomiaru) od wartości
prawdziwej mierzonego elementu. Błędy pomiarów
można podzielić na:
Błędy grube wynikają z

nieuwagi obserwatora

, są

spowodowane omyłkowym odczytem przyrządów użytych
do pomiaru. Są łatwe do wykrycia, przez powtórny
pomiar i wyeliminowane z wyników pomiarów, teoria
błędów i rachunek wyrównawczy nie zajmują się nimi.
Błędy systematyczne powstają wskutek jednostronnego
działania różnych czynników (

wady instrumentów lub

wpływ środowiska

), np. temperatury na pomiar długości.

Znając źródło i prawo powstawania błędu, można

obliczyć poprawkę

i wyeliminować błąd z wyników

pomiarów. Stosowanie specjalnych metod pomiarów
eliminuje niektóre błędy systematyczne.
Błędy przypadkowe mają

charakter losowy

,

spowodowane przyczynami, których nie da się uniknąć
(

niedoskonałość zmysłów

obserwatora, niedoskonałość

instrumentów (przyrządów) użytych do pomiarów.

ROZKŁAD BŁĘDÓW (molekularna teoria)

Hipotezy Hagena:
Błędy przypadkowe mają niewielkie wartości i mogą z
jednakowym prawdopodobieństwem przyjmować
wartości dodatnie i ujemne.
Prawdopodobieństwo wystąpienia błędu dużego jest
bliskie zeru.
Największe prawdopodobieństwo wystąpienia ma błąd o
wartości zerowej.
W ogólnych teoriach rozkładu błędów przyjmuje się
założenie zerowania się wartości średniej błędów oraz
założenie niezależności błędów.

Rozkład błędów przypadkowych w

teorii prawdopodobieństwa

Błędy przypadkowe są

zmiennymi losowymi

.

Charakteryzuje je

rozkład normalny

zwany

rozkładem

Gaussa-Laplace'a

N(μ,σ).

Jest to najczęściej spotykany w naturze

rozkład zmiennej losowej ciągłej.

Rozkład normalny ma dwa parametry:

 μ – wartość oczekiwana,
σ – odchylenie standardowe

.

Funkcja gęstości rozkładu normalnego

2

2

1

(

)

( )

exp(

)

2

2

x

f x





 







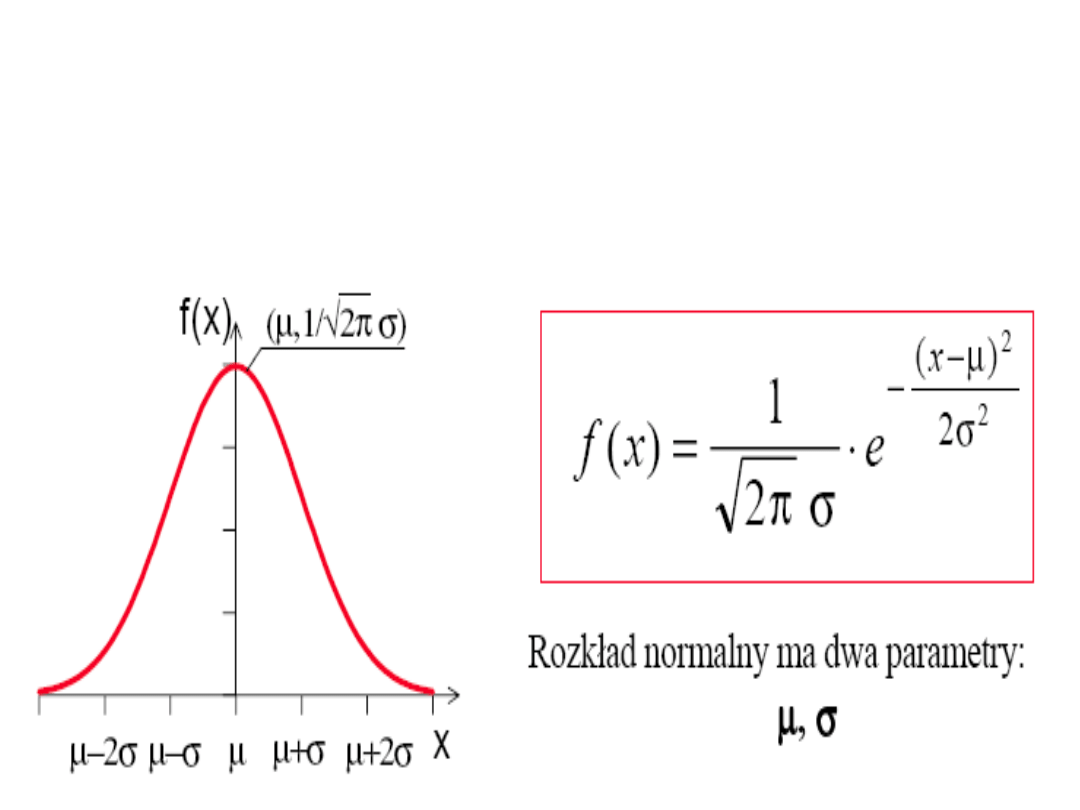
Wykres funkcji gęstości rozkładu normalnego

dla parametrów μ,σ.

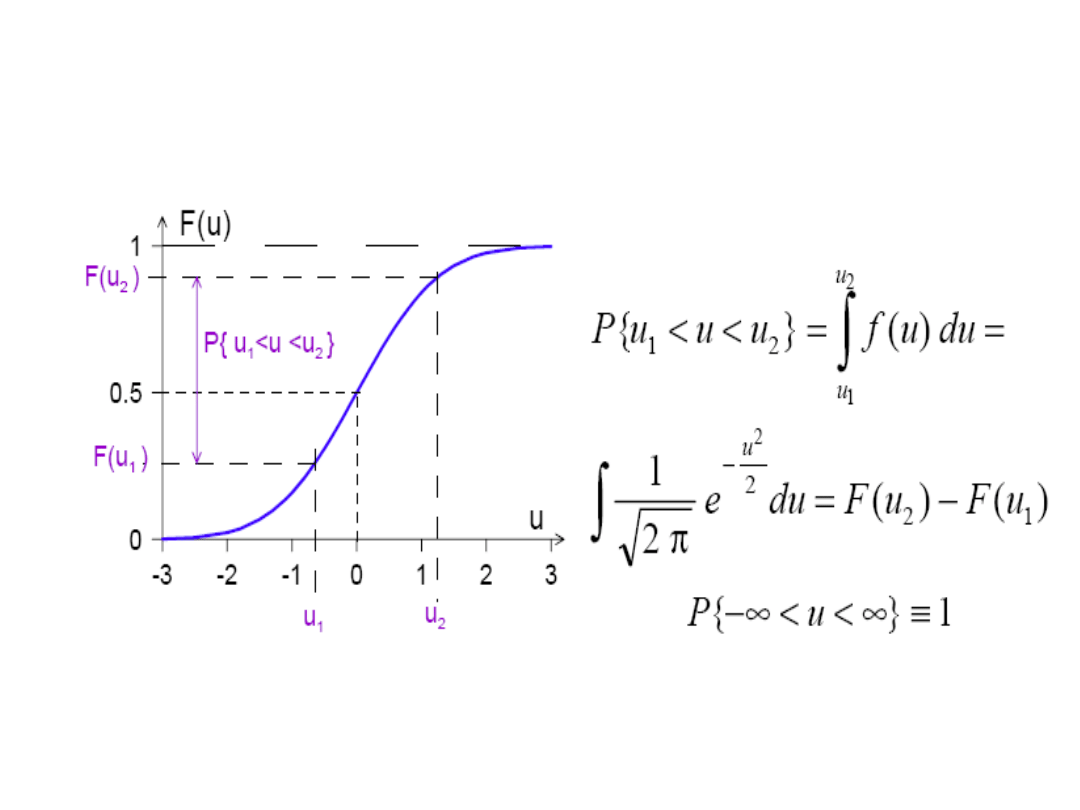
DYSTRYBUANTA ROZKŁADU

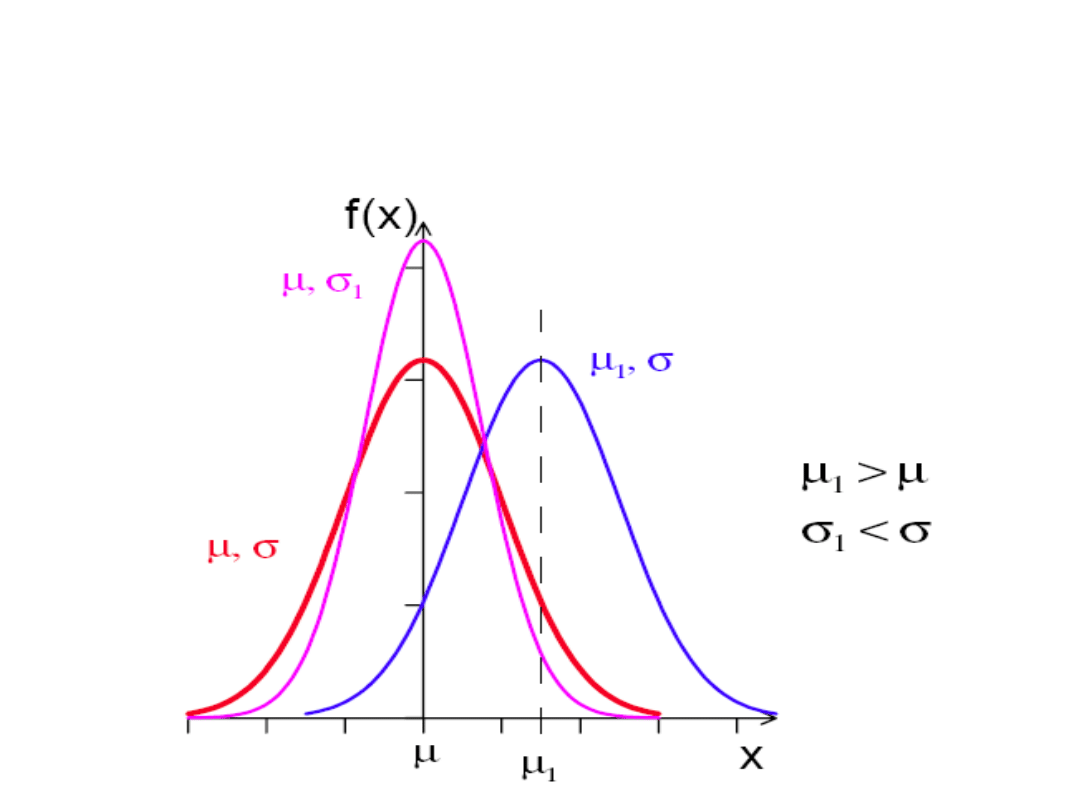
Własności rozkładu normalnego

Empiryczne wartości parametrów rozkładu

normalnego

Brak informacji o wartości błędu  zmusza do operowania

zastępczymi wielkościami do oceny błędu obliczonymi z
próby losowej.

Empiryczne wartości parametrów rozkładu μ,σ
obliczone

z serii pomiarów

:

 

wartość średnia - x

s

błąd średni - m

.

Błąd średni to empiryczna ocena parametru σ,
Definicja: P(|| < m) = 0.68

Różne charakterystyki do oceny błędów:

błąd średni

, błąd przeciętny, błąd prawdopodobny,

błąd graniczny

oraz

błąd względny

.

Różnica między wartością średnią z próby losowej x

s

i obserwacją l

i

nazywa się

błędem pozornym

v

i

v

i

= x

s

- l

i

Ocena dokładności w oparciu o pojęcie niepewności
standardowej

W 1995 roku Międzynarodowa Organizacja
Normalizacyjna (ISO) opublikowała normy dotyczące

niepewności pomiarowych

. Według tych norm,

niepewności

typu A

oblicza się z analizy statystycznej

serii pomiarów {X

1

, X

2

, ....X

n

}. Jako

wynik pomiaru

przyjmuje się średnią arytmetyczną serii X

s

. a

niepewność standardową :

Jeżeli mamy tylko jeden wynik pomiaru, mówimy o
niepewności typu B, Δ

1

= niepewność wzorcowania,

wartość działki podziałki przyrządu pomiarowego,
Δ

2

= niepewność wpływu środowiska pomiaru,

Δ

3

= niepewność wpływu parametrów z literatury,

wyznaczonych doświadczalnie.

2

3

2

2

2

1













X

u











n

i

S

i

X

x

x

n

n

u

1

2

)

(

)

1

(

1

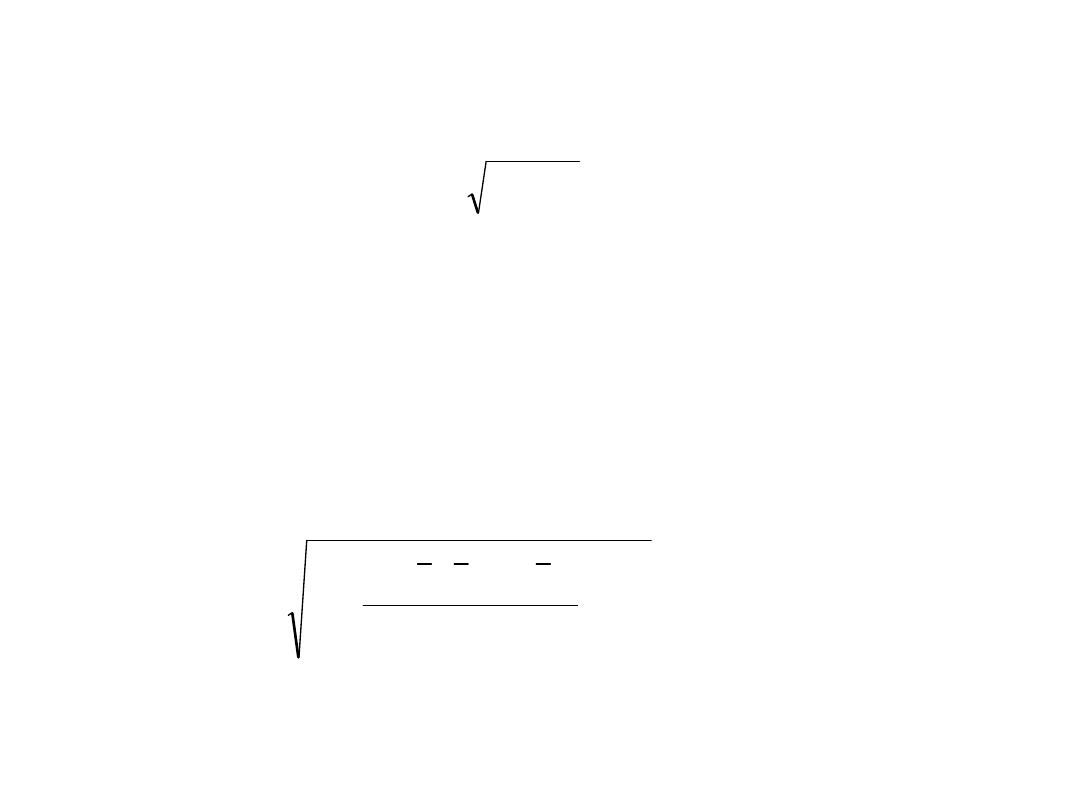
Niepewność standardowa

Gdy występują oba typy niepewności A i B niepewność
standardową obliczamy ze wzoru:

Seria wyników Y

i

, z n

pomiarów pośrednich

jest próbką

podobnie jak w pomiarach bezpośrednich. Przyjmuje się,
że wynikiem pomiaru pośredniego jest Y

s

, a

złożona

niepewność standardowa wyniku:

Y(x) = F(x

1

, x

2

, … x

p

)

2

2

B

A

X

u

u

u



























p

i

i

p

Y

Xi

u

x

x

x

x

F

u

1

2

2

1

)

,

,

,

(



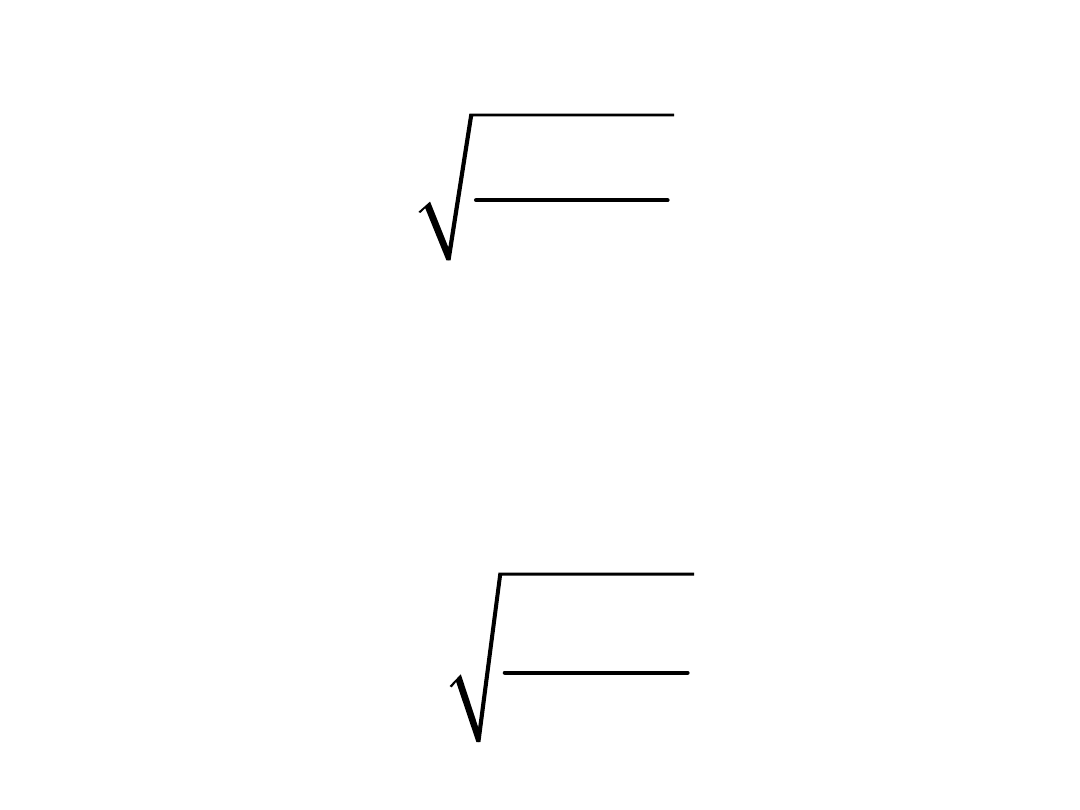
Obliczenie błędu średniego z próby losowej

2

m=

n

e

�

Wielokrotny pomiar tej samej wielkości daje
nadliczbowe elementy i pozwala obliczyć błędy
pozorne v

i

oraz błąd średni m. Dotyczy to zarówno

pomiarów bezpośrednich jak też pośrednich.
v

i

= x

s

- l

i

2

v

m=

n-1



Błąd graniczny

Małe prawdopodobieństwo zdarzenia: P(||

<m)=0.68 nakazuje szukać korzystniejszego
parametru do oceny błędów

: P(|| < m

gr

) = 0.997

,

m

gr

= 3 m

. (0.3% ryzyka wystąpienia błędów ||

większych od błędu granicznego w serii pomiarów).

Błąd graniczny jest przyjmowany do obliczenia

największej wartości błędu (dopuszczalnej) dla
obserwacji. W metrologii w budownictwie, do
określania

odchyłki dopuszczalnej,

często

przyjmuje się 5% poziom istotności,

stąd P(|| < 2 m) = 0.95

Błąd przeciętny t

jest średnią arytmetyczną

bezwzględnych wartości błędów danego szeregu
jednakowo dokładnych obserwacji:

 

| |

t=

n





Błąd względny

Błąd względny to

stosunek bezwzględnej błędu do

wartości mierzonej wielkości (m/L)

.

W pewnych zadaniach przy ocenie błędu korzystniej
jest użyć

miary względnej

. Na przykład porównanie

błędów długości odcinków, pola figur, objętości
obiektów lub ich masy. Błędy pomiaru odcinka
krótkiego i bardzo długiego, ewentualnie błędy
pomiaru objętości lub masy takich obiektów są
trudne do porównania. Takie porównania wymagają

względnej miary dokładności

:

1

w =

L

(

)

|m|

Prawo Gaussa przenoszenia się błędów

średnich.

Błędy obserwacji

powodują, że wszelkie

funkcje

tych

obserwacji

są również obarczone błędami. W

przypadku funkcji liniowych ocena błędu funkcji
obserwacji nie jest skomplikowana. Błąd średni

funkcji nieliniowej

F = f(x, y, z, ...), może być

obliczony dla przybliżonej postaci tej funkcji, przy
założeniu, że daje się ona rozwinąć na szereg
Taylora. Funkcja F (x, y, z) w postaci

szeregu Taylora

w otoczeniu punktu P (x

0

, y

0

, z

0

):

F (x,y,z) = F (x

0

+ dx ,y

0

+ dy, z

0

+ dz) = F (x

0

,y

0

,z

0

)

+

0

0

0

F

F

F

...

x

y

z

dx

dy

dz



















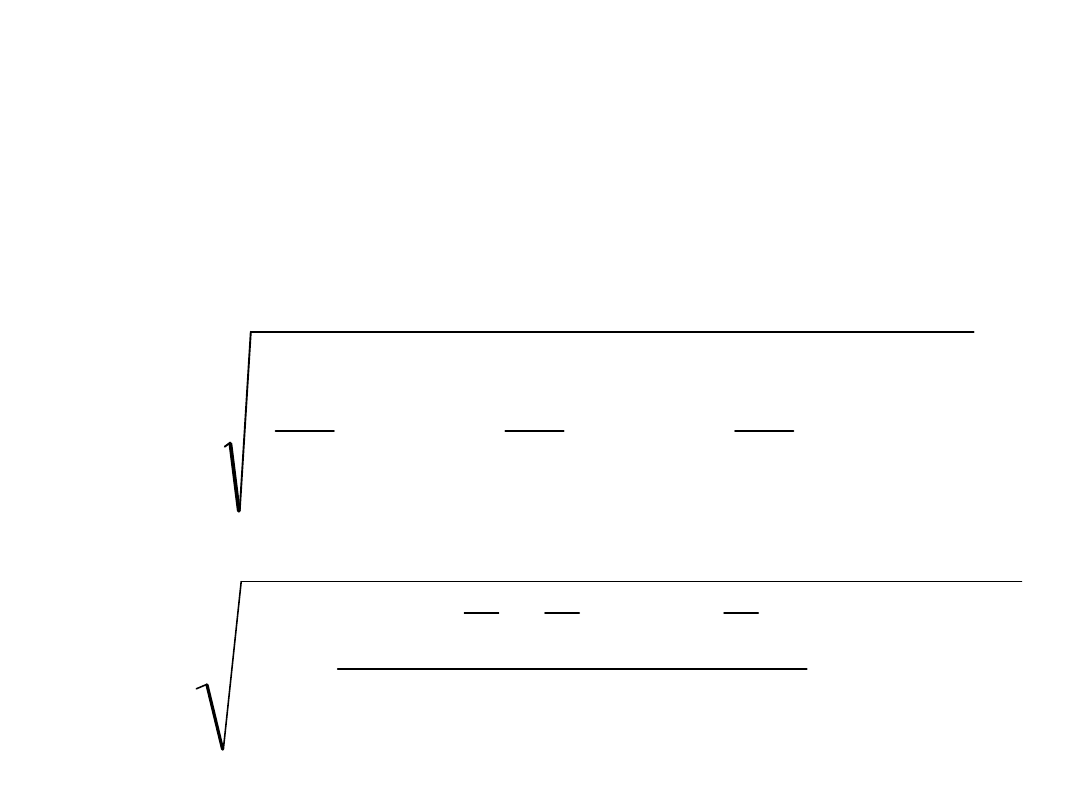
Wzór na średni błąd dowolnej funkcji

 

...

2

2

2

2

2

2



























































z

y

x

F

m

z

F

m

y

F

m

x

F

m























p

i

i

p

F

Xi

m

x

x

x

x

F

m

1

2

2

1

)

,

,

,

(



Utożsamiając zmiany dx, dy, dz z błędami: 

x

, 

y

, 

z

F(x,y,z)=a*X+b*Y+c*Z = F

o

+ a*dx+b*dy+c*dz

Pomiędzy błędem prawdziwym funkcji F i błędani
zmiennych X,Y,Z zachodzi związek:



F

= a*

x

+ b*

y

+ c*

z

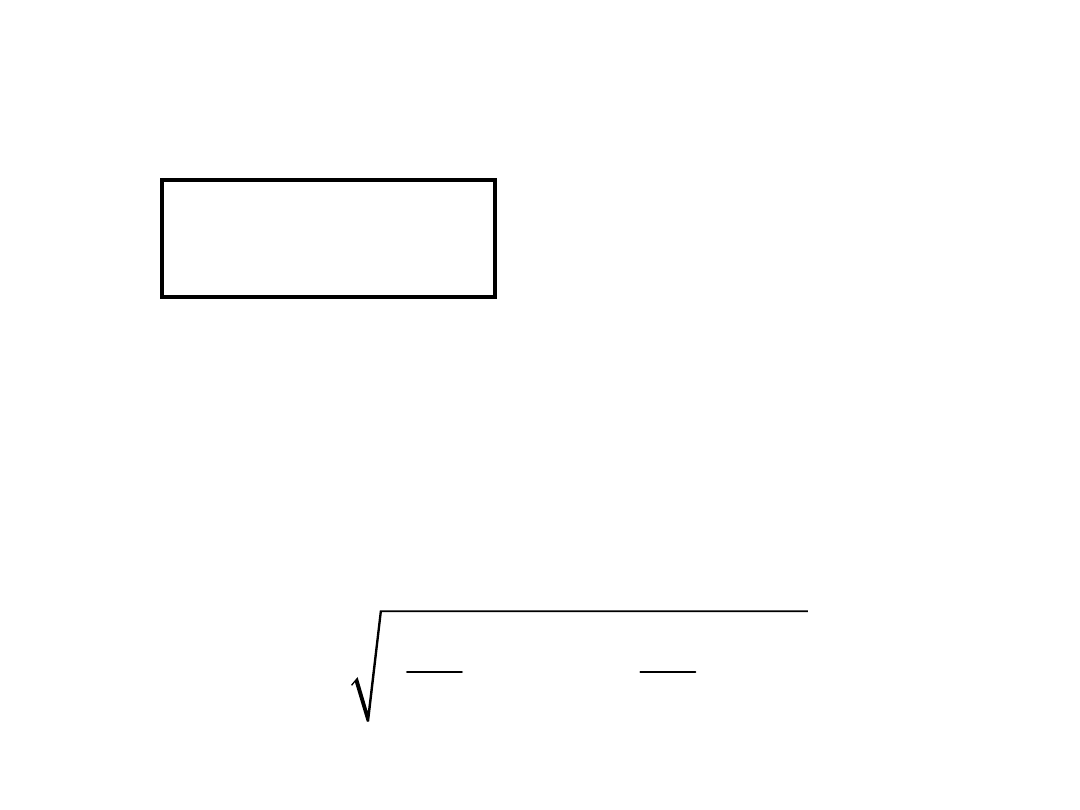
Przykład

: Pole prostokątnej działki o bokach a, b.

 

Z pomiaru długości boków figury: a =300m,
m

a

=0,10 m, b = 20m m

b

= 0,01m

Obliczyć pole figury, błąd średni oraz względny pola.
Funkcja zmiennych a i b - P = F(a,b) = a * b =
6000 m

2

= 60 a.

Średni błąd tej funkcji

:

 

 

 

 

2

2

2

2

P

b

a

P

P

m

m

m

a

b





































a

b

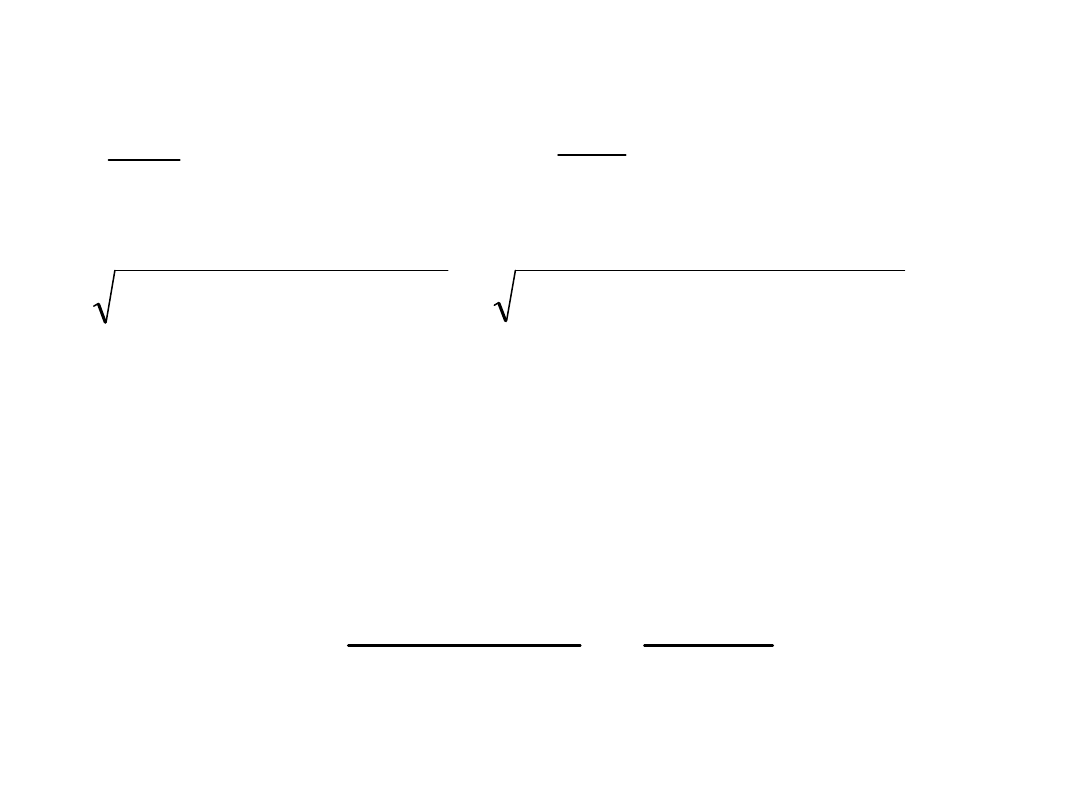
Pochodne cząstkowe:

 

 
 
 

 

 

 

P = 6000 m

2

± 4 m

2

Błąd względny pola figury:

 

b

a

P







a

b

P







2

2

2

2

b

2

a

P

m

3.6

0.01)

*

300

(

0.1)

*

(20

)

m

*

a

(

)

m

*

(b

m













P

1600

1

m

6000

m

3.6

2

2



Wyrównanie obserwacji i ocena dokładności

Obserwacje bezpośrednie:
-

jednakowo dokładne

.

-

niejednakowo dokładne

(o różnej dokładności).

Wzajemny stosunek dokładności wyraża się przez

nadanie wag p

i

dla każdej obserwacji,
Wagi p

i

=1 dla każdej obserwacji jednakowo

dokładnej.

Wagi

to liczby niemianowane, które określają

dokładność

względną poszczególnych

obserwacji.

Wyrównanie i ocena dokładności

obserwacji

bezpośrednich jednakowo dokładnych

Teoria błędów posługuje się błędami pozornymi

przy

obliczaniu

wartości

najbardziej

prawdopodobnej.

W statystyce wyrównanie wyników pomiaru nosi

nazwę estymacji parametrów rozkładu.

 
Wyrównanie obserwacji metodą najmniejszych

kwadratów jest wykonywane przy założeniu v

2

=

minimum dla obserwacji jednakowo-dokładnych.
Dla obserwacji niejednakowo-dokładnych warunek
ten ma postać:

pv

2

= minimum. Wyrównanie takie nazywane jest

wyrównaniem ścisłym.

W zadaniach geodezyjnych często występują

obserwacje pośrednie, których wartości oblicza się
na podstawie innych pomierzonych wielkości.

Próba

złożona z n obserwacji: l

1

, l

2

, ..., l

n

wykonanych z tą samą

dokładnością, Jeżeli

wartość prawdziwa poszukiwanej wielkości
wynosi X, to zgodnie z podaną wcześniej definicją
błędu

prawdziwego można zapisać:



1

= X—l

1



2

= X—l

2

...



n

= X—l

n

Sumując równania, otrzymuje się:

stąd X =

/n dąży do zera,

dąży do wartości prawdziwej

X

Wartość średnia

:

i

nX

l











l

n

n









x

i

l

x

n





Przykład wyrównania obserwacji jednakowo

dokładnych

i

Obs. l

i

v

i

pv

i

1

1.419

-5

25

2

1.408

6

36

3

1.415

-1

1

4

1.410

4

16

5

1.415

-1

1

6

1.418

-4

16

7

1.412

2

4

8

1.415

-1

1

9

1.422

-8

64

10

1.406

8

64

1.414 

=

0

228

 =

14.140

x

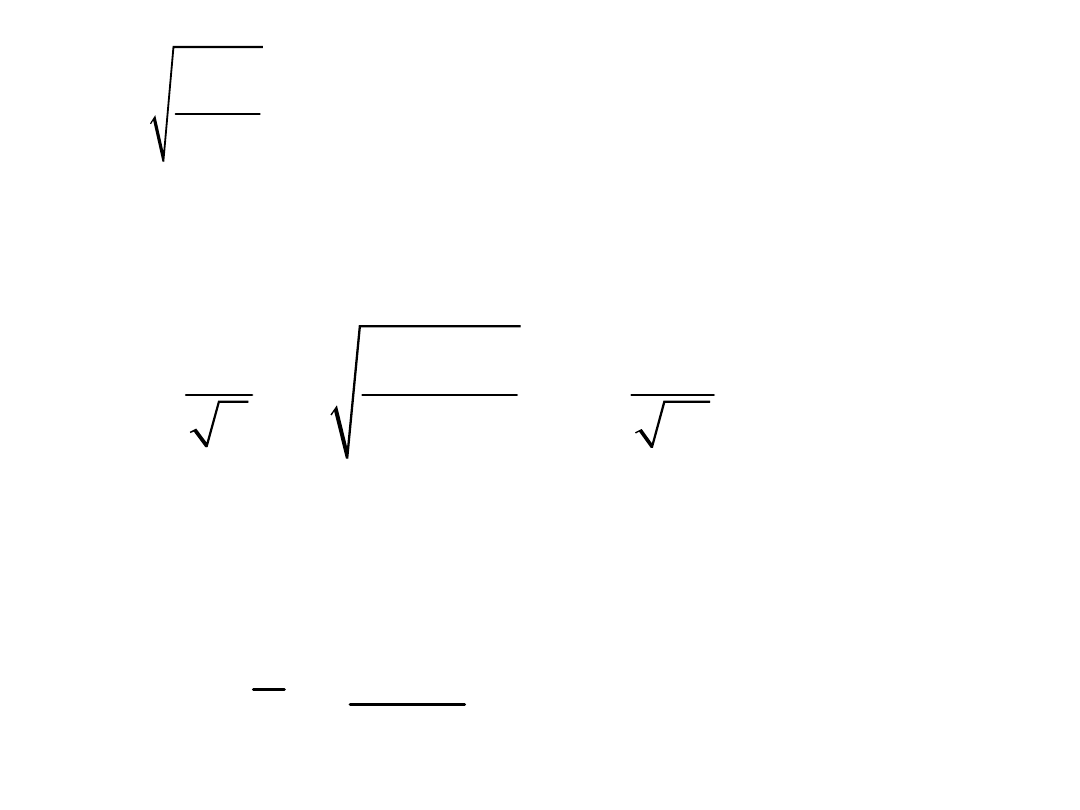
2

v

m

n 1







=

±

5 mm

Błąd średni średniej

arytmetycznej

M:





2

m

5

M

=

= 1.6 mm

n n 1

n

10

v













Średnia

arytmetyczna:

i

l

x

= 1.414

n





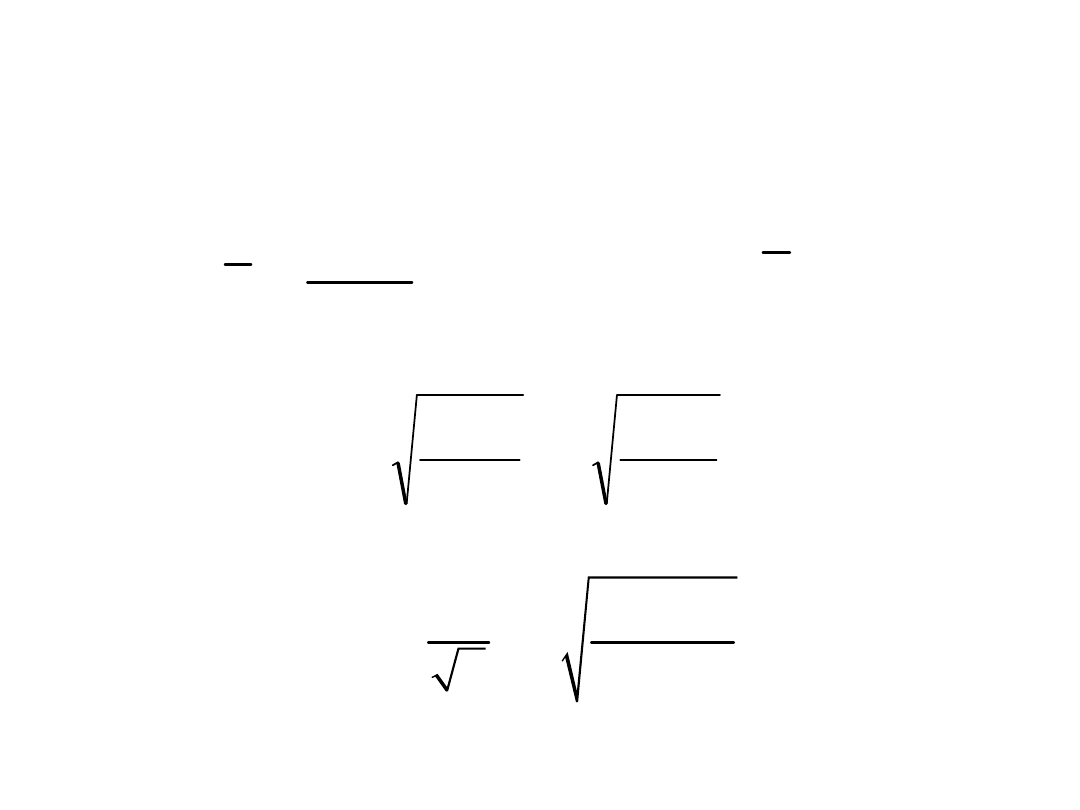
1

2

2















n

v

n

m







2

m

M

n n 1

n

v









Średni błąd pojedynczej obserwacji z próby (m):
Błąd średni średniej arytmetycznej (M):
(po wyrównaniu obserwacji)

n





i

l

x

i

i

v = x- l

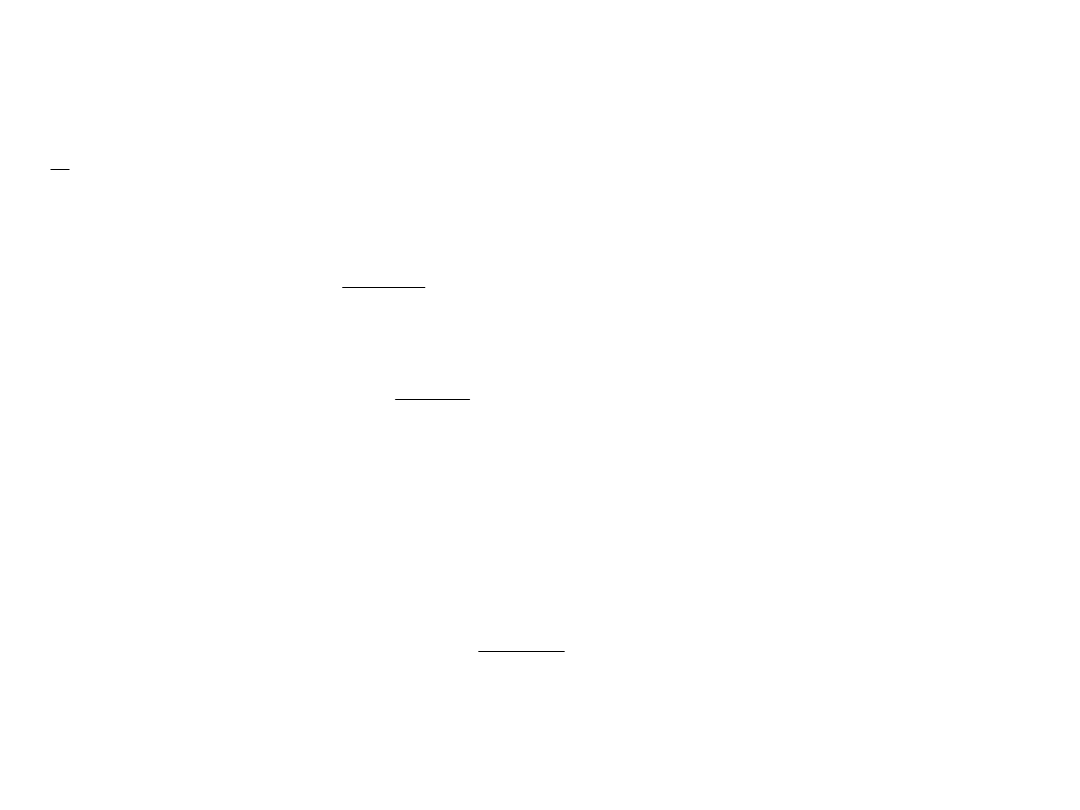
Ocena dokładności pomiarów

Błąd średniej arytmetycznej M można wyznaczyć

jako

błąd

funkcji:

= F(l):
 

 

Przyjmując, że suma obserwacji ma

odchyleni

standardowe σ

x

,

otrzymuje się wzór na tzw. średni

błąd średniej

arytmetycznej

:

x

2

i

2

m

M

n





2

2

2

x

2

M

n











2

2

M

n(n-1)

v





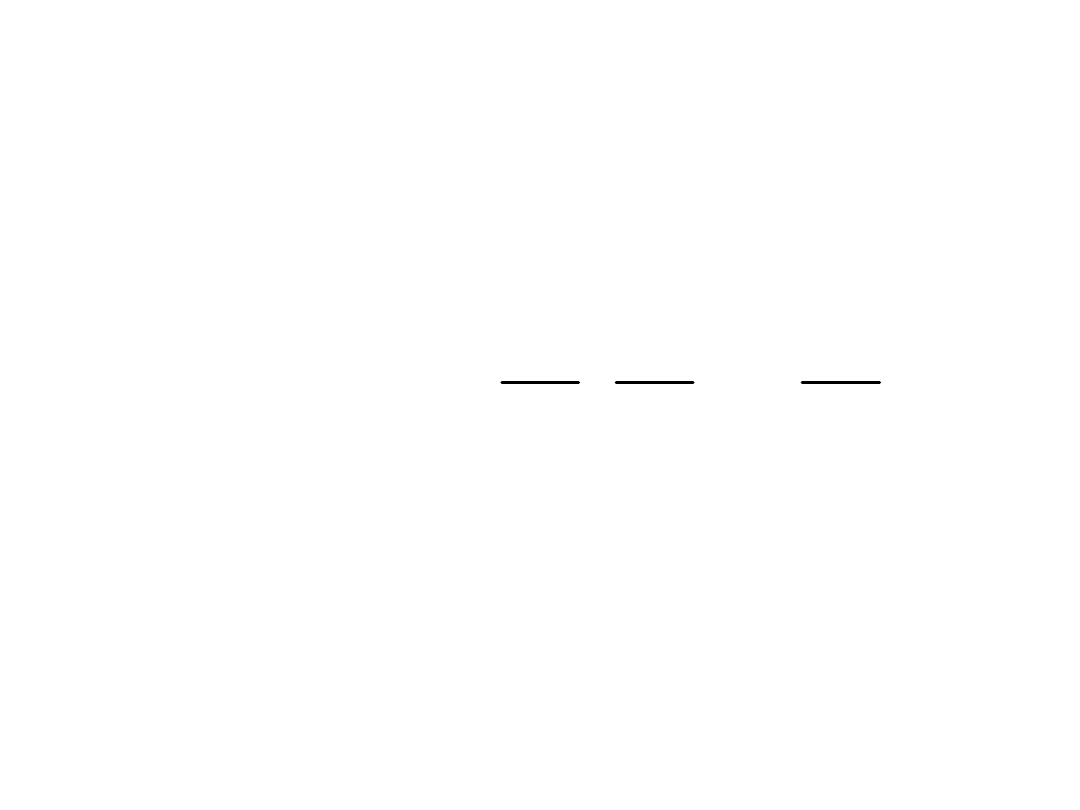
Wyrównanie i ocena dokładności obserwacji

bezpośrednich niejednakowo dokładnych

Próba

losowa

n

obserwacji

niejednakowo

dokładnych: l

1

, l

2

, ..., l

n

średnie błędy

m

1

, m

2

, ..., rn

n

lub

wagi

p

1

, p

2

, ..., p

n

,

lub

2

i

l

p

1/ m



1

2

2

2

2

1

2

1

1

1

p :p :...:p

:

:...:

m m

m

n

n



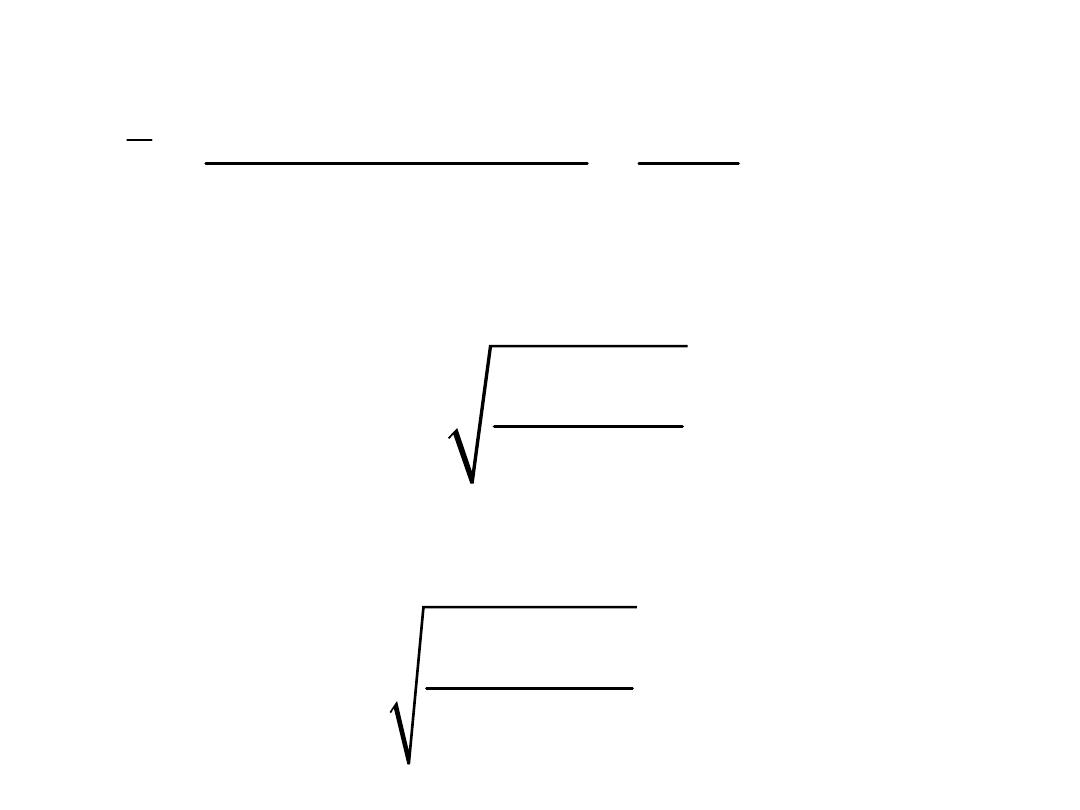
Ogólna średnia arytmetyczna

(ważona):

1 1

2 2

1

2

pl

p l

p l

... p l

p

p

... p

p

n n

n

X



 







 





Błąd średni

typowej obserwacji

o wadze p

0

=1.

2

0

pv

m

n 1







Błąd średni ogólnej średniej arytmetycznej:

2

pv

M

p(n-1)







Przykład wyrównania obserwacji
różnodokładnych

i

Obs. l

i

p

i

v

i

pv

i

pvv

i

1

1.419

0.3

-4.85

-1.455 7.05

6

2

1.408

0.5

6.15

3.075

18.9

11

3

1.415

1.2

-0.85

1.020

0.86

7

4

1.410

0.6

4.15

2.490

10.3

34

5

1.415

1.5

-0.85

-1.275 1.08

4

6

1.418

0.2

-3.85

-0.770 2.96

4

7

1.412

0.4

2.15

0.860

1.84

9

8

1.415

1.5

-0.85

-1.275 1.08

4

9

1.422

0.5

-7.85

3.925

30.8

11

10

1.406

0.4

8.15

3.260

26.5

69

1.414

pl

10.0

4

7.1

0.030

98.5

65

pl
=

10.040

x

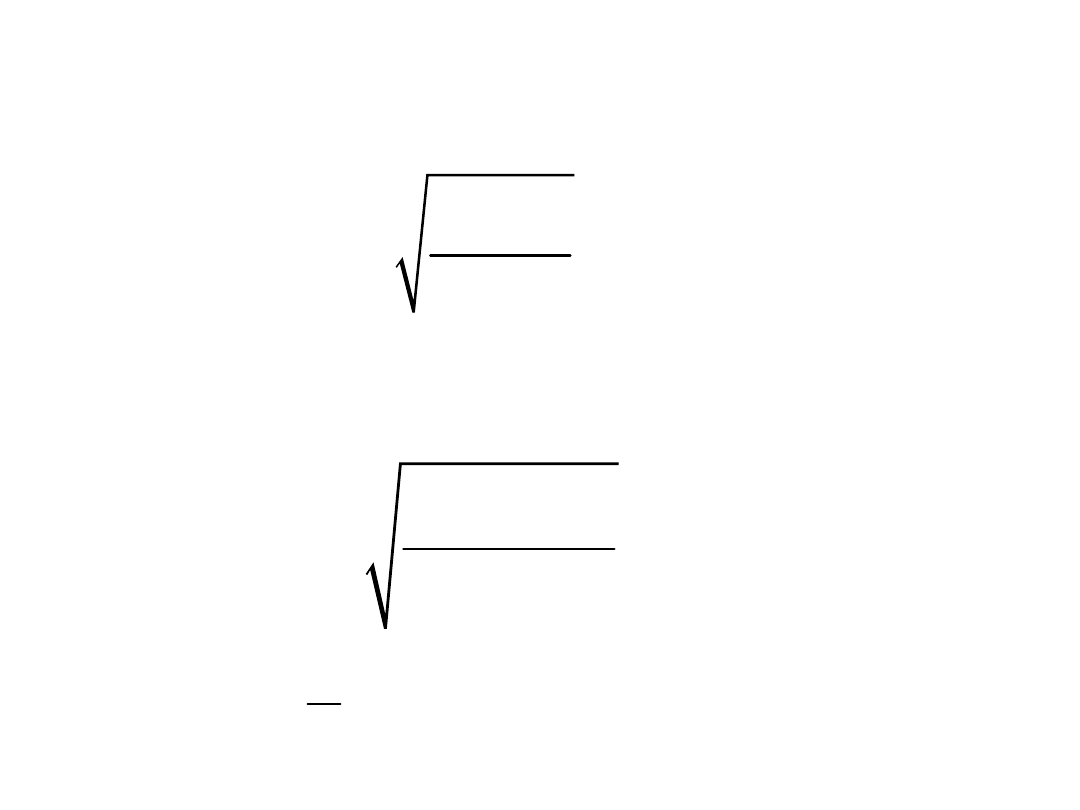
Średni błąd obserwacji typowej:

2

0

pv

m

n 1







2

pv

M

p(n-1)







x

= 1.4141.2 mm

=

3.3

mm

=

1.2

mm

Średni błąd wartości oczekiwanej:

Dla bardzo małych prób wyniki pomiarów podlegają
rozkładowi

tStudenta

. Przyjmując interpretacje

probabilistyczną odchylenia standardowego w rozkładzie
normalnym (prawdopodobieństwo uzyskania wyniku

spoza przedziału

<x

s

- m

x

;x

s

+ m

x

> wynosi 0,3174),

znajdujemy taką

wartość krytyczną

w rozkładzie

Studenta t

n,

, dla której =0.31740.32. Wtedy dla

bardzo małej próby
S

xt

= t

n, 0.32

m

x

m

x

 S

xt

t

n, 0.32

– wartość krytyczna z rozkładu tStudenta

Wartości krytyczne t

n,0.32

dla niektórych wartości n

podane są w tabeli

n

Wart. Krytyczna

t(n,0.32)

3

1.3210

4

1.1966

6

1.1103

8

1.0765

10

1.0585

15

1.0368

Dziękuję za uwagę