1. Zbiory i działania na nich (przykłady): pojęcia pierwotne: •![]()
- a jest elementem zbioru A
• ![]()
- A jest zawarty w B
• ![]()
- A jest podzbiorem B
• A = B - zbiory pokrywają się
• ![]()
- zbiór A jest podzbiorem właściwym zbioru B
Przykłady: N - naturalne, Q - wymierne, R - rzeczywiste, {a1…….an} - zbiór skończony o n elementach, {x: P(x)} zachodzi warunek P(x).
• Zbiór pusty: ø zbiór do którego nie należy żaden element, np. x2+1=0
Działania na zbiorach:
• suma ![]()
wszystkie i tylko te elementy, które należą do A i B, np. ![]()
• iloczyn (przekrój) ![]()
(wszystkie, które należą do A i B)
• różnica A \ B (wszystkie, które należą do A ale nie należą do B
2. Prawa rachunku zbiorów:
• przemienność dodawania ![]()
• przemienność przekroju ![]()
• łączność dodawania ![]()
• łączność przekroju ![]()
• rozdzielność przekroju względem dodawania ![]()
• rozdzielność dodawania względem przekroju ![]()
3. Produkty kartezjańskie i relacje:
X i Y: produktem kartezjańskim tych zbiorów nazywamy zbiór wszystkich uporządkowanych par (x,y), gdzie ![]()
. ![]()
- produkt kartezjański. Przykłady: zbiór punktów płaszczyzny jest produktem kartezjańskim R x R.
Dany jest X x Y, wtedy relacja nazywamy każdy podzbiór tego produktu. ![]()
(x pozostaje w relacji ρ z y). Przykład: X i Y należą do R, wykres y=x2 będzie zbiorem par (x,x2) będzie to relacja.
Rodzaje relacji:
• relacja zwrotna - ![]()
, ![]()
mamy x ρx, np. relacja równości w zbiorze X, x=X, x=X
• relacja symetryczna ![]()
, gdy z warunku xρy wynika yρx, np. relacja równoległości prostych na płaszczyźnie
• relacja przechodnia ![]()
, gdy xρy i yρx implikują warunek xρz, np. relacja nie większości ![]()
• relacja równoważności - ![]()
, jest ona równocześnie zwrotna, symetryczna i przechodnia
• relacja antysymetryczna ![]()
, gdy z xρy i yρx wynika x=y, np. relacja nie większości ![]()
• relacja spójna ![]()
, dla każdych dwóch różnych elementów x i y zbioru X albo xρy i yρx, np. relacja niewiekszości.
def. Relacja, która jest jednocześnie przechodnia, antysymetryczna i spójna nazywa się relacją liniowo porządkującą zbiór X.
4. Zbiór liczb rzeczywistych. Własności. Kresy górny i dolny:
pojęcia pierwotne: zbiór R, relacja niewiększości, działania dodawania i mnożenia.
Aksjomaty dotyczące R:
• x+y=y+x przemienność
• (x+y)+z=x+(y+z) łączność
• istnieje taki element 0 należący do R, taki że x+0=x
• istnieje taki element -x, taki że x+(-x)=0 jest to tzw. Przeciwny znak
Def. Zbiór X nal. do R nazywa się ograniczonym z góry, gdy istnieje taki element spełniający powyższy warunek, mówimy, że ogranicza zbiór X z góry.
Def. Najmniejszy z elementów ograniczających zbiór X z góry nazywamy kresem górnym tego zbioru. K nal. do R nazywa się kresem górnym dla X gdy dla każdego x należącego do X mamy x≤k oraz dla każdego M<k istnieje element x nal. do X taki, że x>M. kres górny oznaczamy symbolem supX (supremum - największy).
Def. Zbiór X nal. do R nazywamy ograniczonym z dołu, gdy istnieje m takie, że dla każdego x nal. do X X≥m
Def. Zbiór, który jest ograniczony z góry i z dołu nazywamy ograniczonym.
Def. Największy z elementów ograniczających zbiór X z dołu nazywa się kresem dolnym i oznaczamy go symbolem inf X można udowodnić, że każdy niepusty i ograniczony z dołu podzbiór zbioru R ma kres dolny.
5. Kwantyfikatory:
Def. Zapis, w którym występują litery x,y,z oznaczające dowolne liczby, a które po podstawieniu za te litery dowolnej liczby stają się albo zdaniem prawdziwym albo zdaniem fałszywym. Niech P(x) oznacza pełną funkcję zdaniową, wówczas zapis ![]()
oznacza zbiór tych wszystkich liczb x należących do zbioru X dla których funkcja zdaniowa P(x) jest prawdziwa. Przy zapisie funkcji zdaniowych używamy często symboli zwanych kwantyfikatorami. P(x) i Q(x) są niektórymi funkcjami zdaniowymi
• ![]()
dla każdego x jest P(x)
• ![]()
istnieje takie x, że zachodzi P(x)![]()
kwantyfikator ogólny![]()
kwantyfikator szczegółowy
Niech P oznacza zdanie orzekające (prawdziwe lub fałszywe) wówczas za jego pomocą możemy utworzyć zdanie zaprzeczające ![]()
nieprawda, że P. Ważne są reguły postępowania z zaprzeczeniami zdań, w których występują kwantyfikatory. ![]()
![]()
6. Ciąg liczbowy. Ograniczony. Monotoniczny:
ciągiem liczbowym nazywamy funkcję odwzorowującą zbiór liczb naturalnych w zbiór liczb rzeczywistych. Wartości tej funkcji dla liczby naturalnej n nazywamy n-tym wyrazem i oznaczamy an lub bn, ciągi o takich wyrazach oznaczamy odpowiednio przez (an) (bn). obrazowo ciąg można traktować jako zbiór ponumerowanych liczb, które są poustawiane według rosnących numerów.
Def. Ciąg an jest ograniczony z góry jeżeli zbiór liczb ![]()
jest ograniczony z góry tzn. jeżeli ![]()
Def. Ciąg an jest ograniczony z dołu jeżeli zbiór liczb ![]()
jest ograniczony z dołu, tzn. ![]()
Def. Ciąg an jest ograniczony ![]()
jest ograniczony i z dołu i z góry.
Def. Ciąg an jest rosnący jeżeli a1<a2<a3<…, tzn. ![]()
obrazowo można powiedzieć, że ciąg jest rosnący, gdy jego wyrazy powiększają się ze wzrostem indeksu, np. ![]()
Def. Ciąg an jest niemalejący ![]()
a1≤a2≤a3≤… albo ![]()
Analogicznie jest dla ciągów malejących i nierosnących.
Monotoniczność ciągu an możemy ustalić badając znak różnicy an+1-an a ciąu bn wyrazach (+) porównując ![]()
z jedynką.
an+1-an |
bn+1/bn |
ciąg |
> 0 |
> 1 |
rosnący |
7. Ciąg zbieżny. Ciąg rozbieżny:
Def. Ciąg (an) jest zbieżny do liczby a ![]()
zachodzi: |an-a|<ε obrazowo można powiedzieć, że ciąg jest zbieżny do liczby a gdy jego dostatecznie dalekie wyrazy dążą dowolnie blisko od liczby a.
Def. (granicy nieskończonej)
Ciąg (an) jest zbieżny do granicy nieskończonej ![]()
zachodzi:
|an|> ε obrazowo możemy powiedzieć, że ciąg jest zbieżny do granicy nieskończonej gdy dostatecznie dalekie moduły wyrazów tego ciągu są większe od dowolnie dużej liczby.
• ciąg an jest zbieżny do +∞ ![]()
zachodzi an>ε
• ciąg an jest zbieżny do -∞ ![]()
zachodzi an<ε
ciągi które nie maja granicy skończonej albo nieskończonej nazywamy ciągami rozbieżnymi.
Tw. (warunek Cauchy'ego zbieżności ciagu)
ciąg an jest zbieżny ![]()
zachodzi |an-am|< ε
8. Podciągi. Twierdzenie Bolzano - Weierstrassa:
Def. Niech an będzie dowolnym ciągiem, oraz niech (nk) będzie rosnącym ciągiem liczb naturalnych. Podciągiem ciągu an nazywamy ciąg bk określony wzorem ![]()
. Możemy powiedzieć, że podciągiem nazywamy ciąg pozostały po skreśleniu niektórych liczb i wyrazów tego ciągu, np. ciąg liczb parzystych jest podciągiem liczb naturalnych.
Tw. (Bolzano - Weierstrassa)
każdy ograniczony ciąg ma zbieżny podciąg. Nieograniczony ciąg ma podciąg zbieżny do +∞ lub -∞ .
9. Arytmetyka granic ciągów:
• zbieżny ciąg jest ograniczony (uwaga! Nie każdy ograniczony ciąg jest zbieżny)
• ciąg an→0 gdy |an|→0
• o arytmetyce ciągu: an→a i bn→b to:
- an![]()
bn → a ![]()
b
- an ∙bn → a ∙ b
- ![]()
- ![]()
- ![]()
10. Twierdzenie o 3 ciągach i o ciągu monotonicznym:
Tw. (o 3 ciagach)
niech ciągi (an), (bn) i (cn) spełniają warunki an≤bn≤cn i niech an→a, cn→a, wówczas bn→a
Tw. (o ciągu monotonicznym ograniczonym)
jeżeli (an) jest niemalejący n>n0 i ograniczony z góry to jest zbieżny do granicy sup{an:n≥n0}.
prawdziwe jest także analogiczne stwierdzenie dla ciągu nierosnącego i ograniczonego z dołu.
11. Twierdzenie o granicach nieskończonych:
Tw. (o 2 ciągach)
niech ciąg an≤bn dla każdego n>n0 i niech an→+∞ wtedy bn→+∞. Podobnie dla ciągów zbieżnych do -∞.
Tw. (o arytmetyce granic nieskończonych)
• +∞ + a = +∞ dla |
• a(+∞)=+∞ dla 0<a≤+∞ |
Symbole nieoznaczone: ![]()
12. Granice specjalne qn, en, ![]()
: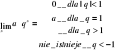
• ![]()
• ![]()
13. Podstawowe określenia funkcji, dziedzina, wykres:
Def. Funkcją określoną na zbiorze X zawierającym się w R o wartościach w zbiorze Y zawierającym się w R nazywamy przyporządkowanie x należące do X dokładnie jednego elementu y należącego do Y. funkcję tą oznaczamy f: X→Y
Zbiór X nazywamy dziedziną funkcji f
Zbiór Y nazywamy przeciwdziedziną.
Zbiór tych liczb {f(x)nal. do Y: x nal. X} nazywamy zbiorem wartości funkcji f.
Wykresem funkcji f nazywamy zbiór {(x,y): x nal. X, a y=f(x)}
14. Klasy funkcji, okresowa, parzysta, ograniczona, monotoniczna:
• funkcje okresowe:
funkcje f: X→R nazywamy okresową jeżeli istnieje T>0 takie ze ![]()
oraz f(x+T)=f(x)
liczbę T nazywamy okresem funkcji
np. y=sin x, sin (x+2π)=sin x T=2π
• funkcje parzyste
f: X→R gdy ![]()
• funkcje nieparzyste
f: X→R gdy ![]()
• funkcje ograniczone z góry (z dołu)
f: X→R gdy zbiór jej wartości na tym zbiorze jest ograniczony z góry (z dołu) tzn. ![]()
funkcję ograniczona z góry i z dołu nazywamy ograniczoną.
• funkcje rosnące (malejące), niemalejące (nierosnące)
gdy ![]()
zachodzi nierówność f(x1)<f(x2) i odpowiednio: f(x1)> f(x2); f(x1)≤ f(x2); f(x1)≥ f(x2)
15. Funkcja odwrotna:
Def. Niech funkcja f: X→Y będzie różnowartościowa, funkcja odwrotną do funkcji f nazywamy funkcję f-1 z dziedziną równa zbiorowi wartości funkcji f i przeciwdziedziną X, która jest określona przez warunek: ![]()
wykres funkcji odwrotnej otrzymujemy z wykresu funkcji f odbijając go symetrycznie względem prostej y=x.
Własności:
• f-1(f(x))=x
• f(f-1(y))=y
np. arcsin x, arccos x, arctg x, arcctg x
16. Funkcje elementarne i nieelementarne:
podstawowymi funkcjami elementarnymi nazywamy funkcje stałe, potęgowe, wykładnicze, logarytmiczne, trygonometryczne oraz cyklometryczne. Funkcje, które można otrzymać z podstawienia funkcji za pomocą skończonej liczby działań elementarnych oraz operacji złożenia funkcji nazywamy funkcjami elementarnymi. Np. •![]()
• wielomian ![]()
• funkcje wymierne, tzn. funkcje które można zapisać w postaci ilorazu 2 wielomianów ![]()
• funkcje hiperboliczne: sh x, ch x, th x, ctg x
Funkcje nie elementarne:
• signum![]()
• funkcja Dirichleta![]()
17. Sąsiedztwo. Definicja Heinego granicy funkcji:
Def. Sąsiedztwem (lewostronnym, prawostronnym) o promieniu r>0 punktu ![]()
nazywamy zbiór ![]()
jeżeli promień r sąsiedztwa nie będzie istotny w naszych rozważaniach, to będziemy mówili prosto o sąsiedztwie S(x0), S(x0+), S(x0-)
Def. (Heinego funkcji w punkcie)
Niech funkcja f będzie oznaczona przynajmniej na sąsiedztwie S(x0) liczba a jest granicą funkcji f w punkcie x0 gdy dla każdego ciągu xn→ a: ![]()
zachodzi: f(xn)→ a![]()
18. Definicja Cauchy'ego. Granica lewostronna i prawostronna:
Def. (granicy funkcji w punkcie Cauchy'ego)
niech funkcja f będzie określona przynajmniej na sąsiedztwie punktu x. Liczba a jest granicą funkcji w punkcie x0 gdy ![]()
, że z nierówności ![]()
Def. (granicy lewostronnej)
niech funkcja f jest określona przynajmniej na sąsiedztwie S(x0-). Liczbę a nazywamy granicę lewostronną funkcji f w punkcie x0 gdy ![]()
zachodzi f(xn)→ a![]()
w podobny sposób określa się granice prawostronną.
19. Granice nieskończone i granice w nieskończoności:
Def. niech funkcja f będzie określona na sąsiedztwie S(x0) i ma granicę +∞ w punkcie x0 gdy dla każdego xn→x0 i xn nal. do S(x0) zachodzi f(xn)→ +∞ ![]()
Def. Sąsiedztwem -∞ nazywamy przedział
S(-∞)=(-∞,a),
Sąsiedztwem +∞ nazywamy przedział S(+∞)=(b,+ ∞)
Def. Niech funkcja f będzie określona przynajmniej na sąsiedztwie S(+∞). Liczba a jest granica funkcji f w +∞ gdy dla każdego xn→+∞ zachodzi f(xn)→a![]()
20. Arytmetyka granic funkcji:
Jeżeli funkcje f i g maja skończone granice a i b w punkcie x0 to dla x→x0 zachodzi:
• ![]()
• f(x) ∙ g(x) → a ∙ b
• c ∙ f(x) → c∙a, c nal. do R
• ![]()
o ile b≠0
• ![]()
o ile a≠0 i b≠0
21. Arytmetyka granic nieskończonych:
• +∞ + p = +∞ dla |
• p(+∞)=+∞ dla -0<p≤+∞ |
22. Granice podstawowych wyrażeń nieoznaczonych: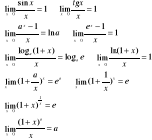
23. Otoczenie. Definicja ciągłości:
Def. Otoczeniem (lewostronnym, prawostronnym) o promieniu r>0 punktu x0 nal. do R nazywamy zbiór ![]()
O(x0)
Def. Niech funkcja f będzie określona przynajmniej na otoczeniu O(x0) punktu x0. funkcja f jest ciągła w tym punkcie, gdy granica ![]()
istnieje. Obrazowo - gdy wykres funkcji nie przerywa się w punkcie x0
24. Ciągłość jednostronna. Ciągłość na przedziale:
Def. Niech funkcja f będzie określona przynajmniej na otoczeniu O(x0-) punktu x0. Jest lewostronnie ciągła w x0 gdy ![]()
podobnie dla prawostronnie ciągłej
Def. Funkcja f jest ciągła na przedziale otwartym, gdy jest ciągła w każdym punkcie tego przedziału. Funkcja jest ciągła na przedziale domkniętym [a,b], gdy jest ciągła w każdym pkt. przedziału otwartego (a,b) oraz prawostronnie ciągła w pkt. a i lewostronnie ciągła w pkt. b.
25. Rodzaje nieciągłości:
mówimy, że funkcja f określona na otoczeniu pkt. x0 jest nieciągła w tym punkcie, gdy granica ![]()
lub nieistineje.
def. funkcja f ma w pkt. x0 nieciągłość 1 rodzaju jeżeli istnieją granice skończone ![]()
oraz ![]()
rozróżniamy dwa podrodzaje:
• funkcja f ma w pkt. x0 nieciągłość 1 rodzaju typu „skok” gdy ![]()
• jeżeli funkcja f spełnia warunek ![]()
, to mówimy że funkcja f ma w punkcie x0 nieciągłość 1 rodzaju typu „luka”.
np.
1. f(x) =![]()
ma w punkcie 0 nieciągłość 1 rodzaju typu „skok”.
def. Funkcja f ma w pkt. x0 nieciągłość 2 rodzaju jeżeli przynajmniej jedna z granic ![]()
nie istnieje lub jest nieskończona.
np. funkcja Dirichleta![]()
ma nieciągłość 2 rodzaju w każdym punkcie x0 należącym do R, ponieważ w każdym takim punkcie nie ma ona granicy lewostronnej ani prawostronnej.
26. Działania na funkcjach ciągłych:
Tw. (o arytmetyce ciągłości)
jeżeli funkcje f i g są ciągłe w pkt. x0, to funkcja f+g, f-g, f∙g, f/g są ciągłe w tym punkcie x0.
Tw. (o ciągłości funkcji złożonej)
jeżeli funkcja y=f(x) jest ciągła w punkcie x0 a funkcja z=g(y) jest ciągła w pkt. y0=f(x0) wtedy funkcja złożona g○f jest ciągła w pkt. x0. z=g(f(x))
Tw. (o ciągłości funkcji odwrotnej)
jeżeli funkcja f jest ciągła i rosnąca w przedziale [a,b], to funkcja odwrotna f-1 jest ciągła i rosnąca w przedziale [f(a),f(b)]
Tw. (ciągłość funkcji elementarnej)
Funkcje elementarne są ciągłe w swoich dziedzinach.
27. Twierdzenie Weierstrassa o funkcji na przedziale domkniętym:
Tw. (Weierstrassa)
Jeżeli funkcja f jest ciągła na przedziale domkniętym i ograniczonym [a,b] to jest ona na nim ograniczona oraz osiąga swe kresy. Tzn. że istnieją takie liczby c i d należące do [a,b], że inf f(x)=f(c) i sup f(x)=f(d).
28. Twierdzenie Darboux o wartości pośredniej:
Tw. (Darboux)
Jeżeli funkcja f jest ciągła na przedziale [a,b] oraz f(a)<f(b), to dla każdego u należącego do (f(a),f(b)) istnieje c należący do (a,b) taka, że f(c)=u
29. Pochodne. Pochodne funkcji elementarnych:
Def. Niech x0 należy do R, oraz niech funkcja f będzie określona przynajmniej na otoczeniu O(x0). Pochodną funkcji f w punkcie x0 nazywamy ![]()
i oznaczamy przez f'(x0).
Niech Δx=x- x0
wtedy mamy: ![]()
.
stosujemy także symbol ![]()
30. Interpretacja geometryczna pochodnej:
Def. Niech funkcja ciągła g będzie określona przynajmniej na otoczeniu O(x0). Prosta jest styczna do wykresu funkcji f w pkt. x0 jeżeli jest granicznym położeniem siecznych funkcji przechodzących przez pkt. (x0,f(x0)) i (x,f(x)), gdy x→x0
f'(x0)=tgα, gdzie α oznacza kąt między styczną do wykresu funkcji f i dodatnią częścią osi .
Równanie stycznej do wykresu funkcji f w pkt. (x0,f(x0))
y=f(x0)+f'(x0)(x-x0)
31. Interpretacja fizyczna pochodnej:
Def. Niech S(t) oznacza położenie na osi punktu materialnego w chwili t. Wtedy szybkość pkt. w chwili t0 ![]()
32. Arytmetyka pochodnej:
Jeżeli funkcje f i g mają pochodne skończone w punkcie x0 to:
• ![]()
• ![]()
• ![]()
• ![]()
33. Pochodna funkcji złożonej:
Tw. ( o pochodnej funkcji złożonej)
Jeżeli funkcja f ma pochodną skończoną w pkt. x0, a funkcja g ma pochodna skończoną w f(x0) to funkcja złożona g○f ma pochodną w pkt. x0 ponadto (g○f)'(x0)=g'(f(x0)f'(x0)
34. Pochodna funkcji odwrotnej:
Tw. Jeżeli funkcja f spełnia następujące warunki:
• jest ciągła na otoczeniu O(x0)
• jest malejąca albo rosnąca na otoczeniu O(x0)
• ma pochodną skończoną w pkt x0 i ta pochodna nie równa się 0
wtedy funkcja odwrotna f-1 ma pochodną w pkt. y0=f(x0), przy czym (f-1)'(y0)=1/f'(x0)
35. Różniczka funkcja. Zastosowanie do obliczeń przybliżonych:
Tw. (różniczka)
niech funkcja f ma pochodną skończoną w pkt. x0 jej różniczką w tym punkcie nazywamy funkcję df od zmiennej Δx=x-x0 określoną wzorem: ![]()
Tw. (o zastosowaniu różniczki do obliczeń przybliżonych)
jeżeli funkcja f ma pochodna skończoną w pkt. x0, ![]()
. Przybliżenie tzn., że błąd jaki popełniamy zastępując przyrost funkcji
Δf=f(x0+Δx)-f(x0) jej różniczką f'(x0)Δx dąży szybciej do 0 niż przyrost zmiennej niezależnej Δx, tzn. ![]()
36. Pochodne wyższych rzędów:
Def. Niech funkcja f jest określona w otoczeniu pkt. x0. Pochodną skończoną n - tego rzędu funkcji f w pkt. x0 definiujemy indukcyjnie: ![]()
Pochodna II rzędu interpretacja fizyczna:
fizyczną interpretacją pochodne II rzędu jest przyspieszenie punktu materialnego: ![]()
37. Twierdzenie Rolle'a o wartości średniej i interpretacja geometryczna:
Jeżeli funkcja f:
• jest ciągła na przedziale domkniętym [a,b]
• ma pochodną na przedziale otwartym (a,b)
• f(a)=f(b)
wtedy istniej punkt c z (a,b), w którym pochodna f'(c)=0
Równość f'(c)=0 oznacza, że styczna do wykresu f=f(x) w pkt. (c,f(c)) jest równoległa do osi x.
38. Twierdzenie Lagrange'a o wartości średniej i interpretacja geometryczna:
niech funkcja f
• jest ciągła na przedziale domkniętym [a,b]
• ma pochodną na przedziale otwartym (a,b)
wtedy istnieje c należące do (a,b), w którym pochodna ![]()
![]()
39. Wnioski z twierdzenia Lagrange'a (monotoniczność, o tożsamości, o nierównościach):
• o monotoniczności: niech I oznacza dowolne przedziały, wtedy dla każdego x należącego do I f spełnia warunki:
- f'(x)=0 funkcja stała
- f'(x)>0 funkcja rosnąca
- f'(x)<0 funkcja malejąca
- f'(x)≥0 funkcja niemalejąca
- f'(x)≤0 funkcja nierosnąca
• o tożsamości: niech funkcje f i g będą określone na przedziale I i pkt. x0 należy dętego przedziału. Jeżeli spełnione SA warunki:
- f(x0)=g(x0)
- f'(x)=g'(x)
to f(x)=g(x)
• o nierówności: niech funkcje f i g będą określone na przedziale I oraz niech x0 jest punktem z tego przedziału. Jeżeli
- f(x0)≤g(x0)
- f'(x)≤g'(x)
to f(x)≤g(x)
40. Twierdzenie Cauchy'ego o wartości średniej:
niech funkcje f i g spełniają takie warunki:
• są ciągłe na przedziale domkniętym [a,b]
• mają pochodne na przedziale otwartym (a,b)
ponadto g'(x)≠0, wtedy istnieje takie c należące do (a,b), takie że ![]()
jest to uogólnienie twierdzenia Lagrange'a.
41. Reguła de L'Hospitala dla symbolu ![]()
:
niech funkcje f i g spełniają:
• ![]()
, przy czym g(x)≠0 dla x należącego do sąsiedztwa S(x0)
• istnieje granica ![]()
, wtedy istnieje granica ![]()
42. Reguła de L'Hospitala dla symbolu ![]()
:
jeżeli:
• ![]()
• istnieje ![]()
, wtedy istnieje ![]()
43. Wzór Taylora z resztą Lagrange'a:
jeżeli funkcja f ma:
• pochodną ciągła rzędu n-1 na przedziale [x0,x]
• pochodną skończoną rzędu n na przedziale (x0,x)
to istnieje takie c należące do (x0,x), taki że ![]()
uwaga: powyższe twierdzenie jest prawdziwe także dla przedziału [x0,x] wtedy punkt c będzie z przedziału (x0,x).Równość występująca w tym twierdzeniu nazywa się wzorem Taylora o wyrazie ![]()
z resztą Lagrange'a.
44. Ekstrema lokalne i twierdzenie Fermata o warunku koniecznym ekstremum:
Def. Funkcja f ma w punkcie x0 minimum lokalne jeżeli istnieje δ>0, taki że ![]()
. Ona ma w pkt. x0 maksimum lokalne jeżeli istnieje δ>0, taki ze ![]()
Tw. (o warunku koniecznym istnienia ekstremum Fermata)
Jeżeli funkcja f ma ekstremum lokalne w pkt. x0 i pochodną f'(x0) to pochodna f'(x0)=0.
Uwaga: implikacja odwrotna jest fałszywa.
45. I warunek wystarczający istnienia ekstremum:
Jeżeli f'(x0)=0 oraz istnieje δ>0, że f'(x)>0 dla x należącego do sąsiedztwa S(x0-,δ) i f'(x)<0 dla x należącego do sąsiedztwa S(x0+,δ) to funkcja f ma w punkcie x0 maksimum lokalne.
O minimum lokalnym analogicznie.
46. II warunek wystarczający istnienia ekstremum:
jeżeli f'(x0)=0 a f''(x0)>0 to funkcja f w pkt. x0 ma minimum lokalne.
O maksimum analogicznie.
47. Algorytm szukania ekstremum globalnego:
Niech funkcja f będzie ciągła na przedziale [a,b] i ma pochodną skończoną wszędzie, możliwe poza skończoną liczba punktów. Ekstremum szukamy postępując następująco:
• znajdujemy punkty c1…..cn zerowania się pochodnej f'(x)=0 oraz punkty d1…..dm w których funkcja f nie ma pochodnej.
• obliczamy wartości funkcji w punktach końcowych a i b i w punktach c1…..cn i d1…..dm
• spośród liczb f(a), f(b), f(c1)…f(cn), f(d1)….f(dm) wybieramy najmniejszą m i największa M.
48. funkcja wypukła i wklęsła. Warunek wystarczający wypukłości:
Def. Funkcja f jest wypukła na przedziale (a,b) jeżeli dla każdej pary x,y liczb: a<x<y<b ma miejsce nierówność: ![]()
λ od 0-1.
Geometrycznie wypukłości oznacza, że każdy odcinek sieczny wykresu leży wyżej lub pokrywa się z fragmentem wykresu położonym między punktami przez które przechodzi sieczna.
Def. Funkcja f jest wklęsła na przedziale (a,b) jeżeli dla każdej pary x,y liczb: a<x<y<b ma miejsce nierówność: ![]()
Geometrycznie wklęsłość oznacza, że każdy odcinek sieczny wykresu leży niżej lub pokrywa się z fragmentem wykresu położonym między punktami przez które przechodzi sieczna.
Tw. (warunek wystarczający wypukłości)
• Jeżeli f''(x)>0 to funkcja f jest wypukła
• jeżeli f''(x)<0 to funkcja f jest wklęsła.
49. Punkty przegięcia warunek konieczny:
Def. Niech funkcja f będzie określona przynajmniej na otoczeniu punktu x0 i ma w tym punkcie pochodną. Punkt (x0,f(x0)) jest punktem przegięcia p.p. wykresu funkcji g gdy istnieje δ>0, że f jest wypukła na sąsiedztwie lewostronnym S(x0-,δ) i f jest wklęsła na sąsiedztwie prawostronnym S(x0+,δ) albo odwrotnie.
Tw. (warunek konieczny punktu przegięcia)
Jeżeli (x0,f(x0)) jest punktem przegięcia wykresu funkcji f i istnieje f''(x0), to f''(x0)=0.
Wniosek: funkcja może mieć punkty przegięcia jedynie w punktach zerowania się jej drugiej pochodnej albo w punktach, w których ta pochodnia nie isnieje.
50. I warunek wystarczający punktu przegięcia):
Jeżeli funkcja f ma pochodną w punkcie x0 oraz istnieje δ>0, że f''(x)<0 dla każdego x należącego do S(x0-,δ), a f''(x)>0 dla każdego x należącego do S(x0+,δ), to punkt (x0,f(x0)) jest punktem przegięcia p.p.
50. II warunek wystarczający punktu p1zegięcia:
Jeżeli f''(x0)=0 a f'''(x0)≠0 to punkt (x0,f(x0)) jest punktem przegięcia p.p.
Warunki dla pochodnych |
Własności |
||
f' |
f'' |
f''' |
|
f'(x)>0 |
f''(x)>0 |
|
rosnąca wypukła |
f'(x)>0 |
f''(x)<0 |
|
rosnąca wklęsła |
f'(x)<0 |
f''(x)>0 |
|
malejąc wypukła |
f'(x)<0 |
f''(x)<0 |
|
malejąca wklęsła |
f'(x0)=0 |
f''(x0)>0 |
|
minimum lokalne |
f'(x0)=0 |
f''(x0)<0 |
|
maksimum lokalne |
|
f'”(x0)=0 |
f'''(x0)≠0 |
punkt przegięcia |
52. Asymptota pionowa. Warunek istnienia:
Def. Prosta x=x0 jest asymptotą pionowa lewostronną jeżeli ![]()
podobnie z prawostronną.
Def. Asymptota pionowa obustronna. Prosta x=x0 jest asymptota pionową obustronną lub krótka asymptotą pionową funkcji f jeżeli jest jednocześnie jej asymptotą lewostronną i prawostronną.
Tw. Funkcja elementarna może mieć asymptoty pionowe jedynie w skończonych krańcach dziedziny, które do niej nie należą.
53. Asymptota ukośna, pozioma. Warunek istnienia:
Def. Prosta y=Ax+B jest asymptotą ukośną dla funkcji f w pkt. +∞ gdy ![]()
obrazowo prosta jest asymptotą ukośną gdy jej wykres dla argumentów bardzo wielkich prawie pokrywa się z tą prostą. Podobnie definiuje się asymptotę ukośną w -∞.
Jeżeli A dla asymptoty ukośnej =0 wtedy mówimy, że asymptota jest pozioma. Warto podkreślić, że asymptota ukośna może przecinać wykres funkcji f nieskończenie wiele razy.
Tw. (warunek istnienia asymptoty ukośnej)
prosta y=Ax+B jest asymptotą ukośną funkcji f na +∞ jeżeli ![]()
Tw. (warunek istnienia asymptoty poziomej)
prosta y=B jest asymptotą poziomą dla funkcji f na +∞ jeżeli ![]()
54.Algorytm badania funkcji
1. Ustalenie dziedziny f-cji
2. Wskazanie podstawowych własności f-cji
a)parzystość lub nieparzystość
b)okresowość
c)miejsca zerowe
d)ciągłość
3. Obliczanie granic lub wartości f-cji na krańcach dziedziny
4. Znalezienie asymptot pionowych i ukośnych
5. Zbadanie I-wszej pochodnej
a)wyznaczenie dziedziny pochodnej i obliczenie
b)wyznaczenie punktów, w których f-cja może mieć ekstremum
c)wyznaczenie przedziału monotoniczności f-cji
d) ustalenie ekstremów
e)obliczenie granic lub wartości f-cji na krańcach jej dziedziny
6. Zbadanie II pochodnej
a)obliczenie II pochodnej
b)wyznaczenie miejsc, w których f-cja może mieć punkty przegięcia
c) ustalenie przedziałów wklęsłości i wypukłości
d)wyznaczenie punktów przegięcia
e) obliczenie wartości w punktach przegięcia
7. Wykres funkcji
55.Funkcja pierwotna, wniosek z twierdzenia Lagrange'a, warunek wystarczający istnienia f-cji pierwotnej
Def. Funkcja F jest funkcją pierwotną dla funkcji f na przedziale I jeżeli jej pochodna F'(x)=f(x) dla każdego x należącego do I
Z tw, Lagrange'a można wysnuć taki wniosek:
Niech F jest funkcją pierwotną dla f na przedz. I wtedy:
1) G(x)=F(x)+C także będzie funkcją pierwotną dla funkcji f
2)Każda f-cja pierwotna dla f-cji f na tym przedziale I ma postać F(x)+C (C-dowolna stała liczba)
Tw.(Warunek wystarczający istnienia funkcji pierwotnej)
Każda f-cja ciągła na przedziale ma f-cję pierwotną na tym przedziale
Uwaga: F-cja pierwotna dla elementarnej nie musi być elementarna
56. Całka nieoznaczona. Twierdzenie o pochodnej całki nieoznaczonej.
Def: Niech F będzie funkcją pierwotną dla funkcji f . Całką nieoznaczoną funkcji f na przedziale I nazywamy zbiór funkci {F(x)+c: c∈R}. Całkę nieoznaczoną funkcji f oznaczamy przez ∫f (x)dx.
Działania na całkach nieoznaczonych oznaczają działania na funkcjach pierwotnych reprezentujących tę całkę.
Twierdzenie o pochodnej całki i całce pochodnej.
Niech funkcja f na funkcję pierwotną na przedziale I wtedy:
1) ∀x∈I [∫f(x)dx]'=f(x)
2) ∫f'(x)dx=f(x) +c
57. Całki nieoznaczone ważniejszych funkcji elementarnych.
∫0dx=c
![]()
(α≠-1)
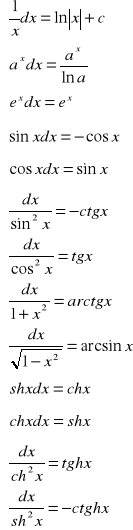
58. Twierdzenie o liniowości całki i o całkowaniu przez części.
Tw o liniowości całki
Jeżeli funkcje f i g mają funkcje pierwotne to całka ∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx
∫a⋅f(x)dx=a∫f(x)dx ∀a≠0.
Tw o całkowaniu przez części
Jeżeli funkcje f i g mają ciągłe pochodne w x∈I wtedy ∫f(x)g'(x)dx=f(x)⋅g(x)-∫f'(x)g(x)dx
59. Twierdzenie o całkowaniu przez podstawianie t=ϕ(x) i x=ϕ(t).
tw t=ϕ(x)
Jeżeli:
1. funkcja f:T→R ma pochodną ciągłą na przedziale T
2. funkcja ϕ:X→T ma pochodną ciągłą na X
∫f(ϕ(x))dx=F(ϕ(x))+c gdzie F jest pierwotna dla funkcji f.
inna postać twierdzenia: Niech mamy obliczyć ∫f(ϕ(x))⋅ϕ'(x)dx= robimy podstawienie t=ϕ(x) wtedy zgodnie z symboliką przyjmujemy w rachunku różniczkowym dt=ϕ'(x)dx =∫f(t)dt obliczamy ostatnią całkę i podstawiamy t=ϕ(x).
tw o całkowaniu przez podstawienie x=ϕ(t)
1. jeżeli funkcja ϕ jest różniczkowalna i różnowartościowa na przedziale T i przekształca go na X.
2.funkcja f ma na przedziale X funkcję pierwotną F to prawdziwe jest na tym przedziale ∫f(x)dx=[f(ϕ(t)⋅ϕ'(t)]⋅ϕ-1
∫f(x)dx=∫f(ϕ(t))ϕ'(t)dt
pamietając, że po wyznaczeniu prawej strony otrzymamy wynik należy złożyć
60. Funkcja wymierna, właściwa. Ułamki proste 1go i 2go rodzaju.
Def: ![]()
Funkcję wymierną W(x) nazywamy właściwą gdy stopień wielomianów w liczniku jest mniejszy od stopnia wielomianu w mianowniku.
Uwaga: każdą funkcję wymierną niewłaściwą można przedstawić w postaci wielomianu funkcji wymiernej właściwej.
Def: funkcję postaci ![]()
nazywamy ułamkiem prostym pierwszego rodzaju, a funkcję postaci ![]()
nazywamy ułamkiem prostym II rodzaju ![]()
.
61. Twierdzenie o rozłożeniu funkcji właściwej wymiernej na ułamki proste.
Każdą funkcję wymierną właściwą można zapisać w postaci sumy ułamków prostych. Przedstawienie to jest jednoznaczne.
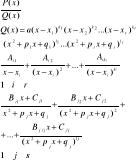
62. Całkowanie ułamków prostych 1go rodzaju.
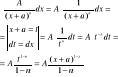
n≠1
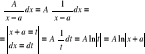
63. Całkowanie ułamków prostych 2go rodzaju.

64. Algorytm całkowania funkcji wymiernych.
1). Funkcje wymierne zapisujemy w postaci sumy wielomianu i funkcji wymiernej właściwej.
2). Mianownik funkcji wymiernej właściwej rozkładamy na czynniki liniowe i kwadratowe nierozkładalne.
3). Zapisujemy rozkład teoretyczny funkcji wymiernej właściwej na ułamki proste I i II rodzaju
4). Znajdujemy nieznane współczynniki tego rozkładu.
5). Obliczamy całki poszczególnych składników rozkładu.
65. Całkowanie funkcji postaci R(sin x,cos x), R-funkcja wymierna.
Dla obliczenia całek postaci ∫R(sin x,cos x) stosujemy podstawienie następujące:
1) t=cosx gdy R(-u,v)=-R(u,v)
2) t=sinx gdy R(u,-v)=-R(u,v)
3) t=tgx gdy R(-u,-v)=R(u,v)
4) ![]()
← podstawienie uniwersalne
66. Całkowanie sinax⋅cosbx; sinax⋅sinbx; cosax⋅cosbx.
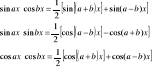
67. Całkowanie funkcji z niewymiernościami.
R(u,v) będzie funkcją wymierną dwóch zniennych u i v
Dla obliczenia całek:
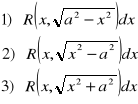
stosujemy
1) x=a sin t
2) x=a ch t
3) x=a sh t
68. Przestrzeń metryczna. Aksjomaty.
Def: Przestrzenią metryczną nazywamy zbiór X, któremu przyporządkowano funkcję dwóch zmiennych d(x,y) x,y∈Rx spełniającego następujące warunki (zwane aksjomatami):
1) d(x,y)≥0 oraz d(x,y)=0 x=y (aksjomat tożsamości)
2) d(x,y)=d(y,x) (aksjomat symetrii)
3) d(x,y)≤d(x,z)+d(z,y) ∀x,y,z∈X (aksjomat nierówności trójkąta)
Elementy przestrzeni metrycznej nazywamy PUNKTAMI. Funkcję d nazywamy METRYKĄ, liczbę d(x,y) nazywamy ODLEGŁOŚCIĄ MIĘDZY PUNKTAMI x i y.
Najprostszym przykładem przestrzeni metrycznej jest zbiór liczb rzeczywistych X=R z metryką d(x,y)=|x-y|
1) d(x,y)≥0
|x-y|=0<=>x-y=0<=>x=y
2) d(x,y)=|x-y|=|-(y-x)|=|y-x|=d(y,x)
3)d(x,y)=|x-y|=|x-z+z-y|≤|x-z|+|z-y|=d(x,z)+d(z,y)
69. Przestrzeń Rn.
Elementem przestrzeni Rn są wszystkie uporządkowane układy liczb rzeczywistych (x1,x2,….,xn). Układy te nazywamy punktami tej przestrzeni, a same liczby x1,x2,….,xn współrzędnymi prostokątnymi tych punktów. Odległość d(A,B) między punktami A=(a1,a2,….,an) B=( b1,b2,….,bn) przestrzeni Rn określamy![]()
Gdy n=2 otrzymamy odległość na płaszczyźnie ![]()
70.Otoczenie i sąsiedztwo w przestrzeni metrycznej.
Otoczeniem o(x,r) punktu x przestrzeni metrycznej X o promieniu r jest zbiorem wszystkich punktów y∈X, dla których d(y,x)<r
SĄSIEDZTWEM S(x,r) punktu x przestrzeni metrycznej X o promieniu r jest zbiorem wszystkich punktów y∈X, dla których 0<d(y,x)<r
71. Zbiór otwarty.
Punkt x przestrzeni metrycznej X nazywamy punktem wewnętrznym zbioru A⊂X jeżeli zbiór ten zawiera pewne otoczenie punktu x np.
1) każdy punkt przediału (a,b)przestrzeni R jest punktem wewnętrznym.
2) punkt a przedziału [a,b] nie jest wewnętrznym
def: Zbiór, którego każdy punkt jest wewnętrznym nazywamy zbiorem otwartym.
Np. zbiór (a,b) jest otwarty w R.
72. Ciąg zbieżny i zbiór domknięty. Punkt brzegowy.
Def: Mówimy, że ciąg xn, element przestrzeni metrycznej X dąży do punktu x o tej samej przestrzeni metrycznej X i zapisujemy xn→x ∨ ![]()
jeżeli d(xn,x)→0 gdy n→∞
Ciąg pkt. Pk przestrzeni metrycznej Rn o współrzędnych Pk =( x1(k),x2(k),….,xn(k)) dąży do P=(x1,x2,….,xn)
x1(k) → x1
x2(k) → x2
x3(k) → x3 gdy k→∞
def: Zbiór A przestrzeni metrycznej X nazywamy domkniętym jeżeli xn∈A ∧ xn→x => x∈A
np. [0,1] domknięty w R
73. Krzywa elementarna. Otwarta i zamknięta. Obszar.
Def: Krzywą elementarną przestrzeni nazywamy zbiór wszystkich punktów tej przestrzeni P=(x1,x2,….,xn) o współrzędnych
x1= x1(t)
x2= x2(t)
……..
xn= xn(t)
gdzie x1(t), x2(t),…, xn(t) są funkcjami ciągłymi określonymi w przedziale (α,β)
Przy czym różnym wartościom zmiennej t∈(α,β) odpowiadają różne punkty P.
Przykład krzywej elementarnej: okrąg x=sint, y=cost, 0≤t≤2π
Krzywą elementarną nazywamy zamkniętą jeżeli xi(α)= xi(β) ∀i=1,2
Krzywą która nie jest zamkniętą nazywamy otwartą.
Obszar jest to taki zbiór otwarty, którego każde dwa punkty można połączyć krzywą elementarną całkowicie w nim zawartą.
74. przestrzeń unitarna. aksjomaty.
Def: Przestrzenią liniową L nazywamy przestrzeń unitarną jeżeli każdej uporządkowanej parze x,y∈L jest przyporządkowana liczba <x,y>∈R taka, że:
1)<x,x〉≥0
2)<α1x1+α2x2,y〉=α1<x1,y〉 +α2<x2,y〉 ∀ x1,x2,y∈L ∀α1, α2∈R
3) <x,y〉=<y,x〉 ∀ x,y∈L
liczby <x,y〉 nazywamy iloczynem skalarnym. Łatwo zobaczyć, że z aksjomatów 2 i 3 wynika:
2' <x,α1y1+α2y2〉=α1<x,y1〉 +α2<x,y2〉 ∀ x,y1,y2∈L ∀α1, α2∈R
def: Normy elementu x przestrzeni unitarnej określamy wzorem ![]()
wzór ten przypomina określenie długości wektora. Norma przestrzeni unitarnej na własności:
1)||x||≥0 ||x||≠0 x=0
2) ||α||=|α|⋅||x|| ∀α∈R ∀x∈L
3) ||x+y||=||x||+||y||
własność 3 zwana nierównością trójkąta wynika z nierówności Schwartza |<x,y〉|=||x||⋅||y||
76. ciąg Cauchiego. Przestrzeń zupełna. Przestrzeń Hilberta.
Def: Mówimy, że ciąg elem. xn przestrzeni metrycznej, jest CIĄGIEM CAUCHIEGO gdy ∀ε>0 ∃N: n,m>N d(xn,xm)<ε Łatwo zobaczyć, że każdy ciąg zbierzny będzie ciągiem Cauchiego, ale nie zawsze ciąg Cauchiego jest zbierzny.
Def: Mówimy, że przestrzeń metryczna jest zupełna, gdy każdy ciąg Cauchiego w niej jest zbierzny. Np. przestrzeń Q liczb wymiernych jest niezupełna, a przestrzeń liczb wymiernych R jest zupełna.
Def: Przestrzeń HILBERTA
Przestrzeń unitarną, która jest zupełna, nazywemy przestrzenią Hilberta. Np. określony w Rn iloczyn skalarny ![]()
P=(x1,x2,….,xn), Q=(y1,y2,….,yn) wzg. tego iloczynu skalarnego Rn będzie przestrzenią Hilberta.
================================
114. Pole powierzchni obrotowej
Niech funkcja nieujemna f ma ciągłą pochodną na przedziale [a,b]. Wtedy pole powierzchni Σ powstałej z obrotu wykresu funkcji f wokół osi ox wyraża się wzorem:
IΣI=2Π ∫ f(x)√1+[f`(x)]2 dx
115. całka niewłaściwa w przedziale nieskończonym. definicje
Jeżeli funkcja f jest całkowalna przedziale [a,T]∀t>a
oraz ∃ granica skończona
lim T→∞ ∫ od a do T z f(x)dx (1)
to nazywamy ją całką niewłaściwą funkcji f na przedziale nieskończonym [a,∞]
i oznaczamy symbolem ∫ od a do ∞ z f(x)dx. Jeżeli granica nieskończona (1) istnieje to mówimy, że całka funkcji f w [a,∞] istnieje lub że ona jest nieskończona.
Jeżeli granica (1) nie istnieje to mówimy że całka niewłaściwa (1) jest rozbieżna.
116. Wartość główna na (-∞,∞):
wartością główną nazywamy granice:
v.p ∫ od -∞ do ∞ f(x) dx= lim T→+∞ z ∫od -T do T z f(x) dx
117. Kryterium porównawcze dla całki niewłaściwej
Na przedziale nieskończonym:
Jeżeli f(x) i g(x) są określone w [a,+∞) i całkowalne w każdym przedziale [a,T]∀T>a oraz 0<=f(x)<=g(x) to zbieżność ∫ od a do ∞ z g(x) dx (4)
zapewnia zbieżność ∫ od a do ∞ z f(x)dx (5) natomiast rozbieżność całki (5) zapewnia rozbieżność całki (4).
118 Bezwzględna i warunkowa zbieżność
w przedziale nieskończonym:
Całkę zbieżną ∫ od a do∞ z f(x) dx (7) nazywamy bezwzględnie zbieżną
jeżeli zbieżna jest ∫ od a do ∞ z | f(x)| dx (8).
Całka (7) nazywa się warunkowo zbieżna jeżeli całka (7)
jest zbieżna a całka (8) rozbieżna.
119. Całka niewłaściwa funkcji nieograniczonej:
Niech f określona na (a,b] jest nieograniczona w lewostronnym sąsiedztwie pkt.b. Jeżeli istnieje granica skończona lim ε→0+ z ∫ od a do b-ε z f(x)dx, to nazywamy ją całką niewłaściwą funkcji f w przedziale [a,b), i oznaczamy symbolem takim jak całkę Reymana ∫ od a do b z f(x)dx. Analogicznie określamy całkę niewłaściwą funkcji f która jest określona w (a,b] nieograniczoną w prawostronnym sąsiedztwie pkt.a
i całkowalną w prawostronnym przedziale [a+ε,b],ε>0 mianowicie:
∫ od a do b z f(x)dx= lim przy ε→0+ ∫ od a+ε do b f(x)dx
120. Wartość główna całki funkcji nieograniczonej:
v.p ∫ od a do b f(x)dx= lim przy ε→0+ [ ∫od a do c-ε f(x)dx + ∫ od c+ε do b f(x)dx]
121. Bezwzględna i warunkowa zbieżność
całki funkcji nieograniczonej:
Całkę niewłaściwa zbieżna drugiego rodzaju ∫ od a do b f(x)dx (1) nazywamy bezwzględnie zbieżną jeżeli jest zbieżna ∫ od a do b If(x)I dx (2). Całkę zbieżną (1) nazywamy warunkowo zbieżną jeżeli całką (2) jest rozbieżna.
122.podstawoweDef całki podwójnej w prostokącie:
Jeżeli dla każdego normalnego ciągu podziału prostokąta P ciąg sum całkowalnych Sn jest zbieżny do tej samej granicy skończonej i niezależnej od wyboru pkt. Ak to te granice nazywamy całką podwójną funkcji f w prostokącie P
i oznaczamy ∫∫ f(x)dσ (1)
∫∫ f(x,y)dσ= lim przy σn→0 ∑ od k=1 po n f(Ak)∆σk (2). Jeżeli całka (1) istnieje to mówimy że funkcja f jest całkowalna w sensie Reymana w prostokącie P.
123. Interpretacje geometryczne i fizyczne całki podwójnej:
• Interpretacja geometryczna Jeżeli funkcja f jest stała w prostokącie P f(x,y)=a, a>0 to dla każdego n: ![]()
, gdzie σ to pole P. Całka podwójna równa się objętości prostopadłościanu o polu podstawy σ i wysokości a.
Jeżeli funkcja f jest ciągła w prostokącie P i f≥0 to suma całkowa ![]()
równa jest sumie objętości prostopadłościanu o polach podstawy Δσk i wysokościach f(Ak). Całka ![]()
równa jest wówczas objętości bryły V ograniczonej płaszczyznami z=0, x=a, x=b, y=c, y=d.
• Interpretacja fizyczna: jeżeli funkcja P(x,y) jest gęstością powierzchniową masy prostokąta P, to całka ![]()
przedstawia masę tego prostokąta.
124. Twierdzenie o zamianie całki podwójnej na całkę iterowaną:
jeżeli funkcja f jest ciągła w prostokącie P, który jest określony wzorem ![]()
, to ![]()
, oraz ![]()
125. Obszar normalny. Całka podwójna w tym obszarze. Zbiór regularny.
zbiór domkniety D określony nierównościami ![]()
gdzie φ(x) i ψ(x) są funkcjami ciągłymi w przedziale [a,b], nazywamy obszarem normalnym względem osi X.
Rozważmy prostokąt ![]()
gdzie c=inf φ(x) w przedziale [a,b] a d=sup ψ(x) w przedziale [a,b]. Niech f(x,y) będzie funkcją ciągła w obszarze D, rozważamy funkcję f*(x,y) określoną w prostokącie P następująco: ![]()
całkę podwójną funkcji f(x,y) w tym obszarze normalnym D oznaczamy symbolem ![]()
lub posługując się wzorem na zamianę całki podwójnej na całkę iterowaną: ![]()
Zbiór D nazywamy regularnym jeżeli jest on sumą ![]()
obszarów normalnych względem X lub Y, które nie mają wspólnych punktów wewnętrznych.
• Interpretacja geometryczna: niech funkcja f(x,y) będzie funkcja ciągłą w obszarze regularnym D, przy czym f(x,y)≥0.
Całka ![]()
przedstawia objętość bryły o podstawie D ograniczonej powierzchnią będącą wykresem funkcji f, oraz powierzchnią walcową utworzoną z prostych równoległych do osi Z i przechodzących przez brzeg obszaru D.
• Interpretacja fizyczna: jeżeli ρ(x,y) jest gęstością powierzchniową masy obszaru regularnego D, to całka ![]()
przedstawia masę m tego obszaru regularnego D.
Całki: ![]()
przedstawiają momenty statyczne Mx i My względem osi X i Y naszego obszaru D.
126. Zmiana zmiennych w całce podwójnej. Jakobian:
zmiana zmiennych w całce podwójnej ściśle związana z odwzorowaniem zbioru płaskiego za pomocą pary funkcji. Rozważmy pary funkcji ciągłych x= x(u,v) i y= y(u,v), które przekształcają zbiór D0 w płaszczyźnie OUV w zbiór D w płaszczyźnie XYZ, wzajemnie jednoznacznie. Jakobianem nazywamy funkcję: ![]()
- odwzorowanie to przekształca wzajemnie jednoznacznie obszar regularny D0 na obszar regularny D
- funkcje te są klasy C1 w obszarze D0
- funkcja f(x,y) jest ciągła w obszarze D
- jakobian J(u,v) przekształcenia nie równa się 0 w obszarze D0
wtedy ma miejsce takie wzór: ![]()
127. Wyprowadzenie zmiennych biegunowych w całce podwójnej:
x= rcosθ, y= rsinθ, wtedy jakobian tego przekształcenia: ![]()
128. Całka potrójna w prostopadłościanie. Podstawowe definicje:
Rozważmy prostopadłościan ![]()
oraz funkcję f(x,y,z) określoną w tym prostopadłościanie. Dzielimy P na n prostopadłościanów Pk 1≤k≤n o objętościach ΔVk. Podział ten oznaczmy symbolem Δn. Niech dk oznacza długość przekątnej prostopadłościanu Pk. Liczbę δn która równa się max dk nazywamy średnicą podziału dk.
Jeżeli dla każdego ciągu normalnego podziału prostokąta P, sumę Sn zmieniają się do tej samej granicy skończonej, niezależnej od wyboru punktu A k, to tą granicę nazywamy całka potrójną funkcji f w prostokącie P. ![]()
129. Interpretacje geometryczne i fizyczne całki potrójnej:
• Interpretacja geometryczna: Jeżeli f(A)≡1 to całka ![]()
przedstawia objętość prostopadłościanu P.
• Interpretacja fizyczna: Jeżeli ρ(A) jest gęstością masy prostopadłościanu P, to całka ![]()
przedstawia masę tego prostopadłościanu.
130. Zamiana całki potrójnej na całkę iterowaną:
Jeżeli funkcja f jest ciągła w prostopadłościanie P ![]()
to całka potrójna ![]()
--------------------------------------------------
139. Twierdzenie o niezależności całki krzywoliniowej od kształtu drogi całkowania. Wnioski:
Jeżeli funkcja P(x,y) i Q(x,y) są klasy C1 w obszarze jednospójnym D, to spełnienie równości Q'x=P'y (2) w każdym punkcie w obszarze D jest warunkiem koniecznym i wystarczającym na to, żeby całka ![]()
po krzywej AB nie zależała od kształtu tej krzywej tylko od punktów A i B.
Wn: (4)1.jeżeli funkcje P i Q są klasy C1 i spełniają warunek 2 to ![]()
=0 po krzywej C, która jest kawałkami gładka i zamkniętą i należy do d równa się 0.
2. Jeżeli funkcja P(x,y) i Q(x,y) są klasy C1 w obszarze jednospójnym D oraz![]()
kawałkami gładkiej krzywej zamkniętej C należącej do D spełniony jest warunek 4 w każdym punkcie tego obszaru to spełniony jest warunek 2.
140. Warunek istnienia funkcji z danymi pochodnymi cząstkowymi:
przypuśćmy, że funkcje P(x,y) i Q(x,y) są klasy C1 w obszarze ![]()
, czy istnieje w tym obszarze funkcja U(x,y) dla której U'x=P i U'y=Q, przypuśćmy, że taka funkcja istnieje wtedy: U''xy=P'y i U''yx=Q'x, ponieważ funkcje P i Q są klasy C1 więc drugie pochodne mieszane są równe sobie. Warunek Q'x=P'y jest konieczny dla istnienia U(x,y), okazuje się, że warunek ten jest wystarczający.
Rozważmy funkcję: ![]()
, gdzie (x0,y0) ustalony punkt należący do D.
U'x=P(x,y)
U'y=![]()
141. Całka krzywoliniowa niekierowana. Podstawowe definicje:
Jeżeli![]()
normalnego ciągu podziału przedziału [α,β] ciąg sum sn=![]()
jest zbieżny do tej samej granicy skończonej, niezależnie od wyboru punktu τk to tą granicę nazywamy całką krzywoliniową nieskierowaną:
![]()
=![]()
![]()
142.Interpretacja geometryczna i fizyczna całki krzywoliniowej niekierowanej:
• interpretacja geometryczna: Jeżeli funkcja f(x,y)=1 to ciąg sn=![]()
zawsze równa się l. Jeżeli f(x,y)>0 i jest ciągła to ![]()
przedstawia pole powierzchni.
• interpretacja fizyczna: Jeżeli ρ(x,y) jest gęstością liniową masy krzywej L to ![]()
przedstawia masę tej krzywej.
143. Zamiana całki krzywoliniowej niekierowanej na całkę oznaczoną: Jeżeli funkcja f(x,y) jest ciągła na otwartej krzywej gładkiej L to całka ![]()
istnieje i jest równa ![]()
144. Całka powierzchniowa niezorientowana. Podstawowe pojęcia:
Jeżeli dla każdego normalnego ciągu podziału prostokąta P ciąg sum sn jest zbieżny do tej samej granicy skończonej, niezależny od wyboru punktu Ak' to tą granicę nazywamy całką powierzchniową niezorientowaną
![]()
=![]()
![]()
=sn
145.Interpretacja geometryczna i fizyczna całki powierzchniowej niezorientowanej:
• interpretacja geometryczna: Jeżeli F(x,y,z)=1 to ![]()
przedstawia pole płata gładkiego Ω
• interpretacja fizyczna: Jeżeli ρ(x,y,z) jest gęstością powierzchniową masy pola Ω to ![]()
przedstawia masę tego pola.
146. Obliczanie całki powierzchniowej niezorientowanej:
Jeżeli funkcja F jest ciągła na gładkim płacie Ω to ![]()
istnieje i oblicza się ją za pomocą wzoru ![]()
=![]()
przykład :F(x,y,z)=z ![]()
Ω-tr. o wierzchołkach (1,0,0), (0,1,0), (0,0,1) f(x,y)=1-x-y
![]()
=![]()
![]()
Wyszukiwarka
Podobne podstrony:
egz, e (4), Egzamin Chemia analityczna
egz, Egzamin 96-113, 95
BIOCHEMIA EGZAMIN, Szkoła Rolnictwo studia, Szkoła, Materiały studia, biochemia cwiczenia, biochemia
Biochemia egzamin, Szkoła Rolnictwo studia, Szkoła, Materiały studia, biochemia cwiczenia, biochemia
Egzamin fizjologia roślin drz, Fizjo I EGZ, EGZAMIN
algebra, egz, EGZAMIN Z ALGEBRY I
Fizjo I EGZ, EGZAMIN
rachunek pra, egz, EGZAMIN Z RACHUNKU PRAWDOPODOBIEŃSTWA
egz, e (5), EGZAMIN Z CHEMII ANALITYCZNEJ DLA II ROKU CHEMII 2003/2004
egz, e (7), EGZAMIN Z CHEMII ANALITYCZNEJ DLA II ROKU CHEMII 2003/2004
pytania egz ekonimak II, OPRACOWANIE PYTAŃ NA EGZAMIN
egz fizjo, II ROK STOMATOLOGIA SUM ZABRZE, FIZJOLOGIA, FIZJOLOGIA EGZAMIN, foldery z pytaniami, egza
pytania egz.fizjot.-1, pedagogika, egzamin
Egz.Gim.Ang2009odpowiedzi, Egzamin gimnazjalny
egz.42, II rok, zimowy, Chemia Fizyczna, zagadnienia do egzaminu
praca egz kinezjologia, Kinezjologia, prace egzaminacyjne
egz 1, Politechnika Krakowska, IV Semestr, Nawierzchnie drogowe, Projekt, materialy, Nawierzchnie dr
więcej podobnych podstron