TRYGONOMETRIA SFERYCZNA

Odległość sferyczną między dwoma punktami A i B leżącymi na sferze nazywamy kąt środkowy ά oparty na łuku koła wielkiego AB przechodzącego przez te punkty

Kąt sferyczny to kąt mdzy stycznymi do łuków kół wielkich w p-cie ich przecięcia się.

Jeżeli 3 dane p-kty leżące na sferze połączymy łukami kół wielkich, to część sfery ograniczona tymi łukami będziemy nazywać trójkątem sferycznym. Elementy Δ sfer. to 3 kąty (A,B,C) i 3 boki (a,b,c) takie, że bok a leży naprzeciwko kąta A. Miarą długości boku Δ sfer. jest odległość sfer. danych wierzchołków. 3 łuki kół wielkich tworzą na sferze 8 Δsfer. Suma kątów Δsfer. jest zawsze większa od 180^o.

Podstawowe wzory tryg.sferycznej:

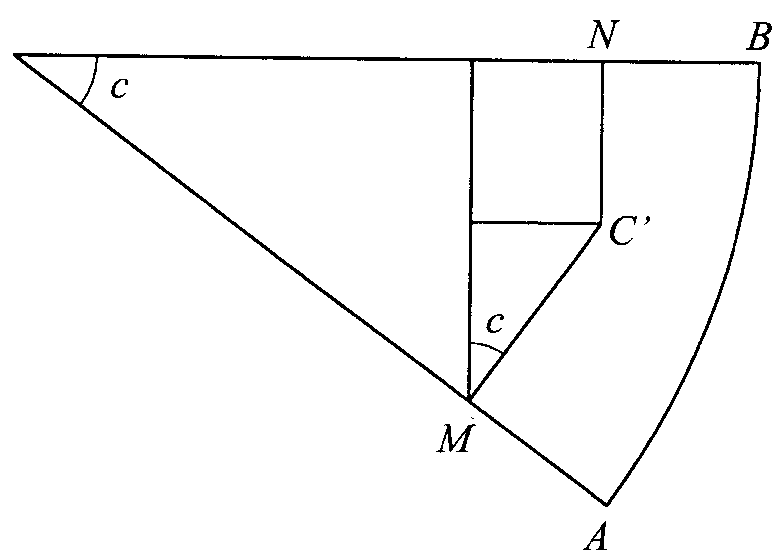
Zależności między bokami i kątami OMC`NO:

ON=OMcosc+C`Msinc

C`N=Omsinc-C`Mcosc

RYS 1

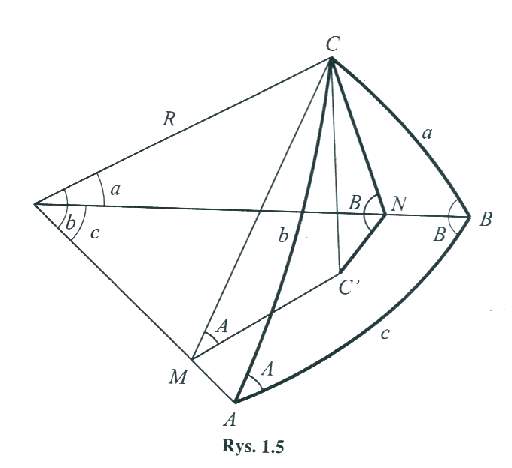
OM=Rcosb; ON=Rcosa

C`M=CmcosA= Rsinb cosA

C`N=CncosB=Rsinb cosA

Podstawiamy do poprz. zależności:

Rcosa=Rcosb cosc+ Rsinb sinc cosA;

Rsina cosB=Rcosb sinc-Rsinb cosc cosA;

dzielimy obie strony przez R:

cosa= cos cosc+ sinb sinc cosA;

sina cosB=cos sinc- sinb cosc cosA

wzory cos i sin-cos; jeżeli uwzględnimy CN=Rsina i CM=Rsinb

to otrzymamy wzór sin postaci:

sina sinB = sinb sinA

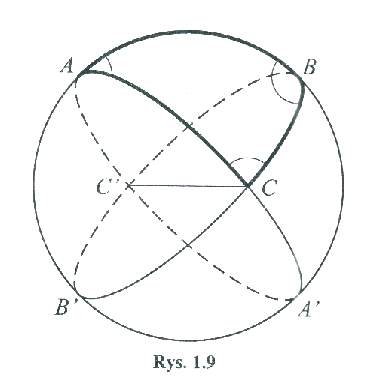
Trójkąt eulerowski jego wszystkie boki i kąty mniejsz od 180^o.RYS 1

Trójkąt sferyczny biegunowy RYS 2

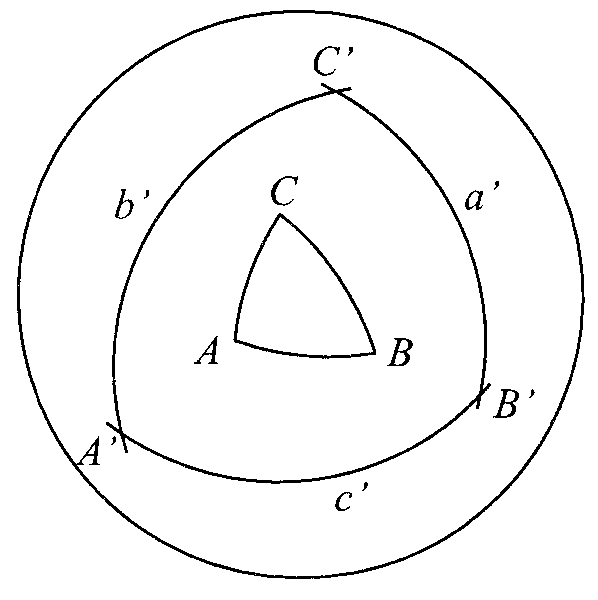
to Δ o bokach a^',b^',c^' względem danego Δ ABC jeżeli pkt. A jest biegun. boku a^', pkt.B jest biegunem boku b^', a pkt. C biegunem boku c^'. Wierzchołki tego Δ o A^',B^',C^' Każdemu Δsfer. odpowiada 8 Δ biegunowych. Z def. Δ biegun. wynika, że A^'B=90⁰ i A^'C=90⁰ co oznacza, że pkt. A^' jest biegun. boku a. Tak można udowodnić, że Δ ABC jest Δbiegun. Δ .A^',B^',C^', więc Δ ABC i A^',B^',C^' są wzajemnie biegun.

RYS 3

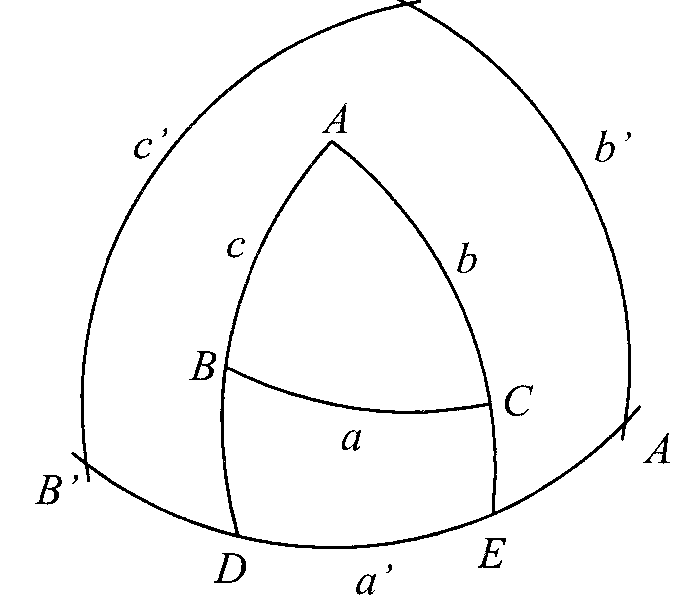
Związki między ich bokami i kątami: B^'C^'=B^'E+DC^'-DE^' ponieważ B^'C^'=a, B^'E=90⁰, DC^'=90⁰, DE=A to a^'=180⁰-A, b^'=180⁰-B, c^'=180⁰-C,podobnie a=180^o-A^', b=180⁰-B^', c=180⁰-C^'.

cosa`=cosb`cosc`+sinb`sinc`cosA`

pdst. powyższe zależnosci:

-cosA=cosBcosC-sinBsinCcosa

cosa=(cosBcosC+cosA)/(sinBsinC)

znajdując katy można obl.boki.

Wzory ctg-sowe:

sinb cosA=cosa sinc-sina cosc cosB sinb sinA=sinB sina

dzielimy przez siebie stronami: ctg sinB=ctgsinc-cosBcosc

i pozostałe 5 wypr. Tak samo!

Wzory połówkowe:

2sin²A/2=1-cosA 2cos²A/2=1+cosA; zatem: tg²A/2=1-cosA/1+cosA

podstawiamy do prawej strony : cosA=(cosa-cosbcosc)/sinbsinc;

po przekształceniach otrzymamy: tg²A/2=sin(s-b)sin(s-c)/sinssin(s-a);

gdzie 2s=a+b+c;podobnie dla pozostałych kątów; Teraz dla boków:

tg²a/2=1-cosa/1+cosa podstawiamy do prawej strony: cosa=(cosA+cosBcosC)/sinBsinC

tg²a/2=-cosScos(S-A)/cos(S-B)cos(S-C); gdzie 2S=A+B+C; tak samo pozos.

Analogie Nepera są to wzory tg(A+B)/2= [cos(a-b)/2] / [cos (a+b) /2]*ctgC/2 tg(A-B)/2=[sin(a-b)/2]/[sin (a+b) / 2]*ctgC/2 tg(a+b)/2=

[cos(A-B)/2] / [cos (A+B) / 2]*tgc/2

tg(a-b)/2= [sin(A-B)/2] / [sin (A+B) / 2]*tgc/2 Podobne wz. można otrzymać dla pozostał. par kątów i boków

Nadmiar sferyczny to suma kątów Δsfer. pomniejszona o 180^o. ε=(A+B+C)-180^o. Nadmiar sfer. zawiera się w przedz. (0;360^o). Jeżeli kąty wyrażamy w radianach to wzór : ε=(A+B+C)-π

Rys.

Pole dwukątów sferycznych ABA`C,BCB`A i CAC`B to odpow.:

P_A=P*A/2π, P_A=P*A/2π, P_A=P*A/2π

P_A+P_B+ P_c =P/2π(A+B+C),a że P=4πR² to wtedy: P_A+P_B+P_c=2R²(A+B+C)

ΣPi=połowa pola sferycznego powiększonego podwójne pole S trójkąta ABC⇒ P_A+P_B+P_c=2πR²+2S zachodzi zależ.:

2R²(A+B+C)=2πR²+2S skąd (A+B+C)-π=S/R²; ε= S/R²,do obliczania nadmiaru służą także wzory L`Huilliera: tg ε/4=√(tg s/2*tg s-a/2*tg s-b/2*tg s-c/2), lub wzór Cagnoli:

sin ε/2=(sin a/2*sin b/2*sin C)/cos c/2

W przypadku Δsferycznych o bokach kilkudziesięciokilometrowych leżących na sferze o prom. R=6371 można stosować wzór uproszczony: ε=ab/2R²*sinC a,b-wyrażone w jednostkach długości. Wzór ten zapewnia dokładność 1”*10^-4 dla trójkątów o bokach 30km i 1”*10^-3-50km

Wzór na nadmiar sferyczny wielokąta:

Σ_i=1ⁿKi=(n-2)π+ P_w/R², P_w-pole tej części sfery znajdującej się w wieloboku.

KULA Najlepiej bryłę ziemską reprezentuje kula o promieniu równym 6371 km. Osią podstawową ukł. wsp. geograficznych jest oś obrotu Ziemi. Oś ta przecina powierzchnię kuli w 2 punktach, zwanych biegunami ziemskimi. Każde połączenie biegunów ziemskich połową łuku koła wielkiego nazywamy południkiem. Południk przechodzący przez określony punkt obserwatorium w Greenwich nosi nazwę południka początkow. Każde koło małe leżące w pł. prostopadłej do osi obrotu jest nazwane równoleżnikiem. Równik jest kołem wielkim, leżącym w pł. prostopadłej do osi obrotu i przechodzącej przez środek kuli. Odległość sferyczna dowolnego punktu równika od bieguna ziemskiego wynosi Π/2. Pozycję punktu leżącego na kuli określamy, podając kąt φ i λ (szer. i długość geograficzna). Szer. geograficzną punktu P leżącego na kuli nazywamy kąt, jaki tworzy normalna do sfery w punkcie P z płaszczyzną równika.

Długością geograficzną punktu P leżącego na kuli nazywamy kąt dwuścienny między płaszczyzną południka punktu P a pł południka początkowego rys

Wsp .prostokątne prostoliniowe Układ wsp. prostokątnych jest zdefiniowany:

-początek układu pokrywa się ze śr. kuli,

-oś z pokrywa się z osią obrotu,

-oś x pokrywa się z krawędzią przecięcia pł. równika i pł. południka początk.

-oś y tworzy z pozostałymi osiami układ prawoskrętny.

Współrzędne x,y,z punktu leżącego na kuli określamy wzorami: x=Rcosφcosλ; y=Rcosφsinλ; z=Rsinφ. Wsp. te spełniają warunek x²+y²+z²=R². Znając współrzędne prostokątne x, y, z punktu leżącego na kuli można obliczyć jego wsp. geograficzne φ, λ wg wzorów: tgλ=y/x; tgφ=z/v(x²+y²) RYS 4

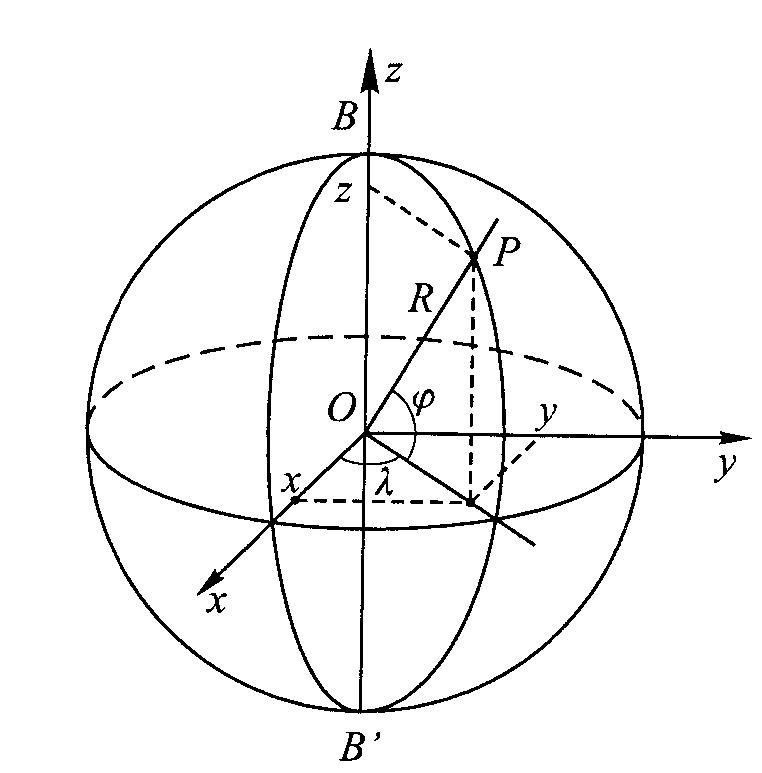
WSP. AZYMUTALNE Punktem głównym układu wsp. azymutaln będzie punkt G leżący na kuli i nie będący biegunem ziemskim,o znanych współrzędnych geograf. (φ_o,λ_o) połączymy łukiem koła wielkiego p-kt główny G i dowolny punkt P leżący na kuli. Pozycja pkt.P będzie jednoznacz określona względem punktu G, jeżeli podamy azymut α i odległość zenitalną ζ. Azymut α jest kątem dwuściennym między płaszcz. połudn. G i płaszcz. koła wielkiego GP, jest równy kątowi sfer., którego lewym ramieniem jest styczna do połud. punktu G, zaś prawym styczna do łuku koła wielkiego GP. Azymut rośnie zgodnie z ruchem wskazówek zegara od północnego kierunku południka punktu G. Wertykał to każde koło wielkie przechodzące przez p-kt główny G Almukantarat to koło małe, którego wszystkie pkt. są jednakowo oddalone od pkt. G

RYS 5

Związek między wsp. geograficznymi i azymutalnymi Rys.

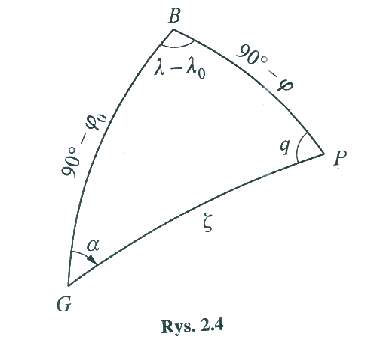
Opiszmy kąty i boki Δsfer. GBP wsp. Azymut. pkt.P (α,ζ) są f-cją wsp. Geograf. pkt. G (ϕ₀,λ₀) i pkt.P(ϕ,λ) cosζ=sinϕ₀sinϕ+cosϕ₀*cosϕcos(λ-λ₀) sinα=sin(λ-λ₀)cosϕ/ sinζ Wzory te nie dają dokł.wyników, gdy odl. zenitalnaζ jest mała. Wtedy stosujem wz. ctgαsin(λ-λ₀)= ctg (90⁰-ϕ)sin(90⁰-ϕ₀)-cos (λ-λ₀)cos(90⁰-ϕ₀) i otrzymujemy tgα=sin(λ-λ₀)/ tgϕ cosϕ₀-cos(λ-λ₀)sinϕ₀ Odl. zenitalną ζ obl.wg. jednego z wz. sinζ=sin(λ-λ₀)cosϕ / sinα sinζ=sinϕcosϕ₀-cosϕsinϕ₀cos(λ-λ₀)/ cosα Wsp. azymut. α,ζ można zamienić na wsp. geograf. ϕ,λ wg.wz. sinϕ=cosζsinϕ₀ +sinζcosϕ₀cosα oraz sin(λ-λ₀)=sinαsinζ/ cosϕ Azymut odwrotny α^, będący kątem dwuściennym między pł.południka pkt. P. I pł.koła wielkiego PG zależy od kąta q(kąt paralaktyczny) α^,=360⁰-q q obl.ze wz. tgq=sin(λ-λ₀)/tgϕ₀* cosϕ-cos(λ-λ₀)sinϕ WSP. PROSTOKĄTNE SFERYCZNE Podstawą ukł. tych współ. jest wybrany połud o długości geograf λ_o. Pkt. pomocniczy C powstaje przez przecięcie wybranego połud z kołem wielkim przechodz przez dany pkt. P i prostopadłym do wybranego połud. Wsp. prostokątnymi są wielkości g i h wyrażone w mierze kątowej. RYS 6

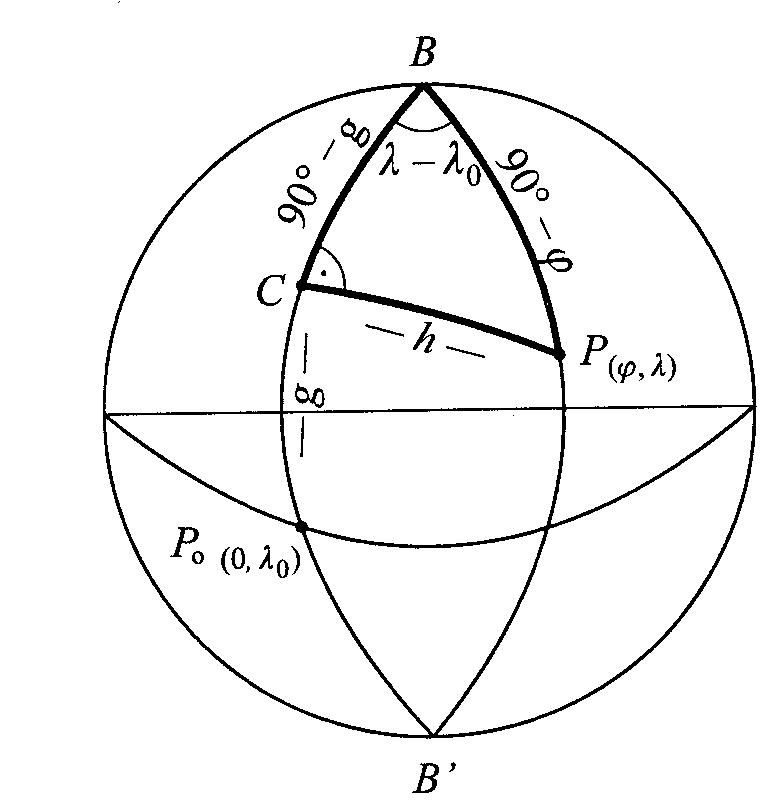
Wsp. h obl.sinh=sin(λ-λ₀)cosϕ wsp.g obl.sin(90⁰-ϕ)cos (λ-λ₀)=coshsin(90⁰-g) lubcos(90⁰-ϕ)=cos(90⁰-g)cosh po podzieleniu stronami dwóch ostatnich wyrażeń mamy ctgg=cos(λ-λ₀) ctgϕ przeliczenia odwrotne wykonujemy wg.sinϕ=singcosh oraz ctg(λ-λ₀)=cosgctgh Wsp. prostokątnym sferycznym g,h można przyporządkować wsp. płaskie x=gR,y=hR

ELIPSOIDA

Elipsoida obrotowa o odpowiednio dobranych parametrach jest znacznie lepszym przybliżeniem kształtu bryły ziemskiej niż kula. Elipsoidą odniesienia nazywamy elips. obrotową o odpowiednio dobranych parametr. i określonym usytuowaniu w bryle ziemskiej, na którą rzutowano punkty danej sieci geodezyjnej. W ukł. współ. prostokątnych XYZ umieszcza się elipsoidę obr. w taki sposób, że środek elips. pokrywa się z początkiem ukł. współ, oś obrotu elipsoidy pokrywa się z osią Z ukł. współ. RYS 7

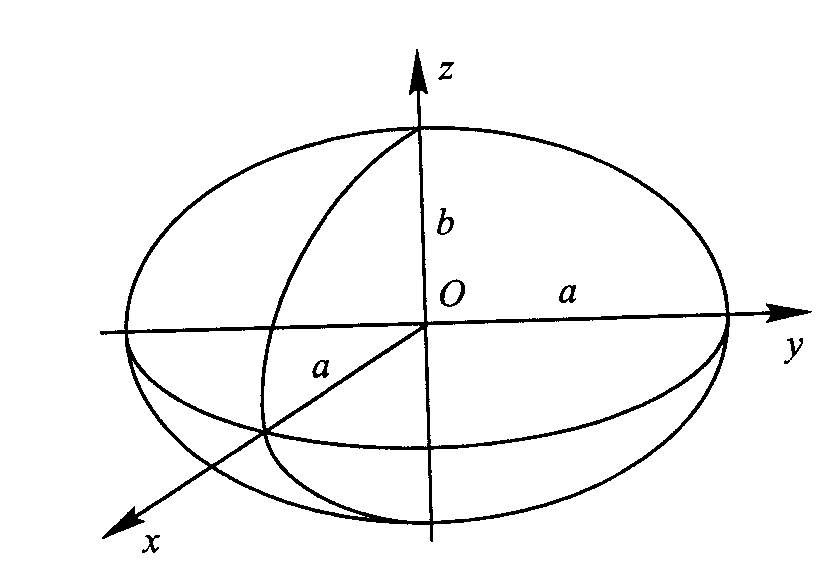
Wsp. każdego pkt leżącego na pow. elipsoidy obrotowej spełniają równanie X²/a²+Y²/a²+Z²/b²=1 Kształt i wielkość elipsoidy obr. określają parametry: półosie a i b lub półoś a i spłaszczenie α [α=(a-b)/a] Zamiast α można posługiwać się mimośrodem elipsoidy

e²=(a²-b²)/a²=α(2-α), także: b²/a² =1- e² wielkość II mimośrodu obliczamy ze wzoru: e'²=(a²-b²)/b² = e²/(1- e²)

Równoleżnikiem punktu P jest ślad przecięcia pow. elipsoidy pł. przech. przez p-kt P i równoległą do płaszczyzny równika. Ma kształt okręgu.

Południkiem punktu P jest ślad przecięcia elipsoidy płaszcz. przech. przez p-kt P i oś obrotu elipsoidy. Ma kształt elipsy. Wprowadza się oś U i powstaje nowy, prostokątny układ UZ. RYS 8

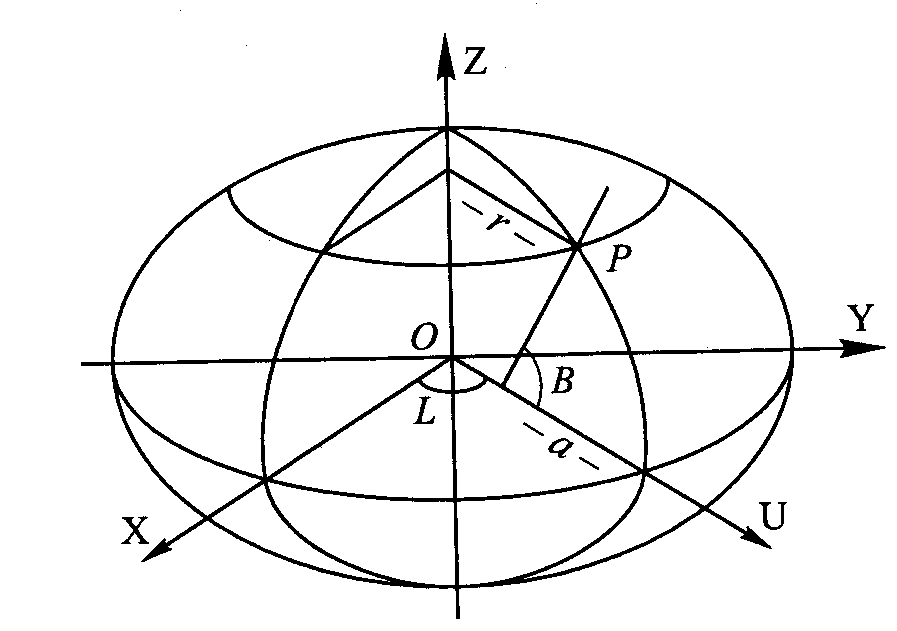
Równanie połud. zawierającego pkt P w tym układzie to U²/a²+Z²/b²=1 Normalna n do elipsoidy leży w płaszcz. południka P. Szerok. elipsoidalną B (sz. geodezyjna) punktu P jest kąt miedzy normalną n do pow. elipsoidy w p-kcie P i płaszcz. równika Dł elipsoidalną L (dł. geodezyjna) p-tu P jest kąt dwuścienny między płaszcz. połud.

p-tu P i płaszcz. połud. początkowego RYS 9

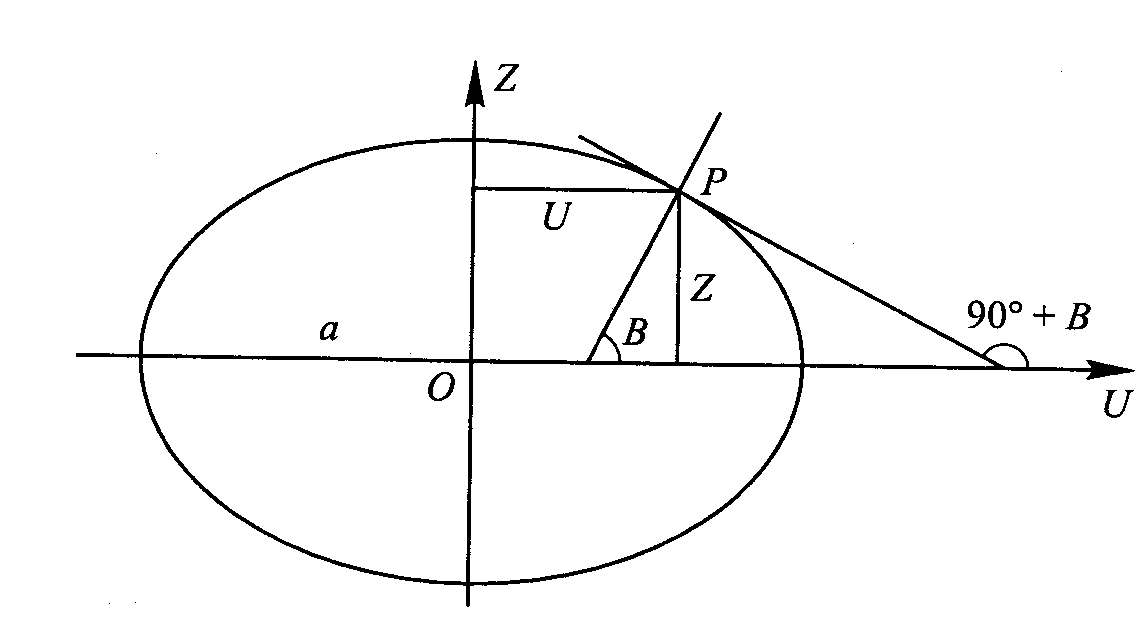
Styczna do pow. elips. w pkt. P tworzy z dodatnim kierunkiem osi U kąt=90⁰+B co pozwala określić zależność pochodnej dZ/dU od szer. elipsoid. B.

dZ/dU=tg(90⁰+B)= -ctgB po przekształc. i uwzględnieniu b²/a²=1-e² mamy: U²=a²/1+(1-e²) tg²B Dla U≥0 mamy : U=(acosB)/√(1-e²sin²B), a promień równoleżnika pkt P r=U Współ. X i Y punktu P oblicz. X=UcosL; Y=UsinL, a współ. Z=[a(1-e²)sinB]/ √(1-e²sin²B)

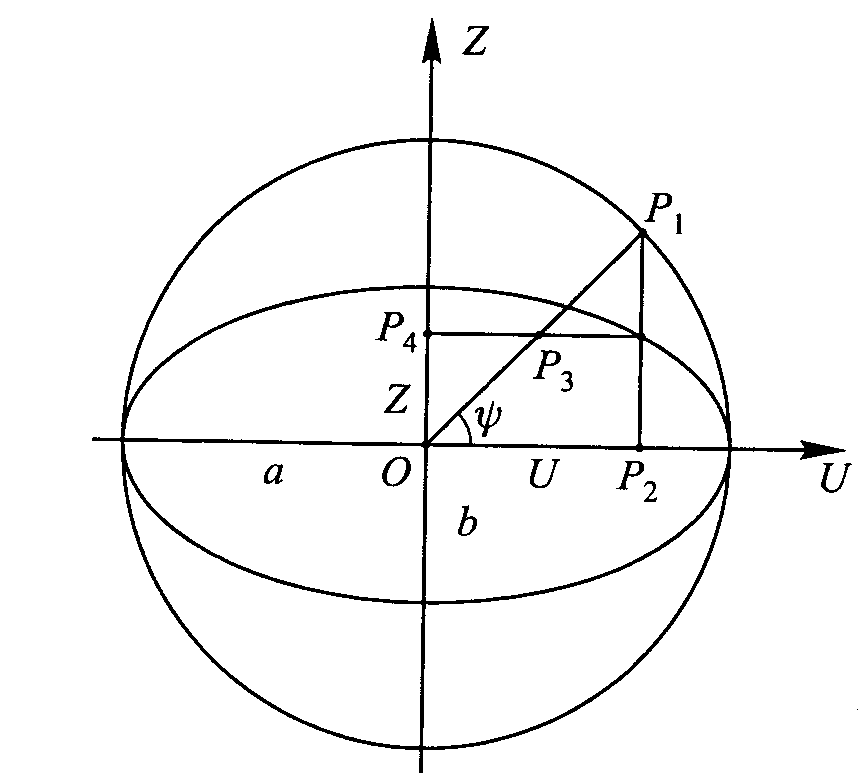
Szerokość zredukowana Przyjmujemy, że środek sfery pokrywa się ze środ. elips. obrot. Jeżeli przez pkt P leżący na elips. poprowadzimy prostą równoległą do osi obrotu Z, to punkt P₁ będzie rzutem punktu P na sferę. Kąt ψ zawarty między promieniem OP₁ a pł. równika będzie szerokością zredukowaną punktu P. RYS10

tgψ=[√(1a²)]×tgB

Przekroje normalne Przez p-kt P leżący na danej, regularnej pow. można poprowadzić tylko jedną prostą prostopadłą do tej pow. zwaną normalną n. Wszystkie płaszcz. zawierające normalną n przecinają daną pow. wzdłuż krzywych zwanych przekrojami normalnymi w punkcie P. Krzywizny z reguły są zmienne. Spośród wszystkich przekrojów normalnych w danym punkcie wyróżniamy 2 przekroje główne. Jeden ma krzywiznę największą spośród krzywizn wszystkich przekr. normalnych w danym punkcie, drugi zaś ma krzywiznę najmniejszą. Płaszcz. przekr. gł. przecinają się pod kątem prostym.

RYS 11.

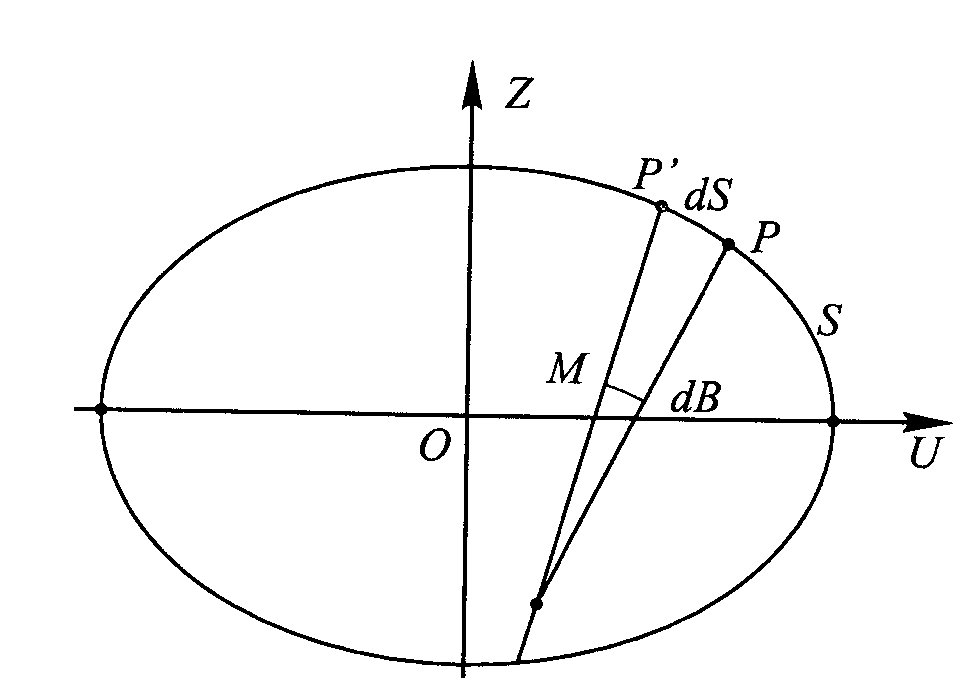
Jednym z przekr. gł. elips. obrotowej jest przekr. płaszcz. połud, zwany przekr. połud, a drugim - przekr. płaszcz. prostopadłą do płaszcz. połud. zwany przekr. poprzecznym Dług. promienia M krzywizny przekr. połudn. M=ds/dB, S- dł. połud, rożniczka dS zależy od dU i dZ czyli: dS.=√(dU²+dZ²), lub

dS= -dU√(1+(dZ/dU)²), znak minusa mówi o tym że ujemnemu przyrostowi dU odpowiada dodatni przyrost dS., uwzględniając dZ/dU= -ctg B, to otrzymamy: dS.=- dU√(1+ctg ²B)=-dU/sin B, zatem M=-dU/dB*1/sin B,

dU/dB=-a(1-e²)sin B/(1-e²sin ²B)^3/2,

Co ostatecznie daje nam wzór na M

M=[a(1-e²)]/(1-e²sin²B)^3/2.

RYS 12

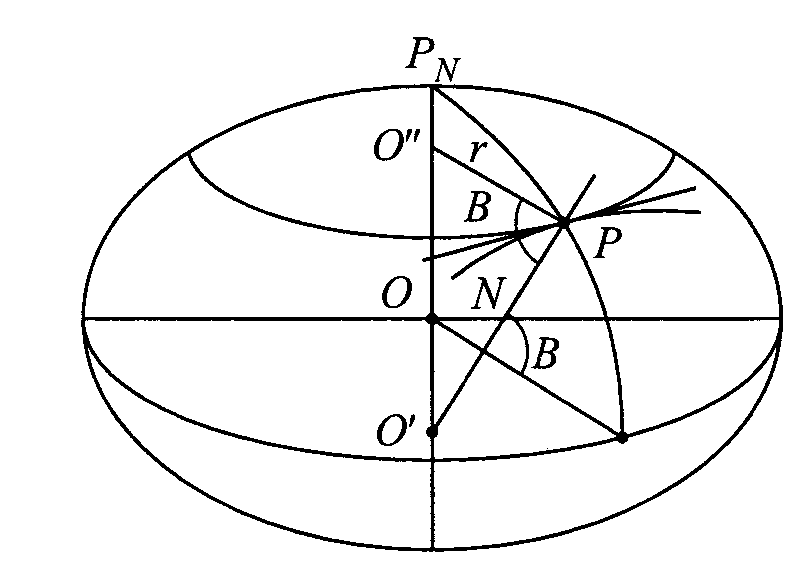
Oba przekroje mają wspólną styczną w punkcie P, a płaszcz. tych przekr. tworzą kąt równy szer. elips. B, możemy zastosować tw. Meusniera: r=Ncos B,r to promień równoleżnika, zatem N=r/cosB, podst. r=U otrzymujemy dł. promienia N krzywizny przekr. poprzecznego to N=a/(1-e²sin²B)^1/2 Zależność tę można wykorzystać do uproszczenia wzorów określające wsp. prostokątne pkt leżącego na pow. elipsoidy: X= NcosBcosL Y= NcosBsinL Z= N(1-e²) sinB. Promień. M jest najmn. a N najw. promieniem krzywizny przekr. normalnych w danym p-kcie. Promień krzywizny dowolnego przekr normalnego (wzór Eulera) 1/R_A=cos²A/M+sin²A/N. Śr. promień krzywizny Q w danym p-kcie elips. definiujemy jako Q=1/2π₀∫^2πR_AdA. Obliczamy ze wzoru Q=√MN=(a√1-e²)/(1-e²sin²B)

Długość łuku południka Wzór wyjściowy dS=MdB S₁₂<60km z dok. 1mm:

S₁₂=M_s(B₂-B₁), M_s=M(B_Sr); Dla 60km<S₁₂<750km z dok. 1mm: S₁₂=[(M₁+4M_s+M₂)*(B₂-B₁)]/6; Dla S₁₂>750km S₁₂=_B1∫^B2MdB =₀∫^B2MdB-₀∫^B1MdB

Pole powierzchni elipsoidy Elementarny czworobok krzywoliniowy. jest zawarty między dwoma południkami i równoleżnik. będącym wycinkiem powierzchni elipsoidy obrotowej. RYS 13

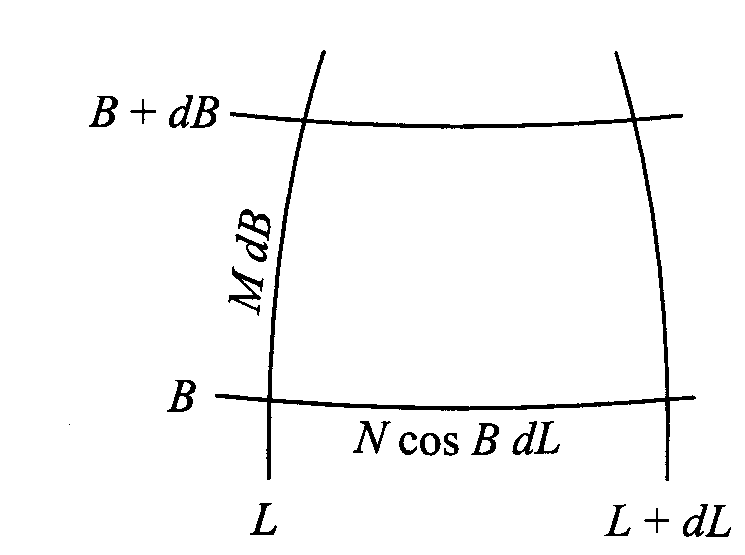
Dł. boków tego czworoboku są równe elementarnym dług. łuku połud. (MdB) oraz równoleżnika (NcosBdL). Pole elementarnego czworoboku można obliczyć ze wzoru dP=MncosBdBdL. Pole czworoboku o wymiarach skończonych określa wzór P=_B1∫^B2_L1∫^L2MncosBdBdL.

Pole całej pow. elips. obr. to

P=a²(1e²)4π[1+²/₃e²+³/₅e⁴+⁴/₇e⁶+...]

Teoria odwzorowań

Odwzorowaniem jednej pow. na drugą nazywamy każdą wzajemnie jednoznacz. odpowiedniość punktową między pow. nazywaną oryginałem a pow. nazwaną obrazem Odwzorowanie nazywamy regularnym, gdy funkcje f i g spełniają warunki: a)każdej parze wartości parametrów u,v przyporządkowują tylko jedną parę wartości parametrów U,V b)są ciągłe i co najmniej 2-krotnie różniczkowalne c)są wzajemnie niezależne. W odwz. tym obrazem pkt jest pkt, krzywej-krzywa, kąta-kąt, obszaru - obszar. Jeżeli oryginałem jest cała pow. elips. obr. lub jej część to rolę parametrów u,v odgrywają zwykle wsp. elipsoidalne B,L. Jeżeli rolę parametrów U,V odgrywają wsp. prostokątne x,y to f-cje odwzorowawcze mają postać x= x(B,L) y= y(B,L). Jeżeli położenie pkt. na płaszcz. opisują wsp. biegun. ρ,δ to f-cje odwzorow. mają postać δ=δ(B,L) ρ=ρ(B,L)

Skale i zniekształcenia odwzorowawcze Skala główna mapy - zmniejszenie wszystkich elementów liniowych obrazu płaskiego w stałym stosunku m₀=1/m

Elementarna skala długości stosunek dł. ds nieskończenie małego łuku na obrazie do dł. ds odpowiadającemu mu łuku na oryginale m=ds/ds. Elementarna skala dł. w danym odwz. zależy od współ. B,L określających położenie p-ktu, i od azymutu A elementu liniowego ds - m= m(B,L,A).Tylko w odwz. równokątnych zależy tylko od współ. p-ktu. Wartość skali dł. mieści się w przedziale (0,∞).

Skala poszczególna m` -stosunek dł. nieskończenie małego odcinka na mapie do długości jego odpowiednika na oryginale. Jest ona iloczynem skali głównej mapy m<sub>0</sub> i elementarnej skali dł. m: m`= m₀ m.

Elementarna skala pól - stosunek nieskończenie małego elementu powierzchniowego na obrazie dP do odpowiadającemu mu nieskończenie małemu elementu powierzchn. na oryginale dP. p=dP/dP. W danym odwzor. skala pól zależy od współ. B,L określających poł. pkt.

Zniekształcenie długości Z_m=m-1, a zniekszt. pól Z_p=p-1.

Odwzorowanie elementów powierzchni elipsoidy obrotowej na płaszczyznę Elementarny czworobok krzywoliniowy - jest zawarty między dwoma połud. i równoleż. będącym wycinkiem pow. elips obr. RYS 20

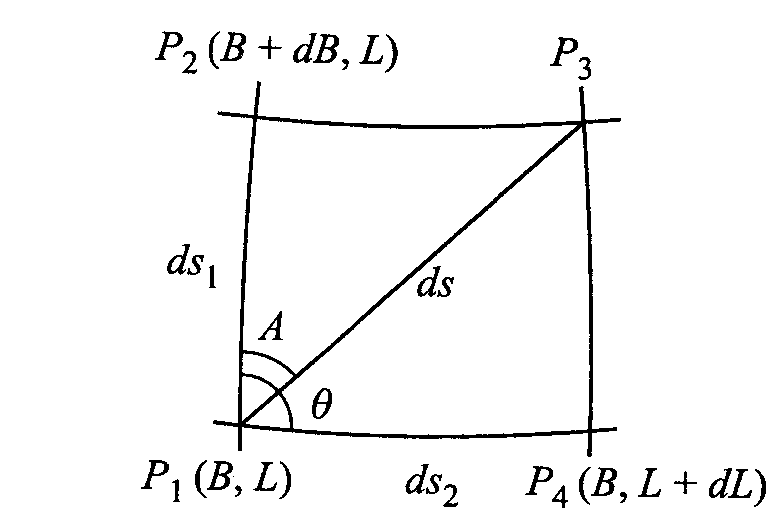
można traktować go jako figurę płaską leżącą w płaszczyźnie stycznej do elipsoidy w pkt.P₁ ponieważ różniczki dB i dL są nieskończenie małe. ds₁=MdB, ds₂=rdL=NcosBdL więc ds²=ds₁²+ds₂²=(MdB)²+(rdL)².

tg A=ds₂/ds₁=rdL/MdB

Kąt θ między połud. a równo. wynosi 90^o wzór na pole elementarnego czworoboku wynosi dP=ds₁ds₂=M*rdBdL

RYS 21

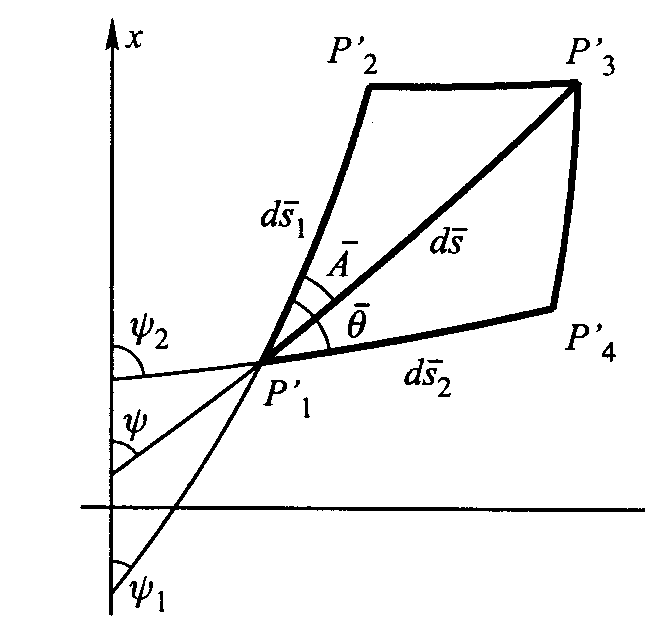
Obrazem elementu liniowego ds będzie element ds wyrażony wzorem ds²=dx²+dy² H²=EG-F² Posługując się wielkościami E,F,G gdzie E=(δx/δB)²+(δx/δ B)²F=(δx/δB*δx/δL)+ (δy/δB*δy/δL)G=(δx/δL)²+(δy/δL)² H= (δx/δB*δy/δL)-(δx/δl*δx/δB) Łatwo można spr.że H²=EG-F² Posługując się wielkościami E,F,G możemy obl. długość elementu liniowego ds²=Edb²+ 2FdbdL +GdL² Długość elementarnego łuku południka otrzymamy przyjmując w odwzorowaniu dL=0 to ds₁=(√E)dB a długość równoleżnika ds₂=(√G)dL. Skala dł. w kierunku połud. m_B=ds₁/ds₁=(√E)/M. a w kierunku równoleż. m_L=ds₂/ds₂=(√G)/r Kąt ψ₁ est szczególnym przypadkiem kątaψ gdy dL=0 tgψ₁= (δy/δB)/(δx/δB) ψ₂ jest natomiast szczególnym przypadkiem ψ gdy dB=0 tgψ₂= (δy/δL)/(δx/δL) Wynika że kąt θ będący obrazem kąta θ=90⁰ równa się różnicy ψ₂-ψ₁ więc tgθ=tg(ψ₂-ψ₁)

Odwzorowanie jest równokątne, jeżeli w każdym punkcie odwzorowywanego obszaru dowolny azymut A odwzorowuje się bez zniekształcenia, tzn. A≡A. Warunki równokątności F=0 i jednocześnie (E/H)*(r/M)=1.

ctgA=(m_BctgA/m_Lsinθ)+ctgθ

Po przekształceniach: odwz. jest równokątne jeżeli spełnione są jednocześnie dwa warunki: 1.obrazy południków przecinają się z obrazami równoleżników pod kątem prostym θ=90^o; 2.w każdym punkcie skala długości w kierunku południków jest równa skali długości w kierunku równoleżników m_B=m_L

Postacie różniczkowe warunku równokątności ∂x/∂L=-r∂y/M∂B; ∂y/∂L=+r∂x/M∂B

Wz na pole czworoboku elementarnego dP=ds₁ds₂sinθ i na skalę pól

P=(ds₁ds₂sinθ)/(ds₁ds₂).

Przy odwzorowaniach równokątnych skale dł. nie zależą od kierunku.

Warunek równopolowości Odwzorowanie jest równopolowe jeżeli w każdym pkt odwzorowywanego obszaru spełniony jest warunek p=1 czyli m_Bm_Lsinθ=1 lub H=Mr Gdy θ=90^o to m_Bm_L=1 RYS od 22 do 27

Kierunki główne

Na powierzchni elipsoidy są dwi krzywe k1 i k2,przecinają się pod kątem 90st. Na obrazie krzywe te przetną się pod kątem różnym od 90 zwiększając w sposób ciągły azymut A1 zauważamy, że przy pewnej wartości tego azymutu kąt między obrazami kierunków osiąga wartość minimalną <90st. I max >90.Oznacza to, że nastąpił taki moment w którym kąt ten =90. istnieją dwie wart. Azym. A_g czyli A_g1 i A_g2, azymuty te określają położenie K1 i K2 =90, na oryginale i obrazie.

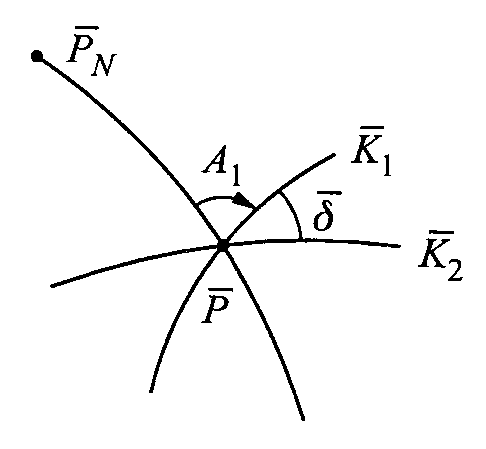
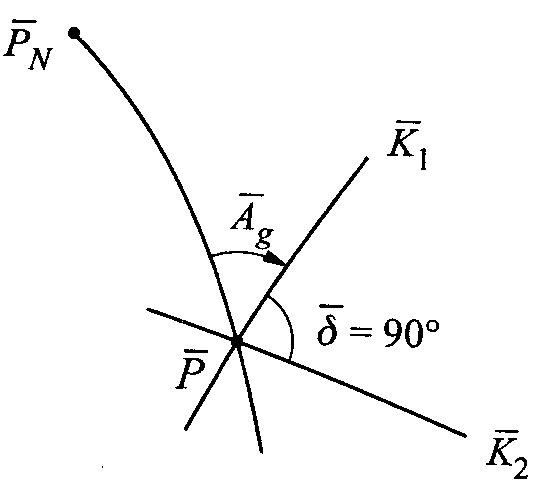
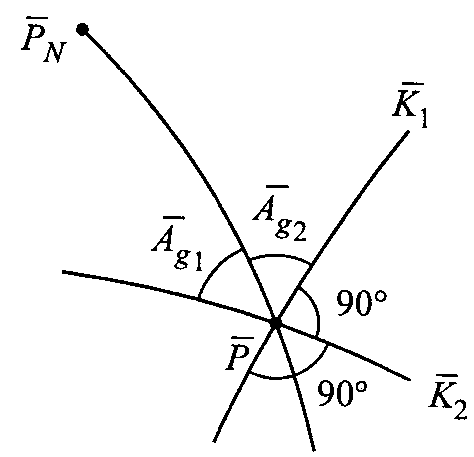
I tw. Tissota W każdym odwzorow. regularnym, nie będącym odwzorow. równokątnym, istnieje na oryginale dokładnie jedna siatka ortogonalnych linii parametrycznych, której obrazem jest także siatka ortogonalna. Kierunki tej siatki nazywamy kierunkami głównymi. Nie są one określone gdy odwzorowanie jest równokątne. Gdy obrazy południków i równoleż. przecinają się pod kątem prostym (θ=90^o) wówczas kierunki główne pokrywają się z nimi. Wzory na azymuty w kierunkach głównych oryginału i obrazu tg2A_g=(2m_Bm_Lcosθ)/(m_B²-m_L²); Po przekształceniach tg2A_g=(m_L²sin2θ)/(m_B²+m_L²cos2θ)

Skala długości w kierunkach głównych.

Kwadrat skali długości można wyrazić wzorem:m²=ds²/ds²=(EdB²+2F dBdL+GdL²)/(M²dB²+r²dL²) , dzielimy licznik i mianownik przez dL² mamy: m²=E(dB/dL)²+2F(dB/dL)+G/M²(dB/dL)²+r² (#). Stosunek dB/dL zależny od azymutu A elementu ds obl.: dB/dL=r/M ctgA ,podstawiając to do wz.(#) mamy:

m²=[E*r²/M²ctg²A+2F*r/MctgA+G]/[r²ctg²A+r²] , ponieważ r²ctg²A+r²=r²(ctg²A+1)=r²/sin²A ostatecznie otrzymujemy :m²=E/M²cos²A+F/Mr sin2A+G/r²sin²A ,z wz.wynika że skala dł. m zależy od E,F,G i azym. A . Skala dł. w kierunku południków: m_B=√E /M E=(δx/δB)²+(δy/δB)², Skala dł. w kier. równoleżników: m_L=√G /r G=(δx/δL)²+(δy/δL)². Z powyższych wzorów otrzymujemy m²= m_B²cos²A+m_Bm_Lcosθsin2A+m_L²sin²A Skala długości jest funkcją okresową azymutu o okresie 180^o. W pełnym zakresie azymutów, od A=0^o do A=360^o, skala m będzie osiągała 2 razy tę samą wartość max i 2 razy tę samą wartość min

Ekstremalne skale długości występują w kierunkach głównych tg2A_e=(m_Bm_Lsinθ)/(m_B²-m_L²) e -ekstremalne wartości skali W odwz. równokątnych kierunki gł. nie są określone dlatego skala dł.w danym pkt. nie zależy od kierunku

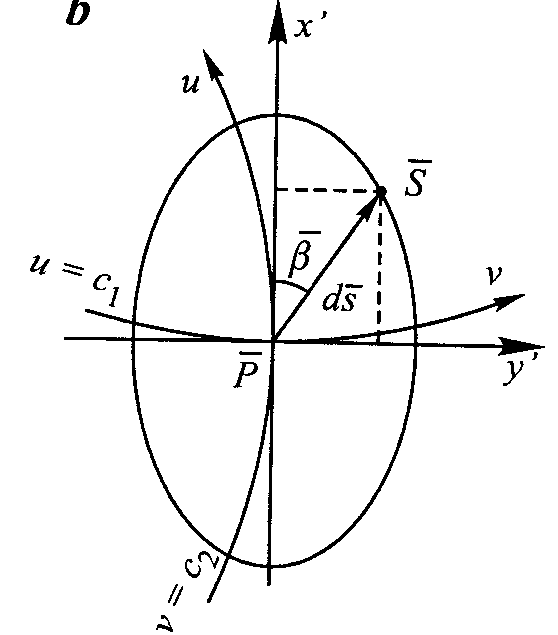
Elipsa zniekształceń RYS 28,29

pamiętaj o jednostce do II Tissota

(wskaźnica Tissota) II tw Tissota „Obrazem graficznym skal długości we wszystkich kierunkach wyprowadzonych z danego punktu jest elipsa o półosiach równych skalom długości w kierunkach głównych”.

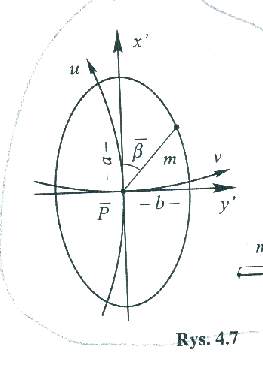
Wskaźnica Tissota ma postać (x^'2/a²)+(y^'2/b²)=1Rys Określenie skali długości jako funkcji kąta B opisuje wzór m²=a²cos²B+b²sin²B Do równania elipsy podstawiamy wartości współ. x'=ds*cosB i y'=ds*sinB Uwzględniając ds/ds=m to otrzymujemy 1/m²=(cos²B/a²)+(sin²B/b²) Skale a,b otrzymujemy z zależności

a+b=√(m_B²+2m_Bm_L sinθ +m_L²);

a-b=√(m_B²-2m_Bm_Lsinθ+m_L²)

Zniekształcenie kątowe jest to największa różnica, co do wartości bezwzględnej, między kątem na obrazie a odpowiadającym mu kątem na oryginale ω=max|α-α| Zniekształcenie kątowe ma postać sin(ω/2)=(a-b)/(a+b). RYS 30

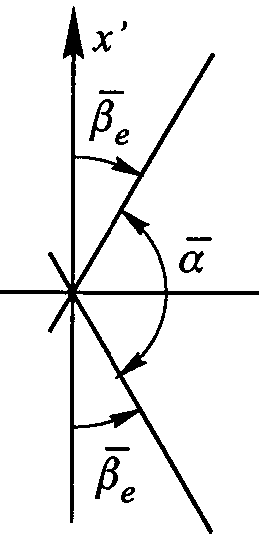
Wsp. izometryczne Zakładamy, że pow. opisana jest równaniami X=X(u,v); Y=Y(u,v); Z=Z(u,v) Długość elementarnego łuku ds na tej powierzchni można wyrazić wzorem(*)ds²=Edu²+2Fdudv+Gdv² Współ. krzywoliniowe u,v są współ. izometrycznymi jeżeli długość elementarnego łuku ds na danej powierzchni można wyrazić wzorem (**) ds²=μ(du²+dv²), gdzie μ jest dowolną, dodatnią funkcją u,v Gdy porównamy wzory (*)i(**) to stwierdzimy, że jeżeli współ. u,v są współ. izometrycznymi, to zachodzą zależności F=0; E=G=μ² Współ. krzywoliniowe u,v są współ. izometrycznymi jeżeli spełniają 2 warunki: 1.Siatka współ. u,v jest siatką ortogonalną 2.Przesunięcie ds wywołane zmianą współ. u o du=ε, jest równe przesunięciu ds wywołanemu zmianą współ. v o dv=ε, gdzie ε jest nieskończenie małą dowolnie obraną liczbą.

Badanie izometryczności współ. B,L Siatka południków i równoleżników jest ortogonalna (spełniony warunek 1). Wzór na dł. elementarnego łuku na elipsoidzie ma postać (@)ds²=M²dB²+N²cos²BdL² Dla dB=ε i dL=0 otrzymamy ds²=M²ε², zaś dla dB=0 i dL=ε ds²=N²cos²Bε² (nie spełniony war 2), więc współ. elipsoidalne B,L nie są współ. izometrycznymi. Przekształcając wzór (@) i podstawiając w miejsce współ. B nową współ. q taka, że dq= MdB/(NcosB) to otrzymamy ds²=N²cos²B(dq²+dL²) Porównując ten wzór ze wzorem (**) stwierdzamy, że współ. q,L są współ. izometrycznymi Współrzędna q : q= ₀∫^B M/NcosB*dB , drugą wsp. L-dług. elipsoidalna-wygodniej zastąpić różnicą dł. elipsoidalnych l, liczoną od wybranego południk L₀: l=L-L₀

Warunki równokątności odwzorowania w przypadku stosowania współ. izometrycznych Warunki równokątności odwzorowania elipsoidy obrotowej na płaszcz.: ∂x/∂L=-r∂y/M∂B; ∂y/∂L=+r∂x/M∂B Przy wyprowadzeniu funkcji odwzrowawczych odwz. równokątnych możemy posłużyć się sposobem: zastąpić współ. geodezyjne B,L współ. izometrycznymi q,l to otrzymamy ∂x/∂l=-r∂ydq/M∂qdB;

∂y/∂l=+r∂xdq/M∂qdB. Uwzględniając r=NcosB oraz dq/dB=M/(NcosB) to otrzymamy warunki równokątności wyraż. zastosowaniem współ. izometrycznych q,l ∂x/∂l=-∂y/∂q; ∂y/∂l=+∂x/∂q (war. Cauchy'ego - Riemanna).Przy wyprowadzeniu f-cji odwzorowawczych odwz. równokątnych możemy:-zastąpić wsp. geodezyjne B,L wsp. izometrycznymi q,l -wykorzystać funkcję analityczną do przedstawienia związku między współ. prostokątnymi płaskimi x,y i współ. q,l

KLASYFIKACJA ODWZ. KARTOGRAFICZNYCH:

1.Ze względu na charakter występujących zniekształceń odwzorow: równokątne, równopolowe, równoodległościowe w jednym z kierunków głównych, dowolne. 2.Ze wzgl. Na kształt siatki kartograficznej: azymutalne, walcowe, stożkowe. 3. Ze wzgl. na sposób przyłożenia pow.rzutowania: normalne, ukośne, poprzeczne.

Klasyfikacja odwzor. ze względu na kształt siatki kartogr. czyli kształt obrazu siatki geograficznej:Rys

1.Odwz.azymutalne.

Obrazami południków są półproste zbiegające się w obrazie bieguna ziemskiego. Kąty między obrazami południków nie ulegają zniekształceniu i są równe różnicom długości geograficznych południków.

RYS 31

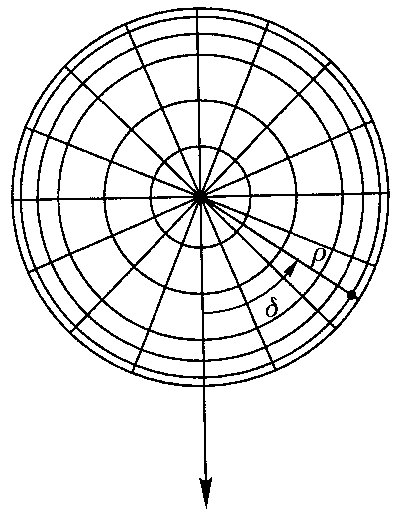
λ=0⁰ P(δ,ρ)

Obrazem równoleż. są okręgi współśrodkowe, których środek jest na obrazie bieguna. Równania ogólne odwz. azymutalnych mają postać w ukł. wsp. biegunowych: ρ = ρ(φ),

δ = λ.

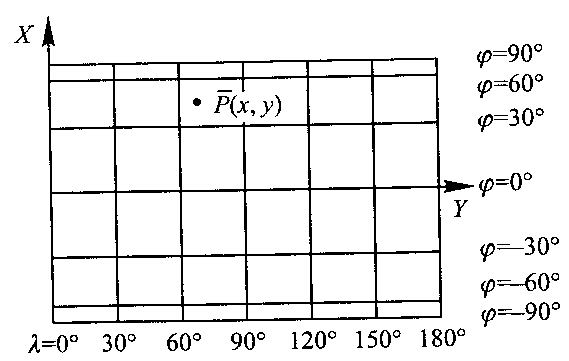
2.Odwz.walcowe.

Obrazami południków są proste lub odcinki równoległe względem siebie i prostopadłe do prostoliniowego obrazu równika. Odległość między obrazami dwóch danych południków jest proporcjonalna do różnicy ich długości geograficznych. Obrazami równoleż. są odcinki równoległe do obrazu równika.

RYS 32

Równanie tych odwz. w ukł. wsp. prostokątnych x,y utworzonym przez obrazy południka początkowego i równika:

X = x(φ), Y = Cλ.

3.Odwz. stożkowe.

Obrazami równoleż. są łuki okręgów współśrodkowych, obrazami południków są odcinki lub półproste prostopadłe do obrazów równoleżników. Kąty między obrazami połud. są proporcjonalne do różnicy długości geograficznych południków.

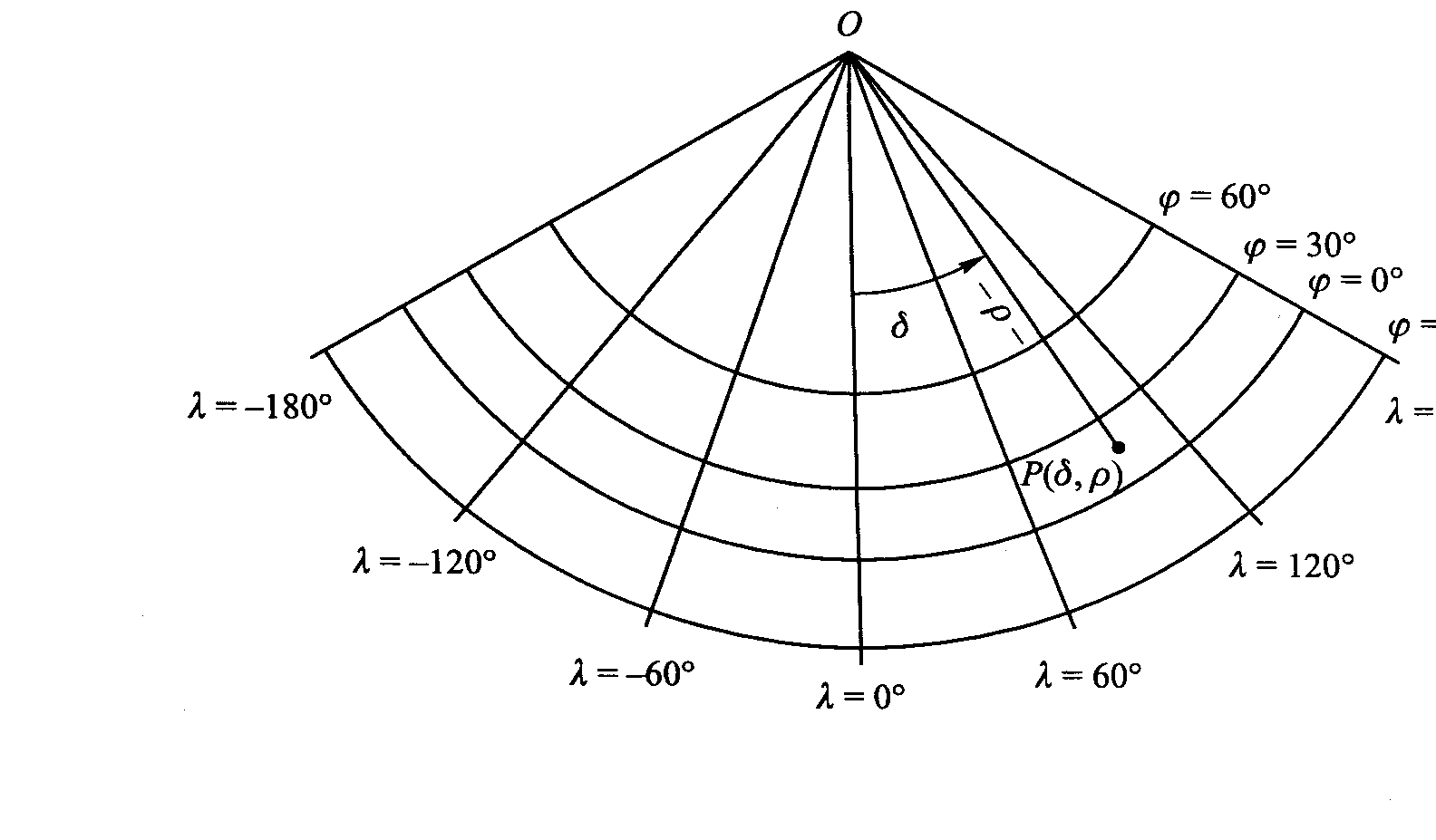
Równanie ogólne: ρ = ρ(φ), δ = Cλ.

ODWZOROWANIE POW.ELIPSOIDY OBROTOWEJ NA POW.KULI

OGÓLNE ZASADY ODWZOROWANIA Niektóre odwz. pow. elipsoidy na pł. można łatwo otrzymać , odwzorowując najpierw pow. elipsoidy na pow .kuli a potem pow. kuli na pł. Przy konstruowaniu map drobnoskalowych przyjmuje się że R=6371km W przypad odwz. niewielkiego fragmentu pow. elipsoidy obrot. na pow. kuli przyjmuje się że pr.kuli=śr.pr. krzywizny w pkt. P₀ leżącym w środku odwzorowawczego obszaru R=*M₀N₀ czyli R=(a*1-e² )/(1-e²sin²B₀) Odwz. pow. elipsoidy na pow. kuli wykonuje się tak aby równoleżniki odwzorowywały się na równoleżniki połud. na południki λ=λ(L) ϕ=ϕ(B) Obrazem elementarnego czworoboku krzywoliniowego na elipsoidzie będzie elementarny czworobok na kuli RYS Kat θ na elipsoidzie i jego obraz na kuli=90⁰ a zatem siatka połud. i równo. jest siatką krzywych gł. a kierunki tej siatki to kierunki gł. Skale dł. m_B i m_L określamy m_B=ds₁/ds₁= Rdϕ/MdB m_L=ds₂/ds₂=Rcosϕ dλ / NcosBdL

Odwzorowanie równokątne pow. elipsoidy na pow. kuli Pierwszy warunek równokątności odwz. o postaci θ=90⁰ jest spełniony dzięki przyjęciu f-cji odwzorowawczych λ=λ(L) ϕ=ϕ(B) drugi warunek ma postać m_B=m_l czyli Rdϕ/MdB =Rcosϕdλ / NcosBdL Szerokość ϕ zależy jedynie od B dlatego dλ/dL musi być wielk. stałą α= dλ/dL Związek między λ i L przyjmuje postać λ=αL+c_λ stawiając warunek aby połud. pocz. na elips. L=0 się połud. pocz. na kuli λ=0 otrzymamy c_λ=0 więc λ=αL wzór na skalę dł. w tym odwz. to m=Rcosϕ / NcosB

Odwzorowanie równopolowe pow. elipsoidy na pow. kuli. Załóżmy ,że promień R kuli obliczono według wzoru R=a√(1-e²)[1+2/3e²+3/5e⁴+4/7e⁶+...] =a[1-1/6e²-17/360e⁴-67/3024e⁶-...]. warunek równopolowości odwz. ma postać m_Bm_L=1 czyli R²/MN*cosφ/cosB*dφ/dB*dλ/dL=1. Aby zapewnić odwzor. całej pow. elipsoidy na pow. kuli, należy przyjąć, że dλ/dL=1.Warunek równopolowości możemy przedstawić w postaci r-nia różniczkowego: R²cosφdφ=MncosBdB , po kolejnych przekształceniach i redukcjach otrzymujemy wzór na skalę dł. w kier. poł. : m_B=1+e²/6cos²B. Skalę m_L otrzymamy jako odwrotność skali m_B m_L=1/m­_B=1-e²/6cos²B. Największe zniekształcenie długości wystąpią na równiku.

ODWZ.AZYMUTALNE KULI PERSPEKTYWICZNE ODWZ. AZYMUTALNE NORMALNE

Powstają one przez rzutowanie pkt. pow. kuli na pł. promienie rzutujące zbiegają się w jednym pkt. zwanym środkiem rzutów. RYS Dla określonego odwzorowania odl. D przybiera konkretną wartość, a promień ρ zależy tylko od szerokości geograficznej φ odwzorowywanych pkt. ρ=ρ(φ)

Umieszczając środek rzutów w środku kuli, otrzymujemy odwz. gnomoniczne, w którym promień ρ obrazu równoleżnika obliczamy: ρ=Rctg φ. Umieszczając śr. rzutów w przeciwległym, biegunie względem pkt. styczności-odwz stereograiczne ρ: ρ=2R cosφ/sinφ+1. Umieszcz. śr. rzut. na osi biegunowej w nieskończoności- odwz. ortograficzne- ρ: ρ=R cosφ RYS

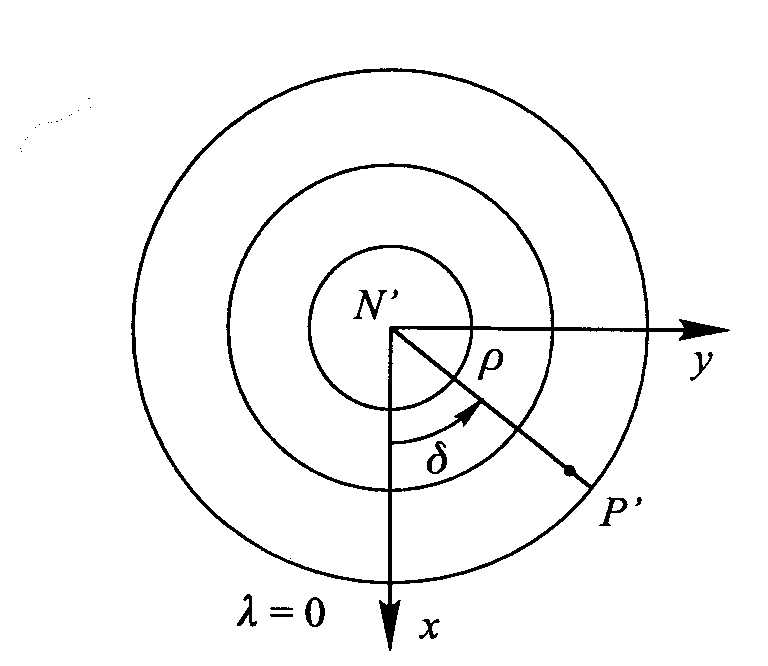
OGOLNA TEORIA ODWZOROWAŃ AZYMUTALNYCH NORMALNYCH KULI W układzie wsp. biegunowych, którego początek to obraz bieguna, a oś podstawowa to obraz południka początkowego , funkcje odwzorowawcze wszystkich odwzorowań azymutalnych normalnych kuli mają następującą postać:

Szerokość geograficzną φ zastępujemy odległością biegunową б, liczoną od bieguna geograficznego: б=90^o-φ . A zatem promień ρ obrazu równoleżnika można wyrazić jako funkcję odległości biegunowej б : ρ=ρ(б) . W określonym przedziale [0, б_max] argumentu б funkcja ρ(б) powinna być ciągła i różniczkowalna. Dla argumentu б=0 funkcja ρ(б) powinna przyjmować wartość 0. Jakobian funkcji odwzorowawczych , mający postać

powinien być różny od zera, a więc pochodna dρ/dб nie może przyjmować wartości 0. W odwzorowaniach użytkowych funkcja ρ(б) jest rosnąca, dlatego dρ/dб >0 . Początek układu współrzędnych prostokątnych N'xy pokrywa się z obrazem bieguna geograficznego, a oś x pokrywa się z obrazem południka początkowego. Współ. prostokątne x,y pkt. P' wyraża się wzorami : x=ρ(б)cosλ, y=ρ(б)sinλ.

RYS 39

Wielkości E,F,G oblicza się: E=(δx/δσ)²+(δy/δσ)²= (δρ/δσ)²cos²λ+(δρ/δσ)²sin²λ=(δρ/δσ)² F=(δx/δσ)(δx/δλ)+(δy/δσ)(δy/δλ)=(δρ/δσ)cosλ(-ρsinλ)+(δρ/δσ)sinλ (ρcosλ)=0 G=(δx/δλ)²+(δy/δλ)²= (-ρsinλ)²+(ρcosλ)²=ρ²

Wielkość F jest równa 0 dla wszystkich wartości б i λ, co prowadzi do wniosku, że linie parametryczne б,λ, a więc południki i równoleżniki są krzywymi głównymi, a kierunki południków i równoleżników są kierunkami głównymi.

Skale dł. w kierunkach głównych można obliczyć za pomocą wzorów : - w kierunku południków: m_б=(√E)/R, a w kierunku równoleżników: m_λ=(√G)/r

ODWZ. AZYM. NORM. RÓWNOODL EGŁOŚCIOWE KULI odwzorowanie równoodległościowe musi spełniać warunek: m_б=1 czyli 1/R*dρ/dб=1 Rozwiązując to równanie różniczkowe, otrzymujemy kolejno: dρ=R*dб , ρ=Rб+C. .Stała C przyjmuje wartość 0, ponieważ dla б=0 powinno zachodzić ρ(б)=0, ostatecznie ρ=Rб .Skala długości w kierunku równoleżników jest w tym odwzorowaniu określona jest wzorem: m_λ=ρ(б)/Rsinб=Rб/Rsinб=б/sinб Odwzorowanie równoodległościowe z kierunku równoleż musi spełniać warunek: m_λ=1 czyli ρ(б)/Rsinб=1. Rozwiązaniem tego równania jest ρ=Rsinб po uwzględnieniu ,że φ=90^o-б ,stwierdzamy że poszukiwane odwz. jest odwzorowanie ortograficznym. Skalę długości w kierunku południków w tym odwz. określa wzór: m_б=1/R*dρ/dб=cosб

ODWZ. AZYM. NORM. RÓWNOKĄTNE KULI Wyprowadzając funkcję odwzorowawczą ρ=ρ(б) odwz. równokątnego, korzystamy z warunków równokątności : pierwszy, mający postać θ=90^o,jest spełniony , ponieważ w odwzorow. azymutal. normalmych obrazy połud. i równoleżników przecinają się pod kątem prostym ; drugi , mający postać m_б=m_λ prowadzi do takiego równ. różniczkowego: 1/R*dρ/dб=ρ/Rsinб . Rozwiązanie tego równania wymaga rozdzielenia zmiennych dρ/ρ=dб/sinб oraz całkowania lewej i prawej strony ln ρ=ln tg б/2+ln C .Ostatecznie ρ=C tg б/2 .Wzór ten przedstawia rodzinę odwz. równokątnych, różniących się wartością stałej C. Korzystając ze wzorów na skalę dł. otrzymujemy wzór na skalę długości: m=C/2Rcos² б/2 .Skala dł przyjmuje dla bieguna (б=0) wartość C/2R .Stawiając warunek m(0)=1 otrzymujemy: C=2R .Po uwzględnieniu wartości stałej C w odpowiednich wzorach mamy: ρ=2R tg б/2 , m=1/cos² б/2 .Porównując wzory m=1/cos² б/2 i ρ=2R cosφ/sinφ+1 i uwzględniając, że φ=90^o-б, możemy stwierdzić, że odwz. stereograficzne jest odwz. równokątnym.

ODWZ. AZYMUT. NORM. RÓWNOPOLOWE KULI Odwzorowanie równopolowe musi spełniać warunek: m_бm_λ=1 czyli 1/R*dρ/dб*ρ/Rsinб=1. Rozwiązanie ego równania sprowadza si do uporządkowania zmiennych: ρ dρ=R²sinб dб i całkowania jego lewej i prawej strony: ρ²/2=-R² cosб+C , ρ²=-2R² cosб+2C .Stałą C należy dobrać tak, aby dla б=0 otrzymać ρ=0. A zatem C=R². Wobec tego ρ²=-2R² cosб+2R²(1-cosб)=4R²sin²б/2 i ostatecznie ρ=2Rsin б/2 .Skale długością są określone wz: m_ρ=cos б/2 , m_λ=1/cos б/2 ODWZ.AZYMUTALNE UKOŚNE I POPRZECZNE We wszystkich rozważanych odwz. azymutal. Normalnych skala dł.=1w biegunie geograficznym jest to pkt.styczności pł.i kuli (pkt. gł. odwz. azym) W miarę oddalania się od pkt. styczności skale dł. coraz bardziej odbiegają od 1.Odwz. azymut. Poprzeczne i normalne kuli można traktować jako szczególne przypadki odwz. ukośnych. Zastępujemy tu dł.geograficz. λ azymutem α oraz odl.biegunową σ odl. zenitalną ζ RYS Wsp. azymutalne α, ζ obl. cosζ=sin

ϕ₀sinϕ+cosϕ₀cosϕcos(λ-λ₀) sinα=[sin(λ-λ₀)cosϕ]/sinζ. Wsp prostokątne obl x=ρcosα y=ρsinα Krzywymi gł.w odwz. azymutalnych ukośnych i poprzeczn. Są koła wielkie przechodzące przez pkt. gł. odwz. zwane wertykałami oraz koła małe prostopadłe do wertykałów zwane almukantarami. Po zastąpieniu wsp.λ,σ przez wsp.α,ζ wprowadzono następ. wz.ρ=2Rsin(ζ/2) m_ζ=cos(ζ/2)-skala dł.w kierunku wertykałów m_α=1/cosζ/2-skala dł.w kier. almukantarów

ODWZ. WALCOWE KULI

OGÓLNA TEOTIA ODWZ. WALCOWYCH NORMALNYCH KULI Odwz. walcowe normalne kuli powstają przez rzutowanie punktów pow. kuli na pow. boczną walca, którego oś pokrywa się z osią obrotu Ziemi. Śr. rzutów zawsze znajduje się na osi walca, ale jego położenie na osi walca zależy od zastosowanych funkcji odwzorowawczych i od szer. geogr. rzutowanego pkt. Skale dług. w kierunku połud. i równoleż. są wyrażone wzorami: m_φ=(E)^1/2/R=1/R*dx/dφ m_λ=(G)^1/2/Rcosφ=1/cosφ .

ODWZ. WALC. NORMALNE RÓWNOODLEGŁOŚCIOWE KULI Podstawiając warunek m_φ=1 otrzymamy odwz. równoodległościowe w kier. połud. Gdy uwzględnimy : m_φ=(E)^1/2/R=1/R*dx/dφ ,wówczas otrzymamy równanie różniczkowe: 1/R*dx/dφ=1 ,które należy rozwiązać następująco: dx=Rdφ ; x=Rφ=C_x . Jeżeli przyjmiemy, że obraz równika ma leżeć na osi y to stała C_x przyjmie wartość 0. Ostatecznie funkcje odwzorowawcze przyjmują następującą postać: x=Rφ , y=Rλ .W tym odwz. siatka kartogr. na postać siatki kwadr. Skala pól: p=1/cosφ ; zniekształcenie kątowe: sin_ω/2=m_λ-1/m_λ+1=1-cosφ/1+cosφ=tg² φ/2 Odwz. walcowe normalne równoodległ. kuli w kierunku równoleżników nie istnieje, ponieważ m_λ=1 tylko na równiku .RYS

ODWZ. WALC. NORMALNE RÓWNOKĄTNE KULI Obrazy połud. przecinają się z obrazami równoleż. pod kątem prostym we wszystkich odwz. walcowych normalnych, spełniony jest pierwszy warunek równokątności. Drugi staje się, po uwzględnieniu m_φ=(E)^1/2/R=1/R*dx/dφ m_λ=(G)^1/2/Rcosφ=1/cosφ równ. różniczkowym: 1/R*dx/dφ=1/cosφ .Rozwiązanie tego równania wymaga uporządkow zmiennych: dx=R*dφ/cosφ i scałkowania obu stron: x=R ln tg(π/4+φ/2)+C_x .Aby obraz równika (φ=0) leżał na osi y (x=0), to stała C_x musi przyjąć wartość 0.Ostatecznie x=R ln tg(π/4+φ/2) , y=Rλ .Takie funkcje nazywamy funkcjami odwzorowawczymi odwzorow. Merkatora. Odwz. to jest szeroko stosowane w nawigacji, bo odcinek linii prostej łączącej dwa pkt. na mapie tworzy z obrazami połudn. stały kąt równy azymutowi trasy. Odcinek ten to obraz linii krzywej na oryginale tzw. loksodromą. Loksodroma nie jest najkrótszą linią łączącą dwa wybrane pkt. ale azymut w każdym jej pkt. jest stały. Ortodroma-wycinek łuku koła wielkiego nie ma tej ważnej cechy. Skala dłg. w odwz. Merkatora: m=1/cosφRYS

ODWZ.WALC. NORMALNE RÓWNOPOLOWE KULI. Warunek równopolowości odwz. ma postać: mφmλ=1, postać równania różniczkowego: 1/R*dx/dφ*1/cosφ=1.Rozwiązanie dx=Rcosφdφ, x=Rsinφ+C_x. Ostatecznie funkcje odwz. mają postać: x=Rsinφ, y=Rλ. Skala dłg. m_φ=1/R*dx/dφ=cosφ. Zniekształcenie kątowe: sinω/2=sin²φ/1+cos²φ.

ODWZ.WALC. UKOŚNE. Funkcje odwz. walcowego ukośnego równokątnego x=Rlntg(π/4+π/4-ζ/2), y=Rln tg(π/4+π/4-ζ/2), y=Rά. Skala dłg. m=1/cos(90^o-ζ)=1/sinζ. Odwz. walcowe ukośne równokątne stosowane są podczas tworzenia map tras lotniczych.

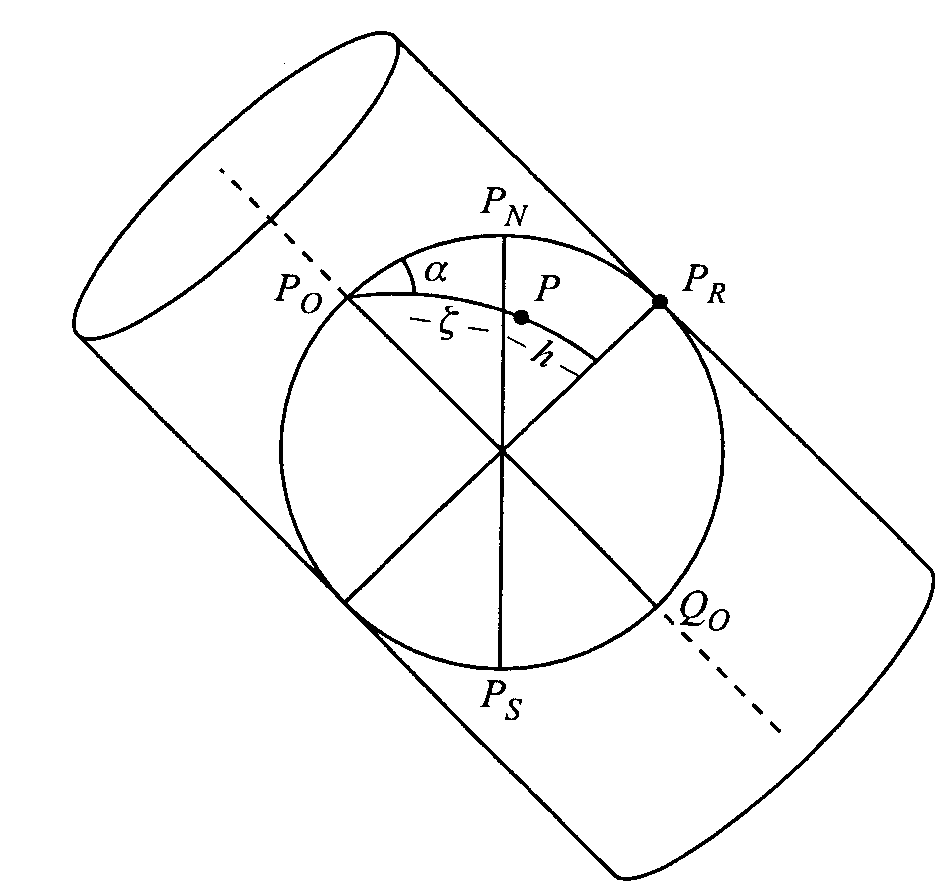
ODWZ.WALC.POPRZECZNE traktuje się jako przypadki szczególne odwz. walcowych ukośnych. Obrazami połud. są odcinki lub proste prostopadłe do osi x,a obrazami równoleżn. odcinki równoległe do osi x. Skala dłg. w kierunku połud.: m₁=1/R*dy/dh, w kierunku równoleż.: m₂=1/cosh, gdzie: g,h- wsp. prostokątne sferyczne.

Odwz. walcowe poprzeczne równoodległościowe kuli jedynie w kierunku równoleż. (m₁=1). Funkcje odwzorowaw: x=Rg, y=Rh.Te odwz. zwane odwz. Cassiniego, a wsp. x,y zwane wsp. prostokątnymi sferycznymi Soldnera. Skala dłg. w kierunku południków: m₂ =sech=secy/R=1+1/2(y/R)²+5/24(y/R)⁴+..

ODWZOROWANIE GAUSSA-KRUGERA jest odwz. równokątnym pow.i elipsoidy obrotowej na pł. Odwz to jest odwzor. walcowym poprz. równokąt. pow. elips. obrotowej. Charakteryzuje się występow. niewielkich zniekształceń w wybranym, wąskim pasie połud. Powierzchnie elipsoidy obrotowej należy podzielić na wąskie pasy połud. i każdy z nich odwzorować oddzielnie na płaszcz. Szerokość pasa połud. (ΔL) zależy od przyjętych dopuszczalnych zniekształceń dług. lub zniekształceń pól. Odwz G-K spełnia 3 warunki: jest odwz. równokątnym, obrazem połud. Śr. danego pasa jest odcinek linii prostej, a obrazami pozostałych połud. są linie krzywe symetrycznie rozłożone względem obrazu połud. śr., połud. śr. pasa odwzorowuje się bez zniekształceń (m₀= 1).

Funkcje odwzorowawcze w postaci funkcji B, l. Wprowadźmy układ wsp prostokątnych x, y w następujący sposób: oś odciętych x pokrywa się z obrazem połud. Śr. L₀ i jest skierowana na północ, oś rzędnych y pokrywa się z prostoliniowym obrazem równika i jest skierowana na wschód. RYS 40

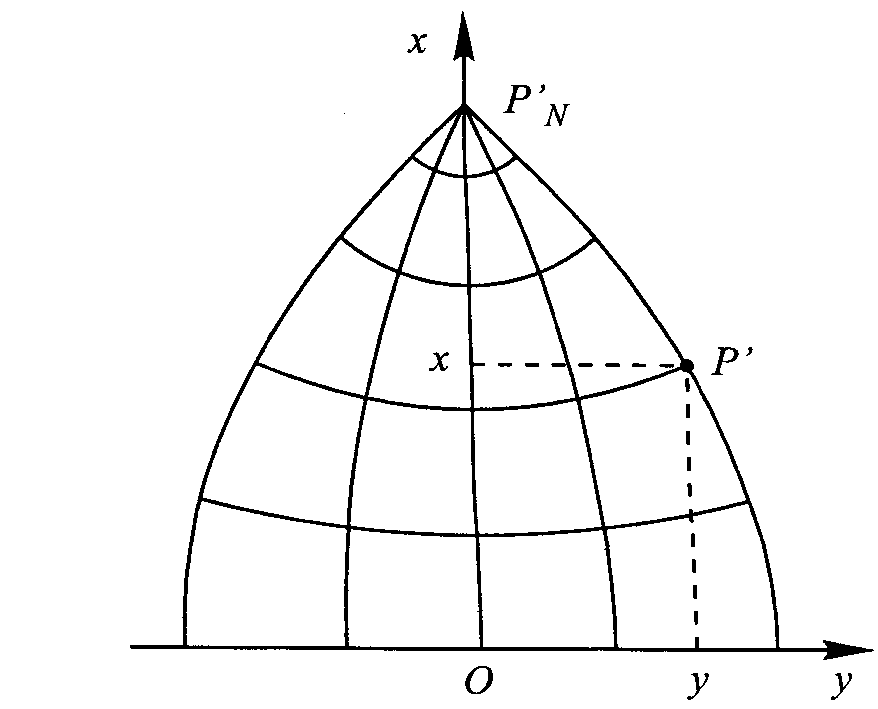
Skoro połud. L₀ ma tak duże znaczenie będziemy się posługiwać różnicą długości geodezyjnych l= L-L₀. funkcje odwzorowawcze można zapisać następująco: x=F₁(B,l), y=F₂(B,l); Podczas wyprowadzania funkcji odwzorowaw. będziemy się posługiwać wsp. izometrycznymi q, l.

Zbieżność południków w odwzorowaniu Gaussa-Krugera.

Zbieżnością południków w odwzorowaniu nazywamy kąt zawarty między styczną do obrazu południka w danym punkcie a linią prostą przechodzącą przez ten punkt

równolegle do osi x.

Rys.

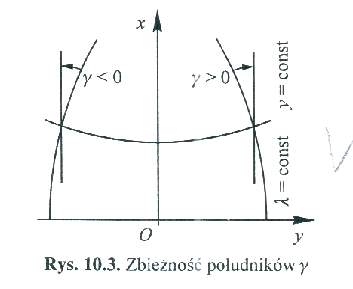
Zbieżnością południków γ mierzona jest od stycznej do obrazu południka w kierunku zgodnym z ruchem wskazówek zegara. We wszystkich punktach odwzorowania G-K, leżących na północ od obrazu równika i na wschód od obrazu południka jest dodatnia. Obierzmy na obrazie punkt P' o współrzędnych B,L oraz punkt P₁' o współrzędnych B,L+dL, przy założeniu, że dL jest wielkością nieskończenie małą. Punkty P' i P₁' leżą zatem na obrazie równoleżnika o szerokości elipsoidalnej B.

(rys.10.4).

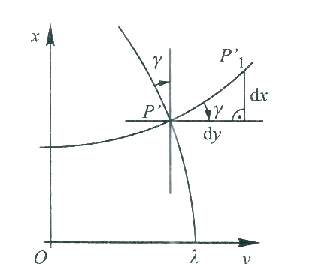
Przyrosty współrzędnych prostokątnych dx=(δx/δl)*dl i dy=(δy/dl)*dl. Różniczki te wykorzystujemy do obliczania zbieżności południków, gdyż tgγ=dx/dy=[δx/dl*dl]:[δy/δl*dl] po podzieleniu licznika i mianownika przez dl otrzymamy prosty wzór: tgγ=δx/δl:δy/δl. Kąt γ nie przekracza 3⁰ w wąskich pasach południków, możemy go więc wyrazić bez stosowania funkcji tangens. Po przekształceniach otrzymujemy wzór na zbieżność południków w odwzorowaniu G-K w radianach: γ=lsinB+l³/3sinBcos²B(1+3η²)+1⁵/15sinBcos⁴B(2-t²) i wzór w sekundach γ”=l”sinB{1+1/3[l”/ρ”]²cos²B(1+3η²)+1/15[l”/ρ”]⁴cos^4-B(2-t²)}

Elementarna skala dł. i pól. W odwzorowaniach równokątnych elementarną skalę dł. można obliczać w dowolnym kierunku. W kierunku równoleżników wg. wzoru:

m=m_λ=√G /r=√(δx/δl)²+(δy/δl)² /NcosB . Elementarna skala pól jest równa kwadratowi elementarnej sk. dł.: p=m²= [(δx/δl)²+(δy/δl)² ] / [N ²cos ²B]

Wybierając odwzorowanie G-K jako podstawę geodezyjnego układu wsp. płaskich x,y, można zmodyfikować trzeci warunek odwz, wprowadzając skalę długości m₀ na połud. środ. mniejszą od 1. Skala dł. m₀ powinna być odwrotnością średniej skali m_sr występującej na odwz. obszarze (w odwz. nie modyfikowanym) m₀=1/m_sr W przypadku odwz. G-K, w którym min. wartośc skali dł. = 1, a max. wartośc skali dł. m_max występuje na skraju pasa połud, m₀= 2/(1+m_max). Skala m₀ zależy więc od m_max, zatem od przyjętej szerokości pasa połud. Skala dł. m₀ jest zwykle zaokraglana do 4 lub 5-ciu miejsc po przecinku. Wykorzyst. w wielu krajach odwz. UTM jest odwz. G-K o szer. pasa 6⁰ i m₀=0,9996 na połud. śr; X=m₀*x; Y=m₀*y + c* n; gdzie n- nr pasa, c-stała dodawania

ODWZOROWANIE QUASI-STEREOGRAFICZNE odwzorowanie quasi-stereo jest odwz. równokątnym elipsoidy obrotowej. Siatka kartograf w tym odwz. jest podobna do siatki w odwzorowaniu stereograf. kuli. Odwzor q-s charakteryzuje się występow. niewielkich zniekształceń w pobliżu punktu głównego, który odpowiada punktowi styczności płaszczyzny i kuli w odwz stereograf. Odwz q-s jest zatem szczególnie przydatne do przedstawiania obszarów, które granice mają kształt regularny, zbliżony do okręgu. Punkt główny P₀ (B₀ , L₀) odwz powinien się znajdować w pobliżu punktu środkowego odwz-go obszaru. Południk przech. przez punkt główny będziemy nazywać połud środkowym, który odwzorowuje się jako odcinek linii prostej. Wprowadźmy układ współrzędnych płaskich x, y w następujący sposób: początek ukł. znajduje się w obrazie p-ktu głów, oś x pokrywa się z obrazem połud środ. i jest skierowana do obrazu bieguna półn, oś y jest prostopadła do osi x i wraz z nią tworzy układ prawoskrętny. Odwz q- s musi spełniać następujące warunki: odwz jest równokątne,

RYS41

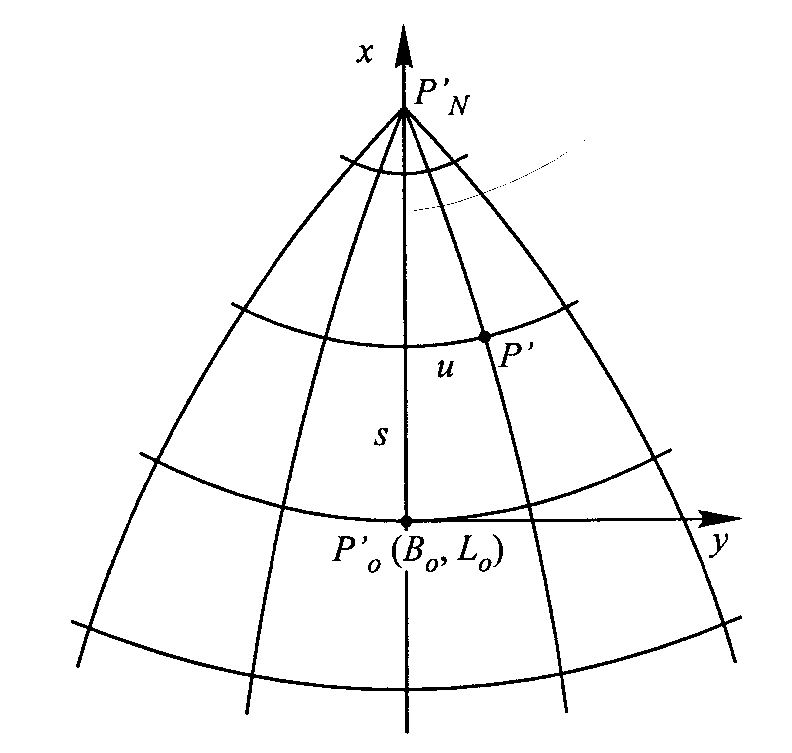
Obrazem połud. środ. jest odcinek linii prostej, a obrazami innych połud są krzywe symetryczne względem połud środk, odcięte x p-tów leżących na połud środk oblicza się wg wzoru: x_m= 2R₀ tg (s/2R₀ ), gdzie R₀ oznacza średni promień krzywizny pow elipsoidy obrotowej w punkcie gł. odwz., s oznacza długość łuku połud. od punktu gł. P₀ do równoleżnika odwz-ego punktu P.

Funkcje odwzorowawcze jako funkcje wielkości B₀, b, l. Odwz będzie równokątne, jeżeli zależność między wsp. prostokątnymi płaskimi x, y i izometrycznymi q, l będą funkcją analityczną: x+ iy= f (q+ il). Początek ukł współ płaskich znajduje się w p-kcie gł. odwz P₀ (B₀, L₀), dlatego dla q=q₀ (B₀) współ. x musi być równa 0. Zależność możemy zastąpić wzorem: x+ iy =f (Δq+ il), w której Δq =q-q₀.

Kolejne funkcje odwzorowawcze : -jako f. wielkości B₀,u,s ; -f. odwzor. odwzorowania odwrotnego

x=(a₀₀+a₀₁b+a₀₂b²+a₀₃b³+…)+

+(a₂₀+a₂₁b+a₂₂b²+...)l²+(a₄₀+ a₄₁b+…)l⁴;

y=(a₁₀+a₁₁b+a₁₂b²+a₁₃b³+… )l+

+(a₃₀+a₃₁b+a₃₂b²+…)l³+(a₅₀+a₅₁b+a₅₂b²+…)l⁵

Współczynnik a_ij można obliczyć jednorazowo dla danego odwz po ustaleniu wsp. B₀ pkt. gł. odwzor. Podane szeregi potęgowe ograniczają się najwyżej do 5-tej potęgi argumentów b i l. Zapewniają dokł. obliczenia wsp. x i y równą 1cm, w przypadku pkt. leżących w pobliżu granicy Polski, pod warunkiem, że pkt. gł. Odwz. będzie umieszczony w pobliżu środka geometrycznego Polski.

Funkcje odwzorowawcze B₀, u, s:

Każdemu punktowi odwzorowywanego obszaru można jednoznacznie przyporządkować parę liczb u i s. (z rys. wyżej), u- jest długością łuku równoleżnika przechodz. przez dany p-kt, obliczoną wg. Wzoru: u=lr=lNcos B, a s to długość łuku połud środk, którą oblicza się: s=f₁b¹+ f₂b² + f₃b³+ f₄b⁴+...; wsp. prostokątne można przedstawić jako f wielkości u i s:x=F₁(u, s), y=F₂(u, s),założenie:F1-parzysta wzgl. u, F2-nieparzysta wzgl. u.

x=(w₀₀+ w₀₁s¹+ w₀₂s²+ w₀₃s³+ w₀₄s⁴+ w₀₅s⁵_+...)+( w₂₀+ w₂₁s¹+ w₂₂s²+ w₂₃s³+...)u²+( w₄₀+ w₄₁s¹+...)u⁴+...; y=(_w10+ w₁₁s¹+ w₁₂s²+ w₁₃s³+ w₁₄s⁴+ w₁₅s⁵_+...)u+( w₃₀+ w₃₁s¹+ w₃₂s²+ w₃₃s³+...)u³+( w₅₀+ w₅₁s¹+...)u⁵+...; wynika z nich, że wsp. prostokątne pkt. leżącego na pd środk będą opisane następującymi równaniami:

x_m= w₀₀+ w₀₁s¹+ w₀₂s²+ w₀₃s³+...; y_m=0; Zgodnie z trzecim war. Odwz. x_m obliczamy: x_m=s+s³/12R²₀+s⁵/120R⁴₀+17s⁷/20160R⁶₀+...Ogólny wzór służący do sekwencyjnego obliczenia wsp.:

(-1)ⁿ⁺¹w_n+1,r=n/n+1[k_rw_n,0+k_r-1w_n,1+...+k₀w_n,r]-r+1/n+1*w_n,r+1.

Odwzorowanie odwrotne:

Równokątne, zatem związek współ. izomet-rycznych Δq i l oraz x i y ma postać funkcji analitycznej F:

Δq +il= F(x +iy); x,y→q,l(u, s)

Zbieżność południków:

Jest kąt zawarty między styczną do obrazu połud w danym p-kcie, a linią prostą przech. przez ten p-kt, równolegle do oX. tgγ=δx/δl:δy/δl, po wielu bardzo, ale to bardzo skomplikowanych przekształceniach γ=sinB₀l+1/2*cosB₀bl-5/4*sinB₀η²₀ b² l +1/12*sinB₀cos²B₀(1+9η²₀)l³+1/24*cosB₀b³l- 1/24*cos³B₀(2t₀²-1)bl³,wielkości b i l powinny być w tym wzorze wyrażone w radianach.

Elementarne skale dł. i pól. W odwz. równokątnych elementarną skalę dł. można obliczać w dowolnym kierunku. Skalę m możemy obliczyć w kierunku równoleżników wg. wzoru : m=√(δx/δl)²+(δy/δl)² /NcosB po przekształ. otrzymujemy wzór uproszczony: m=1+x²+y²/4R²₀-2t₀η²/R³₀*xy², ostatni człon osiąga wart. 0.0000006 dla B₀=52⁰ Oraz x=250km i y=300km, może być zatem pomijany przy wyk. wielu prac geod. zatem taki uproszczony wzór wskazuje, że liniami jednakowych skal dł. są okręgi współśrodkowe, których środek znajduje się w pkt. gł. odwz. Skalę pól p obl. ze wzoru: p=m²=1+ x²+y²/2R²₀ - 4t₀η²₀/R³₀*xy²

---