 | Pobierz cały dokument zadanie.z.wektorow.dla.grup.parzystych.matma.doc Rozmiar 83 KB |
I ROK ARCHITEKTURY GR. 2, 4, 6,8
Zad.1 Wyznaczyć współrzędne końca B wektora 
, jeżeli jego początek znajduje się w punkcie A(-1,5,-3).
Zad.2 Dane są trzy wektory 
, 
, 
. Wyznacz wektor 
.
Zad.3 Oblicz długość przekątnych równoległoboku zbudowanego na wektorach:
a) 
; 
, gdzie 
; 
oraz tworzą kąt 
.
b) 
; 
.
Zad.4 Obliczyć kąt między wektorami 
i 
, jeżeli wiadomo, że wektory 
,
są wzajemnie prostopadłe i 
.
Zad.5 Dla jakiej wartości parametru 
wektory 
i 
są wzajemnie prostopadłe.
Zad.6 Obliczyć pole trójkąta o wierzchołkach w punktach A(3,4,-3); B(6,2,3); C(0,-1,5).
Zad.7 Dane są wierzchołki trójkąta A(-3,1,-1); B(6,-2,-5); C(1,-2,-1).Obliczyć długość wysokości opuszczonej z wierzchołka B na bok AC.
Zad.8 Obliczyć pole równoległoboku zbudowanego na wektorach 
i 
wiedząc, że pole równoległoboku zbudowanego na wektorach 
i 
jest równe 12.
Zad.9 Oblicz sinus kąta zawartego między wektorami 
i 
.
Zad.10 Dany jest czworościan o wierzchołkach w punktach A(3,1,1); B(1,4,1); C(1,1,7) i D(3,4,9). Obliczyć jego objętość oraz wysokość poprowadzoną z wierzchołka D.
Zad.11 Dane są dwa punkty A(1,-5,4) i B(-4,3,7). Znaleźć równanie płaszczyzny przechodzącej przez punkt A i prostopadłej do wektora 
.
Zad.12 Znaleźć równanie płaszczyzny przechodzącej przez punkt A(-2,1,4) i równoległej do dwóch wektorów 
i 
.
Zad.13 Znaleźć równanie płaszczyzny przechodzącej przez punkty A(2,-1,3), B(3,1,2) i równoległej do wektora 
.
Zad.14 Znaleźć równanie płaszczyzny przechodzącej przez punkty M(2,-1,4), N(1,-1,5) i prostopadłej do płaszczyzny x-2y+z-1=0.
Zad.15 Znaleźć równanie prostej przechodzącej przez dwa punkty:
a) A(2,3,1), B(4,6,9).
b) A(1,5,1), B(1,-5,1).
Zad.16 Znaleźć równania parametryczne prostej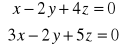 
.
Zad.17 Znaleźć równanie płaszczyzny przechodzącej przez punkt A(2,-1,1) i prostopadłej do prostej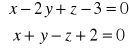 
.
Zad.18 Znaleźć punkt przebicia płaszczyzny 2x+3y+z-1=0 prostą 
.
Zad.19 Znaleźć rzut punktu A(1,-2,1) na prostą 
.
Zad.20 Znaleźć rzut punktu A(2,3,-6) na płaszczyznę x+2y+z+4=0.
Zad.21 Znaleźć punkt B symetryczny do punktu A(5,2,-1) względem płaszczyzny 2x-y+3z+23=0.
Zad.22 Znaleźć rzut prostej 
na płaszczyznę 2x-2y+3z-5=0.
 | Pobierz cały dokument zadanie.z.wektorow.dla.grup.parzystych.matma.doc rozmiar 83 KB |