Wykład11 całki: f: x→R F-funkcja pierwotna funkcji

(F(x)+C)'=F=(x)=f(x)

Na odwrót, jeżeli F₁,F₂ są funkcjami pierwotnymi funkcji f, to (F₁(x)-F₂(x))'-F₁'(x)-F₂'(X)=f(x)-f(x)=0, czyli na podstawie twierdzenia Legrange'a o wartości średniej F₁(x)-F₂(x)=Funkcja,

gdzie C jest odpowiednio dobraną stałą.

Zatem wyrażenie

, C-dowolna ustalona stała, jest ogólną postacią funkcji pierwotnej funkcji f.

Def. Rodzinie wszystkich funkcji pierwotnych funkcji f nazywamy całkę nieoznaczoną z f zapisujemy przy pomocy symbolu
,

Twierdzenie1. Jeżeli funkcja f posiada funkcję pierwotną na przedziale(a,b) to dla każdego(x₀y₀)єR², gdzie x₀є(a,b), istnieje dokładnie jedna funkcja pierwotna F taka, że F(x₀)=y₀.

Twierdzenie2. Jeżeli funkcja f jest ciągła na przedziale<a,b>(lub na (a,b)), to f posiada na ty przedziale funkcję pierwotną.

Twierdzenie3. Jeżeli funkcje f,g są całkowalne na xєX, to dla xєX:

gdzie α,stałe. (*)

Dowód. Ponieważ dla xєX.

=α*f(x)+β g(x),

więc dla xєX:

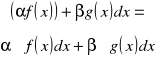
Uwaga! Wzór z tezy Tw.3 należy rozumieć następująco: Dla dowolnie ustalonych stałych Cf i Cg, odpowiadające całce
tak, by zachodziła równość(*)

Podstawowe metody całkowania:

a) całkowanie przez podstawianie:

Twierdzenie4. Jeżeli a) funkcja f jest ciągła na (a,b),

b) funkcja φ ma ciągłą pochodną

φ' na przedziale(α,β),

a<φ(t)<b dla tє (α,β),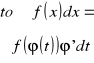

gdziex=φ(t)dlaα<t<β.

Dowód. Niech:

dlaxє(a,b),

a więc F'(x)=f(x) dla xє(a,b), Funkcja złożona F(φ) jest określona dla fє(α,β). Z twierdzenia o pochodnej funkcji złożonej otrzymujemy: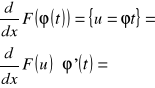

f(u)φ'(t)=f(φ(t))φ'(t)

czyli

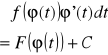
b całkowanie przez części. Twierdzenie5. Jeżeli funkcje u=u(x),v=v(x) posiadają skończone pochodne u', v' ma przedziale(a,b)(lub<a,b>, to dla xє(a,b) (lub xє<a,b>):

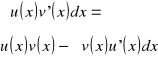
przy założeniu istnienia obu całek.

Dowód Dla xє(a,b)(xє<a,b>) mamy, stosując wzór na pochodną iloczynu(u(x)v(x))'=

u'(x)v(x)+u(x)v'(x),

czyli u(x)v'(x)=

(u(x)v(x))'-u(x)v(x)

Po oustronnym scałkowaniu otrzymujemy:

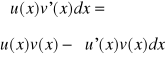
Przykłady:

1)Obliczyć

Rozwiązanie Stosujemy wzór na całkowanie przez części:

u=lnx

du=1/x dx

dv=v²dx=dx

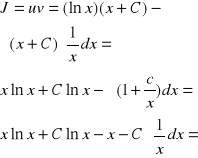
=xlnx+Clnx-x-

Clnx+Co,

gdzie C,Co-dowolne stałe. Zatem

J=x(lnx-1)+C

Sprawdzenie:

[x(lnx-1)+Co]'=

[x(lnx-1)]'=

(x)'(lnx-1)+x(lnx-1)

=lnx-1+x(1/x)=

lnx-1+1=lnx

2)Obliczyć

Rozwiązanie:

b) X<0: Podstawiamy x=-t.

Wtedy t>0,x=-t/( )'

różniczkujemy dwukrotnie

1dx=t1dt, dx=-dt

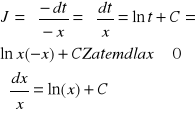
3)Obliczyć:

gdzie f-funkcja ciągła wraz z pochodną f'naprzedziale(a,b) oraz f(x)różne od 0 dla xє(a,b)

Rozwiązanie: f(x)=t

Po obustronnym zróżniczkowaniu otrzymujemy:

f'(x)dx=1dt Stąd

Całki funkcji elementarnych:

f				uwagi
d -stała		dx + C
X^α,x>0
1/x		ln(x)+C
a^x
f			uwagi
ex	ex+C
lnx	x(lnx-1)+C
sinx	-cosx+C
cosx	sinx+C
tgx=sinx/ cosx	-ln(cosx) +C
ctg=cosx/ sinx	ln(sinx)+C

2.Całkowanie funkcji wymiernych: Jeżeli funkcja pod całkowa jest funkcją wymierną, tzn ma postać f(x)=P(x)/Q(x),

gdzie P,Q-wielomiany algebraiczne, to w przypadku, gdy stopień wielomianu Q jest większy niż stopień wielomianu P, wykonujemy dzielenie wielomianów (dzielimy P przez Q).

Otrzymujemy wielomian W=W(x) oraz resztę postaci R/Q, gdzie stopień Q jest większy niż stopień R.

Funkcję wymierną, dla której stopień licznika jest niższy od stopnia mianownika, nazywamy ułamkiem właściwym

Funkcje wymierne postaci: A/(x-a)^k,

Mx+N/(x²+px+q)ⁿ,

gdzie A,a,M,N,p,q-

stałe rzeczywiste,

k,nєN, p²-nq<a,

nazywamy ułamkiem prostym.

Niech funkcja podcałkowa f będzie ułamkiem właściwym f(x)=R(x)/Q(x)

Jeżeli wielomian Q ma pierwiastki rzeczywiste a₁,…,a_n,

odpowiednio rzędów,r₁,…,r_n, oraz pierwiastki zespolone z,ž₁,…,z_m,ž_m,

odpowiednio rzędu s₁,…s_m, to wielomian Q ma postać Q(x)=

A(x-a₁)^r1:.:(x-a_n)^rn*

(x-z₁)^S1(x- ž₁)^S1:.:

(x-z_m)^Sm(x- ž_m)^Sm

gdzie ž_j jest liczbą sprzężoną do z_j.

Ponieważ:

(x- z_j)(x- ž_j)=

x²-(z_j + ž_j)x+ z_j ž_j =

x²+bjx+cjx

gdzie bj,cjєR,

bj²-4cj<0,

więc

Q(x)=A(x-a₁)^r1:.:

(x-a_n)^rn(x2+bjx+c1)^S1

:.:(x2+bmx+cm)^Sm

Twierdzenie1

Każda funkcja

wymierna R(x)/Q(x)

,gdzie stopień R <stopień Q oraz wielomian Q ma postać(1) rozkłada się jednostronnie na sumę ułamków parzystych

R(x)/Q(x)=

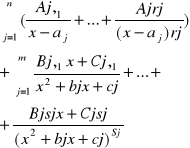
Jest to równość tożsamościowa, czyli dla każdego xєR z wyjątkiem x różnego od Oj, j=1,…,n

---