WSTĘP
Matematyka dyskretna (MD) jest częścią matematyki. Jak wskazuje na to nazwa przedmiotu, jego główną cechą jest dyskretność, tzn. przeciwieństwo ciągłości.
W zadaniach MD mogą być użyte liczby niecałkowite (rzeczywiste, zmiennoprzecinkowe), jednak typ zastosowanych liczb nie odgrywa decydującego znaczenia dla tego przedmiotu. Metody i algorytmy MD często wykorzystywane są w takich dziedzinach jak chemia, ekonomia, badania operacyjne, socjologia, medycyna itp. Wyniki badań uzyskiwane przy pomocy MD wykorzystane są m.in. przy opracowaniu urządzeń technicznych i systemów cyfrowych, projektowaniu algorytmów komputerowych, planowaniu oraz radioelektronice. W MD ważne miejsce zajmują zadania, powiązane z uporządkowaniem niektórych obiektów i budową skomplikowanych konstrukcji na podstawie „prawidłowego” połączenia osobnych elementów. Oto przykłady zadań jakie mogą być rozwiązywane przy użyciu MD:
Na płytce układu scalonego wykonać połączenie elementów bez przecięcia lub
z ich minimalną ilością.Wskazać dla listonosza minimalną drogę.
Dana jest mapa osiedla, na której umieszczono koszt i czas przejazdu każdego odcinka drogi. Wyznaczyć najtańszą trasę dostarczenia towaru od hurtowni do sklepów.
Dana jest tablica możliwości transmisyjnych w sieci telekomunikacyjnej. Wyznaczyć trasę (drogę) szybkiego i w miarę niezawodnego przekazywania informacji, np. E-mail od nadajnika do odbiornika.
Dzisiaj MD jest nie tylko podstawowym elementem cybernetyki matematycznej
i informatyki, ale także ważną częścią wykształcenia matematycznego nowoczesnego inżyniera.
W zasadzie z MD mieliśmy do czynienia już w szkole podstawowej, kiedy używaliśmy algorytm opuszczania nawiasów przy mnożeniu składników w nawiasach, liczb całkowitych do budowy kombinacji, dwumianu Newtona itp. Głównym celem wykładów nie jest rozszerzenie wiedzy szkolnej, lecz poznanie metod i sposobów myślenia, charakterystycznych dla MD. Podczas wykładów, zaznajomimy się również z zastosowaniem pojęcia algorytmu, co jest szczególnie ważne dla specjalistów w dziedzinie programowania oraz matematyki stosowanej.
Treść niniejszych wykładów została przygotowana tak na podstawie opublikowanych materiałów, jak i na osobistym doświadczeniu autora w dziedzinie programowania zadań kombinatorycznych z jednoczesnym wykorzystaniem tablic i grafów. Nie ma wątpliwości, że MD należy do najciekawszych przedmiotów w planach studiów technicznego kształcenia magistrów - informatyków. Można nawet ogólnie zauważyć, że MD jest także nauką o algorytmach rozwiązywania łamigłówek. Na kilku ciekawych przykładach pokażemy, jak można nauczyć komputer sztuki generowania wzorów symbolicznych, szukania najtańszej drogi między dwoma punktami, np. miastami, szukania ścieżek w labiryntach itp.
Niektóre stosunkowo proste algorytmy będziemy notować w postaci operatorów języka PASCAL, co również ułatwi rozszerzenie wiedzy o sztuce programowania komputerów. Przy opracowaniu tematów wykładów wykorzystaliśmy nowoczesną zasadę uczenia ogólnej umiejętności rozwiązywania zadań, a nie podania jak największej ilości definicji, wzorów, komputerowych instrukcji itp. Mechaniczne zapamiętywanie takiej wiedzy ma nikłą szansę na możliwość jej wykorzystania
w przyszłości.
Tematyka wykładów została podzielona na następujące części:
Wstęp. Grafy i tablice. (3 godziny).
Komputerowa reprezentacja tablic i grafów. Analiza kombinatoryczna. Kombinacje. Redukcja wierzchołków digrafu. (3 g.)
Permutacje, inwersje, cykle, znak permutacji. Iloczyn kartezjański.
Generowanie wzorów na przykładzie wyznaczników. (3 g.)
Drzewa grafu oraz ich generowanie. (3 g.)
Zagadnienia transportowe. Problem komiwojażera. Obwody Hamiltona. (3 g.)
Kombinatoryka w badaniach operacyjnych. Sieci transportowe. Sieci czynności. Grafy w teorii ger. (3 g.)
Zastosowanie redukcji oraz didrzew do analizy obwodów elektrycznych (3 g.)
LITERATURA
K. Ross, C. Wright, Matematyka dyskretna, PWN, Warszawa, 1996, s. 899.
N. Deo, Teoria grafów i jej zastosowania w technice i informatyce, PWN, Warszawa, 1980, s. 607.
W. Lipski, Kombinatoryka dla programistów, WNT, Warszawa, 1982, s. 187.
B. Jankowski, GRAFY- algorytmy w PASCALU, MIKOM, Warszawa, 1998, s. 164.
S. Jabłoński, Wstęp do matematyki dyskretnej, PWN, Warszawa, 1991, s. 288.
M.Sysło, N.Deo, J.Kowalik, Algorytmy optymalizacji dyskretnej z programami w języku PASCAL,PWN, Warszawa 1999, s.443.
ZBIORY
W czasie wykładów często będziemy się posługiwać zbiorami, co pozwoli zaoszczędzić czas nauczania oraz ułatwi zgodność traktowania symboli oraz wzorów.
W paragrafie tym zostaną zanotowane symbole oraz definicję, którymi będziemy posługiwać się podczas procesu dydaktycznego.
Pod zbiorem rozumiemy „kolekcję” obiektów. Definicja konkretnego zbioru misi być niedwuznaczną w tym sensie, że musi zostać określone, czy ten lub inny obiekt należy do danego zbioru. Zbiory oznaczamy dużymi, często pochylonymi literami,
a obiekty - małymi, zwykle pochylonymi literami. Obiekt a, który należy do zbioru A zapiszemy w postaci: a∈A, lub a∉A jeśli obiekt a nie należy do zbioru A. Znak ∈ można czytać jako „jest elementem zbioru” lub „należy do” lub „jest w” lub jako spójnik „w”, w zależności od użytego kontekstu.
Zarezerwujemy symbol N dla oznaczania zbioru liczb naturalnych z zerem:
N={0, 1, 2, 3, 4,...}.
Wielokropek „...” oznacza „i tak dalej”. Wielokropka używa się zawsze przy założeniu, że jego znaczenie jest jasne.
Zbiór P to zbiór liczb całkowitych dodatnich lub zbiór liczb naturalnych z wyłączeniem zera.
P={1, 2, 3, 4,...}.
Zbiór C to zbiór wszystkich liczb całkowitych dodatnich lub ujemnych
wraz z zerem
C={...-2, -1, 0, 1, 2, 3, 4,...}, C+={1, 2, 3,...}, C−={-1, -2, -3,...}.
Zbiór R jest zbiorem wszystkich liczb rzeczywistych tzn. zera, liczb ujemnych lub dodatnich. W programach takie zmiennoprzecinkowe liczby oznaczamy jako real, double, extended itp.
Zauważmy, że dla N, P oraz C użyliśmy pogrubione symbole.
Zbiory często będziemy opisywać przez opis własności swych elementów, za pomocą notacji { : }. Zmienna lub obiekt jest wypisana przed dwukropkiem, a własności podane są po dwukropku. Na przykład,
{n: n∈N i n jest parzyste}
czytamy „zbiór wszystkich n takich, że n należy do N i n jest parzyste”. Ten zapis oznacza zbiór {0, 2, 4, 6, 8, 10,...}.
Będziemy również używać rysunków - diagramów Venna, na których zbiory odpowiadają podzbiorom płaszczyzny. Na rys.1.1 pokazano cztery podstawowe diagramy Venna, na których wskazane zbiory zastały zakreskowane.
TABLICE I GRAFY
Umiejętność rysowania jest jednym z darów Natury dla Człowieka. Od dawna używa się rysunków do prac inżynierskich. W ostatnich kilkudziesięciu latach rysunek składający się z punktów (wierzchołków) oraz łączących ich linii traktowany jest jako graf, zawierający pewną informację o badanym obiekcie: sieci komputerów lub sklepów, schemacie blokowym, mapie drogowej, obwodzie elektrycznym itp. Również tablicę można odnieść do klasy najprostszych rysunków, składających się z pionowych i poziomowych linii, między którymi rozłożone są kratki.
Tablice. We wszystkich lub niektórych kratkach (komórkach) tablicy B mogą być liczby, wzory symboliczne lub rysunki (grafy). Każda z danych ma swoje miejsce „zakwaterowania” tzn., że zajmuje kratkę na przecięciu i-tego wiersza i j-tej kolumny. Załóżmy, że numery i, j nie przyjmują wartości zero.
i ≤ m, j ≤ n, i, j, n, m ∈ P.
Zaznaczymy tę kratkę jako (i, j). Zwykle w (i, j) mieści się obiekt matematyczny, który nazwiemy elementem tablicy B i zaznaczymy jako B(ij) lub bij Element bij może mieć jakąś wartość (wagę) ze zbiorów C lub R, na przykład bij = 5 złotych, lub 5 kilometrów, 5 kilogramów, -5 Simensów itd. Wartość bij nie koniecznie musi być równa wartości elementu symetrycznego bji tablicy. Rozróżniamy tablice pełne i rzadkie. Tablica rzadka w odróżnieniu od tablicy pełnej ma co najmniej jedną pustą (zerową) kratkę. To znaczy, że niektóre bij = 0. Głównym przedmiotem naszych ćwiczeń będą tablicę rzadkie.
Grafy. Większość zadań MD opartych jest na wykorzystaniu grafów. Rozdział MD, w którym badane są grafy nazywany jest teorią grafów. Niestety, ograniczona ilość godzin wykładów zmusza nas do ograniczenia do minimum czasu na głębsze poznanie teorii grafów. Więcej czasu zostanie poświęcone zastosowaniu grafów. Dlatego podamy tylko te oznaczenia i definicje, które są niezbędne dla treści naszych wykładów.
Na początku zaznaczymy, że graf w zależności od rodzaju linii na rysunku może należeć do nieskierowanych lub skierowanych. Jeżeli w grafie wszystkie linie nie posiadają strzałek to taki graf nazywamy nieskierowanym, linie bez strzałek nazywamy krawędziami. W przypadku, kiedy w grafie chociażby jedna linia posiada strzałkę, to taki graf nazywamy skierowanym lub digrafem, a linie ze strzałkami nazywamy łukami. Zakładamy, że w ogólnym przypadku, jeśli nie prowadzi to do nieporozumień, termin „graf” może oznaczać tak graf nieskierowany, jak i skierowany (digraf).
W celu opisu wielu sytuacji fizycznych potrzebne są właśnie digrafy, np. mapa miasta z ulicami jednokierunkowymi, sieć przepływowa z zaworami w rurach, obwody elektryczne aktywne itp. Digrafy wykorzystuje się w abstrakcyjnych przedstawieniach programów komputerowych, przy czym wierzchołki zastępują instrukcje programu, a łuki pokazują kolejność wykonywania. Digraf stanowi dogodne narzędzie do badania automatów sekwencyjnych oraz w teorii sterowania.
Ponieważ każdą krawędź grafu można zamienić dwoma przeciwnie skierowanymi łukami z jednakowymi imionami i wagami to każdy graf nieskierowany składający się z krawędzi lub graf mieszany (krawędzie i łuki) można zastąpić digrafem. Z tego powodu oraz dla zaoszczędzenia czasu wykładów przejdziemy od razu do digrafów.
Definicja digrafu
Niech G(V,E) określa graf skierowany, gdzie G oznacza symbol (imię) rozpatrywanego grafu, V jest zbiorem jego wierzchołków: V={0,1,2,...,n-1}, V⊂N, |V|=n, gdzie |V| oznacza moc zbioru V lub ilość jego elementów. Założymy, że wierzchołek oznaczony zerem będzie oznaczać korzeniowy wierzchołek grafu G. Takie grafy nazywamy ukorzenionymi. Zasięg niniejszych wykładów jest ograniczony właśnie do grafów ukorzenionych (rys. 1-3,a). Wierzchołki mogą oznaczać miasta lub sklepy, węzły obwodów elektrycznych, wyspy, operacje w marketingu lub w programie komputerowym, pierwiastki chemiczne itp. Zauważmy, że V również może być zbiorem różnych obiektów, co nie zmienia postaci rzeczy, ponieważ obiekty zawsze można ponumerować.
E jest zbiorem łuków grafu G: E⊆=V×V={e1, e2, ... ,em}. |E|=m. Łuki oznaczono jako uporządkowaną parę (i,j), i,j∈V. Łuk l(i,j) jest skierowany od wierzchołka i do wierzchołka j. Łuk (i,i) nazwiemy pętlą. Pętla niczym nie różni się od krawędzi. Można ją rysować tak ze strzałką jak i bez strzałki. Łuki, skierowane do lub od wierzchołka k, nazywamy incydentnymi do wierzchołka. k. Ilość wychodzących łuków nazwiemy półstopniem wejściowym wierzchołka k, i zaznaczymy jako d+(k). Analogicznie d-(k) oznacza półstopnień wyjściowy wierzchołka k. Dla uproszczenia rysunku dwa przeciwnie skierowane łuki z jednakowymi wagami i imionami podłączone do tej samej pary wierzchołków można zastąpić jedną krawędzią z tą samą wagą i imieniem (rys. 1-3,c). Łuki lub krawędzie mogą oznaczać np.: drogi na mapie, mosty, elementy obwodów elektrycznych, wykonanie operacji, reakcję chemiczną itp. Imię łuku może oznaczać nazwę ulicy, trasę przejazdu, nazwę operacji itp. Jednostki dla wagi krawędzi lub łuku - to kilometry, dolary, rezystancja w Ohmach, czas w sekundach itp.
O dwóch łukach (i,j) oraz (j,i) mówi się, że są równolegle, jeśli są one podłączone do tej samej pary wierzchołków oraz ich strzałki mają zgodny zwrot. Łuki (i,j) oraz (j,i) są symetryczne. Digraf zawierający łuki równoległe nazywa się dimultigrafem.
Digraf, który nie ma ani pętli, ani łuków równoległych nazywa się elementarnym (albo prostym) digrafem. Jeżeli dany graf nie jest elementarny, to można go takim uczynić przez usunięcie wszystkich pętli własnych i zastąpienie każdego zbioru łuków równoległych, na przykład przez taki łuk spośród nich, który ma najmniejszą wagę. W teorii obwodów elektrycznych równoległe łuki są zamieniane ich sumą.
Symetryczne digrafy są to digrafy, w których dla każdego łuku (i, j) istnieje także łuk (j, i).
Pełny digraf określono jako digraf, w którym każdy wierzchołek jest połączony z każdym innym wierzchołkiem przez dokładnie dwa przeciwnie skierowane łuki.
Digraf nazywa się zrównoważonym, jeśli dla każdego wierzchołka k stopień wejściowy równa się stopniowi wyjściowemu, to jest d+(k)=d-(k). Digraf nazywa się regularnym, jeśli każdy wierzchołek ma ten sam stopień wejściowy co każdy inny wierzchołek.
Droga skierowana od wierzchołka i do wierzchołka j jest ciągiem występujących na przemian wierzchołków i łuków, zaczynających się od i i kończących się na j takim, że każdy łuk jest zorientowany od wierzchołka go poprzedzającego do wierzchołka występującego po nim. Jeśli i = j to droga nazywa się zamkniętą. W przeciwnym przypadku droga jest otwarta.
Drogę otwartą, w której żaden wierzchołek nie pojawi się więcej niż jeden raz, nazywamy ścieżką lub drogą elementarną. Drogę zamkniętą, w której żaden z wierzchołków (z wyjątkiem początkowego i końcowego) nie pojawia się więcej niż jeden raz nazywamy obwodem lub cyklem.
Najważniejszymi elementami grafu są wierzchołki oraz krawędzie (łuki). Krawędzie (łuki) mogą przyjąć nazwy (imiona) oraz wartości (wagi). (Rys. 1-1, a, b) Należy zwrócić uwagę, że przy rysowaniu grafu nieistotne jest, czy linie-łuki rysuje się proste, czy krzywe, długie czy krótkie. Ważna jest jedynie incydencja między łukami a wierzchołkami. Na rys. 1-3, a, b pokazano, że wierzchołki grafu można zaznaczać dużymi (wyraźnymi) kropkami lub kołami. Zwykle wierzchołek ma numer lub nazwisko (imię), które piszemy obok kropek (jak na lewym rysunku) lub wewnątrz koła jak pokazano na prawym rysunku. Rysunek grafu dla człowieka ma również estetyczną wartość: graf może wyglądać estetycznie lub niedbale, rys. 1-3, e. Komputer nie rozróżnia takich rozmytych cech, jest „ślepy”, dlatego należy wprowadzać do komputera rysunek grafu, jako specjalnie zdefiniowany zbiór liczb, tablic, symboli, tekstów, danych bitowych itp. Postać danych projektowana jest oczywiście przez człowieka (programistę).
Między tablicą a grafem istnieje jednoznaczna odpowiedniość: element tablicy (macierzy) aij, i≠j odpowiada łukowi (i,j). Element tablicy aii odpowiada pętli grafu (Rys. 1-3, f). Mówi się, że istnieje grafowa interpretacja tablicy oraz tablicowa interpretacja grafu.
KOMPUTEROWA REPREZENTACJA TABLIC I GRAFÓW
Formy wewnętrznego kodowania
Każdy algorytm komputerowy wymaga pewnych danych wejściowych, dzięki którym rozpoczyna on swoje działanie. Danymi wejściowymi dla naszych algorytmów na poziomie człowieka będą tablice lub digrafy. Sposób reprezentacji najbardziej przejrzysty i użyteczny dla człowieka - tzn. przez rysunek punktów i łączących je linii na płaszczyźnie - jest bezużyteczny, jeśli chcemy problemy związane z grafami rozwiązywać za pomocą komputera. Chodzi o to, że komputer „wymaga” specyficznego zestawu danych. Wybór odpowiedniej struktury danych do reprezentacji grafu ma zasadniczy wpływ na efektywność algorytmów, i dlatego zajmujemy się teraz tym zagadnieniem nieco bliżej. Pokażemy kilka sposobów reprezentacji i omówimy pokrótce ich podstawowe wady i zalety.
Kodowanie tablic w zasadzie nie sprawia istotnych problemów, ponieważ większość kompilatorów ma środki kompilacji jedno, dwu lub więcej wymiarowych tablic. Bardziej skomplikowane jest kodowanie grafów, które zwykle podawane są do komputera w jednej z niżej podanych postaci. Od razu zaznaczymy, że nie istnieje najlepsza forma zadania informacji o digrafie. Wybór zależy od struktury digrafu, rozpatrywanego zagadnienia, stosowanego języka, typu procesora i od tego, czy należy modyfikować digraf w trakcie wykonania zadania, czy nie, itp. Innymi słowy od sposobu zadania
w komputerze informacji o strukturze tablicy lub grafu istotnie zależy złożoność oraz czas wykonania programu. Przy kodowaniu grafów również używane są tablice.
1. Macierz przyległości lub macierz sąsiedztw
Przy przypisaniu różnych numerów do każdego z n wierzchołków danego digrafu G do jego prezentacji podczas wprowadzania, przechowywania i wyprowadzania używa się macierzy binarnej X(G) o wymiarach n×n. Na rys. 2-1,b pokazano przykład digrafu oraz jego macierzy X. Ponieważ każdy z n2 jej elementów jest równy 0 lub 1, więc macierz przyległości wymaga n2 bitów. Oczywiście, że bity można łączyć w bajty lub podawać zera i jedynki w postaci bajtów. Należy pamiętać, że macierz przyległości nie może zawierać informacji o łukach równoległych.
2. Macierz incydencji
W teorii grafów klasycznym sposobem reprezentacji grafu jest macierz incydencji (rys. 2-1, c). Jest to macierz A o n wierszach odpowiadających wierzchołkom i m kolumnach odpowiadających krawędziom. Dla digrafu kolumna odpowiadająca łukowi (i,j)∈E zawiera -1 w wierszu odpowiadającym wierzchołkowi i, +1 w wierszu odpowiadającym wierzchołkowi j i zera we wszystkich pozostałych wierszach. Pętle (i,i) wygodnie jest reprezentować przez inną wartość, np. 2 w wierszu i. W przypadku grafu (niezorientowanego) kolumna zawierająca krawędź {i,j} zawiera dwie odpowiednie jedności w wierszach i oraz j.
Z algorytmicznego punktu widzenia macierz incydencji jest chyba najgorszym sposobem reprezentacji grafu jaki można sobie wyobrazić. Oprócz zajmowania dużej pamięci również dostęp do informacji w niektórych przypadkach jest bardzo niewygodny. Odpowiedź na elementarne pytania typu „czy istnieje łuk (i,j)?”, „do jakich wierzchołków prowadzą krawędzi z i?” wymaga w najgorszym przypadku przeszukiwania wszystkich kolumn macierzy, a więc m kroków.
Macierz incydencji A(G) wymaga 2n⋅m bitów pamięci, co może być liczbą większą niż n2 bitów zajmowanych przez macierz X, ponieważ liczba krawędzi m jest zwykle większa niż liczba wierzchołków n. Przykład macierzy A pokazany jest na rys. 2-1, c. Macierze A są szczególnie dogodne przy rozpatrywaniu obwodów elektrycznych
i układów przełączających.
3. Lista łuków
Często stosowanym sposobem reprezentacji grafu jest wypisywanie wszystkich jego łuków jako par wierzchołków. Tak, na przykład, graf skierowany z rys. 2-1,a byłby przedstawiony w formie rys. 2-1,d. Niezbędne zajmowanie pamięci przez listy łuków wynosi 2mb bitów, gdzie b równa się ilości bitów, potrzebnych do zanotowania największego numeru wierzchołka. Podczas porównania z n2 widzimy, że lista łuków jest bardziej ekonomiczna niż użycie macierzy przyległości X, jeżeli digraf jest rzadki.
Lista łuków jest bardzo dogodną formą wprowadzenia grafu do komputera, jednakże przechowywanie i przekształcenie digrafu za pomocą listy łuków nie jest wygodne.
4. Lista następników
Inna efektywna metoda do kodowania digrafów rzadkich polega na użyciu n tablic liniowych. Po przypisaniu wierzchołkom, w dowolnej kolejności, liczb 1, 2, ...,n przedstawimy każdy wierzchołek k za pomocą tablicy, której pierwszym elementem jest k,
a pozostałymi elementami są wierzchołki będące bezpośrednimi następnikami wierzchołka k, tzn. wierzchołki, do których istnieje ścieżka skierowana o długości jeden od wierzchołka k. (W grafie (nieskierowanym) są to po prostu wierzchołki przyległe do k.). Przykład kodowania digrafu pokazano na rys. 2-1, e. Dla grafu nieskierowanego notujemy wierzchołki sąsiednie każdego wierzchołka, a nie następniki. A zatem każda krawędź pojawia się dwukrotnie, co jest oczywistą nadmiarowością.
Zaletą listy następników jest możliwość kodowania łuków równoległych oraz pętli. W wielu algorytmach struktura grafu jest dynamicznie modyfikowana przez dodawanie i usuwanie łuków. W takich przypadkach zakładamy, że w naszych listach incydencji element listy zawiera wskaźnik do następnego elementu. Wtedy usuwając pewien element z listy możemy łatwo - w liczbie kroków ograniczonej przez stałą - usunąć drugi element reprezentujący te samą krawędź, bez konieczności przeszukiwania listy zawierającej ten element.
5. Dwie tablicy liniowe
Nieznaczną modyfikacją listy łuków jest przedstawienie digrafu za pomocą dwóch tablic liniowych, powiedzmy F i H. (Rys. 2-1, f.) Każdy element w tych tablicach jest etykietą wierzchołka. Łuk i-ty, to jest łuk, który prowadzi od wierzchołka fi do wierzchołka hi.
6. Tablica rekordów
Tablica rekordów - jest to kombinowana metoda reprezentacji digrafu. Łączy ona listy łuków, dwie tablice liniowe oraz listy następników. Wewnęczne dane programu są oparte na kodowaniu informacji o każdym łuku typem record. Wymienimy jako przykład fragment deklarowania informacji o łukach digrafów w języku PASCAL:
type
LUK=record
ODw,DOw :integer;
IMIE :string[16];
WAGA :double;
{tu mogą być jeszcze inne dane,
np. postać bitowa łuku, oparta na ODw (Dow) lub
zapis drogi od wierzchołka ODw do wierzchołka Dow itp.}
End;
var
LUKI: array[1...m] of LUK;
LUKI oznacza tablicę łuków digrafu w postaci rekordów. LUK oznacza typ rekordu do zapisu informacji o każdym łuku. ODw (DOw) oznacza numer wierzchołka, OD (DO) którego jest skierowany konkretny łuk. Informacja o początku grupy łuków każdego wierzchołka podana jest w tablicy wskaźników NODE, jak pokazano na rys. 2-2.
Na zakończenie przeglądu sposobów reprezentacji digrafów zauważymy, że omówione metody nie są całkowicie różne, a związane ze sobą w tym sensie, że dostarczają tej samej informacji. Można łatwo napisać programy-konwertery, przekształcające jedną postać na drugą. Można również doraźnie dokonać pewnych dodatkowych zmianw tych reprezentacjach, aby dopasować je do aktualnych wymagań, np. digraf ważony można przedstawić za pomocą macierzy wag (zwanej również macierzą kosztów lub odległości) o wymiarach nxn, która jest taka sama jak macierz przyległości z wyjątkiem tego, że jej elementami zamiast jedynek są wagi krawędzi. Powtórzymy jeszcze raz,efektywność algorytmu zależy od postaci, w której digraf jest przedstawiony. A zatem ważny jest właściwy wybór struktury danych.
Osobliwości programów kombinatorycznych
Jakość algorytmów zwykle ocenia się według trzech parametrów: dokładność obliczeń, ich czas oraz pamięć, zajmowana kodem wykonawczym oraz danymi. Osobliwość algorytmów kombinatorycznych polega na niezależności od parametru dokładności, ponieważ wszystkie obliczenia wykonują się nad zmiennymi logicznymi oraz liczbami całkowitymi. Mając na uwadze pamięć, nowoczesne komputery mają tyle pamięci RAM i ROM, że w algorytmach kombinatorycznych prawie nie mówi się o konieczności zaoszczędzenia pamięci zwłaszcza przy kodowaniu danych wejściowych.
Niestety, czas rozwiązywania większości zadań kombinatorycznych nadal pozostaje głównym wskaźnikiem efektywności programów komputerowych. Chociaż nowoczesne komputery są bardzo szybkie i pracują przy szybkościach nanosekundowych (10-9 sek.), to szybko dochodzą do granic swoich możliwości, jeżeli są wykorzystane do rozwiązywania zagadnień kombinatoryki. Rozpatrzymy, na przykład, zagadnienie znalezienia ścieżki Hamiltona o najmniejszej sumie wag krawędzi w ważonym grafie pełnym o n wierzchołkach, tzn. problem komiwojażera. W grafie tym istnieje ½(n-1)! różnych obwodów Hamiltona. Najprościej byłoby wygenerować wszystkie obwody Hamiltona i porównać ich wagi. Dla grafu o 10 wierzchołkach liczba ścieżek Hamiltona wynosi 0.5 razy 9! =181440 i ta metoda mogłaby być prawidłowa. Ale dla grafu o 20 wierzchołkach mamy już
½(n-1)!≈6⋅1016,
a wykonanie tego algorytmu nawet z szybkością 109 operacji na sekundę wymagałoby około 6⋅1016/109⋅3⋅107 = 2 lat.
Wyraźnie więc widać, że moc obliczeniowa komputera musi być połączona z pomysłowością metod kombinatorycznych. W programach teorii grafów wykorzystuje się bardziej zdolność komputera do podejmowania decyzji niż jego zdolność wykonywania operacji arytmetycznych.
Zewnętrzne kodowanie tablic i grafów
Wyżej wymienione sposoby kodowania tablic i grafów są uciążliwe dla człowieka. Dlatego zazwyczaj używa się uproszczenie „załadowania” danych do komputera wykorzystując specjalny język, formalnie podobny do zapisu informacji przez człowieka
w formie symbolicznej.
Dla wprowadzenia oraz przekształcenia zewnętrznych danych wejściowych do wewnętrznych danych komputera używa się specjalnego programu-konwertera, ogólnie nazywanego jako preprocesor. Niżej podamy jeden z możliwych wariantów języka opisu tablic i grafów, którymi będziemy posługiwać się na wykładach oraz przy wykonaniu projektu. Komputerowa reprezentacja grafu oparta jest na kodowaniu informacji o wszystkich krawędziach i łukach grafu. Na przykład, krawędź A między wierzchołkami 1 i 2 z wagą 3 w danych wejściowych notuje się jako: A 1-2 3. Łuk B skierowany od wierzchołka 1 do wierzchołka 2 o wadze 4 ma postać: : B 1>2 4 itp. Na rys. 2-2 jest pokazany przykład danych wejściowych o digrafie oraz kolejność opracowania tych danych preprocesorem. Kolejność notowania łuków i krawędzi nie ma znaczenia. Zapis informacji o każdym łuku lub krawędzi wykonuje się w trzech grupach symboli: grupa nazwy, grupa incydentności (tzn. wierzchołki podłączenia) oraz grupa wag. Przed każdą z wymienionych grup za wyjątkiem informacji o pierwszym łuku obowiązkowy jest zapis spacji (odstępu). Dane wejściowe mogą być przygotowane jako dane tekstowezapisywane w kodzie ASCII dowolnego edytora.
Preprocesor kolejno ogląda i analizuje dane oraz wypełnia odpowiednie tablice: LUKI. ODw -zawiera numer wierzchołka, od którego łuk wychodzi; LUKI. DOw - zawiera numer wierzchołku, do którego łuk wchodzi, LUKI. Imie - zawiera nazwisko łuku oraz LUKI. Waga - zawiera wartość łuku. W niektórych zadaniach waga łuków nie jest używana. W takim przypadku można zainicjować wagę każdego łuku jako jedność. Każda krawędź zamienia się na dwa symetryczne łuki o jednakowej nazwie oraz wadze. Należy dodać, że w rekordzie LUK mogą być dodatkowo pomieszczone inne dane, np. postać bitowa łuku, oparta na ODw (DOw) lub zapis drogi od wierzchołka ODw do wierzchołka DOw itp.
Kolejnym etapem jest sortowanie łuków według numerów incydentnych wierzchołków. Pierwszym kluczem jest liczba z LUKI. ODw, zaś drugim - z tablicy LUKI. DOw. Na ostatnim etapie pracy preprocesora formuje się tablica Node. W komórce Node[i] notuje się numer rekordu w tablicy LUK który jest pierwszym z grupy łuków, wychodzących z i-go wierzchołka. W przypadku nie obecności w i-tym wierzchołku łuków wychodzących w Node[i] zapisuje się -1. Umożliwia to pracę z digrafami w których nie jest przestrzegana ciągłość liczb przy numerowaniu wierzchołków. W komórce Node[n]+1 preprocesor zapisuje numer pierwszej wolnej komórki w notacji rekordówo łukach w tablice LUKI. Oprócz wyżej wymienionej informacji preprocesor może dodatkowo generować inne niezbędne dane dla realizacji tego lub innego algorytmu: zapis łuków w postaci liści, dane bitowe o incydentności łuków, sortowanie łuków według rosnących lub malejących wag itp.
ANALIZA KOMBINATORYCZNA
Analiza kombinatoryczna bada obiekty, które można utworzyć ze skończonego zbioru E={e1,..., en}, oraz własności takich obiektów. Mogą to być podzbiory zbioru E, podzbiory z powtarzającymi się elementami ze zbioru E, uporządkowanie podzbioru zbioru E itp.
Analiza kombinatoryczna jest działem matematyki dyskretnej, której źródeł należy szukać w starożytności. W obecnych czasach zainteresowanie analizą kombinatoryczną znacznie wzrosło. Wyrosła ona na bardzo bogaty i dynamicznie rozwijający się dział matematyki. Trudno dziś precyzyjnie określić obiekty i własności, które leżą w kręgu zainteresowania analizy kombinatorycznej, zaczniemy wiec od opisu najprostszych (elementarnych) obiektów kombinatorycznych.
Obiekty kombinatoryczne
Rodzina podzbiorów zbioru E.
Niech E={e1,..., en} będzie zbiorem skończonym. Rodzinę wszystkich podzbiorów zbioru E oznaczymy przez Fn.
Przykład 1. E={e1, e2, e3}. Rodzina jego podzbiorów ma postać
F3={∅, {e1}, {e2}, {e3}, {e1, e2}, {e1, e3}, { e2, e3}, {e1, e2, e3}};
Liczba elementów Fn równa się: |Fn|=2n.
Algorytm generowania (wyliczenia) wszystkich podzbiorów polega na tworzeniu wszystkich ciągów n zer i jedynek, zaczynając od (0,...,0). Kolejne ciągi otrzymujemy przez dodawanie jedynki do liczby, której zapisem w systemie dwójkowym jest poprzedni ciąg.
Wariacje bez powtórzeń elementów z E po k.
Wariacje bez powtórzeń elementów z E po k nazywamy uporządkowany podzbiór, złożony z k elementów należących do E.
Przykład 1. E={e1, e2, e3}, k=2. Niżej wypisane są wszystkie wariacje bez powtórzeń z tego zbioru po 2:
Wnk={(e1, e2), (e2, e1), (e1, e3), (e3, e1), ( e2, e3), (e3, e2)};
Liczba elementów Wnk równa się: |Wnk|=(n)k=n(n-1)...(n-k+1), 1≤k≤n.
Permutacje elementów ze zbioru E.
Niech E={e1,..., en}. Permutacjami nazywamy uporządkowane podzbiory złożone
z n elementów należących do zbioru E.
Przykład 2. E={e1, e2, e3}. Permutacjami zbioru E są:
Pn={(e1, e2, e3), (e1, e3, e2), (e2, e1, e3), (e2, e3, e1), (e3, e1, e2), (e3, e2, e1), };
Liczba elementów: |Pn| = |Wnn|=(n)n=n(n-1)...(1)=n!
Kombinacje elementów z E po k..
Niech E={e1,..., en}. Kombinacją elementów z E po k nazywamy (nieuporządkowany) podzbiór złożony z k elementów należących do zbioru E.
Przykład 1. E={e1, e2, e3} i k=2. Kombinacjami z E po 2 są:
Cmn={{e1, e2}, {e1, e3}, {e2, e3}}.
Kombinacja różni się od wariacji bez powtórzeń tym, że porządek elementów
w kombinacji nie jest istotny. Zatem każdej kombinacji odpowiada k! wariacji bez powtórzeń
Liczba wariantów przy kombinacji z m po n :
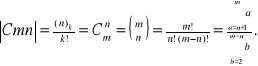
ILOCZYN KARTEZJAŃSKI (IK)
Niech Y1=(y11, y12,...,y1,n1), Y2=(y21, y22,...,y2,n2),..., Yk=(yk1, yk2,...,yk,nk) będą zbiorami liczb naturalnych dla których: |Y1|=n1, |Y2|=n2, |Yk|=nk; n1,n2,...,nk∈C+.
Wtedy wg definicji IK
Y=Y1×Y2×...×Yk=((y11, y21,...,yk1), (y11, y21,...,yk2),..., (y1,n1, y2,n2,...,yk,nk)).
Nawiasy ( ) wskazują, że kolejność notacji elementów w IK uważamy istotną.
Ilość elementów zbioru IK równa się ![]()
.
Prostym przykładem IK jest operacja opuszczenia nawiasów na lekcjach w szkole podstawowej.
(a+b)⋅(c+d+e)⋅(f+h) =
= acf+ach+adf+adh+aef+aeh+bcf+bch+bdf+bdh+bef+bch.
Algorytm generowania IK pokażemy na przykładzie.
Niech dane są cztery źbiory: A1={a,b}, A2={c,d,e}, A3={f,h}, A4={k,m}.
Dane wejściowe umieścimy w tablicach TA oraz TB:
TA= |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
2 |
3 |
4 |
5 |
|
a |
b |
c |
d |
e |
f |
h |
k |
m |
|
|
NA= |
1 |
3 |
6 |
8 |
10 |
Górne indeksy oznaczają numer komórki w tablicy. W tablicy TA zanotowane są kolejno wszystkie elementy zbiorów A1...A4. Dodatkowo w i-tej komórce tablicy NA[i], (i=1,2,3,4) zanotowany jest numer komórki w TA, gdzie zaczynają się elementy zbioru Ai. Ostania (piąta) komórka w TB oznacza początek wolnych komórek w TA.
Zanotujemy najprostszy operator generacji IK, który ma wygląd jednego złożonego operatora typu „pętla w pętli” o zmiennych długościach. Wynikiem działania algorytmu ma być wydruk wszystkich elementów IK.
{moduł GIK -generowanie i drukowanie iloczynu kartezjańskiego-}
for i1:=NA[1] to NA[2]-1 do
for i2:=NA[2] to NA[3]-1 do
for i3:=NA[3] to NA[4]-1 do
for i4:=NA[4] to NA[5]-1 do
writeln(TA[i1],TA[i2],TA[i3],TA[i4]);
Po uruchomieniu operatora otrzymamy następne kombinacje IK :
acfk acfm achk achm adfk adfm adhk adhm aefk aefm aehk aehm bcfk bcfm bchk bchm bdfk bdfm bdhk bdhm befk befm behk behm
Oczywiście, że operator GIK i GP mają raczej dydaktyczną wartość, ponieważ czas ich wykonania rośnie jak O(nn). W następnym wykładzie pokażemy algorytm generowania permutacji o złożoności O(const).
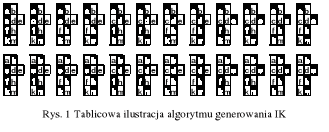
Zauważymy, że powyższy operator ma pętle różnej długości (i1=1,2; i2=1,2,3; i3=1,2; i4=1,2). Algorytm generowania IK pokazany jest na rys. 1.
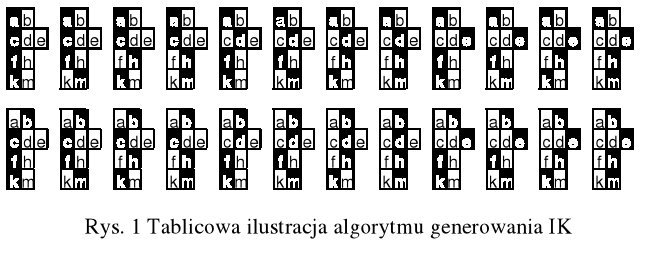
Łatwo udowodnić, że złożoność czasowa algorytmu IK wynosi O(|A|).
Ważną cechą algorytmów opartych na wykorzystaniu IK jest możliwość generowania kolejnych wierszy z minimalną ilością nowych elementów. Istotę algorytmu „pływającego nawiasu” pokazano na rys. 3-5z. Tam że widzimy dwa wykresy średniego czasu szukania kombinacji IK na przykładzie generowania didrzew. Pierwszy wykres oznacza czas szukania tych kombinacji wg. klasycznego algorytmu iloczynu kartezjańskiego. Drugi -to czas szukania wg modyfikowanego algorytmu IK. Właśnie wykorzystanie tego algorytmu pozwala w niektórych przypadkach wykonać automatyczne uproszczenie wzorów obliczeniowych, tzn. na przykład zaoszczędzić ilość arytmetycznych operacji przy generowaniu oraz obliczeniu wzorów symbolicznych.
PERMUTACJE
Ogólne informacje
Permutacją zbioru n -elementowego X nazywamy dowolną wzajemnie jednoznaczną funkcję f:X→X. Jest to dowolny ciąg różnowartościowy długości n o elementach ze zbioru X. Permutację określamy jako tablicę o dwóch wierszach, z których każdy zawiera wszystkie elementy zbioru X, przy czym element f(i) występuje pod elementem i. Dla przykładu permutację f zbioru {0, 1, 2, 3, 4, 5} taką, że
f(0)=2, f(1)=5, f(2)=3, f(3)=0, f(4)=1, f(5)=4
zapisujemy następująco: <2, 5, 3, 0, 1, 4>
Jeśli ustalimy porządek elementów w górnym wierszu, to każdej permutacji odpowiada jednoznacznie ciąg zawarty w dolnym wierszu, np. dla permutacji f jest to
<2, 5, 3, 0, 1, 4> lub (2, 5, 3, 0, 1, 4). W naszych rozważaniach natura elementów zbioru X będzie nieistotna - przyjmujemy dla prostoty X = {0, 1,...,n}. Permutację <0, 1,...,n> nazywamy identycznościową. Łatwo udowodnić, że ogólna liczba permutacji n- elementowego zbioru wynosi n!.
Parę (ai, aj) nazwiemy inwersją, jeśli dla i<j ai > aj. Inwersja permutacji I jest zbiorem wszystkich inwersji w tej permutacji, tzn.
I={(i,j): i<j, ai>aj}.
Liczbą inwersji LI permutacji jest moc jej zbioru I, tzn. LI=|I|. Dla wyżej pokazanego przykładu I={(2,0), (2,1), (5,3), (5,0), (5,1), (5,4), (3,0), (3,1) }, LI=8 i jest parzysta.
Dla dowolnej permutacji f definiujemy jej znak w następujący sposób:
sgn (f) = (-1)LI.
Permutację f nazywamy parzystą, jeśli sgn (f) = 1, oraz nieparzystą, jeśli sgn (f) = -1.
Każdą permutację f możemy reprezentować graficznie za pomocą digrafu
o zbiorze wierzchołków X = {0, 1,...,n}, w którym x → y wtedy i tylko wtedy, gdy
f(x) = y. Od każdego wierzchołka x tego digrafu odchodzi dokładnie jeden łuk, mianowicie <x, f(x)>. Łatwo zauważyć, że startując z dowolnego wierzchołka x0 dochodzimy po skończonej liczbie kroków ponownie do wierzchołka x0 . Stąd wniosek,
że digraf permutacji składa się z pewnej liczby (od 1 do n) cykli elementarnych o rozłącznych zbiorach wierzchołków dających w sumie cały zbiór X. Przedstawienie permutacji w postaci digrafu nazywamy rozkładem permutacji na cykle. Dla wyżej wymienionego przykładu rozkład na cykle zapiszemy w następujący sposób: f= [0, 2, 3] [1, 5, 4]. Permutację o jednym cyklu nazwiemy cyklem (drogą) Hamiltona. Ilość cykli w permutacji oznaczymy jako LC. Istnieje związek między znakiem permutacji a ilością cykli:
sgn (f)=(-1)n+1(-1)LC=(-1)n+LC+1.
Dodatkowa jedynka w potędze jest konieczna ze względu na numerację od 0 do n. Ogólna informacja o permutacji została pokazana na rys. 3-4.
Generowanie permutacji
Zagadnienie generowania wszystkich n! permutacji zbioru n- elementowego ma bogatą literaturę i jeszcze dłuższą historię, których źródeł można się doszukać w początkach XVII wieku, kiedy to w Anglii powstała sztuka bicia w dzwony polegająca na wybiciu na n różnych dzwonach wszystkich n! permutacji. Zostały ułożone pewne proste metody systematycznego generowania wszystkich permutacji bez powtórzeń. Niektóre z tych metod zostały ponownie „odkryte” współcześnie
i zaprogramowane na komputerach. Ciekawe, że słynna Księga Rekordów Guinnesa zawiera informację o wybiciu wszystkich 8! = 40320 permutacji na 8 dzwonach
w 1963 roku - ustanowienie tego rekordu trwało prawie 18 godzin. Oczywiście użycie nowoczesnych komputerów pozwala generować permutację znacznie szybciej: dla zbioru 8-elementowego w ułamku sekundy. Ale przez bardzo szybki wzrost wartości n! generowanie wszystkich permutacji zbioru 14-elementowego może potrwać na komputerze dziesiątki godzin...
Przyczyną naszego zainteresowania algorytmami generowania permutacji jest jego łatwe zastosowanie do szukania obwodów Hamiltona oraz do generowania wzorów obliczenia wyznaczników.
Modyfikujemy poprzedni operator GIK dla generowania permutacji ze zbioru {1, 2, 3}.
Zanotujemy tablice: Y1=[1,2,3], Y2=[1,2,3], Y3=[1,2,3].
Wtedy: TA=[1,2,3,1,2,3,1,2,3], NA=[1, 4, 7, 10]. n:=3;
Niech istnieje pomocnicza tablica. Tbit=[1, 2, 4, 8,...] }
Wtedy:
{moduł GP - generowanie i drukowanie wszystkich permutacji}
for i1:=NA[1] to NA[2]-1 do
for i2:= NA[2] to NA[3]-1 do
for i3:= NA[3] to NA[4]-1 do
if Tbit[TA[i1]]+Tbit[TA[i2]]+Tbit[TA[i3]]=7 {7 = Tbit[n+1]-1}
then writeln(TA[i1], TA[i2], TA[i3],);
Operator GP wydrukuje następne permutację:
123 132 213 231 312 321.
Rozpatrzymy algorytmy znajdowania znaku permutacji. Prosty algorytm wyznaczenia inwersji w permutacji a1, a2,..., an, polega na definicji inwersji permutacji: obliczenie sumy ilości prawych liczb mniejszych od każdej lewej liczby, tzn. mniejszych od a1, plus mniejszych od a2 itd. do an-1. Obliczenie ilości inwersji w permutacji można zaprogramować wykorzystując moduł GP w następujący sposób:
Inv:=0; for i:=1 to n-1 do
for j:=i+1 to n do if TA[j]<TA[i] then Inv:=Inv+1;
writeln(`liczba inwersji=',Inv:2);
Łatwo udowodnić, że algorytm ma złożoność O(n(1+n)/2) = O(n2).
W [3, str.21] podana jest efektywna metoda oraz algorytm (1.9) do wyznaczenia znaku inwersji na podstawie analizy cykli permutacji. Zanotujemy ten algorytm w całości:
Dane: Dowolna permutacja f w postaci ciągu P[1],...,P[n] (P[i]=f(i)).
Wyniki: Po zakończeniu działania algorytmu s=sgn(f).
begin s:=1;
for i:=1 to n do NOWY[i]:=true;
for i:=1 to n do
if NOWY[i] then { znajdź cykl zawierający i}
begin j:=P[i];
while j<>i do
begin NOWY[j]:=false; s:=-s; j:=P[j];
end;
end;
end;
Na starcie algorytmu s ustawia się na 1 oraz utworzona jest pomocnicza tablica NOWY długości n. Algorytm ten przegląda kolejno pozycje 1,...,n permutacji (pętla 4) i za każdym razem gdy element P[i] nie był jeszcze analizowany (NOWY[i]=true) wyznacza cykl, do którego ten element należy (blok 6). Zauważmy, że jeśli cykl ten jest długości k, to pętla 7 jest wykonywana k-1 razy. Po znalezieniu wszystkich cykli s=(-1)p, gdzie p jest liczbą cykli parzystej długości. Łatwo udowodnić, że złożoność czasowa algorytmu wynosi O(n).
Modyfikujemy algorytm 1.9 w celu obliczenia ilości cykli, co jest ważne tak przy ustaleniu znaku permutacji, jak i przy generowaniu obwodów Hamiltona. Dla tego komórkę s przeznaczymy do liczenia ilości i parzystości cykli.
begin
s:= n and 1; { s = 0 dla parzystych n i s=1 dla nieparzystych n}
for i:=1 to n do NOWY[i]:=true;
for i:=1 to n do
if NOWY[i] then {znajdź cykl zawierający i}
begin s:=s+1; j:=P[i];
while j<>i do
begin NOWY[j]:=false; j:=P[j];
end;
end;
if s and 1=0 then s:=1 else s:=-1;
end;
Przy szukaniu cykli Hamiltona wiersze 2 i 11 należy zanotować tak:
2 s:=0;
...
if s=1 then CyklHam:=true
else CyklHam:=false;
W tym przypadku dla przyspieszenia algorytmu należy zmienić wiersz 6.
begin s:=s+1; if s>1 then break; j:=P[j];
Oczywiście, że modyfikowany dla potrzeby generowania obwodów Hamiltona blok szukania cykli ma złożoność O(n) tak samo, jak i podany w [3] algorytm 1.9, chociaż jest szybszy (dzięki zastosowaniu rozkazu break - na przerywanie zbędnych obliczeń).
W [3] podano kilka ciekawych algorytmów generowania wszystkich permutacji. Pierwszy z nich bazuje na prostym algorytmie rekurencyjnym. W wyniku generowania wszystkich permutacji dla n=4 otrzymano następny ciąg permutacji:
1234, 2134, 1324, 3124, 2314, 3214, 1243, 2143, 1423, 4123, 2413, 4213,
1342, 3142,1432, 4132, 3412, 4312, 2341, 3241, 2431, 4231, 3421, 4321.
Drugi algorytm generuje wszystkie permutację przez minimalną liczbę transpozycji (tzn. zamiana miejscem dwóch elementów). W wyniku działania algorytmu otrzymamy ciąg permutacji zbioru {1...n}, w którym każda następna powstaję z poprzedniej przez dokonanie pojedynczej transpozycji niekoniecznie sąsiednich elementów. Dla n=4 otrzymano następny ciąg permutacji:
1234, 2134, 1324, 3124, 2314, 3214, 1243, 2143, 1423, 4123, 2413, 4213
1342, 3142, 1432, 4132, 3412, 4312, 2341, 3241, 2431, 4231, 3421, 4321.
Trzeci algorytm generuje wszystkie permutacje przez minimalną liczbę transpozycji sąsiednich elementów. W wyniku działania algorytmu otrzymamy ciąg permutacji zbioru {1,...,n}, w którym każda następna powstaje przez dokonanie pojedynczej transpozycji sąsiednich elementów. Dla n=4 otrzymano następny ciąg permutacji:
1234, 2134, 2314, 3214, 3124, 1324, 4321, 3421, 3241, 2341, 2431, 4231,
4132, 1432, 1342, 3142, 3412, 4312, 4213, 2413, 2143, 1243, 1423, 4123.
Zastanówmy się teraz, ile zmian wykonują opisane trzy algorytmy przy wygenerowaniu kolejnej permutacji. Łatwo zauważyć, że liczba ta jest zmienna. Chociaż średnia liczba transpozycji [(i) ↔ (i+1)] przypadających na każdą permutację jest niewielka, to jednak w niektórych zastosowaniach lepszy byłby algorytm, w którym każda następna permutacja powstaje z poprzedniej przez dokonanie minimalnej zmiany elementów. Może to być istotne w sytuacji, gdy z każdą permutacją związane są pewne obliczenia, i gdy istnieje możliwość korzystania z częściowych wyników uzyskanych dla poprzedniej permutacji, jeśli kolejne permutacje mało się od siebie różnią. Pokażemy, że algorytm taki jest rzeczywiście możliwy. Należy użyć podstawowego algorytmu, bazowanego na iloczynie kartezjańskim.
WZORY
Jeszcze w szkole podstawowej zapoznaliśmy się z różnymi notacjami matematycznymi, które zwykle nazywano formułami lub wzorami. Terminy "wzór" i "formuła" użyjemy jako synonimy.
Oto niektóre przykłady formuł:
w trygonometrii 2sinx⋅cosx = sin(x+y) + sin(x-y), (1)
w rachunku całkowym ![]()
(2)
przy obliczaniu wyznaczników
![]()
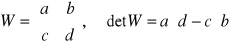
,
lub 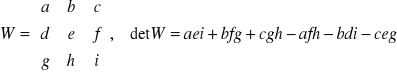
. (3)
Ważną zaletą formuły jest jej uniwersalność w stosunku do wartości liczbowej argumentów zanotowanych jako pewne symbole.
Wyprowadzenie jednych wzorów z innych lub źródłowych uważa sie za cenne intelektualne narzędzie dydaktyczne w naukach matematycznych i technicznych. Uważa się, że wyprowadzenie formuł jest własnością Natury Człowieka oraz że zastosowanie komputerów w tym celu jest bardzo skomplikowane. Często mówi się o sztuce wyprowadzania wzorów. Jednak potężna eksplozja techniki komputerowej w ostatnich kilkudziesięciu latach w sposób naturalny zachęca naukowców do szukania sposobów wykorzystania komputerów do wyprowadzenia i skutecznego zastosowania formuł.
Zaczniemy od ogólnej obserwacji formuł. Widzimy, że niezbędnym atrybutem każdej formuły jest używanie liczbowych współczynników oraz różnych symboli. Te ostatnie można rozdzielić na dwie grupy: symbole operacji oraz symboliczne elementy. Symbole operacji - są to wskaźniki różnych operacji: logicznych, arytmetycznych, trygonometrycznych itp. Symboliczne elementy oznaczają pewne argumenty formuły, które mogą przyjmować różne wartości liczbowe.
Dla uproszczenia wykładu ograniczymy się do analizy struktury najprostszych wzorów typu (3). Są to wzory składające się z sumy lub różnicy iloczynów pewnych symboli lub liczb. Zaczniemy od tego, ze formuła typu (3) uważana jest za wzór całkowicie symboliczny (full-symbolic formula). Jeżeli zaś w przykładzie (3) w macierzy W niektóre symbole zamienimy liczbami to otrzymamy wzór (4) jako wzorzec symboliczno-numerycznej formuły (semi-symbolic formula).
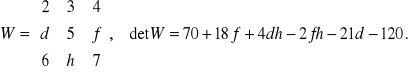
(4)
Generowanie formuł.
Jak już mówiono, wyprowadzenie wzorów w przeszłości było wyłącznym przywilejem Człowieka. Istotny wzrost mocy obliczeniowej nowoczesnych komputerów związany z szybkością procesorów (CPU) oraz większą pamięcią operacyjną (RAM) umożliwia skuteczne generowanie wzorów. Zaczniemy od najprostszych wzorów typu (3) i (4).
Do obliczenia wyznacznika wykorzystamy algorytm na podstawie jego definicji, tzn.
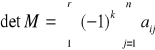
,
gdzie
r - ilość składników detM ( w przypadku pełnej macierzy r = n! ).
j - indeksy w każdym składniku, które tworzą permutację,
k - ilość inwersji w permutacji, tworzonej indeksami j.
Na rys. 3-4c,d,e,f i rys. 3-6 pokazano przykład zastosowania algorytmu IK do obliczenia wyznacznika macierzy.
Dla dogodności podania algorytmu generowania formuły z nawiasami zanotujemy powyższy wzór w postaci kolumn (Rys. 3-4g). Pogrubioną czcionką w każdej kolumnie zaznaczonę nowe elementy. Na dole w każdej kolumnie obliczymy różnicę w ilości nowych elementów w porównaniu z poprzednią kombinacją.
Algorytm generowania nawiasów oparty jest na wykorzystaniu ilości nowych elementów w i-tej kombinacji (kołumnie) w porównaniu z i+1-szą kombinacją, tzn.
k[i]=Ln[i]-Ln[i+1], i=1...Nd,
gdzie k[i] oznacza różnicę nowych elementów pomiędzy i-tą a i+1-szą kolumnami, Ln[i] - liczba nowych elementów i-tej kolumny, Nd- ilość składników (kolumn) wzoru. Ln[1]=Ln[Nd+1]=n.
Dodatnia liczba zanotowana pod i-tą kolumną oznacza ilość kolejno otwierających się nawiasów po pierwszym, drugim itd. nowym elemencie, zaś ujemna oznacza ilość zamykających się nawiasów po ostatnim elemencie. Różnica zerowa oznacza nieobecność nawiasów. Ponieważ w formule ilość otwierających się nawiasów powinna być równa ilości zamykających się nawiasów, to suma liczb w dodatkowym wierszu równa się zero.
Ustawienie znaków w formule
W podanym algorytmie ważną rolę odgrywa poziomowa struktura formuły wyznacznika (rys. 3-4g). Pierwszy poziom wzoru odpowiada pierwszym param otwierającego i zamykającego nawiasu. Drugi poziom odpowiada pierwszym param nawiasów wewnątrz pierwszej (górnej) pary itd. Na ostatnim poziomie w stosunku do odpowiedniej pary nawiasów na pierwszym poziomie występują składniki bez nawiasów. Każdy wzór wyznacznika można podzielić na składniki pewnego poziomu. Na rys. 3-4g przykładowy wzór mieści trzy składniki na pierwszym poziomie. Wewnątrz pierwszego poziomu oznaczonego jako „składnik 1” mamy trzy składniki (lub podskłądniki) drugiego poziomu tzn. składniki 1.1, 1.2, 1.3. Wewnątrz składniku 1.1 są dwa podskładniki trzeciego poziomu: 1.1.1 i 1.1.2.
Algorytm generowania wielunawiasowego wzoru wyznacznika oparty jest na zasadzie minimalnej ilości symboli niezbędnych dla odnotowania tej formuły oraz minimalnej ilości operacji arytmetycznych niezbędnych do jego obliczenia. Łatwo udowodnić, że znaki ujemne lub dodatnie należy zapisywać wyłącznie w środku pary nawiasów lub po ich zamknięciu. To oznacza, że po ostatnim otwartym nawiasie pewnego składnika zawsze musi występować znak plus. Na przykład, zamiast fragmentu wzoru +eh(-ko+ln) składającego się z 11 symboli notujemy krótszy 10 symbolowy wzór -eh(ko-ln).
Algorytm ustalenia znaku przed kolejnym składnikiem zależy od typu i ilości nawiasów. Niech
i oznacza numer bieżącego poziomu formuły,
k - ilość nawiasów bieżącego składnika : k=0 bez nawiasów,
k>0 dla otwierających nawiasów, k<0 dla zamykających nawiasów.
Po - tablica poziomów wzoru: w Po[i] notujemy znak i-tego poziomu formuły
(0 dla plusa i 1 dla minusa).
Znak Po[1] (tzn. dla i =1 ) taki sam jak w bieżącej permutacji.
Bieżący znak w formule dla i >1 notujemy jako wynik operacji XOR między znakiem Po[i] oraz znakiem bieżącej permutacji.
Znak tablicy poziomu ustawiamy tylko przy otwieraniu nawiasów (k>0).
W tym przypadku znaki tablicy poziomu od Po[i+1] do Po[i+k] notujemy jako wynik operacji XOR nad znakami od Po[1] do Po[i-1] oraz bieżącym znakiem .Poziom formuły dla następnej permutacji ustawiamy jako i+k.
Należy zaznaczyć, że wadą opracowanego algorytmu generowania wzorów jest obecność zbędnych nawiasów jak pokazano na przykładzie rys. 3-4g. Dla usunięcia pary nawiasów w niektórym składniku na i-tym poziomie należy w dodatkowej procedurze wykorzystać prosty algorytm oparty na badaniu ilości jego podskładników (rys. 4-3h). Przy jednym podskładniku parę nawiasów usuwamy zaś przy większej ilości - nie usuwamy.
Generowanie i upraszczanie wzorów do obliczenia wyznaczników na podstawie wykorzystania IK oraz efektu pływającego nawiasu (rys.3-5, rys.3-4e) pokażemy na przykładzie macierzy M
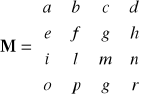
Det M=
+afmr-afnq-aglr+agnp+ahlq-ahmp-bemr+benq+bgir-bgno-bhiq+bhmo
+celr-cenp-cfir+cfno+chip-chlo-delq+demp+dfiq-dfmo-dgip+dglo.
Ilość operacji arytmetycznych wynosi: [*]=72, [±]=23
Ciekawym przykładem generowania wielonawiasowego wzoru jest symboliczny wyznacznik podanej pełnej macierzy 4x4.
DetM =
+a(f(m⋅r-n⋅q)-g(l⋅r-n⋅p)+h(l⋅q-m⋅p))-b(e(m⋅r-n⋅q)-g(i⋅r-n⋅o)+h(i⋅q-m⋅o))
+c(e(l⋅r-n⋅p)-f(i⋅r-n⋅o)+h(i⋅p-l⋅o))-d(e(l⋅q-m⋅p)-f(i⋅q-m⋅o)+g(i⋅p-l⋅o)).
Widzimy, że dzięki wykorzystaniu nawiasów zmniejszono ilość operacji mnożeń {teraz mamy: [*]=40, [±]=23, [(]=16}
W celu dalszej minimalizacji ilości operacji arytmetycznych uproszczenie (faktoryzację) wzoru:
DetM=
(a⋅f-b⋅e) (m⋅r-n⋅q)-(a⋅g-c⋅e)(l⋅r-n⋅p)+(a⋅h-d⋅e)(l⋅q-m⋅p)+
+(b⋅g-c⋅f)(i⋅r-n⋅o)-(b⋅h-d⋅f)(i⋅q-m⋅a)+(c⋅h-d⋅g)(i⋅p-l⋅o).
{mamy: [*]=30,[±]=17, [(]=12}
Dalsze uproszczenie wzoru jest możliwe kosztem jego zagnieżdżania
(ciągu wzorów):
f1=m⋅r-n⋅q; f2=l⋅r-n⋅p; f3=l⋅g-m⋅p; f4=i⋅r-n⋅o; f5=i⋅q-m⋅a; f6=i⋅p-l⋅o;
DetM= a(f⋅f1-g⋅f2+h⋅f3)-b(e⋅f1-g⋅f4+h⋅f5)+c(e⋅f2-f⋅f4+h⋅f6)-d(e⋅f3-f⋅f5+g⋅f6).
Ostatecznie otrzymaliśmy wzór, zawierający następującą ilość operacji:
{[*]=28, [±]=17, [(]=4, [=]=6}.
Na końcu zaznaczymy, że generowanie wielo nawiasowego wzoru wyznacznika bez zastosowania operacji dzielenia jest dodatkowym przykładem zastosowania permutacji oraz inwersji.
2
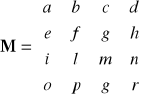
Wyszukiwarka
Podobne podstrony:
Teoria komunikacji jezykowej. Wstep, polonistyka
Wstęp do kulturoznawstwa, Kulturoznawstwo, Teoria Kultury
Teoria psychoanalizy, Religioznawstwo, I rok, Wstęp do psychologii
Wstep do nauki o panstwie i polityce (2), Teoria polityki
Inżynieria - Teoria, OiO - zarz, sem 1, WSTĘP DO INŻYNIERII JAKOŚCI I ZARZĄDZANIA ŚRODOWISKOWEGO
Teoria Polityki Panstwo, Wstęp do nauk o państwie
Gewert M, Skoczylas Z Wstęp do analizy i algebry Teoria, przykłady, zadania wyd 2
Logika i teoria mnogości Wstęp do logiki
wstęp i teoria notki
W10a Teoria Ja wstep
TEORIA I POLITY(1), Wstęp do nauki o państwie i prawie
teoria DHF, Wstęp do informatyki gospodarczej, Wstęp do informatyki gospodarczej
Teoria z Elektrotechniki, 1 Wstęp, Rodzaje Kanałów Transmisyjnych
F2 W11 Teoria względności wstęp
Wykład wstęp teoria
Hempel - wstęp, Studia (europeistyka), nauka o polityce, Teoria polityki, ćwiczenia 3
Logika i teoria mnogości Wstęp do logiki
więcej podobnych podstron