RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH
ZBIORY W PRZESTRZENI Rn
Definicja przestrzeni n-wymiarowej:
Przestrzenią n-wymiarową Rn nazywamy zbiór wszystkich uporządkowanych układów (x1,x2,...,xn) n liczb rzeczywistych, dla n>1.
Układy (x1,x2,...,xn) nazywamy punktami przestrzeni Rn, liczby x1,x2,...,xn - współrzędnymi prostokątnymi tych punktów.
Definicja przestrzeni dwuwymiarowej:
Przestrzenią dwuwymiarową (płaszczyzną) nazywamy zbiór wszystkich par uporządkowanych (x,y), gdzie x,y![]()
R, oznaczamy przez R2. Elementy (x,y) nazywamy punktami płaszczyzny. Liczby x,y nazywamy współrzędnymi kartezjańskimi punktów (x,y).
Definicja przestrzeni trójwymiarowej:
Przestrzenią trójwymiarową (przestrzenią) nazywamy zbiór wszystkich trójek uporządkowanych (x,y,z), gdzie x,y,z![]()
R, oznaczamy przez R3. Elementy (x,y,z) nazywamy punktami przestrzeni. Liczby x,y,z nazywamy współrzędnymi kartezjańskimi punktów (x,y,z).
Definicja odległości punktów:
Odległością dAB punktów A(a1,a2,...,an) i B(b1,b2,...,bn) przestrzeni Rn jest określona wzorem:
![]()
n=1 ![]()
n=2 ![]()
n=3 ![]()
Niech r oznacza dowolną liczbę rzeczywistą dodatnią, tj. r![]()
R+.
Definicja otoczenia:
Otoczeniem Q(P0,r) punktu P0(a1,a2,...,an) o promieniu r nazywamy zbiór wszystkich punktów P(x1,x2,...,xn), dla których ![]()
.
Definicja sąsiedztwa:
Sąsiedztwem S(P0,r) punktu P0(a1,a2,...,an) o promieniu r nazywamy zbiór wszystkich punktów P(x1,x2,...,xn), dla których ![]()
.
Niech O oznacza punkt O(0,0,...,0) ![]()
Rn.
Definicja zbioru ograniczonego i nieograniczonego:
Zbiór Z![]()
Rn nazywamy ograniczonym, jeżeli istnieje taka liczba r>0, że Z![]()
Q(0,r), natomiast nieograniczonym, gdy taka liczba nie istnieje.
Niech n oznacza dowolną liczbę naturalną.
Definicja zbioru skończonego i nieskończonego:
Zbiór nazywamy skończonym, jeżeli należy do niego dokładnie n punktów. Zbiór nazywamy nieskończonym, jeżeli nie jest ani pusty ani skończony.
FAKT:
Zbiór ograniczony może być skończony lub nieskończony. Każdy zbiór skończony jest ograniczony.
Niech Z![]()
Rn.
Definicja punktu wewnętrznego:
Punkt P![]()
Z nazywamy punktem wewnętrznym zbioru Z, jeżeli ten zawiera pewne otoczenie punktu P.
Definicja zbioru otwartego:
Zbiór, którego każdy punkt jest punktem wewnętrznym, nazywamy zbiorem otwartym.
Z={(x,y,z): x2+y2+x2<1}
Definicja łuku zwykłego:
Łuk zwykły w przestrzeni Rn jest to zbiór wszystkich punktów P(x1,x2,...,xn) o współrzędnych:
x1=x1(t), x2=x2(t), ..., xn=xn(t) (1)
gdzie xi(t), i=1,2,...,n są to funkcje ciągłe, określone w przedziale <α,β>, przy czym różnym wartościom parametru t![]()
( α,β) odpowiadają różne punkty P.
Łuk zwykły nazywamy otwartym, jeżeli nie jest spełniona co najmniej jedna z równości xi(α)=xi(β), i=1,2,...,n, natomiast zamkniętym lub zwykłą krzywą zamkniętą, jeżeli każda z tych równości jest spełniona. Jeżeli funkcje (1) mają ciągłe pochodne w przedziale <α,β> oraz:
![]()
, dla t![]()
<α,β> (2)
to łuk zwykły nazywamy gładkim (regularnym).
Jeżeli natomiast przedział <α,β> można podzielić na skończoną liczbę podprzedziałów tak, aby w każdym z nich oddzielnie funkcje (1) miały ciągłe pochodne (na końcach podprzedziałów pochodne jednostronne) oraz spełniony był warunek (2), to łuk nazywamy kawałkami gładkim.
Przykład łuku gładkiego: Przykład łuku kawałkami gładkiego:
Z 1
0<t<2π -1 1
-1
Y
X
Definicja obszaru:
Obszar jest to taki zbiór otwarty, którego każde dwa punkty można połączyć łukiem zwykłym (łamaną) całkowicie w zawartą.
A i B są obszarami
A![]()
B nie jest obszarem
UWAGA: Obszar może być zarówno ograniczony jak i nieograniczony.
Definicja punktu skupienia:
Punkt P nazywamy punktem skupienia zbioru Z, jeżeli w każdym sąsiedztwie punktu P znajduje się punkt tego zbioru.
Definicja zbioru domkniętego:
Zbiór domknięty jest to zbiór, do którego należą wszystkie jego punkty skupienia.
Definicja punktu odosobnionego:
Punkt P![]()
Z, który nie jest punktem skupienia zbioru Z, nazywamy punktem odosobnionym tego zbioru.
Definicja punktu brzegowego:
Punkt P nazywamy punktem brzegowym zbioru Z, jeżeli w każdym otoczeniu tego punktu znajduje się zarówno punkt zbioru Z jak i punkt, który do tego zbioru nie należy.
Punkty brzegowe
Definicja brzegu zbioru:
Brzeg zbioru jest to zbiór wszystkich punktów brzegowych tego obszaru.
Definicja obszaru domkniętego:
Obszar D wraz z brzegiem nazywamy obszarem domkniętym i oznaczamy symbolem ![]()
.
Definicja krzywej Jordana:
Krzywą Jordana nazywamy zwykłą krzywą zamkniętą w przestrzeni R2.
UWAGA: Krzywa Jordana dzieli płaszczyznę na dwa obszary. Jeden z tych obszarów jest ograniczony i nazywamy go wnętrzem krzywej Jordana, drugi z tych obszarów jest nieograniczony.
Definicja obszaru jednospójnego i wielospójnego:
Obszar w przestrzeni R2 nazywamy jednospójnym, jeżeli należy do niego wnętrze każdej leżącej w nim krzywej Jordana. Obszar, który nie jest jednospójny, nazywamy obszarem wielospójnym.
pierścień kołowy
R
Obszar jednospójny Obszar wielospójny
Definicja:
Jeżeli brzeg obszaru w przestrzeni R2 składa się z rozłącznych krzywych Jordana, łuków zwykłych otwartych i punktów, to ich łączną liczbę n nazywamy rzędem spójności i obszar nazywamy n-spójnym.
FUNKCJE WIELU ZMIENNYCH
Definicja funkcji wielu zmiennych:
Funkcją n zmiennych x1,x2,...,xn określoną Z![]()
Rn nazywamy przyporządkowanie każdemy punktowi P(x1,x2,...,xn)![]()
Z dokładnie jednej liczby z![]()
R. Zbiór Z nazywamy dziedziną tej funkcji. Piszemy przy tym:
z=f(x1,x2,...,xn), dla (x1,x2,...,xn)![]()
Z
lub krótko:
z=f(P), dla P![]()
Z
Symbole:
x1,x2,...,xn oznaczają zmienne niezależne
z oznacza zmienną zależną
f oznacza symbol przyporządkowania
UWAGA: Jeżeli funkcja f jest określona pewnym wzorem i jej dziedzina nie jest podana, to należy przyjąć, że jest ni zbiór wszystkich punktów P(x1,x2,...,xn), dla których wzór ten ma sens liczbowy. Jest to tzw. dziedzina naturalna.
Przykład: Wyznaczyć dziedzinę naturalną funkcji f(x,y)=![]()
.
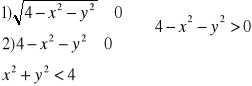
2
Df={(x,y)![]()
R2: x2+y2<4}
-2 2
-2
Definicja funkcji ograniczonej:
Funkcję f(P) nazywamy ograniczoną w zbiorze Z, jeżeli istnieje taka liczba M, że dla każdego P![]()
Z spełniona jest nierówność:
|f(P)| < M
Interpretacja geometryczna funkcji dwóch zmiennych:
Każdemu punktowi P(x,y)![]()
Z![]()
R2 przyporządkowujemy dokładnie jeden punkt (x,y,z) w przestrzeni OXYZ, przy czym Z=f(x,y).
Zbiór wszystkich punktów (x,y,f(x,y)), gdy (x,y)![]()
Z nazywamy wykresem funkcji dwóch zmiennych.
Z
z=f(x,y)
(x,y,f(x,y))
Y
(x,y) Z
X
Przykład: Z
z=2x2+3y2
x=0![]()
z=3y2
y=0![]()
z=2x2
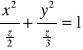
Y
X
GRANICE NIEWŁAŚCIWE FUNKCJI WIELU ZMIENNYCH
Definicja:
Mówimy, że ciąg punktów (Pk), k=1,2,..., w przestrzeni Rn jest zbieżny do punktu P0 i piszemy Pk→P0 wtedy i tylko wtedy, gdy:
![]()
Jeżeli ![]()
oznacza k-ty wyraz ciągu punktów (Pk), a ![]()
punkt stały, to:
![]()
Przykład:
![]()
k→![]()
k→![]()
k→![]()
P0 (0, 2, 0)
Rozważmy zbiór Z![]()
Rn, w którym jest określona funkcja z=f(P). Niech P0![]()
Z będzie punktem skupienia tego zbioru.
Definicja Heinego granicy funkcji:
Liczbę g nazywamy granicą funkcji f(P) w punkcie P0, jeżeli dla każdego ciągu punktów (Pk), Pk![]()
Z, Pk![]()
P0, zbieżnego do P0, ciąg (f(Pk)) jest zbieżny do g. Piszemy przy tym:
![]()
Przykład: Obliczyć ![]()
D={(x,y)![]()
R2: x![]()
y}
Weźmy ciąg punktów Pk(xk,yk)![]()
(0,0)
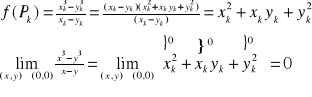
Definicja Cauchy'ego granicy funkcji:
![]()
FAKT:
Definicje Heinego i Cauchy'ego granicy funkcji n-zmiennych są równoważne.
UWAGA: Z definicji Heinego korzystamy często w przypadkach, których celem jest wykazanie, że pewna granica nie istnieje. Wystarczy wówczas udowodnić, że istnieją dwa ciągi (Pk') i (Pk”) punktów dziedziny rozważanej funkcji zbieżnej do punktu P0, Pk'![]()
P0, Pk”![]()
P0, dla których odpowiednie ciągi wartości funkcji (f(Pk')) i (f(Pk”)) nie są zbieżne do tej samej granicy g.
Przykład: Wykazać, że granica podwójna ![]()
nie istnieje.
Niech:
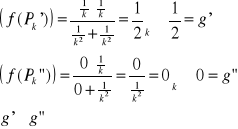
GRANICE ITEROWANE
Niech funkcja f będzie funkcją dwóch zmiennych.
Definicja:
Jeżeli istnieje liczba:
![]()
(1)
to nazywamy ją granicą iterowaną funkcji f(x,y), gdy najpierw y→y0, a następnie x→x0.
Definicja:
Jeżeli istnieje liczba:
![]()
(2)
to nazywamy ją granicą iterowaną funkcji f(x,y), gdy najpierw x→x0, a następnie y→y0.
UWAGA: Istnienie granicy funkcji w punkcie P0(x0,y0) jest niezależne od istnienia granic iterowanych (1) i (2). Granica (podwójna) funkcji f(x,y) może więc nie istnieć, natomiast granice (1) i (2) mogą istnieć i na odwrót. Ponadto, jeżeli granice iterowane istnieją, to mogą być różne.
Przykład: Obliczyć granice iterowane funkcji f(x,y)=![]()
w punkcie (0,0).
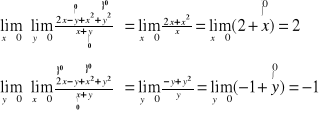
CIĄGŁOŚĆ FUNKCJI n - ZMIENNYCH
Definicja ciągłości funkcji w punkcie:
Funkcja f jest ciągła w punkcie P0 wtedy i tylko wtedy, gdy ![]()
.
UWAGA: Jeżeli funkcja n - zmiennych f(x1,x2,...,xn) jest w tym punkcie ciągła, to dla każdego k=1,2,...,n funkcja ![]()
jednej zmiennej xk jest ciągła w punkcie xk(0). Twierdzenie odwrotne nie jest prawdziwe.
Definicja:
Funkcję f(P) nazywamy ciągłą w pewnym zbiorze, jeżeli jest ciągła w każdym punkcie tego zbioru.
Przykład: Określić wartość funkcji w punkcie (0,3) tak, aby funkcja ![]()
była ciągła w
tym punkcie.
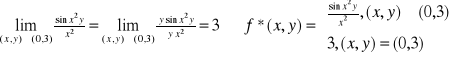
Twierdzenie o lokalnym zachowaniu znaku:
Jeżeli funkcja f(P), określona w pewnym otoczeniu punktu P0, jest w tym punkcie ciągła i f(P0)>0 [albo f(P0)<0], to istnieje takie sąsiedztwo S punktu P0, że dla każdego punktu P![]()
S jest spełniona nierówność f(P)>0 [albo odpowiednio f(P)<0].
Twierdzenie o ograniczoności funkcji:
Jeżeli funkcja f(P) jest ciągła w obszarze domkniętym i ograniczonym ![]()
, to jest w tym obszarze ograniczona.
Twierdzenie Weiestrassa o osiąganiu kresów:
Jeżeli funkcja f(P) jest ciągła w obszarze domkniętym i ograniczonym![]()
, to istnieje taki punkt P1![]()
![]()
, że
![]()
oraz istnieje taki punkt P2![]()
![]()
, że
![]()
Twierdzenie Darboux o przyjmowaniu wartości pośrednich:
Jeżeli funkcja f(P) jest ciągła w obszarze domkniętym i ograniczonym![]()
oraz:
![]()
to istnieje taki punkt P0![]()
![]()
, że f(P0)=μ.
Twierdzenie Cantora o ciągłości jednostajnej:
Jeżeli funkcja f(P) jest ciągła w obszarze domkniętym i ograniczonym![]()
, to dla każdej liczby ε>0 istnieje taka liczba δ>0, że dla każdych dwóch punktów P1![]()
![]()
i P2![]()
![]()
, których odległość ![]()
spełnia warunek ![]()
< δ spełniona jest nierówność:
|f(P1)-f(P2)|<ε
Podana właściwość funkcji ciągłej w zbiorze domkniętym i ograniczonym ![]()
nazywa się jednostajną ciągłością.
POCHODNE CZĄSTKOWE
Niech f oznacza funkcję n - zmiennych określoną w otoczeniu Q punktu![]()
. Oznaczmy symbolem Δxi przyrost zmiennej xi, 1<i<n, różny od zera i taki, żeby punkt ![]()
należał do otoczenia Q.
Definicja pochodnej cząstkowej rzędu pierwszego:
Granicę właściwą:
![]()
nazywamy pochodną cząstkową rzędy pierwszego funkcji f(P) względem zmiennej xi w punkcie P0 i oznaczamy symbolem ![]()
.
Definicja pochodnej cząstkowej rzędu pierwszego funkcji dwóch zmiennych:
![]()
, h1 oznacza przyrost zmiennej x
![]()
, h2 oznacza przyrost zmiennej y
Przykład: Obliczyć pochodne cząstkowe:
f(x,y)=xy
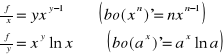
f(x,y,z)=x2yx3-xcox(yz)+
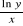
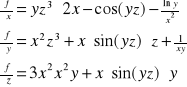
Definicja:
Jeżeli funkcja f(P) ma pochodną cząstkową rzędu pierwszego względem zmiennej x, w każdym punkcie pewnego zbioru Ω![]()
Rn, to mówimy, że funkcja ta ma pochodną cząstkową pierwszego rzędu względem zmiennej xi, w tym zbiorze.
W zbiorze Ω definiujemy funkcję, która każdemu punktowi P![]()
Ω przyporządkowuje ![]()
. Funkcję tą nazywamy pochodną cząstkową pierwszego rzędu funkcji f względem zmiennej xi i oznaczamy symbolem ![]()
, ![]()
, ![]()
.
Przykład: Obliczyć wartości pochodnych cząstkowych rzędu pierwszego funkcji ![]()
w punkcie
P0(2,-3).
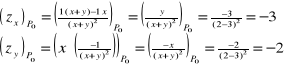
Definicja pochodnej cząstkowej rzędu drugiego:
Pochodne cząstkowe rzędu pierwszego pochodnych cząstkowych ![]()
, 1<i<n, nazywamy pochodnymi cząstkowymi rzędu drugiego funkcji z=f(x1,x2,...,xn).
Oznaczamy: ![]()
, 1<i, j<n
Inne oznaczenie: ![]()
Jeżeli i=j to zamiast ![]()
, piszemy ![]()
lub ![]()
UWAGA: Funkcja n zmiennych może mieć n2 różnych pochodnych cząstkowych rzędu drugiego.
Przykład: Obliczyć pochodne cząstkowe rzędu drugiego z funkcji z=sin(x2+y3).
zx=cos(x2+y3)2x
zy=cos(x2+y3)3y2
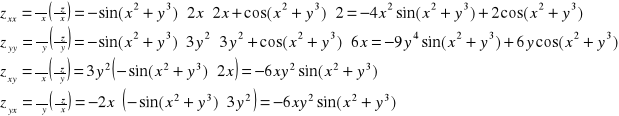
Definicja:
Pochodną ![]()
w przypadku, gdy i![]()
j nazywamy pochodną cząstkową mieszaną rzędu drugiego.
Twierdzenie Schwarza:
Jeżeli funkcja f(x1,x2,...,xn) ma w pewnym obszarze Ω![]()
Rn ciągłe pochodne cząstkowe mieszane rzędu drugiego ![]()
oraz ![]()
, to w każdym punkcie tego obszaru: ![]()
=![]()
.
Definicja pochodnej cząstkowej rzędu trzeciego:
Pochodną cząstkową rzędu pierwszego pochodnej cząstkowej rzędu drugiego nazywamy pochodną cząstkową rzędu trzeciego.
Definicja:
Pochodną cząstkową rzędu n, określoną za pomocą różniczkowań względem co najmniej dwóch różnych zmiennych nazywamy pochodną cząstkową mieszaną rzędu n.
UWAGA: Zachodzi tu również twierdzenie Schwarza, tzn.:
Jeżeli funkcja f(x1,x2,...,xn) ma pochodne cząstkowe mieszane różniące się tylko kolejnością różniczkowania względem zmiennych x1,x2,...,xn, przy tej samej liczbie różniczkowań względem każdej z tych zmiennych i jeżeli pochodne są ciągłe w obszarze Ω![]()
Rn, to są w tym obszarze równe.
Przykład: Obliczyć pochodne cząstkowe rzędu trzeciego funkcji z=x3y+2xy2+5
zx=3x2y+2y2 zxx=6xy zxxx=6x zy=x3+4xy zyy=4x zyyy=0
zxy=3x2+4y zyx=3x2+4y
zxxy=6x zyxx=6x zxyx=6x zyyx=4 zxyy=4 zyxy=4
Niech Z oznacza pewien zbiór w przestrzeni Rn.
Definicja:
Klasą Cn(Z) nazywamy zbiór wszystkich funkcji f(P), mających w zbiorze Z ciągłe pochodne cząstkowe do rzędu n włącznie.
EKSTREMA FUNKCJI WIELU ZMIENNYCH
Niech f(P) będzie funkcją n zmiennych określoną w pewnym otoczeniu punktu P0![]()
Rn.
Definicja ekstremum lokalnego:
Mówimy, że funkcja f(P) ma w punkcie P0 maksimum lokalne [minimum lokalne], jeżeli istnieje takie sąsiedztwo S punktu P0, że dla każdego P![]()
S spełniona jest nierówność:
f(P) < f(P0) [f(P) > f(P0)]
Maksima i minima lokalne nazywamy ekstremami lokalnymi. Jeżeli zamiast nierówności słabych jest spełniona odpowiednia nierówność mocna:
f(P) < f(P0) lub f(P) > f(P0)
to ekstremum nazywamy właściwym, tj. odpowiednio lokalnym maksimum właściwym lub lokalnym minimum właściwym. maksimum: minimum:
f(P0)
f(P)
f(P)
z=f(x,y)
z=f(x,y) f(P0)
P P0 P0 P
Weźmy funkcję f(x,y) określoną w pewnym otoczeniu punktu P0![]()
R2.
Twierdzenie: warunek konieczny istnienia ekstremum:
Jeżeli funkcja f(x,y) ma pochodne cząstkowe rzędu pierwszego w punkcie P0(x0,y0) i ma w tym punkcie ekstremum, to:
fx(P0)=0 i fy(P0)=0 (1)
Definicja:
Punkt P0(x0,y0), w którym spełniony jest warunek (1) nazywamy punktem stacjonarnym.
FAKT: o lokalizacji ekstremów funkcji:
Funkcja może mieć ekstrema tylko w punktach, w których wszystkie jej pochodne pierwszego rzędu są równe zero, albo w punktach, w których choć jedna z tych pochodnych nie istnieje.
Twierdzenie: warunek wystarczający istnienia ekstremów:
Jeżeli funkcja f(x,y) jest klasy C2 w pewnym otoczeniu punktu P0(x0,y0), a ponadto:
fx(P0)=0 i fy(P0)=0
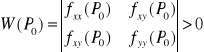
to funkcja f(x,y) ma w punkcie P0 maksimum właściwe, gdy: fxx(P0)<0
natomiast minimum właściwe, gdy: fxx(P0)>0
UWAGA: Jeżeli spełniony jest warunek konieczny istnienia ekstremum oraz W(P0)<0 to funkcja f(x,y) nie ma ekstremum w punkcie P0, natomiast jeśli W(P0)=0, to w punkcie P0 może być ekstremum jak i nie.
Przykład: Zbadać istnienie ekstremum funkcji
a) ![]()
, D:(x,y)![]()
R2.
warunek konieczny
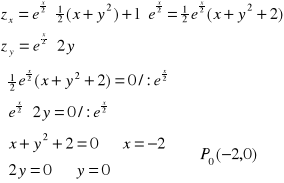
warunek wystarczający
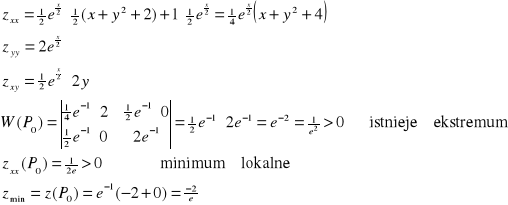
b) f(x,y)=x∙y, D: R2
warunek konieczny
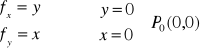
warunek wystarczający
fxx=0
fyy=0 brak ekstremum
fxy=0
Przykład: Wyznaczyć ekstrema funkcji f(x,y)=3x2y-x3-y4, D: R2
warunek konieczny
warunek wystarczający
fxx=6y-6x
fyy=-12y2
fxy=6x
Zauważmy, że jeśli 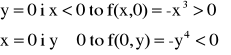
w P0(0,0) nie istnieje ekstremum (nie jest
spełniona definicja).
WARTOŚĆ NAJWIĘKSZA I NAJMNIEJSZA FUNKCJI
Definicja wartości największej i najmniejszej funkcji na zbiorze:
Liczbę m nazywamy wartością najmniejszą na zbiorze A![]()
Df, jeżeli w tym zbiorze istnieje punkt, w którym ta funkcja przyjmuje wartość m oraz dla dowolnego punktu (x,y)![]()
A zachodzi nierówność:
f(x,y) > m
Liczbę M nazywamy wartością największą na zbiorze A![]()
Df, jeżeli w tym zbiorze istnieje punkt, w którym ta funkcja przyjmuje wartość M oraz dla dowolnego punktu (x,y)![]()
A zachodzi nierówność:
f(x,y) < M
Liczby m i M nazywamy także odpowiednio minimum i maksimum globalnym funkcji f na zbiorze A.
UWAGA: Funkcja f określona na obszarze domkniętym ![]()
może przyjmować wartość największa i najmniejszą nie tylko w punktach, w których ma ekstremum lokalne, ale też na brzegu obszaru ![]()
.
FAKT: Poszukując wartości największej i najmniejszej należy:
zbadać istnienie ekstremów funkcji w obszarze
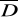
zbadać zmienność funkcji na brzegu
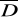
, co sprowadza się do poszukiwania ekstremów funkcji jednej zmiennej
Przykład: Wyznaczyć wartość największą i najmniejszą funkcji z=(x-y)2+xy-x na obszarze
D={(x,y)![]()
R2: 0<x<1 ^ 0<y<13}.
zx=2(x-y)+y-1=2x-y-1
zy=2(x-y)∙(-1)+x=-x+2y
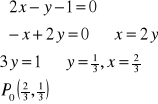
zxx=2
zyy=2
zxy=-1

x=0 0<y<1 f1(y)=y2
y=1 0<x<1 f2(x)=(x-1)2
x=1 0<y<1 f3(y)=y2-y
y=0 0<x<1 f4(x)=x2-x
POCHODNA KIERUNKOWA
Niech f(x,y) będzie funkcją klasy C1 w pewnym otoczeniu Q punktu P0(x0,y0) i niech P0s oznacza półoś o początku w punkcie P0.
Oznaczamy przez P dowolny punkt osi P0s, różny od P0, należący do otoczenia Q punktu P0.
Definicja pochodnej kierunkowej:
Granicę właściwą ![]()
nazywamy pochodną funkcji f kierunku półosi P0s, krótko pochodną kierunkową, w punkcie P0 i oznaczamy symbolem ![]()
, tj.:
![]()
GRADIENT FUNKCJI
Niech f(x1,x2,...,xn) będzie funkcją klasy C1 w pewnym otoczeniu punktu P0![]()
Rn.
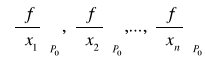
nazywamy gradientem funkcji f w punkcie P0 i oznaczamy symbolem grad f(P0).
FAKT: Interpretacja geometryczna gradientu:
Gradient funkcji w punkcie wskazuje kierunek najszybszego wzrostu funkcji w tym punkcie.
Przykład: Wyznaczyć gradient funkcji f(x,y)=x3y2+3x-y w punkcie P0(-2,1).
grad f=[3x2y2+3, 2yx3-1]
grad f(P0)=[15,-17]
FAKT: Związek gradientu z pochodną kierunkową:
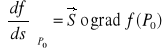
gdzie ![]()
oznacza wersor półosi P0s.
RÓŻNICZKOWANIE FUNKCJI ZŁOŻONEJ
Twierdzenie o pochodnej funkcji złożonej:
Jeżeli funkcja z=f(x1,x2,...,xn), n>0 jest klasy C1 w obszarze D![]()
Rn, a ponadto funkcje xi=xi(t), i=1,2,...,n mają pochodne w przedziale (α,β), oraz (x1,x2,...,xn)![]()
D, gdy t![]()
(α,β), to funkcja złożona zmiennej t:
z=f(x1(t), x2(t),...,xn(t))
ma pochodną w każdym punkcie przedziału (α,β), przy czym:
![]()
z=f(x(t), y(t))
![]()
Przykład: Obliczyć ![]()
funkcji z=x2+ysinx w punkcie t0=0, jeśli x=2t+et, y=et-sint.
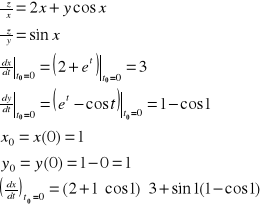
Zauważmy, że pochodne cząstkowe ![]()
oraz ![]()
funkcji złożonej z=f(x(t), y(t)) są także funkcjami złożonymi zmiennej t, tj.: ![]()
Przy założeniu istnienia i ciągłości pochodnych cząstkowych rzędu drugiego funkcji f(x,y) w rozważanym obszarze, istnienia drugich pochodnych funkcji x(t) i y(t) w przedziale (α,β) otrzymujemy wzór na pochodną rzędu drugiego funkcji złożonej w postaci:
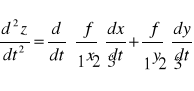
i dalej: pochodna pochodna
Analogicznie otrzymujemy wzory na pochodne cząstkowe wyższych rzędów.
Twierdzenie o pochodnych cząstkowych funkcji złożonej:
Jeżeli funkcja z=f(x1,x2,...,xn), n>2 jest klasy C1 w obszarze D![]()
Rn, a ponadto funkcje xi=xi(u1,u2,...,um)![]()
D1, to funkcja złożona m zmiennych:
z=f(x1(u1,u2,...,um), x2(u1,u2,...,um),..., xn(u1,u2,...,um))
ma pochodne cząstkowe rzędu pierwszego w każdym punkcie obszaru D1, przy czym:
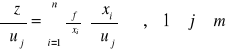
Analogicznie wyprowadzamy wzory na pochodne cząstkowe wyższych rzędów funkcji złożonej.
POCHODNE CZĄSTKOWE FUNKCJI ZŁOŻONEJ DWÓCH ZMIENNYCH
Załóżmy, że f(x,y)![]()
C2 w D1![]()
R2, a x=x(u,v) i y=y(u,v)![]()
C2 w obszarze D1![]()
R2. Niech (x,y)![]()
D, gdy (u,v)![]()
D1.
Na podstawie twierdzenia o pochodnych cząstkowych funkcji złożonej, otrzymujemy pochodne cząstkowe rzędu pierwszego:
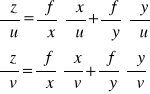
Stąd dalej pochodne cząstkowe rzędu drugiego wyrażają się zależnościami:
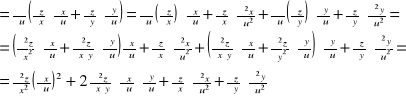
RÓŻNICZKA FUNKCJI DWÓCH ZMIENNYCH
Niech z=f(x,y) będzie funkcją dwóch zmiennych określoną w pewnym otoczeniu punktu P0(x0,y0).
Twierdzenie o przedstawieniu przyrostu funkcji:
Jeżeli funkcja f(x,y) ma w pewnym otoczeniu Q punktu P0(x0,y0) pochodne cząstkowe fx(x,y) i fy(x,y), które są ciągłe w punkcie P0, oraz (x0+Δx, y0+Δy)![]()
Q, to przyrost Δf taj funkcji, tj.:
Δf=f(x0+Δx, y0+Δy) - f(x0,y0)
można przedstawić w postaci:
Δf=fx(x0,y0)Δx + fy(x0,y0)Δy + ερ
gdzie: ![]()
, przy czym ε→0, gdy ρ→0.
WNIOSEK: Jeżeli funkcja f(x,y) ma w pewnym otoczeniu punktu P0(x0,y0) pochodne cząstkowe
rzędy pierwszego, które są ciągłe w tym punkcie, to jest ciągła w punkcie P0.
WNIOSEK: Jeżeli funkcja f(x,y) ma w pewnym otoczeniu punktu P0(x0,y0) ograniczone pochodne
cząstkowe rzędu pierwszego, to jest w tym punkcie ciągła.
Niech Δf i ρ będą określone tak, jak w twierdzeniu o przedstawieniu przyrostu funkcji oraz niech o(ρ) oznacza nieskończenie małą rzędu wyższego, niż ρ, gdy ρ→0.
Definicja
Funkcję f(x,y) nazywamy różniczkowalną w punkcie P0(x0,y0), jeżeli istnieją takie liczby A i B, że dla każdego dostatecznie małego ρ zachodzi:
Δf = AΔx + BΔy + o(ρ)
WNIOSEK: Funkcja f(x,y) jest różniczkowalna w punkcie P0(x0,y0) wtedy i tylko wtedy, gdy:
Δf = fx(x0,y0)Δx + fy(x0,y0)Δy + o(ρ)
Definicja różniczki zupełnej:
Składnik liniowy ze względu na Δx i Δy, tj.:
fx(x0,y0)Δx + fy(x0,y0)Δy
przyrostu Δf funkcji f(x,y), różniczkowalnej w punkcie P0(x0,y0), nazywamy różniczką zupełną funkcji f(x,y) w tym punkcie.
Różniczkę zupełną funkcji z=f(x,y) w punkcie P0(x0,y0), oznaczamy symbolem df(x0,y0), lub krótko df lub też dz.
Przyrosty Δx, Δy nazywamy różniczkami zmiennych niezależnych i oznaczamy odpowiednio symbolami dx i dy. Stąd:
df(x0,y0)![]()
fx(x0,y0)dx + fy(x0,y0)dy
dla każdego punktu P0(x0,y0), w którym funkcja f(x,y) jest różniczkowalna. Piszemy krótko:
![]()
Iloczyny:
![]()
i ![]()
nazywamy różniczkami cząstkowymi funkcji f(x,y) i oznaczamy odpowiednio dxf i dyf.
FAKT: Zastosowanie różniczki zupełnej:
Niech funkcja f ma ciągłe pochodne cząstkowe pierwszego rzędu w punkcie (x0,y0). Wtedy:
f(x0+dx, y0+dy)![]()
f(x0,y0)+df(x0,y0)
przy czym błąd tego przybliżenia, tj.: df - Δf, w stosunku do ρ dąży do zera, gdy ρ→0, tj.:
![]()
Przykład: Obliczyć przybliżoną wartość funkcji ![]()
.
f(x,y)= ![]()
x0=2 dx=0,1
y0=8 dy=0,05

Interpretacja geometryczna funkcji różniczkowalnej w punkcie:
Różniczkowalność funkcji z=f(x,y) w punkcie (x0,y0) oznacza, że istnieje płaszczyzna styczna (niepionowa) do wykresu tej funkcji w punkcie (x0,y0,f(x0,y0)).
FAKT: Równanie płaszczyzny stycznej do wykresu funkcji:
Niech funkcja f ma ciągłe pochodne cząstkowe ![]()
, ![]()
w punkcie (x0,y0). Wówczas płaszczyzna styczna wykresu funkcji f w punkcie o współrzędnych (x0,y0,f(x0,y0)) ma postać:
![]()
Z
(x0,y0,f(x0,y0))
z=f(x,y)
y0 Y
x0 (x0,y0)
X
Przykład: Wyznaczyć równanie płaszczyzny stycznej do wykresu funkcji ![]()
w
punkcie ![]()
. Z
z2=9-x2-y2
x2+y2+z2=9
Y
X
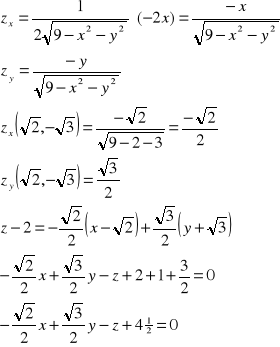
RÓŻNICZKI ZUPEŁNE DRUGIEGO I WYŻSZYCH RZĘDÓW
Niech z=f(x,y) jest klasy C2 w pewnym obszarze. Przy ustalonych wartościach różniczek dx i dy różniczek df jest pewną funkcją zmiennych x i y klasy C-1, w więc różniczkowalną w rozpatrywanym obszarze.
Definicja:
Różniczką zupełną rzędu drugiego funkcji f(x,y) nazywamy różniczkę zupełną funkcji df i oznaczamy d2f(x,y) bądź krótko d2f lub d2z.
Mamy zatem:
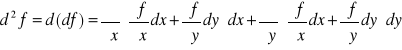
Korzystając z twierdzenia Schwarza o równości pochodnych cząstkowych otrzymujemy:
![]()
Definicja:
Różniczką zupełną rzędu n nazywamy różniczkę zupełną funkcji dn-1f i oznaczamy dnf(x,y), bądź krótko dnf lub dnz.
Stąd:
dnf=d(dn-1f), n=2,3,...
FAKT:
Jeżeli funkcja z=f(x,y) jest klasy Cn w pewnym obszarze, to różniczka dnf istnieje i:
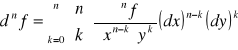
lub:
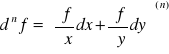
Twierdzenie Taylora:
Jeżeli funkcja f(P) n zmiennych, dla n>2 jest klasy Cn w pewnym otoczeniu Q punktu P0(x1(0),x2(0),...,xn(0)) oraz punkt P(x1(0)+h1,x2(0)+h2,...,xn(0)+hn)![]()
Q i P0![]()
P, to istnieje taka liczba θ![]()
(0,1), że:
![]()
(1)
gdzie ![]()
(x1(0)+θh1,x2(0)+ θh2,...,xn(0)+ θhn), a różniczki dif, i=1,2,...,n są liczone dla przyrostów h1,h2,...,hn.
Wzór (1) nazywamy wzorem Taylora. Ostatni składnik we wzorze Taylora nazywamy n-tą resztą wzoru Taylora i oznaczamy przez Rn.
FUNKCJA UWIKŁANA
Niech F(x,y) oznacza funkcję określoną w pewnym obszarze.
Definicja funkcji uwikłanej:
Jeżeli istnieje funkcja y=f(x), spełniająca w każdym punkcie x pewnego zbioru X warunek
F(x,f(x))=0
to nazywamy ją funkcją uwikłaną określoną w zbiorze X równaniem: F(x,y)=0
Mówimy też, że funkcja y=f(x), jest określona w sposób uwikłany równaniem F(x,y)=0.
Przykład: Funkcja ![]()
jest funkcją uwikłaną określoną równaniem x2+y2-1=0
F(x,y) y=?
Twierdzenie o istnieniu i jednoznaczności funkcji uwikłanej:
Jeżeli funkcja F(x,y) jest klasy C1 w pewnym otoczeniu punktu P0(x0,y0), a ponadto F(x0,y0)=0 i Fy(x0,y0)![]()
0 to istnieje dokładnie jedna ciągła funkcja uwikłana y=f(x) określona w pewnym przedziale (x0 - δ, x0 + δ) za pomocą równania F(x,y) i spełniająca warunek: f(x0)=y0.
Twierdzenie o różniczkowalności funkcji uwikłanej:
Jeżeli funkcja F(x,y) jest klasy C1 w pewnym otoczeniu punktu P0(x0,y0), a ponadto F(x0,y0)=0 i Fy(x0,y0)![]()
0, to funkcja uwikłana y=f(x) posiada w pewnym otoczeniu punktu x0 pochodną f'(x), przy czym:
![]()
Przykład: Obliczyć pierwszą pochodną funkcji uwikłanej y=y(x) danej równaniem: y2-arctgy-ex=0.
I sposób:
F(x,y)=y2-arctgy-ex
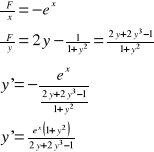
UWAGA: Jeżeli funkcja F(x,y) jest klasy C2 w pewnym otoczeniu punktu P0(x0,y0) oraz F(x0,y0)=0
i Fy(x0,y0)![]()
0, to funkcja ciągła y=f(x), określona w pewnym przedziale (x0 - δ, x0 + δ)
równaniem F(x,y)=0 i spełniająca warunek f(x0)=y0, posiada w pewnym otoczeniu
punktu x0 drugą pochodną.
II sposób:
y2-arctgy-ex=0
y=y(x)
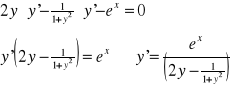
Przykład: Równanie x2+4y2-4=0 określa w pewnym otoczeniu punktu x0=0 dokładnie jedną ciągłą
funkcję uwikłaną y=f(x) spełniającą warunek f(0)=1. Obliczyć y”(0).
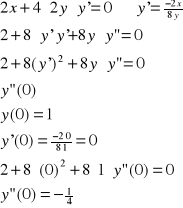
EKSTREMA FUNKCJI UWIKŁANEJ
Twierdzenie o ekstremach lokalnych funkcji uwikłanej:
Niech funkcja F(x,y) jest klasy C2 w pewnym otoczeniu punktu P0(x0,y0), a ponadto spełnione są warunki:
F(x0,y0)=0
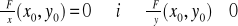
I(x0,y0)=
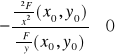
Wówczas funkcja uwikłana y=f(x) określona równaniem F(x,y)=0 przyjmuje w punkcie x0 ekstremum lokalne właściwe, przy czym jest to minimum właściwe, jeśli I(x0,y0)>0, natomiast maksimum właściwe jeśli I(x0,y0)<0.
UWAGA: Równość ![]()
jest warunkiem koniecznym, a nierówność ![]()
warunkiem wystarczającym istnienia ekstremum funkcji uwikłanej.
UWAGA: Algorytm znajdowania ekstremów lokalnych funkcji uwikłanej:
Punkty, w których funkcja uwikłana może mieć ekstrema lokalne, znajdujemy korzystając z warunku koniecznego istnienia ekstremum, tj. rozwiązujemy układ równań:
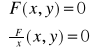
i wyznaczamy jego rozwiązanie postaci (x0,y0). Sprawdzamy dla otrzymanych punktów, czy spełniony jest warunek ![]()
.
W otrzymanych punktach (x0,y0) sprawdzamy warunek wystarczający istnienia ekstremum, tj. badamy, czy zachodzi warunek:
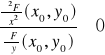
Na podstawie znaku ostatniego wyrażenia ustalamy rodzaj ekstremum.
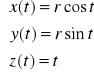
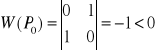
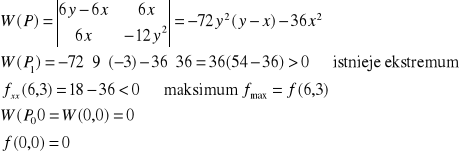
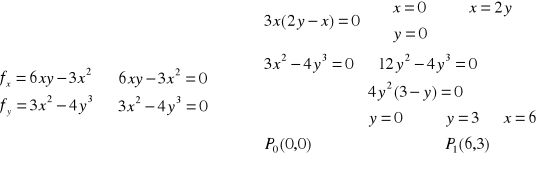
III
II
IV 1
I
P0
1
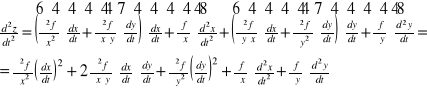
Wyszukiwarka