4.5.3. Lewar - zjawisko kawitacji
Na rys.4.6. przedstawiono przepływ cieczy w rurce ze zbiornika górnego do zbiornika dolnego po uprzednim zassaniu cieczy. Zakrzywioną rurkę wprowadzoną jednym końcem do naczynia (górnego), w celu umożliwienia wypływu cieczy nazywamy lewarem.
Napiszmy równanie Bernoulli'ego dla przekrojów „0” i „2”strugi cieczy.
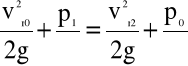
(4.67)
Założymy, że pole powierzchni swobodnej w zbiorniku górnym S0 jest dużo większe od przekroju rurki lewara f. Wykorzystując równanie ciągłości (4.55) mamy:
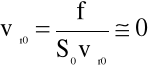
Wtedy średnia prędkość przepływu w lewarze:
![]()
(4.68)
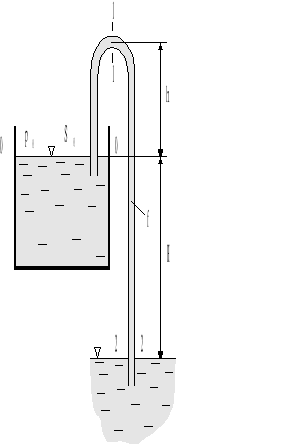
Rys.4.6. Lewar.
Z kolei, z równania Bernoulli'ego zapisanego dla przekrojów „1” i „2”
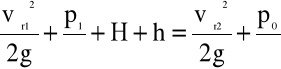
(4.69)
wynika, że ciśnienie w przekroju „1” lewara wynosi:
![]()
(4.70)
Wyciągamy zatem wniosek, że p1<p0
Przy pewnej, dostatecznie dużej wysokości h ciśnienie p1 może obniżyć się do ciśnienia wrzenia pv w temperaturze otoczenia i zaczną wytwarzać się pęcherzyki pary w kolanie lewara (przekroju „1”).
Po wytworzeniu się pary ciśnienie wzrasta i następuje jej skroplenie. Zjawisko takie, mające charakter okresowo zmienny nazywamy kawitacją. Towarzysząca kawitacji korozja i drgania akustyczne są zjawiskami niepożądanymi i niebezpiecznymi, których należy unikać.
4.5.4. Wypływ ustalony cieczy ze zbiornika przez mały otwór
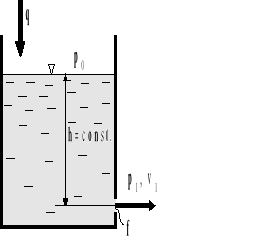
Rys.4.7. Ustalony wypływ cieczy ze zbiornika przez mały otwór.
Zbadajmy ustalony (rys.4.7) wypływ cieczy ze zbiornika przy założeniu, że przekrój otworu wypływowego jest mały.
Warunkiem gwarantującym stacjonarność wypływu jest stałość poziomu cieczy w zbiorniku, tj. h= const. Warunek ten spełniony jest wtedy, gdy strumienie objętościowe cieczy: wpływającej i wypływającej ze zbiornika są takie same. Oznacza to, że ![]()
.
Z równania Bernoulli'ego zapisanego dla przekrojów „0” i „1” (rys.4.7)
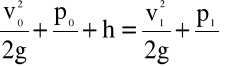
(4.71)
wynika, że
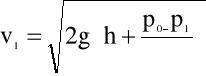
(4.72)
W przypadku, gdy ![]()
mamy:
![]()
(4.73)
Jest to, tzw. wzór Toricellego, określający teoretyczną prędkość wypływu cieczy doskonałej.
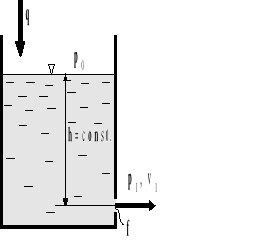
Rys.4.7. Ustalony wypływ cieczy ze zbiornika przez mały otwór.
Prędkość wypływu cieczy rzeczywistej obliczyć można za pomocą wzoru
![]()
(4.74)
gdzie ϕ - współczynnik poprawkowy prędkości uwzględniający lepkość płynu i charakter wypływu.
Rzeczywisty wydatek wypływu (rys.4.7) wynosi
![]()
(4.75)
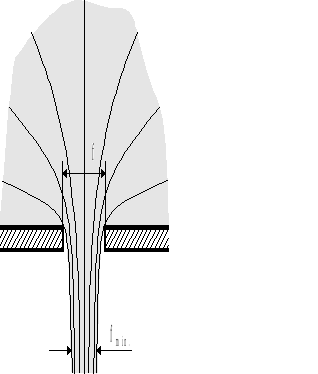
Rys.4.8. Zjawisko kontrakcji.
Wprowadzając tzw. współczynnik poprawkowy kontrakcji
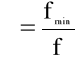
(4.76)
otrzymujemy wzór określający objętościowy strumień wypływu cieczy rzeczywistej:
![]()
(4.77)
gdzie
![]()
(4.78)
jest tzw. współczynnikiem poprawkowym wydatku wypływu.
4.5.5. Czas wypływu nieustalonego cieczy ze zbiornika przez mały otwór
Wypływ nieustalony cieczy ze zbiornika (rys.4.9.) ma miejsce wtedy, gdy:
1/ ![]()
- poziom cieczy w zbiorniku opada,
2/ ![]()
- poziom cieczy w zbiorniku podnosi się.
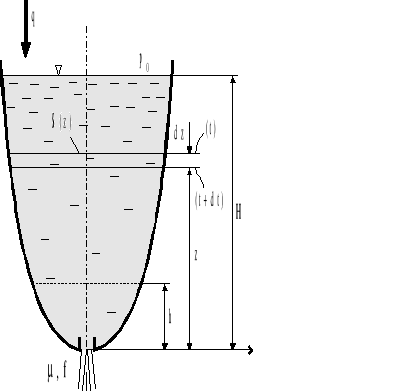
Rys.4.9. Nieustalony przepływ cieczy ze zbiornika przez mały otwór.
Bilans masy cieczy wypływającej i dopływającej do zbiornika w czasie dt jest następujący:
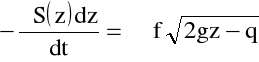
Stąd
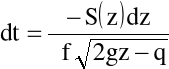
Czas częściowego opróżniania zbiornika obliczyć, zatem, można za pomocą wzoru:
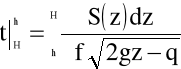
(4.79)
Czas całkowitego opróżniania zbiornika określa z kolei wzór:
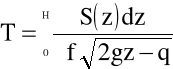
(4.80)
4.6. Zasada pędu w mechanice płynów
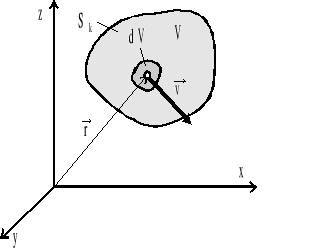
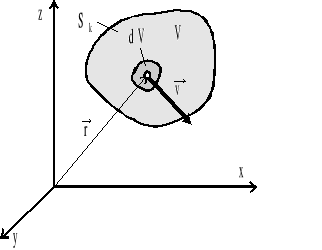
Rozważmy ustalony ruch płynu nieściśliwego (rys.4.10).
Rys.4.10. Obszar płynny płynu
Pęd elementu płynu o objętości dV:
![]()
(4.81)
Pęd bryły cieczy o objętości płynnej V wynosi:
![]()
(4.82)
Zgodnie z zasadą pędu mamy:
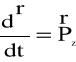
(4.83)
lub, po kolejnych przekształceniach:
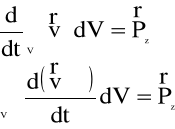
Ponieważ jednak założyliśmy wcześniej, że ruch cieczy jest ustalony, zatem:
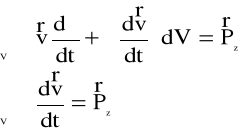
Zrzutujemy to równanie w kierunku osi x. Mamy:
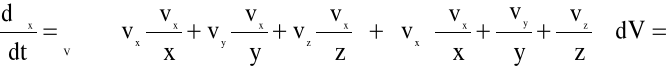
![]()
![]()
(4.84)
Pochodną
![]()
obliczyć, zatem można w sposób następujący:
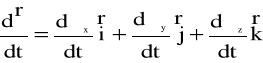
(4.85)
Wracając do równania (4.83) otrzymujemy wzór:
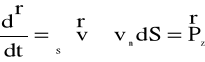
(4.86)
lub
![]()
(4.87)
Wzór (4.87) opisuje tzw. reakcję hydrodynamiczną, (napór hydrodynamiczny), tj. sięłę poruszająca się ciecz oddziaływa na ściankę ciała stałego.
4.7. Napór hydrodynamiczny cieczy na ściankę krzywaka
Zakrzywiony przewód o zmiennym przekroju poprzecznym (rys.4.10) nazywać będziemy krzywakiem.
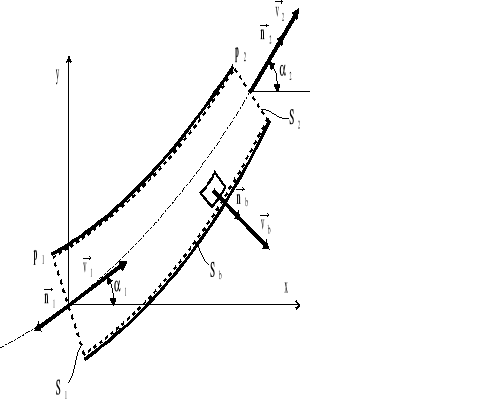
Rys.4.11. Ruch jednowymiarowy cieczy w krzywaku.
Zgodnie z zasadą pędu:
![]()
(4.88)
Zatem w rozważanym przypadku
![]()
(4.89)
Ponieważ powierzchnia ograniczająca rozważany obszar
![]()
(4.90)
otrzymujemy:
![]()
(4.91)
Ale
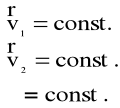
Stąd
![]()
Zatem
![]()
(4.92)
Oznaczmy ![]()
; jest to reakcja hydrodynamiczna (napór hydrodynamiczny cieczy na ściankę krzywaka). W świetle powyższego, po przekształceniu równania (4.92) otrzymujemy wzór opisujący wypadkowy wektor reakcji hydrodynamicznej na ścianki krzywaka.
![]()
(4.92a)
Zakładając, że krzywak usytuowany jest w płaszczyźnie xy, możemy obliczyć składowe reakcji hydrodynamicznej:
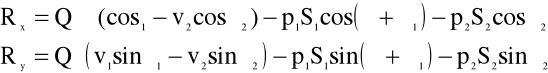
(4.93)
4.8. Zasada, krętu w mechanice płynów
Podobnie jak w p.4.6. rozważymy ustalony ruch płynu nieściśliwego o objętości V.
Rys.4.10. Obszar płynny płynu
Kręt elementu o objętości dV (rys.4.10).
![]()
(4.95)
lub
![]()
(4.96)
Zgodnie z zasadą krętu:
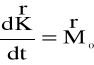
(4.97)
Zatem
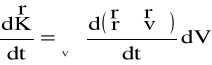
(4.98)
Ale
![]()
(4.99)
Po zrzutowaniu równania (4.98) w kierunku osi x ,mamy:
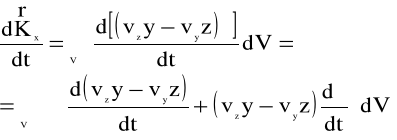
(4.100)
Z kolei, zgodnie z założeniem nieściśliwości płynu ρ=const, otrzymujemy:
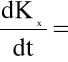
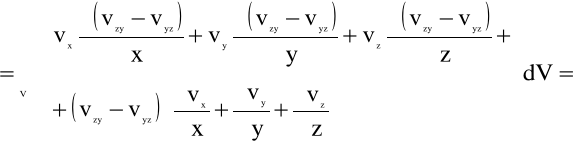
![]()
(4.101)
i następnie
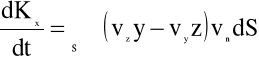
(4.102)
Zasadę krętu w mechanice płynów sformułować można w postaci równania:
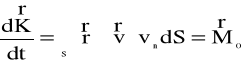
(4.103)
gdzie ![]()
jest momentem głównym sił zewnętrznych działających na rozważany obszar płynu. Moment reakcyjny:
![]()
. (4.104)
5. DYNAMIKA PŁYNÓW RZECZYWISTYCH
5.1. Klasyczne doświadczenie Reynoldsa.
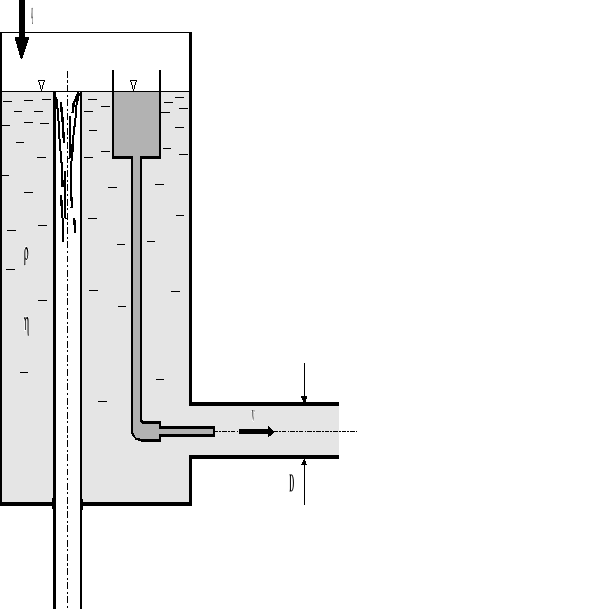
Rys.5.1. Doświadczenie Reynoldsa; schemat stanowiska doświadczalnego.
Reynolds zauważył, po raz pierwszy, że bezwymiarowe wyrażenie,
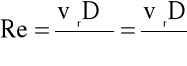
(5.1)
nazwane później na cześć Reynoldsa liczbą Reynoldsa, charakteryzuje rodzaj przepływu.
1) W przypadku, gdy liczba Reynoldsa ![]()
ma miejsce tzw. przepływ laminarny (rys.5.2),tzn. zabarwiona struga cieczy nie miesza się z cieczą bezbarwną, czyli wszystkie elementy płynu poruszają się równolegle do głównego kierunku przepływu. Między sąsiadującymi ze sobą warstewkami cieczy nie ma makroskopowej wymiany pędu.
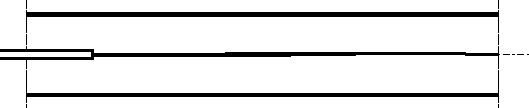
Rys.5.2. Przepływ laminarny.
W przedziale zmienności liczby Reynoldsa
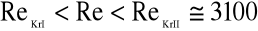
obserwujemy formę przejściową przepływu (rys.5.3), tzn. struga cieczy zabarwionej przyjmuje kształt falisty.
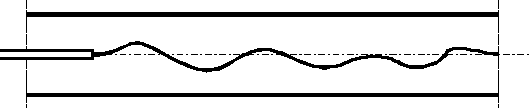
Rys.5.3. Forma przejściowa przepływu.
W szerokim zakresie liczb Reynoldsa
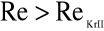
- przepływ jest turbulentny (burzliwy) (rys.5.4), tzn. struga zabarwionej cieczy ulega gwałtownemu rozproszeniu w cieczy bezbarwnej, a zatem występują dodatkowe, pulsacyjne składowe poprzeczne prędkości lokalnej elementów płynu i towarzysząca im makroskopowa wymiana pędu miedzy sąsiadującymi ze sobą warstewkami płynu.
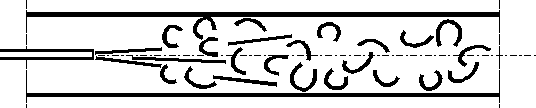
Rys.5.4. Przepływ turbulentny.
5.2. Różniczkowe równania ruchu płynu lepkiego wyrażone w naprężeniach
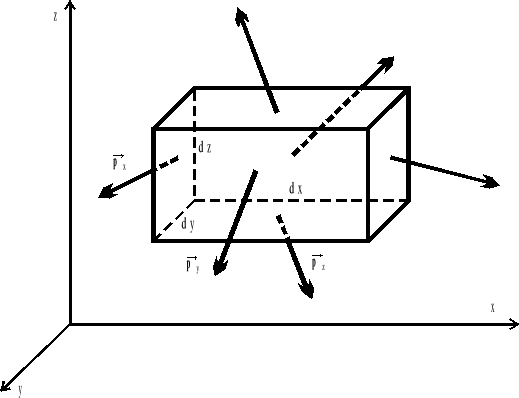
Jak wiadomo stan naprężenia w płynie opisany jest tensorem 2-go rzędu. Wyodrębnijmy element poruszającego się płynu rzeczywistego
Rys.5.5. Naprężenia działające na wyodrębniony element płynu.
Zgodnie z (1.34) na każdą ze ścianek przechodzących przez punkt A(x,y,z), (rys.5.5) po odrzuceniu otaczającego płynu, działają naprężenia:
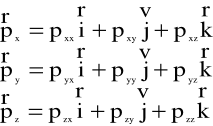
(5.2)
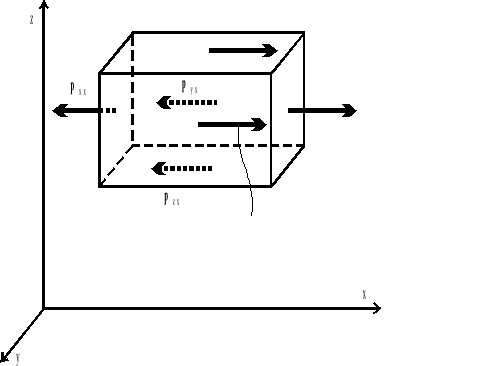
Rys.5.6. Bilans składowych sił powierzchniowych w kierunku osi x.
Natomiast na ścianki elementu przechodzące przez odległy od punktu M o elementarną odległość ![]()
punkt A', działają naprężenia odpowiednio (
), (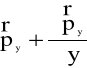
),(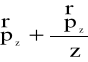
).
Z bilansu sił powierzchniowych i masowych (nie zaznaczonych na rys.5.6) w kierunku osi x wynika następujące równanie:
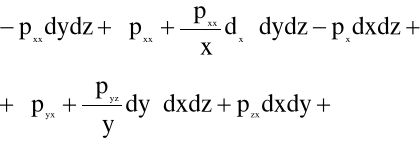
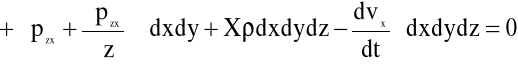
(5.3)
Dwa ostatnie wyrażenia w równaniu (5.3) są małymi wyższego rzędu w porównaniu z pozostałymi; można je zatem zaniedbać.
Po napisaniu podobnych równań wynikających z bilansu wszystkich sił działających na element płynu w kierunkach osi y i z i ich uporządkowaniu otrzymujemy układ różniczkowych równań ruchu płynu rzeczywistego wyrażonych w „naprężeniach”.
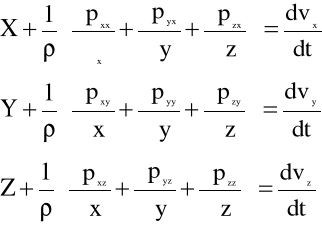
(5.4)
5.3.Postulat Boltzmanna
Zgodnie z zasadą krętu (rys.5.5),
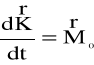
(5.5)
lub
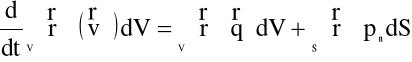
(5.6)
Dokonajmy kolejnych przekształceń równania (5.6), zrzutowanego w kierunku osi x, zakładając że gęstość płynu ρ=const.:
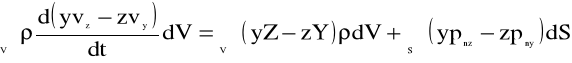
,
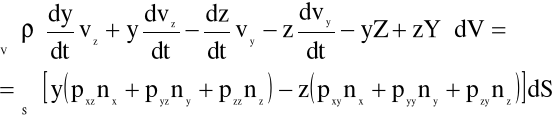
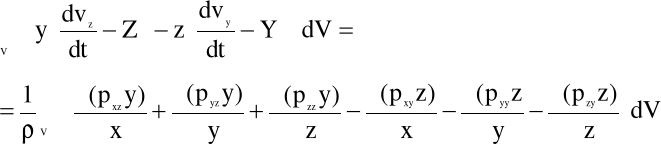
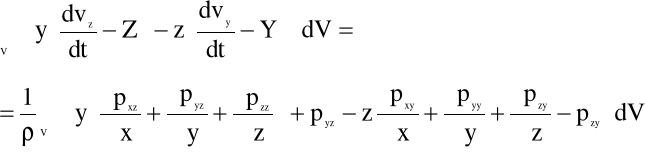
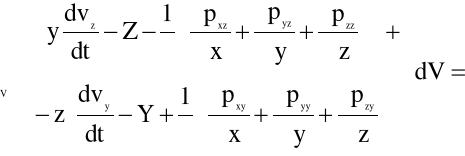
![]()
(5.7)
Postępując podobnie, tzn. rzutując równanie (5.6) w kierunkach osi: y i z a następnie uwzględniając w nich równania (5.4) otrzymujemy związki, które nazywane są w literaturze przedmiotu postulatem Boltzmana:
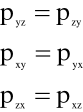
(5.8)
Z równań (5.8) wynika, że
tensor naprężenia w płynie jest symetryczny,
tzn.,
![]()
(5.9)
5.4. Równania konstytutywne
Rozłóżmy tensor naprężenia ![]()
(5.9) na aksjator i dewiator naprężenia:
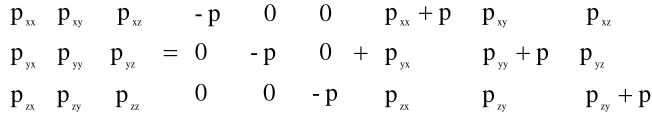
(5.10)
gdzie naprężenie średnie oznacza ujemną wartość ciśnienia hydrostatycznego
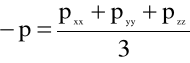
(5.11)
lub
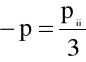
5.11b)
Aksjator naprężenia, występujący w równaniu (5.10) Wyrażony jest następująco:
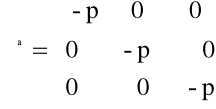
(5.12)
Dewiator naprężenia określony jest natomiast za pomocą wzoru:
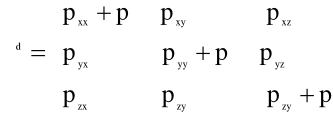
(5.13)
Przedstawmy z kolei tensor prędkości deformacji ![]()
w postaci sumy aksjatora i dewiatora, tj.
![]()
(5.14)
tj.
![]()
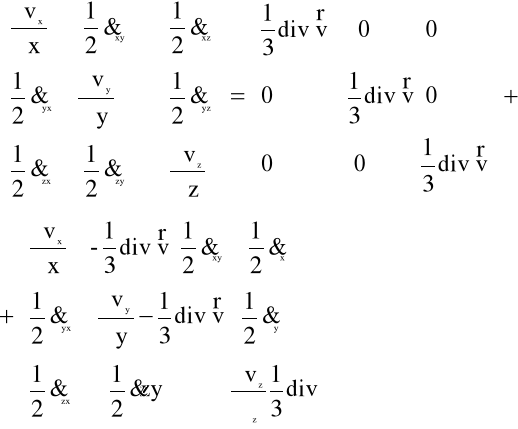
(5.15)
Gdzie aksjator prędkości odkształcenia
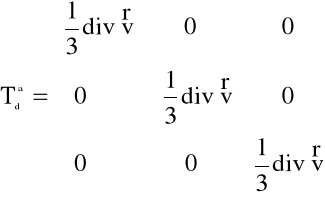
(5.16)
i dewiator prędkości odkształcenia
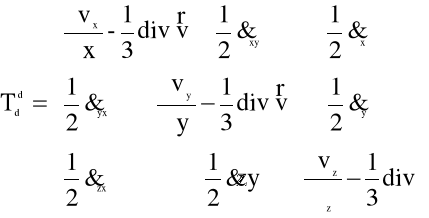
(5.17)
przy czym oznaczenia występujące we wzorach (5.15)-(5.17) są zgodne z definicjami (3.59).
Zgodnie z uogólnioną hipotezą Newtona:
Dewiator naprężenia jest wprost proporcjonalny do dewiatora prędkości odkształcenia.
tj.
![]()
(5.18)
gdzie ![]()
- dynamiczny współczynnik lepkości.
Po rozpisaniu (5.18) otrzymujemy tzw. związki fizyczne lub równania konstytutywne:
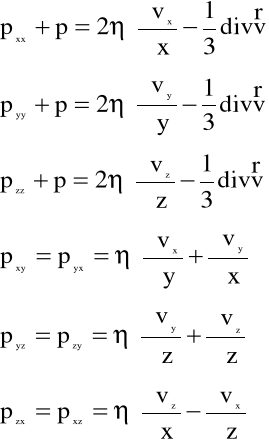
![]()
(5.19)
5.5. Równania Naviera - Stokesa
Równania różniczkowe ruchu płynu wyrażone w naprężeniach (5.4), równanie ciągłości i równania konstytutywne tworzą zamknięty układ 10-ciu równań z dziesięcioma niewiadomymi pxx, pyy, pzz, pxy, pyz, pzx, vx, vy, vz, p.
Wyeliminujmy składowe naprężeń z równań (5.4) wprowadzając doń związki fizyczne (5.19). W przypadku pierwszego z równań (5.4) mamy:
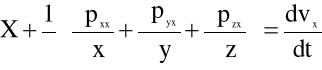
![]()
i dalej:
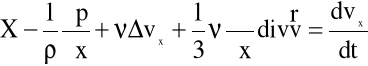
Postępując analogicznie otrzymujemy równania Naviera Stokesa:
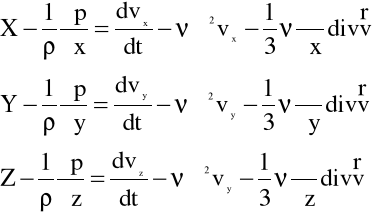
(5.20)
które uzupełnione jest równaniem ciągłości:
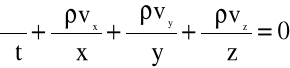
3.38a)
lub w zapisie wektorowym:
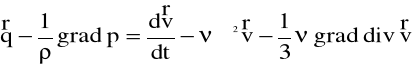
5.20a)
i
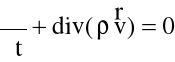
(3.38)
5.6. Przypadki szczególne równań Naviera - Stokesa:
1/ W przypadku płynu ruchu płynu nieściśliwego ![]()
mamy:
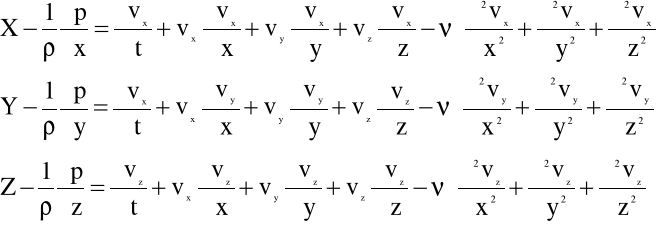
(5.21)
Uzupełnione ono jest równaniem ciągłości
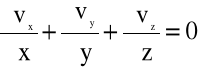
(5.22)
2/ W przypadku ruchu potencjalnego, płynu nieściśliwego
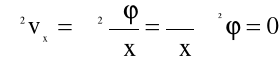
(5.23)
lub płynu doskonałego (nielepkiego), równania Naviera - Stokesa sprowadzają się do równań Eulera, ruchu płynu doskonałego, tj.
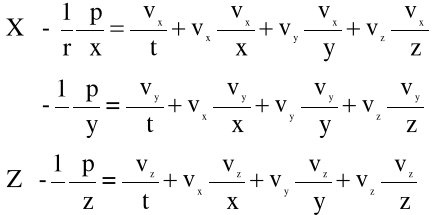
(4.3)
3/ W szczególnym przypadku płynu znajdującego się w stanie równowagi (![]()
), równania (5.20) upraszczają się do równań Eulera:
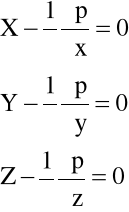
(2.5)
W celu rozwiązania równań Naviera - Stokesa należy podać:
warunki początkowe (jeżeli ruch jest nieustalony), tzn. w chwili t=0 przyjąć postać funkcji vi = vi(xk, 0),
warunki brzegowe, sprowadzające się do warunku zerowania się składowej normalnej prędkości na granicy zetknięcia cieczy z ciałem stałym, oraz warunku równości składowej stycznej prędkości cieczy z prędkością punktu ciała, w którym ciecz styka się z ciałem stałym.
Równania Naviera -Stokesa i równanie ciągłości we współrzędnych cylindrycznych (rys.5.7) mają postaci:
0,
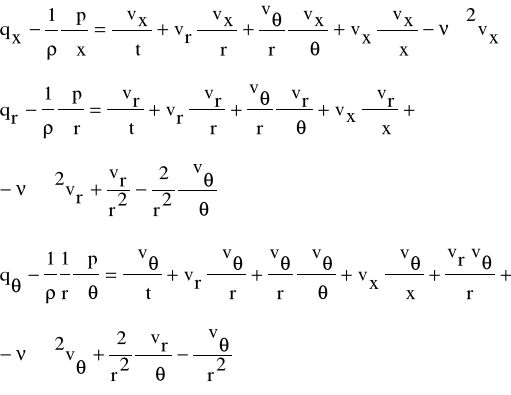
(5.24)
Natomiast równanie ciągłości:
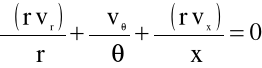
(5.25)
Operator Laplace'a w równaniach (5.24) ma postać:
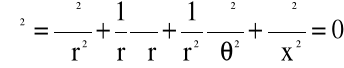
(5.26)
![]()
![]()
![]()
![]()
![]()
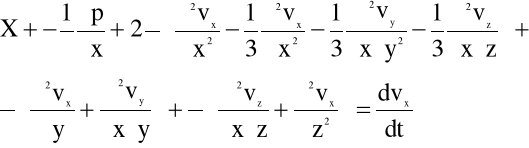
![]()
Wyszukiwarka
Podobne podstrony:
Dynamika płynów rzeczywistych
DYNAMIKA PŁYNÓW RZECZYWISTYCH
Dynamika plynow doskonałych i rzeczywistych
Dynamika plynow, bio, Chemia, Biofizyka, Toksykologia, Wykład PWrocławska
Ostatni wykład z Dynamiki
dynamika plynow poziomo
antropologia Wykład 2. DYNAMIKA ZJAWISK KULTURY; KULTURA I OSOBOWOŚĆ – WZAJEMNE RELACJE
Wyklad1, STATYKA PŁYNÓW
Elementy statyki i dynamiki płynów
4 Podstawowe równwnia dynamiki płynów nielepkich 5
Wykł 09 Statyka i dynamika płynów
statyka i dynamika plynow(1)
Dynamika plynow 13 14
4 Podstawowe równwnia dynamiki płynów nielepkich
więcej podobnych podstron