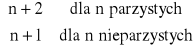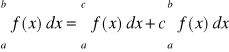METODY NUMERYCZNE W ELEKTROTECHNICE

Metody numeryczne - dział matematyki stosowanej, zajmujący się opracowywaniem i badaniem metod przybliżonego rozwiązywania problemów obliczeniowych w modelach matematycznych innych dziedzin nauki

Przykładowe zastosowania:

• elektrotechnika - obliczanie parametrów obwodów elektrycznych

• medycyna - tomografia komputerowa, opracowywanie nowych leków

• chemia - konstruowanie nowych cząsteczek

• inżynieria - przemysł samochodowy i lotniczy

• informatyka - konstruowanie nowych procesorów

W obrębie klasycznych metod numerycznych możemy wyróżnić m.in. takie zagadnienia jak:

• analiza błędów zaokrągleń

• interpolacja

• aproksymacja

• rozwiązywanie równań i układów równań nieliniowych

• całkowanie i różniczkowanie numeryczne

• rozwiązywanie układów równań liniowych

• obliczanie wartości własnych i wektorów własnych macierzy

• rozwiązywanie zagadnień dla równań różniczkowych zwyczajnych i cząstkowych

• rozwiązywanie równań całkowych i układów równań całkowych

(każdy wynik musi podlegać weryfikacji!)

Reprezentacja liczb w maszynie cyfrowej

Liczby całkowite (stałopozycyjne = stałoprzecinkowe):

, gdzie e_i = 0 lub 1

Jeżeli rejestr ma d-bitów, wówczas liczba całkowita n może zawierać się w przedziale

-2^d-1 < n < 2^d-1-1

przykład: Zapisać liczbę 18 w systemie dwójkowym:

, może być zatem przechowywana w słowie o długości D + 1 > 5 bitów jako

Liczby rzeczywiste (zmiennopozycyjne):

, gdzie ½ < m < 1, m-mantysa, i-cecha

W maszynie cyfrowej mantysa zapisywana jest w t-bitach m_t

w wyniku zaokrąglenia do t-bitów mantysy

Zmiennopozycyjna reprezentacja liczby rzeczywistej x oznaczana jest symbolem rd(x) i jest równa

!	Gdy elementy macierzy są rzędu μ lub n musimy dokonać przekształcenia całego układu. Uciekamy się od operacji na małych liczbach.

Nie prowadzi się operacji na małych liczbach, co oznacza, że:

, gdzie

liczbę 2^-t nazywamy dokładnością maszynową

przykład: Liczba 18,5 daje się przedstawić w postaci:

może być więc przechowywana w słowie o długości d + 1 > 11 bitów o t > 6 bitach mantysy:

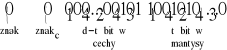
0,5781525

W sytuacji, gdy elementy macierzy są < 1, np. mV, musimy wtedy dokonać przeskalowania całego układu (np. poprzez pomnożenie macierzy przez jakąś liczbę).

Błędy obliczeń

Przy obliczeniach wykonywanych na maszynach cyfrowych spotyka się trzy podstawowe rodzaje błędów:

• błędy wejściowe (danych wejściowych) - występujące, gdy dane wprowadzane do pamięci maszyny cyfrowej odbiegają od dokładnych wartości tych danych. Źródłem tych błędów jest najczęściej skończona długość słów binarnych reprezentujących liczby i w związku z tym nieuniknione jest wstępne ich zaokrąglenie

• błędy odcięcia - powstają podczas obliczeń na skutek zmniejszenia liczby działań, na przykład przy obliczaniu sum nieskończonych. Chcąc obliczyć wartość wyrażenia e^x równego szeregowi:
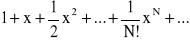
  zastępuje je sumą częściową o odpowiednio dobranej wartości N: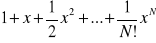
  

Jeżeli liczba N będzie niedostatecznie duża, to uzyskana w ten sposób wartość liczby e^x będzie obliczona niedokładnie, a popełniony w ten sposób błąd jest właśnie błędem odcięcia. Błędy tego typu powstają też często przy obliczaniu wielkości będących granicami. Podobnie zastąpienie wartości pochodnej funkcji jej ilorazem różnicowym powoduje powstanie błędu odcięcia. W wielu przypadkach daje się uniknąć błędu wejściowego i odcięcia przez ograniczenie danych.

Lemat Wilkinsona:

Błędy zaokrągleń powstające podczas wykonywania działań zmiennopozycyjnych są równoważne zastępczemu zaburzeniu liczb, na których wykonujemy działania. W przypadku działań arytmetycznych otrzymujemy:

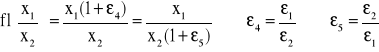
gdzie ε_i są co do modułu niewiększe niż dokładność maszyny ε. Przedrostek fl oznacza, że są to wyniki działań wyznaczone przy użyciu maszyny cyfrowej.

Oszacowanie błędów w obliczeniach iteracyjnych:

Wiele algorytmów obliczeniowych polega na wyznaczeniu ciągu liczb zbieżnego do poszukiwanej wartości.

Przykład:

wyznaczyć wartość funkcji
, przekształcając do równania iteracyjnego. Można to uczynić obliczając ciąg y₀, y₁, y₂..., gdzie y₀ jest dowolnie wybraną liczbą, natomiast każdy element ciągu y_i jest dany wzorem:

, dla i = 1, 2, 3, ...

(niewiadoma musi być po obu stronach równania)

, współczynnik przed funkcją (tutaj 1) musi być < 1 dlatego:

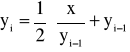
- iteracja i-ta

np.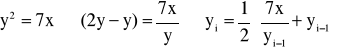
takiego równania nie da się rozwiązać bo 7/2

ale można zrobić tak:

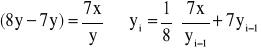
jeśli założyć, że działania wykonywane są dokładnie, to ciąg y₀, y₁, y₂, ... będzie zbieżny do liczby x, ponieważ
, to

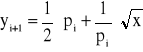
, a ciąg p_o > 0

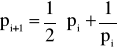
, przy i = 1, 2, 3, ... jest zbieżny do 1

Przykład:

rozwiązanie iteracyjne

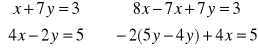
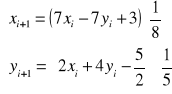
wszystkie składniki przy niewiadomych są < 1 (7/8, -7/8, 3/5)

przyjmujemy dowolnie x_i = 1, y_i = 2

Działania potrzebne do wyznaczania kolejnych wartości ciągu y₀, y₁, y₂, ... nazywamy iteracją. Informację o tym czy w kolejnej iteracji nastąpiło przybliżenie do rozwiązania uzyskujemy obliczając wyrażenie:

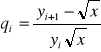
W przypadku dokładnych działań, gdy
i
, więc q_i < 0 dla i = 1, 2, 3, ... jeśli p_i>1/3. Oznacza to, że maleje wartość bezwzględna różnicy
odpowiednio dużego numeru iteracji i.

Dla obliczeń wykonywanych na maszynie cyfrowej, mamy:

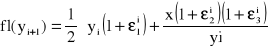
, gdzie
, k = 1, 2, 3, ...

Dla liczby
uzyskamy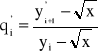

Jeżeli y_i jest już dostatecznie dobrym przybliżeniem liczby
, a więc p_i jest bliskie jedności, to pierwszy składnik powyższego wyrażenia ma pomijalnie małą wartość, natomiast drugi ze składników wynika z błędów zaokrągleń i może mieć tym większą wartość im bliższe jedności jest p_i.

Przykład: dla liczby 4 x=4

Algorytm:

zmienne rzeczywiste x, y, eps

y:= x/4; {pierwsze przybliżenie}

repeat

y:= 0,5*(y+(x/y));

until abs (x-sqr(y))<=eps {eps jest zakładaną dokładnością obliczeń)

Uwarunkowanie zadania i stabilność algorytmów.

Załóżmy, że mamy skończoną liczbę danych rzeczywistych, x = ( x₁, x₂, ... x_n ), na ich podstawie chcemy obliczyć skończenie wiele wyników rzeczywistych y = ( y₁, y₂, ... y_m ). Będziemy więc chcieli określić wartość y według odwzorowania y = φ (x), gdzie ϕ: D → R^m jest ciągłym odwzorowaniem i D ⊆ R^m.

Algorytm to jednoznaczny przepis obliczania wartości odwzorowania φ (x) składający się ze skończonej liczby kroków.

Jeśli zadanie rozwiązujemy numerycznie to zamiast dokładnymi wartościami x₁, x₂, ... x_n posługujemy się reprezentacjami rd (x₁), rd (x₂), ..., rd (x_n). Operacje elementarne nie są więc realizowane dokładnie tylko przez odwzorowanie zastępcze fl. Ta niewielka zmiana danych powoduje, że różne algorytmy rozwiązania tego samego zadania dają na ogół niejednakowe wyniki. Dużą rolę odgrywa tu przenoszenie błędów zaokrągleń. Często niewielkie zmiany danych powodują duże względne zmiany rozwiązania zadania. Zadanie takie nazywamy źle uwarunkowanym. Wielkości charakteryzujące wpływ zaburzeń danych na zaburzenia rozwiązania nazywamy wskaźnikami uwarunkowania zadania.

Przykład:

Zerami tego wielomianu będą liczby naturalne 1, 2, ..., 20. Gdy zakłócimy np. a₁₉ = - 210 i jego wartość wynosi a₁₉(ε) = - (210 + 2^-23), czyli a₁₉ (ε) = a₁₉ (1+ε). Otrzymujemy wtedy wielomian w_ε(x) = w (x) - 2^-23, który posiada już pierwiastki zespolone i np. najbliższe pierwiastkowi 15 wielomianu w(x) są pierwiastki 13,992358137 ± 2,518830070j.

Metodę badania przenoszenia błędów można rozbudować do analizy różniczkowej błędów algorytmu.

Niech δ_x1 = rd (x_i) - x_i dla i = 1, 2, ..., n

dla j = 1, 2, ..., m

We wzorze tym, czynnikiem określającym wrażliwość y_j na bezwzględną zmianę δx_i jest

Analogiczny wzór można wyprowadzić dla przenoszenia się błędów względnych. Jeśli
dla j = 0,1, 2, ..., m i
dla i = 1, 2, ..., n to

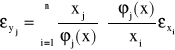
, gdzie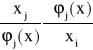
nazywamy wskaźnikiem uwarunkowania. Jeśli wskaźniki uwarunkowania co do wartości bezwzględnej są duże to zadanie jest źle uwarunkowane.

Przykład:

Badamy uwarunkowanie sumy y = a + b + c

=
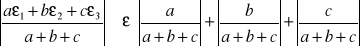
, gdzie ε jest

największą z wartości ε₁, ε₂ i ε₃, gdzie
jest wskaźnikiem uwarunkowania zadania.

Stabilność numeryczna algorytmów

Algorytm jest stabilny, jeżeli posiada tę własność, że małe błędy powstałe w pewnym kroku algorytmu nie są powiększane w innych krokach oraz nie powodują poważnego ograniczenia dokładności wszystkich obliczeń. Oznacza to, że algorytm jest numerycznie stabilny, gdy zwiększając dokładność obliczeń można wyznaczyć (z dowolną dokładnością) istniejące rozwiązanie zadania. Numeryczną stabilność zadania łatwo sprawdzić rozwiązując zadanie raz z dokładnością np. 10^-6, a potem z dokładnością 10^-12.

INTERPOLACJA:

Dana jest funkcja y = f (x),
, dla której znana jest tablica wartości w punktach zwanych węzłami interpolacji. Należy wyznaczyć taką funkcję W(x), aby:

W(x₀) = Y₀, W(x₁) = Y₁, ..., W(x_n) = Y_n

interpolacja funkcji f(x)

Zadaniem interpolacji jest wyznaczenie przybliżonych wartości funkcji zwanej funkcją interpolową w punktach nie będących węzłami interpolacji. Przybliżoną wartość funkcji obliczamy za pomocą funkcji zwanej funkcją interpolującą, która w węzłach ma te same wartości co funkcja interpolowana.

Funkcja interpolująca jest funkcją pewnej klasy. Najczęściej będzie to wielomian algebraiczny, wielomian trygonometryczny, funkcja wymierna i funkcja sklejana.

Interpolację stosuje się najczęściej, gdy nie znamy analitycznej postaci funkcji (jest ona tylko stablicowana) lub gdy jej postać analityczna jest zbyt skomplikowana.

Najczęściej stosowaną metodą wyznaczania funkcji W(x) jest jej dobór w postaci kombinacji liniowej n+1 funkcji bazowych

wyrażenie to nazywamy wielomianem uogólnionym.

Wprowadzając macierz bazową

i macierz współczynników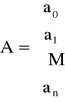

mamy

warunek W(x₀) = Y₀, W(x₁) = Y₁, ..., W(x_n) = Y_n

można zapisać w postaci układu równań liniowych X · A = Y, gdzie

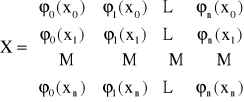
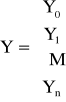
Jeśli macierz X nie jest osobliwa (da się odwrócić), to:

A = X^-1·Y

co ostatecznie daje

W(x) = Φ(x) · X^-1· Y

Interpolacja wielomianowa

W praktyce często używa się bazy złożonej z jednomianów

Baza dla funkcji ciągłych na odcinku skończonym [x_o, x_n] jest bazą zamkniętą, tzn., że każda funkcja tej klasy może być przedstawiona w postaci szeregu złożonego z funkcji bazowych. Wielomian interpolacyjny ma w tym przypadku postać:

dodatkowo musi być spełniony warunek:

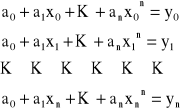
Powyższy układ równań ma jedyne rozwiązanie względem a₁, jeżeli wartości x₀, x₁, ..., x_n są od siebie różne

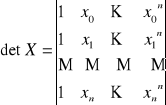
Macierz X^-1 dla bazy wielomianowej
nazywana jest macierzą Lagrange'a

Zauważyć należy, że każdy zbiór węzłów równoodległych x_i+1 - x_i = h = const. można sprowadzić do zbioru podstawowego podstawiając
, wówczas
, a macierz Φ przyjmuje postać

Interpolacja Lagrange'a

Przedstawiony powyżej sposób podejścia do interpolacji nie jest zbyt efektywny, ponieważ macierz X jest macierzą pełną i nie zawsze dobrze uwarunkowaną, co oznacza, że numeryczna procedura jej odwracania może być obarczona dużym błędem.

W interpolacji wielomianowej Lagrange'a dla n+1 węzłów interpolacji

przyjmuje się funkcje bazowe w postaci

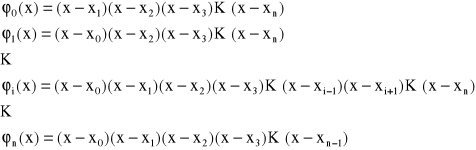
Funkcje te są wielomianami stopnia n zbudowanymi w ten sposób, że w funkcji bazowej φ₁ brakuje czynnika (x-x_i). Zatem wielomian interpolacji wyraża się następującym wzorem:

współczynniki a₀ ... a_n tego wielomianu wyznaczamy z równania:

X · A = Y, przy czym macierz X ma postać:

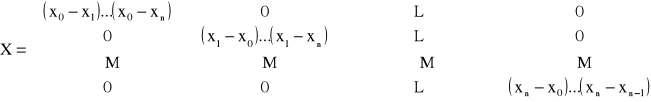
Macierz posiada tylko główną przekątną niezerową w związku z tym układ równań X · A = Y rozwiązuje się natychmiastowo

Można więc wielomian interpolacyjny Lagrange'a zapisać w postaci ułamka:

lub krócej

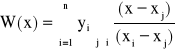
, j = 0, 1, ..., n

Przykład:

Wyznaczyć wielomian interpolacyjny Lagrange'a funkcji f (x) = e^x w przedziale [0,2 ; 0,5] mając dane:

f (0,2) = 1,2214, f (0,4) = 1,4918, f (0,5) = 1,6487

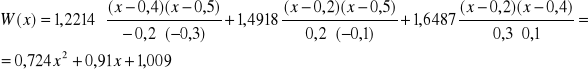
algorytm do wyznaczania wielomianu Lagrange'a dla podanego punktu:

begin

fx:=0;

for i:=0 to n do

begin

p:=1;

for k:=0 to n do

if k<>i then p:=p*(xx-x[k])/(x[i]-x[k]);

fx:=fx+f[i]*p

end;

end;

Należy pamiętać, ze przed przystąpieniem do obliczeń należy sprawdzić czy w wektorze x wartości się nie powtarzają, ponieważ grozi to wystąpieniem błędu dzielenia przez zero.

Różnice skończone

Dla funkcji stabelaryzowanej przy stałym kroku h = x_i+1 - x_i można wyprowadzić pojęcie różnicy skończonej rzędu k

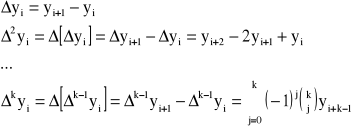
Przykład: Dla funkcji danej w postaci tablicy zbudować tablicę różnic skończonych.

NR	x	y	Δy	Δ^2y	Δ^3y	Δ^4y	Δ^5y
0	1,2	1,728	0,469	0,078	0,006	0	0
1	1,3	2,197	0,547	0,084	0,006	0
2	1,4	2,744	0,631	0,090	0,006
3	1,5	3,375	0,721	0,096
4	1,6	4,096	0,817
5	1,7	4,913

Wzory interpolacyjne dla argumentów równoodległych

Dla zbioru węzłów tworzących ciąg arytmetyczny x₀, x₁ = x₀ + h, x₂ = x₀ + 2h, ..., x_n = x₀ + nh dane są wartości funkcji f(x₀), f(x₁), ..., f(x_n). Szukany wielomian interpolacyjny zapisać możemy w następujący sposób:

W(x) = a₀ + a₁q + a₂q(q - 1) + a₃q(q - 1)(q - 2) + ... + a_nq(q - 1)(q - 2)...(q - n +1),

gdzie

Dla:

x = x₀: q = 0

x = x₁: q = 1

x = x₂: q = 2

...

x = x_n: q = n

Funkcje bazowe dla wielomianu W(x) przyjęto w postaci:

Φ₀(x) = 1 Φ₁(x) = q Φ₂(x) = q(q - 1)

Φ₃(x) = q(q - 1)(q - 2) Φ_n(x) = q(q - 1)(q - 2)...(q - n + 1)

Otrzymujemy następujący układ równań:

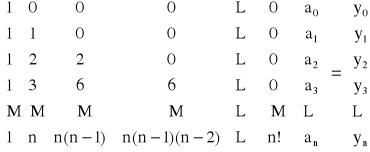
z którego wyznacza się wartości nieznanych współczynników a₀, a₁, a₂, ..., a_n

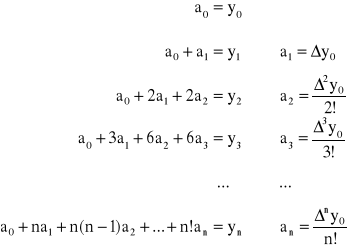
Ostatecznie otrzymujemy I wzór interpolacyjny Newtona w postaci

Przykład: Dla zależności f(T)=T log p znaleźć wielomian interpolacyjny stopnia 3 i obliczyć odchyłki w węzłach interpolacji

T	0,8	1,0	1,2	1,4	1,6	1,8
T log p	0,3566	0,9383	1,5598	2,2169	2,9059	3,6229

Tablica:

T	T log p	Δ	Δ^2	Δ^3	błąd [%]
0,8	0,3566	0,5817	0,0398	-0,0042	0
1,0	0,9383	0,6215	0,0356	-0,0037	0
1,2	1,5598	0,6571	0,0319	-0,0039	0
1,4	2,2169	0,6890	0,0280		0
1,6	2,9059	0,7170			1,9
1,8	3,6229				4,2

przyjmijmy

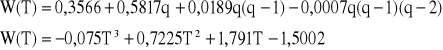
Zauważmy, że I wzór Newtona daje dobrą dokładność w pobliżu punktu T₀, natomiast dla punktów leżących niżej w tabeli błąd wzrasta. Jeśli chcielibyśmy wyzerować odchyłki we wszystkich węzłach tabeli trzeba by podwyższyć rząd interpolacji i w efekcie wzór empiryczny staje się wtedy praktycznie mało przydatny. Wzory interpolacyjne stosuje się też do obliczania wartości funkcji w punktach pośrednich tabeli (do zagęszczenia). Aby obliczyć T log p dla T = 1,3 z dokładnością do Δ² wystarczy przyjąć T₀ = 1,2, a wówczas q = 0,5 i znajdujemy
.

Zadanie takich wartości T = 1,65 byłoby już niewykonalne, ponieważ brakuje różnic. Widać tu ograniczenie tzw. interpolacji w przód, określonej I wzorem Newtona. Do interpolacji wstecz służy II wzór Newtona. Szukamy wielomian interpolacyjny

W(x) = a₀ + a₁q + a₂q(q + 1) + a₃q(q + 1)(q + 2) + ... + a_nq(q + 1)(q + 2)...(q + n - 1),

gdzie

Współczynniki a₀, a₁, a₂, ..., a_n wyznaczamy jak poprzednio i dochodzimy do wzoru:

Przykład: Obliczyć T log p dla T = 1,65 z dokładnością do Δ²

3,6229-0,75*0,717-0,75*0,25*0,028=3,0825

for j:=1 to 2 do

for i:=1 to n-j do

z[i,j]:=z[i+1,j-1]-z[i,j-1];

q0:=(x-x0)/h;

k:=int(q,0);

q:=q0-k;

if k>=n then write (`Brak danych')

else wart:=z[k,0]+q*z[k,1]+0.5*q*(q-1)*z[k,2];

Interpolacja trygonometryczna

Załóżmy, że znamy wartości pewnej ciągłej i okresowej funkcji f(x) o okresie 2π w 2n+1 węzłach. Jako bazę interpolacji przyjmujemy zbiór funkcji trygonometrycznych

Otrzymujemy zatem wielomian interpolacyjny w postaci

zawierający 2n+1 nieznanych parametrów.

Ze względu na uproszczenie obliczeń najistotniejszy jest przypadek interpolacji funkcji określonej na zbiorze równoodległych węzłów x_i∈[0,2π] dobranych według następującej zależności

, gdzie i = 0, 1, ..., 2n

Czyli

Warunek interpolacji prowadzi do układu równań liniowych w postaci

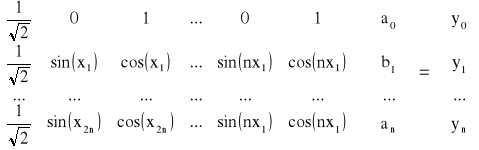
Współczynniki pierwszego wiersza macierzy X wynikają z wartości funkcji sin(hx) i cos (hx) dla x₀ = 0. Przedstawiony układ równań rozwiązuje się natychmiastowo, ponieważ macierz X^-1 można wyznaczyć z zależności

Przykład: Daną funkcję f(x) = 7x - x² przybliżyć wielomianem trygonometrycznym przyjmując n = 3. Współrzędne węzłów interpolacji obliczamy ze wzoru:

x	0	0,898	1,795	2,693	3,590	4,488	5,386
y	0	5,478	9,344	11,598	12,242	11,274	8,695

Baza interpolacji - zbiór funkcji:

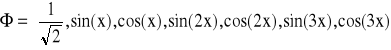
Tworzymy macierz X:

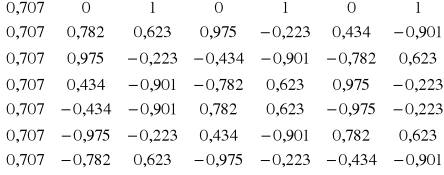
Elementy macierzy X mnożymy przez 2/7, otrzymaną macierz transponujemy i obliczamy współczynniki wzoru interpolacyjnego

Aproksymacja

jest to przybliżanie funkcji f(x) zwanej aproksymowaną inną funkcją Q(x) zwaną funkcją aproksymującą. Aproksymacja bardzo często występuje w dwóch przypadkach:

• gdy funkcja aproksymowana jest przedstawiona w postaci tablicy wartości i poszukujemy dla niej odpowiedniej funkcji ciągłej

• gdy funkcję o dosyć skomplikowanym zapisie analitycznym chcemy przedstawić w „prostszej” postaci

Dokonując aproksymacji funkcji f(x) musimy rozwiązać dwa ważne problemy:

• dobór odpowiedniej funkcji aproksymującej Q(x)

• określenie dokładności dokonanej aproksymacji

Dobór odpowiedniej funkcji aproksymującej Q(x)

Najczęściej stosowane funkcje aproksymujące są dobierane w postaci wielomianów uogólnionych będących kombinacją liniową funkcji q(x)

Jako funkcje bazowe stosowane są:

• jednomiany

• funkcje trygonometryczne

• wielomiany ortogonalne

Przyjęcie odpowiednich funkcji bazowych powoduje, że aby wyznaczyć funkcję aproksymującą należy wyznaczyć wartości współczynników, a₀, a₁, ..., a_m.

Określenie dokładności aproksymacji

Aproksymacja funkcji powoduje powstanie błędów i sposób ich oszacowania wpływa na wybór metody aproksymacji. Jeśli błąd będzie mierzony na dyskretnym zbiorze punktów x₀, x₁, ..., x_n to jest oto aproksymacja punktowa, jeśli będzie mierzony w przedziale (a,b) - aproksymacja integralna lub przedziałowa.

Najczęściej stosowanymi miarami błędów aproksymacji są:

• dla aproksymacji średniokwadratowej punktowej

• dla aproksymacji średniokwadratowej integralnej lub przedziałowej

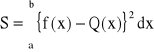
• dla aproksymacji jednostajnej

We wszystkich tych przypadkach zadanie aproksymacji sprowadza się do takiego optymalnego doboru funkcji aproksymującej (dla wielomianu uogólnionych zaś do optymalnego doboru współczynników a₀, a₁, ..., a_m) aby zdefiniowane wyżej błędy były minimalne.

Aproksymacja średniokwadratowa

Niech dana będzie funkcja y=f(x), która w pewnym zbiorze X punktów x₀, x₁, ..., x_n przyjmuje wartości y₀, y₁, ..., y_n. Wartości te znane tylko w przybliżeniu z pewnym błędem (np. jako wyniki pomiarów). Poszukujemy takiej funkcji Q(x) przybliżającej daną funkcję f(x), która umożliwi wygładzenie funkcji f(x), czyli pozwoli z zakłóconych błędami danymi wartości funkcji przybliżonej otrzymać gładką funkcję przybliżającą.

Niech ϕ_j(x), j=0, 1,...,n będzie układem funkcji bazowych. Poszukujemy wielomianu uogólnionego Q(x) będącego najlepszym przybliżeniem średniokwadratowym funkcji f(x) na zbiorze X=(x_j). Funkcja przybliżająca ma postać

Przy czym współczynniki a_i są tak określone, aby wyrażenie

dla i=0, 1, ..., n

było minimalne. Funkcja w(x) jest z góry ustaloną funkcją wagową.

Aby wyznaczyć współczynniki a_i oznaczamy odchylenie

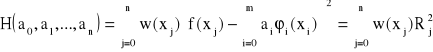
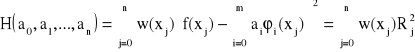
gdzie R_j jest odchyleniem w punkcie x_j.

Następnie obliczamy pochodne cząstkowe funkcji H względem a_i. Z warunku

, gdzie k = 0, 1, ..., n

otrzymujemy układ m+1 równań o niewiadomych a_i zwany układem normalnym

, gdzie k = 0, 1, ..., n

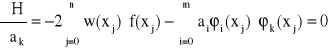
Jeśli wyznacznik tego układu jest różny od zera to rozwiązaniem układu jest minimum funkcji H. W zapisie macierzowym układ przyjmuje postać

gdzie

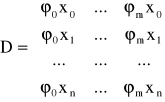
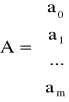
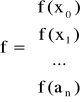
Aproksymacja wielomianowa

Jeżeli za funkcje bazowe przyjmiemy ciąg jednomianów (xⁱ), i = 0, 1, ..., n to układ normalny przyjmuje postać

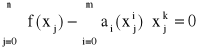
, k = 0, 1, ..., n

co po zmianie kolejności sumowania daje

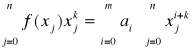
przykład: Odnaleźć zależność między x i y w postaci ax+by=1

x	1	3	4	6	8	9	11	14
y	1	2	4	4	5	7	8	9

Będziemy rozpatrywać odchylenia zarówno wartości x jak i y, ponieważ wiodą one do różnych wyników. Zakładamy, że dane są obarczone błędami, wówczas minimalizujemy wyrażenia

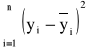
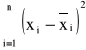
przy czym

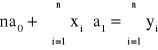
, gdzie:
,

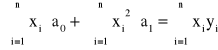
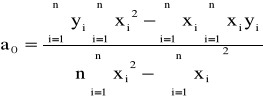
Układ normalny dla danych z tablicy ma rozwiązanie

a₀ = 6/11 i a₁ = 7/11,

więc ma postać

11y - 7x = 6

Minimalizując w ten sam sposób wyrażenie

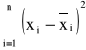
otrzymamy równanie

2x - 3y = -1

Dla obu otrzymanych równań wykresy się pokrywają.

Algorytm

tablice: tab[1..4,1..5], a, p[1..4], s, suma[1..6]

zmienne rzeczywiste: x, y

zmienne indeksowe: i, j, n, k

for j:=1 to n do

begin

write (`Podaj x i y dla węzła:');

readln (x:10:4, y:10:4);

s[1]:=x;

for i:=2 to 6 do s[i]:=x*s[i-1];

for i:=1 to 6 do suma[i]:=suma[i]+s[i];

p[1]:=p[1]+y;

for i:=2 to 4 do p[i]:=p[i]+y*s[i-1];

end;

tab[1,1]:=n;

for i:=1 to 4 do

begin

tab[i,5]:=p[i];

for j:=1 to 4 do

begin

k:=i+j;

if not (k=2 then tab[i,j]:=suma[k-2]

end;

end;

RUKL(tab,a,4,5);

writeln (`Poszukiwane współczynniki to');

for i:=1 to 4 do writeln (a[i]:12:6);

Aproksymacja za pomocą wielomianów ortogonalnych ze wzrostem stopnia wielomianu, obliczenia stają się coraz bardziej pracochłonne a ich wyniki niepewne. Problem ten można usunąć stosując do aproksymacji wielomiany ortogonalne.

Funkcje f(x) i g(x) nazywa się ortogonalnymi na dyskretnym zbiorze punktów x₀, x₁, ..., x_n jeśli

przy czym

Analogicznie ciąg funkcyjny

nazywamy ortogonalnym na zbiorze punktów x₀, x₁, ..., x_n jeśli

dla j≠k

Zastosowanie tej metody powoduje, że znika jedna z trudności obliczeniowych przy aproksymacji wielomianowej, mianowicie złe uwarunkowanie macierzy układu normalnego. Przy aproksymacji wielomianami ortogonalnymi macierz układu normalnego jest macierzą diagonalną, a jej elementy położone na głównej przekątnej dane są wzorem

Załóżmy, że znamy n+1 równoodległych punktów x_i (x_i = x₀+ih, i = 0, 1, ..., n). Za pomocą przekształcenia liniowego

przeprowadzimy te punkty w kolejne liczby całkowite od 0 do n poszukujemy ciągu wielomianów

(dolny indeks oznacza stopień i m ≤ n) spełniających warunek ortogonalności

dla j≠k

przy czym

gdzie

Często używa się unormowanego ciągu wielomianów spełniających warunek

, gdzie k = 0, 1, ..., m

Co po przekształceniu daje nam wzór na wielomiany Grama, zwane też wielomianami Czebyszewa stopni k = 0, 1, ..., m w postaci

, gdzie k = 0, 1, ..., m

Wzór aproksymacyjny oparty na wielomianach Grama ma postać:

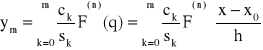
gdzie,

oraz

Przykład:

Na podstawie tablicy wartości f(x) znaleźć najlepszy w sensie aproksymacji średniokwadratowej wielomian przybliżający tę funkcję.

x	1	1,5	2	2,5	3
y	3	4,75	7	9,75	13

Ponieważ węzły są równoodległe posłużymy się wielomianem Grama. Konstruujemy wielomian aproksymacyjny dla n = 4. Wartości F_k(q), q=1, 2,…, 4.

Obliczamy ze wzoru:

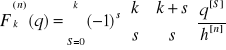
Zestawienie wyników przedstawia tabela:

q	xi	yi	F0(q)	F1(q)	F2(q)	F3(q)	F4(q)
0	1	3	1	1	1	1	1
1	1,5	4,75	1	0,5	-0,5	-2	-4
2	2	7	1	0	-1	0	6
3	2,5	9,75	1	-0,5	-0,5	2	-4
4	3	13	1	-1	1	-1	1

Następnie korzystając ze wzorów:

Obliczamy c_i i s_i oraz b_i= c_i / s_i i ze wzoru:

otrzymujemy:

ci	37,5	-12,5	1,75	0	0
si	5	2,5	3,5	10	70
bi	7,5	-5	0,5	0	2

dla

Aproksymacja trygonometryczna

Często spotykamy się z przypadkiem, gdy funkcja f(x) jest okresowa. Taką funkcję wygodniej jest aproksymować, wielomianem trygonometrycznym o bazie:

1, sin x, cos x, sin 2x, cos 2x, …, sin kx, cos kx

Jeżeli f(x) jest funkcją dyskretną określoną w dyskretnym zbiorze równoodległych punktów i ich liczba jest parzysta i wynosi 2L (dla nieparzystej liczby punktów rozumowanie jest analogiczne), niech:

dla i = 0, 1, …, 2L-1

Baza jest ortogonalna nie tylko na przedziale <0, 2π>, ale też na zbiorze punktów x_i, przy czym warunki ortogonalności mają postać:

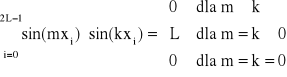
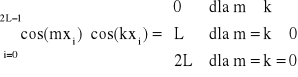
dla m, k dowolnych, przy czym m i k zmieniają się od 0 do L

Przybliżeniem funkcji f(x) na zbiorze punktów x_i jest wielomian trygonometryczny:

, n<L

Współczynniki a_j i b_j wielomianu wyznaczamy tak, aby suma kwadratów różnic

była minimalna.

Korzystając z warunku ortogonalności otrzymujemy rozwiązanie układu normalnego

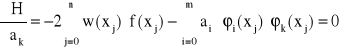
w postaci:

dla j=1, 2, …, n

Algorytm:

const max: … {zdefiniowanie stałej}

type zakres: 1…max;

wektor: array[zakres] of real;

procedure APR (N, K: zakres; var y, a, b: wektor);

var i, j: integer;

PI, A0, S1, S2: real;

begin

write(`Podaj wartość y');

for i:=1 to N do readln(Y[I]);

A0:=0.0;

for j:=1 to N do A0:=A0+Y[I];

A0:=A0/N;

PI:=4.0*arctan(1.0)/N;

for i:=1 to K do

begin

S1:=0.0;

S2:=0.0;

for j:=1 to N do

begin

S1:=S1+Y[J]*cos(PI*J*I);

S2:=S2+Y[J]*sin(PI*J*I);

end;

A[I]:=S1*2/N;

B[I]:=S2*2/N;

end;

end;

Szybka transformata Fouriera

Każdą funkcję w tablicy tablicą wartości w n punktach
, gdzie β = 0, 1, ..., n-1 można przybliżać wielomianem trygonometrycznym w postaci

, j - czynnik urojony

lub

gdzie

Θ = 1
dla n parzystych

Θ = 1
dla n nieparzystych

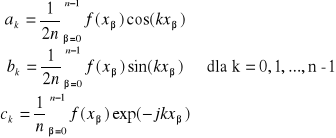
Aproksymacja za pomocą funkcji sklejonych stopnia 3 (funkcji giętych)

Każdą funkcję
można przedstawić w postaci kombinacyjnej liniowej

, a ≤ x ≤ b oraz gdzie
są funkcjami określonymi wzorem:

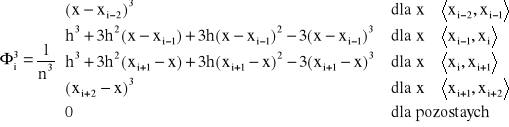
gdzie
,

Aproksymacja na przedziale <a,b>

Współczynniki c_i dobieramy tak, aby odchylenie kwadratowe dane poniższym wzorem było jak najmniejsze:

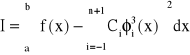
w celu wyznaczenia minimum funkcji I=I(c_-1 , c₀ , … , c_n+1) obliczamy pochodne:

j = -1 , 0, … , n+1

i przyrównujemy je do zera. Otrzymane równania tworzą układ n+3 równań z n+3 niewiadomymi c_i

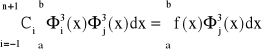
j= -1, 0, 1, … ,n+1

Funkcje
są liniowo niezależne na przedziale <a,b>, więc układ równań ma rozwiązanie w postaci punktu. Funkcji I osiąga minimum. Układ równań możemy zapisać w postaci:

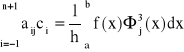
j = -1, 0, 1, … , n+1,

gdzie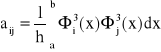

Aproksymacja funkcji określonej na dyskretnym zbiorze punktów

Niech (x_i') dla i= 0, 1, … ,n₁ ; n₁ > n + 3 będzie zbiorem punktów, w których dane są wartości funkcji f(x). Szukane jest minimum wyrażenia:

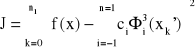
W celu wyznaczenia c_i obliczamy pochodne cząstkowe funkcji J = J (c_-1, c₀,… ,c_n+1) względem zmiennych c_i i przyrównujemy je do zera.

Otrzymane równania tworzą układ:

, gdzie

Jeżeli wyznacznik tego układu jest różny od zera to rozwiązując go możemy wyznaczyć współczynniki c_j takie, że funkcja J osiągnie minimum.

Metody numeryczne rozwiązywania układów algebraicznych równań liniowych.

Rozpatrujemy układ n równań liniowych zawierających n niewiadomych

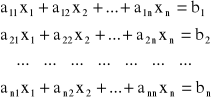
Układ ten można zapisać także w postaci macierzowej A · X = B, gdzie

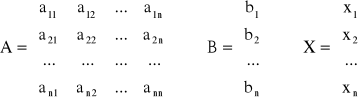
metody dokładne: metoda Cramera, metoda eliminacji Gaussa, metoda Crouta (LU)

metody niedokładne: iteracja prosta, Gaussa-Siedla, metoda sukcesywnej nadrelaksacji (SOR)

O wyborze metody decyduje postać macierzy współczynników A. Jeśli macierz A jest macierzą pełną to na ogół stosujemy metody dokładne. Jeśli macierz współczynników A jest macierzą niepełną (znacząca ilość współczynników jest równa zero) wtedy stosujemy metody iteracyjne.

Macierz A nazywana jest macierzą główną układu, X - wektorem niewiadomych, B - wektorem wyrazów wolnych. Jeśli macierz główna nie jest osobliwa (det A ≠ 0), to układ równań jest oznaczony (posiada dokładnie jedno rozwiązanie).

Gdy macierz A posiada niezerowe elementy tylko na głównej przekątnej, to układ równań rozwiązuje się natychmiastowo.

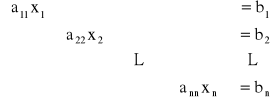
Niewiadome można wtedy obliczyć
, a_ii ≠ 0, i = 0, 1, ..., n.

Łatwo rozwiązuje się trójkątne układy równań

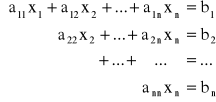
Z ostatniego równania możemy wyznaczyć x_n, z przedostatniego x_n-1

a ogólnie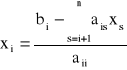
, i = n-1, n-2, ..., 1 przy założeniu, że a_ii ≠ 0, i = 1, 2, ..., n

PRZYKŁAD:

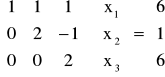
zmienną x₃ mamy daną wprost - x₃ = 3

ALGORYTM:

zmienne indeksowe n, i, j, s

zmienne rzeczywiste suma

tablice a[1..n,1..n], b[1..n], c[1..n]

for i:=n downto 1 do

begin

suma:=0;

for s:=i+1 to n do

suma:=suma+a[i,s]*x[s];

x[i]:=(b[i]-suma)/a[i,i];

end;

Wzory Cramera

Jesli oznaczymy symbolem W wyznacznik główny układu równań

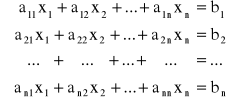
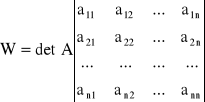
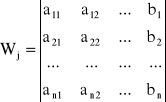
to można wykazać, że
, W ≠ 0, j = 1, 2, ..., n

Metoda ta należy do metod dokładnych. Ze względu na dużą złożoność obliczeniową praktycznie stosowana do numerycznego rozwiązywania równań.

Metoda eliminacji Gaussa

Metoda polega na zapisaniu układu równań w postaci macierzy C, której n pierwszych kolumn zawiera elementy a_ij macierzy głównej A, natomiast kolumnę n+1 tworzą dowolne wyrazy b_i.

Zakładając, że C₁₁≠0, odejmujemy pierwsze równanie pomnożone przez
od i-tego równania (i=2,3,...,n) a obliczonymi współczynnikami zastępujemy przednie wartości. W wyniku tej operacji otrzymujemy układ równań i odpowiadającą mu macierz C₁.

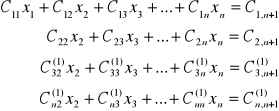
Za pomocą wzorów określających nowe współczynniki

i=2,3,...,n j=2,3,...,n+1

Jeśli
, to odejmiemy drugie równanie układu pomnożone przez
od i-tego równania układu i=3,4,...,n. W wyniku otrzymujemy układ:

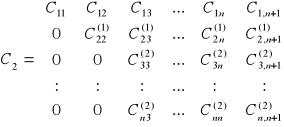
A nowe współczynniki wyrażone są wzorami

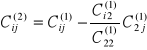
i=3, 4, ..., n j=3, 4, ..., n

Kontynuując takie postępowanie po wykonaniu n kroków dochodzimy do układu trójkątnego

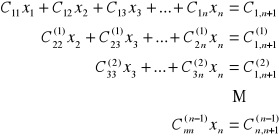
Algorytm dochodzenia od układu trójkątnego do układu równań liniowych

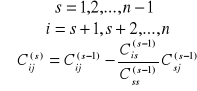
Przykład

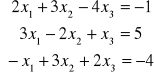
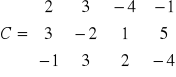
Obliczamy elementy macierzy C₁

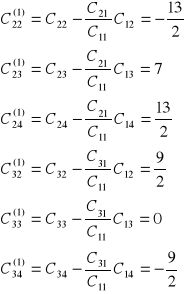
druki krok s=2

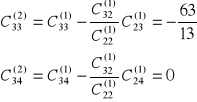
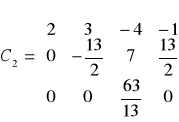
co daje nam macierz C₁:

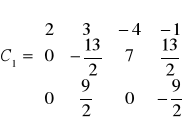
i dalej ze wzorów dla układów trójkątnych mamy x₃=0, x₂=-1, x₁=1

ALGORYTM:

zmienne indeksowe n, i, j, s

zmienne rzeczywiste suma

tablice c[1..n,1..n+1], x[1..n]

for s:=1 to n-1 do

for i:=s+1 to n do

for j:=s+1 to n+1 do

c[i,j]:=c[i,j]-(c[i,s]*c[s,j])/c[s,s];

x[n]:=c[n,n+1]/c[n,n]

for i:=n-1 downto 1 do

begin

suma:=0;

for s:=i+1 to n do

suma:=suma+c[i,s]*x[s];

x[i]:=(c[i,n+1]-suma)/c[i,i];

end;

Metody iteracyjne

Proces iteracyjnego obliczania wrtości x polega na przyjęciu pewnej wartości początkowej X^o, zwanej przybliżeniem początkowym, a następnie wykonaniu określonych operacji arytmetycznych dających w wyniku X¹ (zwanym pierwszym przybliżeniem). Kolejne przybliżenia oblicza się wykonując te same operacje na ostatnio obliczonym przybliżeniu. Jeżeli ciąg przybliżeń {Xⁿ} zmierza do X, to proces iteracyjny jest zbieżny i tylko wtedy metoda iteracyjna jest efektywna. Metody iteracyjnego rozwiązywania układów równań liniowych można stosować dla układów typu...

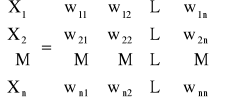
Przykład: Sprowadzić układ do postaci AX=B

2x₁+x₂+x₃=4 x₁=-0,5x₂-0,5x₃+2

x₁+x₂-x₃=1 x₂=-x₁+x₃+1

x₁+x₂+x₃=3 x₃=-x₁-2x₂+4

W pierwszej kolejności macierz A zakładamy na dwie macierze D i R przy czym D zawiera tylko główną przekątną macierzy A, natomiast R pozostałe jej elementy.

A = D + R

Równanie A*X=B sprawdziło się dla

D*X+R*X=B D*X=-R*X+B

Ostatnie równanie pomnożymy lewostronnie przez D^-1 i otrzymujemy:

E*X=D^-1*R*X+D^-1*B

Oznaczając -D^-1*R=W i D^-1*B=Z dochodzimy dorównania: X=W*X+Z

Wracając do zadania:

ponieważ

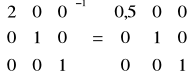
więc jak łatwo sprawdzić mamy taki sam układ jaki znaleziono sposobem „naturalnym”

Metoda iteracji prostej (Jakobiego):

Metoda ta dla równania X=W*X+Z polega na przyjęciu zerowego przybliżenia wektora X=X^o, a następnie przeprowadzenia obliczeń iteracyjnych za pomocą zależności:

Xⁱ⁺¹=W*Xⁱ+Z i=0,1,...

Liczba kroków, które należy wykonać, aby uzyskać wymaganą dokładność rozwiązania, jest z reguły dość duża i istotnie zależy od przyjęcia punktu startowego X^o. Punkt ten najczęściej się dobiera na podstawie dodatkowych informacji o fizycznych aspektach problemu.

Przykład: Metodę iteracji prostej wykorzystano do rozwiązania układu równań będącego różnicową aproksymacją równania Laplace`a z warunkami brzegowymi I rodzaju. Równanie to opisuje stacjonarne pole temperatury w pewnym dwuwymiarowym obszarze, na którego brzegach temperatury są znane. Jako przybliżenie zerowe przyjęto wartość temperatur w wnętrzu obszaru T=50°C, wymiary prostokątne a=b=0,8 cm.

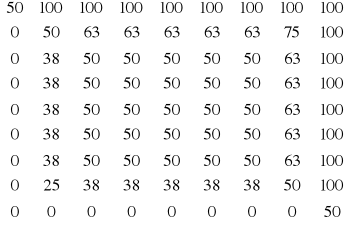
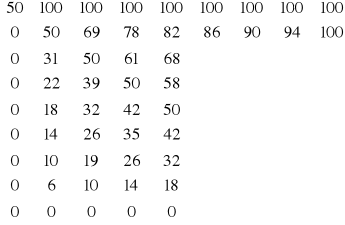
Metoda Gaussa-Seidla

Stanowi ulepszenie metody iteracyjnej prostej polegające na wykorzystaniu obliczonych k pierwszych składowych wektora Xⁱ⁺¹ do obliczenia składowej k+1. Modyfikacja ta znacznie przyspiesza proces obliczania.

Przykład: Rozwiązując układ równań:

dla uproszczenia zapisu oznaczamy składowe z wektora iteracji „i” symbolem „x”, a składowe wektora i iteracji i+1 symbolem „u”. W metodzie iteracji prostej układ ten zapisujemy:

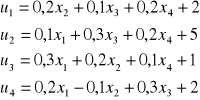
Przyjmujemy teraz punkt startowy np. X⁰ = [3, 6, 4, 3]^T, składowe tego wektora podstawiamy do prawych stron równań wyliczając u₁, ..., u₄, które w następnej iteracji przejmą rolę punktu startowego. Kolejne przybliżenia otrzymane tą metodą

rozwiązaniem dokładnym jest X = [4,59, 7,49, 4,20, 3,44]

Ten sam układ w metodzie Gaussa - Siedla ma postać:

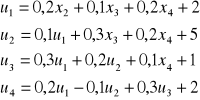
a kolejne przybliżenia:

Formalny zapis algorytmu

Macierz W w równaniu X = W · X + Z przedstawiamy jako sumę dwóch macierzy: górnej trójkątnej W_u i dolnej trójkątnej W_l. Macierz górna trójkątna składa się z elementów macierzy W leżących nad główną przekątną (pozostałe są zerami), natomiast macierz dolna trójkątna składa się z elementów macierzy W leżących pod główną przekątną. Macierz W w tym przykładzie ma zerową główną przekątną

Algorytm metody Gaussa - Siedla realizowany jest następującym wzorem:

czyli mamy:

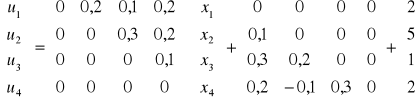
Metoda sukcesywnej nadrelaksacji (SOR)

Jest ulepszeniem metody Gaussa-Seidla mającym poprawić szybkość zbieżności procesu iteracyjnego. Istota polega na sukcesywnym wprowadzaniu w miejsce składowych u_i po prawej stronie układu wartości

x_i + α (u_i - x_i) α - współczynnik nadrelaksacji, α∈<1,2>

i - liczba niewiadomych a nie iteracja

Sposób dobory optymalnego współczynnika α nazywanego czynnikiem nadrelaksacyjnym jest trudny do określenia, chociaż wiadomo, że jest on liczbą z przedziału [1 , 2]. Można zauważyć, że dla α=1 otrzymuje się metodę Gaussa - Siedla. Według źródeł literaturowych zaleca się przyjmowanie α rzędu 1,8.

Algorytm metody nadrelaksacyjnej sprowadza się do wzoru:

Zbieżność metod iteracyjnych

Jeżeli macierz A kwadratowa oraz x jest wektorem niezerowym, wówczas istnieje pewien wektor równoległy do Ax, co oznacza, że istnieje pewna stała λ taka, że:

Ax = λx

Możemy wtedy zapisać równanie charakterystyczne

(A - λI)x = 0, gdzie I - macierz jednostkowa

oraz wielomian charakterystyczny ma postać

p(λ) = det (A - λI)

Jeżeli wielomian macierzy A jest
, wektora x jest n, wówczas p jest wielomianem m-tego stopnia, którego pierwiastki są pojedyncze i zespolone. Jeżeli wektor λ jest pierwiastkiem wielomianu p wówczas:

Jeżeli powyższy warunek jest spełniony, oznacza to, że równanie charakterystyczne ma rozwiązanie x≠0.

Zbieżność metod iteracyjnych (2)

Promień spektralny ρ(A) macierzy A jest zdefiniowany jako:

, gdzie
- oznacza moduł wektora λ

wówczas równanie charakterystyczne jest zbieżne gdy:

Można wykazać, że:

ostatecznie dla metod iteracyjnych można zapisać twierdzenie:

Warunkiem koniecznym i wystarczającym zbieżności procesu iteracyjnego danego wzorem przy dowolnym wektorze początkowym i dowolnym wektorze Z jest, aby wszystkie wartości własne macierzy W były co do modułu mniejsze od jedności.

Zbieżność metod iteracyjnych

W praktyce jest na ogół wygodniej korzystać z twierdzenia:

Jeżeli norma macierzy W jest mniejsza od jedności to proces iteracyjny określany wzorem X^i+1 = W · Xi + Z jest zbieżny.

Z przytoczonych twierdzeń wynika, że zbieżność procesu iteracyjnego nie zależy ani od wartości początkowej
, ani też od wartości danego wektora Z, a wystarczy jedynie spełnienie jednego z następujących warunków:

norma wierszowa

norma kolumnowa

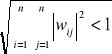
norma energetyczna

Kryterium „stopu” metod iteracyjnych

Obliczenia iteracyjne trwają do momentu kiedy zostanie spełniony warunek

gdzie: X⁽ⁱ⁺¹⁾ oraz X⁽ⁱ⁾ są kolejnymi przybliżeniami rozwiązania Xⁱ⁺¹ = W · Xⁱ + Z oraz δ jest dokładnością obliczeń - dowolna liczba większa od 0

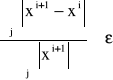
, gdzie ε ∈ <10^-1, 10^-256> - przyjęta dokładność obliczeń

Numeryczne rozwiązywanie równań nieliniowych

Metoda Newtona

Dany jest układ równań nieliniowych z n niewiadomymi

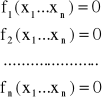
który możemy zapisać w postaci wektorowej

f(x)=0

gdzie:

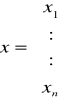
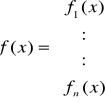
O funkcjach fi(x₁...x_n) dla i = 1, 2, ..., n zakładamy, że mają ciągłe pochodne pierwszego rzędu w pewnym obszarze zawierającym odosobniony pierwiastek układu równań. Niech

x^(k) = {x₁^(k), ..., x_n^(k)}

będzie k-tym przybliżeniem pierwiastka a = {a₁, ..., a_n} równania.

Dokładną wartość pierwiastka wyraża wzór a = x^(k) + ε^(k)

Gdzie
jest błędem pierwiastka przybliżonego
. Skoro istnieje ciągła pochodna funkcji f(x) możemy zapisać:

Zastępując błąd
przyrostem
i porównując prawą stronę powyższego wyrażenia do zera otrzymujemy równanie liniowe:

Wzór ten stanowi zapis rekurencyjny dla metody Newtona w postaci macierzowej.

Pochodna f'(x) jest macierzą Jakobiego

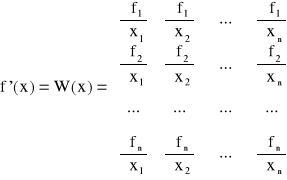
Przyjmując, że
jest macierzą nieosobliwą możemy równanie liniowe przekształcić do postaci:

stąd przyjmując dowolną wartość
otrzymujemy ciąg kolejnych przybliżeń pierwiastka równania
uzyskanych metodą Newtona.

Metoda iteracji

Dany jest układ równań nieliniowych z n niewiadomymi

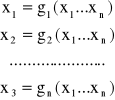
który możemy zapisać w postaci wektorowej

x=g(x)

gdzie:

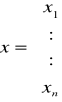
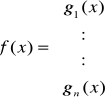
Zakładamy, że funkcja g₁, g₂, ..., g_n są rzeczywiste i ciągłe w pewnym otoczeniu odosobnionego pierwiastka a = {a₁, ..., a_n} układu równań.

Metoda iteracji polega na stosowaniu następującego wzoru

x^k+1 = g(x^(k))

Po przyjęciu przybliżenia
, w rezultacie otrzymujemy ciąg kolejnych przybliżeń
pierwiastka a równania.

Metoda siecznych

Rozpatrujemy układ równań nieliniowych w postaci

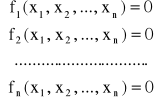
Który możemy ogólnie zapisać w postaci:

f(x)=0

gdzie x jest wektorem n zmiennych.

Metoda iteracji polega na stosowaniu wzoru wyliczającego k-te przybliżenie i-tej zmiennej tych:

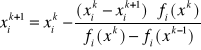
Metoda ma dwie wady:

- potrzebne są 2 zestawy punktów startowych: x₀, f(x₀), x₁, f(x₁)

- wykrywamy jeden wektor x-ów (globalny) (jeden zestaw x-ów), a pierwiastki mogą być wielokrotne

Przykład: Dany jest układ równań w postaci

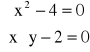
Napisać program wyznaczający rozwiązanie tego układu.

Niezbędne deklaracje typów:

wektor array[1..2] of Extended;

zmienne:

x, X1, Xn, F, F1, Fn: Extended;

iteracja: LongInt;

Funkcja reprezentująca układ równań

function funkcja (z:word):wektor;

begin

funkcja[1]:=sqrt(z[1])-4;

funkcja[2]:=z[1]*z[2]-2;

end;

Realizacja obliczeń:

Procedure oblicz

Begin

x[1]:=4;

x[2]:=7;

X1[1]:=9;

X1[2]:=11;

Repeat

Inc(iteracje);

F:=funkcja(x);

F1:=funkcja(X1);

xn[1]:=x[1]-((x[1]-x1[1])*F[1])/F[1]-F1[1];

Xn[2]:=x[2]-((x[2]-X1[2])*F[2])/F[2]-F1[2];

Fn:=funkcja(xn);

X1:=x;

x:=Xn;

until (abs(Fn[1]+abs(Fn[2])<=0.0000000001;

Po zakończeniu obliczeń wektor x przechowuje wartości zmiennych, natomiast zmienna iteracje zawiera liczbę wykonanych iteracji.

Rozważania dotyczą numerycznego obliczania wartości:

- całek pojedynczych funkcji ciągłych

- całek pojedynczych funkcji niewłaściwych

- całek funkcji osobliwych

- całek wielokrotnych

- całek Monte Carlo

Całkowanie pojedyncze - metody obliczeń

1. kwadratury z ustalonymi węzłami

• kwadratury Newtona-Cotesa

• złożone kwadratury Newtona-Cotesa

• metody Romberga

• metoda adaptacyjna

b) kwadratury Gaussa

- kwadratury Gaussa

- złożone kwadratury Gaussa

Całki pojedyncze właściwe

Całka oznaczona Riemanna

Niech funkcja f(x) będzie określona i ograniczona na przedziale [a,b]. Dokonajmy podziału przedziału [a,b] takiego, że:

a = x₀ < x₁ < ... < x_n+1 = b

i utwórzmy sumę

, gdzie
są dowolnymi punktami pośrednimi

Jeżeli ciąg {S_N} dla
jest zbieżny do tej samej granicy S przy każdym przedziale odcinka [a ; b] takim, że
niezależnie od wyboru punktów C_i to funkcję f(x) nazywamy całkowalną w przedziale [a ; b], a granicę S ciągu (1) nazywamy:

Całką oznaczoną Riemanna funkcji f o oznaczamy:

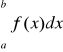
Można wykazać, że funkcja ograniczona w przedziale domkniętym jest całkowalna wtedy i tylko wtedy, gdy jej punkt nieciągłości w przedziale [a ; b] tworzą zbiór miary zero.

Jeżeli przez F(x) oznaczymy funkcję pierwotną funkcji f(x) w przedziale [a,b] (jeżeli F'(x) = f(x)) to ma miejsce wzór

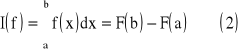
, gdzie E(f) - reszta kwadratury

Interpretacją graficzną całki oznaczonej jest pole pomiędzy osią OX, krzywą.

Wzór (1) jest inaczej nazywany kwadraturą. Nazwa pochodzi od sumowania wyrazów ciągu, które w najprostszym przypadku graficzną interpretację mają w postaci czworokątów.

Całka oznaczona Riemanna

Interpretacją graficzną całki oznaczonej jest pole powierzchni pomiędzy osią OX a krzywą. Rysunek obok to ilustruje

Wyznaczmy S sumę ciągu n-wyrazów, które są określone jako iloczyn wartości funkcji w punktach x_i∈<a,b> oraz współczynników niezależnych od rodzaju funkcji.

Wówczas

(1)
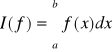
(2)

Można wykazać, że suma ciągu S(f) jest zbieżna do całki oznaczonej I(f) dla

Uwagi ogólne o całkowaniu numerycznym

Całkowanie numeryczne stosujemy wtedy gdy trudno obliczyć całkę w sposób analityczny lub w przypadku gdy znane są tylko wartości funkcji podcałkowej w punktach zwanych węzłami

W celu przybliżonego obliczenia całki oznaczonej funkcji f(x) na skończonym przedziale
, funkcję podcałkową f(x) zastępujemy interpolującą funkcją φ(x), którą łatwo można całkować. Funkcja φ(x) będzie wielomianem interpolującym z węzłami interpolacji x₀, x1, …, x_n. Wówczas całkę możemy zastąpić sumą, współczynniki a_i zależą od metody obliczeń

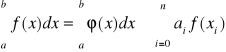
(4)

Kwadratury z ustalonymi węzłami

Kwadratury Newtona-Cotesa

Całkowanie z zastosowaniem kwadratur o ustalonych węzłach polega na zastąpieniu funkcji podcałkowej wielomianem interpolacyjnym Lagrange'a Li(x).

Jeżeli dla skończonego przedziału [a,b] wybierzemy zbiór punktów węzłowych {x₀, ..., x_n} takich, że:

x_i = x₀ + i · h

gdzie:

dla wówczas=(0, 1, …, n)

n - oznacza również stopień wielomianu interpolacyjnego

(5), gdzie:

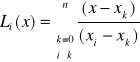
(6)

wówczas

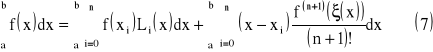
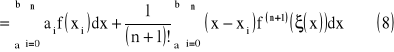
ξ - dowolny punkt pośredni z przedziału (x,x_i)

gdzie:

oraz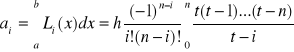
(9)

ostatecznie wzór kwadratury Newtona - Cotesa oraz reszta kwadratury

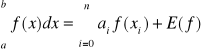
(10)

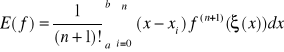
(11)

Twierdzenie 1

Kwadratury Newtona-Cotesa oparte na n+1 węzłach są rzędu

wówczas wzory kwadratur dla n parzystych mają postać

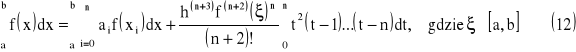
oraz dla nieparzystych mają postać:

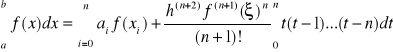
(13)

Kwadratury z ustalonymi węzłami - wzór trapezów

Wyznaczmy wzór kwadratury dla n = 1

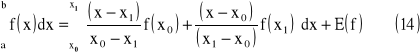
gdzie:

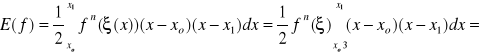
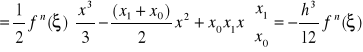
wówczas:

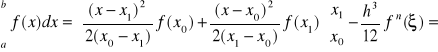
(16)

Ostatecznie otrzymujemy

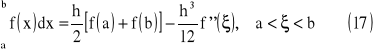
powyższe równanie jest znane jako wzór trapezów - widać, że wzór pozwala dokładnie obliczyć całkę dla dowolnej funkcji, dla której druga pochodna jest zero (wtedy reszta jest 0).

Zauważmy, że dla powyższych rozwiązań końce przedziału całkowania są węzłami kwadratury x₀=a oraz x_n=b. Wzory kwadratur oparte na tych węzłach nazywamy wzorami zamkniętymi Newtona - Cotesa.

Podobnie wyznaczyć można wzory dla innych n.

Kwadratury Newtona-Cotesa - wzory zamknięte

Poniżej znajdują się wzory zamknięte dla n = (1..3):

wzór trapezów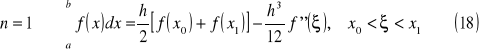

wzór parabol (Simpsona)

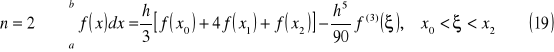
wzór Bessela

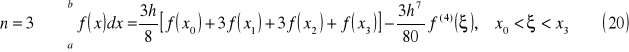
Interpretacja graficzna

wzór parabol (Simpsona)

wzór Bessela

Kwadratury Newtona - Cotesa - wzory otwarte

Wzory kwadratur nie opartych na węzłach będących końcami przedziału całkowania nazywamy wzorami otwartymi Newtona - Cotesa

Jeżeli dla skończonego [a ; b] przedziału wybierzemy zbiór punktów węzłowych {x₀, …, x_n} takich, że :

gdzie:

dla i=(0, …, n)

oraz

W oparciu o Twierdzenie 1 można również wyznaczyć wzory kwadratur otwartych. Wówczas wzory kwadratur dla n parzystych mają postać

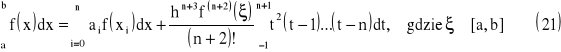
oraz dla n nieparzystych mają postać:

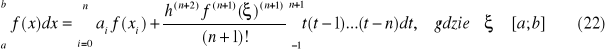
wzór prostokątów

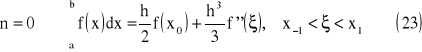
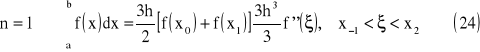
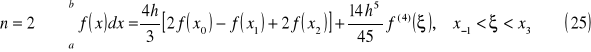
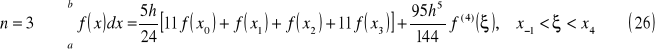
Interpretacja geometryczna

wzór prostokątów

wzór trapezów

Kwadratury Newtona-Cotesa - porównanie

Przykładowe wyniki obliczeń całki

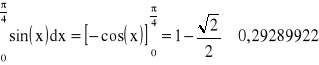
Wyniki obliczeń dla wzorów otwartych i zamkniętych:

n	0	1	2	3
wzory zamknięte		0,27768018	0,29293264	0,29291070
błąd		0,01521303	0,00003924	0,00001748
wzory otwarte	0,30055887	0,29798754	0,29285866	0,29286923
błąd	0,007666565	0,00509432	0,00003456	0,00002399

Kwadratury Newtona-Cotesa - podsumowanie

Kwadratury Newtona-Cotesa dają coraz lepszą dokładność wraz ze wzrostem n. Jednak wraz ze wzrostem n wzór na sumę posiada również rosnącą liczbę czynników. Dlatego kwadratur Newtona-Cotesa nie stosuje się dla dużych n oraz z uwagi na pojawianie się ujemnych współczynników (dla n = 7). Co więcej dla dużych n istnieją funkcje ciągłe, dla których ciąg kwadratur Newtona - Cotesa nie jest zbieżny do całki

W praktyce nie stosuje się kwadratur Newtona - Cotesa wysokiego rzędu.

Jak widać aby obliczyć wartość całki stosując kwadratury Newtona - Cotesa wystarczy wyznaczyć wartość funkcji w punktach węzłowych, a następnie podstawić je do wzoru. Większą trudność sprawia oszacowanie reszty kwadratury, gdyż należy wyznaczyć maksimum pochodnej k rzędu funkcji dla przedziału całkowania.

Obliczyć poniższą całkę stosując metodę Simpsona

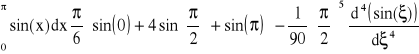
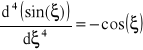
, wtedy

wówczas wyniki:

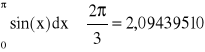
oraz oszacowanie błędu obliczeń:

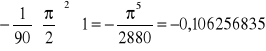
rozwiązanie dokładne:

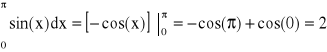
Kody źródłowe:

przykładowa całkowana funkcja:

function f(x:extender):extender,

begin

result:=sin (2*x*x)+2*cos(3x);

end;

wzór prostokątów:

function calka_n_0_wzor_otwarty(a,b:extended):extended;

var h:extended;

begin

h:=(b-a)/2;

result:=2*h*f(a+h);

end;

wzór trapezów:

function calka_n_1_wzor_zamkniety(a,b:extended):extended;

var h:extended;

begin

h:=(b-a);

result:=(h/2)*(f(a)+f(b));

end;

wzór parabol:

function calka_n_2_wzor_zamkniety(a,b:extended):extended;

var h:extended;

begin

h:=(b-a)/2;

result:=(h/3)*(f(a)+f(a+h)=f(b));

end;

Kwadratury z ustalonymi węzłami

Złożone kwadratury Newtona - Cotesa:

W poprzednim punkcie zostały przedstawione kwadratury Newtona-Cotesa. Wiemy, że błąd kwadratury zależy od długości przedziału całkowania oraz rzędu kwadratury. Dlatego w oparciu właśnie o kwadratury Newtona-Cotesa niskich rzędów zdefiniujemy tzw. wzory złożone Newtona-Cotesa. W celu zwiększenia dokładności obliczeń należy zmniejszyć długość przedziału. Wynika z tego, że dzieląc przedział całkowania na m podprzedziałów i obliczając dla każdego przedziału kwadraturę Newtona-Cotesa niskiego rzędu, następnie, gdy zsumujemy wyniki podprzedziałów, uzyskamy wynik zbieżny do rozwiązania dokładnego, natychmiast zwiększy się dokładność obliczeń.

m=1

Otrzymane w ten sposób kwadratury określono na całym przedziale całkowania nazywamy złożonymi kwadraturami Newtona-Cotesa

Twierdzenie 2:

Podzielmy przedział całkowania [a,b] na m części przy pomocy punktów:

, dla
,

mamy wtedy:

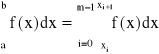
stosując do każdej z całek po prawej stronie równania dowolny wzór kwadratury Newtona-Cotesa ...

Na podstawie poprzedniej zależności możemy wyprowadzić wzory złożonych kwadratur:

złożony wzór prostokątów:

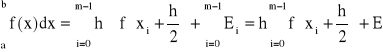
(28)

gdzie błąd przybliżenia
(29)

oraz

złożony wzór trapezów:

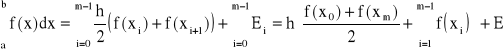
(30)

gdzie błąd przybliżenia
(31)

oraz

złożony wzór parabol - dla m parzystych:

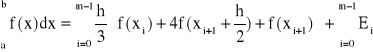
(32)

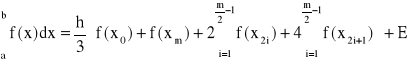
(33)

gdzie błąd przybliżenia
(34)

oraz

Podsumowanie:

Z powyższych wzorów wynika, że jeśli funkcja f jest wystarczająco regularna, to całka tej funkcji może być z dowolnie dużą dokładnością przybliżona przy pomocy złożonych kwadratur. Dla złożonych kwadratur Newtona-Cotesa, również największą trudność sprawia oszacowanie błędu obliczeń.

Twierdzenie 3:

Jeżeli
(jest jednokrotnie całkowalna w przedziale [a,b]), to dla każdego ciągu m złożonych kwadratur Newtona-Cotesa n-tego rzędu dla funkcji f jest zbieżny do całki: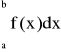
, przy

inaczej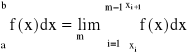

,
,

Przykład:

Obliczyć poniższą całkę:

Rozwiązanie dokładne

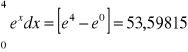
Metoda Simpsona m=1, h=2

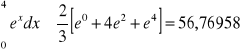
błąd = -3,17143

Metoda Simpsona m=1, h=1

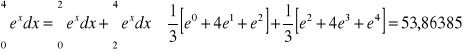
błąd = -0,26570

Metoda Simpsona m=4, h=0,5

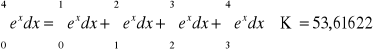
błąd = -0,01807

Przykładowe wyniki obliczeń całki:

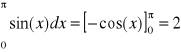
Wyniki obliczeń dla wzorów złożonych w zależności od m:

m		2	4	8	16	32	64
wzór prostokątów	wynik	1,110720735	1,751785441	1,936297295	1,983970758	1,995986709	1,998996147
		błąd	0,889279265	0,248214559	0,066102705	0,016029242	0,004013791	0,001003853
	wzór trapezów	wynik	1,570796327	1,896118898	1,1974231602	1,993570344	1,998393361	1,999598389
		błąd	0,429203673	0,103881102	0,025768398	0,006429656	0,001606639	0,000401611
	wzór parabol	wynik	2,094395102	2,004559755	2,000269170	2,000016591	2,000001033	2,000000065
		błąd	-0,094395102	-0,004559755	-0,000269170	-0,000016591	0,000001033	0,000000065

Kody źródłowe:

Złożony wzór prostokątów:

function Calka_Prostokat_Zlozony(a,b:extended;m:integer):extended;

var h,x,I_0:extended;

begin

h:=(b-a)/m;

I_0:=0.0;

for i:=0 to m-1 do

begin

x:=a+(i*h);

x:=x+(h/2);

I_0:=I_0+f(x)

end;

result:=I_0*h

end;

Złożony wzór trapezów:

function Calka_Trapez_Zlozony(a,b:extended;m:integer):extended;

var h,x,I_0,I_1:extended;

begin

h:=(b-a)/m;

I_0:=f(a)+f(b);

I_1:=0.0;

for i:=0 to m-1 do

begin

x:=a+(i*h);

I_1:=I_1+f(x);

end;

result:=(0.5*I_0+I_1)*h;

end;

Złożony wzór parabol:

function Calka_Simpson_Zlozony(a,b:extended;m:integer):extended;

var h,x,I_0,I_1,I_2:extended;

begin

h:=(b-a)/m;

I_0:=f(a)+f(b);

I_1:=0.0;

I_2:=0.0;

for i:=0 to m-1 do

begin

x:=a+(i*h);

if (i mod 2)=0

then I_2:=I_2+f(x);

else I_1:=I_1+f(x);

end;

result:=(I_0+2.0*I_2+4.0*I_1)*h/3;

end;

Kwadratury z ustalonymi węzłami

Metoda ekstrapolacyjna - Romberga

Metoda adaptacyjna

Kwadratury Gaussa

W poprzednim rozdziale omawiane były metody Newtona-Cotesa, które bazowały na całkowaniu wielomianu interpolacyjnego stopnia n. Pozwalał on na dokładne przybliżenie całki dla funkcji stopnia (n+1) lub (n+2). Wszystkie metody Newtona-Cotesa wykorzystywały wartości funkcji dla punktów węzłów równoległych. Ten warunek jest dogodny dla konstrukcji złożonych wzorów, ale może znacząco zmniejszyć dokładność przybliżenia całek.

Poniżej widać kwadraturę Newtona-Cotesa opartą na końcach przedziału - przybliżenie funkcji nie jest dokładne.

Kwadratury Gaussa dobierają takie węzły, aby osiągnąć optymalne przybliżenie całki: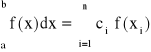

Węzły kwadratury x₁, x₂,..., x_n z przedziału całkowania [a,b] oraz współczynniki c₁, c₂,...,c_n są tak dobrane, aby zminimalizować błąd przybliżenia. Nie zakładamy jednak żadnych ograniczeń na węzły x_i o współczynnikach c_i natomiast chcemy zmaksymalizować rząd kwadratury.

Mamy znaleźć 2n stałe we wzorze, przypuszczamy więc, że rząd kwadratury powinien wynosić 2n, a więc wzór powinien być dokładny dla wielomianów stopnia (2n-1). Dla wielomianu stopnia równego lub wyższego od (2n-1) należy uwzględnić resztę kwadratury E:

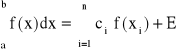
Aby pokazać proces wyboru odpowiednich węzłów oraz współczynników zilustrujemy to na przykładzie:

n=2 - liczba węzłów oraz przedział [-1,1]

Należy wyznaczyć x₁, x₂ oraz c₁, c₂, ponieważ:

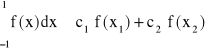
(64)

Zgodnie z założeniami, powyższe przybliżenie będzie dokładne tylko gdy stopień funkcji f(x) mniejszy lub równy
wówczas

(65)

gdzie a₀, a₁, a₂, a₃ - dowolne stałe

a więc możemy zapisać:

Poszukujemy x₁, x₂ oraz c₁, c₂, więc można zapisać:

(67)

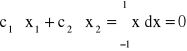
(68)

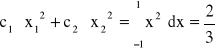
(69)

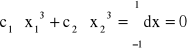
(70)

otrzymaliśmy układ liniowych równań algebraicznych, którego rozwiązanie jest:

ostatecznie otrzymaliśmy wzór na przybliżenie całki dla funkcji danej wzorem (64):

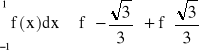
Metoda poszukiwania węzłów oraz współczynników może zostać zastosowana dla funkcji wyższych rzędów, lecz istnieje łatwiejsza metoda. Bazuje ona na wykorzystaniu jednego z wielomianów ortogonalnych. Mają one taką właściwość, że całka z iloczynu dwóch dowolnych wielomianów jest równa 0:

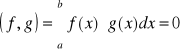
Dla naszych dalszych rozważań, zajmiemy się tylko ciągiem wielomianów Legendre'a

, który posiada właściwości:

1. Dla każdego n, P_n(x) jest wielomianem stopnia n

2.
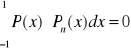
, gdzie P(x) jest wielomianem stopnia wyższego (niższego???) od n

Wzory kilku pierwszych wielomianów Legendre'a:

oraz wzór rekurencyjny do wyznaczania wielomianów krzywych ??? oraz ich pochodnych:

Pierwiastki tego wielomianu są tylko pojedyncze, leżą w przedziale <-1,1> oraz są symetryczne względem początku układu współrzędnych. Najważniejszą właściwością jest to, że bardzo dobrze nadają się do wyznaczania punktów węzłowych oraz współczynników.

Punkty węzłowe potrzebne w celu dokładnego przybliżenia całki funkcji stopnia mniejszego od 2n są pierwiastkami wielomianu Legendre'a n-tego stopnia.

Jeżeli x₁, x₂, ... x_n są pierwiastkami wielomianu Lagrange'a, P_n(x) stopnia n dla każdego i = (1,2,...n) wtedy współczynniki c_i można obliczyć ze wzoru:

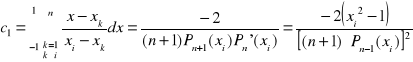
wówczas jeżeli P(x) jest dowolnym wielomianem stopnia mniejszego od 2n wtedy:

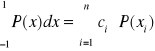
(75)

reszta dla stopnia większego od (2n-1):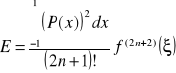

Pierwiastki wielomianu oraz współczynniki c_i są tabelaryzowane - nie obliczamy ich przy każdym całkowaniu. Prawa strona wzoru (75) jest nazwana kwadraturą Gaussa-Lagrange'a. Wzór ten pozwala na obliczenie całki tylko w przedziale
. W celu obliczenia przybliżenia całki w dowolnym przedziale
dla którego f(x) jest ciągła należy wykonać przekształcenie poprzez podstawienie.

Dokonujemy przekształcenia dowolnego przedziału
do przedziału
.

Wówczas możemy zapisać:

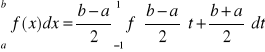
po zastosowaniu kwadratury Gaussa-Lagrange'a otrzymujemy

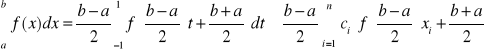
gdzie x_i - pierwiastek wielomianu stopnia n

c_i - współczynnik ze wzoru (74)

przykład:

Obliczyć całkę wykorzystując kwadraturę Gaussa:

dokończyć ??? najpierw przekształcenia przedziału całkowania:

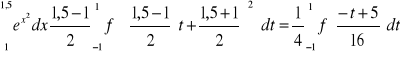
po zastosowaniu kwadratury Gaussa-Lagrange'a, n=2 otrzymujemy:

c₁=1 c₂=1

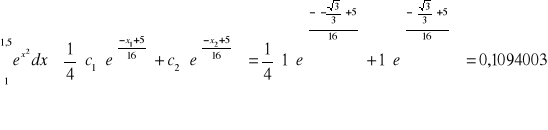
Po zastosowaniu kwadratury Gaussa-Lagrange'a, n=3 otrzymujemy:

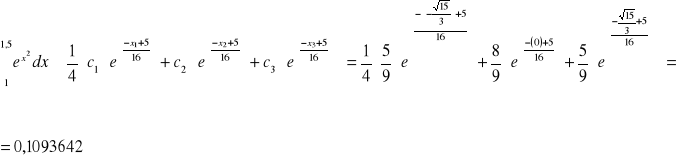
Tablica pierwiastków wielomianu Legendre'a:

n	x0	x1	x2	x3	x4
1	0	-	-	-	-
2	-0,5773509	0,5773509	-	-	-
3	0,7745966	0	-0,77459666	-	-
4	0,86113631	0,33998104	-0,33998104	-0,86113631	-
5	-0,53846931	-0,90617984	0	0,90617984	0,53846931

Kod źródłowy kwadratury Gaussa:

Przykład f. całką wykorzystując kwadraturę G w przedziale
oraz n- oznacz. stopnia met. L.

function Gauss_Legendre (n:Integer; var x:vector); Extended

var k,l,m:Integer;

p0,p1,p2,s,x1,ci:Extended

begin

if n>0 then

begin

s:=0

l:=n div2;

for k:=0 to n do

begin

p0:=1;

x1:=x[k];

p1:=x1

for m:=1 to n-1 do

begin

p2:=((2*m+1)*x1*p1-m*p0)/(m+1);

p0:=p1;

p1:=p2;

end;

ci:=-2*(x1*x1-1)/((n+1)*(n+1)*p1*p1);

s:=s+f(x1)*ci;

end;

Result:=s;

end;

end;

gdzie x - tabl. zawiera pierwiastki wielomianu Legendre'a

oraz n - stopień wielomianu Legendre'a

Obliczanie całek niewłaściwych:

Przy numerycznym całkowaniu w przedziale obustronnie lub jednostronnie nieskończonym, należy stosować takie funkcje wagowe, które zapewniają zbieżność całki, W zależności od przedziału stosujemy odpowiedni wielomian interpolacyjny:

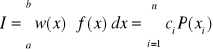
Całkowanie funkcji osobliwych:

W celu obliczenia przybliżonej całki funkcji posiadającej punkty nieciągłości, należy zmodyfikować poznanie metody. Aby dokonać takiego całkowania, należy zlokalizować wszystkie punkty nieciągłości należące do przedziału całkowania.

Przykłady funkcji nieciągłych:

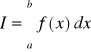
, gdzie f(x):

przypadek 1*	przypadek 2*

Powyższe metody wymagają wielu przekształceń matematycznych, które nie dają wyznaczyć się informatycznie.

Ma to charakter historyczny.

Alternatywną metodą wyliczenia całki jest metoda polegająca na oddalaniu się od punktu nieciągłości o małe ε ???

Metoda zwykłego szeregu Taylora:

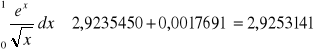
Metoda adaptacyjna:

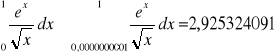
zał. dokładne 0,0001 liczba przedzi. 235 il. wywoł. funkcji 941 ???

Całki wielokrotne:

rozpatrzmy całkę podwójną:

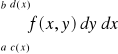
x - stała i stosunek kwadratury do obliczonej całki

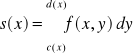
otrzymujemy:

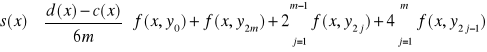
m - liczba przedziałów przedziału [c(x) ; d(x)]

wykorzystanie z kolei kwadratury Simpsona do obliczenia całki:

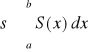
ostatecznie:

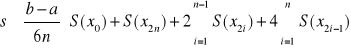
np.: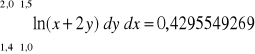

stos. złoż. kwadratury Simpsona:

dla n=4 i m=2

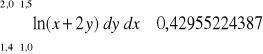
Całkowanie wielokrotne - całka podwójna

kod źródłowy:

function f (x,y:real):real;

begin

Result:=explg (x)???

end;

function c(x:real):real;

begin

Result:=x*x*x

end;

function d(x:real):real;

begin

Result:=x*x

end;

function simpson-Podwojna

(a,b:real; m,n:integer):real;

var i,j:integer

h,hx,j1,j2,j3

k1,k2,k3,x,y,x:real;

begin

h:=(b-a)/(2*n)

j1:=0; j2:=0;

j3:=0

for i:=0 to 2*n do

begin

x:=a+i*h;

nx:=(d(x)-c(x))/(2*m);

k1:=f(x,c(x))+f(x,d(x));

k2:=0

k3:=0

for j:=1 to 2*m-1 do

begin

y:=c(x)+j*hx

z:=f(x,y);

if Odd(j) ???

then k3 :=k3+z

else k2:=k2+z

end

i:=(k1+2*k2+4*k3)+hx/3

if(i=0) or (i=2*n)

then j1:=j1+1

else if Odd (i)

then j3:=j3+l

else j2:=j2+l

end;

Result:=(j1+2*j2+4*h/3)

end;

Kody źródłowe:

Function f(x,y:real):real;

Begin

Result:=exp(y/x);

End;

Function c (x:real):real;

Begin

Result:=x*x*x;

End;

Function d (x:real):real;

Begin

Result:=x*x;

End;

function Simpson_Podwojna (a,b:real; m,n:integer):real;

var i,j:integer;

h,hx,j1,j2,j3,k1,k2,k3,I,x,y,z:real;

begin

h:=(b-a)/(2*n);

j1:=0;

j2:=0;

j3:=0;

for i:=0 to 2*n do

begin

x:=a+i*h; tu tomek napisał ... j*h a ja mam i*h sprawdźcie!!!

hx:=(d(x)-c(x))/(2*m)

k1:=f(x,c(x)+f(x,d(x));

k2:=0;

k3:=0;

for j:=1 to 2*m-1 do

begin

y:=c(x) +j*hx;

z:=f(x,y);

if odd(j)

then k3:=k3+z

else k2:=k2+z

end;

I:=(k1+2*k2+4*k3)*hx/3;

If (i=0) or (i=2*n)

then j1:=j1+I

else if Odd(i) tu też mam troche inaczej

then j3:=j3+l

else j2:=j2+l

end;

Result:=(j1+2*j2+4*j3)*h/3;

End;

Obliczanie całek metodą Monte-Carlo

Metoda Monte Carlo - całka pojedyncza

Mamy obliczyć przybliżoną wartość In całki oznaczonej

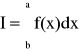
(129)

przy założenie, że f(x) jest funkcją ciągłą w przedziale domkniętym [a;b]

Następnie n-krotnie generujemy realizację x zmiennej losowej X o rozkładzie równomiernym w przedziale [a,b], otrzymujemy w rezultacie ciąg liczb x₁, x₂, ..., x_n,

Przybliżoną wartość całki określa wzór

(130)

Zbieżność przybliżonej wartości całki In do jej dokładnej wartości jest gwarantowana w sensie probalistycznym, tzn., że dla każdego ε>0 zachodzi relacja:

(131)

gdzie P jest prawdopodobieństwem, przy czym błąd metody monte Carlo można określić wzorem

(132)

Maszyny typowe zazwyczaj dysponują generatorem liczb losowych o rozkładzie równomiernym w przedziale [0,1], zachodzi zatem konieczność przeliczania wylosowanej realizacji Y z przedziału [0,1], na realizację zmiennej losowej X o rozkładzie równomiernym w przedziale [a, b]. Wzory poniżej, to ilustrują:

Przeliczanie zmiennych losowych Y na X

X=(b-a)Y+a (133)

Przeliczanie realizacji zmiennych losowych Y na X

x=(b-a)y+a (134)

Kod źródłowy:

Function Calka_MonteCarlo (a,b:extended; n:lingint):extended

Var i:integer;

h,x:extended;

begin

Result:=0;

h:=(b-a)/n;

for :=1 to n do

begin

x:=a+((b-a)*Random);

Result:=Result+f(x);

End;

Result:=Result*h;

end;

Całkowanie - Metody Monte Carlo. Całki wielokrotne właściwe

Dana jest całka wielokrotna:

(135)

Każda ze zmiennych x_i zawiera się w przedziale
(136)

Losujemy n-krotnie punkty Pk kostki, przyjmując że współrzędnymi tych punktów są zmienne losowe X₁^(k), X₂^(k),..., X_m^(k) o rozkładzie równomiernym w odpowiednich przedziałach [a_i,b_i]. Każdemu punktowi Pk odpowiada zatem ciąg m-elementowy wylosowanych realizacji x₁^(k), x₂^(k),..., x_m^(k). Po wylosowaniu sprawdzamy czy każdy punkt Pk należy do obszaru Ω. Możemy zatem po zakończeniu losowań uporządkować wylosowane punkty w następujący sposób:

dla k=(1, 2, ..., n),
dla k=(n+1, n+2, ..., N) (137)

Przy dostatecznej liczbie losowań możemy obliczyć przybliżoną wartość V_Ω objętości m-wymiarowanego obszaru całkowania:

(138),

gdzie

(139)

jest objętością m-wymiarowej kostki. Przybliżona wartość I_n całki (135) określana wzorem:

(140)

Aby uzyskać ciąg realizacji X1, X2, ..., Xm losujemy m-krotnie zmienną losową Y o rozkładzie równomiernym w przedziale [0,1], a następnie przeliczamy realizacje y na realizację x_i^(k) w przedziale [a_i; b_i] korzystając ze zależności:

x_i^(k)=(b_i-a_i)y_i^(k)+a_i

Rozwiązywanie równań różniczkowych

Rozważania dotyczą:

• równań różniczkowych zwyczajnych z warunkami początkowymi i brzegowymi,

• układów równań różniczkowych zwyczajnych z warunkami początkowymi i brzegowymi,

• równań różniczkowych cząstkowych,

• układów równań różniczkowych cząstkowych

Numeryczne obliczanie pochodnej

Aby obliczyć pochodną funkcji f w punkcie x₀, mamy

(1)

W celu wyznaczenia przybliżonej wartości pochodnej f'(x) dla małych wartości h możemy użyć wyrażenia

(2)

Możemy to udowodnić. Dokonujemy interpolacji f(x); zdefiniujemy wielomian Lagrange`a stopnia 1, który będzie oparty na węzłach x₀ oraz x₀+h pod warunkiem, że funkcja f jest dwukrotnie różniczkowalna w przedziale [a; b]

ktoś nie zdązył do końca, a ja nie wiem czy w mianowniku jest 2!, czy co??

Wówczas obliczając pochodną funkcji f, mamy:

(3)

oraz po uproszczeniu

(4)

Jeżeli dokonamy interpolacji funkcji f wielomianem stopnia 2, wówczas

(5)

oraz po uproszczeniu

I(6)

Za pomocą wielomianów wyższych stopni możemy wyznaczyć wzory na przybliżenie pochodnej.

Przykład: Obliczyć pochodną funkcji f(x)=ln(x) dla x₀=1,8 stosując metodę w przód i wstecz stopnia 1.

,

gdzie:

brak textu

	Metoda w przód		Metoda wstecz
h	Wynik	Błąd	Wynik	Błąd
0,1	0,5406772	0,0154321	0,5715841	0,0173010
0,01	0,5540180	0,0015432	0,5571045	0,0015605
0,001	0,5554013	0,0001543	0,5557099	0,0001545

Numeryczne obliczanie drugiej pochodnej.

Jeżeli dokonamy rozwinięcia funkcji f w szereg Taylora 3 rzędu w otoczeniu punktu x₀ dla punktów x₀+h oraz x₀-h, zakładając, że f jest 4-krotnie różniczkowalna na przedziale [x₀-h, x₀+h], wówczas dla x₀-h:

Wzor (8)

gdzie

dodając oba równania stronami otrzymujemy:

wzór (9)

Rozwiązując równanie ze względu na f”(x₀), otrzymujemy:

(11)

oraz

, gdzie

Powyższy wzór otrzymamy różniczkując obustronnie wzór na pierwszą pochodną (5) kroku h/2.

Przykład: Obliczyć drugą pochodną funkcji f(x)=ln(x³) dla x₀=2 stosując powyższą metodę różnych wartości kroku h.

Wzór

Rozwiązanie dokładne

f”(2)=-0,1875

h	Wynik	Błąd	Oszacowanie ε
0,1	-0,1875586182	0,0000586182
0,01	-0,1875005859
0,001	-0,1875000049

Równania różniczkowe zwyczajne z warunkami początkowymi

Równania różniczkowe są wykorzystywane do odwzorowania wielu problemów z zakresu różnych nauk, które dotyczą zmian jednej zmiennej względem innej zmiennej. Wiele problemów świata rzeczywistego opisywanych przez równania różniczkowe jest za bardzo złożonych, aby uzyskać rozwiązanie dokładne (analityczne), należy znaleźć rozwiązanie przybliżone. Są dwa sposoby aby uzyskać rozwiązanie przybliżone. Po pierwsze można dokonać uproszczenia zadanego równania różniczkowego do takiej postaci, dla której znamy rozwiązanie dokładne, wówczas uproszczone równanie będzie przybliżało rozwiązanie równania zadanego. Drugim sposobem jest zastosowanie jednej z metod numerycznych w celu przybliżenia rozwiązania zadanego równania.

Metody różnicowe jednokrokowe:

• metody Eulera;

• metody Rundego-Kutty

• metody Rundego-Kutty-Fehenberga

Metody różnicowe wielokrokowe:

• metody bezpośrednie

• metody pośrednie

• metoda Predictor-Corrector

• metoda trapezów

Metoda Eulera

Rozpatrzmy zadanie znalezienia funkcji y=y(t), które dla
spełnia równanie różniczkowe zwyczajne pierwszego rzędu:

(7)

oraz warunek początkowy

y(a)=y₀ (8),

gdzie f jest daną funkcją dwu zmiennych. Warunek wystarczający istnienia i jednoznaczności rozwiązania zadania (7) oraz (8) jest warunek ciągłości funkcji f(t,y)

Metoda ta rzadko jest używana w praktyce, natomiast ze względu na jej prostotę, zostanie przedstawiona w celu zobrazowania i zrozumienia technik stosowanych w bardziej zaawansowanych metodach, pomijając przy tym złożone działania matematyczne. Przedmiotem rozważań będzie poniższe równanie.

, gdzie
oraz y(a)=a (10)

Na rozwiązanie powyższego zagadnienia będziemy obliczać przybliżone wartości funkcji yi=y(ti), gdzie ti=a+ih, h=(b-a)/N, dla którego i=(0,1, ..., N), gdzie ti nazywane są punktami węzłowymi, natomiast h odległością między nimi.

Rozwiniemy y(t) w szereg Taylora w celu wyprowadzenia metody Eulera. Zakładając, że y(t) jest jedynym rozwiązaniem (10) oraz posiada drugą pochodną, która jest ciągła w przedziale [a, b] wówczas dla każdego i=1, 2, ..., N.

Wykorzystując powyższe założenia możemy zapisać:

(11), gdzie

Oznaczamy h=t_i+1-t_i, wówczas otrzymujemy:

(12)

Użyjemy podstawienia y'(t)=f(t, y), wówczas otrzymujemy:

(13)

Zapisując ω_i≈y(t_i) oraz pomijając błąd przybliżenia otrzymujemy ω_i+1=ω_i+hf(t_i, ω_i) (14)

Powyższy wzór nazywamy metodą Eulera - wzór ten nazywany jest inaczej równaniem różniczkowym, gdyż można zapisać:

(15)

Aby wyznaczyć wartość szukanej funkcji y(x) w następnym kroku h, wykorzystujemy poprzednią wartość funkcji oraz wielkości zmian funkcji - dzięki pochodnej. Natomiast uwzględniając błąd przybliżenia wzór (13) przyjmuje postać:

, gdzie
(16)

Lokalny błąd dyskretyzacji τ_i+1(h)

(17)

dodatkowo możemy określić krok h, dla którego błąd lokalny jest mniejszy od zadanej dokładności δ

, gdzie

Globalny błąd dyskretyzacji g(x)

g(t)= ω(t)-y(t) (19)

Dla wybranego punktu t_i możemy zapisać:

g_i=ω_i-y(t_i) (20), wówczas

, gdzie L- liczba Lipschnitz`a

Lokalny błąd dyskretyzacji

Globalny błąd dyskretyzacji

nie będę wskazywał na tego, kto nie narysował go ;)))

Stosując metodę Eulera rozwiązać następujące równanie różniczkowe

y'=y-t²+1 0<t<2 y(0)=0,5

dla N=10, wtedy h=0,2; t_i=ih, ω=0,5 oraz ω_i+1=ω_i+hf(t_i, ω_i), gdzie f(t,y)=y-t²+1

ω_i+1=ω_i+h(ω_i-t²_i+1)= ω_i+0,2[ω_i-0,04i²+1]=1,2ω_i-0,008i²+0,02 dla i=0, 1, ..., 9

Rozwiązanie dokładne ma postać

y(t)=(t²-1)-0,5e^t

Metoda Eulera - wstecz

Powyższe rozważania dotyczyły metody Eulera w przód, ponieważ krok spełniał warunek h>0. W analogiczny sposób można wyprowadzić metodą Eulera wstecz przyjmując h<0, wówczas otrzymujemy:

w_i+1 = w_i + hf (t_i+1, w_i+1) (22)

w_i+1^(k) = w_i + hf (t_i+1, w_i+1^(k-1)) (23)

Metoda wstecz różni się w stosunku do metody w przód argumentami funkcji f.

Metoda w przód wykorzystuje do obliczenia przybliżenia wartości z poprzedniego kroku, natomiast metoda wstecz jest równaniem uwikłanym, ponieważ aby obliczyć kolejne przybliżenie w_i+1 wykorzystujemy wartości z poprzedniego kroku oraz poszukiwaną wartość w_i+1. Takiego równania nie można rozwiązać w sposób bezpośredni. Aby rozwiązać takie równanie (23) należy zastosować proces iteracyjny, czyli poszukujemy kilkakrotnie w_i+1^(k), stojącej po prawej stronie równania podstawiając jako w_i+1^(k-1) - lewa strona równania, wynik przybliżenia z poprzedniej iteracji (k-1). Proces trwa do momentu, kiedy spełniony zostanie warunek:

|w_i+1^(k) - w_i+1^(k-1)| ≤ ε (24)

gdzie ε - tolerancja obliczeń

Kody źródłowe:

Metoda Eulera w przód:

Function Euler_order_One_Forward (t0, tn, y0:extended; n:integer): extended;

var i:integer;

h, wi, wi_1,t :extended;

Begin

h:= (tn-t0)/n;

yi_1:=y0;

for i:=0 to n-1 do

begin

t:=t0+i*h;

wi:=wi_1+h*f(t,wi_1);

wi_1:=wi;

end;

Result:=wi;

end;

Przykładowa funkcja definiująca równanie różniczkowe

function f(t,y:extended):extended;

begin

result:=y-sqr(t)+1;

end;

Metoda Eulera “wstecz”

function Euler_Order_One_Backward

t0, tn, y0, eps : extended; n:integer):extended;

var i:integer;

h,wi,wi_p,wi_1,t :extended

begin

h:=(tn-t0)/n

wi_1:=y0;

for i:=0 to n-1 do

begin

t:=t0 + i*h;

wi:=wi_1 + h*f (t, wi_1);

repeat

wi_p:=wi;

wi:=wi_1 + h*f (t, wi_p);

until abs(wi-wi_p)<eps;

wi_1:=wi;

end;

Result:=wi;

end;

Przykładowa funkcja definiująca równanie różniczkowe

function f(t,y:extended):extended;

begin

result:=y-sqr(t)+1;

end;

Metody Rungego-Kutty

Powszechnie na całym świecie stosuje się metody Rungego-Kutty czwartego rzędu. Polegają one na rozwiązaniu zagadnienia:

gdzie t∈ [a,b] oraz y(a)=α (25)

i przedstawieniu różnicy funkcji y(t) w punktach t_i+1 oraz t_i w postaci:

w_i+1 - w_i =
lub inaczej w_i+1 - w_i = h0 (t_i,w_i,h) (26)

gdzie m oznacza rząd metody, c_j są stałymi, a

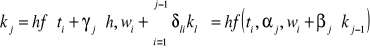
gdzie α_j, β_j, γ_j, _δlj - stałe

h - krok całkowania

Określenie stałych c_j, α_j, β_j otrzymujemy poprzez rozwinięcie funkcji f(t,y) w szereg Taylora w otoczeniu punktu t_i

Metody R-K - metoda 2 rzędu

Metoda wyprowadzona przez rozwinięcie f(t,y) w szereg Taylora 2 rzędu pozwala określić stałe c₁, α₁,β₁, c₂, α₂, β₂ :

Metoda punktu środkowego:

C1 = 0 C2 = 1 α₁ = 0 α₂ = h/2 β1 = 0 β2 = ½ (28)

wówczas możemy zapisać:

k₁=hf (t_i,w_i) k₂=hf (t_i + ½ h, w_i + ½ k₁)

ostatecznie:

w_i+1=w_i+k₂

lub

w_i+1=w_i + hf(t_i + h/2, w_i + h/2 * f(t_i, w_i))

Interpretacja graficzna:

f₁=f(t_i,w_i) f₂=f(t_i + h/2, w_i + h/2 * f₁)

Stosując metody Rungego-Kutty 2 rzędu , rozwiązać następujące równanie różniczkowe:

y'=y-t² + 1 0≤ t ≤2 y(0)=0,5

dla N = 10 wtedy h = 0,2; t_i = i⋅h ; w₀ = 0,5 oraz

metoda punktu środkowego w_i+1 = 1,22 w_i - 0,0088 i² + 0,218

Metoda zmodyfikowana Eulera

w_i+1 = 1,22 w_i - 0,0088 i² + 0,216

Metoda Heana dla i = 0, 1, ..., 9

w_i+1 = 1,22 w_i - 0,0088 i² + 0,2173

Rozwiązanie dokładne ma postać:

y(t) = (t²+1) - 0,5 e^t

Metody R-K rzędu 4

Metoda wyprowadzona przez rozwinięcie f(t,y) w szereg Taylora 4 rzędu, pozwala określić stałe we wzorze (wzór ogólny R-K). Poniżej przedstawiono najczęściej stosowaną metodę 4 rzędu

k₁ = hf (t_i, w_i)

k₂ = hf (t_i + ½ *h, w_i + ½ *k₁)

k₃ = hf (t_i + ½ *h, w_i + ½ *k₂) (37)

k₄ = hf (t_i+h, w_i+k₃)

ostatecznie:

w_i+1=w_i + 1/6 (k₁ + 2k₂ + 2k₃ + k₄) (38)

Interpretacja graficzna:

f₁ = f (t_i, w_i)

f₂ = f (t_i + ½ * h, w_i+1 + h f₁)

f₃ = f (t_i + ½ * h, w_i + ½ * h f₂)

f₄ = f (t_i + h, w_i + h f₃)

linia 3-4 nie jest łamana - jest prosta !!! (na 99%) :)

Metoda R-K jest najczęściej stosowaną metodą do rozwiązywania układów równań różniczkowych

Przykład:

Stosując metodę R-K 4-tego rzędu rozwiązać następujące równanie różniczkowe:

y' = y-t² + 1 0≤ t ≤ 2 y(0) = 0,5

dla N = 10 wtedy h = 0,2 t₁ = i*h w₀ = 0,5 oraz:

Metoda Rungego-Kutty 4-rzedu:

w_i+1 = 1,2214 w_i - 0,008856 i² + 0,00856 i + 0,218593

dla i = 0, 1, ..., 9

Rozwiązanie dokładne ma postać y(t) = (t²+1) - 0,5e^t

Kody źródłowe:

function RK_Rzedu_4 (t0, tn, y0: extended; n:integer):extended;

var i:integer;

h, yi, y_i, t, k1, k2, k3, k4: extended;

begin

h:= (tn-t0)/n

y_i = y0;

for i:=0 to n-1 do

begin

t:=t0 + i*h;

k_1 := h*ft, y_i);

k_2 := h*f(t + 0.5 * h, y_i+0.5 * k1);

k_3 := h*f(t+0.5*h, y_i + 0.5 * k₂);

k_{4 :}= h*f(t+h, y_i + k3);

yi:= y_i+(k1 + 2*k2 + 2*k3 + k4)/6;

y_i:=yi;

end;

Result := yi;

end;

Metody wykorzystujące więcej niż jedną przybliżoną wartość dla poprzednich punktów węzłowych w celu przybliżenia wartości w następnym punkcie węzłowym nazywamy metodami wielokrokowymi.

Ogólny wzór na m-krotną metodę wielokrokową dla rozwiązania równania

gdzie t∈ [a,b] oraz y(a) = α (55)

jest równaniem różniczkowym dla znalezienia przybliżenia w_i+1, dla punktu węzłowego t_i+1, gdzie m>1, które przyjmuje postać:

w_i+1 = a_m-1 * w_i + a_m-2 * w_i-1 + ... + a₀ * w_{i+1_m} + h [b_n f(t_i+1,w_i+1) + b_n-1 f(t_i, w_i) + ... + t + b₀ f(t_{i+1_m}, w_{i+1_m})]

dla i = (m-1, m, ..., N-1),

N - liczba węzłów w przedziale, gdzie h = (b-a) / N

Równania różniczkowe cząstkowe z warunkami brzegowymi - rodzaje:

1. równania różniczkowe eliptyczne

• równanie Laplace'a,

• równanie Poisson'a,

• równanie różniczkowe paraboliczne

• równanie dyfuzji

c) równanie różniczkowe hiperboliczne

• równanie falowe

Równania różniczkowe cząstkowe z warunkiem brzegowym - wstęp

Równania różniczkowe prezentowane w poprzednich rozdziałach pozwalały na wyznaczenie poszukiwanej funkcji jednej zmiennej dla podanych warunków początkowych lub brzegowych. Problemy przedstawione w tym rozdziale będą opisywane funkcjami wielu zmiennych.

W zależności od specyfiki problemu można opisać go za pomocą odpowiedniego równania różniczkowego: Laplace'a, Poisson'a, Dyfuzji, Falowego, itp… . Aby rozwiązać problem opisany odpowiednim równaniem różniczkowym należy określić warunki brzegowe. Warunki brzegowe mogą być opisane w formie warunków Dirichleta lub Neumanna.

Równania różniczkowe cząstkowe - warunek brzegowy Dirichleta

Jeżeli funkcja u(x,y) jest poszukiwana na obszarze R, wówczas musi mieć zdefiniowane warunki w postaci funkcji g(x,y) na brzegu S.

Warunek brzegowy Dirichleta


dla





gdzie: u(x,y) - poszukiwana funkcja w punktach wewnątrz obszaru R, g(x,y) - zadana funkcja dla punktów (x,y) należących do brzegu S obszaru R.

Wynika z tego, że w trakcie obliczeń wartości funkcji g w poszczególnych punktach (x,y) ჎ S nie mogą się zmienić.

Równania różniczkowe cząstkowe - warunek brzegowy Neumanna

Warunek brzegowy Neumanna


dla


gdzie:
- pochodna normalna poszukiwanej funkcji w punktach należących do brzegu S obszaru R, g(x,y) - zadana funkcja dla punktów (x,y) należących do brzegu S obszaru R.

Oznacza to, że na brzegu obszaru zmienność funkcji u(x,y) w kierunku normalnym dla punktów (x,y) ჎ S jest równa funkcji g(x,y).

Dla zmiennej x




Dla zmiennej y




Równania różniczkowe cząstkowe z warunkiem brzegowym - Równania eliptyczne - Poissona i Laplace'a

Równania różniczkowe cząstkowe eliptyczne znane jako równanie Poissona , dla dwóch wymiarów i prostokątnego układu współrzędnych przyjmuje postać:


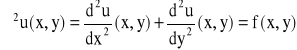
(1)

na


z warunkami brzegowymi
dla


W powyższym równaniu funkcja f opisuje dane wejściowe na płaszczyźnie dla obszaru R ograniczonego brzegiem S. Równania tego typu są stosowane dla różnych problemów fizycznych, które są niezależne od czasu. Najczęściej stosowane są do obliczenia rozkładu potencjału (np. temperatury) w stanie ustalonym.

Szczególnym przypadkiem równania Poissona gdy f(x,y)=0 jest równanie Laplace'a.

Aby rozwiązać równanie cząstkowe eliptyczne (1) zastosujemy metodę różnic skończonych MRS.

W tym celu weźmiemy dwie liczby całkowite m i n, i zdefiniujemy kroki całkowania h = (b-a)/n oraz k = (c-d)/m. Dzięki temu możemy podzielić: przedział [a,b] na n równych części o szerokości h oraz przedział [c,d] na m równych części o szerokości k.

Umieśćmy siatkę na obszarze R poprzez narysowanie pionowych i poziomych linii przechodzących przez punkty (xi, yj), takich że:





dla i = 0,1, .. n

oraz
dla j = 0,1, .. m

Linie x = xi oraz y = yj nazywamy liniami siatki, natomiast ich punkty przecięcia (xi,yj) nazywamy punkami węzłowymi siatki. Dla wewnętrznych punktów węzłowych (xi,yj), które nie należą do brzegu obszaru R, zastosujemy metodę różnic skończonych - MRS. Metoda ta opiera się na zastąpieniu pochodnych cząstkowych rozwinięciem funkcji w szereg Taylora w otoczeniu punktu (xi,yj) - (patrz druga pochodna numeryczna) . Wówczas otrzymujemy:

Dla zmiennej x


(2)

gdzie:


Dla zmiennej y


(3)

gdzie:


Podstawiając wzory (2) oraz (3) do równania Poissona (1) otrzymujemy:



(4)

dla i = 1,2 … n-1 oraz j = 1,2, … m-1

natomiast warunki brzegowe mają postać:


oraz
dla j = 0,1, .. m (5)


oraz
dla i = 1,2, .. n (6)

Ostatecznie wzór na MRS, podstawiając za (xi,yj) = wij oraz wyłączając oszacowanie błędu zapisujemy:


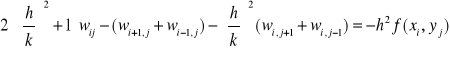
(7)

dla i = 1,2 … n-1 oraz j = 1,2, … m-1

natomiast warunki brzegowe mają postać:


oraz
dla j = 0,1, .. m (8)


oraz
dla i = 1,2, .. n (9)

gdzie w_ij jest przybliżeniem u(x_i,y_j).

Analizując równanie (7) można zauważyć, że w celu wyznaczenia przybliżenie rozwiązania w punkcie (xi,yj), potrzebne są wartości przybliżenia rozwiązania w czterech sąsiednich punktach - patrz rysunek obok.




Postać macierzowa

Jak widać poszukujemy rozwiązania równania Poissona dla wewnętrznych węzłów siatki, w tym celu dla każdego punktu siatki układamy równanie (7). Po uwzględnieniu warunków brzegowych otrzymujemy układ (n-1)Ⴔ(m-1) równań liniowych. Układ równań możemy rozwiązać metodami deterministycznymi bądź iteracyjnymi.

Zakładając, że h = k możemy wyprowadzić uproszczoną postać równania (7) :


(10)

dla i = 1,2 … n-1 oraz j = 1,2, … m-1

natomiast warunki brzegowe są takie same jak (8) i (9) :

Postać iteracyjna

Równanie (7) i (10) można przedstawić również w postaci iteracyjnej, wyprowadzając wij z każdego równania, gdzie l oznacza numer iteracji :

z równania (7)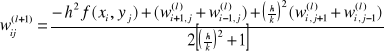
(11)

z równania (10)
(12)

Równania eliptyczne - przykład 1

Wyznaczyć rozkład temperatury w stanie ustalonym dla cienkiej kwadratowej metalowej płytki o wymiarach 0,5 m na 0,5 m. Na brzegu płytki znajdują się źródła ciepła utrzymujące temperaturę na poziomie 0°C dla boku dolnego i prawego, natomiast temperatura boku górnego i lewego zmienia się liniowo od 0°C do 100°C Problem rozwiązać układając układ równań liniowych (postać macierzowa) dla wewnętrznych węzłów siatki 5 x 5 - układ równań rozwiązać metodą Gaussa -Siedla.




Siatka dyskretyzacyjna 5 x 5

Problem ten opisuje równanie Laplace'a




z warunkami brzegowymi:

1) T(0,y) = 0 [°C ]

2) T(x,0) = 0 [°C ]

3) T(0,5,y) = 200y [°C ]

4) T(x,0,5) = 200x [°C ]

Układ równań tworzymy w oparciu o wzór (10)




Rozwiązanie układu równań metodą Gaussa-Siedla, daje wyniki




Ostatecznie wyniki dla założonej siatki mają postać:





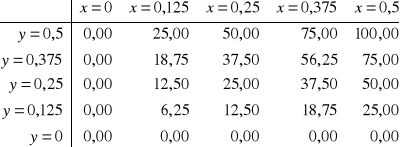
Rozwiązanie dokładne problemu ma postać:




Natomiast oszacowanie błędu obliczeń :


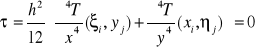
, bo


i


Wynika z tego, że rozwiązanie numeryczne jest równe z rozwiązaniu dokładnemu.

Równania eliptyczne - przykład 1 - kody źródłowe

Funkcje charakteryzujące dane równanie różniczkowe eliptyczne

function F( X,Y : real ) : real;

begin

F := 0;

end;

function G( X,Y : real ) : real;

begin

if X = 0 then G := 0;

if X = 0,5 then G := 200*Y;

if Y = 0 then G := 0;

if Y = 0,5 then G := 200*X;

end;

Definicja wymaganych stałych i typów

const max = 4;

type

Macierz = array [ 0..max, 0..max ] of real;

Vector = array [ 0..max ] of real;

Funkcja obliczająca przybliżenie równania różniczkowego eliptycznego

function PoissonEq(A,B,C,D,TOL : real;N,M,NMAX : integer; var W : Macierz) :boolean;

var

X,Y : Vector; H,K,V,VV,Z,E : real;

M1,M2,N1,N2,I,J,L,LL: integer;

Ok :boolean;

begin

M1 := M - 1; M2 := M - 2;

N1 := N - 1; N2 := N - 2;

H := ( B - A ) / N; K := ( D - C ) / M;

for I := 0 to N do X[I] := A + I * H;

for J := 0 to M DO Y[J] := C + J * K;

for I := 1 to N1 do begin

W[I,0] := g(X[I],Y[0]);

W[I,M] := g(X[I],Y[M])

end;

for J := 0 to M do begin

W[0,J] := g(X[0],Y[J]);

W[N,J] := g(X[N],Y[J])

end;

for I := 1 to N1 do for J := 1 to M1 do W[I,J] := 0.0;

V := H * H / ( K * K ); VV := 2.0 * ( 1.0 + V );

L := 1; OK := false;

while ( ( L <= NMAX ) and ( not OK ) ) do begin

Z := (-H*H*F(X[1],Y[M1])+G(A,Y[M1])+V*G(X[1],D)+V*W[1,M2]+W[2,M1])/VV;

E := abs( W[1,M1] - Z ); W[1,M1] := Z;

for I := 2 to N2 do begin

Z := (-H*H*F(X[I],Y[M1])+V*G(X[I],D)+W[I-1,M1]+W[I+1,M1]+V*W[I,M2])/VV;

if ( abs( W[I,M1] - Z ) > E ) then E := abs( W[I,M1] - Z );

W[I,M1] := Z

end;

Z := (-H*H*F(X[N1],Y[M1])+G(B,Y[M1])+V*G(X[N1],D)+W[N2,M1]+V*W[N1,M2])/VV;

if ( abs( W[N1,M1] - Z ) > E ) then E := abs( W[N1,M1] - Z ); W[N1,M1] := Z;

for LL := 2 to M2 do begin

J := M2 - LL + 2; Z := (-H*H*F(X[1],Y[J])+G(A,Y[J])+V*W[1,J+1]+V*W[1,J-1]+W[2,J])/VV;

if ( abs( W[1,J] - Z ) > E ) then E := abs( W[1,J] - Z );

W[1,J] := Z;

for I := 2 to N2 do begin

Z := (-H*H*F(X[I],Y[J])+W[I-1,J]+V*W[I,J+1]+V*W[I,J-1]+W[I+1,J])/VV;

if ( abs( W[I,J] - Z ) > E ) then E := abs( W[I,J] - Z );

W[I,J] := Z

end;

Z := (-H*H*F(X[N1],Y[J])+G(B,Y[J])+W[N2,J]+V*W[N1,J+1]+V*W[N1,J-1])/VV;

if ( abs( W[N1,J] - Z ) > E ) then E := abs( W[N1,J] - Z ); W[N1,J] := Z

end;

Z := ( -H * H * F( X[1],Y[1] ) + V * G( X[1], C ) + G( A, Y[1] ) + V * W[1,2] + W[2,1] ) / VV;

if ( abs( W[1,1] - Z ) > E ) then E := abs( W[1,1] - Z );

W[1,1] := Z;

for I := 2 to N2 do begin

Z := (-H*H*F(X[I],Y[1])+V*G(X[I],C)+ W[I+1,1]+W[I-1,1]+V*W[I,2])/VV;

if ( abs( W[I,1] - Z ) > E ) then E := abs( W[I,1] - Z );

W[I,1] := Z

end;

Z := (-H*H*F(X[N1],Y[1])+V*G(X[N1],C)+G(B,Y[1])+W[N2,1]+V*W[N1,2])/VV;

if ( abs( W[N1,1] - Z ) > E ) then E := ABS( W[N1,1] - Z );

W[N1,1] := Z;

if ( E <= TOL ) then OK := true

else L := L + 1;

end;

Result := OK;

end;

Równania eliptyczne - przykład 2

Wyznaczyć rozkład temperatury w stanie ustalonym dla cienkiej kwadratowej metalowej płytki o wymiarach 1 m na 1 m. Na trzech brzegach płytki znajdują się źródła ciepła utrzymujące temperaturę na poziomie 100°C dla boku górnego, 50°C dla boku lewego, 0°C dla boku dolnego (warunki Dirichleta), natomiast przy czwartym lewym boku jest umieszczony izolator termiczny (warunek Neumanna - pochodna normalna równa jest 0). Problem rozwiązać wg postaci iteracyjnej dla wewnętrznych węzłów siatki 101 x 101. Tolerancję obliczeń przyjąć na poziomie 10^-6.




Problem ten opisuje równanie Laplace'a




z warunkami brzegowymi:

1) T(0,y) = 0 [°C ]

2) T(x,0) = 50 [°C ]

3) T(1,y) = T(1-h,y) [°C ]

4) T(x,1) = 100 [°C ]

Przybliżenie rozwiązania równania w postaci mapy barwnej po 13484 iteracjach






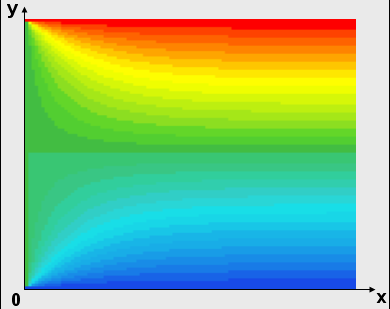
Tabela wyników dla wybranych punków prawego boku płytki - izolator

Numer węzła	Numer iteracji					Dokładne
		0	1000	3000	7000		13000
T100,0	100,00	100,00	100,00	100,00	100,00	100,00
T100,10	0,00	75,17	86,03	89,59	89,92	90,00
T100,20	0,00	52,58	72,46	79,24	79,87	80,00
T100,30	0,00	34,03	59,66	69,00	69,86	70,00
T100,40	0,00	20,27	47,91	58,89	59,90	60,00
T100,50	0,00	11,08	37,37	48,90	49,97	50,00
T100,60	0,00	5,55	28,07	39,03	40,05	40,00
T100,70	0,00	2,55	19,91	29,22	30,09	30,00
T100,80	0,00	1,07	12,70	19,47	20,10	20,00
T100,90	0,00	0,37	6,17	9,73	10,06	10,00
T100,100	0,00	0,00	0,00	0,00	0,00	0,00

Równania eliptyczne - przykład 2 - kody źródłowe

Funkcje charakteryzujące dane równanie różniczkowe eliptyczne

function F( X,Y : real ) : real;

begin

F := 0;

end;

Definicja wymaganych stałych i typów

const max = 100;

type

Macierz = array [ 0..max, 0..max ] of real;

Vector = array [ 0..max ] of real;

function PoissonEquationIteration (a,b,c,d, TOL : real ; N,M ,nmax : integer; var V : Macierz) : boolean;

var EPS,H,K,Vs : real; X,Y : Vector; I,J,L : integer;

begin

H := ( B - A ) / N; K := ( D - C ) / M;

for I := 0 to N do X[I] := A + I * H; for J := 0 to M do Y[J] := C + J * K;

for i:=0 to N do for j:=0 to M do V[i,j]:=0;

L := 0; Result := true;

repeat

eps:=0; L := L + 1;

for i:=0 to N do for j:=0 to M do begin

Vs:=V[i,j];

if j=0 then V[i,j]:=0 else // bok dolny

if j=M then V[i,j]:=100 else // bok gora

if i=0 then V[i,j]:= 50 else // bok lewo

if i=N then V[i,j]:= V[i-1,j] else // bok prawo

V[i,j]:=(- h*h* F(X[i],Y[j] ) + (V[i+1,j]+V[i-1,j])+sqr(h/k)*(V[i,j+1]+V[i,j-1]) )/(2*(sqr(h/k)+1));

If abs(V[i,j]-Vs) > eps then eps := abs(V[i,j]-Vs);

end;

until (eps< TOL ) or ( L > nmax);

if (L > nmax) then Result := false;

end;

Równania różniczkowe cząstkowe z warunkiem brzegowym

Równania paraboliczne - Dyfuzja

Równania różniczkowe cząstkowe paraboliczne znane jako równanie dyfuzji lub przewodnictwa, w zależności od jednego wymiaru oraz czasu przyjmuje postać:






dla oraz (13)



z warunkami brzegowymi dla





i początkowymi dla

Równania tego typu są stosowane dla różnych problemów fizycznych, które są zależne od czasu. Najczęściej stosowane są do obliczenia przepływu ciepła wzdłuż pręta o długości l, przy założeniu że, powierzchnia boczna pręta jest odizolowana od otoczenia. Stała ၡ jest niezależna od położenia oraz czasu i najczęściej określa przewodność cieplną materiału z którego zrobiony jest pręt. Funkcja f określa początkowy rozkład temperatury w pręcie.

Aby rozwiązać równanie cząstkowe paraboliczne (13) zastosujemy metodę różnic skończonych MRS.


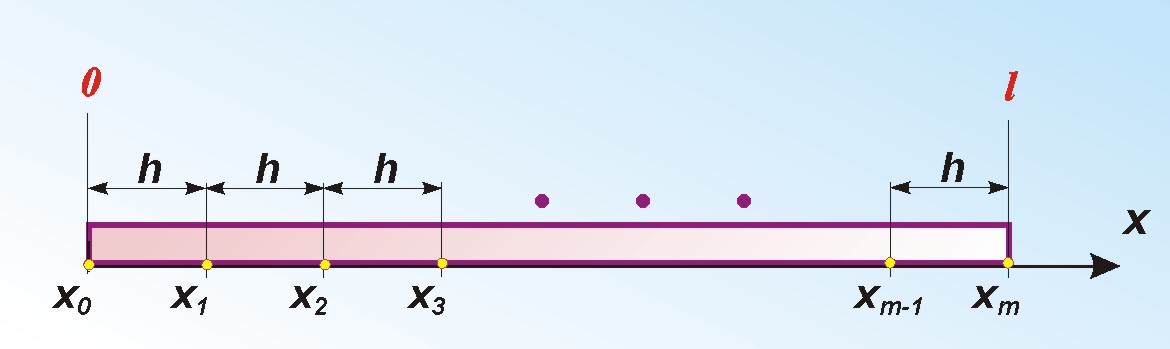
W tym celu weźmiemy liczbę całkowitą m i zdefiniujemy krok całkowania h = (b-a)/m. Dodatkowo ustalimy wartość kroku czasowego k. Dzięki temu możemy wyznaczyć węzły siatki (xi , tj ), gdzie:





dla i = 0,1, .. m oraz dla j = 0,1, ..

Dla wewnętrznych punktów węzłowych (xi,tj), które nie należą do brzegu, zastosujemy metodę różnic skończonych - MRS. Metoda ta opiera się na zastąpieniu pochodnych cząstkowych rozwinięciem funkcji w szereg Taylora w otoczeniu punktu (xi,tj) - (patrz pierwsza i druga pochodna numeryczna) . Wówczas otrzymujemy:




Dla zmiennej x (14)




gdzie:




Dla zmiennej t (15)




gdzie:

Podstawiając wzory (14) oraz (15) do równania dyfuzji (13) oraz wyłączając oszacowanie błędu zapisujemy:




(16)




warunek brzegowy : (17)

dla i = 1,2 … m-1 oraz j = 1,2, …

natomiast lokalny błąd odcięcia jest równy :




(18)





gdzie: oraz

Ostatecznie wzór na MRS, podstawiając za ( xi , tj ) = wi,j oraz wyłączając oszacowanie błędu zapisujemy:




(19)

przekształcając powyższy wzór ze względu na wi,j+1 ,wówczas otrzymujemy:




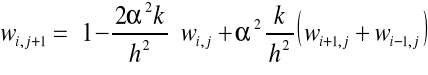
(20)


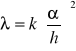
lub




gdzie: (21)

dla i = 1,2 … m-1 oraz j = 1,2, …

Równania paraboliczne - Schemat jawny




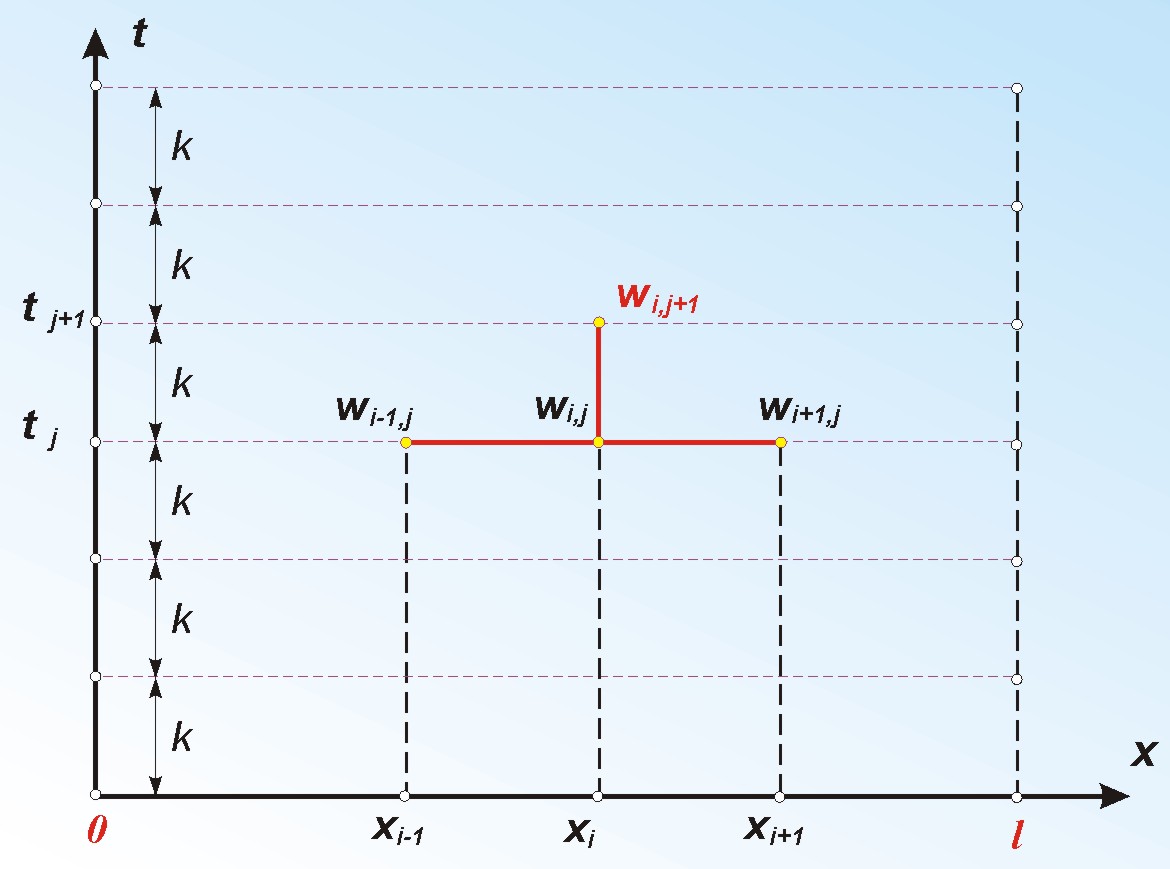
Analizując równanie (21) można zauważyć, że w celu wyznaczenia przybliżenia rozwiązania w punkcie (xi,tj+1), potrzebne są wartości trzech punktów z poprzedniego kroku czasowego tj - patrz rysunek obok. Metoda ta nazywana jest rozwiązywaniem równania parabolicznego wg schematu jawnego

Jak widać poszukujemy rozwiązania równania dyfuzji dla wewnętrznych węzłów siatki, w tym celu dla każdego punktu siatki układamy równanie (21). Obliczenia rozpoczynamy od kroku czasowego j = 1, gdyż najpierw musimy wygenerować wartości początkowe dla t = 0 dla wszystkich punktów u( xi , 0). Obliczmy je zgodnie z warunkami początkowymi u( xi , 0) = f(xi).

A więc mamy do rozwiązania układ (m-1) równań, który powstał poprzez ułożenie równania (21) dla każdego punktu wi,j siatki dla i = 1,2, .. m-1 :




(22)

co rozpisując daje nam:




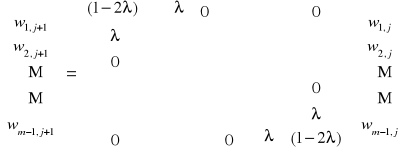
(23)

Czyli w ten sposób możemy wyznaczyć poszukiwane wartości w(j+1). Wystarczy tylko przemnożyć macierz A przez wektor w(j) - wartości dla poprzedniego kroku.

Równania paraboliczne - Dyfuzja - przykład 1

Rozwiązać poniższe równanie przewodnictwa:






dla oraz





z warunkami brzegowymi dla





i początkowymi dla

Obliczenia wykonać dla czasu t = 0.5 używając schematu jawnego najpierw dla h = 0.1 oraz k = 0.0005 , następnie dla h = 0.1 oraz k = 0.01 ,przyjąć ၡ 2 = 1

Rozwiązanie dokładne ma postać:




Tabela wyników - schemat jawny

		Mały krok czasu		Duży krok czasu
xi	u( xi , 0.5 )	wi,1000 k = 0.0005	| u( xi , 0.5 ) - wi,1000|	wi,50 k = 0.01	| u( xi , 0.5 ) - wi,50|
0,0	0	0		0
0,1	0,00222241	0,00228652	6,411 Ⴔ 10-5	8,19876 Ⴔ 107	8,199 Ⴔ 107
0,2	0,00422728	0,00434922	1,219 Ⴔ 10-4	-1,55719 Ⴔ 108	1,557 Ⴔ 108
0,3	0,00581836	0,00598619	1,678 Ⴔ 10-4	2,13833 Ⴔ 108	2,138 Ⴔ 108
0,4	0,00683989	0,00703719	1,973 Ⴔ 10-4	-2,50642 Ⴔ 108	2,506 Ⴔ 108
0,5	0,00719788	0,00739934	2,075 Ⴔ 10-4	2,62685 Ⴔ 107	2,627 Ⴔ 108
0,6	0,00683989	0,00703719	1,973 Ⴔ 10-4	-2,49015 Ⴔ 108	2,490 Ⴔ 108
0,7	0,00581836	0,00598619	1,678 Ⴔ 10-4	2,11200 Ⴔ 107	2,112 Ⴔ 108
0,8	0,00422728	0,00434922	1,219 Ⴔ 10-4	-1,53086 Ⴔ 108	1,531 Ⴔ 108
0,9	0,00222241	0,00228652	6,411 Ⴔ 10-5	8,03604 Ⴔ 107	8,036 Ⴔ 107
1,0	0	0		0

Interpretacja graficzna













Równania paraboliczne - Schemat jawny

Analizując wyniki z przykładu 1 można zauważyć, że metoda wykorzystująca schemat jawny jest warunkowo stabilna, gdyż dla zbyt dużych wartości kroku wyniki są rozbieżne w stosunku do rozwiązania dokładnego. Wynika to wartości własnej macierzy A , dla której powinien być spełniony warunek




(23)

z powyższego wyrażenia wynika, że warunek stabilności tej metody jest:




(24)

Wykorzystując powyższy wzór można wyznaczyć dla przykładu 1 graniczną wartość kroku czasowego, dla której schemat jawny jest stabilny:





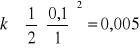
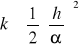
wtedy

Równania paraboliczne - Schemat niejawny

Poprzednia metoda wykorzystująca schemat jawny, była warunkowo stabilna, gdyż należy zwracać uwagę na wielkości kroków całkowania. Metoda opisana poniżej nie ma tej wady, i jest bezwarunkowo stabilna dla różnych wielkości kroków całkowania. Metoda ta wykorzystuje schemat niejawny gdyż zalicz się do metod pośrednich wymagających wielokrotnych iteracji dla danej chwili czasu. Różnica polega na innym określeniu pochodnej cząstkowej po czasie:




Dla zmiennej t (25)


gdzie:


Wówczas podstawiając wzór (25) oraz (14) do równania parabolicznego (13), pomijając błąd obcięcia otrzymamy :

(26)

Modyfikując powyższy wzór, podstawiając za ( xi , tj ) = wi,j zapisujemy:




(27)

lub:





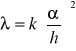
gdzie: (28)

dla i = 1,2 … m-1 oraz j = 1,2, …




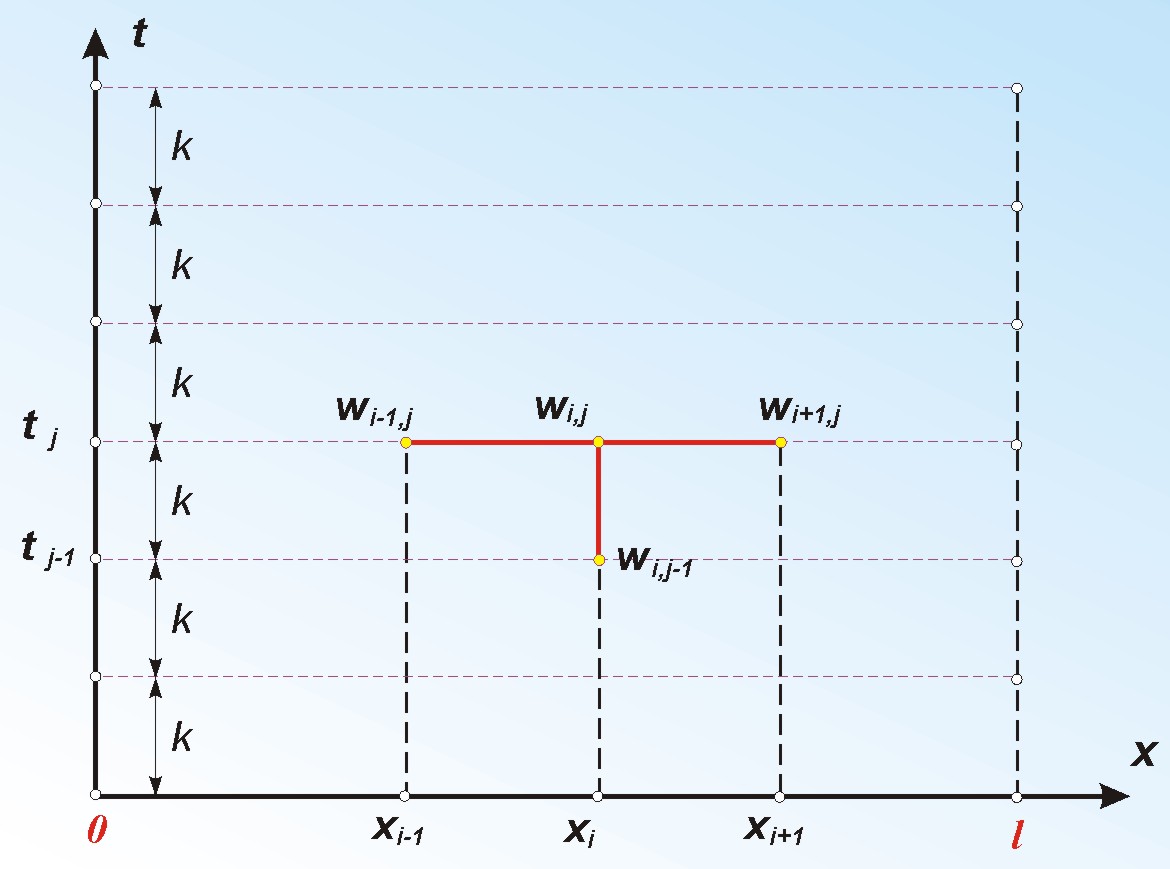
Analizując równanie (28) można zauważyć, że w celu wyznaczenia przybliżenia rozwiązania w punkcie (xi,tj), potrzebne są wartości trzech punktów: dwóch sąsiednich z aktualnego kroku czasowego oraz wartość dla tego samego węzła, ale dla poprzedniej iteracji tj-1 - patrz rysunek obok. Metoda ta nazywana jest rozwiązywaniem równania parabolicznego wg schematu niejawnego

Jak widać poszukujemy rozwiązania równania dyfuzji dla wewnętrznych węzłów siatki, w tym celu dla każdego punktu siatki układamy równanie (28). Obliczenia rozpoczynamy od kroku czasowego j = 1, gdyż najpierw musimy wygenerować wartości początkowe dla t = 0 dla wszystkich punktów u( xi , 0). Obliczmy je zgodnie z warunkami początkowymi u( xi , 0) = f(xi).

A więc mamy do rozwiązania układ (m-1) równań, który powstał poprzez ułożenie równania (28) dla każdego punktu wi,j siatki dla i = 1,2, .. m-1 :




(29)

co rozpisując daje nam:




(30)

Czyli w ten sposób możemy wyznaczyć poszukiwane wartości w(j). Najlepiej do rozwiązania tego typu układów użyć rozkładu Crouta dla macierzy trójdiagonalnych

Równania paraboliczne - Dyfuzja - przykład 2 (1)

Rozwiązać poniższe równanie przewodnictwa:






dla oraz



z warunkami brzegowymi dla



i początkowymi dla

Obliczenia wykonać dla czasu t = 0.5 używając schematu niejawnego dla h = 0.1 oraz k = 0.01 ,przyjąć ၡ 2 = 1




Rozwiązanie dokładne ma postać:

Tabela wyników - schemat niejawny

xi	u( xi , 0.5 )	wi,50 k = 0.01	| u( xi , 0.5 ) - wi,50|
0,0	0	0
0,1	0,00222241	0,00289802	6,756 Ⴔ 10-4
0,2	0,00422728	0,00551236	1,285 Ⴔ 10-3
0,3	0,00581836	0,00758711	1,769 Ⴔ 10-3
0,4	0,00683989	0,00891918	2,079 Ⴔ 10-3
0,5	0,00719788	0,00937818	2,186 Ⴔ 10-3
0,6	0,00683989	0,00891918	2,079 Ⴔ 10-3
0,7	0,00581836	0,00758711	1,769 Ⴔ 10-3
0,8	0,00422728	0,00551236	1,285 Ⴔ 10-3
0,9	0,00222241	0,00289802	6,756 Ⴔ 10-4
1,0	0	0

Równania paraboliczne - Schemat niejawny

Analizując wyniki z przykładu 2 można zauważyć, że metoda wykorzystująca schemat niejawny jest bezwarunkowo stabilna, gdyż jest ona zawsze zbieżna nie zależnie od wielkości kroków całkowania. Wynika to ze spełniania poniższego warunku dla promienia spektralnego macierzy A:




(31)

Równania paraboliczne - kody źródłowe

Funkcja określająca warunki początkowe równania paraboliczne

function F( X,Y : real ) : real;

begin

F := sin( pi * x );

end;

Definicja wymaganych stałych i typów

const

max = 100;

type

Vector = array [ 0..max ] of real;

Funkcji „HeatingForward” - schemat jawny

function HeatingForward (FX,ALPHA ,FT : real; M,N : integer; var W : Vector): boolean ;

var

H,K,VV : real; I,J : integer; W_1 : Vector;

begin

H := FX / M; K := FT / N;

VV := ALPHA * ALPHA * K / ( H * H );

if K <= (0.5*SQR(H/ALPHA)) then begin

W_1[0] := 0; W_1[M] := 0; Result := True;

W[0] := 0; W[M] := 0;

for I := 1 to M-1 do W_1[I] := F( I * H );

for J := 1 to N do begin

for I := 1 to M-1 do W[I] := (1.0 - 2.0 * VV)*W_1[I] + VV*( W_1[I-1] + W_1[I+1] );

W_1 := W;

end;

end

else Result := False;

end;

Funkcji „HeatingBackward” - schemat niejawny

function HeatingBackward (FX,alpha ,FT : real; m,n : integer; var W : Vector): boolean ;

var

L,U,Z : Vector; H,K,VV : real; I1,I,J : integer;

begin

Result := true;

H := FX / M; K := FT / N;

VV := ALPHA * ALPHA * K / ( H * H );

W[0] := 0; W[M] := 0;

for I := 1 to M-1 do W[I] := F( I * H );

L[1] := 1.0 + 2.0 * VV; U[1] := -VV / L[1];

for I := 2 to M-2 do begin

L[I] := 1.0 + 2.0 * VV + VV * U[I-1]; U[I] := -VV / L[I]

end;

L[M-1] := 1.0 + 2.0 * VV + VV * U[M-2];

for J := 1 to N do begin

Z[1] := W[1] / L[1];

for I := 2 to M-1 do Z[I] := ( W[I] + VV * Z[I-1] ) / L[I];

W[M-1] := Z[M-1];

for I1 := 1 to M-2 do begin

I := M-2 - I1 + 1; W[I] := Z[I] - U[I] * W[I+1]

end;

end;

end;

Równanie hiperboliczne - Falowe

Równania różniczkowe cząstkowe hiperboliczne znane jako równanie falowe, w zależności od jednego wymiaru oraz czasu przyjmuje postać:


(32)



dla oraz





z warunkami brzegowymi dla






i początkowymi oraz dla

Równania tego typu są stosowane dla różnych problemów fizycznych, które są zależne od czasu. Najczęściej stosowane są do obliczenia wartości fali płaskiej w dowolnym punkcie pomiędzy 0 a l dla dowolnej chwili czasu większej od zera. Funkcje f(x) i g(x) określają warunki początkowe położenia oraz prędkości rozchodzenia się fali.

Aby rozwiązać równanie cząstkowe paraboliczne (32) zastosujemy metodę różnic skończonych MRS.

W tym celu weźmiemy liczbę całkowitą m i zdefiniujemy krok całkowania h = (b-a)/m. Dodatkowo ustalimy wartość kroku czasowego k. Dzięki temu możemy wyznaczyć węzły siatki (x_i , t_j ), gdzie:






dla i = 0,1, .. m oraz dla j = 0,1, ..

Dla wewnętrznych punktów węzłowych (x_i,t_j), które nie należą do brzegu, zastosujemy metodę różnic skończonych - MRS. Metoda ta opiera się na zastąpieniu pochodnych cząstkowych rozwinięciem funkcji w szereg Taylora w otoczeniu punktu (x_i,t_j) - (patrz druga pochodna numeryczna) . Wówczas otrzymujemy:




Dla zmiennej x (33)




gdzie




Dla zmiennej t (34)




gdzie

Podstawiając wzory (33) oraz (34) do równania falowego (31) oraz wyłączając oszacowanie błędu zapisujemy:


(35)




warunek brzegowy : (36)

dla i = 1,2 … m-1 oraz j = 1,2, …

natomiast lokalny błąd odcięcia jest równy :




(37)



gdzie: oraz

Ostatecznie wzór na MRS, podstawiając za ( x_i , t_j ) = w_i,j zapisujemy:




(38)

przekształcając powyższy wzór ze względu na w_i,j+1 ,wówczas otrzymujemy:





gdzie: (39)

dla i = 1,2 … m-1 oraz j = 1,2, …




z warunkami brzegowymi dla j = 1,2, …




i początkowymi dla i = 1,2, … m-1

Analizując równanie (39) można zauważyć, że w celu wyznaczenia przybliżenia rozwiązania w punkcie (x_i,t_j+1), potrzebne są wartości trzech punktów z poprzedniego kroku czasowego t_j oraz jednej wartości dla czasu t_j-1 - patrz rysunek poniżej.




Jak widać poszukujemy rozwiązania równania falowego dla wewnętrznych węzłów siatki, w tym celu dla każdego punktu siatki układamy równanie (39). Obliczenia rozpoczynamy od kroku czasowego j = 2, gdyż najpierw musimy wygenerować wartości początkowe dla t = 0 dla wszystkich punktów u( x_i , 0)=f(x_i), następnie wygenerujemy z drugiego warunku początkowego wartości punktów dla t = t₁ jako du( x_i , t₁) / dt = g(x_i).

A więc mamy do rozwiązania układ (m-1) równań, który powstał poprzez ułożenie równania (39) dla każdego punktu w_i,j siatki dla i = 1,2, .. m-1 :




(40)

co rozpisując daje nam:




(41)

Czyli w ten sposób możemy wyznaczyć poszukiwane wartości w^(j+1). Wystarczy tylko przemnożyć macierz A przez wektor w^(j) - wartości dla poprzedniego kroku, a następnie odjąć od tego wektor wynikowy dla t_j-1 czyli w^(j-1).

Ponieważ obliczania rozpoczynamy od kroku czasowego j = 2 musimy oprócz warunków początkowych dla j = 0 określić wartości dla j = 1, skorzystamy z drugiego warunku początkowej prędkości fali:





dla (42)

Zamienimy pochodną cząstkową po czasie wykorzystując wzór schematu jawnego dla równań parabolicznych:





(43)


Wyprowadźmy u(x_i,t₁) z powyższego równania, wtedy otrzymujemy:

(44)

Podstawmy do równania (44) wartość pochodnej z równania (42) :




(45)

Podstawmy za u( x_i,t_j ) = w_i,j , pomijając błąd odcięcia, ostatecznie mamy:




dla i = 1,2, .. m-1 : (46)

Powyższy wzór pozwala na określenie warunków początkowych dla j = 1, wadą tego jest duży błąd oszacowania rzędu O(k). Alternatywą do tego jest wzór wyprowadzony jako rozwiniecie funkcji u(x_i,t₁) w szereg Maclurina 2 rzędu:




dla i = 1,2, .. m-1 (47)




gdzie:

:

Równania hiperboliczne - Falowe - przykład 1

Rozwiązać poniższe równanie falowe:






dla oraz



z warunkami brzegowymi dla






i początkowymi oraz dla

Obliczenia wykonać dla czasu t = 1 wykorzystując metodę MRS dla równań falowych, przyjąć: h = 0.1 oraz k = 0.05 ,przyjąć α ² = 4

Rozwiązanie dokładne ma postać:




Tabela wyników




Interpretacja graficzna













Równania hiperboliczne - kody źródłowe

Funkcja określająca warunki początkowe równania paraboliczne

function F( X,Y : real ) : real;

begin

F := sin( pi * x );

end;

function G( X,Y : real ) : real;

begin

G := 0;

end;

Definicja wymaganych stałych i typów

const

max = 100;

type

Vector = array [ 0..max ] of real;

Macierz = array [ 0..max ] of Vector;

Funkcja „WaveEquation” - oblicza przybliżenie rozwiązania równania falowego

function WaveEquation(FX,ALPHA ,FT : real; M,N : integer; var W : Macierz): boolean ;

var H,K,V : real; M1,N1,I,J : integer;

begin

M1 := M + 1; N1 := N + 1; Result := True;

H := FX / M; K := FT / N;

V := ALPHA * K / H;

for J := 1 to N do begin

W[0,J] := 0; W[M,J] := 0;

end;

W[0,0] := F( 0 ); W[M,0] := F ( FX );

for I := 1 to M-1 do begin

W[I,0] := F( H * ( I ) );

W[I,1] := (1-V*V)*F(H*(I))+V*V*(F((I+1)*H) + F(H*(I-1)))/2+K*G(H*(I));

end;

for J := 1 to N-1 do for I := 1 to M-1 do

W[I,J+1] := 2*(1-V*V)*W[I,J]+V*V*(W[I+1,J]+W[I-1,J])-W[I,J-1];

end;

28

































































































































































































































































































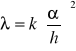
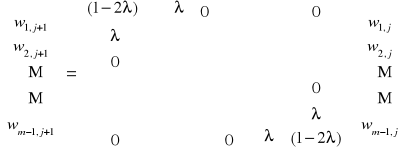
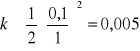
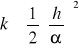
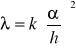
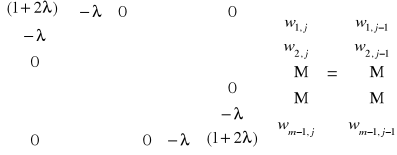
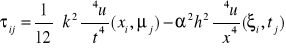
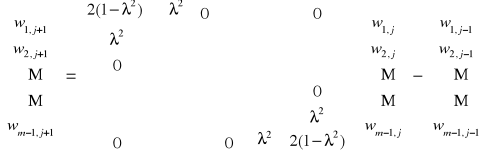
0

0,8090169944

0,8090169944

0,3

0

0,3090169944

0,5877852523

0,8090169944

0,9510565163

1,0000000000

0,9510565163

0,5877852523

0,3090169944

0

u( x_i , 1 )

5,421 × 10^-20

0

0

1,1102 × 10^-16

1,1102 × 10^-16

0

0

0

| u( x_i , 1 ) - w_i,20|

0

0,3090169944

0,5877852523

0,8090169944

0,9510565163

1,0000000000

0,9510565163

0,5877852523

0,3090169944

0

w_i,20

k = 0.05

0,5

0,6

0,7

0,8

0,9

1,0

0,4

0,2

0,1

0,0

x_i

---