Temat: Wyznaczenie momentu bezwładności i sprawdzenie twierdzenia Steinera.			Ocena:

1.WSTĘP TEORETYCZNY.

1.1 Cel ćwiczenia :

- stwierdzenie zależności okresu drgań wahadła od momentu bezwładności ,

- doświadczalne potwierdzenie twierdzenia Steinera ,

- wyznaczanie momentu bezwładności ciał względem osi przechodzącej przez środek masy ( tzw. osi środkowej ).

1.2 Wiadomości ogólne.

Rozpatrzmy jako przykład drgań harmonicznych niewielkie wahania wahadła fizycznego pod wpływem siły cięzkości
. Odchylamy wahadło z położenia równowagi o niewielki kąt . Wówczas z II zasady dynamiki dla ruchu obrotowego mamy : (1)
, gdzie :

(2)
- moment siły
powodującej ruch względem osi , przechodzącej przez punkt zawieszenia ,

m - masa wahadła ,

d - odległość środka masy od osi obrotu ,

I - moment bezwładności wahadła względem tej osi .

(3)
- chwilowe przyspieszenie kątowe

Po podstawieniu we wzorze (1) wartości ze wzorów (2) i (3) otrzymujemy :

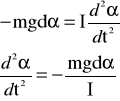
Rozwiązaniem tego równania różniczkowego jest funkcja : =0( t + 0 )

określająca zależność wychylenia kątowego od czasu t gdzie :

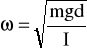
- częstość kołowa ,

0 - amplituda drgań ,

0 - faza początkowa.

(4) Okres drgań harmonicznych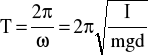

1.2.1 Twierdzenie Steinera.

Po przekształceniu wzoru (4) otrzymujemy wyrażenie na moment bezwładności mierzony względem osi obrotu wahadła :

(5)

W praktyce często przydatna jest znajomość obliczania momentów bezwładności mierzonych względem osi przechodzących przez środki ciężkości tych ciał.

Służy do tego twierdzenie Steinera : różnica momentów bezwładności ciała względem dwu równoległych osi , z których jedna przechodzi przez środek masy , równa jest iloczynowi masy ciała m i kwadratu odległości d między osiami.

Z powyższego twierdzenia wynika następujący wniosek : dla dwu różnych odległości d1 i d2 od osi przechodzącej przez środek masy ciała mamy :

Podstawiając za I1 i I2 wyrażenie (5) otrzymujemy :

Otrymana stała C może służyć jako potwierdzenie twierdzenia Steinera. Stała C pozwala również obliczyć w prosty sposób moment bezwładności ciała względem osi przechodzącej przez środek masy :

2. ZESTAW PRZYRZĄDÓW :

- tarcza metalowa z symetrycznie naciętymi otworami ,

- podpora w postaci metalowej pryzmy ,

- pierścień metalowy ,

- suwmiarka ,

- stoper ,

- waga.

3. WYNIKI POMIARÓW.

3.1 Tarcza metalowa.

m = ( 1061,5 0,1 ) g ; g = 9,81 m/s2 ; = 3,14

3.1.1 2d = ( 139,6 0,1 ) mm d = ( 69,8 0,1 ) mm

LP.	T [ s ]	t [ s ]	C [ m2 ]	I0 [ 10-3 kg m2 ]
1.	0,694 0,002	69,4 0,2
2.	0,694 0,002	69,4 0,2
3.	0,694 0,002	69,4 0,2
< śr. >	0,694 0,002	69,4 0,2	0,1346 0,0245	3,621

3.1.2 2d = ( 90,1 0,1 ) mm d = ( 45,1 0,1 ) mm

LP.	T [ s ]	t [ s ]	C [ m2 ]	I0 [ 10-3 kg m2 ]
1.	0,690 0,005	69,0 0,5
2.	0,680 0,005	68,0 0,5
3.	0,684 0,001	68,4 0,1
< śr >	0,685 0,037	68,5 0,4	0,1274 0,0227	3,427

3.1.3 2d = ( 40,5 0,1 ) mm d = ( 20,3 0,1 ) mm

LP.	T [ s ]	t [ s ]	C [ m2 ]	I0 [ 10-3 kg m2 ]
1.	0,778 0,002	77,8 0,2
2.	0,778 0,002	77,8 0,2
3.	0,778 0,002	77,8 0,2
< śr. >	0,778 0,002	77,8 0,2	0,1043 0,0008	2,806

3.2 Pierścień metalowy.

m = ( 215,7 0,1 ) g ; 2d = ( 95,0 0,1 ) mmd = ( 47,5 0,1 ) mm

2D = ( 119,5 0,1 ) mm D = ( 56,8 0,1 ) mm

LP.	T [ s ]	t [ s ]	C [ m2 ]	I [ * ]	I01 [ * ]	I02 [ * ]
1.	0,670 0,002	67,0 0,2
2.	0,672 0,002	67,2 0,2
3.	0,670 0,002	67,0 0,2
4.	0,670 0,002	67,0 0,2
5.	0,670 0,002	67,0 0,2
6.	0,670 0,002	67,0 0,2
< śr >	0,670 0,002	67,0 0,2	0,1202 0,0016	1,144	0,657	0,591

[ * ] - 10-3kg m2 ; 01 = 0,9 %

4.PRZYK£ADOWE OBLICZENIA.

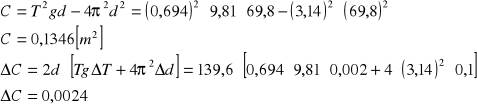
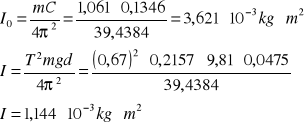
Z twierdzenia Steinera :

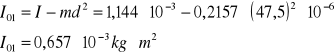
Ze wzoru tablicowego :

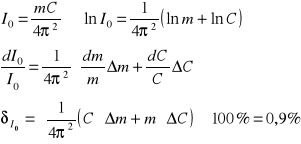
5. UWAGI I WNIOSKI.

Jednym z czynników wpływających na dokładnośc pomiarów i opartych na nich następnie obliczeniach , była bezwładność oka ludzkiego , ponieważ bardzo trudno jest dokładnie określić moment amplitud drgań. Dodatkowo układ pomiarowy narażony był na drgania przenoszone na stół przez podłoże.

Staraliśmy się uniknąc poślizgów tarczy i pierścienia oraz odbić od pryzmy , wychylając wahadło o tak mały kąt , przy którym równanie ruchu ( sin ) zachowuje liniowość.

Błędy przy pomiarach czasu drgań spowodowane były głównie błędami przyrządu pomiarowego (stopera) . Istotny wpływ na wartości odchyleń miały zaokrąglenia wartości oraz stałej g.

Przy obliczaniu momentu bezwładności pierścienia metalowego można zauważyć , że dokładniejszym wzorem jest wzór tablicowy.

5. UWAGI I WNIOSKI.

5.1 Wahadło należy odchylić o mały kąt , aby funkcja sinus była w przybliżeniu liniowa , a także aby uniknąć poślizgu i odbicia tarczy.

5.2 Przy obliczaniu T i t błędem decydującym o odchyłce jest błąd przyrządu ( stopera ). Jest to wynikiem tego , iż liczono czas stu drgnięć.

5.3 Odchyłki spowodowane są także przybliżonymi wartościami oraz g.

5.4 Duże odchyłki powstały przy pomiarze 2D pierścienia wskutek małych szczęk suwmiarki.

---