WYKŁAD I
Za główny przedmiot teorii sygnałów uważa się tworzenia opisu matematycznego sygnałów oraz metod ich analizy i przetwarzania. Pojęcie sygnału już intuicyjnie pojawia się z pojęciem informacji gdyż transmisja informacji możliwa jest dzięki przesyłaniu i przetwarzaniu różnego typu sygnałów, np.: elektrycznych, optycznych, akustycznych, elektromagnetycznych, itp. W procesie transmisji sygnałów występuje zjawisko nakładania się sygnałów na przebieg nośny oraz dodatkowe operacje, które utrudniają odtwarzanie przekazywanej informacji z pobieranego przekazu transmisji w celu efektywnego odtworzenia informacji sygnału odbieranego zachodzi konieczność poznania cech informacji, które stanowią podstawowe opracowanie odpowiednich algorytmów. Wymienione zagadnienia wymagają stosowania odpowiedniego aparatu matematycznego. Teoria sygnałów stanowi pewien dział nauk matematycznych. Charakterystyczną cechą wszystkich sygnałów jest ich trwanie w czasie. Analiza cech czasowych sygnałów nie jest zbyt złożona i w przypadku sygnałów deterministycznych kompletny opis sygnałów możemy uzyskać dzięki analizie fourierowskiej i metodach energetycznych. W przypadku sygnałów losowych ich opis ma postać probabilistyczną a zatem podany jest w postaci rozkładów prawdopodobieństwa sygnałów oraz ich momentów. Sygnały możemy również ustalać według topologiczno-geometrycznej topologii sygnałów gdzie każdy sygnał reprezentowany jest jako wektor, punkt bądź linia w uogólnionej przestrzeni wielowymiarowej. Zbiory punktów, wektorów, linii tworzą przestrzenie sygnałów, w których badamy odległość między sygnałami w sensie ich podobieństwa i możliwości rozróżniania. W tym przypadku ważne są pojęcia iloczynu skalarnego a także ortodonalności. Interpretacje geometryczne są szczególnie ważne przy analizie sygnałów dyskretnych, gdzie w przestrzeni funkcji rozumie się jako składnik funkcji.
Klasyfikacja sygnałów.
Wszelkie spotykane sygnały najogólniej możemy podzielić na:
Stochastyczne (zbiór sygnałów losowych)
Deterministyczne
Zaliczanie sygnałów do pierwszej lub drugiej grupy zależy od zawartości informacji, jaką posiada odbiorca sygnału w stosunku do nadawcy informacji. Jeżeli przekazywana jest nam informacja znana to sygnał dla nas jest deterministyczny. Jeżeli przekazywana jest nam informacja, którą możemy, jedynie przewidzieć jako statystyczną to sygnał traktujemy jako losowy. A zatem sygnał o przyszłości znanej opisanej, np.: matematycznie jest sygnałem deterministycznym. Natomiast sygnał losowy o nieznanej przyszłości posiada model probabilistyczny i z nim związana jest informacja. W praktyce modele stochastyczne sygnałów wynikają często z nieznajomości zjawisk fizycznych, które generują dane sygnały.
Analiza cech losowych.
Przebieg sygnałów rzeczywistych możemy określić dokonując pomiarów ich wartości w kolejnych chwilach czasu t. W ten sposób otrzymujemy tablicę wartości t oraz x(t), która punktowo charakteryzuje przebieg sygnału x(t). Sygnały rzeczywiste oraz niektóre sygnały modelowe opisuje się przy użyciu zbiorów ograniczonych, czyli ![]()
. Jeżeli funkcja czasu opisująca sygnał zanika poza domkniętym pewnym przedziałem, np.: [a, b] to mamy do czynienia z sygnałem o ograniczonym trwaniu, podobnie tworzy się pojęcie sygnału o ograniczonym zakresie wartości. W związku z powyższym klasyfikacja sygnału według zakresu wartości argumentu i wartości funkcji ma postać:
|
Zakres wartości |
||
Czas trwania |
Ograniczony |
Ograniczony |
Nieograniczony |
|
Nieograniczony |
Ograniczony |
Nieograniczony |
Jeżeli przez D oznaczymy skończony zbiór liczb rzeczywistych wybranych ze zbioru ![]()
, ale w pewien określony sposób to klasyfikując sygnały według ciągłości zbiorów możemy utworzyć cztery ich podklasy.
|
|
|
|
Sygnały ciągłe |
Sygnały dyskretne |
|
Sygnały dyskretne |
Sygnały dyskretne |
Sygnały nazywamy ciągłymi przy ![]()
oraz przy ![]()
, nawet w przypadku, jeśli istnieją punkty nieciągłości funkcji x(t). Pozostałe sygnały nazywamy dyskretnymi, przy czym istnieją trzy możliwości nieciągłości zbiorów wartości argumentu i wartości funkcji.
![]()
![]()
![]()
![]()
![]()
![]()
W teorii sygnałów ważne pojęcie stanowi sygnał cyfrowy, który może mieć następujące modele:
Ciąg całkowitoliczbowy.
Ciąg impulsów delta o wadze całkowitoliczbowej
Ciąg wąskich impulsów o amplitudzie całkowitoliczbowej
Ciąg szerokich impulsów o amplitudzie całkowitoliczbowej
Zwykle modele sygnałów są rzeczywistymi funkcjami amplitudycznymi argumentu rzeczywistego, dlatego cechy takich sygnałów możemy opisać energetycznie korzystając z powszechnych konwencji polegającej na wyznaczeniu mocy sygnału prądowego bądź napięciowego na rezystancji jednostkowej. Moc chwilowa sygnałów w tym przypadku będzie równa kwadratowi wartości chwilowej sygnału ![]()
. Energię natomiast określi wyrażenie ![]()
. Korzystając z cech energetycznych sygnału klasyfikujemy je następująco:
Sygnał o energii ograniczonej
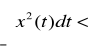
. Średnia moc tych sygnałów jest równa 0.Sygnał o nieograniczonej mocy średniej
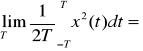
do tej klasy należą pewne modele specjalne sygnałów minimalnych: funkcja grzbietowa.Sygnały o ograniczonej mocy średniej
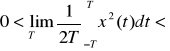
Na sygnałach w dziedzinie czasu możemy dokonywać różnych podziałów algebraicznych, analitycznych i operację uśredniania czasowego. Mówi się całkowo wyznaczając:
1. Wartość średnią sygnału:
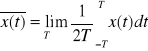
2. Wartość średniokwadratowa:

3. Wartość skuteczna:
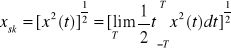
Na sygnałach cyfrowych działania zdefiniowane są na algebrze całkowitoliczbowej i działaniach określonych modulo, przy czym możliwe jest mnożenie i dodawanie jedynie sygnałów w takiej samej postaci. Sygnały te można również przesuwać po osi czasu o całkowitą liczbę n przedziałów elementarnych, N. Operacje analityczne typu różniczkowanie, całkowanie, uśrednianie, splatanie, przekształcanie w La Place' a i Hilberga może być również przeprowadzone na wszystkich typach sygnałów dyskretnych, ale przy wykorzystaniu tzw. dystrybucji.
Analiza częstotliwościowa sygnałów.
Przejście z opisu czasowego sygnału na opis w dziedzinie częstotliwości dokonuje się metodami analizy Furiera. Cechą charakterystyczną takiego opisu jest niezależność od czasu w sensie rozłożenia sygnałów na składowe, okresowe istniejące w czasie bez ograniczenia.
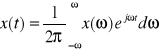
, gdzie x(ω) jest transformatą Furiera sygnału x(t), czyli 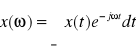
.
W klasycznym ujęciu sygnału x(t) możemy przedstawić w postaci całkowego równania Fouriera, czyli 1.9; 1.10. Najbardziej istotne właściwości przekształcenia Fouriera to:
Liniowość:
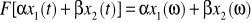
, gdzie: α, β = stałe.Przesunięcie:
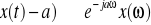
, gdzie: a - liczba rzeczywista.Splot:
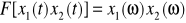
, gdzie: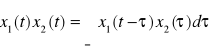
Różniczkowanie:
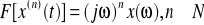
Energia (tw. Parsevala):
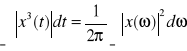
Powyższe właściwości są słuszne dla funkcji zespolonych x(t) bezwzględnie całkowalnych w całej dziedzinie. Dla funkcji rzeczywistych x(t) bezwzględnie całkowalnych zachodzą ponadto relacje:
- Oryginał rzeczywisty parzysty. Jeśli x(t) = x(-t) to: 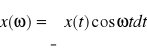
Transformata w tym przypadku jest rzeczywista.
- Oryginał rzeczywisty nieparzysty. Jeśli x(t) = - x(-t) to: 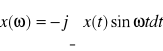
.
Transformata x(ω) jest funkcją widmową określoną w dziedzinie częstotliwości (pulsacji). Transformata ta nazywana jest widmem Fourierowskim bądź widmem zespolonym. Korzystając ze składowych biegunowych transformatę tą możemy zapisać w postaci: ![]()
, gdzie: ![]()
- nazywany jest widmem amplitudowym.
![]()
- jest argumentem od ![]()
i nazywana jest widmem fazowym. W całej dziedzinie pulsacji ![]()
widmo amplitudowe jest parzyste, a widmo fazowe nieparzyste. Transformata w tym przypadku jest rzeczywista.
- oryginał rzeczywisty nieparzysty: jeśli ![]()
to 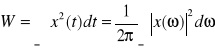
.
Funkcja ![]()
ma sens gęstości energii w dziedzinie pulsacji i nazywana jest widmem gęstości energii. Do podstawowych pojęć analizy częstotliwościowej sygnałów należą ponadto gęstość mocy i widmo mocy. Aby z sygnału x(t) o mocy ograniczonej utworzyć sygnał o energii ograniczonej należy pobrać wycinek tego sygnału, np.: ![]()
wówczas na podstawie wcześniejszego wyrażenia określającego energię możemy zapisać, że energia tego wycinka to: 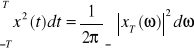
Przejście graniczne ![]()
pozwala odtworzyć moc średnią całego sygnału, która przyjmuje postać: 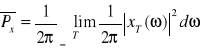
.
Funkcja podcałkowa powyższego wyrażenia stanowi widmową gęstość mody a zatem: ![]()
. Jeżeli granica istnieje gęstość mocy jest funkcją rzeczywistą nieujemną i parzystą a moc średnia: 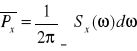
. Podobnie jak widmo mocy sygnału określa jego własności w dziedzinie częstotliwości to funkcja relacji własnej sygnału opisuje własności sygnału w dziedzinie czasu. Funkcja korelacji własnej pewnego sygnału x(t) określona jest zależnością: 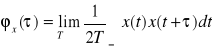
, gdzie ![]()
- funkcja x(t) opóźniona.
Z powyższego wyrażenia widać, że funkcja korelacji własnej jest średnią po czasie z iloczynu ![]()
i stanowi miarę podobieństwa między dwoma wartościami sygnału ![]()
i ![]()
, czyli wartościami odległymi o ![]()
. W przypadku braku podobieństwa, (czyli braku współzależności) między wartościami x(t) odległego o ![]()
i o ile sygnał nie posiada składowych stałych to wartość średnia wspomnianego wyżej iloczynu jest równa 0, a zatem funkcja korelacji również wynosi 0. Jeżeli rozpatrujemy dwa różne sygnały x(t) oraz y(t) to miarą podobieństwa ich wartości odległych o ![]()
jest funkcją korelacji wzajemnej.
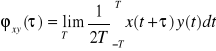
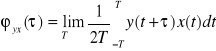
.
Funkcja korelacji i gęstość widmowa mocy związane są ze sobą przekształceniem Fouriera, a zatem można zapisać: 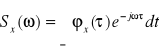
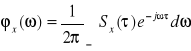
. Korzystając z cech częstotliwościowych sygnałów, a także ich modele możemy klasyfikować według:
a) ciągłości nośnika:
Sygnały rzeczywiste:
Sygnały o widmie ciągłym
Sygnały o widmie prążkowym
Sygnały o widmie złożonym (część ciągła + prążki)
b) szerokości widma:
Sygnały rzeczywiste:
Sygnały monochromatyczne
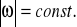
Sygnały pasmowe
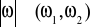
Sygnały wszechpasmowe
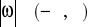
.
WYKŁAD II
Przetwarzanie sygnałów ciągłych - próbkowanie, kwantowanie.
Sygnały fizyczne, chociaż mają naturę ciągłą to jednak z uwagi na stosowane urządzenia techniczne należy przekształcać do postaci cyfrowej przedstawiających ten sygnał w pewnych, wybranych chwilach. Realizuje się to drogą pomiarów w dyskretnych chwilach czasu. Proces ten nazywamy próbkowaniem sygnału. Stosowanie układów cyfrowych w systemach automatyzacyjnych wymaga nie tylko próbkowania, czyli dyskretyzacji w czasie, lecz również dyskretyzacji w poziomie, czyli kwantowania. A zatem efektem operacji próbkowania i kwantowania jest sygnał cyfrowy. W praktyce próbkowanie przeprowadza się podając sygnał ciągły na wejście przetwornika AC (analogowo - cyfrowy), którego sygnał wejściowy jest już ciągiem wartości cyfrowych sygnału. Próbkowanie sygnału może być równomierne lub nierównomierne. Z punktu widzenia zawartości informacji sygnału ważnym problemem próbkowania jest wybór okresu próbkowania. Przyjmowanie długich okresów próbkowania prowadzi do błędów dyskretyzacji zmniejszających dostarczoną informację w sygnale ciągłym. Przyjęcie zbyt krótkich okresów próbkowania prowadzi nie tylko do komplikowania aparatury kontrolno - rejestrującej, ale także obciąża system nieistotną informacją.
Pierwsze twierdzenie o próbkowaniu sygnału o widmie ograniczonym sformułowali Shannon i Kotelnikov, którzy określili warunki, przy których sygnał ciągły x(t) ograniczony w widmie częstotliwości może być zastąpiony bez strat informacji ciągiem wartości chwilowych mierzonych w określonych odstępach czasu. Twierdzenie to mówi, że sygnał x(t) niezawierający składowych o częstotliwości powyżej pewnej częstotliwości granicznej ![]()
jest w pełni określony jego wartościami chwilowymi branymi w odstępach czasu: ![]()
, a zatem każdy sygnał ciągły x(t), jeżeli ma tylko widmo ograniczone możemy przedstawić za pomocą ciągu wartości chwilowych określanych co najmniej dwa razy w każdym okresie składowej o największej częstotliwości.
Proces próbkowania ma postać:
Rys. Sygnał x(t) i odpowiadający im sygnał próbkowy ![]()
.
Widzimy, że twierdzenie Kotelnikova - Shannona dotyczy próbkowania sygnałów x(t) określonych i nieskończonych przedziałów czasu i zanikających w nieskończoności. Realizację sygnału x(t) stacjonarnych procesów losowych powyższych warunków nie spełniają i nie należy do nich stosować powyższego twierdzenia. Sygnały rzeczywiste x(t) są funkcjami określonymi w skończonym przedziale czasu T i mają one transformatę Fouriera ![]()
określoną w paśmie nieograniczonym i także nie spełniają warunków twierdzenia Kotelnikova - Shannona. Ponieważ jednak widma takich sygnałów rzeczywistych szybko maleją w funkcji częstotliwości to można przyjąć częstotliwość graniczną ![]()
, poza którą widmo sygnałów jest praktycznie pomijane. W takim przypadku sygnał x(t) będzie z pewnym przybliżeniem odtworzonym na podstawie swoich wartości chwilowych ![]()
. Wobec przedstawionych badań można uogólnić twierdzenie, Kotelnikova - Shannona i stwierdzić, że sygnał x(t) o ograniczonym czasie trwania, T i widmie ograniczonym w przybliżeniu częstotliwością graniczną ![]()
, przy czym: ![]()
można w przybliżeniu przedstawić za pomocą ![]()
jego wartości chwilowych pobieranych w odstępach czasu ![]()
. Wywód ten wynika ze stwierdzenia Lingwista, który podał, że wystarczy ![]()
dla przedstawienia sygnału o widmie ograniczonym częstotliwością ![]()
i czasie trwania T uzasadniając to rozkładem w szereg Fouriera sygnał x(t) o czasie trwania T.
Kwantowanie sygnałów.
Polega ono na przyporządkowaniu ciągłej wielkości fizycznej pewnej wartości dyskretnej poziomu. Kwantowanie również może być równomierne i nierównomierne, co wpływa na wartość momentu kwantowego. W kwantowaniu nierównomiernym kwantyzator sygnałowi ciągłemu x przyporządkowuje wartości dyskretne x*, co prezentuje rysunek:
Charakterystyka kwantyzatora.
Załóżmy, że sygnał wyjściowy kwantyzatora x charakteryzuje się znaną funkcją gęstości prawdopodobieństwa p(x) wówczas sygnał wejściowy kwantyzatora x* będzie skończoną liczbą wartości ![]()
nazywanych poziomami kwantowania. Kwantyzatory określają, zatem N+1 poziomów kwantowania oraz wartości N punktów ![]()
, w których następują skoki sygnału wejściowego kwantyzatora. Sygnał wyjściowy x* w zależności od sygnału wejściowego x przedstawiamy zależnością:
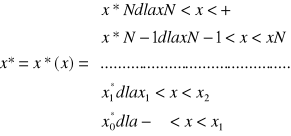
.
Różnicą między wartościami sygnału pierwotnego x i sygnału kwantowanego x*, a zatem różnicę między sygnałem na wejściu i wyjściu kwantyzatora określamy jako ![]()
i nazywamy błędem kwantowania.
Analiza probabilistyczna sygnałów.
Z uwagi na brak możliwości pełnego poznania sygnału losowego bądź zbioru jednorodnych sygnałów losowych, stosuje się analizę probabilistyczną umożliwiającą opis wspólnych cech sygnału ze wspomnianych zbiorów, co polega na określaniu deterministycznych rozkładów prawdopodobieństwa oraz zdeterminowanych licz i funkcji charakteryzujących te rozkłady. Analiza probabilistyczna opiera się na rachunku prawdopodobieństwa, którego podstawy stanowią: zasada alternatywy i zasada koniunkcji. Zasada alternatywy polega na tym, że prawdopodobieństwo wystąpienia jednego z dwóch zdarzeń wzajemnie się wykluczających jest sumą prawdopodobieństw zdarzeń pojedynczych: ![]()
. Należy pamiętać, że A i B są wzajemnie rozłączne jest prawdziwa dla więcej niż dwóch zdarzeń. Zasada koniunkcji polega na tym, że prawdopodobieństwo jednoczesnego wystąpienia dwóch zdarzeń niezależnych równa się iloczynowi prawdopodobieństw zdarzeń pojedynczych: ![]()
. Jest to szczególny przypadek, gdy A i B to zdarzenia niezależne.
Jeżeli zdarzenia A i B są niezależne wówczas w zasadzie koniunkcji występuje prawdopodobieństwo warunkowe i przyjmuje ona postać: ![]()
, gdzie ![]()
to prawdopodobieństwo wystąpienia zdarzenia A przy założeniu, że zdarzyło się B.
Rozkłady prawdopodobieństw.
Przeprowadzając doświadczenia wiele razy otrzymujemy zwykle kilka różnych wyników, graficzne przedstawienie częstości tych wyników w funkcji ich samych nazywamy rozkładem prawdopodobieństw tych wyników, a zatem można powiedzieć, że rozkład prawdopodobieństw określa prawdopodobieństwa różnych zdarzeń w ciągu doświadczeń. Z najprostszą postacią rozkładu mamy do czynienia wówczas, jeżeli eksperyment ma jedynie dwie możliwości: sukces bądź niepowodzenie, rozkład taki nazywamy dwumianowym. Załóżmy, że w każdym eksperymencie prawdopodobieństwo sukcesu wynosi p, a niepowodzenia q, wówczas można zapisać: ![]()
. W przypadku n przeprowadzonych eksperymentów prawdopodobieństwo osiągnięcia sukcesów k razy określa się zależnością: 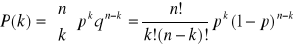
- jest to postać rozkładu dwumianowego. W przypadku, kiedy liczba eksperymentów jest bardzo duża, n >> 1, a prawdopodobieństwo sukcesów każdego z doświadczeń bardzo małe p << 1 to istnieje pewne przybliżenie rozkładu dwumianowego nazywane rozkładem Poisson. Jeżeli przy powyższych założeniach ponadto średnia liczba sukcesów w n próbach określona będzie jako ![]()
to prawdopodobieństwo, że z całkowitej liczby eksperymentów otrzyma się k sukcesów: ![]()
![]()
![]()
. W przypadku badania zdarzeń w kolejnych przedziałach czasu stosuje się zmodyfikowaną postać rozkładu Poissona, w której, przez r oznaczamy średnią liczbę zdarzeń w jednostce czasu i wówczas ![]()
, a prawdopodobieństwo wystąpienia k sukcesów w czasie t: ![]()
.
Rozkład normalny - przypadek dyskretny.
Jest on również w przybliżeniu rozkładu wymiarowego i występuje wówczas, jeżeli zamiast wykreślania prawdopodobieństwa różne liczby sukcesów k w funkcji tej liczby wykreślamy to prawdopodobieństwo w funkcji różnic X między liczbą sukcesów: ![]()
a średnią liczbę sukcesów: ![]()
. W tym przypadku ulegnie przesunięciu początek osi odciętych rozkładu wymiarowego: ![]()
.Jeżeli powyższe zależności podstawimy do wzoru rozkładu dwumianowego otrzymamy: 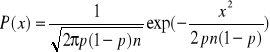
. Przebieg wykresy dyskretnego ma postać:
Ciągłe rozkłady gęstości prawdopodobieństwa.
W omawianych dotychczas rozkładach zmianę przyjmowały wyłącznie wartości całkowite, czyli liczba sukcesów lub niepowodzenia była liczbą całkowitą. W praktyce wiele zmiennych ma naturę dowolną i przyjmuje wartość dodatnią wobec tego w przypadkach ciągłych badań zmiennych obliczane są zawsze dla interesujących nas przedziałów wartości zmiennych a nie dla wartości konkretnych wówczas operujemy pojęciem gęstości prawdopodobieństwa a same prawdopodobieństwa reprezentowane są przez pola powierzchni pod krzywą gęstości prawdopodobieństwa. Przykładem rozkładu gęstości prawdopodobieństwa może być rozkład gęstości prawdopodobieństwa ciężaru noworodków ma postać:
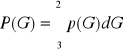
Parametry charakterystyk rozkładu gęstości prawdopodobieństwa.
Wartość średnia:
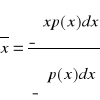
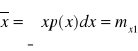
.
Wartość modalna: jest to wartość x, która odpowiada max przebiegu wartości prawdopodobieństwa p(x).
Mediana jest to wartość x odpowiadająca podziałowi pola pod krzywą gęstości rozkładu na dwie równe części.
Wartość średnio - kwadratowa - nazywana jest momentem II rzędu i określana jest wyrażeniem:
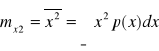
.Wariancja jest to moment II rzędu rozkładu względem wartości średniej:
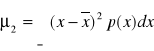
jest miarą szerokości rozkładu lub miarą rozrzutu względem wartości średniej. Często oznaczana jest przez: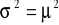
.Pierwiastek z wariancji nazywany jest odchyleniem standardowym. Rozpisując wyrażenie:
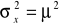
otrzymamy: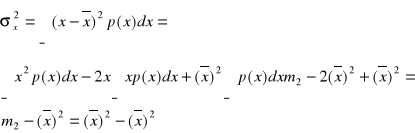
Często zamiast funkcji gęstości prawdopodobieństwa używana jest tzw. dystrybuanta określona wyrażeniem: 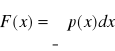
lub ![]()
. Wartość dystrybuanty w każdym punkcie x równa się prawdopodobieństwu, że wartość zmiennej jest mniejsza od x.
Rozkład normalny gęstości prawdopodobieństwa.
Wprowadzony został przez Gaussa dla określenia rozkładu błędów pomiarowych i nazywamy rozkładem błędów. Rozkład ten opisany jest zależnością: ![]()
. W tym rozkładzie prawdopodobieństwo występowania tzw. błędów grubych maleje oraz z oddaleniem się od wartości średniej. Rozkład Gaussa wykorzystywany jest w analizie sygnałów zakłucających, czyli szumów.
WYKŁAD 3
Dyskretne systemy informacyjne i przetwarzania sygnałów.
Składają się one z dyskretnego źródła informacji kanału transmisyjnego oraz dyskretnego odbiornika informacji. Transmitowanym sygnałem jest sygnał losowy ![]()
, który może być transmitowany przez jego realizację ![]()
. Liczba jego realizacji jest ograniczona i wynosi:
i = 1, …, M. Rozpatrywać będziemy pewien zbiór ![]()
utworzony z realizacji ![]()
z sygnału. Każdemu elementowi ![]()
ze zbioru ![]()
przyporządkowana jest pewna liczba ![]()
, określająca prawdopodobieństwo wysłania ze źródła realizacji ![]()
sygnału ![]()
. Zbiór wartości ![]()
oznaczamy ![]()
i stanowi on rozkład prawdopodobieństwa określany na zbiorze ![]()
. Rozkład ten jest probabilistyczną charakterystyką źródła sygnałów a zatem probabilistyczną charakterystyką sygnału nadawanego ![]()
.
![]()
![]()
Rys.: Graficzne przedstawienie przyporządkowań elementów zbioru ![]()
i zbioru ![]()
.
Przykładem dyskretnego źródła informacji, wysyłającego sygnały losowe ![]()
może być zespół urządzeń wytwarzających impulsy prostokątne o znanym czasie trwania i amplitudzie, która w sposób losowy przyjmuje N różnych wartości. Przesyłając sygnał losowy ![]()
kanałem transmisyjnym na jego wyjściu odbierany jest losowy sygnał ![]()
, który zależy od zakłóceń, działających na transmitowany sygnał w kanale transmisyjnym. Losowy sygnał ![]()
opisywany jest przez zbiór jego możliwych realizacji ![]()
. Rozpatrujemy, zatem zbiór ![]()
przez realizację możliwego sygnału odbieranego. Każdemu elementowi ![]()
przyporządkowana jest pewna liczba ![]()
, która określa prawdopodobieństwo odebrania danej realizacji ![]()
sygnału losowego ![]()
. Zbiór prawdopodobieństw ![]()
stanowi probabilistyczną charakterystykę sygnału odbieranego (odbiornika) i jest on określany na zbiorze ![]()
.
Przyporządkowanie prawdopodobieństw ma postać:
![]()
![]()
Rys.: graficzna interpretacja przyporządkowania elementów zbioru ![]()
elementów zbioru ![]()
.
Ponieważ sygnał odbierany ![]()
zależy od sygnału nadawanego ![]()
oraz od obecności kanału transmisyjnego to dla pełnego opisu systemu informacyjnego należy wyznaczyć probabilistyczną charakterystykę zakłóceń działających w kanale. Załóżmy, że na wejście kanału podaliśmy jedną realizację ![]()
sygnału losowego. Na realizację w kanale tym działają zakłócenia i dlatego nie wiemy, którą realizację ![]()
sygnału ![]()
odbieramy. Z uwagi na działania zakłóceń możliwe jest odebranie każdej z realizacji należącej do zbioru ![]()
.
Istnieje jednak możliwość określenia prawdopodobieństwa warunkowego odebrania danej realizacji ze zbioru ![]()
, przy nadaniu realizacji ![]()
ze zbioru ![]()
. A zatem można to zinterpretować graficznie:
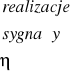
Suma tych prawdopodobieństw warunkowych po wszystkich realizacjach sygnału musi być równa 1:
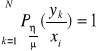
.
Z powyższego widzimy, że dla każdej wartości ![]()
własności zakłóceń działających w kanale transmisyjnym, opisuje się warunkowym rozkładem prawdopodobieństwa: 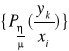
. W związku z tym, że ilość możliwych realizacji sygnału nadawanego jest N, a ilością realizacji sygnału odbieranego jest M, to własności zakłóceń działających w kanale transmisyjnym, będą opisane przez P x M prawdopodobieństw warunkowych 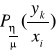
. W związku z tym probabilistyczną charakterystykę kanału możemy przedstawić za pomocą macierzy prostokątnej posiadającej M - kolumn i N - wierszy. Macierz ta ma postać:
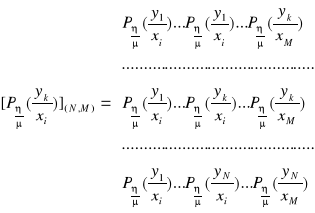
.
Należy pamiętać, że suma kolumn ma być równa ![]()
. Powyższą macierz nazywamy macierzą przejścia kanału transmisyjnego, przedstawiającego zbiory ![]()
i ![]()
w postaci macierzy kolumnowych:
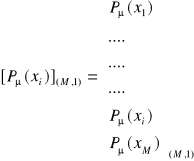
, oraz zbiór ![]()
: 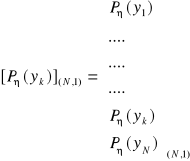
.
Możemy sformułować równanie macierzowe, które opisuje system informacyjny:
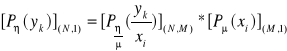
.
Ocena ilości informacji zawartej w sygnale.
W występujących sygnałach, które są przetwarzane w systemach informacyjnych zawarta jest informacja, której ilość określamy za pomocą pojęcia entropii oznaczonej jako H. Chcąc określić ilość informacji zawartej w sygnale nadawanym ![]()
, należy pamiętać, że probabilistyczną charakterystyką tego sygnału jest rozkład tego prawdopodobieństwa apriori, czyli ![]()
. W związku z tym ilość informacji musi być funkcją tego rozkładu, co zapiszemy: ![]()
. Ponieważ ilość informacji związana jest z każdą realizacją sygnału nadawanego, to możemy ją przedstawić w postaci równania: 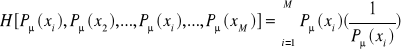
, gdzie ![]()
jest to ilość informacji wynikająca z zajścia zależności ![]()
. Aby spełnić wymagania matematyczne związane z obliczaniem entropii dla jej określenia wprowadzamy logarytm jako funkcję i przy podstawie a > 1 otrzymujemy:
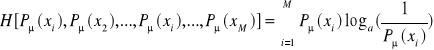
.
Ponieważ entropia jest funkcją prawdopodobieństwa apriori to: 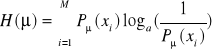
.
W procesie transmisji sygnału ![]()
pewna ilość informacji jest tracona z uwagi na oddziaływanie zakłóceń. Jeżeli na wyjściu kanału transmisyjnego odbierzemy pewną realizację ![]()
sygnału ![]()
to ze względu na losowy charakter sygnału ![]()
i oddziaływanie zakłóceń losowych w kanale nie wiemy, jaka realizacja ![]()
sygnału ![]()
została rzeczywiście nadana. Możemy, jednak dla ustalonego elementu ![]()
sygnału ![]()
wyznaczyć warunkowy rozkład prawdopodobieństwa 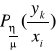
, określającego prawdopodobieństwo z wysłania realizacji ![]()
pod warunkiem odebrania realizacji ![]()
. Interpretacja geometryczna będzie miała postać:
Rys.: Interpretacja geometryczna sytuacji nieznajomości nadanej realizacji ![]()
sygnału ![]()
, przy odbiorze realizacji ![]()
sygnału ![]()
.
Ilość informacji traconej w kanale przez daną realizację ![]()
sygnału ![]()
jest tym mniejsza im większe jest prawdopodobieństwo warunkowe ![]()
. Ilość informacji traconej w kanale jest nieujemną funkcją wszystkich prawdopodobieństw ![]()
i określona jest zależnością: 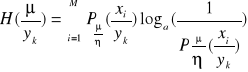
. Aby otrzymać oczekiwaną ilość informacji traconej w kanale z zakłóceniami w przypadku nadania sygnału ![]()
i odebrania pełnego sygnału ![]()
, należy powyższą zależność uśrednić na zbiorze ![]()
. W związku z tym otrzymamy postać: ![]()
. Entropia ![]()
określona wcześniej wymienioną zależnością nazywana jest entropią warunkową a posteriori. Z przedstawionych zależności widzimy, że oczekiwana ilość informacji przesyłanej, przez kanał z zakłóceniami może być określona jako różnica oczekiwanej ilości informacji zawartej w losowym sygnale nadawanym ![]()
oraz oczekiwanej ilości informacji traconej w kanale przesyłowym, co zapiszemy: ![]()
. Wielkość ![]()
określoną wcześniej wymienionym wyrażeniem nazywamy transinformacją bądź szybkością przesyłania informacji lub też informacją wzajemną, wynikającą z zajścia transmisji sygnału ![]()
i odebrania sygnału ![]()
.
Podobnie jak dla źródła informacji możemy obliczyć również ilość informacji zawartej w odbieranym sygnale ![]()
i korzystamy wówczas z wyrażenia: 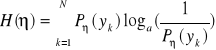
.
Przepustowość kanału transmisyjnego:
Rozpatrzmy system informacyjny, który był omawiany:
![]()
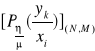
![]()
![]()
![]()
![]()
![]()
Rys.: Graficzne przedstawienie elementarnego dyskretnego systemu informacyjnego.
Należy teraz ocenić zdolność kanału transmisyjnego do przesyłania informacji. Wielkość charakteryzująca zdolność powinna zależeć od charakterystyki probabilistycznej kanału a zatem od zbioru prawdopodobieństwa 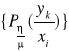
. Jednakże miarą oczekiwanej ilości informacji przesyłanej przez kanał jest transinformacja, będąca funkcją zarówno probabilistycznej charakterystyki źródła informacji jak i probabilistycznej charakterystyki kanału. W celu uniezależnienia wielkości opisującej kanał od charakterystyki probabilistycznej źródła a zatem od rozkładu apriori stosujemy metodę polegającą na wyznaczeniu spośród wszystkich możliwych rozkładów apriori określonych na zbiorze ![]()
takiego, którego transinformacja osiąga wartość maksymalną. Tę maksymalną wartość transinformacji przyjmuje się za wielkość charakteryzującą zdolność kanału do przesyłania informacji i nazywa się ją przepustowością: ![]()
.
Dla oceny sprawności kanału przesyłowego stosuje się tzw. współczynnik sprawności transinformacji określonej wartością: ![]()
. Ilość informacji obliczana jest w jednostkach, które należą od podstawy logarytmu w wyrażeniu na entropię.
Kodowanie sygnałów dyskretnych.
Jest to jedna z metod optymalizacji transmisji informacji a system informacyjny ma wówczas postać:
![]()
![]()
![]()
![]()
![]()
![]()
Rys.: Transmisja sygnałów zakodowanych.
W przedstawionym systemie losowy sygnał ![]()
wysyłany ze źródła w urządzeniu nazywanym koderem zostaje przekształcony w postać zakodowaną ![]()
i w takiej postaci podlega transmisji. Na wyjściu kanału transmisji odbierany jest zakodowany sygnał ![]()
, który w dekoderze przekształcany jest na postać zrozumiałą dla odbiornika.
Proces kodowania.
Źródło wytwarza sygnał losowy ![]()
o realizacjach ![]()
tworzących zbiór ![]()
. Sygnał charakteryzowany jest rozkładem a priori ![]()
oraz dany jest dyskretny zbiór ![]()
, który nazywany jest alfabetem kodu v = 1,…, Q. Operacją kodowania dyskretnego losowego sygnału ![]()
nazywamy przyporządkowania każdej z M realizacji ![]()
sygnału ![]()
pewnego ciągu ![]()
utworzonego z elementów alfabetu kodu ![]()
. W wyniku kodowania zbiorowi ![]()
przyporządkowany zostaje zbiór ![]()
złożony z elementów ![]()
. Regułę przyporządkowania zbioru ![]()
, czyli ciągu ![]()
nazywamy wyrazami kodu, każdy wyraz ![]()
kodu jest ciągiem ![]()
elementów alfabetu ![]()
. Ciągi te mają, zatem postać: 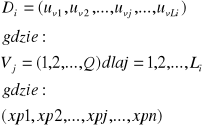
.
Liczbę naturalna ![]()
, czyli liczbę elementów alfabetu kodu tworzących wyraz ![]()
nazywamy długością wyrazu kodu.
WYKŁAD 4 i 5
Zasady kodowania dyskretnych systemów informacyjnych.
Sygnał wytwarzany w źródle ![]()
reprezentowany jest pewnym ciągiem wielkości ![]()
, a zatem ma on postać: ![]()
.
W trakcie kodowania powyższego ciągu, każdej wartości ![]()
, przyporządkowana jest wartość ![]()
, czyli wykaz kodu oznacza to, że danej realizacji sygnału ![]()
w postaci: ![]()
. W celu jednoznacznego odtworzenia realizacji sygnału ![]()
na podstawie otrzymanego na wejściu dekodera ciągu wyrazów ![]()
niezbędne jest wprowadzenie przecinków dla rozdzielenia poszczególnych wyrazów ![]()
kodu. Procedura ta wydłuża jednak czas transmisji, a zatem zmniejsza sprawność transmisji systemu, co jest sprzeczne z celem wprowadzenia kodowania. W związku z powyższym wymaga się stosowania kodów bez przecinkowych, a rolę przecinków mają spełniać, tzw. przedrostki wyrazów kodu, które definiujemy następująco: wyraz ![]()
kodu o długości ![]()
jest ciągiem ![]()
elementów alfabetu kodu, czyli ciągiem ![]()
liter kodu, a zatem ma on postać: ![]()
. Odcinając kolejno pierwszy znak wyrazu kodu, pierwsze dwa znaki wyrazu kodu, itd. aż do ![]()
znaków wyrazu kodu otrzymujemy ![]()
ciągów w postaci:
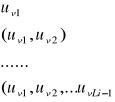
.
Przedstawione powyżej ciągi nazywamy przedrostkami wyrazów kodu ![]()
o długości ![]()
. O kodach bez przecinkowych mówimy, że spełniają one właściwości przedrostkowe. Aby uzyskać maksymalnie współczynnik transmisji informacji dochodzi do uzależnienia długości ![]()
wyrazów ![]()
kodu od prawdopodobieństw ![]()
wystąpienia poszczególnych realizacji ![]()
odpowiadały małe długości ![]()
wyrazów kodu, a rzadko wystąpienia realizacjom ![]()
odpowiadały większe długości wyrazów kodu, czyli długość ![]()
wyrazów kodu ma być rosnącą monotonicznie funkcją odwrotności prawdopodobieństw ![]()
.
Projektowanie kodów Shannona - Fano.
Rozpatrzymy projektowanie kodów binarnych, czyli Q = 2. Załóżmy, że kody mają spełniać właściwość przedrostkową, w przypadku takich założeń, dla zapewnienia dużej sprawności kodowania długości ![]()
wyrazów ![]()
muszą spełniać nierówność: ![]()
.
Na podstawie powyższej nierówności dla danego źródła informacji określamy długości ![]()
wyrazów ![]()
kodu. W taki sposób projektowany kod w ogólnym przypadku nie spełnia jeszcze właściwości przedrostkowej, dlatego należy zastosować metodę Shannona - Fano, którą opiszemy następująco: elementy ![]()
ze zbioru ![]()
w zależności od wartości prawdopodobieństw apriori, czyli ![]()
uszeregujemy w ten sposób, aby spełniona była nierówność: ![]()
. Przez ![]()
oznaczamy dystrybuantę rozkładu prawdopodobieństw ![]()
ma ona postać: ![]()
i następnie wprowadzimy pewien pomocniczy zbiór liczb ![]()
o postaci:
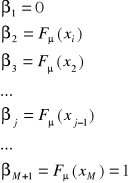
. Zauważyć należy, że ![]()
zmienia się od j = 1, … do ![]()
.
W następnym kroku wartości liczby ![]()
zapisujemy w układzie dwójkowym, czyli każda z liczb będzie ciągiem 0 i 1. Dla określenia i - tego wyrazu ![]()
kodu o długości ![]()
należy wybrać ![]()
kolejnych współczynników, czyli 0 i 1, licząc od kropki w prawo.
Przykład:
Źródło informacji wytwarza losowy sygnał ![]()
charakteryzowany zbiorem realizacji ![]()
, przy czym i = 1, 2, …, 5 oraz rozkładem prawdopodobieństw ![]()
, gdzie ![]()
, ![]()
, ![]()
, ![]()
, ![]()
. Zaprojektować kod binarny Shannona - Fano. Obliczyć ilość informacji zawartą w sygnale ![]()
.
Dane:
![]()
![]()
![]()
![]()
![]()
.
Rozwiązanie:
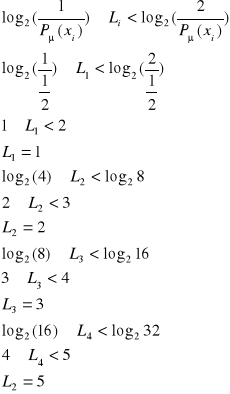

Przetwornik AC - zjawisko aliasingu a twierdzenie Kotelnikowa - Shannona.
Przetwarzanie ciągłego sygnału analogowego x(t) na sygnał cyfrowy składa się z 3 następujących etapów:
Dyskretyzacji sygnału w czasie, czyli próbkowania.
Dyskretyzacji wartości sygnału, czyli próbkowanie w poziomie nazywane kwantyzacją.
Kodowanie uzyskanego sygnału dyskretnego.
Próbkowanie polega na pobieraniu w określonych odstępach czasu próbek wartości x(t)w taki sposób, aby ciąg tych próbek uniemożliwiał jak najbardziej wierne odtworzenie przebiegu funkcji. Podczas próbkowania następuje dyskretyzacji argumentu ![]()
, gdzie k - jest numerem próbki; ![]()
- okresem. A zatem ciąg próbek ![]()
reprezentuje sygnał x(t) w postaci dyskretnej ![]()
.
a)
b)
c)
d)
Rys. Próbkowanie przebiegu: a - przebieg próbkowany, b - impulsy próbkujące, c - przebieg po próbkowaniu w przypadku naturalnego próbkowania punktowego, d - przebieg po próbkowaniu w przypadku próbkowania z zapamiętywaniem.
Przetwarzanie analogowo - cyfrowe.
W przypadku próbkowania idealnego przyjmuje się punktowe pobieranie informacji, co oznacza, że impulsy próbkujące powinny mieć nieskończenie wąską szerokość. Operacja próbkowania będzie, zatem równoważna pomnożeniu przebiegu ![]()
sygnału przez ciąg impulsów o jednostkowej amplitudzie, co daje w rezultacie ciąg impulsów zmodulowanych, w których odpowiedzi zachowana jest informacja o oryginalnym przebiegu będzie to, zatem modulacja iloczynowi realizowana przez ciąg impulsów delta.
Często w torze pomiarowym stosowany jest specjalny układ próbkowania z pamięcią, który nie tylko pobiera próbkę wartości przebiegu sygnału, ale również utrzymuje jej wartość przez określony czas, zwykle do pojawienia się następnego impulsu próbkującego. Ponieważ teoria próbkowania jest ważna przy określaniu dokładności oraz użyteczności każdego systemu cyfrowego to niezbędne jest zrozumienie skutków różnego próbkowania. W dziedzinie częstotliwości istnieje niejednoznaczność związana z próbkami sygnału o czasie dyskretnym, która nie istnieje w przypadku sygnałów ciągłych. Ocena skutków tej niejednoznaczności daje się wyjaśnić drogą zrozumienia próbkowej natury danych dyskretnych. Załóżmy, iż dany jest ciąg próbek o postaci: ![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
. Próbki te reprezentują wartości chwilowe pewnego przebiegu sinusoidalnego w dziedzinie czasu pobrania w równomiernych odstępach czasu pobrane w równomiernych odstępach na osi czasu.
Można zauważyć i udowodnić, że dany ciąg reprezentuje nieskończoną liczbę sinusoid przesuniętych między sobą w dziedzinie częstotliwości o pewną wartość, która stanowi częstotliwość próbkowania przebiegu. Dzieje się tak, dlatego, że proces próbkowania dokonuje powielania widma sygnału z przesunięciem na osi częstotliwości o wielokrotność częstotliwości próbkowania. W związku z tym istotnym zagadnieniem jest określenie minimalnej, niezbędnej częstotliwości próbkowania, (o czym mówi twierdzenie Kotelnikowa - Shannona), przy, której jest możliwe pełne odtworzenie sygnału ciągłego na podstawie pobranych próbek. Problem ten jest przedmiotem rozważań w teorii sygnałów gdzie punktem wyjścia do analizy jest określenie charakterystyki widmowej, czyli Fourierowskiej sygnału, która podlega próbkowaniu. Zakładając, że przebieg ![]()
jest sygnałem ściśle dolnopasmowym o paśmie ograniczonym do pewnej wartości ![]()
uzyskuje się po próbkowaniu widmo sygnału, będące widmem oryginału powielonym nieskończenie wiele razy z przesunięciem na osi częstotliwości o wartości wielokrotności ![]()
. Odtworzenie przebiegu sygnału z ciągu próbek polega na wydzieleniu drogą idealnej filtracji głównej części widma położonej w otoczeniu środka układu współrzędnych. Jest to możliwe tylko wówczas, gdy poszczególne segmenty widma nie zachodzą na siebie, czyli wtedy twierdzenie Kotelnikowa - Shannona (czyli jest dwukrotnie większa od ![]()
). Interpretacja twierdzenia Kotelnikowa - Shannona mówi, że minimalna częstotliwość próbkowania określona jest częstotliwością Nequista.
a)
b)
c)
Rys. Widma częstotliwościowe przy próbkowaniu: a - widmo sygnału próbkowanego; b - nakładanie się segmentów widma w przypadku, próbkowania niedomiarowego (![]()
); c - rozsunięcie segmentów widma w przypadku próbkowania nadmiarowego ![]()
.
Na przedstawionym rysunku b warunek Kotelnikowa - Shannona nie jest spełniony i segmenty widma zachodzą na siebie w takiej sytuacji przy odtwarzaniu sygnału przez wybieranie filtrem dolnopasmowym głównej części widma, zostaje również pobrana część informacji, ale związana z następnymi segmentami i odtworzony przebieg będzie zniekształcony w stosunku do oryginału. Zjawisko to nosi nazwę aliasingu i oznacza nieprawidłowe potraktowanie fragmentu następnego segmentu jako należącego do głównej części widma. Fragment segmentu o większej częstotliwości przybiera cechy części głównej widma, co niekiedy nazywane jest przeplataniem widm. Nakładania segmentów widma i wynikających z tego przekształceń można uniknąć stosując impulsy próbkujące o odpowiednio dużej częstotliwości lub ograniczając pasmo sygnału próbkowanego przez odpowiednią filtrację. W praktyce stosuje się częstotliwości próbkowania większe od minimalnej wartości wynikającej z twierdzenia Kotelnikowa - Shannona. Pozwala to uniknąć nakładania segmentów spowodowaną minimalną nieidealną filtracją i istnieniem szumów o wielkiej częstotliwości omawiane próbkowanie punktowe jest przypadkiem teoretycznym, gdyż w rzeczywistości impulsy próbkujące charakteryzują się pewnym czasem trwania i zachodzi tzw. próbkowanie rzeczywiste z aparaturą.
Procesy sygnałowe DSP.
DSP - Digital Signal Procesor
Zgodnie ze swoją nazwą są to cyfrowe procesory wyspecjalizowane w określonych zadaniach
(przetwarzanie różnego typu sygnałów: akustycznych, wizyjnych itp.) i przetwarzanie w czasie rzeczywistym z wysoką jakością co wykorzystuje się w technice wojskowej np. w hydrolokacji oraz w technice telefonii komórkowej w urządzeniach medycznych do przetwarzania sygnału mowy i obrazu. Procesy sygnałowe są stosowane w technice komputerowej do obróbki danych praktycznie we wszystkich płytach głównych, modemach i k. dźwiękowych. Istnieją rozwiązania k. wielofunkcyjne, których procesy po odpowiednim zaprogramowaniu przetwarzają dane audio lub modemowe. Wszystkie operacje wykonywane są na bazie zadanych algorytmów. Możliwe jest przeprogramowanie procesora sygnałowego w trakcie pracy co zwiększa jego elastyczność. Moc obliczeniowa procesora dorównuje a nawet przewyższa możliwości procesorów PC. Dzięki zastosowaniu układów DSP możliwe jest dowolne manipulowanie w czasie rzeczywistym sygnałami cyfrowymi. Przetworzony sygnał również w postaci cyfrowej pojawia się na wyjściu procesora skąd następnie zwykle przekazywany jest do przetwornika GA. Układ przetwarzania cyfrowego posiada wiele zalet w porównaniu z techniką analogową gdyż bez użycia lutownicy można zmienić jego funkcję. Wyniki przetwarzania w procesach DSP są powtarzalne, co w przypadkach analogowych jest nie do spełnienia z uwagi na rozrzut elementów. Nie występuje w procesorach DSP zjawisko starzenia się elementów, a realizowanie filtrów mają idealne charakterystyki transmitancji.
Ideą przetwarzania procesora DSP możemy przedstawić na poniższym rysunku:
W odstępach czasu określonych przez okres próbkowania T przetwornik analogowo-cyfrowy odczytuje wartości napięcia wejściowego. Wartość ta dostarczana jest do DSP a częstotliwość próbkowania sygnału równa się odwrotności i musi być co najmniej dwukrotnie większa od max. częstotliwości przetwarzanego sygnału.
Filtr dolnoprzepustowy na wejściu przetwornika usuwa wszystkie wyższe częstotliwości z widma analizowanego sygnału a zmierzona przez przetwornik wartości napięcia będzie obarczona błędem zależnym od rozdzielczości przetwornika a-c i nie wzrasta w trakcie cyfrowej obróbki. Właściwa obróbka sygnału zachodzi w procesorze DSP, który przetwarza sygnał w sposób zaprogramowany przez użytkownika. Działanie procesów możemy zmieniać w szerokim zakresie na drodze programowej. Na wyjściu procesora znajduje się przetwornik CA oraz filtr dolnoprzepustowy dla wygładzania skokowego przebiegu sygnału. W niektórych zastosowaniach nie jest konieczne umieszczanie przetwornika AC na wejściu procesora jeśli pracuje on np. jako generator sygnałowy. Architektura procesora DSP różni się od typowej dla mikroprocesora PC, który charakteryzuje się współdzieleniem pamięci przez dane i program. Magistrala procesów DSP pracuje z technologią Harward gdzie pamięć danych jest oddzielona od pamięci programów. Zaletą tego rozwiązania jest możliwość jednoczesnego dostępu do danych. Jednakże nie można dowolnie dzielić całej dostępnej pamięci na program i dane. Procesor DSP posiada kilka wewnętrznych szyn danych i adresowych. Specjalny układ logiczny steruje wewnątrz układu przełącznikami, które łączą odpowiednie magistrale wewnętrzne z zewnętrznymi.
Wyszukiwarka
Podobne podstrony:
K Pedagogika mi-dzykulturowa, Pedagogika ogólna APS 2013 - 2016, I ROK 2013 - 2014, II semestr, 2) K
Wykłady z filozofii - A. Drabarek, STUDIA, aps, I rok ZU - PC pedagogika terappeutyczna, filozofia
program z Podstaw przedsiębiorczości dla APS październik 2013, Studia - Pedagogika Specjalna, Notatk
psychologia Wykład 5, APS, Psychologia Ogólna
A Milerski kierunki pedagogiki wspołczesnej PC, APS Pedagogika specjalna, 2 semestr, Kierunki pedago
PEDEUTOLOGIA-wyklady(1), APS - studia magisterskie, Pedagogika przedszkolna - II stopnia, I rok I se
wyklad - dydaktyka2010, APS pedagogika specjalna, I rok, Dydaktyka, Dydaktyka - Stefan Mieszalski
pedagogika specjalna wyklady, APS różne, Pedagogika specjalna
PEDEUTOLOGIA test, APS - studia magisterskie, Pedagogika przedszkolna - II stopnia, I rok I semestr
Pedagogika specjalna.wyklady, APS, Pedagogika Specjalna
Wyklady dla APS, cz I, repetytorium
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
Wykład 04
więcej podobnych podstron