20. Szeregi potęgowe. Promień zbieżności. Przedział zbieżności.
Wśród szeregów funkcyjnych na szczególną uwagę zasługują szeregi potęgowe - są to szeregi w postaci :
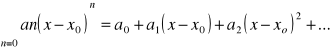
gdzie: x0 - środedek szeregu
a1, a2, a3,..., an - są to współczynniki szeregu.
Dla x0=0 mamy szeregi w postaci:
![]()
Promień zbieżności nazywamy liczbę Rrówną kresowi górnemu zbioru wszystkich x, dla którego szereg jest zbieżny. Przedział (-R;R) nazywamy przedziałem zbieżności szeregu. Możliwe są 3 przypadki:
1. R=0
rys.
2. 0<R<![]()
rys.
3. R=+![]()
rys.
Do wyznaczania promienia zbieżności stosujemy twierdzenie:
1. Jeśli istnieje granica: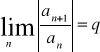
gdy q=![]()
to R=0
gdy0<R<![]()
to R=![]()
gdy q=0 to R=![]()
2. Jeżeli istnieje granica: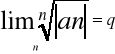
(tak jak wyżej)
21. Szereg Tailora. Rozwinięcie funkcji w szeregu Tailora.
Szereg Tailora to szereg w postaci:
![]()
![]()
np. Rozwinąć funkcję
![]()
![]()
w szereg Tailora
f(x0)=f(1)=3+5+1+2=11
f'(x0)=9x2+10x+1 f'(x0)=f'(1)=9+10+1=20
f''=(x)=18x+10 f''(x0)=f''(1)=18+10=28
f''(x)=18 f'''(x0)==f'''(1)=18
to
![]()
![]()
22.Szereg Maclaurina. Rozwinięcie w szereg Maclaurina funkcji elementarnych.
Gdy x0=0, to szereg Tailora można zapisać wzorem ![]()
Szereg ten nazywa się szeregiem Maclaurina
Rozwinięcia w szereg funkcji elementarnych:
1. ![]()
2.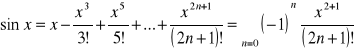
3.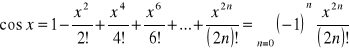
4.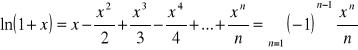
5.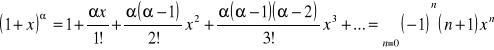
6.![]()
dla /q/<1
Wyszukiwarka