Grupa A

1.Interpolacja trygonometryczna

Załóżmy, że znamy wartości pewnej ciągłej i okresowej funkcji f(x) o okresie 2π w 2n+1 węzłach. Jako bazę interpolacji przyjmujemy zbiór funkcji trygonometrycznych

Otrzymujemy zatem wielomian interpolacyjny w postaci
zawierający 2n+1 nieznanych parametrów.

Ze względu na uproszczenie obliczeń najistotniejszy jest przypadek interpolacji funkcji określonej na zbiorze równoodległych węzłów x_i∈[0,2π] dobranych według następującej zależności

, gdzie i = 0, 1, ..., 2n

Czyli

Warunek interpolacji prowadzi do układu równań liniowych w postaci

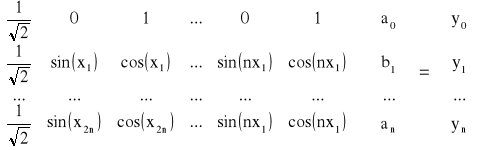
Współczynniki pierwszego wiersza macierzy X wynikają z wartości funkcji sin(hx) i cos (hx) dla x₀ = 0. Przedstawiony układ równań rozwiązuje się natychmiastowo, ponieważ macierz X^-1 można wyznaczyć z zależności

2. Aproksymacja średniokwadratowa

Niech dana będzie funkcja y=f(x), która w pewnym zbiorze X punktów x₀, x₁, ..., x_n przyjmuje wartości y₀, y₁, ..., y_n. Wartości te znane tylko w przybliżeniu z pewnym błędem (np. jako wyniki pomiarów). Poszukujemy takiej funkcji Q(x) przybliżającej daną funkcję f(x), która umożliwi wygładzenie funkcji f(x), czyli pozwoli z zakłóconych błędami danymi wartości funkcji przybliżonej otrzymać gładką funkcję przybliżającą.

Niech ϕ_j(x), j=0, 1,...,n będzie układem funkcji bazowych. Poszukujemy wielomianu uogólnionego Q(x) będącego najlepszym przybliżeniem średniokwadratowym funkcji f(x) na zbiorze X=(x_j). Funkcja przybliżająca ma postać

Przy czym współczynniki a_i są tak określone, aby wyrażenie

dla i=0, 1, ..., n

było minimalne. Funkcja w(x) jest z góry ustaloną funkcją wagową.

Aby wyznaczyć współczynniki a_i oznaczamy odchylenie

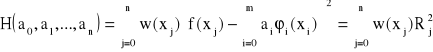
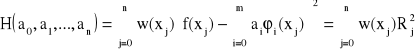
gdzie R_j jest odchyleniem w punkcie x_j.

Następnie obliczamy pochodne cząstkowe funkcji H względem a_i. Z warunku

, gdzie k = 0, 1, ..., n

otrzymujemy układ m+1 równań o niewiadomych a_i zwany układem normalnym

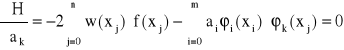
, gdzie k = 0, 1, ..., n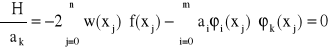

Jeśli wyznacznik tego układu jest różny od zera to rozwiązaniem układu jest minimum funkcji H. W zapisie macierzowym układ przyjmuje postać

gdzie

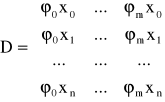
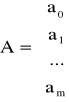
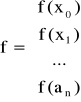
3. Kwadratury Newtona - Cotesa - >wzory zamknięte

Poniżej znajdują się wzory zamknięte dla n = (1..3):

wzór trapezów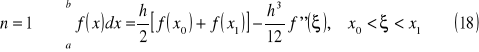

wzór parabol (Simpsona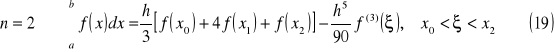

wzór Bessela

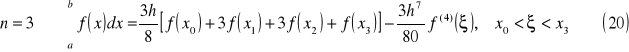
4. Numeryczne rozwiązywanie układów równań liniowych

Metoda iteracji prostej (Jakobiego):

Metoda ta dla równania X=W*X+Z polega na przyjęciu zerowego przybliżenia wektora X=X^o, a następnie przeprowadzenia obliczeń iteracyjnych za pomocą zależności:

Xⁱ⁺¹=W*Xⁱ+Z i=0,1,...

Liczba kroków, które należy wykonać, aby uzyskać wymaganą dokładność rozwiązania, jest z reguły dość duża i istotnie zależy od przyjęcia punktu startowego X^o. Punkt ten najczęściej się dobiera na podstawie dodatkowych informacji o fizycznych aspektach problemu.

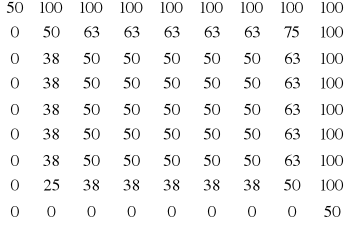
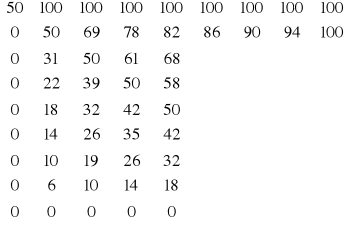
Przykład: Metodę iteracji prostej wykorzystano do rozwiązania układu równań będącego różnicową aproksymacją równania Laplace`a z warunkami brzegowymi I rodzaju. Równanie to opisuje stacjonarne pole temperatury w pewnym dwuwymiarowym obszarze, na którego brzegach temperatury są znane. Jako przybliżenie zerowe przyjęto wartość temperatur w wnętrzu obszaru T=50°C, wymiary prostokątne a=b=0,8 cm.

5. Metoda Rungego - Kutty 4 rzędu rozwiązywania równań różniczkowych I rzędu

Metoda wyprowadzona przez rozwinięcie f(t,y) w szereg Taylora 4 rzędu, pozwala określić stałe we wzorze (wzór ogólny R-K). Poniżej przedstawiono najczęściej stosowaną metodę 4 rzędu

k₁ = hf (t_i, w_i);k₂ = hf (t_i + ½ *h, w_i + ½ *k₁);k₃ = hf (t_i + ½ *h, w_i + ½ *k₂) ;k₄ = hf (t_i+h, w_i+k₃)

ostatecznie: w_i+1=w_i + 1/6 (k₁ + 2k₂ + 2k₃ + k₄) (38)

Interpretacja graficzna:f₁ = f (t_i, w_i);f₂ = f (t_i + ½ * h, w_i+1 + h f₁);f₃ = f (t_i + ½ * h, w_i + ½ * h f₂);f₄ = f (t_i + h, w_i + h f₃)

linia 3-4 nie jest łamana - jest prosta !!! (na 99%) :)

Metoda R-K jest najczęściej stosowaną metodą do rozwiązywania układów równań różniczkowych

6. Rozwiązywanie układów równań różniczkowych I rzędu

Grupa B

1.Interpolacja Lagrange`a

W interpolacji wielomianowej Lagrange'a dla n+1 węzłów interpolacji

przyjmuje się funkcje bazowe w postaci

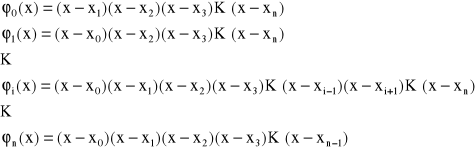
Funkcje te są wielomianami stopnia n zbudowanymi w ten sposób, że w funkcji bazowej φ₁ brakuje czynnika (x-x_i). Zatem wielomian interpolacji wyraża się następującym wzorem:

współczynniki a₀ ... a_n tego wielomianu wyznaczamy z równania:

X · A = Y, przy czym macierz X ma postać:

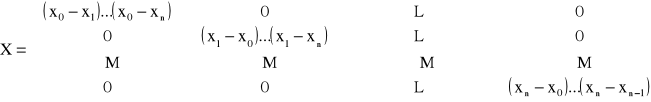
Macierz posiada tylko główną przekątną niezerową w związku z tym układ równań X · A = Y rozwiązuje się natychmiastowo

Można więc wielomian interpolacyjny Lagrange'a zapisać w postaci ułamka:

lub krócej

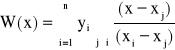
, j = 0, 1, ..., n

2. Aproksymacja trygonometryczna

Często spotykamy się z przypadkiem, gdy funkcja f(x) jest okresowa. Taką funkcję wygodniej jest aproksymować, wielomianem trygonometrycznym o bazie:

1, sin x, cos x, sin 2x, cos 2x, …, sin kx, cos kx

Jeżeli f(x) jest funkcją dyskretną określoną w dyskretnym zbiorze równoodległych punktów i ich liczba jest parzysta i wynosi 2L (dla nieparzystej liczby punktów rozumowanie jest analogiczne), niech:

dla i = 0, 1, …, 2L-1

Baza jest ortogonalna nie tylko na przedziale <0, 2π>, ale też na zbiorze punktów x_i, przy czym warunki ortogonalności mają postać:

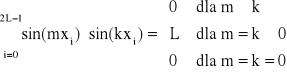
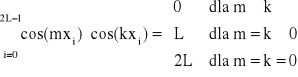
dla m, k dowolnych, przy czym m i k zmieniają się od 0 do L

Przybliżeniem funkcji f(x) na zbiorze punktów x_i jest wielomian trygonometryczny:

, n<L

Współczynniki a_j i b_j wielomianu wyznaczamy tak, aby suma kwadratów różnic

była minimalna.

Korzystając z warunku ortogonalności otrzymujemy rozwiązanie układu normalnego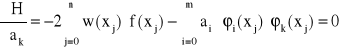

w postaci:
dla j=1, 2, …, n

3. Kwadratury Newtona - Cotesa -> wzory otwarte

Wzory kwadratur nie opartych na węzłach będących końcami przedziału całkowania nazywamy wzorami otwartymi Newtona - Cotesa

Jeżeli dla skończonego [a ; b] przedziału wybierzemy zbiór punktów węzłowych {x₀, …, x_n} takich, że :

gdzie:

dla i=(0, …, n)

Oraz

W oparciu o Twierdzenie 1 można również wyznaczyć wzory kwadratur otwartych. Wówczas wzory kwadratur dla n parzystych mają postać

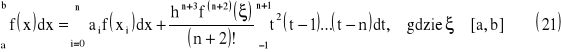
oraz dla n nieparzystych mają postać:

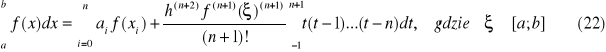
wzór prostokątów

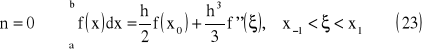
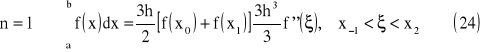
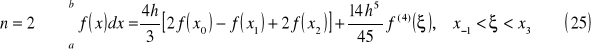
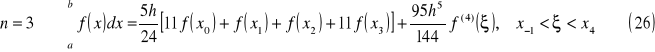
4. Numeryczne rozwiązywanie układów równań nieliniowych

Dany jest układ równań nieliniowych z n niewiadomymi

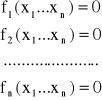
który możemy zapisać w postaci wektorowej

f(x)=0

gdzie:

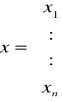
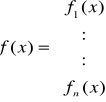
O funkcjach fi(x₁...x_n) dla i = 1, 2, ..., n zakładamy, że mają ciągłe pochodne pierwszego rzędu w pewnym obszarze zawierającym odosobniony pierwiastek układu równań. Niech

x^(k) = {x₁^(k), ..., x_n^(k)}

będzie k-tym przybliżeniem pierwiastka a = {a₁, ..., a_n} równania.

Dokładną wartość pierwiastka wyraża wzór a = x^(k) + ε^(k)

Gdzie
jest błędem pierwiastka przybliżonego
. Skoro istnieje ciągła pochodna funkcji f(x) możemy zapisać:

Zastępując błąd
przyrostem
i porównując prawą stronę powyższego wyrażenia do zera otrzymujemy równanie liniowe:

Wzór ten stanowi zapis rekurencyjny dla metody Newtona w postaci macierzowej.

Pochodna f'(x) jest macierzą Jakobiego

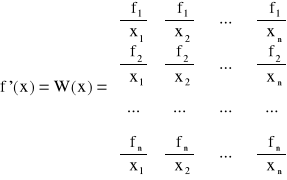
Przyjmując, że
jest macierzą nieosobliwą możemy równanie liniowe przekształcić do postaci:

stąd przyjmując dowolną wartość
otrzymujemy ciąg kolejnych przybliżeń pierwiastka równania
uzyskanych metodą Newtona.

5. Metoda Eulera rozwiązywania równań różniczkowych I rzędu

Rozpatrzmy zadanie znalezienia funkcji y=y(t), które dla
spełnia równanie różniczkowe zwyczajne pierwszego rzędu:

(7)

oraz warunek początkowy

y(a)=y₀ (8),

gdzie f jest daną funkcją dwu zmiennych. Warunek wystarczający istnienia i jednoznaczności rozwiązania zadania (7) oraz (8) jest warunek ciągłości funkcji f(t,y)

Metoda ta rzadko jest używana w praktyce, natomiast ze względu na jej prostotę, zostanie przedstawiona w celu zobrazowania i zrozumienia technik stosowanych w bardziej zaawansowanych metodach, pomijając przy tym złożone działania matematyczne. Przedmiotem rozważań będzie poniższe równanie.

, gdzie
oraz y(a)=a (10)

Na rozwiązanie powyższego zagadnienia będziemy obliczać przybliżone wartości funkcji yi=y(ti), gdzie ti=a+ih, h=(b-a)/N, dla którego i=(0,1, ..., N), gdzie ti nazywane są punktami węzłowymi, natomiast h odległością między nimi.

Rozwiniemy y(t) w szereg Taylora w celu wyprowadzenia metody Eulera. Zakładając, że y(t) jest jedynym rozwiązaniem (10) oraz posiada drugą pochodną, która jest ciągła w przedziale [a, b] wówczas dla każdego i=1, 2, ..., N.

Wykorzystując powyższe założenia możemy zapisać:
(11), gdzie

Oznaczamy h=t_i+1-t_i, wówczas otrzymujemy:

(12)

Użyjemy podstawienia y'(t)=f(t, y), wówczas otrzymujemy:
(13)

Zapisując ω_i≈y(t_i) oraz pomijając błąd przybliżenia otrzymujemy ω_i+1=ω_i+hf(t_i, ω_i) (14)

Powyższy wzór nazywamy metodą Eulera - wzór ten nazywany jest inaczej równaniem różniczkowym, gdyż można zapisać:

(15)

Aby wyznaczyć wartość szukanej funkcji y(x) w następnym kroku h, wykorzystujemy poprzednią wartość funkcji oraz wielkości zmian funkcji - dzięki pochodnej. Natomiast uwzględniając błąd przybliżenia wzór (13) przyjmuje postać:

, gdzie
(16)

Lokalny błąd dyskretyzacji τ_i+1(h)

(17)

dodatkowo możemy określić krok h, dla którego błąd lokalny jest mniejszy od zadanej dokładności δ

, gdzie

Globalny błąd dyskretyzacji g(x)

g(t)= ω(t)-y(t) (19)

Dla wybranego punktu t_i możemy zapisać: g_i=ω_i-y(t_i) (20), wówczas

, gdzie L- liczba Lipschnitz`a

6. Rozwiązywanie równań różniczkowych wyższych rzędów

---