SZEREGI
Def. Szeregiem (od n=1 do ∞ z an) nazywamy ciąg (Sn).
Sn - ciąg sum częściowych szeregu (od n=1 do ∞ z an)
Def. Mówimy, ze szereg (od n=1 do ∞ z an) jest zbieżny jeśli zbieżny jest ciąg sum częściowych (Sn). W przeciwnym wypadku mówimy, że szereg jest rozbieżny.
Jeżeli ciąg (Sn) jest zbieżny to jego granicę ![]()
nazywamy sumą szeregu (od n=1 do ∞ z an)
Tw. Warunek konieczny zbieżności szeregu. Jeżeli szereg (suma od n=1 do ∞ z an jest zbieżny, to (n→∞) lim an=0
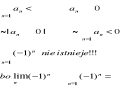
Warunek konieczny zbieżności szeregu nie jest warunkiem wystarczającym !!!
![]()
Szereg harmoniczny rozbieżny,
mimo, że ![]()
![]()
Zbieżny dla α > 1, rozbieżny dla α ≤ 1.
SZEREG DIRICHLETA
![]()
SZEREGI O WYRAZACH NIEUJEMNYCH.
Tw. Kryterium porównawcze (KP). Jeżeli 0 ≤ an ≤ bn, n > N, to:
ze zbieżności szeregu (od n=1 do ∞ z bn) wynika zbieżność szeregu (od n=1 do ∞ z an)
z rozbieżności szeregu (od n=1 do ∞ z an) wynika rozbieżność szeregu (od n=1 do ∞ z bn)
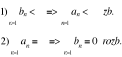
0 ≤ an ≤ bn =>
sn = a1 + an
Sn = b1 + bn sn ≤ Sn ≤ M
Przykład 1):
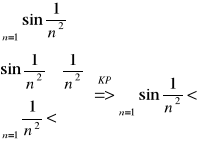
Przykład 2)
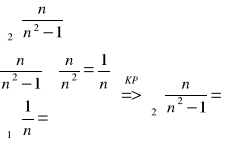
Wniosek z KP (kryterium porównawczego)
Niech an ≥ 0, bn > 0 dla n > N, (n→∞)lim an/bn=g
Jeżeli:
q ≠ 0, ∞, to szeregi an i bn są albo oba zbieżne albo oba rozbieżne
q = 0, to
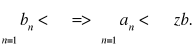
q = ∞, to
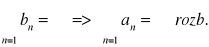
Tw. KRYTERIUM d'ALEMBERTA (ilorazowe)
Niech an > 0, n ∈ N, ![]()
Jeżeli q < 1 to szereg (od n=1 do ∞ z an) < ∞ zbieżny
q > 1, to szereg (od n=1 do ∞ z an) = ∞ rozbieżny
Tw. KRYTERIUM CAUCHY'EGO (pierwiastkowe)
Niech an ≥ 0, n > N, ![]()
Jeżeli q < 1 to szereg ∑an jest zbieżny ∑an < ∞
Jeżeli q > 1 to szereg ∑an jest zbieżny ∑an = ∞
Def. Szereg (od n=1 do ∞ z an) nazywamy szeregiem BEZWZGLĘDNIE ZBIEŻNYM, jeżeli zbieżny jest szereg (od n=1 do ∞ z |an|) (z modułów)
Tw. Szereg bezwzględnie zbieżny jest zbieżny
![]()
Def. Szereg zbieżny, ale nie zbieżny bezwzględnie, nazywamy szeregiem WARUNKOWO ZBIEŻNYM.
Jeżeli szereg (od n=1 do ∞ z |an|) < ∞ => szereg (od n=1 do ∞ z an) jest bezwzględnie zbieżny
Jeżeli szereg (od n=1 do ∞ z |an|) = ∞ => szereg (od n=1 do ∞ z an) może być zbieżny lub rozbieżny
Jeżeli szereg (od n=1 do ∞ z |an|) = ∞ ∧ szereg (od n=1 do ∞ z an) < ∞ jest warunkowo zbieżny
![]()
Def. Szereg w postaci:
![]()
lub
nazywamy szeregiem naprzemiennym jeżeli spełnione są warunki:
an > 0
(n→∞) lim an = 0
(an) jest ciągiem malejącym.
Tw. KRYTERIUM LEIBNITZA. Szereg NAPRZEMIENNY jest zbieżny, jeżeli:
1) ![]()
2) ![]()
rozbieżny
3) ![]()
nie jest zbieżny bezwzględnie.
![]()
SZEREG Z MODUŁÓW
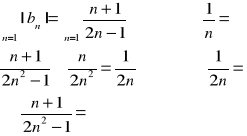
RÓWNANIA RÓŻNICZKOWE
Równaniem różniczkowym zwyczajnym rzędu pierwszego nazywamy równanie postaci F(x,y,y')=0.
Rozwiązanie równania różniczkowego F(x,y,y')=0 nazywamy dowoloną funkcję, która spełnia to równanie.
Równanie liniowe jednorodne: y'+yp(x)=0
Równanie różniczkowe liniowe rzędu 2 o stałych współczynnikach: y''+p1y'+p2y=f(x)
Transformacja Laplace'a
Def. Funkcję zespoloną f(t) zmiennej rzeczywistej nazywamy oryginałem, jeśli spełnione są warunki:
Funkcja w punkcie f(t) i f'(t) są przedziałami ciągłymi w przedziale <0,∞).
Funkcja f(t) = 0 dla t < 0
Istnieją stałe m, λ0 takie, że |f(t)| ≤ Me do potęgi(λ0t) , t∈R
Transformacją Laplace'a nazywamy przyporządkowanie oryginałowi f(t) funkcji zespolonej F(s), gdzie s ∈ C określonej wzorem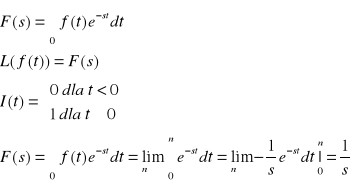
Własności transformacji Laplace'a:
L ( C1 f1 (t) + C2 f2 (t) = C1 L (f1 (t) )+C2 (f2 (t))
L (f' (t)) = s L (f (t)) - f (0+)
L (f'' (t)) = s2 L (f (t)) - s f (0+) - f' (0+)
RACHUNEK RÓŻNICZKOWY WIELU ZMIENNYCH
Sąsiedztwo punktu (a,b) to U(a,b)\{(a,b)}
S(a,b)={(a,y) : 0 < d ((x,y)
Zbiór ograniczony. Zbiór D nazywamy zbiorem ograniczonym jeżeli istnieje kula otwarta K((0,0), r) taka, że DcK((0,0), r) (to nie może być prosta)
Punkt skupienia zbioru. Punkt (a,b) jest punktem skupienia zbioru D jeżeli w każdym sąsziedztwie punktu (a,b) znajduje się element (punkt) zbioru D.
Punkt wewnętrzny zbioru (a,b) jest punktem wewnętrznym zbioru D jeżeli istnieje otoczenie punktu (a,b) U(a,b) ⊂ D
Zbiór otwarty to taki zbiór, którego każdy punkt jest punktem wewnętrznym.
Domknięcie zbioru to suma mnogościowa obu zbiorów D
Krzywą przestrzeni R2 (krzywą płaską) nazywamy zbiór punktów (x,y), których współrzędne określone są równaniami:
![]()
t ∈ <α, β>, gdzie x(t) i y(t) są funkcjami ciągłymi w <α, β>
Zbiór spójny to zbiór, którego każde 2 punkty można połączyć krzywą całkowicie zawartą w tym zbiorze.
Obszar to zbiór otwarty i spójny.
Def. Mówimy, że ciąg punktów ((xn, yn)) jest zbieżny do (x0, y0) ciąg odległości (d((xn, yn), (x0, y0)) jest zbieżny do 0.
Twierdzenie: ![]()
Def. Punkt skupienia D - f: R2 ⊃ D → R, (x0,y0) ∈ D
Funkcja f jest ciągła w punkcie (x0,y0), jeżeli
![]()
Funkcja f jest ciągła w zbiorze, jeżeli jest ciągła w każdym punkcie tego zbioru.
Suma funkcji ciągłych jest funkcją ciągła.
Różnica funkcji ciągłych jest funkcją ciągłą.
Iloraz funkcji ciągłych jest funkcją ciągła poza miejscami zerowymi mianownika.
Złożenie funkcji ciągłych jest funkcją ciągłą.
Własności funkcji ciągłych:
Funkcja ciągła w obszarze domkniętym i ograniczonym jest ograniczona
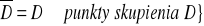
Funkcja ciągła w obszarze domkniętym i ograniczonym przyjmuje wartość najmniejszą i największą.
Jeżeli funkcja f jest ciągła w obszarze domkniętym i ograniczonym
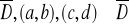
to funkcja f przyjmuje wartości pośrednie pomiędzy f(a,b) i f(c,d)
f. R2 ⊃ D → R, (a,b) ∈ D
ϕ(x)=f(x,b)
![]()
Def. Skończoną granicę ![]()
nazywamy pochodną cząstkową funkcji f względem zmiennej x w punkcie (a,b) i oznaczamy f'x(a,b) lub ![]()
Z=f(x,y) Z'x(a,b)
Def. Skończoną granicę ![]()
nazywamy pochodną cząstkową funkcji f względem zmiennej y w punkcie (a,b) i oznaczamy f'y(a,b) lub ![]()
Z'y (a,b)
Def. Mówimy, że funkcja f jest różniczkowalna w punkcie (a,b), jeżeli istnieje otoczenie tego punktu u(a,b) takie, że dla każdego punktu (a+h, b+k) ∈ U(a,b) ![]()
gdzie A I B są stałymi niezależnymi od przyrostu h I k, ![]()
H jest funkcją spełniającą warunek ![]()
Tw. Funkcja różniczkowalna w punkcie (a,b) jest w tym punkcie ciągła.
Tw. Jeżeli funkcja f jest różniczkowalna w punkcie (a,b) to istnieją pochodne cząstkowe f'x(a,b) I f'y(a,b)
EKSTREMA FUNKCJI
Niech funkcja z=f(x,y) będzie określona w pewnym obszarze D. Mówimy, że funkcja f(x,y) ma w punkcie (x0, y0) należącym do obszaru D maksimum ≤ lokalne słabe (minimum ≥ lokalne słabe), jeżeli istnieje takie sąsiedztwo S punktu (x0, y0), że dla każdego punktu (x,y) należącego do sąsiedztwa S jest spełniona nierówność (słaba)
![]()
lub ![]()
Warunek konieczny na istnienie ekstremum.
Jeżeli funkcja f ma pochodne cząstkowe w punkcie (a,b) względem X I względem y f'x(a,b) I f'y(a,b) oraz ma w tym punkcie ekstremum lokalne, to f'x(a,b)=0 I f'y(a,b)=0
Warunek wystarczający na istnienie ekstremum.
Jeżeli funkcja f ma w otoczeniu U(a,b) punktu (a,b) ciągłe pochodne cząstkowe rzędu drugiego, to:
Jeżeli
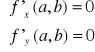
oraz 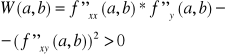
to funkcja f ma w (a,b) ekstremum lokalne właściwe, przy czym jest to maksimum jeśli ![]()
a minimum jeśli ![]()
Jeżeli W(a,b) < 0 to funkcja f nie ma w punkcie (a,b) ekstremum.
CAŁKI PODWÓJNE
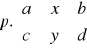
Funkcja f jest ciągła w p.
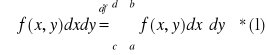
lub
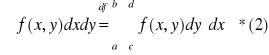
W nawiasach [ ] jest F(y)
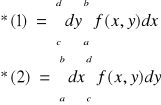
Obszar D normalny względem osi OX 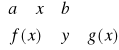
gdzie f I g są funkcjami ciągłymi w <a,b> oraz f(x) ≤ g(x) dla x ∈ <a,b>
Obszar D normalny względem osi OY 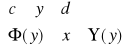
D - norm. wzgl. OX
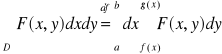
Obszar D nazywamy regularnym, jeżeli można go przedstawić w postaci skończonej sumy obszarów normalnych względem osi OX lub względem osi OY takim, że obszary te mają rozłączne wnętrza.

Tw. Niech obszar D będzie obrazem obszaru Δ poprzez odwzorowanie (*), f będzie funkcją ciągłą w D, wtedy:
![]()
g - jakobien przekształcenia (*)
Współrzędne biegunowe, to para liczb r I Φ określająca położenie punktu P na płaszczyźnie.
r - promień wodzący, który łączy punkt P z pewnym stałym punktem, zw. biegunem współrzędnych.
Φ - kąt pomiędzy promieniem wodzącym r I pewnym ustalonym promieniem o wierzchołku w biegunie, zw. osią biegunową.
Jakobian (wyznacznik Jacobiego), to wyznacznik macierzy zbudowanej z pierwszych pochodnych cząstkowych n funkcji danych (funkcje n zmiennych).
1
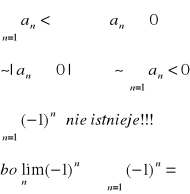
![]()
![]()
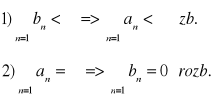
![]()
![]()
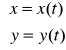
Wyszukiwarka