Zasada zachowania pędu:
Weźmy pod uwagę układ n punktów materialnych. Między nimi mogą działać siły wewnętrzne. Również mogą być przyłożone jakieś siły zewnętrzne. Napiszmy dla każdego punktu równanie wyrażające II zasadę Newtona, oznaczając wskaźnikiem „w” siły wewnę, a „z”z siły zewne.
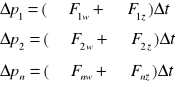
Ponieważ środek masy ma takie przyspieszenie jak gdyby wszystkie masy były w nim skupione i wszystkie siły doń przyłożone, więc dodając wszystkie powyższe równania otrzymalibyśmy dla środka masy równanie:
![]()
Po prawej stronie mamy sumę geometryczną wszystkich sił działających na poszczególne punkty. Między nimi są siły wewn i zewne . Lecz siły wewne według II zasady Newtona są parami równe i mają znaki przeciwne. Ich suma geometryczna równa się zeru. Pozostają tylko siły zewnętrzne:
![]()
Gdy sił zewne nie ma, tzn gdy układ jest odosobniony prawa strona tego równania jest zerem:
![]()
Po lewej stronie mamy wielkość oznaczającą przyrost sumy geometrycznej pędów. Jeżeli przyrost jakiejś wielkości równa się zeru, to znaczy, że jest stała:
![]()
Równanie to wyraża tzw. zasadę zachowania pędu dla układu odosobnionego.
Moment pędu.
Wektor L prostopadły do płaszczyzny przechodzącej przez punkt nieruchomy O i wektor p. Jego długość: L = h * p = h * m V, gdzie h jest ramieniem wektora p. Łącząc dowolny punkt prostej na której leży wektor p z punktem O odcinkiem r o zwrocie od O do p możemy również napisać: ![]()
Drgania harmoniczne.
W środku spiralnie zwiniętej, napiętej sprężyny, której dwa końce są umocowane nieruchomo, umieszczona jest kula o masie m. Położenie w którym ta kulka znajduje się w spoczynku - położenie równowagi. Umieśćmy początek układy współrzędnych w punkcie, gdzie się znajduje wówczas środek kulki. Oś x poprowadźmy poziomo na prawo. Powstanie siła usiłująca cofnąć z powrotem kulkę. Jeżeli kulkę puścimy, przesunie się ona szybko w lewo lecz z powodu rozpędu przejdzie poza położenie równowagi. Lewa sprężyna zostanie ściśnięta, prawa - rozciągnięta. Powstanie siła działająca w prawo. Kulka wkrótce się zatrzyma, potem przesunie się w prawo, znowu z rozpędem przejdzie poza położenie równowagi. Zacznie drgać. Siła tu działająca jest proporcjonalna do wychylenia x kulki z położenia równowagi i jest przeciwnie skierowana niż to wychylenie:
F=-kx : Minus oznacza że siła F i wychylenie x mają przeciwne zwroty: F=ma => ma= -kx
Dzieląc obie strony przez m i oznaczając iloraz k / m przez ω2 możemy zapisać: a = - ω2 x. Równanie to wyraża zależność między przyspieszeniem a i wychyleniem x. Przyspieszenie w rozważanym ruchu jest proporcjonalna do wychylenia i ma znak przeciwny. Każdy ruch mający taką własność nazywamy drganiem harmonicznym. Rys 2.
Środek masy.
Weźmy pod uwagę układ składający się z dwóch punktów 1,2 o masach m1, m2. Poprowadźmy tak układ współrzędnych, aby oba punkty leżały na osi X. Niech ich odcięte będą X1 i X2. Zwróćmy uwagę na punk S dzielący stale odległości punktów 1 i 2 w stosunku odwrotnym do ich mas. Punkt taki nazywamy środkiem masy dwóch rozpatrywanych punktów. Suma pędów obu punktów równa się pędowi, jaki by miał środek ich masy, gdyby w nim obie masy zostały skupione.
Spadek swobodny.
Wielkość przyspieszenia g w przybliżeniu wynosi 9,81 m / s. Równania ruchu ciała swobodnie spadającego będą: V=gt ; S=1/2 gt2
Jeżeli wyrugujemy z tych równań czas, otrzymamy wzór dający zależność końcowej prędkości od wysokości spadania.
![]()
Jeżeli ciało zostanie rzucone w dół z początkową prędkością V0 to równania jego ruchu będą: V=V0 + gt ; S = V0 t + ½ gt2
Rzut poziomy.
Rozpatrujemy rzut ciała rzuconego poziomo z niewielką wielkością. Pole ciężkości na niewielkiej przestrzeni jest jednorodne. Linie jego są pionowe i równoległe. Przyspieszenie siły ciężkości jest stałe w całym obszarze. Poprowadźmy tak układ współrzędnych, aby jego początek 0 znajdował się w punkcie z którego ciało zostaje wyrzucone z prędkością V0. Oś odciętych prowadzimy w kierunku początkowej prędkości ciała, oś rzędnych pionowo w dół. Ruch ciała będzie ruchem złożonym:
1-z ruchu jednostajnego na mocy bezwładności w kierunku osi OX ; 2-z ruchu jednostajnie przyspieszonego w dół z przyspieszeniem g
x = V0 t ; y = 1/ 2 gt2
Rugując z tych równań czas t otrzymujemy zależność y od x, czyli równanie określające kształt toru:
![]()
; ![]()
; ![]()
Jest to równanie paraboli, a więc ciało rzucone poziomo porusza się po paraboli.
Drgania tłumione.
Jeżeli nie doprowadzamy do układu drgającego energii, drgania stopniowo zanikają, ich amplituda maleje i wreszcie układ przechodzi w stan spoczynku. W przypadku drgań prócz siły proporcjonalnej do wychylenia działającej ku środkowi ruchu działa jeszcze siła hamująca ruch. Siła hamująca jest proporcjonalna do prędkości ruchu drgającego i jest skierowana przeciwnie do chwilowej prędkości punktu. Na punkt wychylony OXZ położenia równowagi będą działały dwie siły, jedna proporcjonalna do wychylenia druga - do prędkości.
![]()
![]()
(V)
![]()
mnożymy to przez m / *m
![]()
; ![]()
; ![]()
![]()
-jest to równanie różniczkowe drgań tłumionych.
Fale poprzeczne.
Wyobraźmy sobie układ kulek np.: żelaznych na nitkach i połączonych gumową tasiemką. Gdy pierwszą kulkę wprawimy w ruch wahadłowy, np.: w prawo i lewo - kulka pociągnięta przez taśmę zacznie się też poruszać na prawo. Wychylenie przenosi się coraz dalej. Wzdłuż układu biegnie fala. Gdy więc pierwsza kulka będzie drgać ruchem: y0=Asinωt, to równanie ruchu następnej kulki będzie y1=Asin(ωt-φ), trzeci y2=Asin(ωt-2φ). Odległość między punktami nazywamy długością fali. Jeżeli weźmiemy dwa punkty o odciętych x1 i x2 i równania ich drgań y1=Asin(ωt-kx1) i y2=Asin(ωt-kx2),to gdy ich fazy dla tej samej chwili t będą się różnić o kąt 2Π, odległość między nimi będzie długością fali. Różnica ich faz jest (ωt-kx1)- (ωt-kx2)= 2Π => k(x2-x1)= 2Π. Odległość między punktami x2-x1=λ => k=2Π/ λ. Równanie ruchu fali, możemy zapisać: (ω=2Π/T):
![]()
V=λ/T - prędkość fali.
Energia kinetyczna.
Energię, jaką układ posiada dzięki prędkościom swoich części, nazywamy energię kinetyczną. W szczególności ciało poruszające się z pewną prędkością względem Ziemi może wykonać pewną pracę, która będzie miarą posiadanej przez to ciało energii kinetycznej. Niech wagon o masie m porusza się z prędkością V. Aby obliczyć jego energię przyłóżmy w kierunku przeciwnym jego ruchowi siłę stałą F. Ruch ciała będzie wtedy jednostajnie opóźniony z opóźnieniem określonym równaniem: a = F / m. Droga przebyta przez to ciało A do chwili, gdy się ona zatrzyma:
S - Vt - ½ at2 Ponieważ prędkość końcowa jest równa zeru to:
0 = V - at
![]()
Wzór na wykonaną przez siłę zewnętrzną pracę będzie:
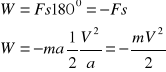
Znak minus wskazuje że praca będzie wydana prze układ A więc zapas pracy ciała rozpędzonego czyli jego energia kinetyczna:
Ek = mV2 / 2
Moment bezwładności.
Mamy n cząsteczek z których wszystkie poruszają się po okręgach około wspólnej osi OO. Gdy na cząstkę działa siła o memencie M względem osi obrotu to jej kręt wzrasta. Przyrost krętu: ΔL=r Δp=rm ΔV=M Δt, lecz V=r ω, zatem ΔV=rΔω, gdzie ω jest prędkością kątową, otrzymujemy mrΔω=MΔt. Gdy na punkt działa siła o momencie odmiennym od zera, prędkość kątowa cząstki wzrasta. Jakiemu warunkowi musiałaby odpowiadać inna cząstka o masie m1 znajdująca się w odległości T1 os osi obrotu, aby przy działaniu siły o takim samym momencie uzyskiwała w takim samym czasie taki sam przyrost prędkości kątowej. Jeżeli do się znaleźć cząstkę odpowiadającą takiemu warunkowi, to masy takich cząstek będziemy nazywali równoważnymi, ze względu na obrót dookoła osi. Przyrost krętu tej drugiej cząstki: m1r12Δ ω. Jeżeli działa na tę cząstkę siła o momencie M to:
m1r12Δω=MΔt. Przyrost prędkości kątowej Δω ma być taki sam jak poprzednio. WZÓR 7. Iloczyn masy cząstki przez kwadrat jej odległości od osi obrotu nazywamy momentem bezwładności cząstki. Dwie cząstki są równoważne ze względu na obrót dookoła osi, gdy ich momenty bezwładności są równe.
Praca w polu grawitacyjnym.
Podnosząc ciało do góry, np.: od punktu A do B, wykonujemy pracę przeciwko sile ciężkości. Energia układu złożonego z tego ciała i Ziemi rośnie. Wartość wykonanej pracy zależy od punktu początkowego i końcowego drogi, nie zależy od drogi po której przenosimy ciało. Ponieważ droga przejścia od punktu A do B jest obojętna, to dla obliczenia pracy możemy wybrać taką drogę aby to obliczenie było możliwe najprostsze. Jako drogę przejścia obieramy odcinek lini prostej AB=l, a więc po równi pochyłej. Oznaczając kąt nachylenia tego odcinka do poziomu przez α na pracę wykonaną otrzymamy wzór:
W = Pl cos (900 - λ ) = Pl sin λ
Oznaczając przez h1 wysokość punktu A nad powierzchnią Ziemi, wysokość B - przez h2 otrzymamy wzór:
W = P (h2 - h1)
Praca wykonana przy podnoszeniu ciała ciężkiego nie zależy od drogi po której ciało zostało podniesione, ani od położenia punktów początkowego i końcowego, lecz zależy jedynie od różnicy wysokości poziomów, na których znajdują się punkt początkowy i końcowy. Jeżeli różnica poziomów jest duża, wtedy trzeba uwzględnić zmianę ciężaru w polu grawitacyjnym.
![]()
![]()
; ![]()
R oznacza promień kuli ziemskiej, G - stałą grawitacji.
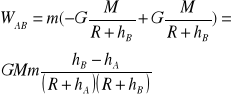
Praca jest zależna tylko od wysokości hB i hA nad powierzchnią Ziemi. Gdy hB i hA są małe wobec promienia Ziemi B, to w mianowniku możemy je opuścić:
![]()
A więc obojętną jest rzeczą, po jakiej drodze wznosi się ciało o ciężarze P. Praca zależy tylko od różnicy potencjałów między powierzchniami ekwipotencjalnymi znajdującymi się w odległości hA i hB od powierzchni Ziemi.
Prawa Keplera.
1). Tory planet są elipsami, w ognisku każdej z tych elips znajduje się słońce.
2). Promienie wodzące planet wychodzące ze Słońca (promieniem wodzącym planety będzie odcinek prostej łączący środek Słońca ze środkiem planety) zakreślają w równych czasach równe pola.
3). Kwadraty czasów obiegu planet mają się do siebie jak sześciany ich środków odległości od Słońca.
Zasada zachowania energii.
Gdy układ wydaje pracę (w<0), wtedy E2-E1 < 0 stąd E2 <E1, a więc energia w stanie końcowym jest mniejsza od energii w stanie początkowym o ilości wydanej pracy. Przy wydawaniu pracy energia układu maleje. Stąd wynika niemożliwość zbudowania perpetum mobile tj. takiej maszyny czy układu, który by wiecznie wydawał pracę. Według zasady zachowania energii musiałaby maleć energia układu, który by stale wydawał pracę i wreszcie musiałaby się wyczerpać. Gdy na układ nie działają żadne siły zewnętrzne układ nazywamy odosobnionym albo izolowanym. Praca wtedy nie może być ani pobierana, ani wydawana (W=0)
E2 - E1 = 0 ; czyli E2 = E1 = const
Energia układu w jakimkolwiek stanie późniejszym równa się energii tegoż układu w stanie początkowym. Możemy więc dla układu odosobnionego napisać: E=const. Gdzie E jest całkowitą energią mechaniczną układu, To równanie nazywamy zasadą zachowania energii.
Zasada Huggensa.
Każdy punkt do którego dochodzi powierzchnia fazowa (nazywana często czołem fali), można uważać za źródło rozchodzącej się na wszystkie strony kulistej fali cząstkowej. Powierzchnię fazową w nowym położeniu tworzy powierzchnia styczna, wszystkich tych fal. Rys 6. Rozchodzenie się fal kołowych wg zasady Huggensa.
Superpozycja.
Dwie fale rozchodzące się w pewnym ośrodku spotykają się nie przeszkadzając sobie wzajemnie. Jeżeli w jakimś środowisku np: w wodzie, rozchodzą się fale wychodzące z dwóch lub więcej punktów, to po dojściu tego samego punktu powierzchni wody wywołają jego wychylenie, które będzie sumą algebraiczną wychyleń wywołanych przez poszczególne fale. Fala będą przechodzić jedna przez drugą, po czym po dojściu do gładkiej powierzchni będą biec niezmienione.
Interferencja fal.
Specjalnie ważny przypadek stanowią drgania wywołane przez dwie fale mające takie same amplitudy i częstości, a różniące się tylko fazami. Jedna fala dochodząc do pewnej cząstki pobudza ją do drgania harmonicznego y1=Asin(ωt-φ1), druga zaś y2=Asin(ωt-φ2). Wychylenie wypadkowe cząstki będzie sumą ich obu: y=y1+y2
![]()
B p
y = B sin (ωt - φ)
A więc drgania harmoniczne o tej samej częstości. Amplituda tego drgania B zależy od różnicy faz (φ1- φ2). Gdy φ2= φ1 tzn. gdy fale spotykają się w zgodnych fazach, B=2A, amplituda drgania wypadkowego równa się podwójnej amplitudzie każdego z drgań składowych. Gdy φ2= φ1+Π, cos (φ2- φ1/2 )= 0
B=0 to cząstka nie drga zupełnie.
Fale stojące.
Jeżeli jeden koniec linki wprawimy w ruch harmoniczny, to wzdłuż linki będą biec fale ku drugiemu końcowi. Jeżeli oba końce linki wprawimy w ruch harmoniczny tej samej częstości to powstaną dwa ciągi fal: jeden biegnący w lewo, drugi w prawo. Obraz ten szybko się zmieni. Nie będzie już widać posuwających się fal, linka podzieli się na odcinki drgające, oddzielone na wskutek nakładania się obu fal. Weźmy równania fali biegnącej w kierunku ujemnym i dodatnim osi X: y1= Asin(ωt-kx), y2= Asin(ωt-kx). Wychylenie dowolnego punktu linii będzie sumą algebraiczną obu wychyleń: y1 + y2
![]()
y=Bsin ωt
Dudnienia.
Gdy dwie fale dochodzące do tego samego punktu różnią się nieco ale niewiele częstotliwością. Weźmy pod uwagę drgania: y1= Asinω1t, y2= Asinω2t, gdzie ω1=/= ω2 (bardzo niewiele się różnią). Drgania wypadkowe y=y1+y2 =>
![]()
y=Bsinωt. Dla zilustrowania weźmy przykład dwóch drgań mało się różniących częstością. Niech jedno drganie ma częstość f2=1001, drugie f1=999. W przedziale:
![]()
![]()
- amplituda raz osiągnie max dla t=0 )B=2A). W przedziale:
![]()
czyli gdy:
![]()
amplituda również raz osiągnie max dla t=1/2 s. To samo będzie się następnie powtarzać w każdej ½ sekundy. Zatem amplituda osiągnie dwa razy w sekundzie max i również dwa razy w sekundzie będzie się równała zeru.
I zasada termodynamiki.
Każde ciało dzięki ruchom molekuł ma pewien zapas energii kinetycznej, dzięki zaś siłom działającym między molekułami - pewien zapas energii potencjalnej. Suma tych energii stanowi tzw. energia wewne ciała U. Ogrzewamy ciało doprowadzając pewną ilość ciepła Q oraz wykonujemy nad nim pewną pracę W. Energia doprowadzona w postaci pracy i ciepła musi pozostać w ciele, powiększając jego energię wewne. Jeżeli energia wewne początkowa ciała była U1, to wzrośnie do U2.
W + Q = U2 - U1
Ciepło właściwe.
Ilość ciepła potrzebna do ogrzania 1 kg danej substancji o 1 stopień nazywa się ciepłem właściwym tej substancji:
C = Q / m*Δt - średnie ciepło właściwe [c] = kcal / kg * deg
C = Q / m(t2 - t1)
Równanie Clapeyrona dla gazu doskonałego.
Gdy oznaczamy przez M masę jednego kilomola gazu, to dowolna jego masa m będzie zawierała m/M kilomoli,a więc stała po prawej stronie równania stanu będzie (m/M)R. Zatem dla dowolnej masy m gazu możemy zapisać równanie.
pV = m/M *RT
Dla kilomola gazu idealnego zapisujemy: pV=RT
Prawo Pascala.
Jeżeli na ciecz będącą w równowadze działają jedynie ciśnienia na powierzchnię zewnętrzną, wówczas ciśnienie wewnątrz cieczy jest wszędzie jednakowe i równe ciśnieniu zewnętrznemu.
Rozkład Maxwella.
Istnieje pewien przedział prędkości Vp, Vp+ΔV najwięcej prawdopodobny tzn. największa liczba molekuł spośród wszystkich IV molekuł ma prędkości zawarte w tym przedziale prędkość to jest związana z temperaturą gazu:
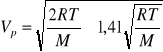
gdzie M oznacza masę 1 kilomola. Stosunek prędkości V molekuł do najprawdopodobniejszej prędkości Vp: U=V/Vp. Dla molekuł których prędkości zawarte są w przedziale V, V+ ΔV powyższe stosunek będzie zawarty w przedziale U, U+ ΔU. Liczba takich molekuł wg Maxwella jest
![]()
gdzie e=2,71828
Odłóżmy na osi odciętych u, zaś na osi rzędnych ΔN / ΔNu
Krzywa ma max dla u=1. Ułamek ΔN/N całkowitej liczby molekuł o prędkości zawartych w przedziale V, V+ ΔV daje iloczyn
![]()
Najwięcej molekuł ma prędkości zbliżone do najprawdopodobniejszej prędkości. Prędkość średnia Vśr jest większa od najprawdopodobniejszej.
![]()
Prędkość średnia kwadratowa jeszcze nieco większa.
![]()
Ciecz doskonała. Lepkość (tarcie wewnętrzne ) Struga
Gdy do jednego z naczyń połączonych wlejemy więcej cieczy niż do innych, tak aby powierzchnia swobodna znajdowała się w nim na wyższym poziomie, natychmiast ciecz zacznie płynąć do naczynia, gdzie powierzchnia swobodna znajduje się wyżej, do naczynia o niżej położonej powierzchni swobodnej. Gdy ciśnienie w tej samej płaszczyźnie poziomej w cieczy jest wszędzie jednakowe, ciecz jest w równowadze. Różnica ciśnień zaś natychmiast wywołuje ruch. Przy ruchu cieczy przez rurę łączącą naczynia cząstki cieczy poruszają się z różnymi prędkościami. Najprędzej poruszają się cząstki znajdujące się w środku. W miarę zmniejszania się odległości od ścian płyną coraz wolniej, przy samej ścianie prędkość cząstek równa się zeru. Powodem tego zjawiska jest tarcie wewnętrzne cieczy(LEPKOŚĆ).
Jeżeli oznaczymy przez T wielkość ciśnienia stycznego, wywierającego przez warstwę 2 na warstwę 1 to ciśnienie to jest proporcjonalne do różnicy prędkości warstw, a odwrotnie proporcjonalne do ich odległości Δy, a więc:
![]()
Wprowadzamy współczynnik proporcjonalności η:
![]()
Współczynnik proporcjonalności η zależy od rodzaju cieczy i od temperatury nazywa się jej współczynnikiem lepkości. Ciecz dla której ten współczynnik η=0, nazywa się cieczą IDEALNĄ.
Jeżeli wewnątrz płynącej cieczy nakreślimy linię AB, po której poruszała się pewna cząstka cieczy to i następnie cząstki poruszające się za pierwszą będą się poruszać po tej samej drodze. Będzie to tzw. linia prądu. Za pomocą linii prądu możemy podzielić płynącą ciecz na oddzielne jakby rurki nazywane STRUGAMI. Wewnątrz każdej strugi ruch odbywa się tak jak gdyby była ona otoczona stałą ścianką.
Gaz doskonały.
Gaz który się stosuje w każdej temperaturze i pod wszelkim ciśnieniem do prawa Boyle'a i Gay-Lussaca tzn. którego zachowanie określałoby dokładnie równanie:
![]()
to gaz doskonały.
Prawo Boyle'a: W danej objętości można zmieścić większą lub mniejszą ilość gazu. Objętość i ciśnienie danej masy gazu są wielkościami odwrotnie proporcjonalnymi. Jeżeli objętość danej masy gazu m pod ciśnieniem p1 oznaczamy przez V1, zaś pod ciśnieniem p2 przez V2 to między tymi wielkościami zachodzi związek p1 V1=p2V2, ponieważ ten związek zachodzi dla dowolnych objętości gazu, to pV=const.
p / q = const ; V = m / q
Prawo Gay-Lussaca: ![]()
Wyszukiwarka