Na początek pojęcie przestrzeni probabilistycznej. Jest to nic innego, jak matematyczny model (matematyczne przedstawienie) doświadczenia losowego. Na ten model składają się trzy elementy: ![]()
. Ten pierwszy element to przestrzeń zdarzeń elementarnych, albo inaczej zbiór możliwych wyników doświadczenia. S to podzbiory zbioru ![]()
oznaczające zbiór zdarzeń. Może to być więc także pojedyncze zdarzenie spośród wszsytkich (![]()
). No i P to prawdopodobieństwo, czyli funkcja przyporządkowująca zdarzeniom szansę ich zajścia w skali od 0 do 1, czyli: ![]()
. Skoro S jest podzbiorem zbioru ![]()
, oznacza to, że możemy wykonywać działania na zdarzeniach. Na matematyce dyskretnej omówione zostały pojęcia sumy, iloczynu, różnicy. Dodatkowo jednak czasem skorzystamy z dopełnienia zbioru. Niech A będzie podzbiorem zbioru ![]()
. Wówczas A', czyli nasze dopełnienie będzie wynosiło ![]()
\ A, a graficznie:
Mówimy, że zdarzenie A pociąga zdarzenie B, gdy ![]()
(A zawiera się w B), co oznacza, że zdarzeniu A sprzyjają pewne wyniki (zdarzenia) elementarne, a zdarzeniu B sprzyjają te same plus jeszcze jakieś inne. Mówimy także, że zdarzenia A i B się wykluczają (są rozłączne - ich część wspólna jako zbiory jest zbiorem pustym, albo inaczej, że nie ma żadnego wyniku który by sprzyjał jednocześnie zdarzeniu A lub zdarzeniu B) wtedy, gdy ![]()
. Zbiór zdarzeń S, aby był zbiorem zdarzeń (ciałem zdarzeń ![]()
) powinien spełniać nastepujące trzy warunki:
1. ![]()
(cała przestrzeń powinna być zdarzeniem)
2. Jeśli ![]()
, to ![]()
3. Jeśli mamy ciąg zdarzeń, to ich suma też musi być zdarzeniem, czyli jeśli![]()
,
to ![]()
.
Kolejna ważna rzecz, z której będziemy korzystali, to aksjomaty prawdopodobieństwa. Mamy trzy:
1. ![]()
- Prawdopodobieństwo powinno być nieujemne
2. ![]()
- Zdarzenie pewne, gdzie każdy wynik mu sprzyja.
3. ![]()
- Prawdopodobieństwo sumy równe jest sumie
prawdopodobieństw, a inne zdarzenia się parami
wykluczają (![]()
.
Następne to własności prawdopodobieństwa i jest ich 5:
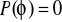
- Zdarzenie niemożliwe (prawdopodobieństwo zerowe)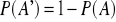
, gdzie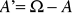
jest zdarzeniem przeciwnym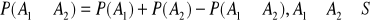
- Prawdopodobieństwo sumy dwóch dowolnych zdarzeń równy jest sumie prawdopodobieństw z uwzględnieniem korekty na część wspólną.
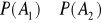
dla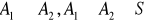
- Prawdopodobieństwo jest monotoniczne ze względu na inkluzję.Jeśli

, to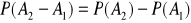
i tylko wtedy.
Teraz przejdziemy do definicji prawdopodobieństwa. Jeśli zdarzeń elementarnych jest skończenie wiele i są one jednakowo prawdopodobne, to możemy skorzystać z takzwanej klasycznej definicji prawdopodobieństwa, czyli:
![]()
Aby lepiej to zrozumieć rozpatrzmy nastepujący przykład. W portfelu mamy umieszczone w przypadkowy sposób 1000 złotych w banknotach po 200 złotych i 100 złotych. Wiadomo, że banknotów po 200 złotych jest dwa razy więcej niż banknotów po 100 złotych. Wyjmujemy losowo z portfela 3 banknoty. Jakie jest prawdopodobieństwo, że wyjęte banknoty będą łączną wartość 500 złotych ?
Wiemy, że banknotów 200 zlotowych było 4, a banknotów 100 złotowych - 2. Razem 1000 złotych. To 500 złotych, które mamy wylosować można uzyskać jedynie z banknotów 2 razy po 200 i raz po 100. Obliczamy zatem ![]()
:
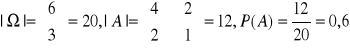
czyli 60 % !!
Rozpatrzmy teraz dyskretną przestrzeń probabilistyczną. Niech ![]()
(2 do omega to rodzina wszystkich podzbiorów). Jeśli określimy prawdopodobieństwo dla zdarzeń jednoelementowych, to: ![]()
, gdzie ![]()
.
Wtedy dla ![]()
mamy: ![]()
.
Popatrzmy na przykład zastosowania tej metody w postaci rozkładu Poissona. Powiedzmy, że mamy ![]()
, gdzie lambda to parametr rozkładu (pewna stała). Wówczas ![]()
(prawdopodobieństwo od zbioru jednoelementowego k).
Kolejne ważne zagadnienie, jakie dziś poruszymy, to prawdopodobieństwo geometryczne. Jeśli zdarzenia elementarne są podzbiorem w mierze skończonej przestrzeni ![]()
(jeśli n = 1, to miara jest długość. Dla n = 2 - pole, a dla n = 3 - objętość) i są one jednakowo prawdopodobne, to stosujemy takzwane prawdopodobieństwo geometryczne określone wzorem:
![]()
I rozpatrzmy taki przykład odnoszacy się do powyższego strwierdzenia. W trójkącie równobocznym ABC o boku a losowo wybieramy punkt D. Jakie jest prawdopodobieństwo, że trójkąt ABD ma pole nie większe niż pole trójkąta ABC?
Widać, że niektóre położenia punktów D będą sprzyjały rozpatrywanemu zdarzeniu, a niektóre nie. Ten punkt przykładowy na rysunku jest punktem sprzyjającym. Punkty niesprzyjające to będą te, które wybiegają poza prostą e (przecinająca trójkąt na pół), czyli te, które znajdują się na płaszczyźnie poprowadzonej od prostej e do punktu A. Widzimy, że te 2 trójkąty zarówno ABC, jak i BCD mają tą samą podstawę. Aby obliczyć pole wystarczy znać podstawę i wysokość. A więc ważna jest tu wysokość. I teraz jak obliczyć prawdopodobieństwo. Najlepszym sposobem będzie tu odcięcie tej prostej e. Powstanie nam trapez i trójkąt o wierzchołku A. Wystarczy wówczas podzielić pole trapezu (E) przez pole trójkąta ABC i to będzie nasze prawdopodobieństwo. Ale też istnieje drugi sposób prostszy, który polega na dostrzeżeniu, że ten nasz mniejszy trójkąt jest podobny do tego dużego ABC. I jest on podobny w skali 1:2. A pola w stosunku 1:4 (skala podobieństwa podniesiona do kwadratu), czyli 25 %. Jednakże jest to zdarzenie przeciwne, a zatem P(E) wyniesie ¾, czyli 75 %.
I na zakończenie wykładu taka uwaga. Jeśli mamy możliwość wielokrotnego powtarzania (niezależnie) doświadczenialosowego w tych samych warunkach, to możemy wyznaczyć przybliżoną wartość prawdopodobieństwa wybranego zdarzenia za pomocą wzoru:
![]()
,
gdzie n to liczba wykonanych doświadczeń, a k to liczba tych doświadczeń, w którtch zaszło zdarzenie A. Sposób ten jednak nie znajduje zastosowania w statystyce.
A
![]()
A', czyli ![]()
bez zbioru A
![]()
![]()
![]()
A B
B
A
C
D
e
E
Zdarzenia sprzyjające
Wyszukiwarka
Podobne podstrony:
Z Wykład 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Ćwiczenia 01.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 16.03.2008, Zajęcia, II semestr 2008, Techniki Internetowe
Z Wykład 29.03.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Wykład 30.03.2008, Zajęcia, II semestr 2008, Teoria informacji i kodowania
Z Wykład 02.03.2008, Zajęcia, II semestr 2008, Algorytmy i struktury danych
Z Wykład 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Wykład z dnia 10.05.2008, Zajęcia, II semestr 2008, Matematyka dyskretna i logika
Z Ćwiczenia 29.03.2008, Zajęcia, II semestr 2008, Wstęp do kryptologii
Z Ćwiczenia 15.03.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 19.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 23.02.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 06.04.2008, Zajęcia, II semestr 2008, Rachunek prawdopodobieństwa
Z Wykład 24.02.2008, Zajęcia, II semestr 2008, Teoria informacji i kodowania
Z Wykład 05.04.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Wykład 10.05.2008, Zajęcia, II semestr 2008, Analiza matematyczna
Z Ćwiczenia 01.06.2008, Zajęcia, II semestr 2008, Rachunek prawdopodobieństwa
Z Wykład 17.05.2008, Zajęcia, II semestr 2008, Algorytmy i struktury danych
Z Wykład 20.04.2008, Zajęcia, II semestr 2008, Algorytmy i struktury danych
więcej podobnych podstron