Lewa strona równania jest z definicji częstotliwością drgań f

Dla ruchu harmonicznego więc otrzymujemy
(13.8)

Jest to okres drgań masy m przyczepionej do końca sprężyny o stałej sprężystości k.

okres drgań harmonicznych T jest niezależny od amplitudy drgań A (o ile jest spełnione prawo Hooke'a). Tę właściwość drgań harmonicznych prostych zauważył Galileusz i wykorzystał ją do skonstruowania zegara wahadłowego.

45. Wahadło proste

Wahadło proste jest to wyidealizowane ciało o masie punktowej, zawieszone na cienkiej, nieważkiej, nierozciągliwej nici. Kiedy ciało wytrącimy z równowagi to zaczyna się ono wahać w płaszczyźnie poziomej pod wpływem siły ciężkości. Jest to ruch okresowy. Znajdźmy okres tego ruchu.

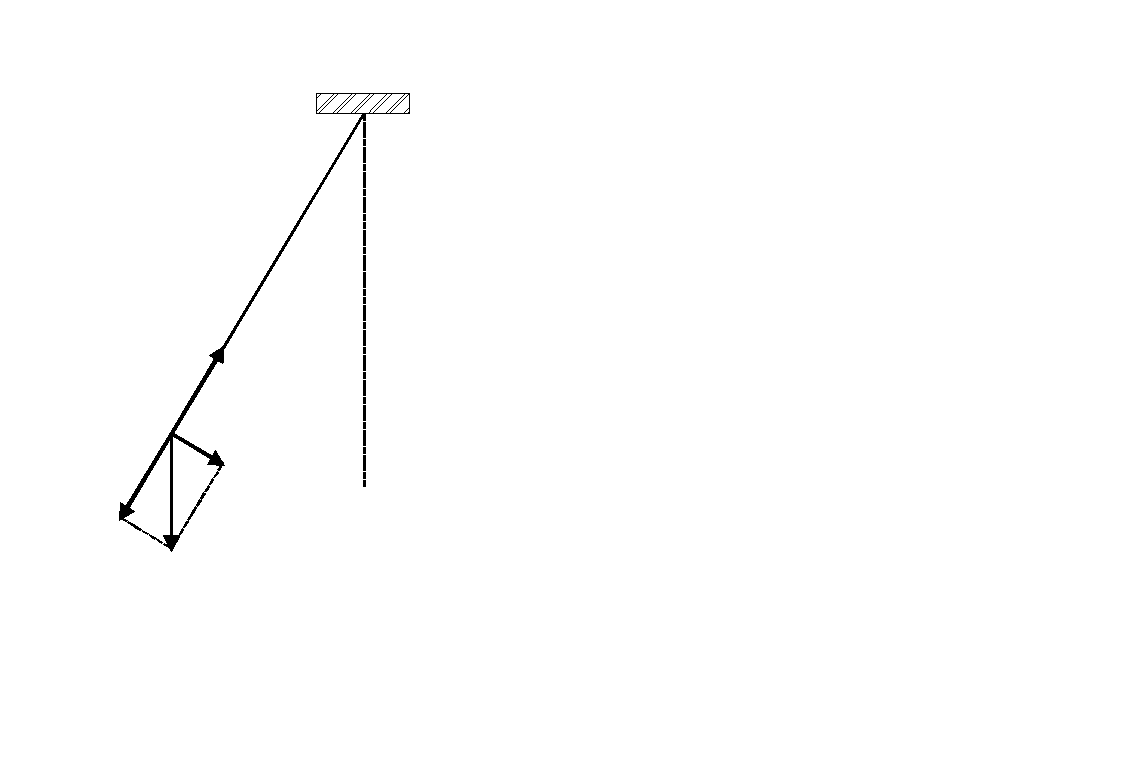
Rysunek przedstawia wahadło o długości l i masie m, odchylone o kąt θ od pionu. Na masę m działają: siła przyciągania grawitacyjnego mg i naprężenia nici N. Siłę mg rozkładamy na składową radialną i styczną. Składowa styczna jest siłą przywracającą równowagę układu i sprowadza masę m do położenia równowagi. Siła ta wynosi F = mgsinθ

siła jest proporcjonalna do sinθ, a nie do θ, więc nie jest to ruch prosty harmoniczny. Jeżeli jednak kąt θ jest mały (mniejszy niż 10°) to sinθ jest bardzo bliski θ (różnica mniejsza niż 0.5%). Przemieszczenie wzdłuż łuku (z miary łukowej kąta) wynosi x = lθ. Przyjmując zatem, że sinθ ≅ θ otrzymujemy

F jest więc proporcjonalna do przemieszczenia (ze znakiem "-"). Jest to kryterium ruchu harmonicznego. Stała mg/l określa stałą k w równaniu F = - kx. Przy małej amplitudzie okres wahadła prostego wynosi więc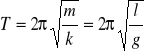

Zauważmy, że okres wahadła nie zależy od amplitudy i od masy wahadła.

Wahadło fizyczne Dowolne ciało sztywne zawieszone tak, że może się wahać wokół pewnej osi przechodzącej przez to ciało nazywamy wahadłem fizycznym.

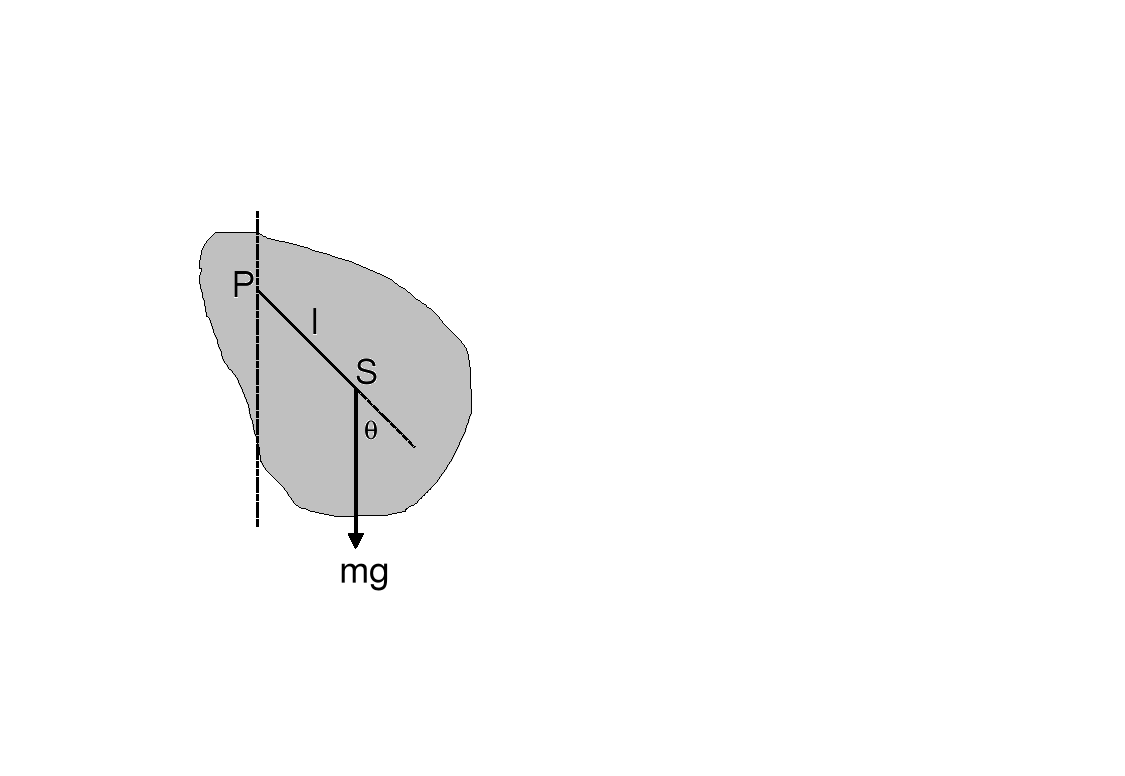
P jest punktem zawieszenia ciała, a punkt S, znajdujący się w odległości l od punkt P, jest środkiem masy. Moment siły τ działający na ciało wynosi τ = - mglsinθ

Korzystając ze związku τ = Iα =I(d²θ /dt²)

Otrzymujemy
Dla małych wychyleń, dla których sinθ ≅ θ dostajemy równanie

To równanie ma tę samą postać co równanie dla ruchu harmonicznego więc

Lub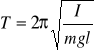
(13.10)

Jako przypadek szczególny rozpatrzmy masę punktową zawieszoną na nici o długości l. Wówczas I = ml² i otrzymujemy znany wzór dla wahadła prostego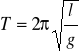

Wahadło fizyczne stosuje się do precyzyjnych pomiarów przyspieszenia g.

46. Energia ruchu harmonicznego prostego

Energią potencjalną sprężyny zajmowaliśmy się na wykładzie 6 przy okazji dyskusji o pracy wykonywanej przez siły zmienne. Pokazaliśmy wtedy, że energia potencjalna (nagromadzona) sprężyny

(13.11)

Jeżeli masę przymocowaną do sprężyny pociągniemy na odległość x = A to energia układu (nagromadzona w układzie) jest równa (1/2)kA² (E_k = 0). Jeżeli teraz zwolnimy sprężynę, to przy założeniu, że nie ma tarcia ani sił oporu, zgodnie z zasadą zachowania energii w dowolnej chwili suma energii kinetycznej i potencjalnej równa się (1/2)kA²

(13.12) stąd
Ponieważ k/m = ω² więc

Obliczmy teraz wartości średnie czasowe) energii potencjalnej i kinetycznej. (Wartości średnie oznaczamy kreską umieszczoną ponad symbolem.)
czyli
Natomiast
czyli

Wartość średnia
jest taka sama jak
i wynosi 1/2. Oba wykresy są takie same (tylko przesunięte). Poza tym sin²ωt + cos²ωt = 1 i średnia każdego składnika jest taka sama. Widać, że

47.składanie ruchów harmonicznych ( figury Lissajousa)

48.Ruch harmoniczny tłumiony.

Oscylator harmoniczny tłumiony

W przypadku drgań mechanicznych siłą hamującą (tłumiącą) ruch cząstki jest siła oporu F_op ośrodka. Siła oporu ma zwrot przeciwny do prędkości i w najprostszej postaci jest wprost proporcjonalna do prędkości F_op ≈ v czyli F_op = γ dx/dt (13.13)

Gdy działa tylko siła tłumienia to

lub

Jeżeli wprowadzimy zmienną (o wymiarze czasu) τ = M/γ to otrzymamy równanie

dv/dt = - (1/τ)v co można przepisać w postaci dv/v = - dt/τ

Całkujemy to równanie obustronnie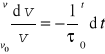
Skąd otrzymujemy lnv - lnv₀ = - (t/τ) lub

ln(v/v₀) = - (t/τ) a po przekształceniu
(13.14)

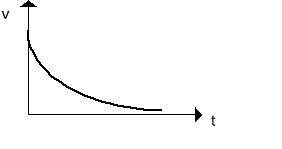
Prędkość maleje wykładniczo z czasem czyli prędkość jest tłumiona ze stałą czasową τ (rysunek).

Jeżeli włączymy siłę hamującą do oscylatora to wówczas równanie ruchu przyjmie postać

Wprowadzając τ = M/γ oraz oznaczając częstość drgań nietłumionych ω₀² = (k/M) otrzymujemy
(13.15)

Szukamy rozwiązania w postaci drgań okresowo zmiennych tłumionych np.
(13.16) Rozwiązanie zawiera czynnik oscylacyjny (cost) i tłumiący (exp(-t)) i jest pokazane na rysunku poniżej. Współczynnik β = 1/2τ określający wielkość tłumienia nazywamy współczynnikiem tłumienia. Teraz obliczamy odpowiednie pochodne (13.16) i podstawiamy do równania (13.15). W wyniku rozwiązania dostajemy warunek na częstość drgań tłumionych
(13.17) Opór zmniejsza więc (oprócz amplitudy) również i częstość Funkcja (13.16) jest rozwiązaniem równania opisującego ruch harmoniczny tłumiony przy warunku (13.17). Widzimy, że opór zmniejsza zarówno amplitudę jak i częstość drgań, czyli powoduje spowolnienie ruchu. Wielkość tłumienia określa współczynnik tłumienia  (lub stała czasowa ). Wykres ruchu harmonicznego tłumionego w zależności od czasu jest pokazany na rysunku

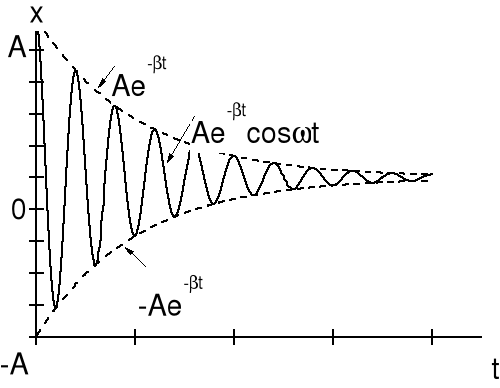
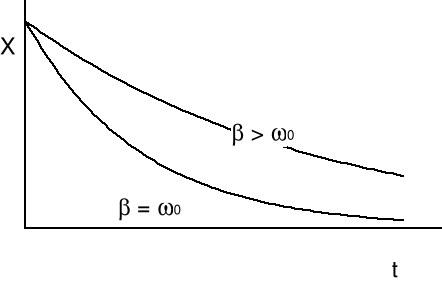
Powyższe rozważania dotyczą sytuacji "słabego tłumienia" tj. β < ω₀. Gdy tłumienie wzrośnie powyżej pewnej krytycznej wartości (β = ω₀) ruch nie jest ruchem drgającym ale obserwujemy, że ciało wychylone z położenia równowagi powraca do niego asymptotycznie. Takich ruch nazywamy ruchem pełzającym (aperiodycznym). Zależności wychylenia od czasu dla ruchu tłumionego krytycznie (β = ω₀) i ruchu pełzającego (β > ω₀) są pokazane na wykresie poniżej.

49.Rezeonans ( drgania wymuszone)

Jeżeli oprócz tarcia istnieje siła zewnętrzna F(t) (która ma za zadanie podtrzymywać gasnące drgania) przyłożona do oscylatora to równanie ruchu ma postać
albo po podstawieniu τ = M/γ oraz ω₀² = k/M otrzymujemy

Gdy układ jest zasilany częstością ω różną od ω₀ wówczas drgania będą odbywały się z częstością siły zewnętrznej a nie z częstością własną. Siłę taką nazywamy siłą wymuszającą.

Załóżmy, że siła wymuszająca ma postać
gdzie α₀ = F₀/M.

Mamy dwie wielkości okresowo zmienne położenie x oraz siłę wymuszającą F. W najogólniejszym przypadku suma (złożenie) dwóch funkcji okresowych daje w wyniku też funkcję okresową (rysunek).

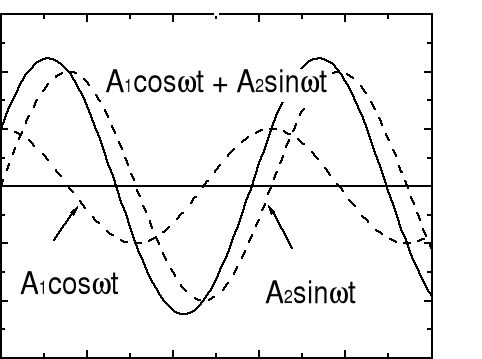
A₁cosωt + A₂sinωt = Asin(ωt + ϕ)

Szukamy więc rozwiązania postaci Asin(ωt + ϕ).

Musimy znaleźć amplitudę A oraz przesunięcie fazowe ϕ.

Przesunięcie fazowe ϕ mówi nam o jaki kąt maksimum przemieszczenia wyprzedza maksimum siły (o ile przesunięte są wykresy x(t) i F(t)).

Np. siła osiąga swoje maksimum gdy przemieszczenie jest równe zeru (i rośnie w kierunku dodatnim). Oznacza to, że x opóźnia się względem siły o π/2.

Poszukiwanie rozwiązania zaczynamy od obliczenia pochodnych dx/dt= ωAcos(ωt + ϕ), orazd²x/dt² = -ω²Asin(ωt + ϕ) Równanie ruchu ma teraz postać (ω₀² - ω²) Asin(ωt + ϕ) + (ω/τ)Acos(ωt + ϕ) = α₀sinωt Równanie to przekształcamy korzystając ze związków sin(ωt + ϕ) = sinωt cosϕ + cosωt sinϕ, cos(ωt + ϕ) = cosωt cosϕ − sinωt sinϕ

Wtedy otrzymujemy

[(ω₀² − ω²)cosϕ − (ω/τ)sinϕ] Asinωt + [(ω₀² − ω²)sinϕ − (ω/τ)cosϕ] Acosωt = α₀sinωt

Równanie to może być tylko spełnione gdy czynniki przy sinωt będą sobie równe, a czynnik przy cosωt będzie równy zeru. Ten ostatni warunek można zapisać jako

Z tego warunku znam już ϕ. Teraz możemy wyznaczyć amplitudę

gdzie już podstawiono za cosϕ i sinϕ. Łącząc wzory (13.22) i (13.23) otrzymujemy rozwiązanie

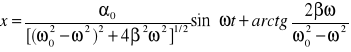
(13.24)

to jest rozwiązanie postaci x = Asin(ωt + ϕ)).

Rezonans

Zauważmy, że chociaż drgania odbywają się z częstością w siły wymuszającej to amplituda i faza zależą od relacji pomiędzy częstością wymuszającą , a częstością własną ₀. W szczególności gdy częstość siły wymuszającej osiągnie odpowiednią częstotliwość, to amplituda drgań może wzrosnąć gwałtownie nawet przy niewielkiej wartości siły wymuszającej. Zjawisko to nazywamy rezonansem.

Wykres przedstawiający rezonansowy wzrost amplitudy drgań w funkcji częstości siły wymuszającej pokazany jest na rysunku poniżej dla różnych wartości współczynnika tłumienia  (₀<₁<₂<₃<₄).

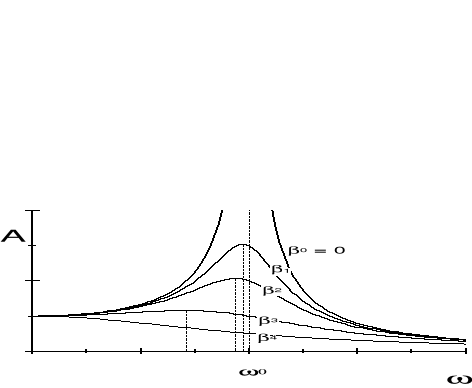
Częstość rezonansową _r i amplitudę rezonansową A_r możemy obliczyć z warunku na maksimum amplitudy drgań danej wzorem (13.23). Funkcja  A() osiąga maksimum

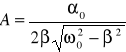
dla częstości rezonansowej

im mniejsze tłumienie  (dłuższy czas τ) tym większa amplituda A. Jeżeli tłumienie jest słabe ( << ω₀) to wówczas maksymalna amplituda odpowiada częstości drgań własnych ω_r = ω₀. moc pochłaniana przez oscylator zasilany siłą wymuszającą F zależy od prędkości P = Fv

Trzeba więc, żeby to prędkość (a nie wychylenie) była zgodna w fazie z siłą, a to oznacza, że siła musi wyprzedzać wychylenie o π/2. Gdy x = 0 to v = v_max i wtedy siła też ma być maksymalna. Skutki rezonansu mogą być zarówno pozytywne jak i negatywne. Z jednej strony staramy się wyeliminować przenoszenie drgań np. z silnika na elementy nadwozia w samochodzie, a z drugiej strony działanie odbiorników radiowych i telewizyjnych jest możliwe dzięki wykorzystaniu rezonansu elektrycznego. Dostrajając odbiornik do częstości nadajnika spełniamy właśnie warunek rezonansu. Zjawisko rezonansu jest bardzo rozpowszechnione w przyrodzie.

50. Prawo powszechnego ciążenia.

Newton - 1665 spadanie ciał. Skoro istnieje siła przyciągania pomiędzy dowolnym ciałem i Ziemią, to musi istnieć siła między każdymi dwoma masami m₁ i m₂. Skoro siła jest proporcjonalna do masy ciała to musi być proporcjonalna do każdej z mas m₁ i m₂ oddzielnie czyli: F ∼ m₁m₂

Newton zastanawiał się również, czy siła działająca na ciała będzie malała wraz ze wzrostem odległości. Doszedł do wniosku, że gdyby ciało znalazło się w odległości takiej jak Księżyc to będzie ono miało takie samo przyspieszenie jak Księżyc bowiem natura siły grawitacyjnej pomiędzy Ziemią i Księżycem jest taka sama jak pomiędzy Ziemią i każdym ciałem.

Przykład 1

Obliczmy jakie jest przyspieszenie Księżyca i jaki jest stosunek przyspieszenia Księżyca do przyspieszenia grawitacyjnego przy powierzchni Ziemi?

Zastosujemy równanie na przyspieszenie dośrodkowe (wykład 3 - ruch jednostajny po okręgu). Wówczas: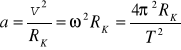

gdzie R_K jest odległością od Ziemi do Księżyca. Ta odległość wynosi 3.86·10⁵ km, a okres obiegu Księżyca T = 27.3 dnia. Otrzymujemy więc a = 2.73·10^-3 m/s²

W pobliżu powierzchni Ziemi przyspieszenie wynosi 9.8 m/s². Stąd stosunek przyspieszeń wynosi: a/g = 1/3590 ≅ (1/60)²

W granicach błędu a/g =
.

Newton wykonał takie obliczenia i wyciągnął wniosek, że siła przyciągania między dwoma masami maleje odwrotnie proporcjonalnie do kwadratu odległości między nimi (odległość między środkami mas). Sformułował więc prawo powszechnego ciążenia

Stałą proporcjonalności oznacza się G, więc
(6.1)

Newton oszacował wartość stałej G zakładając średnią gęstość Ziemi ρ = 5·10³ kg/m³ (porównać to z gęstością pierwiastków z układu okresowego np. ρ_Si = 2.8·10³ kg/m³, ρ_Fe = 7.9·10³ kg/m³).

Punktem wyjścia jest równanie:

Jeżeli weźmiemy r = R_Z to otrzymamy:

Zgodnie z II zasadą Newtona F = ma, gdzie a = g.

Stąd

więc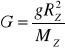

Wiemy, że M_Z = ρV_Z więc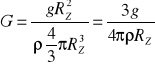

Uwzględniając R_Z = 6.37·10⁶ m otrzymamy G = 7.35·10^-11 Nm²/kg² co jest wartością tylko o 10% większą niż ogólnie przyjęta wartość 6.67·10^-11 Nm²/kg².

Porównując przyspieszenie grawitacyjne na orbicie Księżyca i na powierzchni Ziemi, Newton zakładał, że Ziemia zachowuje się tak jakby jej cała masa była skupiona w środku. Zgadywał, że tak ma być ale dowód matematyczny przeprowadził dopiero 20 lat później (wtedy też sformułował rachunek całkowy).

Równanie (6.1) nazywa się prawem powszechnego ciążenia, ponieważ dokładnie to samo prawo stosuje się do wszystkich sił grawitacyjnych. To samo prawo wyjaśnia spadanie ciał na Ziemię, tłumaczy ruch planet, pozwala obliczyć ich masy i okresy obiegu.

51.Wyznaczanie stałej g

Newton oszacował wartość stałej G zakładając średnią gęstość Ziemi ρ = 5·10³ kg/m³ (porównać to z gęstością pierwiastków z układu okresowego np. ρ_Si = 2.8·10³ kg/m³, ρ_Fe = 7.9·10³ kg/m³).

Punktem wyjścia jest równanie:

Jeżeli weźmiemy r = R_Z to otrzymamy:

Zgodnie z II zasadą Newtona F = ma, gdzie a = g.

Stąd

więc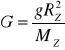

Doświadczenie Cavendisha

Newton obliczył wartość stałej G na podstawie przyjętego założenia o średniej wartości gęstości Ziemi. Gdyby Ziemia miała tak jak gwiazdy jądro o super wielkiej gęstości to wynik uzyskany przez Newtona byłby obarczony dużym błędem

W tym celu trzeba zmierzyć siłę oddziaływania dwóch mas m₁ i m₂ umieszczonych w odległości x (rysunek).

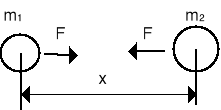
Wówczas siła F = Gm₁m₂/x²

czyli

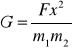
Zauważmy, że dla mas każda po 1 kg oddalonych od siebie o 10 cm siła F ma wartość F = 6.67·10^-9 N tj. 10⁹ razy mniej niż ciężar 1 kg i jest za mała by ją wykryć (dokładnie) zwykłymi metodami.

Problem ten rozwiązał Henry Cavendish w 1797 r. Wykorzystał on fakt, że siła potrzebna do skręcenia długiego, cienkiego włókna kwarcowego o kilka stopni jest bardzo mała. Cavendish najpierw wykalibrował włókna, a następnie zawiesił na nich pręt z dwiema małymi kulkami ołowianymi na końcach (rysunek a). Następnie w pobliżu każdej z kulek umieścił większą kulę ołowianą i zmierzył precyzyjnie kąt o jaki obrócił się pręt (rysunek b). Pomiar wykonane metodą Cavendisha dają wartość G = 6.67·10^-11 Nm²/kg².

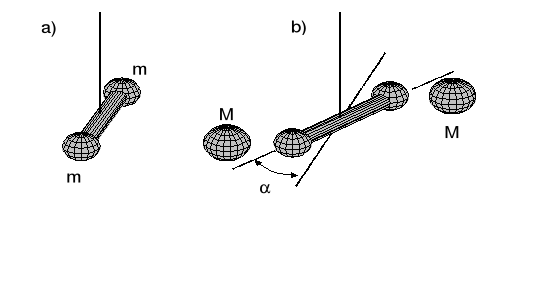
Ważenie Ziemi

Mając już godną zaufania wartość G, Cavendish wyznaczył M_Z z równania:

Wynik pomiaru jest równie dokładny jak wyznaczenia stałej G.

52. Zmiany przyspieszenia ziemskiego.

53. Prawa Kepplera

Zanim Newton zapostulował prawo powszechnego ciążenia, Johannes Kepler stwierdził, że ruch planet stosuje się do trzech prostych praw. Dogmatem był pogląd, że planety poruszają się wokół Ziemi po skomplikowanych torach, które są złożeniem pewnej liczby okręgów. Np. do opisania orbity Marsa trzeba było około 12 okręgów różnej wielkości.

Kepler poszukiwał nieskomplikowanej geometrycznie orbity, żeby udowodnić że Mars i Ziemia muszą obracać się wokół Słońca. Po latach pracy odkrył trzy proste prawa, które zgadzały się z wynikami pomiarowymi pozycji planet z bardzo dużą dokładnością. Te prawa stosują się też do satelitów okrążających jakąś planetę.

Pierwsze prawo Keplera

Każda planeta krąży po orbicie eliptycznej, ze Słońcem w jednym z ognisk tej elipsy.

Drugie prawo Keplera (prawo równych pól)

Linia łącząca Słońce i planetę zakreśla równe pola w równych odstępach czasu.

Trzecie prawo Keplera

Sześciany półosi wielkich orbit dowolnych dwóch planet mają się do siebie jak kwadraty ich okresów obiegu. (Półoś wielka jest połową najdłuższej cięciwy elipsy).

Dla orbit kołowych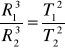

Newton rozwijając swoją teorię potrafił dowieść, że tylko wtedy, gdy siła jest odwrotnie proporcjonalna do kwadratu odległości, orbita dowolnej planety jest elipsą ze Słońcem w jednym z ognisk oraz, że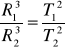
. Newton wyprowadził prawa Keplera z zasad dynamiki. Przykładowo wyprowadźmy III prawo Keplera dla planet poruszających się po orbitach kołowych.

Korzystając z otrzymanego uprzednio wzoru na masę Słońca otrzymamy dla pierwszej planety: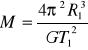

a dla drugiej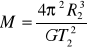

Porównując otrzymamy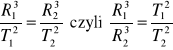

Drugie prawo Keplera wynika z zasady zachowania pędu

Cavendish wyznaczył też masę Słońca, Jowisza i innych planet, których satelity zostały zaobserwowane. Np. na rysunku poniżej niech M będzie masą Słońca, a m masą planety krążącej wokół Słońca np. Ziemi.

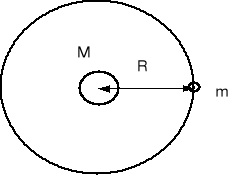
Wtedy F = GMm/R²

Ponieważ przyspieszenie a = 4π²R/T

to z równania F = ma otrzymujemy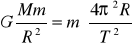
czyli

Jeżeli R jest odległością Ziemia - Słońce, T = 1 rok, to M jest masą Słońca. Podobne obliczenia można przeprowadzić dla innych planet.

54. Pole grawitacyjne

rozważania rozpoczynamy od umieszczenia masy M w początku układu. W punkcie przestrzeni opisanym wektorem r znajduje się natomiast masa m. Wektor r opisuje położenie masy m względem masy M więc siłę oddziaływania grawitacyjnego między tymi masami
możemy zapisać w postaci wektorowej

Zwróćmy uwagę, że siłę tę możemy potraktować jako iloczyn masy m i wektora γ(r) przy czym

Jeżeli w punkcie r umieścilibyśmy inną masę np. m' to ponownie moglibyśmy zapisać siłę jako iloczyn masy m' i tego samego wektora γ(r)

Widzimy, że wektor γ(r) nie zależy od obiektu na który działa siła (masy m) ale zależy od źródła siły (masa M) i charakteryzuje przestrzeń otaczającą źródło (wektor r). Oznacza to, że masa M stwarza w punkcie r takie warunki, że umieszczona w nim masa m odczuje działanie siły. Inaczej mówiąc masie M przypisujemy obszar wpływu (działania), czyli pole.

rozdzieliliśmy siłę na dwie części. jedna masa wytwarza pole, a następnie to pole działa na drugą masę. Taki opis pozwala uniezależnić się od obiektu (masy m) wprowadzanego do pola. Z pojęcia pola korzysta się nie tylko w związku z grawitacją. Jest ono bardzo użyteczne również przy opisie zjawisk elektrycznych i magnetycznych. Źródłami i obiektami działania pola elektrycznego są ładunki w spoczynku, a pola magnetycznego ładunki w ruchu, gdy mamy do czynienia z wieloma masami, możemy najpierw obliczyć w punkcie r pole pochodzące od tych mas, a dopiero potem siłę działającą na masę umieszczoną w tym punkcie.

Z polem sił wiąże się nie tylko przestrzenny rozkład wektora natężenia pola, ale również przestrzenny rozkład energii.

55. Energia potencjalna i potencjał pola grawitacyjnego

56. prędkości kosmiczne

Pierwsza prędkość kosmiczna to prędkość jaką należy nadać na powierzchni ziemi by ciało nie spadło lecz zaczęło krążyć wokół ziemi

Druga prędkość kosmiczna ( prędkość ucieczki)jest to minimalna prędkość jaką trzeba nadać ciału na powierzchni ziemi aby opuściło pole grawitacyjne (wyprowadzenia na kartce)

a) . Miedzy innymi stwierdzono, że ta transformacja zastosowana do równań Maxwella nie daje tych samych wyników dla omawianych układów inercjalnych. W szczególności z praw Maxwella wynika, że prędkość światła jest podstawową stałą przyrody i powinna być taka sama w każdym układzie odniesienia.

Oznacza to na przykład, że gdy impuls światła rozchodzący się w próżni w kierunku x jest obserwowany przez dwóch obserwatorów (patrz na tekst i rysunek powyżej) to zarówno obserwator nieruchomy jak poruszający się z prędkością V (względem pierwszego) zmierzą identyczną prędkość impulsu c = 2.998⋅10⁸ m/s. Tymczasem zgodnie z transformacją Galileusza i ze zdrowym rozsądkiem powinniśmy otrzymać wartość
c - V. Wykonano szereg doświadczeń, w których próbowano podważyć równania Maxwella, a w szczególności próbowano pokazać, że prędkość światła, tak jak prędkość dźwięku zależy od układu odniesienia (stosuje się do transformacji Galileusza). Najsławniejsze z nich, to doświadczenie Michelsona-Morleya mające na celu wykrycie wpływu ruchu orbitalnego Ziemi na prędkość światła poprzez pomiar prędkości światła w kierunku prostopadłym i równoległym do ruchu Ziemi. Wszystkie te doświadczenia dały wynik negatywny i musimy uznać, że prędkość światła w próżni jest jednakowa we wszystkich inercjalnych układach odniesienia.

Prędkość światła c = 2.988⋅10⁸ m/s we wszystkich układach odniesienia.

57.Prawa Pascala

Na rysunku widzimy ciecz w naczyniu zamkniętym tłokiem, na który możemy działać ciśnieniem zewnętrznym p₀.

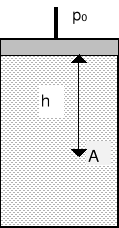
W każdym punkcie A znajdującym się na głębokości h od górnej powierzchni cieczy, ciśnienie jest dane wyrażeniem p = p₀ + ρgh

Możemy powiększyć ciśnienie zewnętrzne o wartość Δp₀. Ponieważ ciecze są nieściśliwe więc gęstość pozostaje praktycznie bez zmian i dlatego ciśnienie teraz wynosi p = p₀ +Δp₀+ ρgh

Wynik ten został sformułowany przez Blaise Pascala i nazywa się prawem Pascala. Prawo to formułuje się następująco: ciśnienie wywierane na zamknięty płyn jest przekazywane niezmienione na każdą część płynu oraz na ścianki naczynia.

58. Prawo Archimedesa

Prawo to jest konsekwencją praw mechaniki płynów podobnie jak prawo Archimedesa.

Kiedy ciało jest zanurzone w całości lub częściowo w spoczywającym płynie (cieczy lub gazie) to płyn ten wywiera ciśnienie na każdą, będącą z nim w kontakcie, część powierzchni ciała. Wypadkowa siła jest skierowana ku górze i zwie się siłą wyporu.

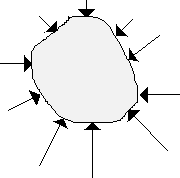
Ponieważ ciśnienie wywierane na ciało nie zależy od materiału, z którego zrobiono ciało więc zastąpmy w naszym rozumowaniu rozpatrywane ciało przez ten sam płyn co płyn otoczenia. Na ten płyn będzie działało to samo ciśnienie co na ciało, które zastąpił. Poza tym płyn będzie nieruchomy. Stąd działająca nań siła będzie równa ciężarowi płynu i skierowana ku górze tak, żeby ten ciężar zrównoważyć. Otrzymujemy prawo Archimedesa: ciało w całości lub częściowo zanurzone w płynie jest wypierane ku górze siłą równą ciężarowi wypartego przez to ciało płynu. Tak więc F_wyporu = m_{wypartego płynu} g = ρVg

gdzie ρ jest gęstością płynu, a V objętością części zanurzonej ciała.

Pomiar

59. Barometry, prasa hydrauliczna.

60.Równanie Bernouliego

Rozważmy nielepki, ustalony, nieściśliwy przepływ płynu przez rurę (rysunek poniżej). Ciecz na rysunku płynie w stronę prawą. W czasie t powierzchnia S₁ przemieszcza się o odcinek v₁t do położenia S₁'. Analogicznie powierzchnia S₂ przemieszcza się o odcinek v₂t do położenia S₂'. Na powierzchnię S₁ działa siła F₁ = p₁S₁ a na powierzchnię S₂ siła F₂ = p₂S₂. Zwróćmy uwagę, że efekt sumaryczny przepływu płynu przez rurkę polega na przeniesieniu pewnej objętości V płynu ograniczonej powierzchniami S₁S₁' do położenia S₂S₂'.

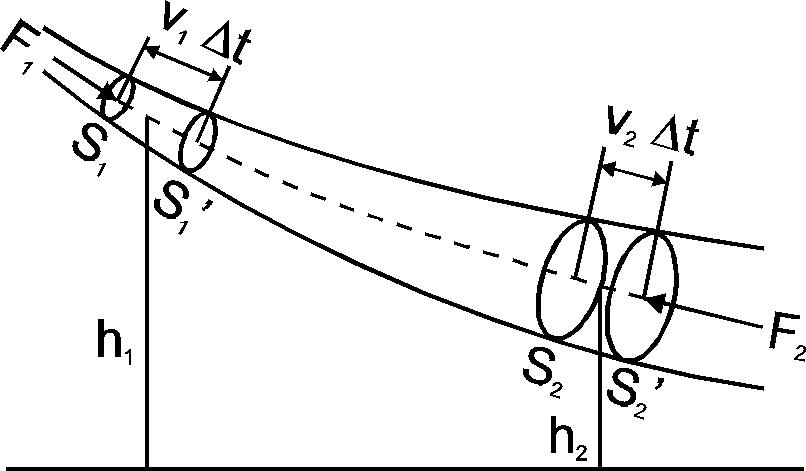
Twierdzenie o pracy i energii mówi, że praca wykonana przez wypadkową siłę jest równa zmianie energii układu. Siłami, które wykonują pracę są F₁ i F₂. Obliczamy więc pracę

oraz zmianę energii strugi

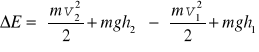
Ponieważ W = ΔE to przy założeniu nieściśliwości płynu (ρ = const)

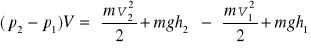
Związek ten można przekształcić do postaci

czyli

Równanie to nosi nazwę równania Bernoulliego dla przepływu ustalonego, nielepkiego i nieściśliwego. Jest to podstawowe równanie mechaniki płynów. Może być stosowane do wyznaczenia prędkości płynu na podstawie pomiarów ciśnienia (rurka Venturiego, rurka Pitota). Można też w oparciu o nie wyznaczyć dynamiczną siłę nośną.

Dynamiczna siła nośna jest to siła jaka działa na np. skrzydło samolotu, nartę wodną, śmigło helikoptera, i wywołana jest ruchem tych ciał w płynie w odróżnieniu od statycznej siły nośnej, która jest siła wyporu działającą np. na balon czy statek zgodnie z prawem Archimedesa. Na rysunku poniżej pokazane są schematycznie linie prądu wokół skrzydła samolotu.

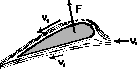
Analizując te linie prądu zauważymy, że ze względu na ustawienie skrzydła (kąt natarcia) linie prądu nad skrzydłem są rozmieszczone gęściej niż pod skrzydłem. Tak więc v_g ponad skrzydłem jest większa niż pod skrzydłem v_d a to oznacza zgodnie z prawem Bernoulliego, że ciśnienie nad skrzydłem jest mniejsze od ciśnienia pod skrzydłem i otrzymujemy wypadkową siłę nośną F skierowaną ku górze. Wynika to również z trzeciej zasady dynamiki Newtona. Prędkość v₀ powietrza zbliżającego się do skrzydła jest pozioma podczas gdy powietrze za skrzydłem jest skierowane na ukos w dół (składowa pionowa). Oznacza to, że skrzydło pchnęło powietrze w dół więc w reakcji powietrze pchnęło skrzydło do góry.

---