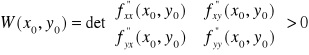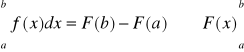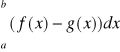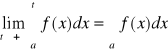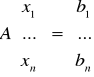Tautologia - nazywamy zdanie złożone, które wartością logiczną jest prawda niezależnie od wartości logicznych zdań prostych tworzących to zdanie. Funkcja zdaniowa - nazywamy wyrażenie P(x1, x2, ..., xn) zawierające zmianę (x1, x2, ..., xn), które staje się zdaniem po podstawieniu za zmianę konkretnych wartości (np. nazw, liczb, itp.) Iloczynem kartezjańskim dwóch zbiorów A i B nazywamy zbiór AxB={(a,b):a ε A ^ b ε B} Relacja to matematyczne ujęcie zależności lub związków zachodzących między pewnymi obiektami.
Relacją między elementami A i B nazywamy podzbiór iloczynu kartezjańskiego AxB. Relacją w zbiorze A nazywamy podzbiór iloczynu kartezjańskiego AxA. Właściwości relacji: a) relacja Poziomicą funkcji f: XxY -> R na wysokości h ε R nazywamy zbiór P(h)={(x,y) ε XxY: f(x,y) = f}
Własności funkcji: a) funkcja jest różnowartościowa w zbiorze A Ciągiem (liczbowym) skończonym nazywamy dowolną funkcję odwzorowującą zbiór {1, 2, ..., n} w R. Liczbę n nazywamy długością ciągu. Ciągiem (liczbowym) nieskończonym nazywamy dowolną funkcję odwzorowującą zbiór liczb naturalnych w zbiór liczb rzeczywistych. Ciąg (an)n ε N jest okresowy, jeśli istnieje liczba naturalna t taka, że an+t = an dla wszystkich liczb naturalnych n. Właściwości ciągów: a) mówimy, że ciąg liczbowy (an)n ε N jest rosnący, gdy an+1 > an, dla każdej liczby naturalnej n. b) mówimy, że ciąg liczbowy (an)n ε N jest malejący, gdy an+1 < an, dla każdej liczby naturalnej n. c) mówimy, że ciąg liczbowy (an)n ε N jest różnowartościowy, gdy am ≠ an, dla wszystkich par różnych od liczb naturalnych m, n. Macierze kwadratowe - czyli liczba wierszy jest równa liczbie kolumn. Wektory kolumnowe - to macierze, które mają tylko jedną kolumnę i m wierszy. Wektory wierszowe - to macierze, które mają tylko jeden wiersz i n kolumn. Transpozycja - macierzą transponowaną macierzy M jest macierz MT otrzymana z M przez utworzenie wierszy z kolumn. Macierz symetryczna - to macierz, która jest równa swojej macierzy transponowanej. Własności wyznaczników: a) wyznacznik macierzy, w której jeden wiersz lub jedna kolumna składa się z samych zer, jest równa zeru. b) gdy macierz B powstaje z macierzy A przez zmianę dwóch kolumn lub wierszy, to detB = -detA. c) jeśli w macierzy dwie kolumny lub dwa wiersze są identyczne, to jej wyznacznik jest równy zeru. d) gdy macierz B powstaje z macierzy A przez pomnożenie wszystkich elementów jednego wiersza lub kolumny przez c, to: detB = cdetA. e) wyznacznik nie zmienia wartości, gdy do elementów jednej kolumny (wiersza) dodać odpowiednie elementy innej kolumny (wiersza) pomnożenie przez dowolną stałą. f) wyznacznik macierzy kwadratowej jest równy wyznacznikowi jej macierzy transponowanej, tzn. detA = detAT g) wyznacznik iloczynu macierzy jest równy iloczynowi tych wyznaczników, tzn. detAB = detA*detB
Macierze odwrotne: a) macierz odwrotną do macierzy A nazywamy taką macierz B, że AB = I, BA = I. b) jeśli macierz posiada macierz odwrotną, to jest macierzą kwadratową. Macierz odwrotna do macierzy A oznaczamy A-1. c) jeżeli B=[bij] jest macierzą odwrotną do macierzy A=[aij], to bij=(-1)i+j Metoda Gaussa: Jeśli macierz układu równań można przedstawić w postaci A=[I/A'], to taki układ nazywamy bazowym. Metoda Gaussa polega na sprowadzeniu układu równań przy pomocy operacji elementarnych do postaci bazowej. Takie postępowanie nazywamy eliminacją niewiadomych. Operacje elementarne zmieniają układ równań, lecz nie zmieniają zbioru rozwiązań układu. Operacją elementarną nazywamy każde z następujących przekształceń układu równań liniowych: a) pomnożenie pewnego równania układu przez dowolną liczbę i dodanie do innego równania tego układu. b) pomnożenie lub podzielenie pewnego równania układu przez liczbę różną od zera. c) zmiana kolejności równań w układzie. d) dopisanie lub usunięcie z układu równania zerowego postaci 0x1+...+0xn=0.
Dwa układy równań nazywamy równoważnymi, jeśli jeden z nich można otrzymać z drugiego przez wykonanie ciągu operacji elementarnych. Twierdzenia: 1. Każdy układ równań można za pomocą ciągu operacji elementarnych sprowadzić do układu bazowego, tzn. każdy układ równań liniowych jest równoważny z pewnym układem bazowym. 2. Równoważne układy równań liniowych mają równe zbiory rozwiązań. 3. a) układ równań liniowych równoważy z układem bazowym postaci
Macierz zredukowana: wskaźnikiem wiodącym niezerowego wektora Mówimy, że macierz jest zredukowana, jeśli ciąg wskaźników wiodących jej wektorów jest słabo rosnący (niemalejący) i wszystkie wskaźniki wiodące wektorów niezerowych są parami różne. Dwie macierze nazywamy równoważnymi, jeśli jedną z nich można otrzymać z drugiej przez wykonanie ciągu operacji elementarnych. Tw: każda macierz jest równoważna z pewną macierzą zredukowaną. Rzędem macierzy zredukowanej nazywamy liczbę niezerowych wierszy tej macierzy. Rzędem (dowolnej) macierzy nazywmy rząd dowolnej macierzy zredukowanej równoważnej z daną macierzą. Działania na wektorach: wektorem (n-wymiarowym) nazywamy każdy n-elementowy ciąg licz rzeczywistych. Wektor może być zapisany jako macierz jednowierszowa lub jednokolumnowa. Zbiór wszystkich wektorów n-wymiarowych oznaczamy Rn.
Wiązka towarowa - to wektor
Wektorem cen nazywamy wektor
Wartości wiązki towarowej
Załóżmy, że Zbiór wiązek towarowych, spośród których konsument może dokonać wyboru przy założeniu ograniczeń budżetowych, nazywamy go zbiorem budżetowym.
Programowanie liniowe: znalezienie wektora decyzyjnego Model matematyczny: a)zmienne decyzje; b)warunki ograniczające; c)funkcja celu. Funkcje jednej zmiennej: Każde jednoznaczne przyporządkowanie f elementu zbioru X elementów zbioru Y nazywamy funkcją określoną na zbiorze X.: f: X→Y. Zbiór X nazywamy dziedziną funkcji (ozn. Df), z zbiór Y przeciwdziedziną.
Zbiorem wartości funkcji (ozn. Vf) nazywamy zbiór tych elementów należących do Y, które zostały przyporządkowane pewnym elementem zbioru X.:
Wektorem funkcji f: X→Y nazywamy podzbiór iloczynu kartezjańskiego XxY postaci: Każda funkcja przekształcająca zbiór XxY jest relacją pomiędzy elementami zbioru X i zbioru Y. Odwrotnie, relacja W ε XxY jest funkcją, jeśli pierwsze elementy par należących do W są różne.
Podstawowe własności funkcji: a) Funkcja jest f. różnowartościową w zbiorze A Funkcja odwrotna: jeśli funkcja X→Y jest różnowartościowa i odwzorowuje zbiór X na zbiór Y, to dla każdego y ε Y, istnieje dokładnie jeden element x ε X, takie, że y = f(x). Przyporządkowanie g w wyniku, którego każdemu y ε Y przyporządkowany jest jedyny x ε X, taki, że y = f(x) nazywamy funkcja odwrotną do f. Funkcję odwrotną do f oznaczamy symbolem f -1. Jeżeli dziedziną i zbiorem wartości jest zbiór liczb rzeczywistych, to wykres funkcji odwrotnej f -1 jest symetryczny do wykresu funkcji f względem prostej o równaniu y = x. Funkcja złożona: Jeśli w zbiorze X jest określona funkcja y = f(x), której przeciwdziedziną jest zbiór Y oraz w zbiorze Y jest określona funkcja z = g(y) z przeciwdziedziną Z, to mówimy, że w zbiorze X jest określona funkcja z = (g ◦ f)(x) = g(f(x)) o wartościach w zbiorze Z. Funkcję g ◦ f nazywamy funkcją złożoną (superpozycją) funkcję f nazywamy funkcją wewnętrzną, a g nazywamy funkcją zewnętrzną. Granicę ciągów liczbowych: Ciągiem nieskończonym nazywamy dowolną funkcję odwzorowującą zbiór liczb naturalnych w zbiorze R.
Liczbę g nazywamy granicą nieskończonego ciągu liczbowego (an)n ε N, co zapisujemy
Z def. otoczenia o promienia ε > 0 liczby g wynika, że Granica ciągu jest podstawowym pojęciem i służy do definiowania wielu pojęć matematycznych, np. pochodnej. Ponadto z granicy korzystamy w wielu zastosowaniach metod matematycznych. Twierdzenie 1.
Jeśli ciągi an oraz bn są zbieżne oraz Twierdzenie o trzech ciągach
Jeżeli Kryterium zbieżności ciągów Każdy ciąg monotoniczny i ograniczony jest zbieżny.
Mówimy, że ciąg an jest zbieżny do nieskończoności, jeśli prawie wszystkie wyrazy tego ciągu są większe od dowolnie wybranej liczby R.
Podobnie mówimy, że ciąg an jest zbieżny do minus nieskończoności, jeśli prawie wszystkie wyrazy tego ciągu są mniejsze od dowolnie wybranej liczby R. W obu przypadkach mówimy, że ciąg ma granicę niewłaściwą.
Granica funkcji w punkcie: Liczbę g nazywamy granicą funkcji f w punkcie x0, jeśli dla każdego ciągu xn spełniającego warunek: a) xnεDf dla wszystkich liczb naturalnych n b) xn≠x0 c) Granica funkcji w nieskończoności: Załóżmy, że funkcja f jest określona w przedziale (a, +∞) dla pewnego rzeczywistego a. Liczbę g nazywamy granicą funkcji f przy x → +∞, jeżeli dla każdego ciągu xn rozbieżnego do nieskończoności ciąg wartości funkcji (f(xn)) jest zbieżny do g. Asymptoty: jeśli funkcja f(x) jest określona w otoczeniu punktu a (z wyjątkiem być może samego punktu a) oraz przynajmniej jedna z granic jednostronnych jest nieskończona, to prostą o równaniu x=a nazywamy asymptotą pionową tej funkcji w punkcie a.
Prostą o równaniu y=ax+b nazywamy asymptotą ukośną krzywej o równaniu y=f(x), jeżeli zachodzi:
Szczególnym przypadkiem asymptoty ukośnej, gdy a=0, jest asymptota pozioma o równaniu y=b. Jeśli krzywa o równaniu y=f(x) ma asymptotę ukośną o równaniu y=ax+b, to
Ciągłość funkcji: Niech funkcja f będzie określona w przedziale Df oraz niech x0εDf. Mówimy, że funkcja f(x) jest ciągła w punkcie x0, jeżeli |
*Jeżeli zachodzi warunek Własność Darboux: jeżeli funkcja f(x) jest ciągła w przedziale domkniętym [a, b] i f(a) ≠f(b) oraz liczba y0 jest zawarta między f(a) i f(b), to istnieje taki punkt x0ε(a, b), że f(x00=y0. Własność Weierstrassa: Jeśli funkcja f(x) jest ciągła w przedziale domkniętym [a, b], to istnieje w tym przedziale punkt, w którym f przyjmuje wartość najmniejszą oraz punkt, w którym f przyjmuje wartość największą.
Pochodna funkcji jednej zmiennej: Wykorzystamy pojęcie granicy funkcji do zdefiniowania jednego z największych pojęć w matematyce - pochodnej. Wyrażenie
Pochodną funkcji f w punkcie x0 nazywamy granicę ilorazu różnicowego przy h→0: Jeżeli funkcja ma pochodną w punkcie x0, to mówimy, że jest różniczkowalna w tym punkcie.. Jeśli f jest różniczkowalna w każdym punkcie x ε(a, b), to mówimy, że f jest różniczkowalna w przedziale (a, b). To pociąga, że możemy mówić o nowej funkcji f' - pochodnej funkcji f. Wartość pochodnej w punkcie x0 interpretujemy geometrycznie jako współczynnik kierunkowy stycznej do wykresu funkcji f w punkcie (x0, f(x0)). Równanie stycznej: y - f(x0) = f'(x0)(x-x0) Interpretacja pochodnej w ekonomii: Funkcję C:[0, ∞)→R nazywamy funkcją kosztów producenta, jeśli wyprodukowanie x jednostek pewnego produktu kosztuje C(x) jednostek pieniężnych. Koszt całkowity: C(x)
Koszt średni: Koszt krańcowy: C'(x)
Twierdzenie Lagrange'a: jeśli funkcja f(x) jest ciągła w pewnym przedziale [a, b] i posiada pochodną w każdym punkcie wewnątrz tego przedziału, to istnieje taki punkt c ε(a, b), że Załóżmy, że funkcja f(x) jest różniczkowalna w przedziale (a, b). 1) jeśli f'(x)=0 w każdym punkcie przedziału (a, b), to funkcja jest stała w tym przedziale. 2) jeśli f'(x)>0 w każdym punkcie przedziału (a, b), to funkcja jest rosnąca w tym przedziale 3) jeśli f'(x)<0 w każdym punkcie przedziału (a, b), to funkcja jest malejąca w tym przedziale. Przedziały, w którym pochodną zachowuje stały znak, są przedziałami monotoniczności funkcji. Warunek konieczny istnienia ekstremum: jeżeli funkcją różniczkowalna f(x) ma w punkcie x0 ekstremum lokalne, to f'(x0)=0. Nie zachodzi twierdzenie odwrotne. Funkcja może mieć ekstremum lokalne tylko t tych punktach, w których pochodna nie istnieje lub jest równa 0. Warunek wystarczający istnienia ekstremum: jeśli funkcja f(x) jest różniczkowalna w pewnym otoczeniu punktu x0, f'(x0)=0 oraz w pewnym otoczeniu punktu x0 pochodna zmienia znak, przy czym gry f'(x)<0, gdy x0-δ<x<x0 i f'(x)>0, gdy x0<x< x0+δ, to funkcja f(x) ma w punkcie x0 minimum lokalne, jeżeli natomiast spełnione są warunki: f'(x)>0, gdy x0-δ<x<x0 i f(x)<0, gdy x0<x< x0+δ, to funkcja f(x) ma w punkcie x0 maksimum lokalne. Pochodne wyższych rzędów: Pochodną pochodnej funkcji f(x) nazywamy drugą pochodną funkcji i oznaczamy symbolem f”(x). Warunek wystarczający istnienia ekstremum: Niech f(x) będzie funkcją dwukrotnie różniczkowalną w pewnym otoczeniu punktu x0 i niech f'(x0)=0. *Jeżeli f”(x0)>0 to funkcja f(x) ma w punkcie x0 minimum lokalne. *Jeżeli f”(x0)<0 to funkcja f(x) ma w punkcie x0 maksimum lokalne. Wypukłość, wklęsłość i punkty przegięcia. Funkcję f(x) nazywamy wypukłą w przedziale (a, b), jeżeli dla dowolnych dwóch punktów x1, x2 ε(a, b) i dowolnej liczby α ε(0, 1) spełniony jest warunek: f(αx1+(1- α)x2)≤αf(x1)+(1- α)f(x2). Funkcję f(x) nazywamy wklęsłą w przedziale (a, b), jeżeli dla dowolnych dwóch punktów x1, x2 ε(a, b) i dowolnej liczby α ε(0, 1) spełniony jest warunek: f(αx1+(1- α)x2)≥αf(x1)+(1- α)f(x2). Jeżeli z jednej strony punkt x0 funkcja f(x) jest wypukła, zaś z drugiej wklęsła, to punkt x0 nazywamy punktem przegięcia krzywej y=f(x). Twierdzenie: 1) jeżeli druga pochodna funkcji f(x) jest dodatnia w każdym punkcie przedziału (a, b), to krzywa o równaniu y=f(x) jest w tym przedziale wypukła. 2) jeżeli druga pochodna funkcji f(x) jest ujemna w każdym punkcie przedziału (a, b), to krzywa o równaniu y=f(x) jest w tym przedziale wklęsła. 3) jeżeli druga pochodna funkcji f(x) ma wartość 0 w punkcie x0 i w otoczeniu punktu x0 zmienia znak, to punkt P0(x0, f(x)) jest punktem przegięcia krzywej o równaniu y=f(x). Wyznaczanie ekstremum warunkowego: Aby wyznaczyć największą wartość funkcji jednej zmiennej ciągłej w przedziale domkniętym, należy wyznaczyć wszystkie maksima lokalne tej funkcji należące do tego przedziału oraz obliczyć wartości funkcji na końcach przedmiotu i wybrać największą z otrzymanych wartości.
Reguła de I'Hospitala: załóżmy, że
Elastyczność funkcji: dana jest funkcja f(x) określona dla x>0 przyjmująca tylko wartości dodatnie i różniczkowalna w obszarze istnienia oraz h - przyrost argumentu x. Iloraz
Granicę stosunku przyrostu względnego funkcji do przyrostu względnego argumentu, gdy h→0. Elastyczność funkcji f w punkcie x0 jest przybliżoną miarą % zmiany (wzrostu lub spadku) wartości funkcji f(x0) odpowiadającej przyrostowi wartości argumentu. Pochodne cząstkowe: jeżeli obliczamy pochodną funkcji f(x1, ..., xn) względem zmiennej xi przyjmując, że pozostałe zmienne mają ustalone wartości, to otrzymaną funkcję nazywamy pochodną cząstkową (rzędu pierwszego) funkcji f(x1, ..., xn) względem zmiennej xi.
Twierdzenie Schwarza: jeżeli pochodne mieszane funkcji f(x, y) w punkcie (x0, y0) są ciągłe i istnieją w pewnym otoczeniu tego punktu, to pochodne te w punkcie (x0, y0) są sobie równe, czyli Ekstrema funkcji dwóch zmiennych: otoczeniem punktu P(x0, y0) o promieniu δ>0 na płaszczyźnie nazywamy wnętrze koła K(x0, y0, δ) o środku w punkcie P i promieniu δ.
Warunek konieczny istnienia ekstremum: jeżeli funkcja f(x, y) ma w punkcie P(x0, y0) ekstremum lokalne i ma w tym punkcie pochodne cząstkowe rzędu pierwszego, to Punkt P(x0, y0), w którym f'(x0, y0)=[0, 0] nazywamy punktem stacjonarnym funkcji f. Punkty te są potencjalnymi miejscami, w których funkcja różniczkowalna f może, lecz nie musi mieć ekstrema lokalne. Jeżeli w punkcie stacjonarnym funkcja f nie ma ekstremum lokalnego, to nazywamy go punktem siodłowym.
Warunek wystarczający istnienia ekstremum: Niech funkcja f(x, y) ma w pewnym otoczeniu punktu P(x0, y0) ciągłe pochodne cząstkowe drugiego rzędu oraz Jeżeli W(x0, y0)<0, to funkcja f(x, y) nie ma w punkcie P(x0, y0) ekstremum lokalne. Jeżeli W(x0, y0)=0, to nie wiemy, czy w punkcie P(x0, y0) jest ekstremum, czy go nie ma. Całka oznaczona i nieoznaczona: Dana jest funkcja f(x). Funkcję F(x) taką, że F'(x)=f(x) nazywamy funkcją pierwotną f(x). Poszukiwanie funkcji pierwotnej nazywamy całkowaniem. Jest to operacja odwrotna do różniczkowania. Jeśli F(x) jest funkcją pierwotną f(x), to każda funkcja postaci F(x)+C, gdzie C jest dowolną stałą , jest również funkcją pierwotną f(x). Zbiór wszystkich funkcji pierwotnych danej funkcji f(x) nazywamy całką nieoznaczoną. Parametr C nazywamy stałą całkowitą.
Twierdzenie (Podstawowe twierdz. rachunku całkowitego lub twierdz. Newtona-Leibniza): Jeżeli F(x) oznacza funkcję pierwotną funkcji f(x) określonej i ciągłej w przedziale [a, b], to
Jeżeli f(x) oraz g(x) są ciągłe w przedziale [a, b] oraz g(x)≤f(x) dla xε[a, b] , to pole obszaru pomiędzy wykresami funkcji oraz prostymi x=a, x=b dane jest wzorem:
Całka niewłaściwa: f(x) - jest ciągła w przedziale [a,+∞)
Twierdzenie Cramera: niech
Własności działań na macierzach: A+B = B+A - przemienność dodawania (A+B)+C = A+(B+C) - łączność dodawania (A±B)T = AT±BT - zgodność transpozycji z dodawaniem i odejmowaniem A+Ө = A - Ө jest macierzą neutralną względem dodawania (A*B)*C = A*(B*C) - łączność mnożenia (A*B)T = BT*AT - “antyzgodność” transpozycji z mnożeniem A*I = A - I jest macierzą neutralną względem mnożenia A*(B±C) = A*B±A*C - rozdzielność mnożenia względem dodawania i odejmowania |
Wyszukiwarka
Podobne podstrony:
Marketing - sciaga, bankowość i finanse - pomoce naukowe
Finanse publiczne - sciaga, bankowość i finanse - pomoce naukowe
Psychologia - sciaga, bankowość i finanse - pomoce naukowe
ekonometria - sciaga, bankowość i finanse - pomoce naukowe
Socjologia - sciagi, bankowość i finanse - pomoce naukowe
rachuna ćwiczenia, bankowość i finanse - pomoce naukowe
Bankowość - wykresy 2, bankowość i finanse - pomoce naukowe
Bankowość - wykresy, bankowość i finanse - pomoce naukowe
Bankowość - wykresy 3, bankowość i finanse - pomoce naukowe
Ćwiczenia III RZ KW I KDP, bankowość i finanse - pomoce naukowe
Marketing4, bankowość i finanse - pomoce naukowe
Marketing2, bankowość i finanse - pomoce naukowe
Marketing1, bankowość i finanse - pomoce naukowe
rachunkowosc zarzadcza, bankowość i finanse - pomoce naukowe
finanse międzynarodowe, bankowość i finanse - pomoce naukowe
UBEZPI~1, bankowość i finanse - pomoce naukowe
prawo - 2 cz, bankowość i finanse - pomoce naukowe
sciaga na przedsiebiorstwo, Pomoce Naukowe-ściągi
ocena fiskalizmu w polsce, UEK, Polityka finansowa, Pomoce naukowe
więcej podobnych podstron