Matematyka dyskretna ogólnie rzecz biorąc to nauka o zbiorach skończonych. I to będzie przedmiotem naszych rozważań. Na samym początku zajmiemy się równaniami rekurencyjnymi. Nim się tym zajmiemy, należy wiedzieć co to jest ciąg liczbowy, żeby to zrozumieć. Jest to funkcja przekształcająca zbiór liczb naturalnych w wartości rzeczywiste (
), przy czym liczby naturalne to w tym wypadku będą takie, które liczy się od 0 do nieskończoności dodatniej. Będziemy tu mieli do czynienia z zależnością
co znaczy, że n naturalne odpowiada wartości funkcji f należącej do zbioru liczb rzeczywistych. Jeśli
, to w skutek tego otrzymamy pewien ciąg liczbowy, czyli albo ciąg wartości tej funkcji, który możemy oznaczyć f(0), f(1), … f(n), albo który możemy oznaczyć jako
. Używa się jednak pewnych oznaczeń skrótowych dla ciągu liczbowego. A mianowicie:
, czy też
. I to dotyczy ciągów nieskończonych, ale też będziemy prócz tego rozpatrywali ciągi skończone. To są ciągi (
). Te przykładowe ciągi to ciągi n wyrazowe dla ustalonego n. I te ciągi liczbowe ogólnie rzecz biorąc mogą być zadawane na dwa sposoby. Wzorem
dla n naturalnego, albo także rekurencyjnym sposobem. My na tych wykładach będziemy rozpatrywali rekurencję postaci
, ale tu trzeba zadać pewne warunki początkowe. I tak przyjmijmy, że
są dane, a a i b rzeczywiste to współczynniki rekurencji. I tak obliczając z początkowych warunków mamy
. Widzimy tu, że przy tym drugim sposobie rekurencyjnym zadania tego ciągu, to te dwa pierwsze są dane, a dwa kolejne są rekurencyjnie obliczone. To jedynie jeden z przykładów ciągu. Kolejnym dobrym przykładem może być ciąg okreslony wzorem
. Teraz rozpatrzmy sobie taki problem. Załóżmy, ze mamy ciąg
zadany rekurencją z pierwszego przykładu. Należy znaleźć wzór na ten ciąg
, czyli znaleźć funkcję
taką, że
, co oznacza, że wszystko prócz n to parametry, a n jest argumentem tej funkcji. Będzie to przykład ciągu Fibonacciego zadanego rekurencyjnie o postaci
, gdzie mamy dane
, oraz współczynniki a = b = 1. Obliczając kolejne wyrazy otrzymamy właśnie ciąg liczbowy Fibonacciego: 1, 1, 2, 3, 5, 8, 13, … I tak
. Przedstawmy rozwiązanie tego problemu w postaci twierdzenia, czy też założenia. Mamy zależność rekurencyjną
, gdzie mamy dane, że a i b to rzeczywiste liczby, jak również
. Rozpatrzymy teraz tak zwane równanie charakterystyczne związane z tym ciągiem rekurencyjnym, a mianowicie
. Jeśli równanie charakterystyczne ma dwa pierwiastki (miejsca zerowe
, gdzie
), to ten wzór ma postać
, gdzie
są stałymi wyznaczonymi przez parametry równania
. Z kolei jeśli jest tylko jeden pierwiastek tego równania z miejscem zerowym r, to wtedy
. I taka postać słuzy do wyznaczania stałych
z ponizszego układu równań:

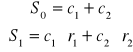
dla dwóch rozwiązań układu i dla jednego rozwiązania: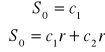
.

I to twierdzenie rozwiązuje cały ten problem. Teraz zobaczmy, jak to wygląda dla tego naszego ciągu Fibonacciego, czyli spójrzmy na przykład zastosowania twierdzenia dla ciągu Fibonacciego. Zobaczmy, jak wygląda to równanie charakterystyczne dla tego ciągu. Jest ono postaci
. Należy policzyć deltę i je rozwiązać. A zatem liczymy. Widzimy, że delta wynosi 5. A zatem nasze miejsca zerowe wyniosą
. Korzystając z naszych wzorów otrzymujemy w rezultacie wzór ciągu

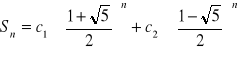
. Z tego stałe
są równe:
.

I ostatecznie otrzymujemy wzór ciągu na liczby Fibonacciego:

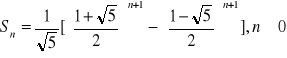
Teraz natomiast przejdziemy do takiego działu, co się nazywa zliczanie funkcji. Pod pojęciem funkcji będziemy tu rozumieli przekształcenie
, gdzie X to dziedzina funkcji, a Y - zbiór wartości. Inaczej można to przedstawić w postaci
. Pamiętać należy, że danemu argumentowi odpowiada tylko jedna wartość funkcji:

I my będizemy rozpatrywali taki przypadek, że X, Y to będą zbiory skończone zawierające skończoną liczbę elementów. Z kolei |X| = n to liczba elementów zbioru X, zaś |Y| = m to liczba elementów zbioru Y. Jeśli m będzie równe 0, oznaczać to będize, że Y jest zbiorem pustym. Zwykle elementy zbioru X oznaczamy w taki sposób:
, albo w postaci ciągu n - elementowego: (
). Nas będzie interesował problem związany ze zbiorem wszystkich funkcji. Jeśli napiszemy Fun(X,Y)={f:X->Y}, to będzie to oznaczało, ze jest to zbiór wszystkich funkcji przekształcających zbiór X w zbiór Y. Z kolei jeśli napiszemy Fun(X,Y)|, to to oznaczać będzie liczbę wszystkich funkcji X -> Y. No i teraz przytoczymy takie pierwsze twierdzenie, że Fun(X,Y)| =
, gdzie n to |X|, a m - |Y|. Jednak z takim szczególnym przypadkiem mamy do czynienia, gdy |Y| = 2. Wówczas jeśli |Y| = n, to Fun(X,Y)| =
, co daje nam wzór na ciąg zerojedynkowy.

X

---