Badania operacyjne - ćwiczenia

Prowadzący: Piotr Danielczyk

Ćwiczenia 1 26 luty 2003

Optymalizacja liniowa

Przykład 1.

Rafineria ropy naftowej zakupuje do przerobu 2 gatunki ropy R1 i R2 w cenach odpowiednio 7 i 14 jednostek pieniężnych za jednostkę przerobową. Proces technologiczny odbywający się w wieży rektyfikacyjnej daje 3 produkty. Z jednostki przerobowej ropy R1 otrzymuje się 16 hektolitrów benzyny, 20 hektolitrów oleju i 24 hektolitry pozostałości. Z jednostki przerobowej ropy R2 otrzymuje się 48 hektolitrów benzyny, 10 hektolitrów oleju i 14 hektolitry pozostałości. Ile należy zakupić ropy R1 i R2 aby wyprodukować 48000 hektolitrów benzyny oraz 20000 hektolitrów oleju napędowego przy minimalnym koszcie nabycia surowca. Należy wziąć pod uwagę, że zdolność przerobowa wieży mierzona łączną objętością produktów wynosi 144 tys. hektolitrów.

1. Sformułuj model matematyczny;

2. Rozwiązać metodą graficzną;

ROZWIĄZANIE:

a) ustalenie zmiennych decyzyjnych (niewiadomych):

x1 - ilość ropy R1

x2 - ilość ropy R2

b) definicja funkcji celu (wyrażenie, które ma osiągnąć ekstremum - MIN lub MAX):

min koszt nabycia surowca

c) Ograniczenia:

16x1+48x2 ≥ 48000 tyle ma być w sumie benzyny

20x1+10x2 ≥ 20000 tyle ma być oleju

60x1+72x2 ≤ 144000 ograniczenie możliwości przerobowych

x1, x2 ≥ 0

Rozwiązanie graficzne patrz Ćwiczenia 2

Przykład 2.

Dwaj sąsiedzi postanowili wymienić stare drewniane przęsła płotu na nowe metalowe. Dysponując metalowymi prętami o długości 300 cm chcą zminimalizować marnowanie materiału wynikłe z nierozsądnego rozcinania. Do wykonania mają 6 przęseł po 20 prętów o długości 140 cm, 6 przęseł na które składa się 10 prętów o długości 110 cm oraz 20 przęseł po 34 pręty o długości 40 cm. Zaplanuj cięcie minimalizujące odpad materiału.

ROZWIĄZANIE:

Możliwości pocięcia pręta 300 cm

długość pręta	I	II	III	IV	V	VI		ilość prętów	Ilość przęseł	Razem prętów
140 cm	2	1	1	0	0	0			20	6	120
110 cm	0	1	0	2	1	0			10	6	60
40 cm	0	1	4	2	4	7			34	20	680
Odpad	20 cm	10 cm	0 cm	0 cm	30 cm	20 cm

a) ustalenie zmiennych decyzyjnych (niewiadomych):

x_i - sposób cięcia i=1...6 (ile razy dany sposób cięcia będzie użyty)

b) definicja funkcji celu (odpad ma być minimalny):

c) Ograniczenia:

z każdego cięcia x1 otrzymamy 2 pręty 140 cm + z każdego cięcia x2 otrzymamy 1 pręt 140 cm itd.

x_i>0

Przykład 3.

Do ogrzania dwóch pomieszczeń o jednakowych temperaturach początkowych wynoszących 0 stopni używa się węgla i koksu. Spalenie 1 kg węgla powoduje wzrost temperatury w pierwszym pomieszczeniu o 3 stopnie, a w drugim o 2 stopnie. Spalenie 1kg koksu powoduje wzrost temperatury w pierwszym pomieszczeniu o 1 stopień a w drugim o 2 stopnie. Minimalny wzrost temperatury powinien wynosić; w pomieszczeniu „1” - 18 stopni, w pomieszczeniu „2” - 20 stopni. Ze względu na przepisy ochrony środowiska koks powinien stanowić 1/3 masy całego opału.

Ustalić jakie ilości węgla i koksu należy spalić aby łączny koszt opału był najmniejszy. Tona węgla kosztuje 600 a tona koksu 900 jednostek.

ROZWIĄZANIE:

a) ustalenie zmiennych decyzyjnych (niewiadomych):

x1 - ilość węgla

x2 - ilość koksu

b) definicja funkcji celu (minimalny koszt opału):

min.

c) Ograniczenia:

pomieszczenie „1”

(spalenie x1 kilogramów węgla razy wzrost o 3^O na każdy spalony kilogram + spalenie x2 kilogramów koksu razy wzrost o 1^O na każdy spalony kilogram ma dać temp 18^O )

pomieszczenie „2”

1/3 całej masy ma stanowić koks

Ćwiczenia 2 12 marzec 2003

Graficzne rozwiązywanie zadań z optymalizacji liniowej.

Do przykładu 1 z Ćwiczeń 1 (zadanie z ropą).

min koszt nabycia surowca

1) 16x1+48x2 ≥ 48000 tyle ma być w sumie benzyny

2) 20x1+10x2 ≥ 20000 tyle ma być oleju

3) 60x1+72x2 ≤ 144000

Równania powyżej są to równania prostych postaci y=ax+b. Zbiorem rozwiązań nierówności jest półpłaszczyzna wyznaczana przez prostą i to co jest powyżej lub poniżej tej prostej (należy uważać aby wziąć dobry obszar, najlepiej podstawić dowolny punkt i sprawdzić czy nierówność zachodzi). Prosta należy do rozwiązania, gdy są znaki ≤ lub ≥ .

Szukamy co najmniej dwóch punktów aby te proste narysować:

1. (0, 1000), (3000, 0)

2. (0, 2000), (1000, 0)

3. (0, 2000), (2400, 0)

Rysujemy te proste w układzie współrzędnych:

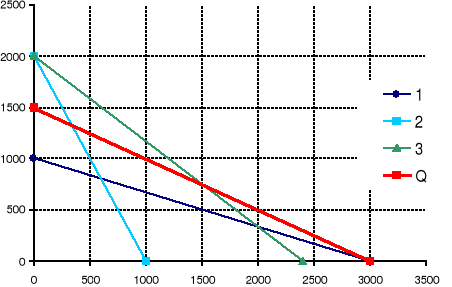
Jak ustalamy punkt optymalny?

Zakładamy dowolną („rozsądną”) wartość funkcji celu Q:

np. 21000 (tyle, ponieważ nierówności też mają wartości podobnego rzędu)

Szukamy dwóch punktów o wsp. x1 i x2, aby narysować prostą funkcji celu:

(0,1500) (3000,0)

Rysujemy „prostą celu” czerwona prosta na wykresie

Jeżeli chcemy rozwiązać zadanie szukania MINIMUM funkcji celu to przesuwamy prostą celu równolegle tak, aby przecięła obszar dopuszczalny możliwie blisko punktu początku układu współrzędnych (tak odległość punktu 0,0 od prostej celu była minimalna) - czerwona linia przerywana na wykresie. Jeżeli szukamy MAXIMUM to przesuwamy prostą celu równolegle tak, aby przecięła obszar dopuszczalny możliwie jak najdalej od punktu początku układu współrzędnych (tak aby odległość punktu 0,0 od prostej celu była maksymalna).

Otrzymany w ten sposób punkt przecięcia wyznacza nam optymalne rozwiązanie zadania.

Dla przykładu jest to:

x1=600 i x2=800 a funkcja celu Q ma wartość

Trochę teoretycznych sformułowań (nazewnictwo):

• jeżeli w punkcie optymalnym lewa strona ograniczenia równa się prawej to mówimy, że to ograniczenie jest wiążące;

w nierów. 1 16*600 + 48*800 = 48000 zatem 48000 ≥ 48000

w nierów. 2 20000 ≥ 20000

Widać to na wykresie, ponieważ punkt optymalny leży na przecięciu wykresu 1 i 2.

• jeżeli nie są równe to mówimy, że mamy luz (w nierów. 3 93600 ≤ 144000, oznacza to, że mamy ponad 50000 mocy przerobowej wieży nie wykorzystywane).

DENEGERACJE ZADANIA:

• Jeżeli się okaże, że te obszary nie mają części wspólnej to obszar dopuszczalny jest zbiorem pustym, tzn. zadanie jest sprzeczne

• jeżeli mamy do wyznaczenia maksimum funkcji celu Qmax a obszar dopuszczalny jest taki jak na rysunku poniżej to mówimy, że funkcja celu jest nieograniczona (nie znajdziemy maksimum, ale co najwyżej minimum)

• obszarem dopuszczalnym może być również odcinek

A Q

Q'

B

• jeżeli mamy do wyznaczenia maksimum funkcji celu Qmax a obszar dopuszczalny jest taki jak na rysunku i jednocześnie prosta funkcji celu jest równoległa do ograniczenia 3 to wtedy rozwiązaniem jest zbiór punktów należących do odcinka AB

3

Q

• jeżeli zbiorem dopuszczalnym jest punkt powstały w wyniku przecięcia się ograniczeń to wtedy zadanie traci sens

ĆWICZENIE:

Dobrać wartość parametru α tak, aby uniknąć nieskończenie wielu rozwiązań zadania (degeneracji).

Dane:

Q=αx₁+x₂ MIN

Ograniczenia:

x₁+x₂ ≤ 60 rów. 1. (60, 0) (0, 60)

6x₁+2x₂ ≥ 120 rów. 2. (20, 0) (0, 60)

x₁+4x₂ ≥ 60 rów. 3. (0, 15) (60, 0)

x₁-3x₂ ≤ 0 rów. 4. (60, 20) (30, 10)

x₂ ≤ 45 rów. 5.

x₁, x₂ ≥ 0

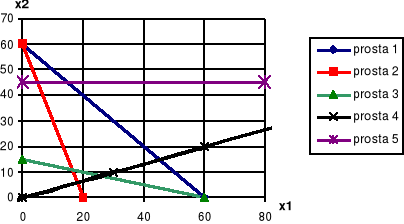
punkt optymalny dla Qmin

Aby zadanie nie uległo degeneracji (nie miało wielu rozwiązań) to prosta funkcji celu nie może być równoległa do ograniczenia 3 (prosta 3). Zatem z rów. 3 mamy:

x₁ + 4x₂ = 60

4x₂= 60 - x₁ /:4

x₂ = 15 - ¼x₁

Przekształcając funkcję celu otrzymujemy:

Q = αx₁ + x₂

x₂ = Q - αx₁

Porównując współczynniki przy x₁ mamy:

-α =-¼

α = ¼

Aby proste tych dwu funkcji (Q i ograniczenia 3) nie były równoległe to muszą mieć różne te współczynniki przy x₁. Ostatecznie zatem wsp. α musi być różny od ¼.

Odp. α ≠ ¼

ĆWICZENIE:

Znajdź punkt optymalne mając daną następującą funkcję celu i ograniczenia:

Dane:

Q=x₁+x₂ MAX

Ograniczenia:

2x₁+x₂ ≥ 4 rów. 1. (0, 4) (2, 0)

5x₁+2x₂ ≤ 40 rów. 2. (10, -5) (0, 20)

5x₁+6x₂ = 60 rów. 3. to ograniczenie spełniają tylko punkty leżące

na prostej (żółty odcinek) (0, 15) (60, 0)

x₁ ≥ 1 rów. 4.

0 ≤ x₂ ≤ 8 rów. 5.

x₁, x₂ ≥ 0

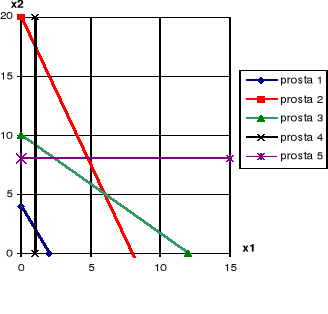
wynika z ograniczenia 5

Q

Odp. Rozwiązaniem optymalnym jest punkt (6, 5)

Ćwiczenia 3 26 marzec 2003

Postacie zadania programowania liniowego.

Zagadnienie omówione na przykładzie zadania z ropą:

min

1) 16x1+48x2 ≥ 48000 tyle ma być w sumie benzyny

2) 20x1+10x2 ≥ 20000 tyle ma być oleju

3) 60x1+72x2 ≤ 144000

Pierwsza postać to POSTAĆ OGÓLNA :

Q=c^T x MIN

[A] x ≤ b

gdzie:

• Q - funkcja celu;

• c - wektor kosztów;

• x - wektor niewiadomych

Postać ta zwykle wynika z treści zadania.

Druga postać to POSTAĆ STANDARDOWA

Q=c^T x MIN

[A] x = b (“=” bo rozwiązania zadań programowania liniowego leżą w wierzchołkach wielościanu, zawężamy poszukiwania)

JAK SPROWADZIĆ ZADANIE Z POSTACI OGÓLNEJ DO STANDARDOWEJ?

Sprowadzenie to polega na wprowadzeniu zmiennych uzupełniających (dodaniu lub odjęciu tych zmiennych). Odejmujemy/dodajemy tyle ile jest za dużo/za mało aby uzyskać w nierównościach ograniczających znak równości.

Dla naszego zadania wygląda to następująco:

1) 16 x1+48 x2 - x3 = 48000 // tu -x3 bo był znak ≥

2) 20 x1+10 x2 - x4 = 20000 // tu -x4 bo był znak ≥

3) 60 x1+72 x2 + x5 = 14400 // tu +x5 bo był znak ≤

Dodatkowe zmienne nie mogą zmieniać funkcji celu Q dlatego wchodzą one do tej funkcji ze współczynnikami 0:

Q=7 x1 + 14 x2 + 0 x3 + 0 x4 + 0x5 MIN

Jeżeli w funkcji celu szukalibyśmy MAX to aby zadanie było w postaci standardowej musimy tę funkcję zamienić na funkcję szukania MIN. Aby z zadania na maksymalizację przejść do zadania poszukiwania minimum celu to składowe wektora c (składniki funkcji celu) mnożymy przez -1.

Postać trzecia to POSTAĆ KANONICZNA

Jeżeli macierz [A] uda nam się rozłożyć na macierz bazową i resztę oraz wektor x uda się rozłożyć na część bazową i resztę, czyli [B N]*
=b i jeżeli macierz bazowa B jest macierzą jednostkową to taką postać zadania nazywamy kanoniczną. Jeżeli macierz B nie jest jednostkowa to trzeba ją doprowadzić do tej postaci (poprzez odpowiednie operacje na wierszach i kolumnach macierzy). Dla algorytmu sympleks b musi być ≥ 0.

Zad. dom. Sprowadź zadanie z ropą do postaci kanonicznej i rozwiąż wykorzystując algorytm sympleks.

PRZYKŁAD na zadaniu z cięciem.

1)

2)

2)

To zadanie jest już w postaci standardowej, ponieważ Q MIN oraz w ograniczeniach są znaki równości „=”.

Trzeba je doprowadzić do postaci kanonicznej (czyli trzeba znaleźć jakąś macierz jednostkową). W tym celu np. od równania 1 i 3 odejmiemy równanie 2:

2x1 + 0x2 + 1x3 - 2x4 - 1x5 = 60 /:2

0x1 + 1x2 + 0x3 + 2x4 + 1x5 = 60

0x1 + 0x2 + 4x3 + 0x4 + 3x5 + 7x6 = 620 /:7

Następnie w celu uproszczenia podzielimy równanie 1 przez liczbę 2 oraz równanie 3 przez liczbę 7:

1x1 + 0x2 +
x3 - 1x4 -
x5 + 0x6 = 30

0x1 + 1x2 + 0x3 + 2x4 + 1x5 + 0x6 = 60

0x1 + 0x2 +
x3 + 0x4 +
x5 + 1x6 =

Otrzymaliśmy już macierz jednostkową. Zatem zgodnie z postacią kanoniczną możemy zapisać:

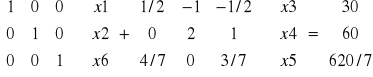
B x_B N x_N b

Mając postać kanoniczną możemy przejść do algorytmu SYMPLEKS.

ALGORYTM SYMPLEKS.

KROK 1.

Dana jest taka baza B, że x_B=B^-1 • b ≥ 0 (musi być spełniony ten warunek).

W naszym zadaniu z cięciem wygląda to następująco:

x_B= I •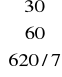
=

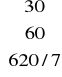
gdzie: I - macierz jednostkowa (macierzą odwrotną do macierzy jednostkowej jest macierz jednostkowa)

x_B - nazywa się to pierwszym rozwiązaniem bazowym.

KROK 2.

Wyznaczamy wektor mnożników sympleksowych:

λ^T = c_B^T • B^-1 = [20 10 20] • I = [20 10 20]

gdzie:

• c_B^T - to jest wektor tych współczynników z funkcji celu, które stoją w macierzy bazowej x_B ( w naszym zadaniu są to współczynniki stojące przy x1, x2, x6)

KROK 3.

Wyznaczamy wektor względny funkcji celu:

p^T = c_N^T -λ^T • N = [0 0 30] - [20 10 20] •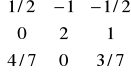
=

gdzie:

• c_N^T - to jest wektor części niebazowej współczynników funkcji celu (czyli te współczynniki przy x-ach z funkcji celu, które nie stoją w macierzy bazowej x_B ( w naszym zadaniu są to współczynniki stojące przy x3, x4, x5)

• N - część niebazowa wektora A

Wśród składowych wektora p wybieramy składową najmniejszą ujemną („najbardziej ujemną”). Kolumna odpowiadająca tej składowej zostaje wprowadzona do bazy. W przypadku, gdy w wektorze p nie ma składowych ujemnych algorytm ustaje, a bieżące rozwiązanie jest rozwiązaniem optymalnym. (na razie rozwiązaniem optymalnym u nas jest x_B z kroku 1).

W naszym zadaniu najmniejszą ujemną liczbą jest -150/7, a odpowiada jej kolumna x3. Tę kolumnę wprowadzamy do bazy.

KROK 4.

W kroku 4 ustalamy z kolei, która zmienna ma bazę opuścić:

y= B^-1 * a_k

gdzie k to numer kolumny, która ma wejść do bazy (u nas do bazy wchodzi x3).

Następnie wybieramy najmniejszą liczbę ze zbioru:

min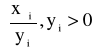

Dla naszego zadania wygląda to następująco:

y= B^-1 * a_k = I *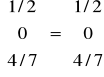
to są te y_i

min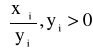
= min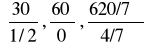
= min
=60

Zatem bazę opuszcza kolumna odpowiadająca zmiennej x1.

Po zamianie kolumn w macierzach otrzymujemy:

B x_B N x_N b

Wyznaczamy nowe rozwiązanie bazowe. Potrzebna do tego jest macierz odwrotna do B (ale teraz nie jest to macierz jednostkowa, bo B nie jest też macierzą jednostkową):

B^-1=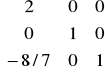

nowe rozwiązanie bazowe:

x_B=B^-1 • b =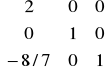
•
=

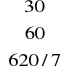
Obliczamy wartość funkcji celu przed pierwszą iteracją, dla pierwszego rozwiązania bazowego x_B:

Q⁰=c^Tx=
•
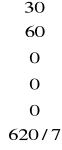
=2971

oraz wartość funkcji celu po pierwszej iteracji, dla nowego rozwiązania bazowego:

Q¹=c^Tx=
•
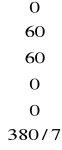
=1686

Wartość funkcji celu zmalała, więc możemy przypuszczać, że nasze obliczenia są poprawne.

Dalej liczymy podobnie jak w pierwszej iteracji.

- z kroku 2 wyznaczamy wektor mnożników sympleksowych:

λ^T = c_B^T • B^-1 = [0 10 20] •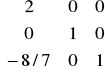
=

- z kroku 3 wyznaczamy wektor względny funkcji celu:

p^T = c_N^T -λ^T • N = [20 0 30] -
•
=

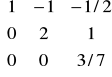
Najmniejszą ujemną liczbą jest -300/7, a odpowiada jej kolumna x4. Teraz tą kolumnę wprowadzamy do bazy.

- z kroku 4 - ustalamy, która zmienna ma bazę opuścić:

y= B^-1 * a_k =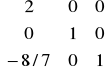
*

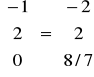
min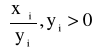
= min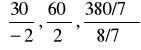
= min
=30

Bazę opuszcza kolumna odpowiadająca zmiennej x2.

Po zamianie kolumn w macierzach otrzymujemy:

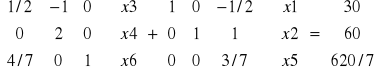
B x_B N x_N b

Wyznaczamy kolejne rozwiązanie bazowe.

B^-1=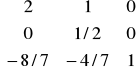

nowe rozwiązanie bazowe:

x_B=B^-1 • b =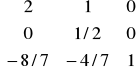
•
=

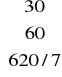
Obliczmy wartość funkcji celu, dla nowego rozwiązania bazowego:

Q²=c^Tx=
•
=400

Wartość funkcji celu zmalała, więc możemy przypuszczać, że nasze obliczenia są poprawne.

Dalej liczymy podobnie jak w pierwszej i drugiej iteracji.

- z kroku 2 wyznaczamy wektor mnożników sympleksowych:

λ^T = c_B^T • B^-1 = [0 0 20] •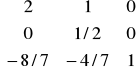
=

- z kroku 3 wyznaczamy wektor względny funkcji celu:

p^T = c_N^T -λ^T • N = [20 10 30] -
•
=

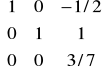
Wszystkie wartości są dodatnie. Tu algorytm się kończy, a bieżące rozwiązanie bazowe jest rozwiązaniem optymalnym. Końcowa odpowiedź brzmi:

Aby uzyskać odpowiednią ilość patyków to pierwszy sposób cięcia należy wykorzystać x1=0 razy, z2=0, x3=120, x4=30, x5=0, x6=20, a odpad jaki pozostanie wyniesie 400.

Ćwiczenia 4 9 kwiecień 2003

Rozwiązanie zad. Domowego:

Sprowadź zadanie z ropą do postaci kanonicznej i rozwiąż wykorzystując algorytm sympleks.

•

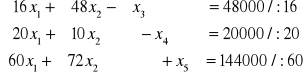
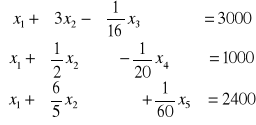
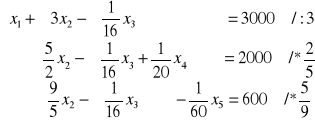
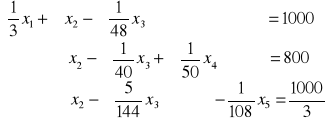
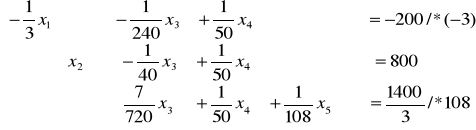
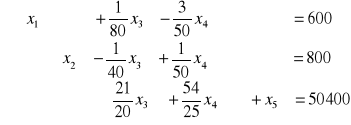
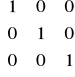
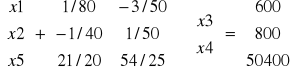
ODWRACANIE MACIERZY

W przypadku zadań programowania liniowego, rozwiązywanych metodą sympleks można łatwo znaleźć macierz odwrotną do danej macierzy bazowej. Potrzebna jest znajomość wcześniejszej macierzy bazowej (pierwszą macierzą bazową jest macierz jednostkowa), odwrotnej do niej oraz wektora y.

W zadaniu, na którym omówiona była metoda sympleks mieliśmy następującą macierz bazową B₁

B₁=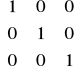
zamieniana była pierwsza kolumna

Po pierwszej wymianie macierz bazowa B₂ wyglądała następująco:

B₂=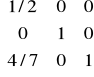

Wektor y wynosił y=

Jak utworzyć macierz odwrotną B₂^-1?

Można zastosować wzór B₂^-1=E * B₁^-1 (dla macierzy jednostkowej B₁ macierz odwrotna B₁^-1 jest również macierzą jednostkową).

Jak tworzy się macierz E?

• na pewno ma wymiar macierzy B

• dla tych kolumn B₁ i B₂, dla których macierze te się nie różnią, macierz E jest macierzą jednostkową:

E=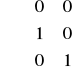

• wartości dla kolumny którą macierze B­₁ i B₂ różnią się obliczamy następująco:

• odnosimy wszystkie działania do tego elementu z wektora y który ma ten sam numer co kolumna którą się te macierze różnią - w naszym przypadku jest to element pierwszy czyli ½ (nazwijmy go „głównym”).

• Element z macierzy E o tym samym numerze co kolumna różniąca się jest równy odwrotności wybranego („głównego”) elementu z y. W naszym przypadku jest to pierwszy element z macierzy E i jest on odwrotnością pierwszego elementu z y.

• Pozostałe elementy macierzy E są równe odpowiadającym im numerami elementom wektora y podzielonymi przez element „główny” wektora y i ze znakiem „-„. W naszym przypadku:

• Drugi element E to drugi element z y podzielony przez pierwszy element z y i ze znakiem -

• Trzeci element E to trzeci element z y podzielony przez pierwszy element z y i ze znakiem -.

E=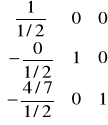
=

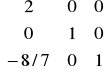
Ostatecznie :

B₂^-1=E*B₁^-1 =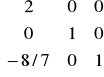
*
=

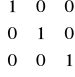
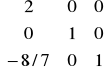
Kolejny przykład:

B₂=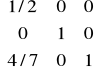
B₃=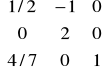
y=

Kolumny 1 i 3 nie różnią się więc dla nich jest macierz jednostkowa:

E=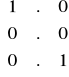

Różnią się kolumną 2, zatem:

• drugi element drugiej kolumny macierzy E jest równy odwrotności drugiego elementu y, czyli ½.

• Pierwszy element drugiej kolumny macierzy E jest równy pierwszemu elementowi y podzielonemu przez drugi element y i ze znakiem „-„ czyli -(-2/2 )=1

• Trzeci element drugiej kolumny macierzy E jest równy trzeciemu elementowi y podzielonemu przez drugi element y i ze znakiem „-„ czyli -(8/7 : 2 )=-4/7

E=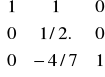

B₃^-1=E * B₂^-1 =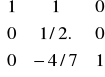
*
=

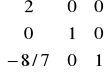
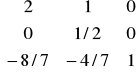
Ćwiczenia 5 23 kwiecień 2003

PROGRAMOWANIE ZERO-JEDYNKOWE.

Sformułowanie ogólne zadania 0/1.:

Q=c^Tx MIN

[A] x ≤ 0

x∈ {0, 1} - x mogą przyjmować tylko wartości 0 lub 1

Jeżeli mamy n=2 punkty (x) to mamy 2ⁿ=2²=4 możliwe kombinacje 0 i 1 (00,01,10,11).

Zadanie:

(rozwiązanie za pomocą arkusza Excel - dołączone w pliku excel1.xls - plik do ściągnięcia ze strony http://www.lectures.z.pl/)

Przedsiębiorstwu produkującemu materiały budowlane podlegają 4 zakłady. W każdym z nich może produkować dowolny spośród pięciu następujących wyrobów:

• cegła pełna

• cegła dziurawka

• cegła kratówka

• pustaki ścienny

• pustaki stropowe

Ze względu na niejednakowe warunki produkcji, zróżnicowane są koszty jednostkowe produkcji poszczególnych asortymentów. Koszty te podane są w tabeli:

Zakład	C. pełna	C. dziur.	C. krat.	P. ścienny	P. strop.
Z1	400 (x1)	320 (x2)	340 (x3)	1800 (x4)	1600 (x5)
Z2	320 (x6)	296 (x7)	280 (x8)	1750 (x9)	1340 (x10)
Z3	336 (x11)	285 (x12)	316 (x13)	1980 (x14)	1160 (x15)
Z4	388 (x16)	288 (x17)	332 (x18)	1960 (x19)	990 (x20)

Zakładając, że popyt na materiały jest tak duży, że każda ilość zostanie sprzedana, rozdzielić produkcję materiałów budowlanych pomiędzy poszczególne zakłady z punktu widzenia minimalizacji kosztów.

Należy pamiętać, że przedsiębiorstwo powinno:

1. dostarczać pełny asortyment wyrobów

2. każdy zakład powinien produkować co najmniej 1 wyrób.

Rozwiązanie:

Oznaczmy każdy wyrób w każdym zakładzie przez x_i - powstanie 20 niewiadomych.

Funkcja celu przyjmie postać:

Q=c^Tx=400x₁ + 320x₂ + ... +1960x₁₉ + 990x₂₀ MIN

Z drugiego ograniczenia (każdy zakład produkuje conajmniej 1 wyrób) mamy:

x₁ + x₂ + x₃ + x₄ + x₅ ≥ 1

x₆ + x₇ + x₈ + x₉ + x₁₀ ≥ 1

x₁₁ + x₁₂ + x₁₃ + x₁₄ + x₁₅ ≥ 1

x₁₆ + x₁₇ + x₁₈ + x₁₉ + x₂₀ ≥ 1

Z pierwszego ograniczenia (przedsiębiorstwo powinno dostarczać pełny asortyment) mamy:

x₁ + x₆ + x₁₁ + x₁₆ ≥ 1

x₂ + x₇ + x₁₂ + x₁₇ ≥ 1

x₃ + x₈ + x₁₃ + x₁₈ ≥ 1

x₄ + x₉ + x₁₄ + x₁₉ ≥ 1

x₅ + x₁₀ + x₁₅ + x₂₀ ≥ 1

Oraz:

x_i∈{0, 1}

Rozwiązanie zadania wykonać w Excel'u (plik excel1.xls)

ZADANIE DOMOWE:

Dla szachownicy 4x4 rozmieścić 4 królowe tak aby nie biły się:

≤ ≥ ≠ Φ ∈ ⊂ λ ∅
•

18

x3

x4

x6

X1 x4 x5

x3 x2 x6

x3 x2 x6 x2

x1 x4 x5

x3

x2

x6

x1 x2 x6 x1

x1

x2

x6

x3 x4 x5

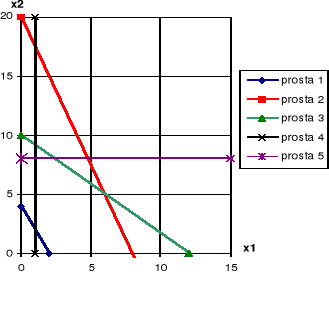
Punkt optymalny (rozwiązanie)

Q'

Jest to tzw. obszar dopuszczalny, każda para x2 i x2 z tego obszaru spełnia nierówności

---