5.2. Teorie i determinanty ceny pieniądza. Stopa procentowa a ryzyko. Wyznaczanie stopy forward. 140
Rozdział V: Cena i wartość pieniądza w czasie.
5.1. Wprowadzenie
Pieniądz jak każdy inny zasób będący towarem ma swoją cenę. Jest ona wyrażana w postaci stopy procentowej. Cena pieniądza wynika z faktu, że nie jest to „dobro wolne” dostępne każdemu w nieograniczonej ilości. Na rynku pieniądza tak jak na każdym innym występuje podaż i popyt. W relacjach odnoszących się do pożyczek i kredytów, podaż reprezentują pożyczkodawcy, a popyt - pożyczkobiorcy. Cenę pieniądza na tym rynku stanowi stopa procentowa, którą płacą pożyczkobiorcy, a uzyskują pożyczkodawcy. Należy tu podkreślić, że cena pieniądza wywiera olbrzymi wpływ w warunkach gospodarki rynkowej na wszystkie sfery życia gospodarczego i społecznego.
O pieniądz konkurują różne podmioty. Ostatecznie pozyskują te, które są (przy sprawnym rynku finansowym) efektywniejsze i są w stanie zapłacić wyższą cenę. W ten sposób zostają wyeliminowane te podmioty, które będąc mniej efektywne, nie są w stanie uzyskać od pożyczonych pieniędzy równie wysokiego efektu (stopy zwrotu) i nie mogą zaoferować za pieniądz tak wysokiej ceny.
Rosnący popyt na pieniądz powoduje wzrost jego ceny (stopy procentowej), co wywołuje z kolei wzrost podaży. Oznacza to, że więcej pożyczkodawców decyduje się wówczas na odłożenie w czasie swojej konsumpcji i udzielanie pożyczek. W praktyce przybiera to postać wzmożonego oszczędzania poprzez zwiększanie oszczędności w bankach. Gdy popyt na pieniądz z kolei spada, wówczas, jeżeli nie zmienia się podaż, na ogół pożyczkobiorcy domagają się obniżki jego ceny (stopy procentowej). Ogólnie można zatem powiedzieć, że cena pieniądza jest funkcją popytu i podaży środków pieniężnych. Znajomość zależności popytu i podaży na pieniądz umożliwia wyznaczanie takiej stopy procentowej, która w danym czasie równoważy rynek. Jest zatem oczywiste, że ten kto niezależnie od popytu i podaży posiada możliwość oddziaływania na cenę pieniądza może również wpływać na czynniki ją kształtujące (popyt i podaż). Takie możliwości mają banki centralne. Z kolei podmioty mające możliwości oddziaływania na popyt (w szczególności państwo) pośrednio wpływają również na cenę pieniądza (stopę procentową). Należy tu pamiętać, że zależność między ceną i popytem jest ujemna (wzrostowi ceny towarzyszy ceteris paribus spadek popytu). Analogicznie więc zależność między stopą procentową i popytem na pieniądz jest skorelowana ujemnie, co oznacza, że rosnącym stopom procentowym odpowiada spadek popytu. Natomiast, jeśli będziemy rozpatrywać zależność między podażą i ceną, to wiadomo, że wzrostowi ceny towarzyszy wzrost podaży. Wobec czego zależność między podażą funduszy pożyczkowych i stopą procentową jest dodatnia. Kształtowanie się ceny na rynku jako funkcji popytu i podaży przedstawia poniższy schemat.
Wykres 2. Popyt, podaż i cena na rynku pieniądza.
Źródło: opracowanie własne.
W rozdziale tym najpierw omawia się teorie wyjaśniające kształtowanie się stopy procentowej (ceny pieniądza), a następnie inne zmienne mające na nią wpływ oraz wyjaśnimy na przykładach wyznaczanie tzw. stopy forward przy znajomości stopy spot.
Po omówieniu determinant wpływających na cenę pieniądza w kolejnym punkcie zajmiemy się zagadnieniem zmiany wartości pieniądza w czasie. Omówimy takie pojęcia jak aprecjacja, deprecjacja, renta (w tym również tzw. renta dożywotnia) oraz zaprezentujemy szereg przykładów na obliczanie wartości przyszłej i obecnej. W końcowej części niniejszego rozdziału prezentuje się pojęcia i zależności między roczną nominalną i efektywną stopą procentową oraz stopą procentową dla podokresu kapitalizacji.
5.2. Teorie i determinanty ceny pieniądza. Stopa procentowa a ryzyko. Wyznaczanie stopy forward.
Malejący popyt na fundusze pożyczkowe wraz ze wzrostem stopy procentowej wyjaśnia teoria malejącej krańcowej użyteczności kapitału. W myśl tej teorii, pożyczkobiorcy przeznaczają pożyczone środki pieniężne w pierwszej kolejności na przedsięwzięcia o najwyższej dochodowości. Każde kolejne przedsięwzięcie będzie miało niższą stopę dochodu. Krańcowa produktywność netto angażowanego kapitału („jednostka dodatkowego zysku netto do jednostki dodatkowo angażowanego kapitału”) ulega w ten sposób systematycznemu obniżaniu, aż do zrównania ze stopą procentową. Obniżająca się stopa krańcowej produktywności kapitału powoduje, że jest coraz mniej podmiotów gotowych korzystać z funduszy pożyczkowych. Trzeba bowiem pamiętać, że poszczególne podmioty (firmy) mają różny poziom efektywności, stąd zrównywanie krańcowej stopy produktywności ze stopą procentową następuje najpierw w grupie podmiotów najmniej efektywnych, a następnie z funduszy pożyczkowych rezygnują podmioty o średniej efektywności i w końcu również pożyczkobiorcy najefektywniejsi.
Z kolei dodatnia zależność podaży funduszy pożyczkowych i stóp procentowych wyjaśniana jest działaniem „preferencji czasowej konsumenta” w zachowaniu jednostek (neoklasycy), albo „preferencją płynności” (keynsiści).
Według poglądów klasyków głównym źródłem podaży funduszy pożyczkowych są oszczędności konsumentów, którzy to bardziej cenią sobie konsumpcję bieżącą od przyszłej. Za odroczenie konsumpcji (utrata użyteczności z tytułu odroczenia w czasie) żądają oni wynagrodzenia w postaci oprocentowania swoich oszczędności. Im wyższe oprocentowanie, tym bardziej są oni skłonni odroczyć bieżącą konsumpcję na rzecz przyszłej znacznie większej. Poziom oprocentowania oszczędności przy którym konsumenci godzą się oszczędzać nosi nazwę „stopy preferencji czasowej”. Stopa ta nie jest równa dla każdego oszczędzającego, a zatem każdy sam subiektywnie określa przy jakiej stopie oprocentowania swoich oszczędności zgodzi się rezygnować z bieżącej konsumpcji na rzecz zwiększonej w przyszłości. W każdym razie, gdy stopa oprocentowania oszczędności na rynku pożyczkowym spadnie poniżej stopy preferencji czasowej, konsument przestaje oszczędzać i dlatego maleje podaż funduszy pożyczkowych. Natomiast wyższa stopa oprocentowania oszczędności na rynku od stopy preferencji czasowej konsumentów powoduje znaczny wzrost funduszy pożyczkowych, co z kolei sprawi, że na część z nich (przy danej stopie procentowej kredytów i pożyczek) nie będzie popytu. W konsekwencji nastąpi obniżenie stopy procentowej.. Zrównanie stopy oprocentowania oszczędności ze stopą preferencji czasowej konsumentów jest zatem w tej teorii poziomem równowagi popytu i podaży na pieniądz. Na podobnej koncepcji opiera się centralna część teorii finansów, tj. wartość pieniądza w czasie o której szerzej powiemy w kolejnym punkcie tegoż opracowania.
Z kolei „keynsiści” dodatnią zależność podaży funduszy pożyczkowych i stopy procentowej oszczędności wyjaśniają na podstawie zjawiska „preferencji płynności”. Istotą tego zjawiska jest dążenie każdej jednostki gospodarującej do utrzymywania części bieżącego dochodu oraz majątku w zasobach pieniężnych. Daje im to odpowiednią płynność finansową, która umożliwia realizację pojawiających się dochodowych przedsięwzięć. Zatem jednostka pożyczająca (oszczędzająca) środki pieniężne, niejako wyrzeka się możliwości wykorzystania pojawiających się okazji. Uzyskany procent jest więc premią za to wyrzeczenie. Wyższa od stopy preferencji płynności rynkowa stopa procentowa skłania jednostki do udzielania pożyczek, a zatem do ograniczania swoich preferencji płynności i odwrotnie. Tak więc cenę pieniądza (stopę procentową) przy której podmioty będą zaciągać i udzielać pożyczki pieniężne określa nie tylko krańcowa produktywność kapitału, ale również stopa preferencji czasowej lub stopa preferencji płynności.
Oprócz opisanych powyżej determinant wielkości stopy procentowej bardzo istotnymi zmiennymi objaśniającymi cenę pieniądza są oczekiwana stopa inflacji oraz ryzyko nieotrzymania spłaty pożyczonego kapitału. Uwzględniając te wszystkie wielkości zależność stopy procentowej od czynników kształtujących jej poziom wyraża następująca formuła:
![]()
(5.2.1)
gdzie:
Rnom - roczna nominalna stopa procentowa kredytu lub oprocentowanie obligacji (inaczej: stopa procentowa wymagana przez pożyczkodawcę),
kRF - stopa procentowa instrumentów wolnych od ryzyka,
PINFL - premia z tytułu spodziewanej inflacji,
Pnd - premia z tytułu ryzyka niewypłacalności dłużnika,
Pop - premia z tytułu ograniczenia płynności,
Pt - premia za termin (ryzyko podwyższone przez upływ czasu)
Korzystając z powyższej zależności poziom wymaganej przez pożyczkodawcę stopy procentowej dla instrumentów wolnych od ryzyka (np. lokat w obligacjach skarbowych) opisuje się następująco:
![]()
(5.2.2)
gdzie oznaczenia jak poprzednio.
W tym miejscu należy powiedzieć, że na rynku finansowym w zależności od różnych determinant wyróżnia się rozmaite rodzaje stóp procentowych. Jako przykładowe i najczęściej spotykane można by wymienić:
stopa procentowa z aktywów wolnych od ryzyka,
stopa aktywów o ryzyku niezerowym,
stopa procentowa nominalna (z uwzględnieniem wpływu oczekiwanej inflacji),
stopa procentowa realna,.
Należy przy tym jeszcze raz wskazać, że zawsze poziom stopy procentowej związany jest z poziomem ryzyka co oznacza, jak już zostało powiedziane w rozdziale pierwszym, że oczekiwanemu wyższemu poziomowi ryzyka aktywów, pożyczkodawca wyznacza wyższą stopę procentową (cenę) pożyczki. Przy tym samym poziomie ryzyka aktywów finansowanych, wysokość stopy procentowej różnicuje się ponadto w zależności od czasu spłaty pożyczki. Oznacza to, że stopa procentowa (cena pożyczanego pieniądza) jest wyższa w przypadku dłuższych terminów spłaty pożyczki, stąd kredyt długoterminowy jest z reguły droższy (wyższa stopa procentowa), aniżeli kredyt krótkoterminowy. Można tutaj wskazać również, że wyemitowane przez tego samego emitenta (a więc identyczna klasa ryzyka) instrumenty o różnym terminie zapadalności (wykupu) mają różne stopy zwrotu. Tak więc porównując na przykład oprocentowanie obligacji rocznych i trzyletnich zauważamy, że zazwyczaj wyższa stopa procentowa występuje w przypadku obligacji trzyletnich. W praktyce występują jednak często zjawiska wyższej stopy procentowej dla instrumentów finansowych (należących do tej samej klasy ryzyka) mających krótszy termin zapadalności. Można tu chociażby porównać dane na temat stóp WIBOR.
Ze względu na zróżnicowany poziom stopy procentowej w zależności od okresu zapadalności w finansach operuje się pojęciem tzw. „struktury czasowej stopy procentowej”, przez którą rozumie się relację między stopą procentową a okresem zapadalności aktywów w określonej klasie ryzyka. Na podstawie analizy struktury czasowej można określić jaką stopę inwestorzy akceptują dla przyszłych okresów. Dla przykładu znając rynkową stopę procentową dla obligacji rocznych i dwuletnich można wyliczyć poziom stopy procentowej akceptowany aktualnie przez inwestorów na okres zawierający się pomiędzy końcem pierwszego a końcem drugiego roku. Jest to tzw. stopa procentowa typu „forward” lub „future”. Zagadnienie to zostanie zilustrowane poniższym przykładem.
Przykład 6.
Inwestor „A” kupując obligację dwuletnią otrzyma stopę dochodu 14% w stosunku rocznym, natomiast inwestor „B” nabywa obligację roczną o stopie dochodu 12%. Jaką stopę dochodu musiałby uzyskać w drugim roku inwestor „B”, aby po dwóch latach ich oszczędności były równe?
Rozwiązanie.
Jeżeli obligacja inwestora „A” będzie wykupiona po dwóch latach jego stopa dochodu wyniesie:
![]()
.
Aby stopa dochodu inwestora „B” była taka sama musiałby on w drugim roku uzyskać stopę dochodu 16,035%, co wynika z prostego wyliczenia:
1,2996 : 1,12 = 1,16035 = 16,035%.
Stopy procentowe 12% i 14% to stopy „spot”, stopa 16,035% to stopa forward (hipotetyczna stopa procentowa, uzyskana w drugim roku oszczędzania). Znając realne stopy „spot” można wyznaczać hipotetyczne stopy „forward” („future”) dla różnych okresów. Korzystamy wówczas z następującej formuły:
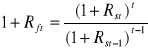
(5.2.3)
gdzie:
Rft - stopa procentowa typu forward dla roku t,
Rst - stopa procentowa typu spot dla roku t,
Rst-1 - stopa procentowa typu spot dla roku t-1,
t - numer okresu.
W naszym przykładzie, korzystając z powyższej zależności, stopę forward dla roku drugiego otrzymujemy:
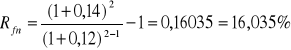
A zatem wyznaczona stopa typu forward według podanej formuły jest identyczna z obliczoną poprzednio.
Na zakończenie tych rozważań przeanalizujmy jeszcze jeden przykład.
Przykład 7.
Stopa od kredytu dwuletniego wynosi 20% a od kredytu rocznego 18%. Oba kredyty są spłacane na końcu okresu (tzn. odpowiednio po pierwszym i drugim roku). Oblicz jaka jest hipotetyczna stopa forward dla drugiego roku w przypadku kredytu rocznego.
Rozwiązanie.
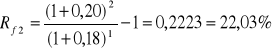
Obliczona stopa forward od kredytu pomiędzy końcem pierwszego i drugiego roku wynosi 22,03 % (wyjaśnij dlaczego?).
Znając poziom stopy „forward” (jak w przykładzie podanym powyżej) inwestor może przykładowo rozstrzygnąć, czy korzystniej będzie zaciągnąć kredyt dwuletni, czy też roczny, a następnie po roku go odnowić. W tym przykładzie jeżeli inwestor oszacuje, że realna roczna stopa oprocentowania kredytu (spot) w drugim roku ukształtuje się na poziomie niższym od 22,03% (i jest to jedyne kryterium), to z pewnością korzystniejsze będzie zaciągnięcie kredytu rocznego, a następnie odnowienie go na kolejny rok.
Podejmowanie prawidłowych decyzji na temat pozyskiwania i okresowego lokowania kapitałów firmy wymaga od menedżera finansowego nie tylko dobrej znajomości instrumentów, ale także stałego i uważnego analizowania cen pieniądza na rynkach finansowych.
5.3. Wartość pieniądza w czasie.
5.3.1. Istota i determinanty zmian wartości pieniądza w czasie.
Wskazywano już, że pieniądz jak każde inne dobro ma swoją wartość, którą wyraża jego cena - stopa procentowa (odsetki) zmieniająca się pod wpływem wielu czynników takich jak popyt i podaż, inflacja, ryzyko wierzyciela. Wspominano również, że cena pieniądza odzwierciedlająca jego wartość podlega wahaniom w czasie. Zmieniająca się w czasie wartość pieniądza powoduje, że nominalnie identyczna kwota ma różną wartość w różnych momentach. Spowodowane jest to występowaniem zjawiska deprecjacji oraz aprecjacji pieniądza polegającym na zmianach jego wartości pod wpływem ogólnych zmian cen towarów i usług. Zmiany polegające na spadku cen towarów i usług (deflacja) powodują zjawisko aprecjacji - wzrostu siły nabywczej pieniądza, natomiast wzrost cen towarów i usług (inflacja) powoduje deprecjację pieniądza. Jednakże w większości przypadków mamy do czynienia z malejącą wartością pieniądza w czasie. Wynika to ze znacznie powszechniejszego występowania w rzeczywistości gospodarczej inflacji niż deflacji. Poza tym konsumenci z reguły przedkładają bieżącą konsumpcję nad przyszłą a przez to wolą otrzymać pieniądz dzisiaj niż w przyszłości. Gdy nawet nie zdecydują się go natychmiastowo wydać mogą go zainwestować (np. założyć lokatę w banku). Dochody uzyskane w przyszłości dzięki dzisiejszym nakładom z reguły przewyższają wartość tych nakładów (w naszym przypadku uzyskany wkład będzie powiększony o odsetki).
Większość decyzji z zakresu zarządzania finansami związana jest z porównywaniem wartości strumieni pieniężnych teraz i w przyszłości (należy porównać bieżące nakłady i przyszłe efekty działalności osiągnięte dzięki przeprowadzonej inwestycji). Zainwestowanie środków pieniężnych obecnie ma na celu ich pomnożenie w przyszłości i jest równoznaczne z zamianą obecnych możliwości konsumpcyjnych na przyszłe. Jednakże dopiero określenie tempa zmian wartości pieniądza pozwala wyznaczyć parytet owej „zamiany obecnych możliwości konsumpcyjnych na przyszłe”, a tym samym ocenić racjonalność decyzji „dzisiejszego” wydatkowania środków pieniężnych z punktu widzenia kreowania wartości. Według wielu współczesnych teoretyków, wartość pieniądza w czasie jest centralną koncepcją finansów i wokół niej koncentrują się zainteresowania tejże nauki..
5.3.2. Wartość przyszła.
Podstawowe narzędzia analityczne umożliwiające prawidłowe porównywanie strumieni pieniężnych w czasie stanowią formuły na wyznaczanie wartości przyszłej (Future Value FV) i wartości zaktualizowanej (Present Value PV). Relację pomiędzy FV i PV wyznacza stopa procentowa „r” (cena pieniądza) oraz ilość jednostek czasu „n”. W niniejszym punkcie skoncentrujemy się na wyznaczaniu wartości przyszłej.
Wartość przyszła (FV) jest to wielkość do jakiej będzie rosnąć przepływ środków pieniężnych lub wiele przepływów środków pieniężnych w danym okresie. Inaczej jest to wartość środków pieniężnych jaką otrzymamy na końcu analizowanego okresu. Wynika ona głównie ze stopy procentowej przyjętej do obliczeń. Możliwe jest wyznaczanie wartości przyszłej zarówno poprzez zastosowanie tzw. prostej stopy procentowej, jak i złożonej stopy procentowej.
Prosta stopa procentowa (stosowana raczej rzadko) to stopa od „nie kapitalizowanej podstawy”. Stosujemy ją wówczas, gdy odsetki nie podlegają kapitalizacji tzn. po zakończonym podokresie nie są doliczane do kapitału. Jako przykład można podać naliczanie odsetek w przypadku 3-letnich obligacji skarbowych. Odsetki są wypłacane co kwartał jednakże, jeśli nabywca obligacji ich w terminie nie podejmie, „leżą” one na nie oprocentowanym koncie. Z kolei na następny kwartał odsetki są naliczane tylko od nominalnej wartości zakupionej obligacji. Znając stopę procentową dla zadanego okresu podstawowego wartość przyszłą w przedstawionym powyżej przypadku możemy wyznaczyć z następującego wzoru:
![]()
(5.3.2.1)
gdzie:
FV - wartość przyszła,
PV - wartość obecna (czyli wartość w dniu dzisiejszym - tzn. w dniu inwestycji),
n - liczba okresów.
r - stopa procentowa,
Dla lepszego zrozumienia omawianych zagadnień wszystkie przykłady będziemy przedstawiać na tzw. osi czasu. Oś taka wygląda następująco:
________→
t1 t2 t3
↓___↓___↓___↓
T0 T1 T2 T3
Na powyższej osi T0, T1, T2, T3 oznaczają początkowe momenty okresów, natomiast t1, t2, t3 symbolizują czas trwania poszczególnych okresów. Strzałka nad osią skierowana w prawo oznacza, że obliczamy wartość przyszłą (czyli wartość pieniądza na końcu okresu analizy; tu w momencie T3).
Przeanalizujmy powyżej omówione zagadnienie na przykładzie.
Przykład 8.
Wpłacamy na początku pierwszego okresu 1.000 PLN. Roczna stopa procentowa w danym okresie jest stała i wynosi 10%. Ile otrzymamy po trzech latach, przy założeniu, że odsetki nie są kapitalizowane.
Rozwiązanie:
Prezentacja graficzna dla powyższego przykładu wygląda następująco:
________→
t1 t2 t3
↓___↓___↓___↓
1.000 ?
Aby rozwiązać to zadanie korzystamy z przytoczonego wyżej wzoru. Podstawiając odpowiednie wielkości otrzymujemy:
FV = 1.000⋅(1+3⋅0,1) = 1.300.
Odpowiedź. Po trzech latach otrzymamy 1.300 PLN.
Zgodnie z założeniami odnośnie powyższego przykładu otrzymany wynik możemy również zinterpretować jako wartość przyszła dzisiejszych pieniędzy. Tak więc „dzisiejszy 1.000 PLN” będzie po trzech latach wart 1300 PLN (oczywiście przy założeniu 10% stopy procentowej oraz nie kapitalizowania odsetek). Wróćmy jednak do sposobu obliczenia tejże kwoty. Zamiast korzystać z przytoczonego wzoru moglibyśmy również obliczać „stopniowo” odsetki przysługujące nam po każdym okresie. Postępowalibyśmy wówczas następująco:
1000 ⋅ 0,1 = 100 odsetki po pierwszym roku
1000 ⋅ 0,1 = 100 odsetki po drugim roku
1000 ⋅ 0,1 = 100 odsetki po trzecim roku
__________
300 RAZEM ODSETKI
+ 1000 KAPITAŁ POCZĄTKOWY
________________
= 1300 OTRZYMANA KWOTA PO TRZECIM ROKU
Zatem w przypadku stosowania prostej stopy procentowej odsetki pierwszego, drugiego i trzeciego roku (ogólniej wszystkich podokresów) są identyczne.
Inaczej sytuacja się przedstawia, gdy zastosujemy tzw. złożoną stopę zwrotu. Zastosowanie takiej stopy oznacza, że odsetki są kapitalizowane tzn. po skończonym podokresie są one dopisywane do kapitału i w następnym podokresie odsetki obliczamy od podstawy, którą stanowi wartość początkowa powiększona o odsetki z poprzednich podokresów. Tak więc stosując złożoną stopę procentową posługujemy się regułą procentu składanego od aktualnie posiadanej kwoty pieniądza PV. Formuła na obliczenie wartości przyszłej w takim przypadku będzie miała następującą postać:
![]()
(5.3.2.2)
gdzie wszystkie wielkości jak w formule poprzedniej.
Przykład 9.
Dane jak w poprzednim przykładzie, z tym, że odsetki są co roku kapitalizowane (tzn. doliczane do kapitału).
Rozwiązanie:
Prezentacja graficzna wygląda tak samo jak w przykładzie poprzednim, czyli przedstawia się następująco:
________→
t1 t2 t3
↓___↓___↓___↓
?
Korzystając z formuły na obliczenie wartości przyszłej, gdy odsetki są kapitalizowane i podstawiając odpowiednie wielkości otrzymujemy:
FV = 1.000⋅(1+0,1)3 =1.331
Podobnie jak w przykładzie pierwszym możemy wyjaśnić skąd powstała ta wielkość analizując naliczanie odsetek krok po kroku. I tak otrzymujemy:
1.000 ⋅ (1+0,1) = 1.100 wartość po pierwszym roku
1.100 ⋅ (1+0,1) = 1.210 wartość po drugim roku
1.210 ⋅ (1+0,1) = 1.331 wartość po trzecim roku
Ogólnie wartość przyszła (FV) zależy od trzech czynników: wartości początkowej (PV), stopy procentowej (ceny pieniądza - r), ilości okresów (tutaj lat) naliczania odsetek n. Z kolei z porównania powyższych przykładów wnioskujemy, że przy tej samej wartości początkowej, tej samej stopie procentowej i równej ilości okresów wartość otrzymana po roku „X” jest zawsze większa, gdy odsetki są kapitalizowane.
Stopa procentowa „r” jest jednym z podstawowych wyznaczników decyzji finansowych firmy, gdyż odzwierciedla tzw. koszty utraconych korzyści (lub płynności) tj. cenę wynikającą z możliwości alternatywnych form zaangażowania kapitału przy identycznym poziomie ryzyka. Procent składany (1 + r)n dostarcza informacji o tempie przyrostu wartości PV (inwestycji) w okresie n. W tablicach finansowych można znaleźć wartości powyższego wyrażenia dla różnych wartości „r” oraz „n”, co przy przyjętej wartości „PV” ułatwia obliczanie „FV”.
Dotychczas rozważaliśmy przypadki wpływu i wypływu pieniądza jedynie w dwóch momentach, a mianowicie obecnie i w przyszłości. Jednak znacznie częściej konieczne jest obliczanie wartości przyszłej w sytuacji nieregularnych w czasie przepływów pieniądza. W takim przypadku będziemy posługiwać się następującym wzorem:
![]()
(5.3.2.3)
gdzie:
FVCF - wartość przyszła przepływów pieniężnych,
CFt - przepływ pieniężny w okresie t,
t - numer okresu
pozostałe oznaczenia jak poprzednio.
Dla lepszego zilustrowania tego zagadnienia posłużmy się następującym przykładem.
Przykład 10.
Firma „X” posiada obecnie w banku na rachunku depozytowym 1.000,0 PLN. Po roku wpłaci na ten rachunek 2.000,0 PLN, za dwa lata 3.000,0 PLN, a za trzy lata 4.000,0 PLN. Po trzech latach firma będzie musiała uregulować zobowiązania finansowe. Jaką kwotę zgromadzi do tego czasu, jeżeli oprocentowanie rachunku wynosi w skali rocznej 8%?
Rozwiązanie:
Na początek przedstawmy tą sytuację na osi czasu:
________→
t1 t2 t3
↓___↓___↓___↓
1.000 2.000 3.000 4.000
?
Jak widać początkowy wpływ finansowy będzie oprocentowany przez trzy lata, wpływ po pierwszym roku - przez dwa lata, po drugim roku - przez rok, natomiast wpływ po trzech latach - nie będzie oprocentowany (gdyż zostanie natychmiast wypłacony). Tak więc wartość na końcu trzeciego roku obliczymy odpowiednio:
FV = 1.000(1+0,08)3 + 2.000(1+0,08)2 + 3.000(1+0,08)1 + 4.000 =10.832,5PLN
W tym miejscu należy zwrócić uwagę na znaczenie momentu, w którym następują przepływy pieniężne. Jeżeli przepływy następują na początku okresu wówczas mówimy, że mamy do czynienia z przepływami płaconymi „z góry”, jeśli natomiast przepływy następują na końcu okresów wówczas są to przepływy płatne „z dołu”. Przeanalizujemy teraz jak będzie różnić się wartość przyszła przepływów pieniężnych w zależności od tego, czy wpływy będą następować z góry, czy z dołu.
Przykład 11.
Oblicz wartość przyszłą następujących przepływów pieniężnych (FVCF) płatnych na końcu okresów: CF1 = 1.000 PLN, CF2 = 2.000 PLN, a CF3 = 3.000 PLN.
Rozwiązanie:
a) prezentacja graficzna:
________→
t1 t2 t3
↓___↓___↓___↓
0 1.000 2.000 3.000
?
b) podstawienie do wzoru:
FVCF = 0 x (1 + 0,1) + 1.000 (1+0,1)2 + 2.000(1+0,1)1 + 3.000(1+0,1)0 = 1.210 + 2.200 + 3.000 = 6.410.
Tak więc wartość przyszła powyższych płatności płatnych na końcu okresów wynosi 6.410 PLN.
Zastanówmy się teraz, jaka byłaby wartość przyszła tych samych płatności jednakże płatnych „z góry”.
Przykład 12.
Oblicz wartość przyszłą następujących przepływów pieniężnych (FVCF) płatnych na początku okresów: CF0 = 1.000 PLN, CF1 = 2.000 PLN, a CF2 = 3.000 PLN.
Rozwiązanie:
a) prezentacja graficzna:
________→
t1 t2 t3
↓___↓___↓___↓
1.000 2.000 3.000 0
?
b) podstawiając do wzoru otrzymujemy:
FVCF = 1.000(1+0,1)3 + 2.000(1+0,1)2 +3.000(1+0,1)1 = 1.331 + 2.420 + 3.300 = 7.051
Zatem widać, że przy identycznych wpłatach ale dokonywanych raz „z dołu”, a raz „z góry” wartość przyszła jest wyższa dla wpływów dokonywanych „z góry”, gdyż każdy przepływ „procentuje” o okres dłużej. I tak w pierwszym przypadku 1.000PLN „procentowało przez dwa okresy w drugim przypadku - przez trzy okresy. Z kolei 2.000PLN „procentowało” w pierwszym przypadku przez jeden okres, natomiast w drugim przypadku - przez dwa okresy. Analogicznie 3.000PLN w pierwszym przypadku nie „procentowało” w ogóle (gdyż zaraz je podjęliśmy), natomiast w drugim przypadku „procentowało” przez jeden okres.
Ostatnią kwestią jaką poruszymy w tym podrozdziale będzie obliczanie wartości przyszłej strumieni pieniężnych (FVA) czyli przepływów równych płatności okresowych. Poprzednio zajmowaliśmy się przepływami, które następowały na początku lub na końcu okresów i były dokonywane w różnych wysokościach. Jeśli natomiast przepływy te byłyby w równych wysokościach wówczas moglibyśmy skorzystać z uproszczonych formuł obliczeniowych. I tak strumień równych płatności dokonywanych z góry obliczymy z następującego wzoru:
![]()
. (5.3.2.4)
gdzie:
FVA - wartość przyszła płatności okresowych,
An - płatność okresowa,
pozostałe wielkości jak poprzednio.
Natomiast strumień równych płatności dokonywanych z dołu obliczamy z formuły:
![]()
(5.3.2.5)
gdzie: wszystkie oznaczenia jak poprzednio.
Dla lepszego zilustrowania powyższych zagadnień przeanalizujmy następne przykłady.
Przykład 13.
Rodzice osoby odbywającej studia licencjackie wpłacają do banku co roku 1.000PLN. Wiedząc, że oprocentowanie wynosi 10% oblicz jaka będzie wartość przyszła tej lokaty w momencie ukończenia studiów przez syna/ córkę
w przypadku, gdy rodzice wpłacają pieniądze na początku roku akademickiego,
w przypadku, gdy rodzice wpłacają pieniądze po ukończeniu przez syna/ córkę roku akademickiego.
Rozwiązanie:
Przypadek a.
prezentacja graficzna
________→
t1 t2 t3
↓___↓___↓___↓
1000 1000 1000 0
?
Obliczenia:
FVA = 1000⋅{[(1+0,1)3+1 - 1] / 0,1} - 1 = 3.641
Przypadek b.
prezentacja graficzna:
________→
t1 t2 t3
↓___↓___↓___↓
0 1.000 1.000 1.000
?
Obliczenia:
FVA = 1000⋅ [(1+0,1)3 - 1] / 0,1 = 3.310
Tak więc widzimy ponownie, że wartość przyszła płatności dokonywanych „z góry” jest większa aniżeli płatności „z dołu”
5.3.3. Wartość obecna.
Wartość obecna (zaktualizowana) „PV” jest odwrotnością w stosunku do przedstawionej powyżej wartości przyszłej. Wartość zaktualizowana wyraża „obecną” (to jest w dniu dzisiejszym - dniu inwestycji) wartość przychodów spodziewanych w przyszłości. Jest to swoisty proces „powracania wartości w czasie”, który nosi nazwę dyskontowania, a stosowana stopa (cena pieniądza) nazywa się stopą dyskontową i jest oznaczana jako „k”. Wartość obecną możemy w związku z tym wyznaczyć na podstawie następującej formuły (powstałej z przekształcenia na obliczanie wartości przyszłej):
![]()
(5.3.3.1)
Oznaczenia są analogiczne do stosowanych poprzednio, jednakże stopa procentowa „r” została tutaj zastąpiona przez stopę dyskontową „k”.
Kwestią zasadniczą pozostaje dobór odpowiedniej stopy dyskontowej. W analizowanych przykładach w niniejszym rozdziale będziemy posługiwali się zadaną stopą określoną w zadaniach. Wyznaczaniem stopy dyskontowej zajmiemy się szerzej w rozdziale poświęconym kosztowi kapitału.
Przeanalizujmy poniższy przykład na wyznaczanie wartości obecnej pieniądza.
Przykład 14.
Oblicz, jaka jest obecna wartość 1.000 PLN, którą uzyskamy:
po roku,
po dwóch latach,
po trzech latach.
Zakładamy, że stopa dyskontowa wynosi:
10%
20 %
Rozwiązanie:
Prezentacja graficzna:
←________
t1 t2 t3
↓___↓___↓___↓
a) 1.000 b) 1.000 c) 1.000
?
Na powyższej osi czasu zostały umieszczone wszystkie trzy przypadki określone w zadaniu (to znaczy, gdy pieniądze otrzymamy po roku, po dwóch latach, po trzech latach). Należy tutaj zwrócić uwagę na kierunek strzałki nad wykresem. Ponieważ obliczamy wartość obecną przyszłego strumienia środków pieniężnych (czyli, jak gdyby cofamy w czasie) więc strzałka skierowana jest w lewo.
Podstawiając odpowiednie wielkości do przedstawionego powyżej wzoru otrzymujemy odpowiednio:
dla stopy dyskontowej 10%:
PV = 1000 ⋅ 1 / (1+0,1)1 = 909,1
PV = 1000 ⋅ 1 / (1+0,1)2 = 826,4
PV = 1000 ⋅ 1 / (1+0,1)3 = 751,3
a dla stopy dyskontowej 20%:
PV = 1000 ⋅ 1 / (1+0,2)1 = 833,3
PV = 1000 ⋅ 1 / (1+0,2)2 = 694,4
PV = 1000 ⋅ 1 / (1+0,2)3 = 578,7.
Zatem jak widać dla tej samej wartości nominalnej FV i przy tej samej stopie dyskontowej (cenie pieniądza) wartość PV spada w miarę wydłużania się okresu oczekiwania realizacji inwestycji (przyszłego dochodu). I tak mamy zawsze niższą wartość PV z tej samej wartości FV po trzecim roku aniżeli po drugim oraz porównując wielkości te po drugim i po pierwszym roku niższa jest ta pierwsza wartość. Oczywiście w kolejnych latach ta sama wartość FV będzie miała coraz niższą wartość PV. Wzrost stopy dyskontowej działa podobnie na zależność PV i FV tzn. wartość PV spada wraz ze wzrostem stopy dyskontowej „k”. Podsumowując te rozważania możemy stwierdzić, że wartość zaktualizowana jest tym niższa im bardziej oddalony jest w czasie moment uzyskania danej kwoty oraz im wyższa jest stopa dyskontowa.
Podane powyżej formuły umożliwiają nie tylko obliczanie wartości przyszłej i bieżącej, ale również rozwiązywanie szeregu istotnych problemów finansowych. Ilustruje to poniższy przykład.
Przykład 15.
Stopa procentowa na terminowym dwuletnim depozycie wynosi 10,0%. Jaką kwotę należy złożyć w banku aby na koniec drugiego roku otrzymać 100.000,0 PLN?
Rozwiązanie:
Na początek zilustrujmy ten przykład na osi czasu. Znamy wartość przyszłą (wartość jaką chcemy uzyskać po dwóch latach) w związku z tym nanieśmy ją na moment T2. Pytanie postawione w zadaniu dotyczy teraźniejszości (jaką wartość musimy dzisiaj złożyć w depozycie?), w związku z czym zaznaczmy w punkcie T0 „?” jako wielkość szukaną. Ponieważ szukamy wartości obecnej strzałkę kierujemy w lewo. Przedstawione zostało to na poniższej osi czasu.
←_____
t1 t2
↓___↓___↓
100.000
?
Wiedząc, że mamy obliczyć wartość obecną korzystamy z formuły na obliczenie wartości zaktualizowanej podstawiając odpowiednio:
PV = 100.000 ⋅ 1 / (1+0,1)2 = 826,4
Odpowiednie wielkości współczynników wartości przyszłej (1+r)n i zdyskontowanej 1/(1+k)n dla stopy procentowej (dyskontowej) od 0,5% do 50% oraz ilości okresów „n” od 1 do 50 można znaleźć w tablicach. Tablice te są niezwykle pomocne przy obliczeniach. Przykładowo aby obliczyć wartość FV po pięciu latach przy następujących założeniach:
PV równa się 50.000,0 PLN,
roczna stopa dyskontowa 12%,
wystarczy ustalić na podstawie właściwej tablicy współczynnik wartości przyszłej, który wynosi 1,76234 i pomnożyć go przez wartość PV. Zatem wartość FV wyniesie 50.000,0 ⋅ 1,76234 = 88.117,0 PLN.
Podobnie postępujemy przy obliczaniu wartości obecnej przy danej wartości przyszłej, stopie dyskontowej „k” oraz ilości okresów dyskontowania „n”. Na przykład, aby obliczyć PV dla FV = 88.117,0 PLN, „r”=12% i „n”-5 lat w tablicach znajdujemy wartość współczynnika dyskontowego dla tych wartości, która wynosi 0,56743, a następnie mnożymy tak odczytany współczynnik przez wartość FV. Zatem wartość PV wyniesie 88.117,0 PLN ⋅ 0,56743 = 50.000,2 PLN.
Zajmiemy się teraz obliczaniem wartości bieżącej PV dla regularnych przyszłych wpływów o różnej wartości. Aby w takim przypadku obliczyć wartość obecną należy posłużyć się następującą formułą:
![]()
(5.3.3.2)
gdzie:
PVCF - wartość obecna przepływów pieniężnych,
CFt - przepływ pieniężny w okresie “t”,
k - j.w.,
Aby lepiej zilustrować to zagadnienie przeanalizujmy następujący przykład.
Przykład 16.
Firma „X” na początku roku wydatkowała 10.000 PLN Dzięki tej inwestycji spodziewa się następujących wpływów gotówki:
na koniec roku pierwszego: 5.000,0 PLN
na koniec roku drugiego: 5.000,0 PLN,
natomiast na koniec roku trzeciego: 7.000,0 PLN.
Zakładając, że stopa dyskontowa „k” wynosi 10%, oblicz ile wynosi wartość obecna tych przepływów.
Rozwiązanie.
przedstawienie podanych przepływów pieniężnych na osi czasu
←________
t1 t2 t3
↓___↓___↓___↓
-10.000 5.000 5.000 7.000
?
uwzględniając momenty wpływów i wydatków podstawienie odpowiednich wielkości do zaprezentowanej powyżej formuły:
PVCF = 1/(1+10.000)0 + 1/(1+5.000)1 + 1/(1+5.000)2 + 1/(1+7.000)3 = 3.936,90 PLN
lub korzystając z tablic obliczamy wartość zaktualizowaną każdego strumienia gotówkowego z osobna:
CF0 na początku pierwszego roku =-10.000 ⋅ 1 =-10.000,0 PLN
CF1 na koniec pierwszego roku = 5.000 ⋅ 0,82643 = 4.545,5 PLN
CF2 na koniec drugiego roku = 5.000 ⋅ 0,75131 = 4.132,2 PLN
CF3 na koniec trzeciego roku = 7.000 ⋅ 0,68301 = 5.259,2 PLN
Razem PV = 3.936,9 PLN
Warto zwrócić uwagę, że CF1 = - 10.000,0 ⋅ 1, gdyż współczynnik wartości zdyskontowanej (k,n) dla okresu zerowego (n=0) zawsze wynosi 1 niezależnie od wartości „k”.
Jeśli określone płatności występujące na koniec lub na początek okresów są tej samej wielkości to wówczas, podobnie jak to robiliśmy w przypadku obliczania wartości przyszłej możemy skorzystać z uproszczonych formuł. I tak, jeśli przepływy następują na początku okresów, wówczas stosujemy formułę:
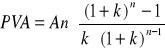
. (5.3.3.3)
gdzie:
PVA - wartość obecna płatności okresowych,
An - płatność okresowa,
pozostałe oznaczenia jak poprzednio.
Gdy przepływy występują na końcu okresów, to korzystamy ze wzoru:
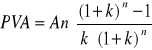
. (5.3.3.4)
gdzie: oznaczenia jak poprzednio.
Przeanalizujmy poniższy przykład.
Przykład 17.
Sprawdź, jaka jest wartość obecna płatności 1.000 PLN rocznie gdy:
zapłata następuje w trzech rocznych ratach na początku okresów („z góry”),
zapłata następuje w trzech rocznych ratach na końcu okresów („z dołu”).
Zakładana stopa dyskonta wynosi 10%.
Rozwiązanie:
punkt a:
←________
t1 t2 t3
↓___↓___↓___↓
1.000 1.000 1.000
?
obliczenia:
PVA = 1.000⋅ [(1+0,1)3 - 1] / [0,1⋅(1+0,1)3-1 = 1.000⋅[0,331 / 0,121] = 2.735,54 PLN
punkt b:
prezentacja graficzna:
←________
t1 t2 t3
↓___↓___↓___↓
1.000 1.000 1.000
?
obliczenia:
PVA = 1000⋅ [(1+0,1)3 - 1] / [0,1⋅(1+0,1)3 ]= 1000⋅[0,331 / 0,1331] = 2.486,85 PLN
Jak więc widać, w przypadku płatności z góry wartość obecna tychże przepływów pieniężnych wynosi 2.735,54 PLN, natomiast w przypadku płatności z dołu 2.486,85 PLN. Podobnie więc wartość obecna strumieni pieniężnych, tak samo jak i wartość przyszła, jest wyższa, kiedy przepływy następują z góry.
W przypadku omawiania wartości obecnej należy również poruszyć zagadnienie tzw. renty wieczystej rozumianej jako ciąg nieskończenie wielu takich samych płatności następujących w równych odstępach czasu. Stosując formułę renty wieczystej uzyskujemy odpowiedź na pytanie, ile należy zainwestować dzisiaj, aby dożywotnio otrzymywać rentę (stałe płatności) w ustalonej wysokości. Jeśli przepływy te miałyby występować na końcu okresów, wówczas korzystamy z następującej formuły:
![]()
(5.3.3.5)
gdzie:
PVP - wartość bieżąca renty wieczystej (perpetuity)
pozostałe oznaczenia jak poprzednio.
Natomiast dla renty wieczystej płatnej z góry, wartość bieżącą obliczamy z poniższego wzoru:
![]()
. (5.3.3.6)
gdzie: oznaczenia jak poprzednio.
Zagadnienia renty wieczystej zobrazujemy poniższym przykładem.
Przykład 18.
Ile należy zainwestować dzisiaj, aby dożywotnio co miesiąc otrzymywać rentę w wysokości 1.000PLN zakładając, że miesięczna stopa dyskontowa wynosi 0,5% przy czym:
płatności następowałyby na końcu okresów,
płatności następowałyby na początku okresów?
Rozwiązanie:
punkt „a”
prezentacja graficzna:
←___________
t1 t2
↓___↓___↓_…__↓_
0 1.000 1.000 1.000
? (razem ?)
obliczenia:
PVP = 1.000PLN ⋅ 1/0,005 = 200.000 PLN
punkt „b”
prezentacja graficzna:
←___________
t1 t2
↓___↓___↓_…__↓_
1000 1000 1000 1000
? (razem ?)
obliczenia:
PVP = 1.000,0 PLN. + 1.000/0,005=201.000,0PLN
Tak więc aby otrzymywać w nieskończoność 1.000 PLN na końcu okresów przy miesięcznej stopie dyskonta 0,5% należy zainwestować 200.000 PLN, natomiast przy wpływach na początku okresów należy zainwestować 201.000 PLN.
Zagadnienie renty dożywotniej jest często wykorzystywane w praktyce gospodarczej do wyceny akcji (model Gordona), a także wyceny całego przedsiębiorstwa (metoda DCF). Jak bowiem zostało powiedziane w rozdziale pierwszym spółka akcyjna nie ma ograniczonego czasu działalności wobec czego akcjonariusze kupując jej akcje mogą oczekiwać dywidend wypłacanych im w nieskończoność oraz, że spółki (perspektywiczne) będą wypracowywały zyski w bardzo długim horyzoncie czasu. Do zagadnień tych powrócimy jeszcze w dalszych rozdziałach niniejszego opracowania.
5.4. Nominalna, efektywna i realna roczna stopa procentowa. Stopa procentowa dla podokresu.
Czasami zdarza się, że lokata jest kapitalizowana częściej niż raz w roku. Wówczas, gdy znamy stopę procentową dla podokresu kapitalizacji możemy obliczyć roczną efektywną stopę procentową. Roczna efektywna stopa procentowa oznacza stopę procentową, jaką byśmy osiągnęli utrzymując lokatę przez rok. Do obliczenia rocznej efektywnej stopy procentowej przy znajomości stopy procentowej dla podokresu dla podokresu kapitalizacji wykorzystujemy następującą formułę:
![]()
(5.4.1)
gdzie:
Ref - roczna efektywna stopa procentowa,
r - stopa procentowa dla podokresu kapitalizacji odsetek,
n - liczba podokresów w roku.
Czasami zamiast stopy procentowej dla podokresu kapitalizacji znamy nominalną roczną stopę procentową. W takim przypadku, aby obliczyć roczną efektywną stopę procentową posłużymy się następującą formułą:
![]()
(5.4.2)
gdzie:
Ref - roczna efektywna stopa procentowa,
Rnom - roczna nominalna stopa procentowa,
n - liczba podokresów (kapitalizacji) w roku.
Stąd też jasno wynika, że zależność między stopą procentową dla podokresu kapitalizacji, a roczną nominalną stopą procentową jest następująca:
![]()
(5.4.3)
gdzie: oznaczenia jak poprzednio.
Tak więc roczna nominalna stopa procentowa oznacza, jakie jest nominalne oprocentowanie lokaty. Gdy w roku jest więcej niż jedna kapitalizacja, wówczas efektywna roczna stopa procentowa jest wyższa niż nominalna roczna stopa procentowa ponieważ w kolejnych podokresach wartość początkowa jest powiększana o wartość narosłych odsetek, co zwiększa podstawę opodatkowania w kolejnym podokresie. Gdy w roku jest tylko jedna kapitalizacja (tzn. odsetki są wyłącznie naliczane i dopisywane do podstawy na koniec roku) wówczas nominalna roczna stopa procentowa równa jest efektywnej rocznej stopie procentowej. Należy tu również zauważyć, że stopa procentowa dla podokresu kapitalizacji jest zarówno (dla tego podokresu) nominalną, jak i efektywną stopą procentową ponieważ w danym podokresie odsetki są kapitalizowane tylko raz. Powyższe zagadnienia zostaną zilustrowana przykładami.
Przykład 19.
Ile wyniesie roczna efektywna stopa procentowa, jeśli miesięczna stopa procentowa wynosi 0,5%? (Odsetki są kapitalizowane co miesiąc.)
Rozwiązanie:
Ref= (1+0,005)12-1 = 6,16%
Tak więc roczna efektywna stopa procentowa wynosi 6,16%. Należy tu zwrócić jeszcze raz uwagę, że jest ona wyższa niż roczna nominalna stopa procentowa, która w tym przypadku wynosi:
Rnom=0,005 ⋅ 12 = 6%.
Kolejny przykład z tego zagadnienia.
Przykład 20.
Roczna nominalna stopa procentowa wynosi 32%, oblicz efektywną roczną stopę procentową
przy kapitalizacji półrocznej
przy kapitalizacji kwartalnej.
Oblicz jaka byłaby wartość po roku depozytu w wysokości 1.000 PLN w przypadku kapitalizacji półrocznej i kwartalnej.
Rozwiązanie.
Punkt a.
Efektywna roczna stopa procentowa dla kapitalizacji półrocznej (tzn. będą w ciągu roku dwie kapitalizacje odsetek, które nastąpią po pół roku i po roku) wyniesie:
![]()
Punkt b.
Efektywna roczna stopa procentowa dla kapitalizacji kwartalnej (kapitalizacje następują na koniec kolejnych kwartałów) wynosi:
![]()
Należy tu zauważyć, że w przypadku kapitalizacji kwartalnej roczna efektywna stopa procentowa jest wyższa aniżeli dla kapitalizacji półrocznej. Ogólnie można powiedzieć, że przy tej samej nominalnej stopie procentowej lecz o różnej liczbie kapitalizacji w ciągu roku efektywna stopa procentowa będzie zawsze większa dla przypadku o większej liczbie kapitalizacji.
Znając efektywne stopy procentowe łatwo już jest obliczyć, jaką otrzymamy kwotę z zainwestowanego 1.000 PLN.
W przypadku „a” będzie to:
FV = 1.000 ⋅ 1,3465 = 1.346,5 PLN,
natomiast w przypadku „b” otrzymamy kwotę:
FV = 1.000 ⋅ 1,36049 = 1.360,49 PLN.
Oczywiście ponieważ w drugim przypadku otrzymaliśmy wyższą roczną efektywną stopę procentową to również otrzymana kwota z zainwestowanego 1.000 PLN będzie wyższa.
Można również obliczyć, jaką uzyska się kwotę po roku z określonej inwestycji bez wcześniejszego obliczania efektywnej rocznej stopy procentowej. Wówczas, znając jedynie stopę procentową dla podokresu skorzystamy ze wzoru:
![]()
(5.4.4)
Ostatnią kwestią, którą tutaj poruszymy jest obliczanie realnej stopy procentowej w warunkach inflacji. Gdy znana jest stopa inflacji oraz nominalna stopa procentowa, realną stopę procentową wyliczymy z następującego wzoru:
![]()
(5.4.5)
gdzie:
Rreal - realna roczna stopa procentowa (tzn. po wyłączeniu inflacji),
Rnom - efektywna roczna stopa procentowa,
INFL - stopa rocznej inflacji.
Dopuszczalne jest również obliczenie realnej rocznej stopy procentowej w sposób uproszczony tzn.:
![]()
(5.4.6)
gdzie: oznaczenia jak poprzednio.
Przeanalizujmy poniższy przykład na wyznaczanie realnej stopy procentowej.
Przykład 21.
Oblicz, jaka jest roczna realna stopa oprocentowania lokat oszczędnościowych, gdy nominalna stopa procentowa wynosi 15%, a roczna stopa inflacji kształtuje się na poziomie 10%?
Rozwiązanie:
Korzystając z przytoczonego powyżej wzoru otrzymujemy:
Rreal = ((1 + 0,15)/(1 + 0,10)) - 1 = 0,045 = 4,5%.
W przypadku uproszczonego sposobu liczenia otrzymamy:
Rreal = 0,15 - 0,10 = 0,05 = 5,0 %.
Tak więc realne oprocentowanie tych lokat wynosi 4,5%.
5.5. Podsumowanie.
W niniejszym rozdziale podjęliśmy kwestie ceny i wartości pieniądza w czasie. Już na wstępie zostało powiedziane, że ceną pieniądza jest stopa procentowa ukształtowana przez popyt zgłaszany ze strony pożyczkobiorców oraz podaż funduszy pożyczkowych. Jak zostało to również zauważone specyficzną, ale bardzo ważną rolę w regulowaniu tego rynku odgrywa Bank Centralny i państwo.
Istnieje szereg teorii wyjaśniających kształtowanie stóp procentowych wśród których najważniejsze to: teoria malejącej krańcowej użyteczności kapitału, teoria preferencji czasowej oraz teoria preferencji płynności. W myśl pierwszej z wymienionych tu teorii każda kolejna jednostka kapitału jest mniej efektywnie inwestowana. Z kolei przedsiębiorstwa będą tak długo skłonne korzystać z funduszy pożyczkowych, dopóki stopa zwrotu z inwestycji przez nie czynione będzie wyższa (lub co najmniej równa) płaconej stopie procentowej. Kolejna teoria definiuje tzw. stopę preferencji czasowej jako stopę procentową przy której konsumenci są skłonni zrezygnować z bieżącej konsumpcji na rzecz przyszłe-większej dzięki uzyskanym dochodom (np. odsetkom od lokat). W odróżnieniu od teorii pierwszej, która wyjaśniała, kiedy pożyczkobiorcy będą skłonni skorzystać z oferty funduszy pożyczkowych, ta teoria wyjaśnia, kiedy konsumenci będą skłonni odłożyć konsumpcję i zaoferować swój kapitał do dyspozycji innych podmiotów. Od wysokości ich oszczędności zależy bowiem skala możliwych do zaoferowania środków pieniężnych. Ostatnia z wymienionych teorii - preferencji płynności, kładąca również nacisk na wysokość oszczędności, traktuje stopę procentową jako cenę za wyrzeczenie się możliwości wykorzystania pieniądza do nadarzających się atrakcyjnych inwestycji.
W dalszej kolejności zostały określone inne czynniki wpływające na stopę procentową takie jak inflacja, ryzyko nieotrzymania spłaty pożyczonego kapitału, długość okresu do momentu wymagalności oraz podano przykłady różnych „rodzajów” stopy procentowej (np. nominalna i realna stopa procentowa). Wyjaśniono również pojęcie struktury czasowej stopy procentowej jako relację między stopą procentową, a okresem zapadalności oraz zdefiniowano stopę spot i forward, a także zobrazowano na przykładach wyznaczanie stopy forward przy znajomości stopy spot.
W części poświęconej wartości pieniądza w czasie wskazano na możliwe kierunki zmian wartości, przy czym zauważono, iż w zdecydowanej większości przypadków pieniądz wraz z upływem czasu traci swoją wartość. Wymieniono również trzy podstawowe przyczyny tego zjawiska: inflacja, przedkładanie przez konsumentów bieżącej konsumpcji nad przyszłą oraz to, że dochody uzyskiwane w przyszłości dzięki dzisiejszym nakładom z reguły przewyższają wartość tych nakładów. Poza tym omówiono tu takie pojęcia jak aprecjacja, deprecjacja, deflacja, inflacja.
Kolejnym poruszonym zagadnieniem było obliczanie wartości przyszłej i obecnej. Obliczanie wartości przyszłej polegało na ustaleniu wielkości do jakiej będzie rosnąć przepływ środków pieniężnych (lub wiele przepływów) w danym czasie. Przypomnijmy, że proces ten nazywa się kapitalizacją (nie mylić z kapitalizacją odsetek!) i odbywa się za pomocą ustalonej stopy procentowej. Z kolei obliczanie wartości obecnej to ustalanie na dzień dzisiejszy wartości przyszłego przepływu środków pieniężnych. Proces ten odbywa się za pomocą stopy dyskontowej i nosi nazwę dyskontowania. W analizowanych przykładach zostały zaprezentowane różne możliwe warianty: jednorazowa wpłata (procent prosty i składany), przepływy pieniężne w różnej wysokości oraz równe strumienie płatności okresowych. Omówiono również przykład na obliczenie wartości obecnej nieskończenie wielu płatności (renta dożywotnia) oraz wskazano na szerokie znaczenie praktyczne tego sposobu kalkulowania. Ogólne wnioski jakie zostały sformułowane na podstawie analizowanych przykładów to:
wartość przyszła z kapitalizacją odsetek jest zawsze wyższa niż wartość bez kapitalizacji odsetek;
gdy wpływy są na początku okresów wartość przyszła (obecna) jest zawsze większa niż w przypadku wpływów na końcu okresów.
Na koniec omówiono interpretację oraz zależności między roczną efektywną (czyli efektywnie uzyskiwaną stopą procentową) i nominalną stopą procentową (czyli wg której w rzeczywistości są naliczane odsetki) oraz stopą procentową dla podokresu (będącą jednocześnie stopą nominalną i efektywną). Najważniejsze ustalone tu wnioski to:
roczna efektywna stopa procentowa jest zawsze większa lub równa nominalnej rocznej stopie procentowej;
jeżeli występują podokresy kapitalizacji pierwszym etapem rozwiązywania tego typu zadań jest wyznaczenie stopy procentowej dla podokresu kapitalizacji,
znając nominalną stopę procentową w warunkach inflacji można wyznaczyć stopę realną (dokładną wartość lub przybliżoną korzystając z formuły uproszczonej)
5.6. Pytania sprawdzające.
Jak jest wyrażana cena pieniądza?
Opisz mechanizm kształtowania ceny pieniądza.
Omów teorię malejące krańcowej użyteczności kapitału.
Omów teorie wyjaśniające zależności między podażą funduszy pożyczkowych, a ceną pieniądza (teoria preferencji czasowej konsumenta i teoria preferencji płynności).
Omów determinanty wpływające na ceną pieniądza.
Wyjaśnij co to jest „struktura czasowej stopy procentowej”?
Wyjaśnij pojęcia stopa swot i stopa forward. Jakie występują między nimi zależności?
Wyjaśnij następujące pojęcia związane z wartością pieniądza w czasie: inflacja, deflacja, aprecjacja, deprecjacja, wartość przyszła, wartość obecna, kapitalizacja, dyskontowanie, stopa procentowa, stopa dyskontowa.
Wymień podstawowe przyczyny powodujące zmniejszenie wartości pieniądza w czasie.
Od czego zależy wartość przyszła i wartość obecna przepływów środków pieniężnych?
Wyjaśnij pojęcie „kapitalizacja odsetek” oraz „prosta” i „złożona stopa procentowa”. Porównaj wartość przyszłą uzyskaną w obu przypadkach.
Porównaj wartość przyszłą i wartość obecną płatności okresowych dokonywanych „z góry” i „z dołu”. Z czego wynikają różnice?
Co to jest renta wieczysta? W jakich sytuacjach z praktyki gospodarczej jest ona wykorzystywana?
Przeanalizuj zależności występujące między roczną nominalną i efektywną stopą procentową oraz stopą procentową dla podokresu kapitalizacji.
Porównaj wartości przyszłe uzyskane po roku przy tej samej nominalnej stopie procentowej, ale różnej liczbie kapitalizacji.
W jaki sposób można wyznaczyć realną stopę procentową w warunkach inflacji znając nominalną stopę procentową?
5.7. Zadania do samodzielnego wykonania.
Załóżmy, iż można nabyć obligację o oprocentowaniu stałym w wysokości 8%, która będzie przynosiła rocznie 900 PLN odsetek (dożywotnio). Ile jest warta ta obligacja dzisiaj dla płatności, która po raz pierwszy będzie miała miejsce po roku („z dołu”), a ile, gdy pierwsza płatność odsetek nastąpi w dniu nabycia lub na następny dzień, („z góry”) ?
Oblicz, który z banków oferuje najwyższą efektywną roczną stopę procentową, gdy oprocentowanie lokaty 12 miesięcznej i kapitalizacja odsetek wynoszą:
w banku „A” oprocentowanie 38,5% kapitalizacja roczna,
w banku „B” oprocentowanie 38% kapitalizacja kwartalna,
w banku „C” oprocentowanie 36% kapitalizacja miesięczna.
ZADANIE KOMPLEKSOWE
Ile będzie zgromadzonych pieniędzy w trzecim filarze funduszu emerytalnego po czterdziestu latach oszczędzania, jeśli miesięcznie będziemy wpłacać 50 PLN, przy założeniu, że roczna efektywna stopa realnego zysku wyniesie 6%. Koszty manipulacyjne pomijamy. Płatności dokonujemy z góry.
Ile będziemy otrzymywać miesięcznie jeśli zażyczymy sobie, że cały zgromadzony kapitał ma nam zostać wypłacany co miesiąc przez 10 lat od momentu przejścia na emeryturę w równych ratach. Efektywna roczna stopa procentowa pozostaje nadal 6%. Płatności następują z góry.
Ile nominalnie wpłaciliśmy do funduszu?
Podpowiedź: najpierw należy obliczyć stopę procentową dla podokresu.
Ilość
Cena
Cena pieniądza
Wyszukiwarka