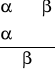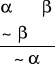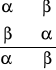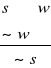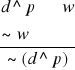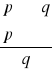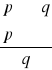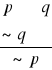Logika formalna Przedmiotem są formy (schematy) niezawodnych rozumowań. Logika formalna to teoria wynikania. Wynikanie między zdaniami Z: Każdy student jest inteligentny Z1: Niektórzy inteligentni ludzie są studentami Ze zdania Z1 wynika zdanie Z wtedy i tylko wtedy gdy (<=>) Z1 jest prawdziwe to i Z musi być prawdziwe p,q - to wyrażenia Stałe logiczne (wyrażenia kt. nazywamy funktorami)muszą być ściśle określone i jednoznaczne;p,q,r,s-to zmienne logiczne(podstawiamy treść zdania) kwantyfikatory - funktory, które określają ilość (dla każdego, dla niektórych) nawiasy - porządkują sens zdania Logikę dzielimy na : teorię zdań i teorię kwantyfikatorów Rachunek kwantyfikatorów nazywany jest RACHUNKIEM NAZW Prawda - zdanie jest prawdziwe wtedy i tylko wtedy gdy stan rzeczy stwierdzony przez to zdanie zachodzi w rzeczywistości. Gdy ten stan nie zachodzi zdanie jest fałszywe. Prawda polega na zgodności zdania z tym, co zdanie stwierdza Zdanie musi być orzekające. Musi wyraźnie stwierdzać pewien stan rzeczy Prawda i fałsz to logiczne wartości zdania Prawda - 1 Fałsz - 0 Logika, która opiera się na założeniu, że zdanie w sensie logicznym posiada jedną z wartości logicznych (1,0)nazywa się logiką dwuwartościową (klasyczną)
Logika wielowartościowa - Jan Łukasiewicz - wprowadził wartość ½(połowiczną) Zdanie jest złożone, gdy zawiera funktor zdaniotwórczy od argumentów zdaniowych Funktory zdaniotwórcze: -)Nieprawda że, i, albo, lub, jeżeli to, wtedy i tylko wtedy -)argument zdaniowy (to co stoi przy funktorze)
Wartość logiczna zdania złożonego przy użyciu funktorów możliwe że ,wie że nie zależy jedynie od wartości logicznej zdania, ale również od jego treści Wyróżniamy spójniki prawdziwościowe i nieprawdziwościowe F. prawdziwościowy -określa wartość logiczną zdania jedynie na podstawie jednego argumentu F. nieprawdziwościowy -wartość logiczna złożonych przy ich użyciu zdań nie zależy od wartości logicznej argumentów, lecz od ich treści, ”możliwe że, wie że” p-funktor q-argument
symbol Schemat zdania czytanie Nazwa zd złożonego
~ ~p nieprawda,że p NEGACJA
^ P^q p i q KONIUNKCJA
v P vq p lub q ALTERNATYWA
→ p→q Jeżeli p to q IMPLIKACJA
↔ p↔q p wtedy i tylko wtedy gdy q RÓWNOWAŻNOŚĆ
ki zdanie jest złożone wtedy i tylko wtedy gdy zawiera funktor zdaniotwórczy od argumentów zdaniowych. Możemy wyróżnić dwa funktory zdaniotwórcze: - od argumentu zdaniowego - wiąże jedno zdanie proste, - od argumentów zdaniowych - wiąże dwa zdania proste. To co stoi przy funktorze to argument zdaniowy.
Wartość logiczna zdania złożonego przy użyciu funktorów „możliwe, że” i „wie, że” nie zależy jedynie od wartości logicznej zdania składowego czyli argumentu ale take od jego treści. Z tego względu wyróżniamy: a) spójniki prawdziwościowe, b) spójniki nieprawdziwościowe. Spójniki prawdziwościowe to inaczej spójniki ekstensjonalne - jest to funktor, który określa wartość logiczną zdania jedynie na podstawie jego argumentu. „Nieprawda, że”, „i”, „lub”. Spójniki nieprawdziwościowe to inaczej funktory intensjonalne - jest to funktor , którego wartość logiczna nie zależy od wartości logicznej argumentów lecz od ich treści. „możliwe, że”, „wie, że”. S Schemat zdania Sposób czytania Nazwa zdania złożonego
~ ~p Nieprawda, że p negacja
^ p ^ q p i q koniunkcja
v p v q p lub q alternatywa
→ p→q jeżeli p, to q implikacja
↔ p↔q p wtedy i tylko wtedy gdy q równoważność
10. Pojęcie tautologii, sprawdzanie formuł metodą matrycową Słownik języka rachunku zdań: -zmienne zdaniowe p,q,r,s -stałe zdaniowe ~,^,v, →, ↔ -nawiasy Dowolne zdania języka potocznego lub naukowego można przedstawić schematycznie za pomocą odpowiedniej formuły języka zdań (p ^ q) → r Zbiór formuł klasycznego rachunku zdań dzielimy na: 1.Schematy tautologiczne (tautologia) 2.Schematy nietautologiczne Ad. 1 Schematy tautologiczne są to schematy zdań wyłącznie prawdziwych, czyli takie formuły, które tworzą zdania prawdziwe przy wszelkich możliwych podstawieniach zdań (prawdziwych bądź fałszywych) za występujące w nich zmienne zdaniowe. Ad. 2 W schematach nietautologicznych wyróżniamy tzw. kontrtautologie. Jest to schemat zdań wyłącznie fałszywych. Pozostałą podgrupę w schemacie zdań nietautologicznych stanowią formuły, które nie są ani tautologiami ani kontrtautologiami czyli takie, które przy pełnych podstawieniach za zmienne przybiorą postać prawdy przy innych zaś wartość fałszu. Nie wnikając w treść (intencjonalność zdania)potrafimy za pomocą pewnych schematów stosując METODĘ MATRYCOWĄ(zerojedynkową)sprawdzić prawdziwość zdania. p v ~p prawo wyłączonego środka lub inaczej prawo logicznego rachunku zdań jest to tautologia,kt.zawsze daje prawdę 1° p = 1 2° p=0 1 v ~ 1 0 v ~ 0 1 v 0 0 v 1 1 1 ~ (p ^ ~ p) prawo sprzeczności czy niesprzeczności cokolwiek podstawimy za p zawsze otrzymamy prawdę 1° p=1 2° p=0 ~ (1 ^ ~ 1) ~ (0 ^ ~ 0) ~ (1 ^ 0) ~ (0 ^ 1) ~ 0 ~ 0 1 1 Prawo wyłączonego środka mówi nam, że z dwóch zdań sprzecznych przynajmniej jedno musi być prawdziwe. Prawo sprzeczności mówi, że dwa zdania sprzeczne nie mogą być zarazem prawdziwe, czyli że z dwóch zdań sprzecznych przynajmniej jedno musi być fałszywe. Prawa te stanowią fundamenty logiki klasycznej, zasadę dwuwartościowości logiki klasycznej, która stwierdza, że z dwóch zdań sprzecznych dokładnie jedno musi być prawdziwe i dokładnie jedno fałszywe.
(p→q) ↔ (~q → ~p) (prawo transpozycji) 1° p = 1, q = 1 2° p = 1, q = 0 (1→1) ↔ (~1 → ~1) (1→0) ↔ (~0 → ~1) 1 ↔ (0 → 0) 0 ↔ (1 → 0) 1 ↔ 1 0 ↔ 0 1 1
3° p = 0, q = 1 4° p = 0, q = 0 (0→1) ↔ (~1 → ~0) (0→0) ↔ (~0 → ~0) 1↔ (0 → 1) 1 ↔ (1→ 1) 1 ↔ 1 1↔ 1 1 1
Zgodnie z definicją formuła jest tautologią jeśli przy wszelkich możliwych układach wartości jej zmiennych przybiera wartość prawdy.
(p→q) ↔ (~p → ~q) - kontrtautologia
1° p = 1, q = 1 2° p = 1, q=0 (1→1) ↔ (~1 → ~1) (1→0) ↔ (~1 → ~0) 1 ↔ (0 → 0) 0 ↔ (0 → 1) 1 ↔ 1 0 ↔ 1 1 0
3° p = 0, q = 0 4° p = 0, q = 1 (0→0) ↔ (~0 → ~0) (0→1) ↔ (~0 → ~1) 1 ↔ (1 → 1) 1 ↔ (1→ 0) 1 ↔ 1 1 ↔ 0 1 0 Metoda aksjomatyczna - przyjmujemy w niej pewne aksjomaty jako pewniki i z tych aksjomatów za pomocą rozumowań wyprowadzamy tzw. tezy, wnioski. Metoda założeniowa (dedukcji naturalnej) - metoda intuicyjna. System założeniowy klasycznego rachunku zdań polega na tym, że każdą tezę systemu da się w sposób intuicyjny udowodnić za pomocą dokładnie określonych reguł. Przy tym systemie nie zakładamy żadnych aksjomatów czyli tez przyjmowanych bez dowodów. Każdą tezę systemu da się tu w sposób naturalny udowodnić za pomocą odpowiednich reguł. Wyróżniamy ich dwa rodzaje:
Wnioskowanie i dowodzenie jako rodzaje rozumowań Wnioskowanie i dowodzenie są pewnymi formami rozumowania. Rozumowanie to proces, który zaczyna się punkcie A i kończy w punkcie B. Punkt A to punkt, w którym nic nie wiemy, punkt B to punkt, w którym wiemy więcej niż w punkcie A. w zależności od tego jak rozumujemy wyróżniamy dwa typy rozumowań: *wnioskowanie - wyprowadzanie tezy głównej której jesteśmy pewni *dowodzenie.
|
q - wniosek, konkluzja kreska ułamkowa - zatem, przeto, a więc
jeżeli Paweł ma gorączkę, to jest chory Sprawdzamy niezawodność rozumowania p q p → q (przesłanka) p (przesłanka) q (wniosek)
1 1 1 1 1
1 0 0 1 0
0 1 1 0 1
0 0 1 0 0
Wniosek okazuje się fałszywy w dwóch przypadkach.
Z rozumowania niezawodnego wynika prawdziwy wniosek przy prawdziwych przesłankach. Z rozumowania niezawodnego wynika prawdziwy wniosek przy prawdziwych przesłankach. Przy przyjmowaniu nieprawdziwych przesłanek mamy do czynienia z błędem materialnym. Schemat jest niezawodny wtedy, kiedy każde wnioskowanie przeprowadzone wg tego schematu będzie formalnie poprawne.
Przykład 2: p→q Jeśli wykręcę bezpiecznik to żarówka zgaśnie ~ p
p q p → q (przesłanka) ~p (przesłanka) ~q (wniosek)
1 1 1 0 0
1 0 0 0 1
0 1 1 1 0
0 0 1 1 1
Wnioskowanie zawodne Kodeks reguł wnioskowania Kodeks podstawowych reguł wnioskowania obejmuje 3 rodzaje reguł i są to: - reguły opuszczania poszczególnych spójników - reguły dołączania poszczególnych spójników - reguły negowania formuł złożonych
1. Reguła opuszczania koniunkcji (OK)
Jeżeli ktoś uznaje koniunkcję, to wolno mu (musi) uznać dowolny człon tej koniunkcji. Zatem z koniunkcji musi wynikać każdy jej człon.
2. Reguła dołączania koniunkcji (DK)
Wolno uznać koniunkcję (musi się uznać koniunkcję) o ile uznane zostały obydwa jej człony. Przykład: Gdynia jest miastem portowym ( 3. Reguła opuszczania alternatywy (OA)
Jeżeli ktoś uznaje alternatywę i negację jednego z jej członów to wolno mu (musi) uznać drugi człon tej alternatywy. Przykład: Przepalił się bezpiecznik ( 4. Reguła dołączania alternatywy (DA)
Wolno uznać alternatywę (musi się uznać alternatywę) jeżeli uznany został któryś z jej członów. Przykład: Mickiewicz jest autorem Pana Tadeusza ( 5. Reguła odrywania (RO), reguła modus ponens (MP)
Jeżeli ktoś uznaje implikację oraz jej poprzednik to wolno mu uznać (musi uznać) następnik tej implikacji. Przykład: Jeżeli bezpiecznik się przepali to zgaśnie żarówka (
6. Reguła odrywania modus tollens (MT)
Jeżeli ktoś uznaje implikację oraz negację jej następnika to wolno mu uznać (musi uznać) negację poprzednika tej implikacji. Przykład: Jeżeli bezpiecznik się przepali to żarówka zgaśnie (
7. Reguła opuszczania ekwiwalencji, opuszczania równoważności (OE)
Jeżeli ktoś uznaje równoważność to wolno mu (musi) uznać zarówno implikację, której poprzednikiem jest lewa strona tej równoważności a następnikiem jej prawa strona, jak też implikację odwrotną. Przykład: Otrzymam pozytywną ocenę wtedy i tylko wtedy gdy potrafię samodzielnie rozwiązać tego typu zadania (
8. Reguła dołączania ekwiwalencji, dołączania równoważności (DE)
Wolno uznać równoważność (musi się) jeżeli uznana została implikacja której poprzednikiem jest lewa strona tej równoważności a następnikiem jej prawa strona jak też uznana została implikacja odwrotna. Przykład: Jeżeli jest mróz to woda zamarza ( 9. Reguła negowania implikacji (NI)
Jeżeli ktoś uznaje negację implikacji, to wolno mu uznac (musi) zarówno poprzednik tej implikacji jak też negację jej następnika. Przykład: Okazało się nieprawdą, że jeżeli Piotr rozwiąże to zadanie to otrzyma piątkę z logiki. Wniosek: A więc Piotr rozwiązał to zadanie i nie otrzymał piątki z logiki. .
10. Reguła negowania ekwiwalencji - równoważności (NE)
Jeśli ktoś uznaje negację równoważności to wolno mu (musi) uznać tę równoważność po zanegowaniu jednego i tylko jednego z jej członów. Przykład: Ponieważ nieprawda, że (Kowalski jest krytyczny wtedy i tylko wtedy gdy jest on naiwny). Wniosek: A więc nieprawda, że Kowalski jest krytyczny wtedy i tylko wtedy gdy jest on naiwny. 11.Reguła opuszczania podwójnej negacji(ON)lub negowania negacji ~~α α Jeżeli ktoś uznaje podwójną negację jakiegoś zdania to wolnemu (musi)uznać to zdanie.Skoro negacja ma wartość logiczną przeciwną niż wartości jej argumentu (p),to z negacji zdania już zanegowanego ~(~p)wynika zdanie wyjściowe→p 12.Reguła dołączania negacji (DN) α ________ ~~α 13.Reguła negacji koniunkcji(NK) ~(α^β) I Prawo De Morgana ~αv~β
Jeśli ktoś uznaje negację koniunkcji to wolno mu (musi)uznać alternatywę zanegowanych członów tej koniunkcji 14.Reguła negowania alternatywy(NA) II Prawo De Morgana
~(αvβ) ~(α^~β)
~(αvβ)↔~α^~β
Jeżeli ktoś uznaje negację alternatywy to wolno mu uznać (musi) koniunkcję zanegowanych członów tej alternatywy
|
PRAKTYCZNE PRZYKŁADY ZWIĄZANE Z DOWODZENIEM Zadanie 1 1) Przyczyną pożaru było zwarcie elektryczne lub ogień wznieciły dzieci - z(zwarcie) v d (dzieci wznieciły ogień) z v d 2) pożar nie był zaraz widoczny w(widoczny) ~w 3) Jeśli przyczyną pożaru było zwarcie elektryczne to palił się najpierw strych
z(zwarcie)
4) Jeżeli (zarazem) ogień wznieciły dzieci (d) a świadek powiedział prawdę (p) to pożar był zaraz widoczny (w). (d ^ p)
5) Jeżeli palił się najpierw strych (s) to pożar był zaraz widoczny (w). s Odpowiadamy na pytania: z - czy było zwarcie? p - czy świadek powiedział prawdę
Wniosek: (7)Nieprawda, że przyczyną pożaru było zwarcie elektryczne {MT: 3,6}
Wniosek: (8) Dzieci wznieciły ogień {OA: 1,7}
Wniosek (9) - Nieprawda, że (zarazem) dzieci wznieciły ogień i świadek powiedział prawdę {MT:4,2}
Zadanie 2
1)
2)
3) 4) p {OK.:3} 5) r {OK.:3} 6) q{MT:1}
7) q v s {RO: 2,4} 8) ~(~q) 9) s {DA: 7,8} Reguły tworzenia dowodów założeniowych
1. Dowód założeniowy wprost - wnioskowanie, które w przypadku implikacji prowadzi do stwierdzenia prawdziwości następnika Przykład:
(p
Założenie 1: p
Założenie 2: q Założenie 3: p
Założenie 4: q na podstawie {RO:1,3}
Założenie 5: r na podstawie {RO:2,4} Dowód założeniowy wprost obejmuje 3 etapy: a) zapoczątkowanie, b) rozwijanie c) zakończenie Ad a)
Zapoczątkowanie rozpoczynamy od wypisania założeń. Jeżeli dowodowy schemat jest implikacją to jej poprzednik stanowi pierwsze założenie Ad b) Do dowodu wolno dołączyć dowolny wniosek zgodnie z niezawodnymi regułami wnioskowania, dla którego przesłanki już w tym dowodzie występują. Wolno też do dowodu dołączyć prawa wcześniej udowodnione. Ad c)
Dowód jest zakończony z chwilą otrzymania ostatniego następnika
Zadanie:
[(p
Zał. 1. p Zał. 2. p
3) p
4) q 5) q {RO: 3,2} 6) r {RO:4,5}
Zdanie do tego schematu: Jeżeli (jest prawdą, że jeśli dzisiaj jest poniedziałek to jutro będzie wtorek i jeśli jutro będzie wtorek to pojutrze będzie środa) to musi być prawdą, że jeśli dziś jest poniedziałek to pojutrze będzie środa.
Zadanie:
[(p
Zał 1. p Zał. 2 p
3) p
4) p 5) q {RO:3,2} 6) r {RO:4,2} 7) q ^ r {DK:5,6} Zdanie do tego schematu: Jeśli jest prawdą, że jeśli ktoś dobrze zna język angielski, to potrafi mówić po angielsku i jeśli ktoś zna język angielski to potrafi pisać po angielsku to musi być prawdą, że jeśli ktoś dobrze zna język angielski to potrafi mówić i pisać po angielsku..
2. Dowód założeniowy nie wprost (przyjmujemy, że następnik jest fałszywy, dodajemy nowe założenie, które jest zaprzeczeniem następnika.
Przykład:
Zał. 1 p Zał. 2 p v q Zał. 3 (założenie dowodu nie wprost) ~r
4) p
5)q 6) ~r {MT:3,4} 7) ~q {MT:5,3} 8) q {OA: 2,6} {sprzeczność 7,8}
Założeniowy dowód nie wprost rozpoczynamy podobnie jak założeniowy dowód wprost, czyli od wypisania założeń z tą jednak różnicą, że dochodzi tu jeszcze jedno założenie nazywane założeniem dowodu nie wprost (z.d.n), który jest negacją ostatniego następnika Zadanie
Zał.1 (p ^ q) Zał. 2 p ^ ~r Zał. 3 z.d.n. q 4) p {OK.:2} 5) ~r {OK.:2} 6) p ^ q {DK:3,4} 7) r {RO:1,6} {sprzeczność 5,7} Zdanie do tego schematu: jeżeli jest prawdą, że jeśli pada deszcz i jest mróz to powstaje gołoledź to musi być prawdą, że jeśli pada deszcz a nie powstaje gołoledź to nie ma mrozu.
Zadanie: p v ~p Chcąc to udowodnić korzystamy z idei dowodu nie wprost i w przeciwieństwie do implikacji tu negujemy cały schemat. 1)ZDN. ~(p v ~p) 2) ~p ^ ~~p {NA:1} 3) ~p {OK.:2} 4) ~~p {OK.:2} 5) p {ON:4} {sprzeczność 3,5} Tego rodzaju dowód przyjęto nazywać zwykłym dowodem nie wprost, zwykłym gdyż nie ma tu innych założeń oprócz założenia dowodu nie wprost. Jeśli formuła do udowodnienia nie jest implikacją ani równoważnością stosujemy wówczas zwykły dowód nie wprost, którego jedynym założeniem jest założenie dowodu nie wprost będące negacją dowodzonej formuły. Zadanie:
1) z.d.n.w
2) p 3) p^~q {OK.:1} 4) p {OK.:3} 5) ~q {OK.:3} 6) q {RO:2,4}{sprzeczność 5,6}
Aby udowodnić tautologiczność formuły o postaci równoważności
a) dowód dla implikacji, której poprzednikiem jest lewa strona tej równoważności a następnikiem prawa
b) dowód dla implikacji, gdzie poprzednikiem jest prawa strona równoważności a następnikiem lewa
c) tzw. Zwykły dowód wprost dla równoważności, w którym korzysta się wyłącznie z tez wcześniej uzasadnionych
Zadanie
a)
Zał. 1: p^q Zał 2: p Zał. 3: q 4)p^q {DK:2,3} 5) r {RO:1,4}
b)
Zał. 1: p Zał.2: p^q 3) p {OK.:2} 4) q {OK.:2}
5) q 6) r {RO:5,4}
c) {DK:1,2} Definicja wynikania logicznego
Ze zdania z1 wynika logicznie zdanie z wtedy i tylko wtedy gdy implikacja z1
Jeśli wniosek wynika logicznie z przesłanek, to prawdziwość przesłanek stanowi gwarancję prawdziwości wniosku. Wolno nam wówczas wnioskować w sposób subiektywnie pewny, czyli uznać wniosek z takim samym stopniem pewności, z jakim uznajemy przesłanki.
Wnioskowanie, w którym wniosek wynika logicznie z przesłanek nazywa się wnioskowaniem dedukcyjnym. O wnioskowaniu dedukcyjnym mówi się, że jest ono zawsze formalnie poprawne. Możemy jednak spotkać się z dwoma błędami w tym wnioskowaniu: 1.Błąd formalny polega na tym, że wnioskowanie nie jest dedukcyjne a mimo to jest subiektywnie pewne (wniosek nie wynika logicznie z przesłanek a zostaje uznany z tym samym stopniem z jakim uznano przesłanki). Wnioskowanie, w którym popełniono błąd formalny może, choć nie musi prowadzić od prawdziwych przesłanek do fałszywego wniosku. 2.Błąd materialny wnioskowania - zachodzi wówczas, gdy przynajmniej jedna z przesłanek jest fałszywa a mylnie uważana jest za prawdziwą. W takim przypadku również wniosek tego wnioskowania może ale nie musi być fałszywy. Naukami, które zajmują się wyłącznie wnioskowaniem dedukcyjnym są logika i matematyka, a pozostałe nauki tzw. Empiryczne oprócz metod dedukcyjnych wnioskowania stosują inne wnioskowania.
|
3
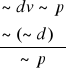
![]()
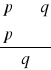
![]()
Wyszukiwarka