Wykład 4
Analiza współzależności
Współzależność (korelacja)
Graficzna ocena korelacji
Tabelaryczna ocena korelacji
Miary korelacji
Miary nieparametryczne - dH
Miary parametryczne - rp, rk
s. 68 -88
Analiza współzależności pozwala określić czy między wybranymi cechami (zmiennymi lub zjawiskami) istnieje zależność tzn. czy jedna cecha wpływa na drugą.
Wyróżnia się następujące metody badania współzależności:
Metoda graficzna
Metoda tabelaryczna
Metody formalne:
parametryczna
nieparametryczna
Ad. I). Metoda graficzna
- polega na wzrokowej ocenie diagramu korelacyjnego
Diagram korelacyjny to wykres punktowy umieszczony w układzie współrzędnych .
Diagram można sporządzić dla danych zapisanych w postaci szeregów statystycznych. Na wykresie zaznacza się punkty o współrzędnych (xi ; yi), gdzie:
xi - i -ta wartość cechy X,
yi - i -ta wartość cechy Y.
Y (tys. szt.) - wielkość sprzedaży pewnego produktu
X - w tys. zł - wydatki na reklamę tego produktu
Lp. (i) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
xi |
35 |
50 |
10 |
45 |
55 |
25 |
30 |
40 |
20 |
50 |
yi |
100 |
150 |
50 |
130 |
175 |
90 |
100 |
110 |
70 |
155 |
Ad II.) Metoda tabelaryczna
- najczęściej polega na analizie rozkładów w tablicy korelacyjnej
W tablicy korelacyjnej wyróżnia się następujące typy rozkładów:
Rozkład łączny - symbol nij lub fij
Rozkłady brzegowe - symbol nj oraz ni
Rozkłady warunkowe - symbol xyj oraz yxi
Przykład: Pracowników pewnej firmy w Jeleniej Górze zbadano ze względu na średnie miesięczne wynagrodzenie otrzymywane w 2002 r. (cecha Y - wynagrodzenie podane zostało w $) oraz poziom wykształcenia (cecha X). Uzyskano następujące wyniki (źródło: dane umowne):
Lp. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
xi |
W |
Ś |
W |
Ś |
W |
Z |
W |
Z |
W |
Z |
W |
yi |
570,28 |
300 |
550,9 |
490,32 |
400 |
200 |
620,59 |
250,83 |
643,75 |
285,21 |
500 |
lp. |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
xi |
Ś |
W |
Ś |
Z |
W |
Ś |
W |
W |
Ś |
W |
Z |
yi |
350,76 |
530,48 |
470,99 |
300 |
699,95 |
450,7 |
680,88 |
599,99 |
420,4 |
580,39 |
237 |
lp. |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
|
xi |
Ś |
W |
W |
W |
Z |
Ś |
Z |
W |
Ś |
W |
|
yi |
400,15 |
600 |
450,64 |
670,94 |
258,61 |
390 |
226 |
590,33 |
325,43 |
480,62 |
|
gdzie: Z - wykształcenie zawodowe, Ś - wykształcenie średnie, W - wykształcenie wyższe.
Ocenić zależność między cechami na podstawie analizy rozkładów w tablicy korelacyjnej.
Ad. III) Metody formalne - Miary współzależności
Podział miar współzależności:
Miary nieparametryczne
w metodzie nieparametrycznego, tzw. stochastycznego badania współzależności
Miary parametryczne
w metodzie parametrycznego, tzw. korelacyjnego badania współzależności
Podział miar współzależności:
Miary nieparametryczne
współczynnik zbieżności Czuprowa- dc
współczynnik zależności Hellwiga - dH
Miary parametryczne
współczynnik korelacji liniowej Pearsona - rp
stosunek korelacyjny - rk
współczynnik korelacji liniowej Spearmana - rs
Idealna miara współzależności powinna posiadać następujące własności:
niemianowana
unormowana
o jednolitej preferencji
symetryczna
uniwersalna
stosowana dla dowolnego układu rodzajowego cech
określająca siłę i kierunek zależności
prosta pod względem rachunkowym
Metoda nieparametryczna polega na badaniu podobieństwa rozkładów warunkowych w tablicy korelacyjnej.
Jeżeli rozkłady warunkowe cechy zależnej tzw. zmiennej objaśnianej są identyczne (lub proporcje między nimi są takie same) oznacza to, że między cechami nie ma związku stochastycznego.
Studenci III roku WWSZiP ze względu na płeć i poziom inteligencji
inteligencji
płeć |
wysoki
|
bardzo wysoki |
Razem (ni) |
kobieta |
50 |
70 |
120 |
mężczyzna |
50 |
70 |
120 |
Razem (nj) |
100 |
140 |
240 |
Źródło: dane umowne
Studenci III roku WWSZiP ze względu na płeć i poziom inteligencji
inteligencji
płeć |
wysoki
|
bardzo wysoki |
Razem (ni) |
kobieta |
60 |
100 |
160 |
mężczyzna |
30 |
50 |
80 |
Razem (nj) |
90 |
150 |
240 |
Źródło: dane umowne
Współczynnik zależności Hellwiga - dH
oblicza się dla tablicy korelacyjnej
Własności miary Hellwiga:
zalety:
niemianowana
unormowana w przedziale <0;1> interpretacja:
dH = 0 - niezależność stochastyczna,
dH (0; 0,34) - zależność słaba,
dH <0,34; 0,67) - zależność średnia,
dH <0,67; 1) - zależność silna,
dH = 1 - zależność ścisła (funkcyjna),
jednolitej preferencji
symetryczna
uniwersalna
stosowana dla dowolnego układu rodzajowego cech
wady:
nie pokazuje kierunku zależności
Współczynnik zależności Hellwiga
- oblicza się dla danych w tablicy korelacyjnej
wzór:
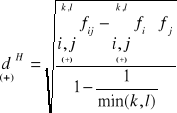
fij - częstość w rozkładzie łącznym,
fi , fj - częstości brzegowe,
min(k,l) - minimum z liczby wariantów
cechy X i Y
Kolejność obliczeń:
w tablicy zamienić liczebności na częstości - (fij, fi, fj)
obliczyć iloczyn częstości brzegowych dla każdego pola w rozkładzie łącznym tablicy - (fi fj),
od częstości w rozkładzie łącznym odjąć iloczyn częstości brzegowych - dla każdego pola w rozkładzie łącznym tablicy - (fij - fi fj),
zaznaczyć pola z różnicami dodatnimi (fij-fifj ှ0),
zsumować z zaznaczonych pół częstości w rozkładzie łącznym
(ქ fij),
zsumować z zaznaczonych pół iloczyny częstości brzegowych
(ქ fifj ),
podstawić sumy do wzoru.
Przykład obliczania współczynnika Hellwiga:
Na podstawie tablicy korelacyjnej zbadać zależność wydajności pracy pracowników pewnego działu produkcyjnego (cecha Y - w szt./ godz.) od typu zmiany (cecha X).
Rozwiązanie:
Dla ułatwienia obliczeń pierwsze cztery działania można wykonać w tablicy (wyniki zostały podane z dokładnością do trzeciego miejsca po przecinku):
Typ zmiany |
190 - 250 |
250 - 310 |
310 - 370 |
ni (fi) |
I zmiana |
6 (6/50)= 0,12 (0,60,18)= 0,108 (0,12 - 0,108)= + 0,012 |
9 (9/50)= 0,18 (0,60,28)= 0,168 (0,18 - 0,168)= + 0,012 |
15 (15/50)= 0,3 (0,60,54)= 0,324 (0,12 - 0,108)= - 0,024 |
30
0,6 |
II zmiana |
3 (3/50)= 0,06 (0,40,18)= 0,072 (0,06 - 0,072)= - 0,012 |
5 (5/50)= 0,1 (0,40,28)= 0,112 (0,1 - 0,112)= - 0,012 |
12 (12/50)= 0,24 (0,40,54)= 0,216 (0,24 - 0,216)= + 0,024 |
20
0,4
|
nj (fj) |
9 0,18 |
14 0,28 |
27 0,54 |
N = 50 F=1 |
działanie 5: ქ( + ) fij = 0,12 + 0,18 + 0,24 = 0,54
działanie 6: ქ( + ) fifj = 0,108 + 0,168 + 0,216 = 0,492
działanie 7: ponieważ cecha X ma 2 warianty (k = 2), a cecha Y - 3 warianty (l = 3), to w mianowniku za wyrażenie min(k,l) należy podstawić mniejszą liczbę wariantów tj. 2
Zależność wydajności pracy od typu zmiany jest słaba (dH<0; 0,34)
Metoda parametrycznego badania współzależności
polega na badaniu podobieństwa parametrów obliczonych z rozkładów warunkowych.
Jeżeli parametry rozkładów warunkowych cechy zależnej są identyczne, to nie ma zależności w sensie korelacyjnym.
Jeżeli natomiast parametry poszczególnych rozkładów różnią się - istnieje zależność korelacyjna.
Przykład 1.6. W celu ustalenia czy liczba posiadanego rodzeństwa wpływa w dorosłym życiu na preferencje kobiet co do ilości dzieci, zapytano 100 losowo wybranych kobiet o ilość dzieci, które chciałyby wychować (cecha Y) oraz o liczbę rodzeństwa (cecha X). Na podstawie danych przedstawionych w poniższej tablicy zbadać czy istnieje zależność korelacyjna między liczbą rodzeństwa kobiet a preferowaną przez kobiety liczbą dzieci.
|
1 |
2 |
3 |
ni |
0-1 |
19 |
18 |
3 |
40 |
2-3 |
22 |
12 |
6 |
40 |
4 i więcej |
10 |
8 |
2 |
20 |
nj |
51 |
38 |
11 |
100 |
Rozwiązanie: Aby zbadać czy istnieje zależność korelacyjna należy obliczyć np. średnie arytmetyczne z rozkładów warunkowych (tzw. średnie warunkowe) cechy zależnej. W tym przypadku cechą zależną (czyli skutkiem w badanej zależności) jest preferowana przez kobietę liczba dzieci - Y (ponieważ może ona zależeć od liczby rodzeństwa tej kobiety). W tablicy występują 3 rozkłady warunkowe cechy Y (ponieważ można nałożyć 3 warunki na cechę X). Należy więc obliczyć 3 średnie warunkowe cechy Y:
Takie same wartości średnich warunkowych wskazują, że niezależnie od ilości rodzeństwa średnia preferowana liczba dzieci nie zmienia się, co oznacza niezależność korelacyjną między cechami. Przykład 1.6. pozwala zauważyć wzajemne powiązania metody stochastycznego i korelacyjnego badania współzależności. Metoda stochastyczna jest bardziej rygorystyczna ponieważ, aby istniała niezależność stochastyczna, liczebności w rozkładach warunkowych muszą być identyczne. W metodzie korelacyjnej rozkłady nie muszą być identyczne, aby istniała niezależność korelacyjna - wystarczy jeśli obliczone z nich parametry (np. średnie warunkowe) były takie same.
Dlatego też niezależność w sensie stochastycznym zawsze oznacza również niezależność w sensie korelacyjnym (parametry np. średnie warunkowe obliczone z identycznych rozkładów warunkowych będą zawsze jednakowe). Natomiast niezależność korelacyjna nie zawsze oznacza niezależność stochastyczną (może oznaczać - jeśli rozkłady warunkowe są takie same, ale nie musi - jeśli rozkłady różnią się, a parametry są identyczne - patrz przykład 1.6.)
Współczynnik korelacji liniowej Pearsona
Własności rp:
zalety:
niemianowana,
unormowana w przedziale: <-1,1>;
rP = 0 niezależność korelacyjna, rP ၼ (0; 0,34) ၼ zależność słaba
rP ၼ <0,34; 0,67) ၼ średnia,
rP ၼ <0,67; 1) ၼ silna,
rP = 1 lub rP= -1 zależność funkcyjna
rP < 0 kierunek zależności ujemny
rP > 0 kierunek zależności dodatni,
jednolitej preferencji,
symetryczna,
mierzy siłę oraz określa kierunek zależności,
wady:
tylko do zależności prostoliniowych
tylko dla dwóch cech mierzalnych
Współczynnik korelacji liniowej Pearsona
- rp - wzór teoretyczny:
![]()
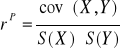
gdzie:
cov (X,Y) - kowariancja
S(X) - odchylenie standardowe cechy X
S(Y) - odchylenie standardowe cechy Y
Licznik wzoru Pearsona, czyli kowariancja decyduje o kierunku zależności
Wzór dla tablicy korelacyjnej:
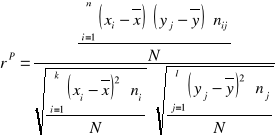
gdzie:
xi - wartości cechy X,
yj - wartości cechy Y,
nij - liczebności w rozkładzie łącznym
nj - liczebność cechy Y,
ni - liczebność cechy X
x - - średnia arytmetyczna cechy X
y - średnia arytmetyczna cechy Y
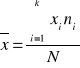
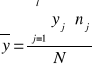
Przykład
Pracowników pewnego przedsiębiorstwa zbadano ze względu na liczbę uzyskanych upomnień w 2001 r. (cecha X) oraz staż pracy (cecha Y - w latach). Wyniki przedstawiono w tablicy korelacyjnej. Należy zbadać siłę i kierunek zależności między cechami.
|
1-3 |
3-5 |
5-7 |
7-9 |
1 |
- |
- |
- |
9 |
3 |
- |
2 |
9 |
1 |
5 |
1 |
8 |
2 |
- |
7 |
8 |
- |
- |
- |
Rozwiązanie:
W tym przypadku zastosowanie miary Pearsona jest możliwe ponieważ obie cechy są mierzalne, a kierunek zależności można uznać za prostoliniowy (liczebności skupiają się na głównej przekątnej; pola tworzące główną przekątną tablicy zostały zacieniowane).
Należy zwrócić uwagę, że warianty cechy Y zostały przedstawione w postaci przedziałów. We wszystkich wzorach zamiast wartości cechy Y -“yi” należy wprowadzić środek przedziału - “”.
Kolejność obliczeń:
po obliczeniu liczebności brzegowych: ni oraz nj, należy obliczyć średnie arytmetyczne obu cech:
y = 5,1 (lat) [(29+410+611+810)/40=(18+40+66+80)/40 = 204/40]
x = 3,9 (upomnień) [(19+ 312+511+78)/ 40 = (9+36+55+56)/40 = 156/40]
Większość obliczeń można wykonać w tablicy:
obliczenia składowe kowariancji - w polach rozkładu łącznego tablicy:
ქ (xi - x) (yi - y) nij = -75,69+1,98-7,29-2,61-3,41-9,68+1,98-76,88 = -171,6
obliczenia dotyczące cechy Y będą wykonywane w kolejno dodawanych wierszach tablicy (ponieważ wartości cechy Y znajdują się w główce tablicy) ქ = 191,6
obliczenia dotyczące cechy X znajdują się- w kolejnych kolumnach. ქ = 175,6
|
1-3 |
3-5 |
5-7 |
7-9 |
ni |
|
|
|
|
- (-2,9თ -3,1თ 0)=
|
-
|
- |
9 (-2,9თ 2,9თ 9)=
|
9 |
- 2,9 |
8,41 |
75,69 |
|
-
|
2 (-0,9თ-1,1თ2)= |
9 (-0,9თ0,9თ9)=
|
1 (-0,9თ 2,9თ1)=
|
12 |
-0,9 |
0,81 |
9,72
|
|
1 (1,1თ -3,1თ1)= |
8 (1,1თ -1,1თ8)= |
2 (1,1თ 0,9თ 2)= |
- |
11 |
1,1 |
1,21 |
13,31
|
|
8 (3,1თ -3,1თ 8)= |
- |
-
|
-
|
8 |
3,1 |
9,61 |
76,88
|
nj |
9 |
10 |
11 |
10 |
40 |
|
|
ქ=175,6 |
|
2 |
4 |
6 |
8 |
|
|
|
|
|
-3,1 (2-5,1) |
-1,1 (4-5,1) |
0,9 (6-5,1) |
2,9 (8-5,1) |
|
|
|
|
|
9,61 (-3,1)2 |
1,21 (-1,1)2 |
0,81 (0,9)2 |
8,41 (2,9)2 |
|
|
|
|
|
86,49 (9,619) |
12,1 (1,2110) |
8,91 (0,8111) |
84,1 (8,4110) |
ქ = 191,6 (86,49+12,1+8,91+84,1) |
|
||
odpowiednie sumy należy podstawić do wzoru:
cov(X,Y) = -171,6/ 40 = -4,29 (upomnień lat)
S2(X) = 175,6 / 40 = 4,39 (upomnień)2 S(X) = 2,1 (upomnień)
S2(Y) = 191,6 / 40 = 4,79 (lat)2 S(Y) = 2,19 (lat)
rP = -4,29/2,1 2,19 = -4,29/ 4,6 = -0,93 zależność liczby upomnień od stażu pracy jest silna, o kierunku ujemnym tzn. że w miarę wzrostu stażu pracy silnie maleje liczba upomnień.
Wzór dla szeregów statystycznych:
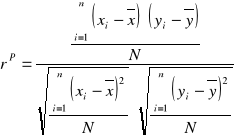
![]()
gdzie:
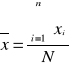
![]()
![]()
Kolejność obliczeń:
obliczyć średnie arytmetyczne cechy X i Y
obliczyć różnice:
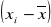
oraz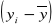
obliczyć iloczyny
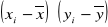
i zsumowaćpodnieść do kwadratu różnice:
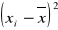
i zsumowaćpodnieść do kwadratu różnice:
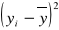
i zsumować,odpowiednie sumy podstawić do wzoru.
Przykład
Pracowników produkcyjnych pewnego działu zbadano ze względu na staż pracy (Y - w latach) oraz średnią wydajność (X - w szt/h). Na podstawie zebranych danych zbadać zależność między cechami:
Lp. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
2 |
8 |
9 |
6 |
5 |
7 |
5 |
3 |
6 |
7 |
Y |
10 |
17 |
18 |
14 |
14 |
15 |
13 |
12 |
15 |
16 |
Rozwiązanie:
Informacje przedstawione są w szeregach statystycznych (ponieważ liczebność badanej zbiorowości jest mała: N = 10), obie cechy są mierzalne, a z wykresu korelacyjnego wynika, że zależność jest prostoliniowa - to oznacza, że spełnione są wszystkie warunki wykorzystania wzoru Pearsona dla szeregów statystycznych.
Większość obliczeń można wykonać w tabeli. Dla wygody informacje można przedstawić pionowo (w kolejnych kolumnach):
Lp. |
xi |
yi |
|
|
|
|
|
1 |
2 |
10 |
-3,8 (2-5,8) |
-4,4 (10-14,4) |
16,72 (-3,8Ⴔ-4,4) |
14,44 (-3,8)2 |
19,36 (-4,4)2 |
2 |
8 |
17 |
2,2 |
2,6 |
5,72 |
4,84 |
6,76 |
3 |
9 |
18 |
3,2 |
3,6 |
11,52 |
10,24 |
12,96 |
4 |
6 |
14 |
0,2 |
-0,4 |
-0,08 |
0,04 |
0,16 |
5 |
5 |
14 |
-0,8 |
-0,4 |
0,32 |
0,64 |
0,16 |
6 |
7 |
15 |
1,2 |
0,6 |
0,72 |
1,44 |
0,36 |
7 |
5 |
13 |
-0,8 |
-1,4 |
1,12 |
0,64 |
1,96 |
8 |
3 |
12 |
-2,8 |
-2,4 |
6,72 |
7,84 |
5,76 |
9 |
6 |
15 |
0,2 |
0,6 |
0,12 |
0,04 |
0,36 |
10 |
7 |
16 |
1,2 |
1,6 |
1,92 |
1,44 |
2,56 |
Razem |
ქ = 58 |
ქ= 144 |
Ⴔ |
Ⴔ |
ქ = 44,8 |
ქ = 41,6 |
ქ = 50,4 |
średni staż pracy wynosi: 5,8 (lat), średnia wydajność wynosi: 14,4 (szt./h)
cov(X,Y) = 44,8/ 10 = 4,48 (szt/h lat)
S2(X) = 41,6 / 10 = 4,16 (szt/h)2 S(X) = 2,04 (szt/h)
S2(Y) = 50,4 / 10 = 5,04 (lat)2 S(Y) = 2,25 (lat)
rP = 4,48 / 2,04 2,25 = 4,48/ 4,59 = 0,98 zależność wydajności pracy od stażu pracy jest silna, o kierunku dodatnim.
Stosunek korelacyjny
zalety:
niemianowana,
unormowana w przedziale: <0,1>; Interpretacja:
rk = 0 niezależność korelacyjna,
rk (0; 0,34) zależność słaba,
rk <0,34; 0,67) zależność średnia,
rk <0,67; 1) zależność silna,
rk =1 zależność ścisła tzw. funkcyjna
spełnia warunek jednolitej preferencji,
uniwersalna - służy do badania zależności krzywoliniowych i prostoliniowych
wady:
nie jest symetryczna tzn. rk xy Ⴙ rk yx ; dlatego w przypadku zależności przyczynowo-skutkowej należy ustalić która cecha jest cechą zależną i zastosować odpowiedni wzór,
na ogół nie pokazuje kierunku zależności
można stosować miarę zawsze dla dwóch cech mierzalnych
oraz dla układu cech: mierzalna - niemierzalna, ale tylko wtedy, gdy cecha mierzalna jest cechą zależną.
Stosunek korelacyjny jest ilorazem odchylenia standardowego średnich warunkowych cechy zależnej oraz odchylenia standardowego cechy zależnej:
rk =
|
odchylenie standardowe średnich warunkowych cechy zależnej |
|
odchylenie standardowe cechy zależnej |
Dlatego też najważniejszym zadaniem jest ustalenie która z cech jest cechą zależną oraz gdzie zostały umieszczone jej warianty - w główce czy też w boczku tablicy. Położenie cechy zależnej w tablicy decyduje o wyborze wzoru, z którego oblicza się rk.
W przypadku zależności dwustronnej należy obliczyć dwa stosunki korelacyjne:
rk(yx) - mierzy korelację cechy Y względem cechy X (Y zależy od X - Y jest cechą zależną),
rk(xy) - mierzy korelację cechy X względem cechy Y (X zależy od Y - X jest cechą zależną).
Zależność cechy Y od X oblicza się z wzoru (gdy cecha Y znajduje się w główce tablicy):
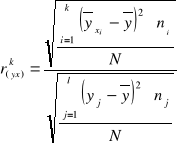
gdzie:
yj - wartość cechy Y
y - średnia arytmetyczna cechy Y - obliczona z rozkładu brzegowego cechy Y według wzoru:
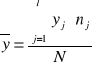
yxi - średnia warunkowa cechy Y - obliczana z rozkładu warunkowego cechy Y według wzoru:
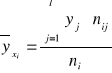
Zależność cechy X od Y służy wzór (gdy cecha X znajduje się w boczku tablicy):
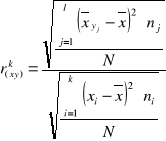
![]()
gdzie:
xi - wartość cechy X
x - średnia arytmetyczna cechy X - obliczona z rozkładu brzegowego cechy X według wzoru:
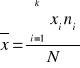
xyj - średnia warunkowa cechy X - obliczana z rozkładu warunkowego cechy X według wzoru:
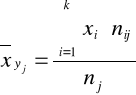
Przykład
Uczniów pewnej klasy Liceum Ekonomicznego zapytano o wysokość otrzymywanego co miesiąc kieszonkowego (cecha X w zł) oraz miesięczny dochód na jedną osobę w rodzinie ucznia (cecha Y - w zł). Na podstawie wyników przedstawionych w tablicy korelacyjnej zbadać zależność między cechami wykorzystując metodę korelacyjną.
|
600-900 |
9000-1200 |
1200-1500 |
ni |
30-180 |
5 |
5 |
4 |
14 |
180-330 |
2 |
4 |
9 |
15 |
330-480 |
2 |
2 |
7 |
11 |
nj |
9 |
11 |
20 |
40 |
Rozwiązanie:
Ponieważ należy zbadać zależności metodą korelacyjną, to nie można wykorzystać miar nieparametrycznych. Nie można również wykorzystać współczynnika korelacji liniowej Pearsona (miara omówiona w punkcie 1.2.2.) ponieważ z układu liczebności w tablicy wynika, że zależność nie jest prostoliniowa. Nie da się również zastosować miary Spearmana (miara omówiona w punkcie 1.2.3.), ponieważ informacje przedstawione są w postaci tablicy.
Można natomiast zastosować stosunek korelacyjny, ponieważ obie cechy są mierzalne. Należy ustalić, która cecha jest cechą zależną: oraz określić położenie cechy zależnej w tablicy. W analizowanym przykładzie cechą zależną jest kieszonkowe (może zależeć od dochodu); cecha zależna znajduje się w boczku tablicy, co oznacza, że należy wykorzystać wzór rkxy (zależność cechy X od Y - gdy X umieszczone jest w boczku).
Kolejność działań jest następująca:
wyznaczyć środki przedziałów cechy X: x*1= 105, x*2 = 255, x*3 = 405
obliczyć średnią arytmetyczną cechy X:
średnie miesięczne kieszonkowe ucznia w tej klasie wynosi: 243,75 zł [10514+25515+40411/40] = [1470+3825+4455/40]=[9750/40]
obliczyć średnie warunkowe cechy X - z rozkładów warunkowych cechy X (pierwsza, druga i trzecia kolumna):
średnie miesięczne kieszonkowe uczniów o dochodzie na 1 osobę w rodzinie, mieszczącym się w przedziale <600-900) zł wynosi: 205 zł.
średnie miesięczne kieszonkowe uczniów o dochodzie na 1 osobę w rodzinie, mieszczącym się w przedziale <900-1200) zł wynosi: 214,09 zł,
średnie miesięczne kieszonkowe uczniów o dochodzie na 1 osobę w rodzinie, mieszczącym się w przedziale <1200-1500) zł wynosi: 277,5 zł,
Średnie warunkowe ułożyły się rosnąco, co oznacza, że można uznać domyślny kierunek zależności za dodatni (wzrost dochodu powoduje wzrost kieszonkowego).
Kolejne obliczenia wykonano w tablicy:
wszystkie obliczenia dotyczące odchylenia standardowego cechy X umieszczono w kolejno dodawanych kolumnach tablicy (ponieważ wartości cechy X znajdują się w boczku tablicy) ქ = 557.437,4
obliczenia dotyczące odchylenia standardowego średnich warunkowych cechy X znajdują się- w kolejnych wierszach (ponieważ cecha na którą nakładany jest warunek znajduje się w główce tablicy - cecha Y) ქ =45.972,16
xi |
600-900 |
900-1200 |
1200-1500 |
ni |
x*i |
(x*i -x) |
(x*i -x)2 |
(x*i -x)2ni |
|||
30-180 |
5
|
5
|
4 |
14 |
105 |
138,75
(105-243,75) |
19.251,56
(138,75)2 |
269.521,84
(19.251,56·14) |
|||
180-330
|
2 |
4
|
9 |
15 |
255 |
11,25
(255-243,75) |
126,56
(11,25)2 |
1898,4
(126,56·15) |
|||
330-480
|
2 |
2 |
7 |
11 |
405 |
161,25
(405-243,75) |
26.001,56
(161,25)2 |
286.017,16
(26.001,56·11) |
|||
nj |
9 |
11 |
20 |
40 |
|
|
ქ |
557.437,4 |
|||
xyj
|
205 |
214,09 |
277,5 |
|
|
|
|
|
|||
(xyj- x) |
-38,75 (205-143,75) |
-29,66 (214,09-243,75 |
33,75 277,5-243,75 |
|
|
|
|
|
|||
(xyj- x)2 |
1501,56 (-38,75)2 |
879,72 (-29,66)2 |
1139,06 (33,75)2 |
|
|
|
|||||
(xyj- x)2nj |
13.514,04 (1501,56·9) |
9.676,92 (879,72·11) |
22.781,2 (1139,06·20) |
ქ = 45.972,16 (13.514,04+9.676,92+22.781,2) |
|
|
|||||
odpowiednie sumy należy podstawić do wzoru - zależność kieszonkowego od dochodu przypadającego na 1 os. w rodzinie jest słaba, o domyślnym kierunku dodatnim.
[obliczenia z pełnego wzoru: S2(Y) = 557.437,4/40=13935,94 zł2; S(Y) =118,05 zł
S2(xyj) = 45.972,16/40=1149,3 zł2; S(xyj) =33,9 zł
rkxy = 33,9/ 118,05 = 0,29]
Zadania z odpowiedziami
Zad. 25. W 2001 r. zbadano losowo wybraną grupę podatników ze względu na wiek (Y - w latach oraz wysokość dochodów uzyskanych poza pierwszym miejscem pracy (X - w tys zł). Zbadać zależność między cechami:
X Y |
0-8 |
8-16 |
16-24 |
18-24 |
15 |
11 |
10 |
24-30 |
8 |
- |
6 |
30-36 |
1 |
7 |
15 |
36-42 |
5 |
18 |
19 |
(odp. rkxy = 0,36. Zależność X od Y jest średnia - kierunku nie można określić; średnie warunkowe: 10,89 tys.zł, 16,87 tys.zł, 14,67 tys.zł).
Zad. 27. Pracowników firmy “A” zbadano ze względu na dwie cechy: wykształcenie (cecha X) oraz wynagrodzenie brutto w $ w lipcu 1998 r. (cecha Y). Otrzymano następujące wyniki:
Lp. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
w |
ś |
w |
z |
p |
p |
z |
p |
ś |
p |
Y |
690 |
510 |
699 |
460 |
300 |
310 |
370 |
300 |
420 |
310 |
Lp. |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
X |
ś |
z |
p |
ś |
w |
p |
z |
p |
w |
z |
Y |
399 |
400 |
320 |
550 |
570 |
310 |
370 |
310 |
580 |
420 |
Przedstawić wyniki w postaci tablicy statystycznej.
Zad. 1. W restauracjach miasta „A” zebrano dane dotyczące oceny jakości usług (wystawionej przez klientów - cecha Y w punktach) oraz średniej miesięcznej liczby klientów (cecha X). Wyniki przedstawiono w tablicy korelacyjnej:
Y X |
50-100 |
100-150 |
150-200 |
ni |
2-4 |
7 |
1 |
- |
8 |
4-6 |
- |
9 |
- |
9 |
6-8 |
- |
2 |
6 |
8 |
nj |
7 |
12 |
6 |
25 |
zbadać siłę i kierunek zależności między cechami. (odp. rP = 0.9),
Zad. 21. Uzupełnij tablicę tak, aby między cechami występowała zależność funkcyjna. Uzasadnij.
X Y |
y1 |
y2 |
y3 |
ni |
x1 |
|
|
|
5 |
x2 |
|
|
|
|
x3 |
|
|
|
|
nj |
|
10 |
|
30 |
Zad.2. W 30 wybranych losowo gospodarstwach indywidualnych zebrano dane dotyczące rocznej wielkości plonów pszenicy w q/ha ( cecha X ) oraz zużycia nawozów mineralnych w kg/ha (cecha Y). Wyniki przedstawiono w tablicy korelacyjnej:
X Y |
40-45 |
45-50 |
50-55 |
ni |
20-30 |
9 |
3 |
- |
12 |
30-40 |
- |
8 |
- |
8 |
40-50 |
- |
2 |
8 |
10 |
nj |
9 |
13 |
8 |
30 |
zbadać siłę i kierunek zależności między cechami. (rP = 0.88),
Zad.3. Pracowników pewnego działu zbadano ze względu na staż pracy (X - w latach) oraz % braków w miesiącu maju'2005 (Y - w %). Scharakteryzować zależność między cechami. Uzasadnić wybór miary.
Lp. |
X |
Y |
1 2 3 4 5 6 7 8 9 10 11 |
1 1,5 4 4 2 3 5 2 3 3,5 3 |
4 3,5 1 2 2,5 3 1 3 2 2 3,5 |
Odp. rp = -0,86. Zależność silna o kierunku ujemnym tzn., że pracownicy z wyższym stażem pracy „produkują” mniej braków. Uzasadnienie: obie cechy są mierzalne, zależność można uznać za prostoliniową (wykres), rp można wykorzystywać do informacji przestawionych w szeregach.
Zad. 24. W 25 województwach zebrano dane dotyczące liczby miejsc noclegowych (X - w tys.) oraz występujących na terenie województwa naturalnych walorów wypoczynkowych (Y - w punktach). Zbadać zależność między cechami wykorzystując miarę niesymetryczną.
X Y |
5-15 |
15-25 |
25-35 |
0-10 |
2 |
1 |
- |
10-20 |
2 |
3 |
- |
20-30 |
3 |
4 |
1 |
30-40 |
4 |
2 |
3 |
(odp. rkxy = 0,36. Zależność X od Y jest średnia - kierunku nie można określić; średnie warunkowe: 23,18 tys., 22 tys. 32,5 tys.).
Zad. 4 Która z podanych wartości nie może być wynikiem miary Pearsona: 0,68; - 0,9; 1.05; - 1,5. Odpowiedź uzasadnić. (1,05 oraz -1,5 ponieważ wynik rp <-1; >).
Zad.5 Wybraną losowo grupę modelek zbadano ze względu na wzrost ( Y ) oraz wiek (cecha X). Wyniki przedstawiono w tablicy korelacyjnej:
X Y |
wysoki |
bardzo wysoki |
ni |
16-20 |
80 |
20 |
100 |
20-24 |
70 |
80 |
150 |
nj |
150 |
100 |
250 |
czy można zbadać zależność miarą rp- uzasadnić (odp. Nie można ponieważ wzrost został przedstawiony w sposób opisowy)
Zad. 6. Pracowników pewne firmy zbadano z względu na płeć (X) oraz stosunek o pracy (Y). Zbadać zależność między cechami
X Y |
dobry |
zły |
kobieta |
30 |
10 |
mężczyzna |
32 |
8 |
(odp. dH = 0,22 )
Zad. 13. Pracowników pewnego działu zbadano ze względu na staż pracy (X - w latach) oraz % braków w miesiącu maju'99 (Y - w %). Scharakteryzować zależność między cechami.
Lp. |
X |
Y |
1 2 3 4 5 6 7 8 9 10 |
0,5 2 1 2 3 5 7,5 3 4 4 |
6 4 5 3,5 3 2 0,5 2 3 4 |
Odp. Można wykorzystać albo rp albo rs. rp = -0,88; rs = -0,78 - zależność silna, o kierunku ujemnym tzn., że im dłuższy staż pracy, tym mniejszy procent braków w miesiącu.
Zad. 7 Pracowników pewnej firmy zbadano z względu na rodzaj wykształcenia (X) oraz częstość spóźnień do pracy (Y). Zbadać zależność między cechami
X Y |
dobry |
zły |
zawodowe |
14 |
15 |
średnie |
15 |
14 |
wyższe |
14 |
15 |
(odp. dH = 0,17 - zależność słaba).
2008-10-11 Wykład 4 Analiza Współzależności
8
-76,88
0
0
0
0
-3,41
1,98
-9,68
0
1,98
-7,29
-2,61
0
0
0
-75,69
Średnie warunkowe ułożyły się rosnąco
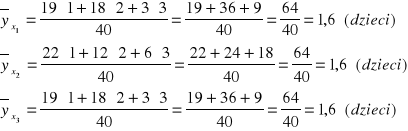
Y
X
Wyszukiwarka