I. ANALIZA STRUKTURY

1) Określenie populacji generalnej, jednostki statystycznej i próby.

Populacja (zbiorowość) statystyczna - zbiór dowolnych elementów (osób, przedmiotów, faktów) podobnych pod względem określonych cech (ale nie identycznych) i poddanych badaniom statystycznym.

Populacja (zbiorowość) generalna - wszystkie elementy będące przedmiotem badania, co do których chcemy formułować wnioski ogólne.

Zbiorowość próbna (próba) - podzbiór populacji generalnej, obejmujący część jej elementów, wybranych w określony sposób. Liczba elementów próby to n.

Jednostka statystyczna - element składowy zbiorowości podlegający bezpośredniej obserwacji lub pomiarowi.

2) Jaki charakter może mieć badanie statystyczne? W jakim badaniu statystycznym występuje próba?

Badanie statystyczne - ogół prac mających na celu poznanie struktury określonej zbiorowości statystycznej.

Etapy badania statystycznego:

1/ przygotowanie badania czyli:

• sprecyzowanie celu badania

• określenie zbiorowości statystycznej i jednostki statystycznej

• określenie charakteru badania (pełne czy częściowe)

• określenie sposobu pozyskiwania danych i źródła z jakich będą pochodziły

• przygotowanie materiałów do przeprowadzenia badania (formularze ankietowe, programy do opracowania danych)

• sporządzenie planu finansowego badania

2/ gromadzenie materiału statystycznego (obserwacja statystyczna)

3/ opracowanie zebranego materiału w postaci tablic i wykresów (grupowanie i prezentacja zebranych informacji)

4/ analiza wyników obserwacji - otrzymujemy tu opis statystyczny (przy badaniu statystycznym pełnym) lub wnioski dotyczące populacji generalnej (przy badaniu statystycznym częściowym).

Obserwacja statystyczna - proces zbierania informacji statystycznych

Obserwacje statystyczne można uzyskać na podstawie badania statystycznego:

- całkowitego (wyczerpującego) - obserwacji podlegają wszystkie elementy zbiorowości generalnej

- częściowego - obserwacji podlega tylko część zbiorowości generalnej, tzw. próba.

Badania całkowite to spis statystyczny, inwentaryzacja, rejestracja bieżąca, sprawozdawczość statystyczna. Badania częściowe to badania reprezentacyjne, monograficzne i ankietowe.

Aby uzyskane wyniki badania próby można było odnieść do zbiorowości generalnej z określoną dokładnością, próba musi być reprezentatywna, muszą być spełnione 2 warunki:

* musi być wybrana losowo - tzn. każda jednostka danej zbiorowości ma znane, różne od zera prawdopodobieństwo znalezienia się w próbie

* powinna być dostatecznie liczna.

3) Jakie rodzaje cech statystycznych podlegających badaniu wyróżniamy?

Cechy statystyczne - jednostki statystyczne wchodzące w skład zbiorowości statystycznej, charakteryzujące się pewnymi właściwościami.

Aby określić populację generalną należy wszystkie jednostki określić pod względem: rzeczowym (co lub kogo badamy?), przestrzennym ( jaki obszar obejmuje badanie?), czasowym (kiedy badanie się odbywa lub jakiego czasu dotyczy?).

Wymienione atrybuty cech to tzw. cechy stałe (rzeczowe, przestrzenne, czasowe); są wspólne wszystkim jednostkom danej zbiorowości i nie podlegają badaniu, decydują tylko o zaliczeniu jednostki do określonej zbiorowości.

Natomiast właściwości, które różnią poszczególne jednostki statystyczne to cechy zmienne.

Cechy zmienne dzielimy na:

1/ cechy niemierzalne (jakościowe) - własności jednostek statystycznych nie dające się zmierzyć. Można jedynie stwierdzić, które z wariantów cechy występuje u danej jednostki; określane słownie np. płeć, cechy geograficzne, wykształcenie, zawód; te cechy opisane są w skali porządkowej.

2/ cechy mierzalne ( ilościowe) - właściwości które można zmierzyć i wyrazić za pomocą odpowiednich jednostek fizycznych np. kg, cm, sztuki. Do tych cech zalicza się też cechy quasi-ilościowe zwane porządkowymi (przedstawiają daną właściwość w sposób opisowy, porządkując w ten sposób zbiorowość np. ocena wiadomości studenta: bardzo dobra, dobra albo 5, 4, itp.).

Cechy mierzalne dzielimy na :

a) skokowe (dyskretne) - przyjmują skończony lub przeliczalny zbiór wartości na danej skali liczbowej (najczęściej jest to zbiór liczb całkowitych dodatnich np. liczba osób w rodzinie, oceny studenta)

b) ciągłe - mogą przyjąć każdą wartość z określonego przedziału liczbowego <a,b>, przy czym liczba miejsc po przecinku jest uzależniona od dokładności dokonywanych pomiarów np. waga detalu.

Wyróżniamy też cechy quasi-ciągłe (skokowa, ciągła) - skala wartości jakie te cechy mogą przybierać jest bardzo duża np. płace w Polsce.

Cechy mierzalne (zmienne) oznaczamy X, Y, Z a wartości tych cech - x_i, y_i, z_i.

4) W jaki sposób porządkujemy dane statystyczne? Jakie rodzaje szeregów statystycznych możemy utworzyć?

Dane statystyczne otrzymane w wyniku przeprowadzonej obserwacji statystyczne (lub pomiaru) porządkujemy i grupujemy w postaci tzw. szeregów statystycznych. Istotą grupowania jest usystematyzowanie jednostek badania wg interesującej nas cechy statystycznej (zmiennej). Grupowanie materiału stosujemy po przeprowadzeniu jego kontroli pod względem formalnym i merytorycznym.

Metody grupowania mogą być związane z cechą mierzalną (ilościową) np. wiek, płaca, bądź cechą niemierzalną (jakościową) np. płeć, pochodzenie społeczne, rodzaj kredytu.

Rodzaje grupowania:

1/ typologiczne (na podstawie cech jakościowych) - np. wg cech terytorialnych, rzeczowych, czasowych; ma na celu wyodrębnienie gryp różnych jakościowo; grupowanie typologiczne grupuje zbiorowość niejednorodną na grupy jednorodne.

2/ wariancyjne (mechaniczne, opiera się na cesze ilościowej) - ma na celu uporządkowanie danej zbiorowości i poznanie jej struktury; polega na łączeniu w klasy jednostek statystycznych o odpowiednich wartościach cech statystycznych.

Dla cechy niemierzalnej kolejność zapisywania wariantów cechy jest dowolna, natomiast dla cechy mierzalnej - dane porządkujemy z reguły niemalejąco.

Liczebności odpowiadające poszczególnym wariantom cechy oznaczamy n_i gdzie i = 1,2,...k. Ogólna liczebność badanej zbiorowości to suma poszczególnych zbiorowości.

Dane statystyczne grupujemy w postaci tzw. szeregów statystycznych.

Szereg statystyczny to ciąg wielkości statystycznych, uporządkowany i pogrupowany wg określonych kryteriów. Szeregi statystyczne dzielimy na:

1/ szczegółowe

2/ rozdzielcze:

- szeregi z cechą mierzalną (ilościową): punktowe i przedziałowe

- szeregi z cechą niemierzalną (jakościową)

3/ czasowe

Szeregi mogą być konstruowane różnie. Idealnie zbudowanym szeregiem, który daje możliwość wykorzystania szerokiego wachlarza parametrów jest szereg o równych przedziałach klasowych, zamknięty górą i dołem. Buduje się również szeregi rozdzielcze:

• o nierównych przedziałach klasowych

• otwarte dołem lub górą

• otwarte dołem i górą.

Szereg statystyczny otwarty dołem - od strony najmniejszej wartości

Szereg statystyczny otwarty górą - od strony największej wartości.

Jeżeli mamy szereg o nierównych przedziałach klasowych i otwarty górą lub dołem to znaczy że nie możemy stosować klasycznych miar statystycznych w analizie struktury zbiorowości.

Dla cechy mierzalnej porządkowanie danych uzależnione jest od liczebności zbiorowości i liczby różnych wariantów cechy. W zależności od tego mamy 3 sytuacje:

1/ Szereg szczegółowy (prosty) - uporządkowany ciąg wartości badanej cechy statystycznej; budujemy go gdy badana zbiorowość jest mała; ustawiamy wartości cechy wg kolejności rosnącej.

Szereg rozdzielczy stanowi zbiorowość statystyczną podzieloną na części (klasy) wg określonej cechy jakościowej lub ilościowej, z podaniem liczebności lub częstości każdej z wyodrębnionych klas. Szereg rozdzielczy określa strukturę badanej zbiorowości.

2/ W przypadku gdy badana zbiorowość jest liczna, ale liczba różnych wariantów cechy niewielka budujemy szereg rozdzielczy punktowy (jednojednostkowy); budujemy je dla cechy skokowe np. liczba dzieci w małżeństwie.

n =
tzn. ogólna liczebność badanej zbiorowości to suma poszczególnych zbiorowości

W szeregach rozdzielczych do określenia struktury badanej zbiorowości obok liczebności bezwzględnej stosuje się tzw. wskaźnik struktury (częstość) oznaczany w_i.

Wskaźnik struktury (w_i) - częstość występowania danego wariantu cechy - jest to stosunek liczby jednostek o danej wartości cechy do liczebności próby: w_i =
i = 1,2,...k.

w_i - wskaźnik struktury

n_i - poszczególne liczebności n - liczebność całej zbiorowości

Obok prostego szeregu rozdzielczego wyróżniamy też szeregi rozdzielcze o liczebnościach (częstościach) skumulowanych. Szeregi rozdzielcze skumulowane uzyskuje się poprzez przyporządkowanie kolejnym wariantom cechy odpowiadających im liczebności (częstości) skumulowanych.

Skumulowany wskaźnik struktury oznaczamy w_sk =
gdzie i = 1,2, ... k

n_isk - liczba jednostek, których cechy odpowiadają wartościom nie większym niż x_i

3/ W przypadku gdy próba jest liczna i cecha mierzalna ciągła lub mieszana, skokowa, ale przyjmująca wiele różnych wartości - budujemy szereg rozdzielczy z przedziałami klasowymi (wielojednostkowy) dzieląc otrzymane wyniki na klasy.

Liczba przedziałów klasowych jest ustalana w zależności od liczebności badanej zbiorowości. Podawane są różne metody ustalania tej liczby przedziałów.

Liczebności (n_i) to liczebności poszczególnych przedziałów klasowych. W zapisie często podaje się wartość prawego krańca przedziału wyższego i lewego krańca przedziału niższego. Na początku ustalamy czy w danym szeregu przedziały będą domknięte z prawej czy z lewej strony. Najwygodniej jest jeśli można ustalić przedziały klasowe o jednakowej rozpiętości.

5) W jaki sposób możemy ocenić czy dwie zbiorowości statystyczne są podobne czy nie, ze względu na badaną cechę?

Do pomiaru podobieństwa zbiorowości stosuje się różne miary. Jedną z nich jest wskaźnik podobieństwa struktur. w_p =
przy czym 0 < w_p ≤ 1

Im w_p jest bliższe jedności, tym struktury badanych zbiorowości są bardziej podobne.

w_p ≤ 0,7 struktury nie są podobne

0,7 < w_p ≤ 0,8 niewielkie podobieństwa

0,8 < w_p ≤ 0,9 znaczące podobieństwa

0,9 < w_p ≤ 0,95 duże podobieństwa

0,95 < w_p ≤ 1 bardzo duże podobieństwa

wp = 1 struktury identyczne

6) Jakie miary położenia stosujemy do opisu struktury zbiorowości? Które z tych miar są miarami klasycznymi, a które pozycyjnymi?

Analiza danych statystycznych dotyczących cechy mierzalnej ma na celu uzyskanie syntetycznego przedstawienia wyników badania przy pomocy odpowiednich charakterystyk liczbowych (parametrów statystycznych).

W analizie struktury zbiorowości stosowane są najczęściej następujące grupy parametrów:

1/ miary położenia - określają poziom wartości cechy

2/ miary zmienności (rozproszenia, dyspersji, zróżnicowania) - badają stopień zróżnicowania wartości cechy

3/ miary asymetrii (skośności) - badają kierunek zróżnicowania wartości cechy.

W każdym z podanych typów miar występują miary klasyczne (ich wartości obliczamy na podstawie wszystkich wyników z próby) i miary pozycyjne (ich wartości ustalane są na podstawie podziału uporządkowanego ciągu wartości cechy lub też wyboru wartości cechy występującej najczęściej).

Miary położenia dzielą się na przeciętne i kwantyle. Miary przeciętne charakteryzują średni lub typowy poziom wartości cechy. Są to więc takie parametry, wokół których skupiają się wszystkie pozostałe wartości analizowanej cechy.

Miary przeciętne dzielą się na 2 grupy: średnie klasyczne i pozycyjne. Wszystkie te parametry są wielkościami mianowanymi (mają miana takie same jak analizowana cecha).

Miary położenia

Klasyczne Pozycyjne

- średnia arytmetyczna - modalna - kwantyle:

- średnia harmoniczna (dominanta, * kwartyl pierwszy

- średnia geometryczna wartość najczęstsza) * kwartyl drugi (mediana)

- inne * kwartyl trzeci

* decyle

7) Jakie własności ma średnia arytmetyczna? Czy dla każdego szeregu można ją wyznaczyć?

Średnia arytmetyczna - klasyczna miara położenia; jest to suma wartości cechy mierzalnej podzielona przez liczbę jednostek skończonej zbiorowości statystycznej.

Wyróżniamy:

* średnią arytmetyczną nieważoną (prostą) - obliczamy dla szeregów szczegółowych

* średnią arytmetyczną ważoną - obliczamy dla szeregów rozdzielczych punktowych i i szeregów rozdzielczych z przedziałami klasowymi.

Własności średniej arytmetycznej:

1/ wartość średniej arytmetycznej zawiera się między najmniejsza i największą wartością cechy. Tą własność stosujemy przy kontroli logicznej obliczonej średniej. x_min ≤
≤ x_max

2/ średnia arytmetyczna wyraża się w takich samych jednostkach jak wartości cechy

3/ jest miarą wrażliwą na skrajne wartości cechy, zatem dobrze charakteryzuje przeciętny poziom wartości cechy w zbiorowościach o niewielkim stopniu zróżnicowania ze względu na badaną cechę

4/ średnią arytmetyczną obliczamy w zasadzie dla szeregów o zamkniętych skrajnych przedziałach klasowych. W sytuacji gdy skrajne przedziały są otwarte, ale ich liczebności bardzo małe możemy w obliczeniach średniej je umownie domknąć.

Warunkiem obliczenia średniej arytmetycznej w szeregu rozdzielczym jest szereg zamknięty górą i dołem - o ile tak nie jest, to można dokonać zamknięcia szeregu, jeżeli w otwartym przedziale znajduje się nie więcej niż 5% ogółu jednostek badanej zbiorowości. Jeżeli ten warunek nie został spełniony to nie wolno nam zamknąć przedziału i obliczać średniej arytmetycznej.

5/ średnią arytmetyczną możemy obliczać tylko dla zbiorowości jednorodnych

Średnią arytmetyczną wyznaczamy dla:

• szeregu szczegółowego

• szeregu rozdzielczego punktowego

• szeregu rozdzielczego z przedziałami klasowymi.

W przypadku gdy nie mamy możliwości obliczenia średniej arytmetycznej, analizę struktury prowadzimy w oparciu o pozycyjne miary położenia.

8) Kiedy istnieje dominanta w szeregu statystycznym i jakich informacji o zachowaniu cechy w badanej zbiorowości nam dostarcza?

Dominanta (modalna, moda, wartość najczęstsza) - wartość cechy statystycznej, która w danej zbiorowości występuje najczęściej; oznaczamy Mo lub D.

Nie dla każdego szeregu istnieje dominanta. Nie istnieje ona gdy:

1. nie ma przedziału o wyraźnie większej liczebności

2. przedział o wyraźnie większej liczebności istnieje, ale jest to przedział skrajny.

Dominanta dla szeregu szczegółowego i rozdzielczego punktowego jest to taka wartość cechy, która w danym szeregu występuje najczęściej, o ile nie jest to wartość skrajna tzn. największa lub najmniejsza.

O istnieniu dominanty w szeregu rozdzielczym z przedziałami klasowymi możemy mówić tylko wtedy gdy istnieje przedział o wyraźnie większej liczebności i nie jest to przedział skrajny (możemy tu bezpośrednio określić tylko przedział w którym znajduje się dominanta).

Przedział klasowy w którym znajduje się dominanta oraz 2 przedziały z nią sąsiadujące muszą mieć jednakowe rozpiętości.

Dominanta informuje o wartości cechy zmiennej, której odpowiada maksymalna liczba spostrzeżeń, lub wokół której koncentrują się spostrzeżenia. Charakteryzuje ona typowy poziom badanej cechy zmiennej, najliczniej reprezentowany w zbiorowości.

Właściwości dominanty:

1/ wyraża się w takich samych jednostkach w jakich występują wartości cechy

2/ jest miarą niewrażliwą na skrajne wartości cechy

3/ wartość dominanty mieści się między: Xmin < D < Xmax

Jeżeli w szeregu rozdzielczym największe liczebności występują w skrajnych przedziałach, wyznaczanie dominanty nie ma sensu.

9) Co to są kwartyle i jakich informacji o zachowaniu cechy w badanej zbiorowości nam dostarczają?

Kwartyle są to miary pozycyjne przeciętne, tzw. wartości ćwiartkowe. Są to najczęściej stosowane kwantyle czyli wartości które dzielą uporządkowany niemalejąco szereg wartości cechy na części równe pod względem liczebności.

Wśród kwartyli wyróżniamy:

1/ kwartyl pierwszy Q₁ (dolny) - dzieli uporządkowany szereg na dwie części tak, że ¼ jednostek zbiorowości przyjmuje wartości niższe bądź równe kwartylowi pierwszemu Q₁, a ¾ jednostek zbiorowości ma wartości równe bądź wyższe od kwartyla Q₁ (25% na 75%)

2/ kwartyl drugi - mediana Me - dzieli zbiorowość na 2 równe części; 50% jednostek ma wartości cechy mniejsze lub równe Me, a połowa wartości cechy równe lub większe od Me (50% na 50%); Me inaczej wartość środkowa

3/ kwartyl trzeci Q₃ (górny) - dzieli zbiorowość na dwie części w ten sposób, że 75% jednostek ma wartości cechy niższe bądź równe Q₃ , a 25% równe bądź wyższe od kwartyla trzeciego (75% na 25%).

Kwartyle wyznaczamy w następującej kolejności:

1. mediana inaczej kwartyl drugi - Me

2. kwartyl pierwszy (dolny)- Q₁

3. kwartyl trzeci (górny) - Q₃

Wyznaczanie kwartyli:

1/ Szereg szczegółowy i rozdzielczy punktowy:

1. kwartyl dolny: wyznaczamy biorąc pod uwagę elementy szeregu stojące przed Me, a jeśli Me jest elementem szeregu to łącznie z tą Me i wyznaczamy go tak jakby był Me dla tej części szeregu

2. kwartyl górny: wyznaczamy biorąc pod uwagę elementy szeregu stojące za medianą, a jeśli Me jest elementem szeregu to łącznie z tą Me i wyznaczamy go tak jakby był Me dla tej części szeregu.

UWAGA: przy wyliczaniu kwartyli korzystamy z liczebności skumulowanej.

2/ szereg rozdzielczy z przedziałami klasowymi:

wyznaczanie Me i pozostałych kwartyli rozpoczynamy od znalezienia odpowiednich przedziałów klasowych dla tych miar. Korzystamy przy tym z szeregów liczebności skumulowanej, wyznaczając przedziały zawierające numery odpowiednich kwartyli.

Pozostałe kwartyle wyznaczamy korzystając z odpowiednich wzorów.

Własności kwartyli:

1/ kwartyle wyrażają się w takich samych jednostkach w jakich występują wartości cechy

2/ Me podobnie jak pozostałe kwartyle może być wyznaczana również w takich szeregach, dla których nie występuje dominanta i nie można obliczyć średniej arytmetycznej; przedziały muszą mieć jednakową rozpiętość.

3/ Me jest miarą nie wrażliwą na skrajne wartości cechy; jest więc dobrą miarą przeciętną dla takich szeregów, w których występują wartości cechy nietypowe dla danej zbiorowości

4/ kwartyl pierwszy i trzeci wyznaczają zbiór wartości cechy dla 50% środkowych jednostek szeregu

5/ kwartyle spełniają nierówność Xmin ≤ Q₁ ≤ Me ≤ Q₃ ≤ Xmax (tzw. kontrola logiczna)

10) Które miary położenia opisują przeciętny poziom zjawiska w badanej zbiorowości?

Przeciętny poziom wartości cechy opisują miary położenia takie jak:

• średnia arytmetyczna (pytanie 7)

• mediana Me

• dominanta.(pytanie 8)

Mediana - wartość środkowa; wartość jednostki statystycznej dzielącej zbiorowość statystyczną na 2 części tak, że połowa jednostek zbiorowości charakteryzuje się wartościami nie wyższymi od mediany, a połowa nie niższymi od mediany. Me dzieli zbiorowość na dwie równe części.. Warunkiem jej wyznaczenia jest uporządkowanie szeregu od x_min do x_max. Jest to parametr centralnego skupienia. Sposób jej wyznaczania zależy od formy szeregu (jego budowy).

Mediana może być wyznaczana w szeregach o otwartych przedziałach klasowych; nie jest wrażliwa na wartości skrajne; może być wyznaczana w szeregach o nierównych rozpiętościach przedziałów klasowych.

11) Jakie miary zmienności stosujemy do opisu struktury zbiorowości? Które z tych miar są miarami klasycznymi, a które pozycyjnymi?

Miary zmienności (zróżnicowania, dyspersji) charakteryzują zachowanie cechy mierzalnej w zbiorowości statystycznej. Przy ich pomocy określamy zróżnicowanie jednostek w zbiorowości ze względu na badaną cechę. Miary te pozwalają na ocenę wartości poznawczej miar średnich. Im mniejsze zróżnicowanie zbiorowości tym wyższa jest wartość poznawcza miar przeciętnych. Miary zmienności podobnie jak miary położenia dzielimy na dwie grupy: klasyczne i pozycyjne.

Siłę dyspersji oceniamy przy pomocy miar klasycznych i pozycyjnych. Ocena przy pomocy miar klasycznych przyjmuje za punkt odniesienia średnią arytmetyczną, a dla miar pozycyjnych z wyjątkiem rozstępu, punktem odniesienia jest Me.

Miary zmienności

1/ KLASYCZNE:

- wariancja (
) gdzie x - to cecha

jest to średnia arytmetyczna kwadratów odchyleń poszczególnych wartości cechy od średniej arytmetycznej zbiorowości (
).Nie stosowana w analizie dyspersji.

- odchylenie standardowe, które jest równe pierwiastkowi z wariancji σ_x =

(oznaczenie σ dla badań pełnych, s dla próby); jest to pierwiastek kwadratowy z wariancji. Parametr ten określa przeciętne zróżnicowanie poszczególnych wartości cechy od średniej arytmetycznej.

Odchylenie standardowe (
) informuje o ile przeciętnie poszczególne jednostki badanej zbiorowości różnią się in
od średniej arytmetycznej badanej zmiennej;

Dla obliczenia tego parametru konieczna jest znajomość średniej arytmetycznej.

Odchylenie standardowe wykorzystuje się do obliczenia typowego przedziału zmienności badanej cechy; w obszarze tym mieści się 68% wszystkich jednostek zbiorowości.

- odchylenie przeciętne d_x gdzie x to cecha jest to średnia arytmetyczna bezwzględnych odchyleń wartości cechy od jej średniej arytmetycznej. Określa ono, o ile jednostki danej zbiorowości różnią się średnio, ze względu na wartości cechy, od średniej arytmetycznej.

- współczynniki zmienności obliczane przy pomocy miar klasycznych V_σx, V_dx

Współczynnik zmienności jest wartością niemianowaną. Wartości liczbowe współczynników zmienności najczęściej podawanej są w procentach. Jeżeli współczynnik zmienności jest poniżej 10% to cechy wykazują zróżnicowanie statystyczne nieistotne.

Klasyczne współczynniki zmienności to: V
=
x 100 lub V_dx =
x 100
gdzie

Mówią o tym, jakim procentem
jest odchylenie standardowe i przeciętne.

Duże wartości tego współczynnika świadczą o zróżnicowaniu, a więc niejednorodności zbiorowości.

Współczynnik zmienności stosujemy zwykle gdy chcemy ocenić zróżnicowanie:

• kilku zbiorowości pod względem tej samej cechy

• tej samej zbiorowości pod względem kilku różnych cech.

0% do 15% - małe zróżnicowanie; zbiorowość dość jednorodna; średnia arytmetyczna dobrze charakteryzuje średni poziom badanego zjawiska; można uznać że badana zbiorowość jest jednorodna

15% do 35% - przeciętne zróżnicowanie; średnia arytmetyczna dość dobrze charakteryzuje poziom badanego zjawiska;

35% do 60% - duże zróżnicowanie; średnia arytmetyczna ma małą wartość poznawczą

powyżej 60% - zróżnicowanie jest bardzo duże; średnia arytmetyczna nie jest miarą dobrze charakteryzującą tendencję centralną.

2/ POZYCYJNE:

- rozstęp szeregu R - najprostsza miara zmienności; R = x_max - x_min;

jest to różnica między największą i najmniejszą wartością zmiennej w badanej zbiorowości, w szeregu uporządkowanym;

jest miarą charakteryzującą empiryczny obszar zmienności badanej cechy, nie daje jednak informacji o zróżnicowaniu poszczególnych wartości cechy w zbiorowości;

- dla szeregu szczegółowego i rozdzielczego punktowego rozstęp możemy wyznaczyć dokładnie.

- dla szeregu rozdzielczego z przedziałami klasowymi o zamkniętych przedziałach skrajnych rozstęp wyznaczamy w przybliżeniu, jako różnicę między prawym krańcem przedziału największych wartości cechy minus lewy kraniec najmniejszych wartości cechy;

jeżeli szereg rozdzielczy z przedziałami klasowymi ma otwarte klasy to nawet przybliżone określenie obszaru zmienności jest niemożliwe.

- odchylenie ćwiartkowe (kwartylowe) Q =

mierzy poziom zróżnicowania tylko tej części jednostek, która pozostaje po odrzuceniu 25% jednostek o najniższych wartościach cechy i 25% jednostek o najwyższych wartościach cechy; jest ono miarą zmienności szczególnie dla tych szeregów w których nie można wyznaczyć miar klasycznych; określa odchylenie wartości cechy od mediany; jest to połowa różnicy między trzecim a pierwszym kwartylem;

- współczynniki zmienności obliczane przy pomocy kwantyli to:

V_Q =
x 100 gdzie Me > 0, i V_Q1,Q3 =

Pozycyjny współczynnik zmienności mierzy zróżnicowanie jednostek o wartościach cechy zawartych miedzy dolnym i górnym kwartylem. Występowanie w zbiorowości jednostek o nietypowych wartościach cechy nie wpływa na jego wartość.

Współczynnik zmienności jest wartością niemianowaną. Wartości liczbowe współczynników zmienności najczęściej podawanej są w procentach. Jeżeli współczynnik zmienności jest poniżej 10% to cechy wykazują zróżnicowanie statystyczne nieistotne.

Duże wartości tego współczynnika świadczą o zróżnicowaniu, a więc niejednorodności zbiorowości. Współczynnik zmienności stosujemy zwykle gdy chcemy ocenić zróżnicowanie:

• kilku zbiorowości pod względem tej samej cechy

• tej samej zbiorowości pod względem kilku różnych cech.

12) Które z miar zmienności wyrażają się w takich samych jednostkach jak wartości cechy, a które są wielkościami niemianowanymi?

Miary zmienności, które wyrażają się w takich samych jednostkach jak wartość cechy:

• rozstęp szeregu - R

• odchylenie ćwiartkowe - Q

• odchylenie przeciętne

• odchylenie standardowe.

Nie mianowane miary zmienności to współczynniki zmienności:

• obliczane przy pomocy kwartyli

• obliczane przy pomocy miar klasycznych

które bardzo często podajemy po pomnożeniu przez 100 w procentach.

13) W jakich sytuacjach ważne zastosowanie znajduje współczynnik zmienności?

Odgrywają znaczącą rolę w 2 sytuacjach:

1/ gdy chcemy porównać zróżnicowanie kilku zbiorowości ze względu na jedną cechę

2/ gdy chcemy porównać zróżnicowanie jednej zbiorowości ze względu na kilka cech.

Służy do porównywania zmienności cech mierzonych w różnych jednostkach, a także do porównywania kilku zbiorowości pod względem tej samej cechy, ale będącej na różnym poziomie (określonym średnią arytmetyczną lub inną miarą średnią).

Ułatwia porównanie stopnia rozproszenia w zakresie cechy zmiennej w kilku zbiorowościach. Ponadto pozwala na ocenę stopnia jednorodności zbiorowości, co jest bardzo ważne dla analizy statystycznej.

14) W jaki sposób możemy wyznaczyć typowy dla danej zbiorowości przedział zmienności cechy? Podaj taki przedział dla miar klasycznych i pozycyjnych.

Przy pomocy mediany i odchylenia kwartylowego możemy wyznaczyć typowy przedział zmienności cechy dla miar pozycyjnych o następującej postaci: Me - Q < x_typ < Me + Q

Natomiast przy pomocy średniej arytmetycznej i odchylenia standardowego możemy wyznaczyć przedział zmienności cechy dla miar klasycznych:

Typowe przedziały zmienności cechy to przedziały do których należą wartości cechy jednostek typowych dla badanej zbiorowości.

15) Jakie rodzaje asymetrii wyróżniamy?

Do określenia asymetrii (skośności) rozkładu bierzemy pod uwagę średnią arytmetyczną, medianę, i dominantę.

Z punktu widzenia asymetrii rozróżniamy następujące typy szeregów statystycznych:

1. szereg symetryczny - taki w którym wszystkie te miary przeciętne maja jednakowe wartości (cecha ma rozkład symetryczny). W takim szeregu najliczniejsza grupa jednostek ma wartości cechy równe w przybliżeniu średniej arytmetycznej.
   ;

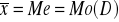
rozkład symetryczny to taki , w którym poszczególne wartości badanej cechy rozkładają się równomiernie po obu stronach średniej arytmetycznej.

2. szereg o asymetrii prawostronnej (cecha ma rozkład prawostronnie asymetryczny); w takim szeregu najliczniejsza grupa jednostek ma wartości cechy poniżej średniej arytmetycznej:
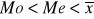
   (asymetria prawostronna);

asymetria prawostronna oznacza, ze w zbiorowości dominują jednostki statystyczne o wartości cechy niższym niż średnia arytmetyczna

3. szereg o asymetrii lewostronnej (cecha ma rozkład lewostronnie asymetryczny); w takim szeregu najliczniejsza grupa jednostek ma wartości cechy powyżej średniej arytmetycznej:
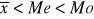
   (asymetria lewostronna)

asymetria lewostronna - dominują w zbiorowości jednostki statystyczne o wartości cechy wyższym niż średnia arytmetyczna.

16) O czym świadczy dodatnia, a o czym ujemna wartość współczynnika asymetrii?

Miary asymetrii:

1/ wskaźnik skośności (asymetrii)

2/ współczynnik skośności (asymetrii)

Miara bezwzględna przyjętą do określania asymetrii to wskaźnik skośności. W_s określa tylko kierunek asymetrii, nie wskazuje jej siły, gdyż jest wielkością nieunormowaną. Nie używa się go do porównywania asymetrii w zbiorowościach, w których wartość zmiennej jest wyrażona w różnych jednostkach miary.

Miarą określającą zarówno kierunek jak i siłę asymetrii jest współczynnik asymetrii (skośności). Wszystkie współczynniki skośności przyjmują zasadniczo wartości z przedziału domkniętego <-1,1>, przy czym dla szeregów o bardzo wysokiej asymetrii mogą przekraczać krańce tego przedziału. Im większa jest wartość współczynnika skośności, tym silniejsza jest asymetria badanego rozkładu.

W_s =
- jest to różnica między średnią arytmetyczną, a modalną..

Dla miar klasycznych:

W_s = 0 dla szeregów symetrycznych (
)

W_s > 0 dla rozkładów o asymetrii prawostronnej (
)

W_s < 0 dla rozkładów o asymetrii lewostronnej. (
)

Współczynnik skośności jest miara względną. Może być obliczany w stosunku do odchylenia przeciętnego (A_d) lub w stosunku do odchylenia standardowego (A_s).

A_d =
A_s =

Współczynniki nawzajem wykluczające się; odpowiadają na pytanie jaką część odchylenia przeciętnego lub standardowego stanowi różnica między średnią arytmetyczną a modalną.

Wskaźnik skośności dla miar pozycyjnych: (w sytuacji jeżeli nie możemy obliczyć średniej arytmetycznej, lub gdy nie istnieje dominanta):

- gdy (Q₃ - Me) - (Me - Q₁) = 0 mamy rozkład symetryczny

- gdy (Q₃ - Me) - (Me - Q₁) > 0 mamy rozkład o asymetrii prawostronnej

- gdy (Q₃ - Me) - (Me - Q₁) < 0 mamy rozkład o asymetrii lewostronnej

Do oceny siły i kierunku w takich szeregach stosujemy pozycyjny (kwartylowy) współczynnik skośności (A_Q).

A_Q =

Współczynnik ten określa tylko asymetrie jednostek statystycznych zawartych między Q₁ i Q₃. nie uwzględnia więc wpływu na siłę asymetrii jednostek o skrajnych wartościach cechy.

= 0 rozkład symetryczny

0 <
≤ 0,1 rozkład zbliżony do symetrycznego

0,1 <
≤ 0,2 asymetria słaba (niewielka)

0,2 <
≤
asymetria znacząca istotna

<
≤ 0,7 asymetria silna

0,7 <
asymetria bardzo silna

II. BADANIE WSPÓŁZALEŻNOŚCI CECH

Dla określenia stopnia zależności między badanymi zmiennymi można posłużyć się:

1/ współczynnikiem korelacji - opisują intensywność zależności miedzy badanymi zmiennymi, a w przypadku zależności liniowej dwóch zmiennych wskazują na jej kierunek. Badane zmienne mogą być zarówno mierzalne jak i niemierzalne. Wyróżniamy tu następujące miary:

- współczynnik korelacji liniowej Pearsona (dotyczy zjawisk lub zmiennych ilościowych, mierzalnych)

- współczynnik korelacji kolejnościowej (rang) Spearmana (dotyczy zjawisk lub cech mierzalnych)

lub

2/ funkcją regresji - bada kształt relacji zachodzących miedzy zmiennymi. (zmienne mierzalne).

Miary korelacji nie są substytucyjne w stosunku do miar regresji.

1) Sposoby porządkowania danych dotyczących dwóch cech badanych w populacji (szereg szczegółowy i tablica korelacyjna).

Gdy badamy zbiorowość ze względu na 2 cechy zachodzi konieczność uporządkowania danych z uwzględnieniem wariantów obu tych cech.

a) W przypadku gdy badana zbiorowość jest nieliczna dane porządkujemy w szeregu szczegółowym, podając dla każdej jednostki parę (X_k,Y_k) wariantów lub wartości dla obu tych cech.

b) Dla licznych zbiorowości dane porządkujemy w tablicy korelacyjnej.

2) Jakie rodzaje zależności miedzy cechami mogą wystąpić?

Badanie zbiorowości ze względu na 2 cechy ma zazwyczaj na celu poszukiwanie zależności między tymi cechami. Ma ono sens tylko wtedy gdy między cechami może istnieć logicznie uzasadniony związek przyczynowo skutkowy. Analizując ten związek między cechami ustalamy, która z cech może być traktowana jako niezależna, a która jako zależna. Niekiedy można stwierdzić zarówno wpływ cechy X na cechę Y, jak i odwrotnie. Mówimy wówczas o współzależności cech.

Zależność między cechami może mieć charakter:

- funkcyjny - każdej wartości zmiennej X odpowiada dokładnie jedna wartość zmiennej Y, np. cena i wartość towaru; zmiana wartości jednej zmiennej powoduje ściśle określoną zmianę drugiej zmiennej;

X - zmienna niezależna (objaśniająca); Y - zmienna zależna (objaśniana)

- stochastyczny - określany przy pomocy pojęć rachunku prawdopodobieństwa; wraz ze zmianą jednej zmiennej zmienia się rozkład prawdopodobieństwa drugiej zmiennej; ta zależność (inaczej probabilistyczna) miedzy cechami polega na tym, że zależne są rozkłady prawdopodobieństwa zmiennych X i Y; wpływ jednej zmiennej na drugą zależy również od czynników losowych, działających wspólnie na obie zmienne (oprócz czynników losowych działających na każdą z nich oddzielnie);

Szczególnym przypadkiem zależności stochastycznej jest zależność korelacyjna, występująca między cechami mierzalnymi lub quasi-mierzalnymi (porządkowymi). Zatem jeśli dla cech mierzalnych stwierdzimy występowanie zależności korelacyjnej to nie badając możemy stwierdzić też, że cechy są stochastycznie zależne. Jeśli między badanymi zmiennymi nie ma związku stochastycznego (brak zależności) to nie ma również związku korelacyjnego. Twierdzenie odwrotne nie jest prawdziwe. Jeżeli cechy są niezależne to mówimy że są nieskorelowane.

3) Jakie miary możemy zastosować do oceny istnienia zależności stochastycznej i w jakich sytuacjach możemy je stosować?

Do oceny istnienia zależności stochastycznej możemy zastosować miary zbudowane na podstawie funkcji chi-kwadrat
. Funkcja chi-kwadrat służy do oceny w jakim stopniu rzeczywiste liczebności różnią się od teoretycznych.
= 0 wtedy, gdy wszystkie liczebności empiryczne (n_ij) są równe liczebnościom teoretycznym (
).

Jedną z takich miar jest współczynnik zbieżności T-Czuprowa. Współczynnik zbieżności T-Czuprowa przyjmuje wartości z przedziału domkniętego 0 ≤ T ≤ 1. Im większa jest jego wartość tym silniejsza zależność między cechami.

Gdy T=0 to cechy uznajemy za stochastycznie niezależne. Współczynnik ten nie wskazuje która z cech jest od której zależna. W interpretacji kierujemy się logicznie uzasadnionym związkiem przyczynowo skutkowym. Współczynnik ten stosujemy do mierzenia współzależności zarówno cech mierzalnych jak i niemierzalnych (zaleta). Wadą - nie wskazuje kierunku korelacji (jest zawsze nie ujemny).

4) Na czym polega zależność korelacyjna między cechami? W jaki sposób można wstępnie ocenić czy między cechami istnieje zależność korelacyjna?

Zależność korelacyjna polega na tym, że określonym wartościom jednej cechy odpowiadają ściśle określone średnie wartości drugiej cechy.

Aby uzyskać wstępną ocenę istnienia zależności korelacyjnej między cechami możemy posłużyć się:

a) uporządkowanymi szeregami statystycznymi - szczegółowymi - zbudowanymi dla obu cech jednocześnie, zbudowanymi w następujący sposób:

- jeżeli wartości cech w obu porównywanych szeregach mają tendencję wzrostową, to możemy oczekiwać korelacji dodatniej

- jeżeli wzrostowi wartości jednej cechy towarzyszy tendencja spadkowa w szeregu wartości drugiej cechy to wskazuje to na istnienie korelacji ujemnej

- brak regularności w zachowaniu wartości cechy w szeregach wskazuje na brak korelacji między cechami.

b) korelacyjnym wykresem rozrzutu - na płaszczyźnie zaznaczamy punkty Xk, Yk o współrzędnych odpowiadających wartościom obu cech; otrzymujemy w ten sposób diagram korelacyjny; jego punkty mogą układać się wzdłuż pewnych linii. Jeżeli układają się wzdłuż prostej, która jest wykresem liniowej funkcji rosnącej, to wskazuje to na istnienie liniowej korelacji dodatniej; jeżeli układają się wzdłuż prostej, która jest wykresem funkcji liniowej malejącej - istnieje liniowa korelacja ujemna.

Ułożenie punktów wzdłuż pewnej krzywej wskazuje na istnienie korelacji krzywoliniowej.

Brak regularności w ułożeniu punktów wskazuje na brak zależności korelacyjnej między cechami.

5) Jakie rodzaje korelacji (ze względu na kierunek) mogą występować między cechami? Czym one się charakteryzują?

Pod względem kierunku wyróżniamy korelację:

a/ dodatnią - występuje wtedy gdy wzrostowi wartości jednej cechy odpowiada wzrost średniej wartości drugiej cechy, np. wzrost i waga ludzi (zmiany jednokierunkowe)

b/ ujemną - występuje wtedy gdy wraz ze wzrostem wartości jednej cechy, maleją średnie wartości drugiej cechy (zmiany różnokierunkowe)

6) Kiedy mówimy, że między cechami występuje korelacja liniowa?

Korelacyjny wykres rozrzutu -diagram korelacyjny - jego punkty mogą układać się wzdłuż pewnych linii. Jeżeli układają się wzdłuż prostej, która jest wykresem liniowej funkcji rosnącej, to wskazuje to na istnienie liniowej korelacji dodatniej; jeżeli układają się wzdłuż prostej, która jest wykresem funkcji liniowej malejącej - istnieje liniowa korelacja ujemna.

7) Jakie miary stosujemy do oceny kierunku i siły zależności korelacyjnej między cechami?

a) kowariancja - cov(x,y) - ocenia kierunek zależności korelacyjnej

b) współczynnik korelacji rang Spearmana (współczynnik zgodności uporządkowania) - R_xy - tylko dla szeregu szczegółowego - ocenia siłę korelacji liniowej w przypadku gdy:

- cechy są mierzalne a badana zbiorowość jest nieliczna

- gdy cechy mają charakter jakościowy i istnieje możliwość ich uporządkowania.

c) współczynnik korelacji liniowej Pearsona - r_xy - mierzy siłę korelacji liniowej i wynosi:

mniej niż 0,2 - praktycznie brak korelacji

0,2 - 0,4 - korelacja słaba

0,4 - 0,7 - korelacja umiarkowana

0,7 - 0,9 - korelacja silna

powyżej 0,9 - korelacja (zależność) bardzo silna

8) Jakie własności ma współczynnik korelacji liniowej Pearsona - r_xy?

- może być stosowany tylko dla cech mierzalnych; dane dotyczące tych cech mogą być uporządkowane zarówno w szeregu szczegółowym jak i w tablicy korelacyjnej;

- ocenia zarówno kierunek i jak i siłę (natężenie) korelacji liniowej między cechami

- dodatni znak współczynnik wskazuje na istnienie współzależności dodatniej, ujemny - ujemnej

- im wartość tego współczynnika jest bliższa 1 tym zależność korelacyjna między badanymi cechami jest silniejsza

- przyjmuje wartości z przedziału <-1,1> (jest miarą unormowaną); wielkość współczynnika korelacji Pearsona zależy od zakresu zmienności badanych cech, tzn. zwiększenie liczby obserwacji sprawia, że współczynnik korelacji może ulec zmianie, podlega on wpływom skrajnych wartości.

- jest miarą symetryczną tzn. r_xy=r_yx

- jest miarą niemianowaną (nie jest wyrażony w jednostkach fizycznych)

- jest podatny na wartości skrajne

9) Jakie własności ma współczynnik korelacji rang Spearmana - R_xy?

- stosowany wyłącznie dla danych w szeregu szczegółowym, gdy zbiorowość nie jest dostatecznie liczna

- obliczamy gdy dwie cechy są niemierzalne, ale istnieje możliwość sensownego uporządkowania obserwacji wg każdej z tych cech

- może być stosowany dla cech mających charakter jakościowy lub quasi-mierzalnych

Aby wyznaczyć jego wartość nadajemy poszczególnym wariantom lub wartościom cech - w każdym szeregu oddzielnie - rangi, w następujący sposób:

(rangowanie - polega na przyporządkowaniu kolejnych numerów obydwu wariantom cechy x_i i y_i wg kolejności rosnącej lub malejącej (od 1 do n). W przypadku gdy występują jednakowe wartości badanych cech, przyporządkowujemy im średnią arytmetyczną obliczoną z ich kolejnych numerów).

a/ wartości lub warianty każdej z cech oddzielnie porządkujemy niemalejąco

b/ jednostkom w każdym z tych uporządkowań nadajemy liczbę odpowiadającą ich miejscy w tym uporządkowaniu. A jeżeli występuje ta sama wartość kilka razy to każdej jednostce, której ta wartość odpowiada nadajemy liczbę będącą średnią arytmetyczną numerów tych miejsc. Tak określone liczby nazywamy rangami

Przyjmuje wartości z przedziału <-1,1>; im współczynnik korelacji rang Spearmana jest bliższy liczbie 1 (lub -1), tym silniejsza jest badana zależność

R_xy =0 w przypadku niezależności cech (x,y)

R_xy = +1 oznacza dodatni związek funkcyjny

R_xy = -1 oznacza ujemny związek funkcyjny

Własności r_xy, R_xy (dotyczy pytania nr 8 i 9)

1) są symetryczne, tzn. ich wartość nie zależy od wyboru zmiennej niezależnej (r_xy = r_yx i R_xy = R_yx), zatem w interpretacji kierujemy się logicznie uzasadnionym związkiem przyczynowo-skutkowym

2) przyjmują wartości z przedziału <-1, 1>

3) analogiczna jest interpretacja ich znaku i wartości:

„-„ wskazuje na istnienie korelacji ujemnej, a „+” - korelacji dodatniej

Im wyższa jest wartość bezwzględna współczynników tym silniejszy związek między cechami.

4) wskazują siłę związku tylko dla korelacji liniowej: jeżeli
≤ 0,2 uznajemy, że brak jest korelacji liniowej między cechami

5) określają nie tylko siłę ale również kierunek korelacji

6) wartości
wskazują w jakim procencie zmiany w poziomie zmiennej zależnej, można wyjaśnić zmianami w poziomie zmiennej niezależnej

10) Jaka jest interpretacja współczynników regresji w liniowej funkcji regresji?

Liniowa funkcja regresji - funkcja której wykres jest miejscem geometrycznym średnich wartości zmiennej zależnej przy ustalonych wartościach zmiennej niezależnej.

W zależności od tego, którą z badanych cech uznamy za zmienną niezależną otrzymujemy 2 funkcje linii regresji:

1/ funkcja regresji zmiennej zależnej (objaśnianej) Y przy danych wartościach zmiennej niezależnej (objaśniającej) X

2/ funkcja regresji zmiennej zależnej (objaśnianej) X względem zmiennej niezależnej (objaśniającej) Y

Występujące w tych równaniach współczynniki b_x i b_y nazywamy współczynnikami regresji. Mają one następujące własności:

- wartość współczynnika regresji w odpowiednim równaniu wskazuje o ile jednostek wzrośnie lub zmaleje wartość zmiennej zależnej, gdy wartość zmiennej niezależnej wzrośnie o jedną jednostkę; parametry b_x i b_y tylko niekiedy mają sensowną interpretację ekonomiczną.

- obydwa współczynniki regresji mają zawsze taki sam znak i taki sam znak ma współczynnik korelacji liniowej Pearsona, wyznaczony dla badanych cech

- współczynniki regresji i współczynnik korelacji łączy następujący związek - ich iloczyn jest równy kwadratowi współczynnika korelacji Pearsona

11) Jaki związek łączy współczynnik korelacji liniowej Pearsona i współczynniki regresji?

Obydwa współczynniki regresji mają zawsze taki sam znak i taki sam znak ma współczynnik korelacji liniowej Pearsona, wyznaczony dla badanych cech

Gdy r_xy = 1 korelacja zachodząca miedzy zmiennymi jest doskonała, dodatnia (obie linie regresji wznoszą się i pokrywają).

Gdy r_xy = -1 korelacja jest doskonała, ujemna (obie linie regresji opadają i pokrywają się);

Gdy 0< r_xy <1 korelacja jest dodatnia, niedoskonała (linie regresji przecinają się w punkcie o współrzędnych x,y i mają kierunek dodatni;

Gdy -1< r_xy <0 korelacja jest niedoskonała, ujemna (linie regresji przecinają się w punkcie o współrzędnych x,y i mają kierunek ujemny.

12) W jaki sposób możemy ocenić, dla cech związanych zależnością korelacyjną, w jakim procencie zmiany jednej z tych cech wpływają na zmiany drugiej?

Dla oceny natężenia miedzy zmiennymi X i Y wykorzystuje się - obok współczynnika zbieżności Czuprowa - również współczynnik determinacji: 100% · T
. Miara ta wskazuje w ilu procentach zmienność zmiennej zależnej jest określona zmiennością zmiennej niezależnej. Z rachunkowego punktu widzenia T ocenia zarówno zależność cechy X od cechy Y, jak i Y od X (T_xy=T_yx). Natomiast interpretacja współczynnika zbieżności musi jednoznacznie określać charakter zmiennych, tzn. która z nich jest zmienną zależną, a która zmienną niezależną. Współczynnik determinacji określa, ile % zmienności Y zostało wyjaśnione przy pomocy oszacowanej funkcji regresji (ile % zmienności wynika z czynników uwzględnionych w równaniu regresji)..

Współczynnik ten jest przede wszystkim miarą zależności stochastycznej dwóch zmiennych. Możemy go też wykorzystywać jako miarę siły związku korelacyjnego ponieważ zależność korelacyjna jest pojęciem węższym od zależności stochastycznej.

Przyjmuje wartości z przedziału <0,1>, przy czym im większa jest jego wartość tym lepsze dopasowanie funkcji.

III. SZEREGI CZASOWE

1) Co to jest szereg czasowy?

Szeregi czasowe są podstawą analizy zmian poziomu zjawiska w czasie.

Szeregiem czasowym (dynamicznym) nazywamy ciąg wartości badanego zjawiska obserwowanego w kolejnych jednostkach czasu (t,y_t) t= 1,2, ..., n lub t=0,1,2, ..., n zaś y_t oznacza wielkość badanego zjawiska w jednostce czasu t. W szeregach czasowych zmienną niezależną jest czas, a zmienną zależną - wartości liczbowe badanego zjawiska.

2) Jakie rodzaje szeregów czasowych wyróżniamy, czym one się charakteryzują?

- szereg czasowy okresów (strumieni) - jednostkami czasu są krótsze lub dłuższe przedziały czasowe (okresy) np. lata, kwartały, miesiące

- szereg czasowy momentów (stanów) - poziom zjawiska badany jest w ściśle określonym momencie, np. określonych dniach, miesiącach, godzinach, itp.

3) Jakie średnie są odpowiednimi miarami przeciętnymi dla poszczególnych typów szeregów czasowych? UWAGA: przy założeniu równości przedziałów

- dla szeregów czasowych okresów - przeciętny poziom zjawiska badamy za pomocą średniej arytmetycznej

- dla szeregów czasowych momentów - za pomocą średniej chronologicznej.

Właściwości średniej chronologicznej:

a/ wyraża się w takich samych jednostkach jak wartości cechy

b/ jej wartość zawiera się między y_min≤
≤ y_max

4) Jakie miary stosujemy do badania dynamiki szeregu czasowego?

W jakich jednostkach wyrażają się te miary?

Miary dynamiki szeregu czasowego:

- przyrosty: absolutne(bezwzględne) i względne (stosunkowe): mogą być dodatnie lub ujemne; obydwie miary dzielą się na jednopodstawowe i łańcuchowe;

- przyrost Δ>0 oznacza wzrost (większą wartość)

- przyrost Δ<0 oznacza spadek (mniejszą wartość)

Przyrosty absolutne (bezwzględne) mogą być obliczane w stosunku do:

1/ jednego okresu Δ_t/k

2/ stale zmieniającego się okresu bazowego Δ_t/t-1

Przyrosty absolutne informują o ile wzrósł (zmalał) poziom zjawiska w okresie badanym w porównaniu z jego poziomem w okresie bazowym.

Przyrosty absolutne jednopodstawowe - wielkość zjawiska w kolejnych okresach (momentach) porównywana ze stała wielkością okresu bazowego (najczęściej wyjściowego) - różnica

Przyrosty absolutne łańcuchowe - za bazowy przyjmuje się okres (moment) poprzedzający okres 9moment) badany.

- indeksy inaczej wskaźniki dynamiki (zawsze dodatnie): indywidualne i zespołowe (agregatowe) - j.w.

Miary te wyrażają się w liczbach dziesiętnych lub po pomnożeniu przez 100 w %. Interpretując indeksy, zawsze wyrażamy je w %.

5) Co to są indeksy dynamiki? Jakie rodzaje indeksów stosujemy do opisu dynamiki zmian zjawisk jednorodnych opisanych pojedynczym szeregiem czasowym?

Indeksy dynamiki (są zawsze dodatnie) - mierniki określające stosunek wielkości badanego zjawiska w 2 okresach lub momentach, są to wielkości niemianowane. Do interpretacji mnożymy je przez 100 i podajemy w %. Wartość indeksu < 1 (lub 100%) oznacza spadek poziomu zjawiska, zaś wartość indeksu > 1 oznacza wzrost poziomu zjawiska; wartość indeksu < 0 oznacza błąd merytoryczny.

% zmiana (
) - szukamy indeksu najbardziej oddalonego od 1, tzn. największego spośród tych >1 (gdy są wzrosty) lub najmniejszego spośród tych < 1 (gdy są spadki).

Do opisu dynamiki zmian zjawisk jednorodnych (np. zmiany wydajności pracy w jednej firmie), opisanych pojedynczym szeregiem czasowym, stosujemy indywidualne indeksy dynamiki. Dzielimy je na:

- jednopodstawowe (i_t/k) - iloraz wielkości zjawiska w okresie t (badanym) i wielkości zjawiska w okresie 0 bazowym; przy ustalonej podstawie możemy je zamieniać na indeksy o innej podstawie lub na indeksy łańcuchowe i na odwrót.

- łańcuchowe (i_{t/ t-1}) - iloraz wielkości zjawiska w okresie (momencie) t czyli badanym i wielkości zjawiska w okresie (momencie) t-1, czyli bezpośrednio poprzedzającym.

Miedzy przyrostami względnymi a indeksami zachodzi związek pozwalający na wyznaczanie jednych z tych miar poprzez drugie.

6) Jaką średnią stosujemy do oceny średniego tempa zmian zjawiska jednorodnego w czasie?

Do oceny średniego tempa zmian zjawiska jednorodnego w czasie stosujemy średnią geometryczną indeksów łańcuchowych. Wynik podajemy po pomnożeniu przez 100 w %. Średnia geometryczna mieści się między najmniejszym a największym z indeksów indywidualnych.

Tempo zmian informuje, o ile % poziom zjawiska w danym okresie jest wyższy (niższy) od poziomu w okresie przyjętym za podstawę porównań.

7) Jaki związek zachodzi między indywidualnymi indeksami cen, ilości i wartości?

Indeksy cen - p₀ Indeksy ilości - q₀ Indeksy wartości - w₀

Indeksy indywidualne stosujemy do charakterystyki dynamiki jednego zjawiska (pojedynczego szeregu statystycznego).

Indywidualne indeksy cen, ilości i wartości informują o zmianie (wzroście/spadku) tych wielkości w okresie badanym w porównaniu z okresem przyjętym za podstawę porównań. Między nimi zachodzi związek określany jako równość indeksowa dla indeksów indywidualnych tzn. i_w=

Indeks wartości jest iloczynem indeksu cen i ilości..

Indeksy indywidualne są stosowane do badań dynamiki zjawisk jednorodnych. Indeks indywidualny to stosunek poziomów tego samego zjawiska z dwóch różnych okresów (momentów).

Rodzaje indywidualnych indeksów: indeksy cen, ilości i wartości.

Indeks indywidualny cen (i_p) wyraża relację poziomu cen określonego dobra w okresie badanym i w okresie podstawowym.

Indeks indywidualny ilości (_q) oblicza się jako stosunek ilości określonego wyrobu w okresie badanym i w okresie podstawowym.

Iloczyn ilości wyrobu wytworzonego w okresie badanym i ceny tego wyrobu z okresu badanego daje wartość wyrobu w okresie badanym. Podobnie obliczamy wartość wyrobu w okresie podstawowym.

Indywidualny indeks wartości (i_w) to iloraz wartości wyrobu wytworzonego w okresie badanym i w okresie podstawowym.

8) Jakie indeksy nazywamy zespołowymi (agregatowymi) indeksami dynamiki wielkości absolutnych?

Indeksy agregatowe to miary dynamiki, które stosuje się do kategorii będących niejednorodnym agregatem, składającym się z różnych składników. Najczęściej indeksy te liczone są w celu wyodrębnienia ze zmian w czasie, wartości pewnego agregatu, wpływu zmian ilościowych oraz zmian cen.

Rozróżniamy 3 podstawowe indeksy agregatowe: wartości, ilości i cen.

Agregatowy indeks wartości wyraża zmiany jakie nastąpiły w okresie badanym w porównaniu okresem bazowym zarówno w ilościach określonego zespołu artykułów jak i w ich cenach.

Agregatowy indeks ilości informuje o tym, o ile - przeciętnie biorąc - wzrosła lub zmalała ilość określonego zbioru artykułów (wyrobów, produktów) w okresie badanym w porównaniu do okresu podstawowego przy odpowiednim założeniu przyjętym w formule standaryzacyjnej.

Agregatowy indeks cen informuje o tym, jak zmieniły się - przeciętnie biorąc - ceny danego zbioru artykułów w okresie badanym w porównaniu do okresu podstawowego, przy unieruchomieniu ilości w obu okresach, zgodnie z przyjętą formułą standaryzacyjną.

9) Na czym polega standaryzacja w zespołowych indeksach cen i ilości?

Standaryzacja inaczej eliminacja współczynników polega na przyjęciu stałego poziomu jednego z dwóch czynników - cen lub ilości - w przypadku agregatowego indeksu wartości, tzn. dla indeksu cen ustala się (unieruchamia) poziom ilości wszystkich artykułów, a dla indeksu ilości ustala (unieruchamia) się poziom cen wszystkich artykułów.

Formuły standaryzacji: okres bazowy - „0” okres badany - „n” lub „1”

1/ formuła Laspeyresa - polega na przyjęciu jako niezmiennych, wielkości z okresu bazowego (podstawowego); polega na ustaleniu na poziomie bazowym cen gdy wyznaczamy indeks ilości, a ilości gdy wyznaczamy indeks cen.

2/ formuła Paaschego - polega na przyjęciu jako niezmiennych, wielkości z okresu badanego; polega na ustaleniu na poziomie badanym cen gdy wyznaczamy indeks ilości, a ilości gdy wyznaczamy indeks cen.

Zespołowe indeksy cen informują, jak zmieniłyby się przeciętnie ceny danego zespołu artykułów w okresie badanym w porównaniu z cenami w okresie bazowym przy założeniu stałej ilości zgodnie z przyjętą formułą standaryzacji.

Pozwalają one na ocenę jak zmieniłaby się wartość całego zespołu w okresie badanym w porównaniu z okresem bazowym tylko na skutek zmiany cen przy odpowiednio przyjętej formule standaryzacji.

Zespołowe indeksy ilości informują, jak zmieniłaby się przeciętnie ilość produktów danego zespołu w okresie badanym w porównaniu z okresem bazowym przy założeniu stałych cen zgodnie z przyjętą formułą standaryzacji.

Pozwalają one na ocenę jak zmieniłaby się wartość całego zespołu w okresie badanym w porównaniu z okresem bazowym na skutek zmian ilościowych przy odpowiednio przyjętej formule standaryzacji.

10) W jakich sytuacjach stosujemy zespołowe indeksy dynamiki wielkości absolutnych?

Stosujemy je do badania dynamiki całego zespołu zjawisk - zwykle niejednorodnych i nie sumowalnych, opisanych kilkoma szeregami czasowymi..

11) Jaki związek zachodzi między zespołowymi indeksami dynamiki wielkości absolutnych?

Związek o nazwie równości indeksowej dla indeksów zespołowych mówi o tym, że jeśli dysponujemy informacjami o poziomach dwóch spośród trzech omawianych indeksów agregatowych, to możemy obliczyć wielkość trzeciego indeksu.

STATYSTYKA Strona 1 z 12

---