EKONOMETRIA

Wykład 1. 07.10.2008

Ekonometria - zajmuje się empiryczną weryfikacją praw ekonomicznych. Dane wykorzystywane do weryfikacji otrzymuje się z obserwacji.

Ekonometria zajmuje się modelami.

Model ekonometryczny to sformalizowany zapis istniejących prawidłowości ekonomicznych.

Budowa modelu ekonometrycznego

y_t= β₀ + β₁ * x_t1 + β₂ * x_t2 +…+ β_k * x_tk +ζ_t

y_t- zmienna objaśniona (endogeniczna)

x_t1, x_{t2, …,} x_tk- zmienne objaśniające (egzogeniczne)

β_0, β_1, β_{2, …,} β_k- parametry strukturalne (nie są znane, nie zmieniają się w czasie)

ζ- składnik losowy (nie jest znany)

t- zmienia się w czasie w różnych momentach (t=1, 2…, T)

Liczba zmiennych objaśniających w modelu oznaczona jest „k”

Liczba parametrów strukturalnych to „k+1”

T- oznacza jak liczna była próba

Macierz Y wymiaru Tx1 - nazywamy macierzą obserwacji na zmiennych objaśnianych modelu.

Macierz X wymiaru Tx(k+1) nazywana macierzą obserwacji na zmiennych objaśniających modelu.

Macierz β wymiaru (k+1)x1 nazywana macierzą parametrów strukturalnych.

Macierz ζ wymiaru Tx1 nazywana macierzą składników zakłócających (losowych)

Wykład 2. 27.10.2008

Parametr przeciętny - to stosunek wartości, jaką przybiera jedna zmienna do wartości jaką przybiera druga zmienna. Parametr przeciętny określa ile jednostek jednej zmiennej (y_t) przypada na jedną jednostkę drugiej zmiennej (x_ti)

PP(y_t,x_ti)=

Parametr krańcowy - to stosunek przyrostu wartości jednej zmiennej do przyrostu wartości drugiej zmiennej. Parametr krańcowy określa ile jednostek średnio wzrośnie (spadnie, w zależności od znaku) zmienna y_t, jeśli zmienna x_ti wzrośnie o jednostkę, ceteris paribus.

PK(y_t,x_ti)=
pochodna

Elastyczność cząstkowa - to stosunek parametru krańcowego do parametru przeciętnego. Elastyczność cząstkowa określa o ile średnio procent wzrośnie (spadnie, w zależności od znaku) zmienna endogeniczna (y_t) jeśli zmienna egzogeniczna (x_ti) wzrośnie o 1%, przy założeniu stałości pozostałych zmiennych. Cp.

E(y_t,x_ti)=

Krańcowa stopa substytucja - stosunek dwóch zmiennych PK politycznych względem różnych zmiennych. Określa jaki jest niezbędny wzrost oddziaływania i-tej zmiennej (x_ti), kompensowany spadkiem oddziaływania j-tej zmiennej (x_tj) o jednostkę, przy niezmienionym poziomie oddziaływania pozostałych zmiennych, tak aby wartość zmiennej endogenicznej (y_t) nie zmieniła się.

KSS(x_ti, x_tj)=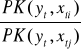

Etapy analizy ekonometrycznej:

1. interpretacja parametrów strukturalnych (β)

2. interpretacja miar przeciętnych, krańcowych, elastyczności cz astkowych

3. interpretacja miar dopasowania

4. testowanie własności struktury stochastycznej modelu (składnika zakłócającego)

- normalność rozkładu

- homoskedastyczność

- struktura autoregresyjna

Model liniowy (β-krańcowy):

- jeśli zmienna objaśniająca(x_ti) wzrośnie o 1, a pozostałe zmienne nie ulegną zmianie, to zmienna y_t wzrośnie (lub zmaleje, w zależności od znaku przed β_i) średnio o β_i jednostek.

Model potęgowy (β-elastyczny):

- jeśli zmienna objaśniająca(x_ti) wzrośnie o 1%, a pozostałe składniki zmienne nie ulegną zmianie, to zmienna y_t wzrośnie (lub zmaleje, w zależności od znaku przed β_i ) średnio o β_i procent.

Model wykładniczy (β-krańcowy):

- jeśli zmienna objaśniająca(x_ti) wzrośnie o 1, a pozostałe zmienne nie ulegną zmianie, to zmienna y_t wzrośnie(lub zmaleje, w zależności od znaku przed β_i ) średnio o (e ^βi -1) * 100%, czyli w przybliżeniu o β_{i *} 100%.

Miary dopasowania:

- ogólny zapis (teoretyczny) y_t=β₀ + β₁ * x_t1 + β₂ * x_t2 + ζ_t

ζ_t- składnik zakładający

- model oszacowany (najmniejszych kwadratów)

ζ_t- składnik resztowy

- przypuszczenie kształtowania się y_t

y_t= nasze przypuszczenie kształtowania się y + błąd

zmienność zmiennej objaśnianej= zmienność zmiennych objaśniających + zmienność reszt

Ogólna suma kwadratów Syy Resztowa suma kwadratów RSS

Regresyjna(objaśniona)suma kwadratówESS

Współczynnik determinacji informuje ile % zmienności zmiennej endogenicznej powodowane jest zmiennością zmiennych objaśniających

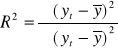
Współczynnik zbieżności informuje ile % zmienności zmiennej endogenicznej powodowane jest przez czynniki nieuwzględnione w modelu.

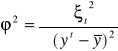
Skorygowany współczynnik zbieżności informuje ile % zmienności zmiennej endogenicznej powodowane jest przez czynniki nieuwzględnione w modelu

Skorygowany współczynnik determinacji informuje ile % zmienności zmiennej endogenicznej powodowane jest zmiennością zmiennych objaśniających

Wariancja resztowa

Średni błąd resztowy informuje jakie jest przeciętne odchylenie wartości empirycznych od teoretycznych modelu

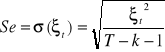
Współczynnik zmienności losowej informuje jaki jest udział średniego błędu resztowego w przeciętnej wartości zmiennej objaśnionej (musi być poniżej 10%, czasem nawet 5%)

Wykład 3, 04.10.2008

Założenia schematu Gaussa-Markova

dany jest model: y_t=β₀ + β₁ * x_t1 + β₂ * x_t2 + ζ_t

1. E(ζ_t)=0 t=1,…,T

2. σ² (ζ_t)= σ^2=const t=1,…,T

3. cov(ζ_t, ζ_s)=0 t,s=1,…,T t≠s

4. cov(x_t1, ζ_t)=0 i=1,…,k t=1,…,T

5. ζ_t ~ N(0, σ²) t=1,…,T

6. rz(X)=k+1

Aby używać MNK (metoda najmniejszych kwadratów) muszą być spełnione wszystkie założenia.

Jeśli warunek 2,3,4 jest spełniony, to estymator MNK jest najlepszy.

Testowanie hipotez

Jeśli spełnione są założenia klasycznego schematu Gaussa-Markova, wówczas estymatory MNK parametrów strukturalnych, oraz estymatory wariacji składnika losowego mają następujące własności:

1. są nieobciążone

2. mają najmniejszą wariancję w klasie nieobciążonych estymatorów liniowych, oznacza to, że są estymatorami efektywnymi

3. są zgodne, czyli wraz ze wzrostem liczebności próby wartości estymatora są stochastycznie zbieżne do rzeczywistej nieznanej wartości parametru w populacji

4. estymator
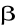
   ma rozkład normalny o wartości oczekiwanej i macierzy wariancji kowariancji danej formułami:

Co można zapisać:

5. zmienna y_t ma rozkład normalny o wartości oczekiwanej i wariancji danej formułami:

Wymienione cztery własności, wraz z założeniem mówiącym o normalności rozkładu składników losowych, stanowią podstawę statystycznej weryfikacji oszacowanego klasycznego modelu ekonometrycznego.

Z własności d) wynika, że zmienna losowa zdefiniowana w następujący sposób:

ma standaryzowany rozkład normalny.

Oznacza to, że moglibyśmy wykorzystać rozkład normalny dla potrzeb wnioskowania o nieznanym parametrze β_i pod warunkiem znajomości wariancji składnika losowego σ_ξ².

Wariancja składnika losowego σ_ξ² nie jest znana, stąd nie jest znana macierz wariancji i kowariancji σ_ξ²*(x^Tx)^-1. zastępując wariancją składnika losowego jest nieobciążonym estymatorem σ_ξ² otrzymujemy
, empiryczną macierz wariancji i kowariancji. pierwiastki kwadratowe głównej przekątnej tej macierzy są ocenami (estymatorami) średniego błędu szacunku parametru, w przypadku estymacji nieobciążonej są również estymatorami odchylenia standardowego.

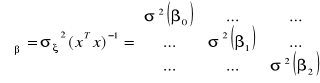
Z kursu statystyki wiadomo, że zmienna losowa zdefiniowana jako:

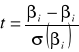
(1)

gdzie
jest estymatorem nieznanej
ma rozkład t-Studenta o T-k-1 stopniach swobody.

Z kursu statystyki wiadomo również, że dowolna statystyka t-Studenta spełnia równanie:

(2)

Równanie jest równoważne z następującą formułą:

(3)

gdzie:

α- poziom istotności

t_α/2 - wartość krytyczna odczytana z rozkładu t-Studenta o liczbie stopni swobody T-k-1

Kładąc prawą stronę równania (1) do (3) otrzymujemy:

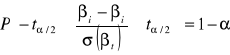
(4)

Przekształcając formułę (4), otrzymujemy formułę (5):

(5)

Wyrażenie (5) określa 1-α procentowy przedział ufności parametru strukturalnego β_i.

Interpretując przedział ufności można stwierdzić, ze przedział o końcach
w (1-α)*100 przypadkach na 100 zawiera rzeczywistą, nieznaną wartość parametru β_i.

Test t-Studenta

Test istotności indywidualnej zwany również testem t-Studenta polega na wykorzystaniu informacji z próby do weryfikacji prawdziwości tzw. hipotezy zerowej (H₀). Decyzję o odrzuceniu lub braku podstaw do jej odrzucenia, podejmujemy na podstawie porównania wartości statystyki z próby z tzw. wartością krytyczną.

Jeśli sformułujemy hipotezę zerową w taki sposób, że parametr przyjmuje konkretna wartość, oznaczoną np. jako
i jeżeli rozkład składnika jest zgodny z rozkładem normalnym wówczas zgodnie z formułą (4) można zapisać przedział ufności w sposób następujący:

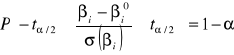
(6)

gdzie:

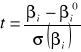
(7)!!!

Formuła (7) jest to statystyka testowa testu istotności indywidualnej.

Z formuły (6) wynika :
(8)

W praktyce zapisując hipotezy w następujący sposób:

wyliczamy wartość statystyki testowej zgodnie z formułą (7) i na podstawie formuły (8) podejmujemy decyzję:

- jeśli |t|>t_α/2 , odrzucamy H₀ na rzecz H_A na α procentowym poziomie istotności.

- jeśli |t|≤ t_{α/2 ,} brak podstaw do odrzucenia H₀ na α procentowym poziomie istotności.

Wykład 4, 18.11.2008

Testowanie istotności parametrów

Stawiamy hipotezy badawcze

Statystyką testową jest:

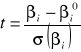
Uwaga! Proszę zauważyć, że licząc powyższą formułę przyjmuje się
, co wynika z hipotezy zerowej.

- jeśli |t|>t_α/2 , odrzucamy H₀ na rzecz H_A na α procentowym poziomie istotności.

- jeśli |t|≤ t_{α/2 ,} brak podstaw do odrzucenia H₀ na α procentowym poziomie istotności.

t_α/2 to wartość krytyczna odczytana jest z rozkładu t-Studenta o liczbie stopni swobody T-k-1

TEST F (testowanie łączne- Fishera)

Wykorzystuje analizę wariancji składnika resztowego, można przeprowadzić podobnego typu rozumowanie dotyczące istotności wszystkich parametrów wyjąwszy wyraz wolny

Stawiamy hipotezę:

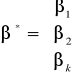
Wyliczamy wartość statystyki testowej zgodnie z formułą:

Następnie porównujemy wartość statystyki testowej F_t z wartością krytyczną odczytaną z rozkładu Fishera o stopniach swobody licznika k i mianownika T-k-1 i α procentowym poziomie istotności:

- jeśli F_t>F_α (k,T-k-1) - wówczas odrzucamy H₀ na rzecz H_A na α procentowym poziomie istotności.

- jeśli F_t≤F_α (k,T-k-1) - wówczas stwierdzamy brak podstaw do odrzucenia H₀ na α procentowym poziomie istotności.

Testy diagnostyczne

-testuje się w celu weryfikacji założeń uczynionych w trakcie konstruowania modelu. w szczególności założeń struktury stochastycznej modelu - czyli składnika zakłócającego modelu.

Odnośnie struktury stochastycznej modelu (składnika zakłócającego) czyni się następujące, tzw. klasyczne założenia:

- brak autokorelacji (czyli skorelowania w czasie z własnymi opóźnionymi obserwacjami)

- stałość wariancji

- normalność rozkładu składników losowych w klasycznym modelu regresji

Testowanie autokorelacji

Do testowania autokorelacji najczęściej używa się jednego z trzech testów:

- Durbina-Watsona (DW)

- h-Durbina

- Godfreya

Test DW można stosować jeśli jednocześnie spełnione są następujące założenia:

- w modelu występuje wyraz wolny

- zmienne objaśniające się nielosowe

- nie występują zmienne endogeniczne opóźnione w czasie w roli zmiennych objaśniających (model nie jest dynamiczny)

- składniki losowe charakteryzują się zależnością autoregresyjną rzędu co najwyżej pierwszego

μ- składnik losowy o wartości oczekiwanej równej zero, stałej wariancji i zerowej kowariancji

Statystyką testową jest:

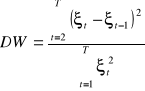
Można wykazać, że 0≤DW≤4 oraz, że autokorelacja nie zachodzi dla DW=2. W praktyce uznaje się autokorelację za nieistotną dla 1,5≤DW≤2,5

Hipotezy stawiamy w zależności od wartości DW:

dla DW<2 dla DW>2

Odczytujemy z tablic rozkładu DW dwie wartości krytyczne, dolną d_L i górną d_U

Dla DW<2 reguła decyzyjna jest następująca:

Jeśli DW>d_U nie mamy podstaw do odrzucenia H₀, brak autokorelacji.

Jeśli DW< d_L odrzucamy H₀, występuje autokorelacja dodatnia.

Jeśli d_L≤DW≤ d_U test nie daje rozstrzygnięcia.

Dla DW>2 liczymy DW^*=4-DW:

Jeśli DW^*> d_U nie mamy podstaw do odrzucenia H₀, brak autokorelacji.

Jeśli DW^*< d_L odrzucamy H₀, występuje autokorelacja ujemna.

Jeśli d_L≤DW^*≤ d_U test daje rozstrzygnięcia.

Heteroskedastyczność - testowanie

jak testować?

Test ilorazu wiarygodności

Dany jest model: y_t=β₀ + β₁ * x_t1 + β₂ * x_t2 + ζ_t

1. Szacujemy parametr modelu, stosujemy MNK, wyznaczamy reszty relacji, otrzymujemy macierz
   .

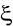
2. Macierz reszt dzielona jest na L podmacierzy (grup).

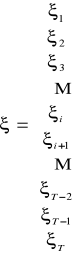
3. Osobno dla grup liczymy średnie arytmetyczne i wariancje reszt, ocenę wariancji dla dowolnej np. i-tej grupy oznaczamy
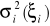
   . Ocen takich jest dokładnie L.

4. Liczymy wariancję błędu w całej próbie (bez podziału na grupy), ocenę wariancji oznaczamy
   .

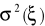
5. Wyznaczamy statystykę χ

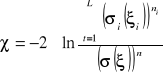
Statystyka χ ma rozkład χ² z (L-1) stopniami swobody

6. Stawiamy hipotezy

7. Reguła decyzyjna

Jeśli λ≤χ² (L-1) dla wybranego poziomu istotności α, wówczas nie mamy podstaw do odrzucenia hipotezy zerowej, wnioskujemy o jednorodności wariancji w przeciwnym przypadku hipotezę zerową odrzucamy i wnioskujemy o heteroskedastyczności.

Posługując się pakietami ekonometrycznymi (np. GRFTL) hipotezy zerowej nie odrzucamy, jeśli wartość (prób) jest większa od poziomu istotności α.

JARQUE - BERA

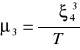
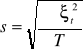
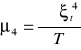
(miara wysmukłości; kurtoza(płaski))

Wykład 5, 02.12.2008

BADANIA OPERACYJNE -dział zajmujący się modelami decyzyjnymi, w których nie występuje ξ

Model decyzyjny

matematyczny opis można przedstawić następująco:

jest uporządkowanym zbiorem zmiennych decyzyjnych

q₁(X)- jest funkcją, której argumenty są zmienne decyzyjnie, zbiór tych funkcji określa warunki wewnętrznej zgodności modelu.

D- jest zbiorem rozwiązań dopuszczalnych, czyli zbiorem tych wszystkich rozwiązań które spełniają warunki wewnętrznej zgodności.

Jeśli funkcja celu i wszystkie funkcje tworzące warunki wewnętrznej zgodności są liniowe, mówimy o liniowych modelach decyzyjnych.

W literaturze przedmiotu wyróżnia się kilka typów takich modeli. Do najbardziej znanych zalicza się: model optymalnego wykorzystania środków produkcji, model diety, model rozkroju, model transportowy, model przydziału.

Wiele sytuacji decyzyjnych mimo iż nie mają nic wspólnego z produkcją, dietą, rozwojem itp. daje się sprowadzić tj. zapisać przy pomocy jednego z modeli wspomnianego typu.

Klasyczny model produkcyjny

- przedsiębiorstwo wytwarza n produktów: P₁,…,P_n

- produkcja odbywa się przy pomocy m środków produkcji: S₁,…,S_m mierzonych w

umownych jednostkach

- środki produkcji dane są w ilościach: b₁,…,b_m

- znana jest technologia produkcji: wyrażona w postaci zużycia jednostkowego środka produkcji S_i niezbędnego do wytworzenia (jednostki) produktu P_j, zużycie to oznacza się symbolem a_ij

- zadanie decydenta polega na takim rozplanowaniu produkcji, by zapewnić przedsiębiorstwu maksymalny zysk, przychód, wiedząc iż cena produktów wynoszą odpowiednio: c₁,…,cn

Uporządkowanym zbiorem (nieznanych) zmiennych decyzyjnych jest zatem zbiór
gdzie dowolna zmienna x_j oznacza ilość produktów typu P_j

Pamiętajmy, że matematyczny opis jest następujący:

Zacznijmy konstrukcję modelu produkcyjnego funkcji celu. pamiętajmy, że zadanie polega na maksymalizacji zusku. Pamiętając, ze cena produktów wynosi C₁,…,Cn przedsiębiorstwo produkuje zaś x₁,…,x_n wyrobów P₁,…,P_n, funkcję celu można zapisać:

W praktyce (czyli w zdecydowanej większości publikacji i aplikacji) zapis ten upraszcza się i powszechnie stosuje następującą notację funkcji celu:

(1)

W powyższym wzorze następujące symbole oznaczają:

c₁- cena jednego produktu P₁, cena jednostkowa, zysk jednostkowy za sprzedaży jednego wyrobu P₁

x₂- ilość produktów typu P₂

c₃x₃- zysk ze sprzedaży wszystkich wyrobów P₃

Σc_jx_j- całkowity zysk za wszystkich wyrobów przedsiębiorstwa

Skoro „rozprawiliśmy” się z funkcja celu, pozostaje zdefiniowanie zbioru rozwiązań dopuszczalnych D

Przypomnijmy, znana jest technologia produkcji, są dane w postaci zużycia jednostkowego

a_ij, znane również zasoby środków produkcji b₁,…,b_m.

Korzystając z dobrodziejstwa zapisu/notacji macierzowej jednostkowe zużycie środków produkcji a_ij możemy przedstawić w postaci tzw. macierzy technologii wytwarzania:

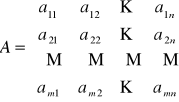
Przypomnijmy, dowolne a_ij to zużycie środka produkcji i-tego niezbędne do wytworzenia jednostki produktu j-tego.

Wygodnym zapisem jest: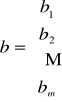

Dysponujemy zatem:

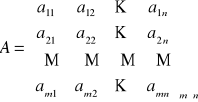
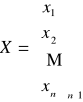
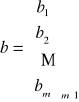
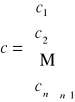
Zużycie pierwszego środka produkcji S₁, do wytworzenia wyrobów P₁,…,P_n można zapisać:

-całkowite zużycie S₁ środka produkcji pierwszego do produkcji poszczególnych wyrobów P₁.P_2,P₃

całkowite zużycie środku produkcji pierwszego

do wytworzenia wszystkich produktów P₁

b₁- całkowity zapas jaki mamy

Zużycie to nie może przekroczyć posiadanego przez przedsiębiorstwo zapasu środka S₁, zatem nie może przekroczyć wielkości b₁, z tego wynika:

-dla środka S₁

Podobnie dla środka produkcji drugiego otrzymujemy:

Ponieważ środków produkcji jest m, zatem:

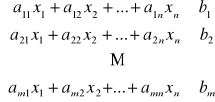
(2)

Układ nierówności liniowych (2) w warunek brzegowy zakładający nieujemność zmiennych decyzyjnych x jednoznacznie wyznacza zbiór rozwiązań dopuszczalnych D.

1. + (2) + warunek brzegowy - liniowy model decyzyjny wykorzystania środków produkcji

Łącząc zapis (1), (2) i warunek brzegowy otrzymujemy klasyczny model produkcyjny:

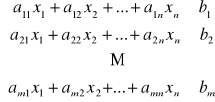
Lub w postaci macierzowej:

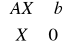
Przykład:

a₃₅- zużycie środka produkcji trzeciego do produkcji jednego produktu P₅

a₃₅x₅- zużycie środka produkcji trzeciego do produkcji wszystkich wyrobów P₅

a₃₁x₁+a₃₂x₂+…+a_3nx_n- całkowite zużycie środka produkcji trzeciego

x₇- ilość produkcji środka x₇ jaką należy wytworzyć

X- cala macierz, wektor mówi ile poszczególnych produktów mamy wyrobić

b₄-zapas środka produkcji czwartego

b- macierz zawierające informacje o zasobach środków produkcji

Klasyczny model diety

- do dyspozycji jest n produktów odżywczych: P₁,…,P_n

- każdy z produktów odżywczych zawiera m składników odżywczych S₁,…,S_m mierzonych w umownych jednostkach

- znane jest minimalne zapotrzebowanie na składniki odżywcze S₁,…,S_m wynosi ono odpowiednio b₁,…,b_m jednostek

- znane są wartości poszczególnych składników odżywczych S₁,…,S_m w jednostce produktu odżywczego P₁,…,P_n. Zawartość składnika S₁ w jednostce produktu P_j oznacza się symbolem a_ij

- zadanie decydenta polega na takim zaprojektowaniu diety (sposobu żywienia) aby zminimalizować jej koszty wiedzą, że ceny jednostkowe produktów odżywczych wynoszą odpowiednio: c₁,…,c_n

b₁ - zapotrzebowanie na składnik odżywczy S₁

b₂ - zapotrzebowanie na składnik odżywczy S₂

Uporządkowanym zbiorem (mierzonych) zmiennych decyzyjnych jest zatem zbiór
gdzie dowolna zmienna x_j oznacza ilość zakupionych i zastosowanych w diecie produktów odżywczych typu P_j

Funkcje celu ogólnie zapisywaliśmy następująco:

W modelu diety chodzi jednak nie o maksymalizację, ale minimalizację kosztu, zatem jak przekształcić powyższy (ogólny) zapis?

Twierdzenie!!!

Jeśli funkcja rzeczywista f(x) określona w zbiorze D osiąga w punkcie x₀ wartość najmniejszą, co można zapisać:

wówczas funkcja -f(x), określona w zbiorze D osiąga w punkcie x₀ wartość największą, co zapisujemy:

Twierdzenie „działa” również w drugą stronę, czyli:

Korzystając z powyższych twierdzeń, możemy skonstruować funkcję celu modelu diety.

Pamiętamy, że zadanie polega na minimalizacji kosztu. ceny jednostkowe produktów c₁,…,c_n, decydent kupuje zaś x₁,…,x_n jednostek produktów odżywczych P₁,…,P_n, zatem funkcję celu można zapisać:

gdzie g(x)= -f(x)

Upraszczając zapis, otrzymujemy:

(1)

c₃- cena za jedną jednostkę produktu P₃

x₄- ilość produktu P₄ jaka kupimy

c₂x₂- całkowity koszt nabycia wszystkich produktów P₂

Σc_jx_j- całkowita cena jaką zapłacimy za wszystkie produkty

Ilość składnika odżywczego S₁ dostarczana wraz z produktem odżywczym P₁ powinna być oznaczona: a₁₁x₁

Ilość składnika odżywczego S₁ dostarczona wraz z produktami odżywczymi P₁,…,P_n:

-całkowita ilość składnika odżywczego pierwszego jaką dostarczamy wraz ze wszystkimi produktami P₁,…,P_n

Ilość składnika S₁ nie może być mniejsza niż zgłoszone zapotrzebowanie b₁, zatem:

Dla środka S₂ + warunek brzegowy

Model klasyczny diety:

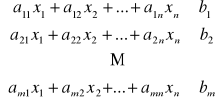
W postaci macierzowej:

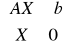
Wykład 6, 16.12.2008

Zad.

Przedsiębiorstwo produkuje dwa rodzaje wyrobów A i B. W procesie produkcji wykorzystywane są trzy środki produkcji S₁, S₂ , S₃ dane w ograniczonych ilościach 2000, 4200, 1200 jednostek odpowiednio.

Do wytworzenie jednego wyrobu A należy zużyć 4, 6 i 3 jednostki środków produkcji S_1, S₂ S_3. Do wytworzenia jednego wyrobu B zużywa się 2 i 6 jednostek środków S₁ i S_2. Jednostkowe zyski ze sprzedaży wyrobów A i B wynoszą odpowiednio 70 i 50 jednostek pieniężnych.

Zapisać odpowiedni model decyzyjny. Rozwiązać wszelkimi znanymi metodami.

Środki produkcji	A	B
S1	4	2	2000
S2	6	6	4200
S3	3	0	1200
	70	50

Model w postaci układu nierówności:

- warunki ograniczające

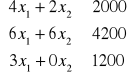
-warunek brzegowy

- funkcja celu

Model decyzyjny:

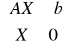
Model w postaci macierzowej:

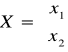
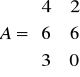
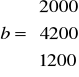
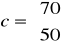
Metoda simpleksowa - przechodzenie od wierzchołka do wierzchołka i szukanie MAX

Twierdzenie (jak znaleźć ten jeden najlepszy punkt P gdzie będzie MAX albo MIN)

Rozwiązanie optymalne liniowego modelu decyzyjnego znajduje się w punkcie wierzchołkowym w zbiorze rozwiązań dopuszczalnych D.

Mamy 5 wierzchołków:

x_1, x₂

P₁ (0, 0) Z (P₁) = 70 * 0 + 50 * 0 = 0

P₂ (0, 700) Z (P₂) = 70* 0 + 50 * 700 = 35000

P₃ (300, 400) Z (P₃) = 70 * 300 + 50 * 400 = 41000 max (rozwiązanie)

P₄ (400, 200) Z (P₄) = 70 * 400 + 50 * 200 = 38000

P₅ (400, 0) Z (P₅) = 70 * 400 + 50 * 0 = 28000

Czyli wytwarzam 400 szt. produktu A i 0 szt. produktu B.

Odp. Optymalny plan produkcji polega na wytworzeniu 300 szt. wyrobu A, 400 szt. wyrobu B. Przy takim planie produkcji przedsiębiorstwo wygeneruje zysk 41000 jednostek pieniężnych.

Model transportowy: (najbardziej skomplikowany, łączy w sobie modele diety i decyzyjny)

- danych jest m dostawców jednorodnego towaru D₁, … , D_m

- dostawcy D₁, … , D_m oferują na rynek odpowiednio d₁, … , d_m jednostek towaru

- danych jest n odbiorców jednorodnego towaru O₁, … , O_n

- odbiorcy O₁, … , O_n składają zamówienie na towar w ilościach o₁, … , o_n

- znane są tzw. odległości taryfowo - ekonomiczne (koszty jednostkowe transportu) pomiędzy odbiorcami i dostawcami, odległość między i-tym dostawcą a j-tym odbiorcą oznaczamy symbolem a_ij.

- zadanie decydenta (czyli nasze) polega na takim wyborze tras bu odległość/koszt transportu był minimalny przy założeniu, iż odbiorcy i dostawcy dokonują wymiany towarów zgodnie z zgłoszonym zapotrzebowaniem.

Klasyczny model transportowy

Sformułowanie modelu:

W klasycznym zagadnieniu produkcyjnym zakłada się, że popyt i podaż są sobie równe, czyli że zachodzi:

(3)

W ogólnym przypadku tak być nie musi.

Zakładamy teraz, że założenie (3) jest spełnione.

Ogół informacji o sytuacji decyzyjnej korzystnie jest zapisać przy użyciu notacji macierzowej, wówczas:

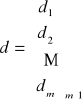
macierz podaży, d_i = podaż generowana przez i-tego dostawcę

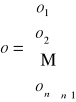
macierz popytu, o_j - popyt generowany przez j-tego odbiorcę

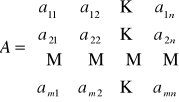
macierz odległości taryfowo-ekonomicznych

(1) a_ij - odległość dostawcy i-tego od odbiorcy j-tego

(2) a_ij - koszt transportu jednostki towaru od dostawcy i-tego do odbiorcy j-tego

(3) a_ij - czas transportu towaru od dostawcy i-tego do odbiorcy j-tego

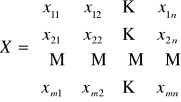
macierz zmiennych decyzyjnych

- w przypadku macierzy A zdefiniowanej zgodnie z (2) dowolny element x_ij oznacza ilość towaru przewiezionego od dostawcy i-tego do odbiorcy j-tego

- jeśli macierz A zdefiniowana jest zgodnie z (1) lub (3) wówczas x_ij jest zmienną 0-1 zależnie od rezygnacji lub wyboru trasy od dostawcy i-tego do odbiorcy j-tego.

Z(x) = a₁₁* x₁₁* a₁₂ * x₁₂ * a₁₃ * x₁₃ * a₂₁ * x₂₁ * a₂₂ * x₂₂ * a₂₃ * x₂₃ MIN

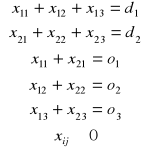
Wykład 7, 13.01.09

SIMPLEKS - TEORIA

- niech dany jest układ m równań liniowych o n niewiadomych, taki, że liczba niewiadomych jest większa od liczny równań (m < n)

- niech w układzie tym rzędy macierzy podstawowej i uzupełniona są równe liczbie równań (czyli rz(x) = rz(U) = m)

Układ ten można zapisać w postaci macierzowej: Ax = b

Zgodnie z twierdzeniem Kroneckera-Cappeliego układ ten posiada nieskończenie wiele rozwiązań (dlaczego?)

Układ ten posiada również co najwyżej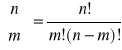
rozwiązań bazowych.

Macierze A i X można zapisać w postaci macierzy blokowych, w następujący sposób:

A = [ BP ] ;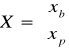

Macierz B to nieosobliwa macierz kwadratowa stopnia m, składająca się (z liniowo niezależnych) kolumn macierzy A.

Macierz P to macierz pozostałych kolumn macierzy A (czyli tych , które nie zostały „wykorzystane” w macierzy B).

Macierz X_b to macierz zmiennych bazowych.

Macierz X_p to macierz zmiennych niebazowych.

Zapis blokowy pozwala na następujące przekształcenie:

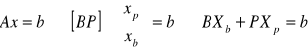
Ponieważ macierz B jest kwadratowa, nieosobliwa, więc możliwe jest obustronne wymnożenie (z lewej strony) równanie przez macierz odwrotną do B (czyli B^-1).

Dla dowolnego rozwiązania bazowego macierz X_p jest macierzą zerową, zatem dowolne rozwiązanie bazowe można zapisać: X_b=B^-1b

Przykład.

Dany jest układ równań:

2x₁ + 1x₂ + 1x₃ + 0x₄ + 0x₅ = 3

3x₁ + 2x₂ + 0x₃ + 0x₄ + 1x₅ = 5

1x₁ + 1x₂ + 1x₃ + 1x₄ + 0x₅ = 4

Wyznaczyć dowolne rozwiązanie powyższego układu.

Macierzowa postać układu jest następująca: X_b=B^-1b

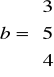
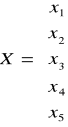
Niech bazowymi zmiennymi są x₁, x₂, x₃ wówczas: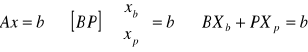

·
=

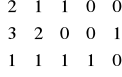
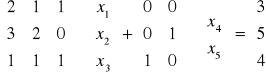
Zmienne niebazowe zanikają (z definicji rozwiązania bazowego), rozwiązanie bazowe można zapisać:

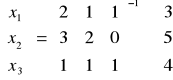
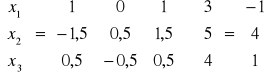
Ostatecznie rozwiązaniem bazowym jest uporządkowana piątka liczb

x₁ = -1 ^ x₂ = 4 ^ x₃ = 1 ^ x₄ = 0 ^ x₅ = 0

Rozwiązań bazowych powinno być co najwyżej:

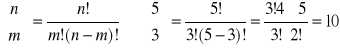
Niech zmiennymi bazowymi będą x₁ , x₂ , x₄ wówczas:

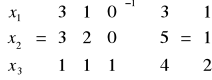
Rozwiązaniem bazowym jest uporządkowana piątka liczb:

x₁ = 1 ^ x₂ = 1 ^ x₃ = 0 ^i x₄ = 2 ^ x₅ = 0

(istnieje co najmniej 10 takich kombinacji)

Przypomnijmy, model decyzyjny został zapisany:

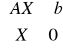
(1)

I jeśli m<n wówczas dowolne bazowe rozwiązanie takiego modelu (de facto - układy równań) można zapisać następująco: X_b=B^-1b

Definicja: Dopuszczalnym rozwiązaniem bazowym układu równań modelu postaci (1) nazywamy rozwiązanie bazowe spełniające układ warunków wewnętrznej zgodności modelu.

Twierdzenie

Dopuszczalne rozwiązanie bazowe modelu (1) wyznacza współrzędne wierzchołka zbioru wielościennego wypukłego D utworzonego z rozwiązań dopuszczalnych modelu (1)

Wniosek:

Zbiór wszystkich dopuszczalnych rozwiązań bazowych wyznaczają jednoznacznie współrzędne wszystkich wierzchołków simpleksu modelu (1)

Wniosek:

Jednoznaczne rozwiązanie analityczne liniowego (niesprzecznego) modelu decyzyjnego można wyznaczyć znajdując wszystkie rozwiązania bazowe układu tworzącego warunki wewnętrznej zgodności.

- Metoda simpleks jest iteracyjną metodą wyznaczania kolejnych bazowych rozwiązań układu warunków wewnętrznej zgodności modelu (1)

- W metodzie simpleks dzięki specyficznym cechom algorytmu, każde kolejne rozwiązanie jest „lepsze” od poprzedniego, aż do uzyskania rozwiązania optymalnego lub stwierdzenia braku rozwiązań, ewentualnie stwierdzenia nieograniczoności funkcji kryterium

- algorytm simpleksowy jest sformalizowany, a obliczenia prowadzone są w tzw. tablicy metody simpleks.

Zad. Treść - jak wyżej

model decyzyjny został zapisany:

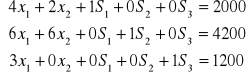
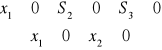
Z(x)=70x₁+50x₂+OS₁₊OS₂+OS₃ max

Ogólna postać tablicy metody simpleks:

		X^T	Wyraz wolny
Baza	cj	c^T
Xb	cb	B^-1A	B^-1b
	zj	C^T-Cb ^TB^-1A	Cb ^TB^-1b
				cj- zj

		X1	X2	S1	S2	S3	Wyraz wolny
Baza	cj	70	50	0	0	0
S1	0	4	2	1	0	0	2000
S2	0	6	6	0	1	0	4200
S3	0	3	0	0	0	1	1200
	zj	0	0	0	0	0	0
		cj- zj	70	50	0	0	0

0

d_L

d_U

4

<

?

DW→ H₀

H_A← DW

grupa pierwsza, liczebność n₁

grupa i-ta, liczebność n_i

grupa L-ta, liczebność n_L

ten wers mówi, który środek produkcji zużyłem

ten wers mówi, do produkcji którego wyrobu zużyłem środek produkcji

---