1. Definicja funkcji

Funkcją określoną na zbiorze

o

wartościach w zbiorze

nazywamy przyporządkowanie

każdemu elementowi

dokładnie jednego elementu

. Funkcję taką

oznaczamy np.:

Wartość funkcji f w punkcie x

oznaczamy przez f(x).

2. Definicja funkcji rosnącej i

malejącej.

Funkcja f jest rosnąca (niemalejąca

) na zbiorze
, jeżeli

.

.

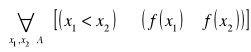
Funkcja f jest malejąca (nierosnąca) na

zbiorze
, jeżeli

.

.

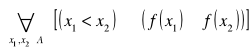
3. Definicja funkcji parzystej i nieparzystej.

Funkcja
jest parzysta, j

eżeli

Obrazowo: funkcja jest parzysta, Gd

y oś Oy jest osią symetrii

jej wykresu.

Funkcja
jest

nieparzysta, jeżeli

Obrazowo: funkcja jest nieparzysta, gdy

początek układu

współrzędnych jest środkiem symetrii jej

wykresu.

4. Definicja granicy ciągu liczbowego.

Niech
będzie ciągiem

liczb rzeczywistych

(lub zespolonych). Wówczas, jeżeli

istnieje taka liczba g, że

,

to nazywamy ją granicą ciągu

i

Oznaczamy

lub

5. Definicja ciągu rosnącego i

malejącego.

Ciąg (a_n) jest rosnący, jeżeli

Ciąg (a_n) jest niemalejący, jeżeli

Uwaga. Analogicznie definiuje się

ciąg malejący i nierosnący.

Ciągi rosnące, malejące, nierosnące i

niemalejące nazywamy

monotonicznymi.

6. Twierdzenie o trzech ciągach.

Jeżeli ciągi (a_n), (b_n) i (c_n) spełniają

warunki:

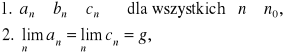
to

7. Definicja granicy funkcji w punkcie wg

Heinego (ciągowa).

Dla funkcji i liczba

rzeczywista q jest granicą funkcji f w

punkcie x₀, co

zapisujemy symbolicznie:
lub

gdy ,
gdy dla każdego ciągu jeśli

, to .

8. Definicja granicy funkcji w punkcie

wg Cauchy'ego (epsylonowa).

dla każdej liczby rzeczywistej

istnieje

liczba rzeczywista taka, że:
jeśli , to

9. Definicja ciągłości funkcji w punkcie.

Funkcja y = f(x) jest ciągła w

punkcie
 wtedy i

tylko wtedy, gdy spełniony jest

warunek: istnieje

granica funkcji w punkcie
,

równa wartości

funkcji w tym punkcie, czyli:

10. Definicja pochodnej funkcji w

punkcie.

Ilorazem różnicowym funkcji f w

punkcie
dla przyrostu

zmiennej niezależnej x

(gdzie
)

nazywamy stosunek

,

przy
.

11. Wzory na pochodną sumy, różnicy,

iloczynu i ilorazu.

a)

b)

(a-stała)
c)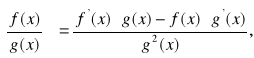
przy

12. Reguła de l'Hospitala.

Jeżeli funkcje f i g są określone w pewnym

sąsiedztwie

S punktu
oraz spełnione są

warunki:
1)

2) istnieją pochodne

i
dla każdego x* S,
3)
dla każdego x* S,
4) istnieje granica

(właściwa lub niewłaściwa),
to istnieje granica

(odpowiednio właściwa

lub niewłaściwa),

przy czym

Analogicznie, jeżeli:
1)

2), 3), 4) jak wyżej,
to istnieje granica

(odpowiednio właściwa lub niewłaściwa), przy czym

13. Definicja ekstremum funkcji.

Funkcją określoną na zbiorze
o

wartościach w zbiorze

nazywamy

przyporządkowanie

każdemu elementowi

dokładnie jednego elementu

. Funkcję taką

oznaczamy np.:

Wartość funkcji f w punkcie x

oznaczamy przez f(x).

14. Warunek konieczny istnienia

ekstremum funkcji.

Jeżeli funkcja f(x) ma w punkcie
 ekstremum i

jest w tym punkcie różniczkowalna, to:

15. Warunek dostateczny istnienia

ekstremum funkcji.

Niech f będzie funkcją różniczkowalną na

przedziale (a, b) i niech f ′ (c) = 0 dla pewnego

punktu c ∈ (a, b).
Jeśli f ′ (x) > 0 dla a < x < c i f ′ (x) < 0

dla c < x < b, to f(c) jest maksimum
lokalnym funkcji

f w przedziale (a, b).
Jeśli f ′ (x) < 0 dla a < x < c i f ′ (x) > 0

dla c < x < b, to f(c) jest minimum

lokalnym funkcji

f w przedziale (a, b).
Jeśli f ′(x) > 0 lub f ′ (x) < 0 dla

wszystkich x w (a, b) z wyjątkiem x = c, to f(c)

nie jest ekstremum lokalnym.

Jest natomiast punktem przegięcia.

Niech f będzie funkcją różniczkowalną

na przedziale (a, b) i

niech f ′ (c) = 0 dla pewnego punktu

c ∈ (a, b).
Jeśli f ″(c)< 0 to f(c) jest maksimum

lokalnym funkcji

f w przedziale (a, b).
Jeśli f ″ (c) > 0 to f(c) jest minimum

lokalnym funkcj

i f w przedziale (a, b).
Jeśli f ″ (c) = 0, to mamy przypadek

wątpliwy i należy

badać zachowanie pochodnej

pierwszego rzędu na lewo i na prawo

od c.

16. Monotoniczność funkcji a znak

jej pochodnej.

17. Definicja krzywej wklęsłej

i krzywej wypukłej.

Krzywa o równaniu

nazywa się

wypukłą w przedziale (a, b),

jeżeli jest

położona nad styczną

poprowadzoną do niej

w dowolnym punkcie o

odciętej z tego przedziału.

Krzywa o równaniu

nazywa

się wklęsłą w przedziale (a, b),

jeżeli jest

położona pod styczną

poprowadzoną do

niej w dowolnym punkcie o

odciętej z tego przedziału.

18. Definicja punktu przegięcia krzywej.

Punkt
gdzie

nazywamy

punktem przegięcia krzywej o równaniu

jeżeli krzywa ta jest:

wypukła w sąsiedztwie

i wklęsła w sąsiedztwie

wklęsła w sąsiedztwie

i wypukła w sąsiedztwie

19.

20. Warunek konieczny i dostateczny

istnienia punktu przegięcia krzywej.

Warunkiem koniecznym na to, a

by punkt

był

punktem przegięcia krzywej o

równaniu

o jest

Uwaga. Warunek ten nie

jest wystarczający

, na przykład dla funkcji

druga pochodna

, ale

punkt

nie jest

punktem przegięcia wykresu tej funkcji.

Twierdzenie (warunek

dostateczny

istnienia punktu przegięcia): Niech

i

Jeżeli druga pochodna

i

przechodząc przez punkt

zmienia znak, to wykres funkcji

ma punkt

przegięcia w

.

21. Definicja funkcji

pierwotnej.

Funkcję F(x) nazywamy

funkcją pierwotną funkcji

f(x) w przedziale X, jeżeli

dla każdego

spełniony jest warunek

Jeżeli przedział X jest

jedno- lub obustronnie

domknięty, to pochodną

w

każdym z należących do

niego końców

rozumiemy jako

odpowiednią pochodną

jednostronną.

22. Twierdzenie o funkcjach

pierwotnych.

Jeżeli funkcja F jest funkcją

pierwotną funkcji

f w przedziale X, to:

• funkcja

• 
  

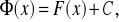
• gdzie C - stała, jest także funkcją

• pierwotną funkcji f w przedziale X,

• każdą funkcję pierwotną
  

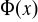
• funkcji f w przedziale X

• można przedstawić w

• postaci sumy
  

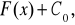
• gdzie
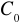
  jest stałą

• odpowiednio dobraną dla
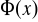
  i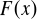
  .

Wniosek: Jeżeli F jest funkcją

pierwotną funkcji f w

przedziale X, to suma

(C - stała),

przedstawia wszystkie funkcje

pierwotne funkcji f w tym przedziale.

23. Twierdzenie o całkowaniu

przez części dla całki nieoznaczonej.

Jeżeli funkcje f i g mają w

pewnym przedziale X ciągłe pochodne , to

dla każdego
.

Wzory rekurencyjne:

1)

gdy

2)

gdy

3)

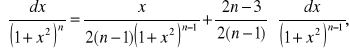
gdy

24. Twierdzenie o całkowaniu przez

podstawianie dla całki nieoznaczonej.

Jeżeli funkcja
jest

różniczkowalna w przedziale

i odwzorowuje ten

przedział na przedział
, w

którym funkcja f(t) jest całkowalna,

to zachodzi wzór

dla
.

25. Twierdzenie o całce oznaczonej z

funkcji ciągłej.

Niech

będzie ciągła oraz niech F będzie

jej funkcją pierwotną w przedziale

Całką

oznaczoną z

funkcji f w przedziale

nazywamy liczbę

,

co zapisujemy

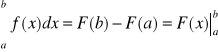
Liczby a i b nazywamy odpowiednio

dolną i górną granicą całkowania.

26. Twierdzenie o całkowaniu

przez części dla całek oznaczonych.

Jeżeli funkcje f i g mają ciągłe

pochodne w
, to

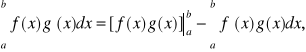
Gdzi

27. Twierdzenie o całkowaniu

przez podstawianie dla całek oznaczonych.

Jeżeli funkcja
ma ciągłą pochodną

w przedziale
,

funkcja
jest ciągła w zbiorze

wszystkich wartości, jakie przyjmuje

funkcja
w
, to

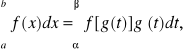
gdzie
.

---