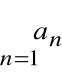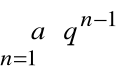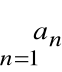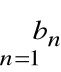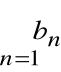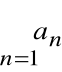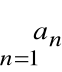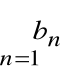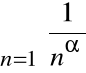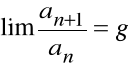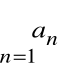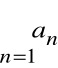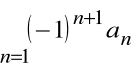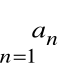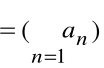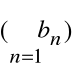WYKŁAD 2

SZEREGI LICZBOWE

Szereg liczbowy

Niech
oznacza ciąg liczbowy

który może być zbieżny albo rozbieżny.

Ciąg sum częściowych oznacza ciąg liczbowy

którego n-ty wyraz jest sumą n początkowych wyrazów ciągu

Mamy więc:

……………….

Ogólnie: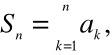
dla każdego naturalnego n.

Przykład

Niech ciąg
o n-tym wyrazie:

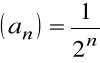
Ciąg
jest ciągiem sum:

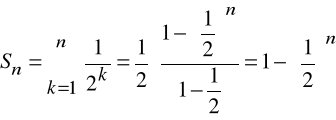
Ciąg
jest więc w tym przypadku następujący:

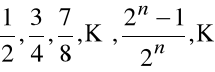
Definicja

Ciąg
sum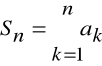

nazywamy szeregiem liczbowym i oznaczamy symbolem

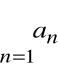
Zamiast tego symbolu piszemy także

Definicję szeregu liczbowego można wyrazić za pomocą równości:

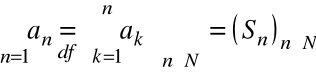
Definicja

• Liczby
  

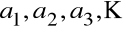
nazywamy wyrazami szeregu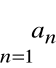
.

Szereg ma nieskończenie (przeliczalnie) wiele wyrazów, niekoniecznie różnych.

• Wyraz n-ty ciągu
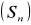
  , określony wzorem

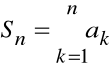
nazywamy n-tą sumą częściową szeregu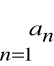
.

Wyraz ten jest sumą n początkowych wyrazów tego

szeregu.

Szereg jest ciągiem swoich sum częściowych
.

Uwaga

• Z określenia szeregu liczbowego
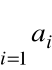
  wynika,

że jest to pewien ciąg liczbowy.

Definicja

Szereg liczbowy nazywamy zbieżnym, jeżeli ciąg jego sum częściowych jest zbieżny do granicy właściwej

natomiast rozbieżnym w przypadku przeciwnym.

Definicja

Granicę
nazywamy sumą szeregu.

Szereg zbieżny ma sumę,

natomiast szereg rozbieżny nie ma sumy.

Zamiast
piszemy też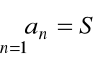

Należy jednak pamiętać, że:

szereg i suma szeregu są to pojęcia różne,

więc równość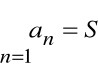
ma charakter umowny.

Przykład

Szereg: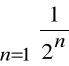
,

Czyli: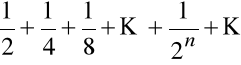

jest zbieżny, ponieważ jego ciąg sum częściowych, którego n-tym wyrazem jest:

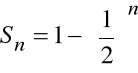
ma granicę właściwą:

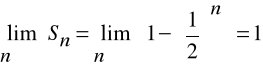
Suma szeregu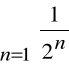
jest równa jedności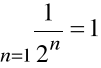
.

1/2

1

1/8

1/4

1/16 itd.

Przykład

Szereg:

jest rozbieżny, ponieważ n-ty wyraz ciągu jego sum częściowych

więc
nie istnieje.

Przykład

Zbadać zbieżność szeregu: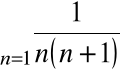

Wyraz n-ty ciągu sum częściowych tego szeregu można przekształcić następująco:

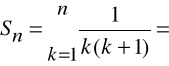
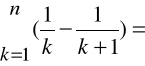
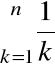
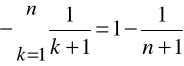
Stąd:

a więc rozpatrywany szereg jest zbieżny i jego suma wynosi 1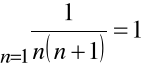

Definicja

Jeżeli w szeregu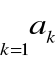
pominiemy n początkowych wyrazów, to otrzymamy szereg

R_n =

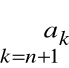
który nazywamy n-tą resztą R_n szeregu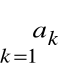
.

Twierdzenie

Szereg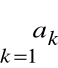
i szereg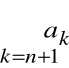

mają tę właściwość, że dla każdego n

obydwa są zbieżne albo obydwa są rozbieżne.

Tzn:

Jeśli w szeregu zbieżnym (albo rozbieżnym) pominiemy pewną liczbę początkowych wyrazów, to otrzymamy szereg zbieżny (albo odpowiednio - rozbieżny).

Definicja

Szereg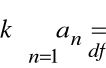

przy czym k oznacza dowolną liczbę.

Definicja

Szereg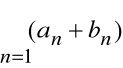

nazywamy sumą szeregów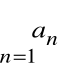
i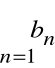
.

Zbieżność szeregów zapewnia zbieżność ich sumy, ale twierdzenie odwrotne nie zachodzi.

Przykład

,

który jest sumą dwóch szeregów rozbieżnych:

oraz
.

Uwaga

Jeżeli szeregi:
i

są zbieżne oraz sumy ich wynoszą odpowiednio A i B, to

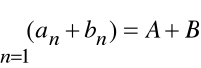
oraz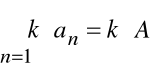

gdzie k jest dowolną liczbą.

Warunek konieczny zbieżności szeregu

Jeżeli szereg jest zbieżny, to

Dowód

Zauważmy, że

gdzie
i
oznaczają odpowiednio:

(n-1)-szą i n-tą resztę szeregu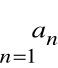
.

Szereg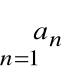
jest zbieżny, więc:

i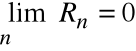
,

a zatem: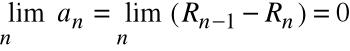

Warunek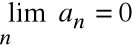
nie jest warunkiem wystarczającym zbieżności szeregu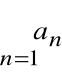
.

Przykład

Szereg rozbieżny spełniający warunek

(szereg harmoniczny)

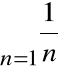
, czyli szereg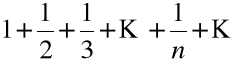

Dowód (nie wprost)

rozbieżności szeregu harmonicznego

Załóżmy, że szereg harmoniczny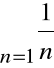
jest zbieżny.

Dla każdego N zbieżny byłby wtedy także szereg:

=

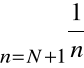
przy czym mielibyśmy:
,

Pokażemy, że założenie takie prowadzi do sprzeczności:

Ponieważ wyrazy powyższych szeregów są dodatnie, więc

,

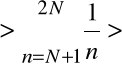
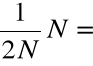
a zatem dla każdego N jest spełniony warunek

Jest to sprzeczne z założeniem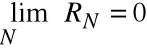
.

Zatem założenie o zbieżności szeregu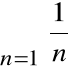
jest fałszywe.

Szereg harmoniczny jest więc rozbieżny, cnd.

Szereg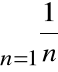
nazywa się harmoniczny dlatego, że każdy jego wyraz (z wyjątkiem pierwszego) jest średnią

harmoniczną wyrazu poprzedniego i wyrazu następnego,

tzn. że odwrotność n-tego wyrazu
jest równa

połowie sumy odwrotności wyrazów: (n-1)-go i (n+1)-go.

Zbieżność szeregu geometrycznego

Szereg geometryczny jest zbieżny wtedy i tylko wtedy, gdy lub . Jego sumą jest wówczas liczba

Badanie zbieżności szereg geometrycznego

Zbieżność szeregu geometrycznego.

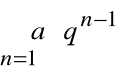
, czyli
.

• Jeżeli
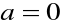
  , to szereg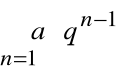
  jest oczywiście zbieżny i jego suma równa się 0.

• Jeżeli
  , to rozróżniamy dwa przypadki:

1. 
   

Ponieważ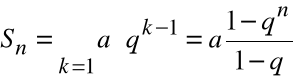
,

więc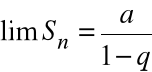
. Szereg geometryczny jest w tym przypadku zbieżny i jego sumą jest liczba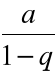
.

2.

Ponieważ dla każdego naturalnego n: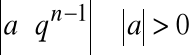
,

więc szereg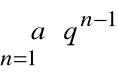
nie spełnia w tym przypadku warunku koniecznego zbieżności, a zatem jest rozbieżny.

Kryteria zbieżności szeregów o wyrazach nieujemnych

• Kryterium ograniczenia z góry

Jeżeli: ciąg sum częściowych Sn szeregu o wyrazach an ≥ 0 jest ograniczony z góry Sn ≤ M, to: szereg ten jest zbieżny (jako ciag monotoniczny i ograniczony )

Przykład

Zbadać zbieżność szeregu: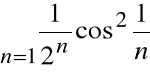

Wyrazy szeregu:
są dodatnie.

Ponieważ dla każdego n:

,

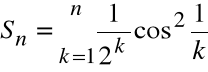
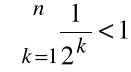
więc ciąg
jest ograniczony z góry liczbą 1

a zatem szereg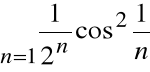
jest zbieżny.

Kryterium porównawcze

Jeżeli: wyrazy szeregów oraz są nieujemne, to: zbieżność szeregu zapewnia zbieżność szeregu rozbieżność szeregu zapewnia rozbieżność szeregu

Kryterium porównawcze można wykorzystać zarówno

• w dowodzie zbieżności,

• w dowodzie rozbieżności szeregu liczbowego

Przykład

Szereg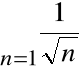
jest rozbieżny, ponieważ dla każdego n

(szereg harmoniczny)

a szereg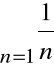
jest rozbieżny.

Przykład

Szereg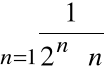
jest zbieżny, ponieważ dla każdego n

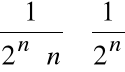
(szereg geometryczny)

a szereg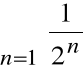
jest zbieżny.

Szereg harmoniczny i szereg geometryczny przyjmujemy często za szeregi porównawcze.

Równie często przyjmowany jest za szereg porównawczy tzw. szereg Dirichleta

,

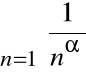
gdzie
oznacza dowolną liczbę rzeczywistą.

Zbieżność szeregu Dirichleta

Szereg jest: rozbieżny dla , zbieżny dla

Przykład

Zbadać zbieżność szeregu: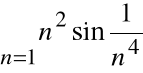
.

Ponieważ dla każdego naturalnego n:

,

przy czym szereg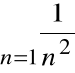
jest zbieżny,

więc szereg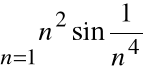
jest także zbieżny

na podstawie kryterium porównawczego.

Przykład

Zbadać zbieżność szeregu: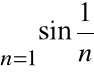
.

Ponieważ dla każdego naturalnego n: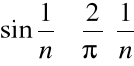
,

przy czym szereg: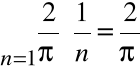

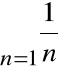
jest rozbieżny, więc szereg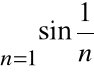
jest także rozbieżny.

Przykład

Zbadać zbieżność szeregu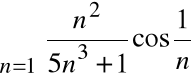
.

Ponieważ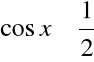
dla
, a ponadto
,

więc dla każdego n :

,

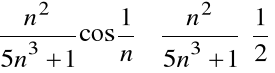
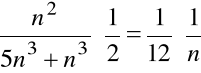
a zatem szereg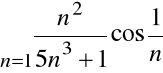
jest rozbieżny.

Kryterium d'Alemberta (ilorazowe)

Jeżeli istnieje granica (właściwa albo niewłaściwa) , to szereg o wyrazach dodatnich jest zbieżny, gdy , rozbieżny, gdy . (Jeśli g = 1, wówczas kryterium to nie rozstrzyga o zbieżności lub rozbieżności szeregu)

Przykład

Zbadać zbieżność szeregu: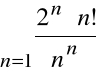
.

Mamy tu: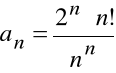
,

,

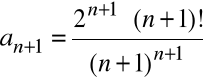
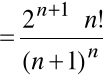
Więc: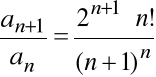

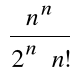
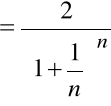
Stąd: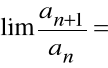

,

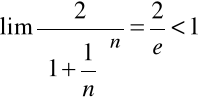
a więc szereg: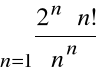

jest zbieżny na podstawie kryterium d'Alemberta.

Przykład

Zbadać zbieżność szeregu: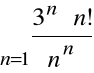
.

Postępując tak, jak w przykładzie poprzednim,

otrzymamy: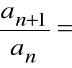

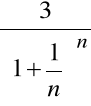
Stąd: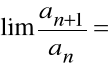

,

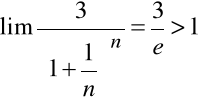
a więc szereg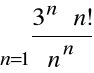
jest rozbieżny

na mocy kryterium d'Alemberta.

Kryterium Cauchy'ego (pierwiastkowe)

Jeżeli istnieje granica (właściwa albo niewłaściwa) , to szereg o wyrazach nieujemnych jest zbieżny, gdy , rozbieżny, gdy . (Jeśli g = 1, wówczas kryterium to nie rozstrzyga o zbieżności lub rozbieżności szeregu)

Przykład

Zbadać zbieżność szeregu: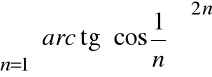
.

Mamy tu: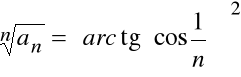

Stąd: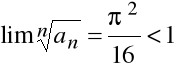
,

a więc szereg: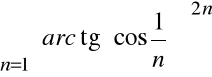
jest zbieżny.

Szeregi o wyrazach dowolnych

Definicja

Szereg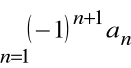
;

nazywamy szeregiem naprzemiennym.

Wyrazy tego szeregu są na przemian dodatnie i ujemne.

• Kryterium Leibniza.

Jeżeli ciąg jest nierosnący, tzn. oraz to szereg naprzemienny jest zbieżny

Przykład

Szereg: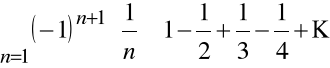

jest zbieżny, ponieważ spełnia założenia kryterium Leibniza:

• jest to szereg naprzemienny,
  

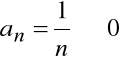
• dla każdego n mamy
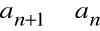
  , gdyż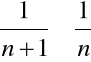
  .

Można udowodnić, że suma S szeregu

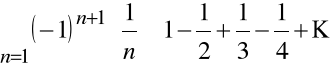
równa jest
.

Przykład :

Szereg:

jest zbieżny na podstawie kryterium Leibniza.

Definicja

Szereg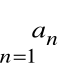
nazywamy bezwzględnie zbieżnym,

jeżeli jest zbieżny szereg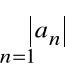
.

Definicja

Szereg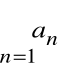
nazywamy warunkowo zbieżnym,

jeżeli jest zbieżny szereg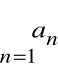

ale szereg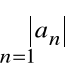
jest rozbieżny.

Przykład

Szereg:

jest zbieżny na mocy kryterium Leibniza.

Ponieważ szereg: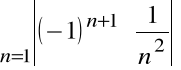

,

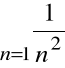
jest zbieżny, więc szereg:

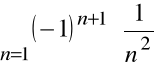
jest zbieżny bezwzględnie.

• Kryterium zbieżności bezwzględnej

Jeśli szereg jest zbieżny bezwzględnie to jest zbieżny.

Twierdzenie odwrotne nie jest prawdziwe:

Przykład:

Szereg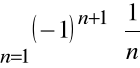

jest zbieżny na mocy kryterium Leibniza.

Natomiast szereg wartości bezwględnych:

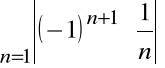
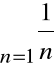
jest rozbieżny.

Zatem szereg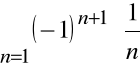
jest zbieżny warunkowo

Przykład

Zbadać zbieżność szeregu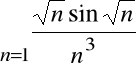
.

Rozważmy szereg utworzony z bezwzględnych wartości wyrazów szeregu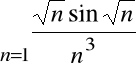
:

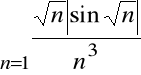
do którego możemy zastosować kryterium porównawcze.

Ponieważ dla każdego naturalnego n

,

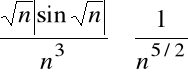
więc szereg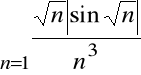
jest zbieżny.

Na podstawie twierdzenia wynika stąd, że szereg

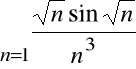
jest zbieżny i to bezwzględnie.

Podsumowując metody badania zbieżności szeregów

możemy dokonać następującego zestawienia:

Warunek konieczny
szereg rozbieżny warunek dostateczny
Warunek dostateczny
Grupa A - wyrazy nieujemne	Grupa B - wyrazy dowolne
Kryterium ograniczenia z góry	Kryterium Leibniza
Kryterium porównawcze
Kryterium ilorazowe		Kryterium zbieżności bezwzględnej
Kryterium pierwiastkowe

Przy badaniu zbieżności bewzględnej mamy do czynienia z szeregiem o wyrazach nieujemnych zatem stosujemy kryteria zbieżnosci dla grupy A szeregów.

Podstawowe konsekwencje wynikające ze zbieżności warunkowej i bezwzględnej podają poniższe twierdzenia:

Twierdzenie o szeregu zbieżnym warunkowo (Riemanna)

Odpowiednie permutacje wyrazów pozwalają uzyskać: a) szereg zbieżny do zadanej z góry sumy b) szereg rozbieżny do +∞ lub -∞ c) szereg nie posiadający sumy

Dzielenie wyrazów na grupy,obliczanie sumy wyrazów w grupach i tworzenie nowych sum częściowych nie zmienia sumy szeregu (prawo łączności sumy szeregu)

Twierdzenie o szeregu zbieżnym bezwzględnie (zasada dowolnego grupowania wyrazów)

Dowolne permutacje nie zmieniaja sumy tego szeregu (prawo przemienności sumy szeregu)

Dowolne grupowania wyrazów nie zmieniają sumy tego szeregu (prawo łączności sumy szeregu)

Ogólniej: prawo przemienności i łączności jest prawdziwe dla szeregów o wyrazach nieujemnych.

Mnożenie szeregów

Definicja

Szereg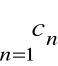
o wyrazach

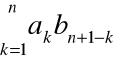
nazywamy iloczynem Cauchy'ego szeregów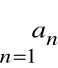
i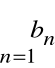
.

Uwaga:

Zbieżność szeregów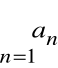
i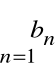
nie zapewnia zbieżności ich iloczynu Cauchy'ego.

Można tak dobrać dwa szeregi warunkowo zbieżne, żeby ich iloczyn Cauchy'ego był szeregiem rozbieżnym.

Twierdzenie (o zbieżności iloczynu szeregów)

Jeżeli: oba szeregi i są zbieżne oraz co najmniej jeden z nich jest bezwzględnie zbieżny, to: ich iloczyn jest zbieżny, przy czym

Przykład

Szereg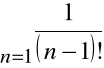
jest bezwzględnie zbieżny.

Obliczymy iloczyn Cauchy'ego

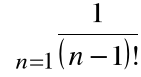
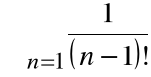
Mamy tu

=

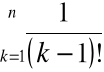
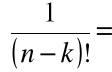
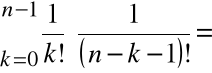
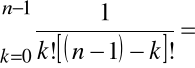
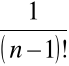
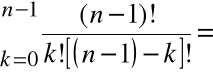
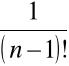
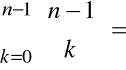
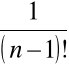
Stąd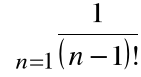

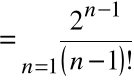
Analiza Matematyczna I

1

8