LICZBY ZESPOLONE
Niech a i b oznaczają dowolne elementy niekoniecznie należące do tego samego zbioru. Symbolem (a,b) oznaczać będziemy parę uporządkowaną, złożoną z tych elementów, przy czym a nazywamy poprzednikiem, zaś b następnikiem pary.
Dwie pary (a,b) i (c,d) uważamy za równe wtedy i tylko wtedy, gdy mają identyczne poprzedniki i następniki.
Zbiór wszystkich uporządkowanych par (a,b), których poprzednik należy do zbioru A, zaś następnik do zbioru B, nazywamy iloczynem (produktem) kartezjańskim zbiorów A, B i oznaczamy ![]()
Liczbami zespolonymi nazywamy uporządkowane pary liczb rzeczywistych, dla których określamy równość, dodawanie i mnożenie w następujący sposób
![]()
![]()
Liczbę (0,0) nazywamy zerem zespolonym, a liczbę (1,0) jedynką zespoloną.
Jeżeli z1=(x1,y1) i z2=(x2,y2) są dowolnymi liczbami zespolonymi, to różnicą z1-z2 nazywamy taką parę z=(x,y), która jest jedynym rozwiązaniem równania:
z1=z2+z
tzn.
(x1,y1)=(x2,y2)+(x,y).
Jeżeli z1=(x1,y1) i z2=(x2,y2) są dowolnymi liczbami zespolonymi, przy czym z2≠(0,0), to ilorazem z1/z2 nazywamy taką parę z=(x,y), która jest jedynym rozwiązaniem równania
z1=z2∙z,
tzn.
(x1,y1)=(x2,y2)∙(x,y)
Liczbę zespoloną (0,1) nazywać będziemy jednostką urojoną i oznaczać małą literą i tzn. i=(0,1)
i2=-1
Płaszczyznę, której każdy punkt jest obrazem geometrycznym liczby zespolonej, nazywamy płaszczyzną Gaussa. Oś Ox na płaszczyźnie Gaussa jest obrazem zbioru liczb rzeczywistych i nosi nazwę osi rzeczywistej, zaś oś Oy - obrazem zbiory liczb czysto urojonych i nosi nazwę osi urojonej.
Modułem liczby zespolonej z=x+iy nazywamy nieujemną liczbę rzeczywistą ![]()
określoną wzorem:
![]()
Dwie liczby zespolone, których części rzeczywiste są równe, a części urojone są liczbami przeciwnymi, nazywamy liczbami sprzężonymi.
Argumentem liczby zespolonej z=x+iy nazywamy każdą liczbę rzeczywistą φ spełniającą warunki:
![]()
Ten spośród argumentów liczby z, który spełnia warunek:
-π<Argz≤π,
będziemy nazywać argumentem głównym i oznaczać go arg z.
Tw. Jeżeli z1=r1(cosφ1+isinφ1), a z2=r2(cosφ2+isinφ2), to:
z1∙z2=r1∙r2(cos(φ1+ φ2)+isin(φ1+ φ2)),
a przy z2≠0
![]()
Niech ![]()
, wówczas:
1˚ przyjmijmy z1=z,
2˚ jeżeli dla liczby ![]()
została już określona potęga zn, to dla następnika n+1 liczby n przyjmujemy: zn+1=zn∙z
Tw. Jeżeli z=r(cosφ+isinφ), to:
![]()
Wzór Moivre'a:
![]()
Każdą liczbę zespoloną w, której n-ta potęga równa się liczbie zespolonej z, nazywamy pierwiastkiem n-tego stopnia z liczby z i piszemy:
![]()
Tw. Każda liczba zespolona z≠0 posiada dokładnie n różnych pierwiastków określonych następującymi wzorami:
![]()
gdzie φ oznacza argument (dowolny) liczby z, a ![]()
arytmetyczny pierwiastek stopnia n z modułu liczby z, tzn. ![]()
Tw.: Równanie Wn(x) = 0, gdzie Wn(x) jest wielomianem stopnia n, ma dziedzinę liczb zespolonych dokładnie n pierwiastków, przy czym pierwiastek k-krotny należy liczyć k razy.
Jeżeli równanie Wn(x) = 0 o współczynnikach rzeczywistych a0, a1, ... , an ma pierwiastek xk = αk + iβk, to xk = αk - iβk też jest pierwiastkiem tego równania.
Zasadnicze twierdzenie algebry
W zbiorze liczb zespolonych każdy wielomian Wn (z) stopnia n>=1 posiada przynajmniej jeden pierwiastek, zatem w zbiorze liczb zespolonych:
Wn (z)=a0(z-z1)(z-z2)…(z- zn)
zi mogą się powtarzać.
Macierz to prostokątna tablica liczb. Mówimy, że mamy do czynienia z macierzą A jeżeli każdej parze (i, k) zostanie przyporządkowana liczba aik.
(i, k) -> aik
i= 1, …, m
k= 1, …, n
A= [aik]mxn (m- liczba wierszy, n- liczba kolumn)
a11 a12 … a1k … a1n
a21 a22 … a2k … a2n
A= ………………………………………….
ai1 ai2 … aik … ain
………………………………………….
an1 an2 … ank … ann
Jeśli m=n to macierz A nazywamy kwadratową stopnia n.
Z macierzą kwadratową związane jest pojęcie wyznacznika.
[a11] |a11| = (z def.) a11
a11 a12 a11 a12
a21 a22 a21 a22 =(z def.) a11*a22 - a21*a12
a11 a12 a13 a11 a12 a13
a21 a22 a23 a21 a22 a23 a22 a23 a21 a23
a31 a32 a33 a31 a32 a33 =(z def.) a11 a32 a33 - a12 a31 a33 +
a21 a22
a13 a31 a32 =
=a11(a22*a33-a23*a32)-a12(a21*a33-a23*a31)+a13(a21*a32-a31*a22)
Mik - minor (podwyznacznik) danego wyznacznika, powstaje z danego wyznacznika przez skreślenie i-tego wiersza i k-tej kolumny.
Aik=(-1)i+k Mik - dopełnienie algebraiczne elementu Aik.
Własności wyznaczników:
wartość wyznacznika nie zmieni się jeśli zamieni się wiersze na kolumny;
jeżeli zamieni się 2 równoległe linie to wartość wyznacznika zmieni znak;
jeżeli w wyznaczniku są 2 identyczne linie to wartość wyznacznika = 0;
jeżeli w wyznaczniku pewną linię pomnożymy przez k, to wartość wyznacznika zostanie pomnożona przez liczbę k;
jeżeli w wyznaczniku pewna linia jest sumą 2 składników to wartość tego wyznacznika jest równa sumie wartości wyznaczników przy czym w pierwszym wyznaczniku jest pierwszy składnik sumy a w drugim drugi składnik sumy przy niezmienionych pozostałych elementach;
wartość wyznacznika nie zmieni się jeżeli do pewnej linii dodamy inną linę pomnożoną przez pewną liczbę.
rozwinięcie wyznacznika względem dowolnej kolumny lub wiersza ( rozwinięcie Laplace' a) :
n
W=ai1*Ai1+ai2*Ai2+…+aik*Aik+…+ain*Ain=Σ aikAik
k=1
Tw.
Jeżeli wyznacznik układu równań liniowych W różne od 0 to:
x1=![]()
, x2=![]()
, xn=![]()
Wzory Cramera
Wi powstaje z wyznacznika W przez zastąpienie i-tej kolumny kolumną wyrazów wolnych.
Rząd macierzy- stopień największego wyznacznika, który można wybrać z macierzy.
Do wyznaczenia rzędu macierzy służy twierdzenie:
Rząd macierzy nie zmieni się jeżeli przestawimy linie macierzy, pomnożymy linię przez liczbę różną od 0, dodamy do linii inną linię pomnożoną przez liczbę.
Jeżeli układ równań posiada dokładnie 1 rozwiązanie (x1, …, xn) to mówimy, że jest to układ oznaczony.
Jeżeli układ posiada nieskończenie wiele rozwiązań to jest to układ nieoznaczony.
Brak rozwiązań - układ sprzeczny.
Twierdzenie Kroneckera - Capellie' go
Układ równań m x n posiada rozwiązanie wtw, gdy rząd macierzy r(M)=r(M'). Jeżeli wspólna wartość rzędu macierzy jest równa r=n to układ równań jest oznaczony ( posiada dokładnie jedno rozwiązanie).
Jeżeli r<n to układ jest nieoznaczony i posiada nieskończenie wiele rozwiązań zależnych od n-r parametrów.
Gdy rzędy macierzy są równe r(M) różne od r(M') to układ jest sprzeczny.
Układ równań jednorodnych - układ ten posiada zawsze rozwiązanie.
Układ posiada rozwiązanie niezerowe, gdy r(M)<n ( r(M) - rząd macierzy, n - liczba niewiadomych)
Kąt na płaszczyźnie między wektorami
Kątem zwykłym między wektorami a, b, którego miara spełnia warunek 0![]()
φ ![]()
П na płaszczyźnie określamy kierunek obrotu jako przeciwny do ruchu wskazówek zegara.
Kątem skierowanym nazywamy każdy obrót, który sprowadza ramię jednego do zgodnego pokrycia z ramieniem drugim, w kierunku dodatnim.
Miara rzutu wektora a na oś X jest równa iloczynowi długości tego wektora i cosinusa kąta zwykłego między wektorem a osią.
Iloczyn skalarny 2 wektorów
Iloczynem skalarnym 2 wektorów nazywamy liczbę, która jest równa długości tych wektorów i cosinusa kąta między nimi zawartego.
a ͦ b = |a| * |b| * cosφ
φ - kąt zwykły między wektorami a i b.
Własności iloczynu skalarnego:
a ͦ b = b ͦ a
a ͦ b = 0 <=> a prostopadłe do b (a,b niezerowe)
a ͦ a = |a|*|a|*cos0=|a|2
l(a ͦ b) = la*b=a*lb
a ͦ (b+c)= ab+Ac
wyrażanie iloczynu skalarnego we współrzędnych
a= [ax, ay, az] , b= [bx, by, bz]
a ͦ b = axbx + ayby + azbz
(axi+ayj+azk)(bxi+byj+bzk) = axbx + ayby + azbz
Iloczyn wektorowy
Iloczynem wektorowym 2 wektorów niezerowych a i b nazywamy taki wektor w, który ma następujące własności:
|w| = |a| |b| sinφ
w prostopadły do a i b
a, b, w - sgodnie skrętna z przyjętym układem współrzędnych. w = a x b
Jeżeli jeden z wektorów jest zerowy to a x b = 0.
Własności iloczynu wektorowego:
a x b = - b x a
χ(a x b) = (χa) x b = a x (χb)
a x (b+c) = a x b + a x c
a x b = 0 a || b dla a,b niezerowych
Zastosowanie :
|a x b| = |a| |b| sinφ = P
P = a * h = |a| |b| sinφ
P = ½ |a x b|
Iloczyn mieszany
a= [ax, ay, az]
b= [bx, by, bz]
c= [cx, cy, cz]
(a x b) ͦ c => iloczyn mieszany ( JEST LICZBĄ)
i j k
a x b = ax ay az
bx by bz
(a x b) ͦ c = cx cy cz
ax ay az
bx by bz
Interpretacja geometryczna iloczynu mieszanego
Vr= P * h
P = ( a x b)
a x b = q
(a x b) ͦ c = q ͦ c = |q| |c| * cosφ = +/- |q| h = +/- Vr
Vr = +/- (a x b) ͦ c
Vr = | (a x b)c|
a, b, c leżą w jednej płaszczyźnie wtw, gdy ( a x b)c = 0
Równanie ogólne płaszczyzny
Ax + By + Cz + D = 0
Jeżeli D = 0 to płaszczyzna przechodzi przez początek układu współrzędnych.
Jeżeli B = 0 to wektor n prostopadły do OY płaszczyzna || do OY
Jeżeli A = 0 to płaszczyzna || do OX
Jeżeli A i B = 0 płaszczyzna || do OXY
Równanie odcinkowe:
![]()
a, b, c - współrzędne punktów przecięcia płaszczyzny z osiami układów.
Prosta - równanie kanoniczne :
![]()
Postać parametryczna:
x = mt + x0
y = nt + y0
z= pt + z0
Równanie krawędziowe :
A1x + B1y + C1z + D1 = 0
A2x + B2y + C2z + D2 = 0 ~ ( ![]()
)
ANALIZA
Niech A jest zbiorem liczbowym np. liczb R.
Kresem górnym zbioru A nazywamy największą liczbę tego zbioru ( o ile ona istnieje) lub najmniejszą z ograniczających ten zbiór z góry.
Liczbę k - nazywamy kresem dolnym zbioru A jeśli jest to liczba najmniejsza ( o ile istnieje) lub największa z ograniczających ten zbiór z dołu.
W analizie przyjmuje się tzw. pewnik ciągłości - każdy zbiór liczb R (niepusty) i ograniczony z góry posiada kres górny.
g, Ɛ > 0 ; O(g, Ɛ) = ( g-Ɛ, g+ Ɛ)
Otoczeniem liczby g o promieniu Ɛ (Ɛ > 0) nazywamy przedział ( g-Ɛ, g+ Ɛ).
Sąsiedztwo - otoczenie bez punktu g : O(g, Ɛ)\{g} = S(g, Ɛ)
Własności ciągów zbieżnych:
Jeżeli ciąg {an} jest zbieżny, to ma on tylko jedną granicę.
Jeżeli ciąg {an} jest zbieżny, to jest on ograniczony.
Jeżeli ciąg {an} jest monotoniczny i ograniczony, to jest on zbieżny
Twierdzenie o 3 ciągach.
Jeżeli dane są trzy ciągi {an},{bn},{cn} ; ( ![]()
) dla n >δ i ![]()
to:
![]()
.
Twierdzenie o zachowaniu nierówności:
Jeżeli ![]()
; ![]()
an![]()
bn ; n > δ to g1![]()
g2
Tw. o działaniach arytmetycznych na granicach ciagu.
Jeżeli ![]()
, ![]()
to :
![]()
- analogicznie odejmowanie, mnożenie i dzielenie ( przy czym w dzieleniu bn różne od 0).
SZEREGI LICZBOWE
Niech {an} będzie pewnym nieskończonym ciągiem liczbowym, {Sn} zaś ciągiem, którego n-tym wyrazem jest suma n początkowych wyrazów ciągu {an}. Ciąg:
![]()
,
nazywamy szeregiem liczbowym nieskończonym i symbolicznie oznaczamy:
![]()
lub a1+a2+…+an+…
Szereg liczbowy nazywamy zbieżnym, jeżeli jego ciąg sum częściowych {Sn} jest zbieżny do granicy właściwej S.
Warunek konieczny zbieżności szeregu
Tw. Jeżeli szereg
a1+a2+…+an+…=![]()
jest zbieżny, to ![]()
.
Tw. (kryterium porównawcze). Jeżeli istnieje taka liczba naturalna n0, że dla każdego n>n0 jest spełniona nierówność 0≤an≤bn, to:
1˚ ze zbieżności szeregu ![]()
wynika zbieżność szeregu ![]()
2˚ z rozbieżności szeregu ![]()
wynika rozbieżność szeregu ![]()
Tw. (kryterium d'Alemberta). Niech ![]()
będzie szeregiem o wyrazach dodatnich i załóżmy, że istnieje granica ![]()
(właściwa lub niewłaściwa). Wówczas:
1˚ jeżli 0≤q<1, to szereg ![]()
jest zbieżny,
2˚ jeżeli q>1, to szereg ![]()
jest rozbieżny,
3˚ jeżeli q=1, to szereg może być zbieżny lub rozbieżny (szereg nie reaguje na kryterium d'Alemberta - nie rozstrzyga).
Tw. (kryterium Cauchy'ego). Niech ![]()
będzie szeregiem o wyrazach nieujemnych i załóżmy, że istnieje granica ![]()
(właściwa lub niewłaściwa). Wówczas:
1˚ jeżli 0≤q<1, to szereg ![]()
jest zbieżny,
2˚ jeżeli q>1, to szereg ![]()
jest rozbieżny,
3˚ jeżeli q=1, to szereg może być zarówno zbieżny jak i rozbieżny (szereg nie reaguje na kryterium Cauchy'ego - nie rozstrzyga).
Szereg ![]()
, gdy ![]()
, nazywamy szeregiem Dirichleta.
Tw. Szereg Dirichleta ![]()
jest zbieżny dla α>1 i rozbieżny dla α≤1.
Szeregi o wyrazach dowolnych.
Szereg ![]()
nazywamy bezwzględnie zbieżnym, jeżeli zbieżny jest szereg
![]()
.
Jeżeli szereg ![]()
jest zbieżny, a szereg ![]()
rozbieżny to szereg ![]()
nazywamy warunkowo zbieżnym.
Tw. Jeżeli szereg ![]()
jest zbieżny to ![]()
też jest zbieżny.
Szereg: ![]()
lub ![]()
nazywamy szeregiem naprzemiennym jeżeli:
1˚ ![]()
,
2˚ an+1<an
3˚ ![]()
.
Tw. Leibniza.
Każdy szereg naprzemienny jest zbieżny.
Jeżeli szereg bezwzględnej wartości jest zbieżny to nie badamy zbieżności warunkowej.
Jeżeli szereg wartość bezwzględnej jest rozbieżny to należy badać zbieżność warunkową (czyli zbieżność szeregu wyjściowego).
Funkcja złożona
Niech y=f(u) ; u![]()
U ;u=g(x) ; x![]()
X
y=f[g(x)] x![]()
g(x) - f. wewnętrzna, f(u) - f. zewnętrzna
Funkcja odwrotna
Jeżeli dla każdego x1, x2 ![]()
Df; x1 ![]()
x2 => f(x1) ![]()
f(x2) => F. różnowartościowa![]()
Niech y=f(x) jest funkcją różnowartościową, gdzie x ![]()
<a,b>, y![]()
<c,d>.
Ponieważ f. jest różnowartościowa, więc każdemu elementowi x ![]()
<a,b> odpowiada 1 i tylko 1 element y![]()
<c,d>.
Rozumowanie możemy odwrócić i y![]()
<c,d> przyporządkować x ![]()
<a,b>.
Możemy więc mówić o funkcji x=g(y) określonej na przedziale <c,d> o wartościach z przedziału <a,b>.
Funkcję g(y) nazywamy funkcją odwrotną do f(x).
Wykresy y=f(x), x=g(y)są identyczne.
Ponieważ zmienną niezależną zaznaczamy zwykle na osi poziomej i oznaczamy przez x, więc we wzorze x=g(y) dokonujemy zamiany zmiennych i otrzymujemy funkcję y=g(x), y![]()
<a,b>, x![]()
<c,d>.
Powoduje to, że wykres funkcji y=g(x)jest odbiciem symetrycznym wykresu y=f(x) względem dwusiecznej I i III ćwiartki układu.
Funkcje odwrotne do f. trygonometrycznych to funkcje cyklometryczne.
Szczególne właściwości funkcji liczbowych:
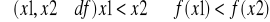
funkcja rosnąca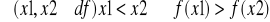
funkcja malejąca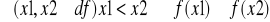
funkcja niemalejąca f. monotoniczne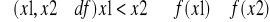
funkcja nierosnąca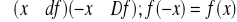
funkcja parzysta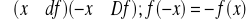
funkcja nieparzysta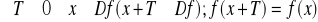
funkcja okresowa
Granica funkcji w nieskończoności :
A. Cauchy
B. Heine
Granica funkcji w punkcie x0:
A. Heine:
Jeżeli dla każdego ciągu xn spełniający postulaty 1º Λn xn ∈ X; 2º Λn xn ≠ xo; 3º limx→∞ xn=xo, odpowiadający ciąg {f(xn)} ma granicę równą g i granica ta nie zależy od wyboru ciągu {xn}, to nazywamy ją granicą funkcji f w punkcie xo.
B. Cauchy:
limx→∞=g Λε>0 Vδ>0 Λx∈Df 0<| x-xo | < δ ⇒ | f(x)-g|<ε.
Granice jednostronne
Jeżeli w def. Cauchy'ego dodamy warunek xn>xo (xn<xo), to taką granicę nazywamy granicą prawostronną (lewostronna) funkcji f w punkcie xo limx→xo+ f(x)=g ( limx→xo- f(x)=g ).
TW.: Funkcja f określona w pewnym zbiorze X zawartym w zbiorze liczb rzeczywistych. Po prawej i po lewej stronie punktu xo ma granicę zwykłą gdy obie granice jednostronne istnieją i są sobie równe.
Granica funkcji w nieskończoności:
Niech f będzie funkcją nieskończoną w przedziale nieokreślonym otwartym. Mówimy, że f→g (+∞; -,∞) gdy x→+∞ jeżeli dla każdego ciągu xn→+∞ ciąg {f(xn)} ma granicę równą g (+∞; -∞).
Asymptota pionowa
x0L
![]()
x0P
![]()
x=x0 - asymptota pionowa
Asymptota pozioma
Prosta y=b jest as. poziom. lewostronną (prawostronną) wykresu funkcji f, jeśli limx→-∞ f(x)=b (limx→+∞ =b).
Asymptota ukośna
Prosta o równaniu y=ax+b jest as. uk. prawostronna (lewostronna) wykresu funkcji y=f(x), jeżeli limx→+∞ [f(x)-(ax-b)]=0 (limx→-∞ [f(x)-(ax-b)]![]()
=0).
Jeżeli funkcja w +/-∞ posiada asymptotę poziomą to nie ma ukośnej.
Twierdzenia o działaniach arytmetycznych na granicach funkcji:
Jeżeli ![]()
, ![]()
to :
![]()
=g1+g2
Analogicznie mnożenie i dzielenie( przy czym w dzieleniu g2![]()
0.
Twierdzenie to jest też prawdziwe również przy x![]()
oraz dla granic jednostronnych.
Symbole nieoznaczone :
[0 * ![]()
], [![]()
], [1![]()
], [![]()
0 ], [00], [![]()
-![]()
], [![]()
]
Twierdzenie o granicy funkcji złożonej:
f[g(x)] = f(u); u=g(x)
![]()
; ![]()
to :
![]()
![]()
przy czym: g(x) ![]()
a dla x ![]()
S(x0)
Ważniejsze granice :
Ciągłość funkcji
Niech y=f(x) jest określona w sąsiedztwie punktu x0
Jeżeli:
istnieje wartość funkcji w x0, f(x0)
istnieje granica
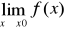
g=f(x0)
to mówimy, ze funkcja jest ciągła w punkcie x0.
Własności funkcji ciągłych :
Do funkcji ciągłych należą:
wielomiany
f. wymierne ( z wyjątkiem miejsc zerowych mianownika)
f. trygonometryczne ( sin, cos, tg, ctg w obszarze określoności)
f. wykładnicza
Zachodzą twierdzenia:
funkcja odwrotna do funkcji ciągłej jest funkcją ciągłą ( cyklometryczne, logarytmiczne, pierwiastkowe)
złożenie funkcji ciągłych jest funkcją ciągłą.
Funkcja jest ciągła w przedziale (a,b) jeśli jest ciągła w każdym punkcie tego przedziału.
Funkcja jest ciągła w przedziale <a,b> jeżeli jest ciągła w przedziale (a,b) a na końcach zachodzi jednostronna ciągłość.
Tw.
Suma, iloczyn, iloraz ( z wyjątkiem miejsc zerowych mianownika), różnica funkcji ciągłych są funkcjami ciągłymi.
Własności:
tw. o zachowaniu znaków
Jeżeli y=f(x) jest ciągła w otoczeniu punktu x0 i f(x0)>0, [f(x0)<0] to istnieje takie otoczenie punktu x0, że do wszystkich x z tego otoczenia zachodzi nierówność f(x)>0 [f(x)<0].
tw. Weierstrassa
Funkcją ciągłą w przedziale domkniętym osiąga swój kres dolny i górny.
tw. Darboux ( tw. o przechodzeniu funkcji przez wartości pośrednie)
Jeżeli y=f(x) określona w <a,b>; f(a)![]()
f(b) i y0 ![]()
, f(a) < y0 < f(b) to istnieje c, że c ![]()
(a,b), f(c)=y0.
Wniosek:
Jeżeli f(a)*f(b)<0 to istnieje c![]()
(a,b), że f(c) =0.
Pochodna funkcji
Niech y=f(x) jest określona w otoczeniu punktu x0
A(x0, f(x0))
B(x0+Δx, f(x0+Δx))
Prosta łącząca A i B nazywamy sieczną.
Równanie kierunkowe prostej ( siecznej przechodzącej przez A i B ) :
y-f(x0)=a(x-x0)
![]()
- iloraz różnicowy w punkcie x0
W interpretacji geometrycznej iloraz różnicowy to tangens nachylenia siecznej do dodatniego kierunku OX:
tgβ=![]()
Niech B![]()
A po krzywej. Sieczna wówczas przechodzi w graniczne położenie, która nazywa się styczna.
Pochodną funkcji w punkcie x0 nazywamy granicę właściwą ilorazu różnicowego przy Δx![]()
0
f'(x0)= ![]()
Równanie stycznej ma zatem postać : y-f(x0)=f'(x0)(x-x0)
Pochodna funkcji w punkcie jest liczbą !
Jeżeli funkcja posiada pochodną w punkcie x0 to mówimy, że jest różniczkowalna w punkcie x0.
Funkcja jest różniczkowalna w (a,b) jeżeli posiada pochodną w każdym punkcie tego przedziału.
F(x)->f'(x) Można mówić wtedy o pochodnej jako funkcji.
Funkcja jest różniczkowalna w (a,b) jeżeli posiada na końcach granice jednostronne.
Tw.
Funkcja różniczkowalna w punkcie x0 jest w tym punkcie ciągła.
Ważniejsze pochodne :
(c)'=0 , c - liczba stała
(
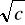
)'=0(x)'=1
(
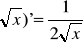
(2x)'=1
(xn)'=n*xn-1
(lnx)'=

(sinx)'=cosx
(cosx)'= -sinx
(ex)'=ex
(arcsinx)'=
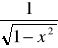
(arccosx)'=
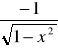
(arctgx)'=
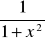
(arcctgx)'=
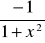
(tgx)'=
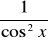
(ctg)'=
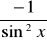
(ax)'=axlna
(
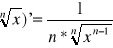
(xα)' =αxα-1
(A*B)'=A'*B+A*B'
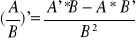
Tw.
Jeżeli y=f(x) jest funkcją odwrotną do x=g(y) monotonicznej i g'(y) ![]()
0 to f'(x)= ![]()
Pochodna logarytmiczna
Jeżeli funkcja f(x) ma w punkcie x pochodną oraz istnieje ln z f(x) to wówczas [ln f(x)]'=![]()
Tw. o pochodnej funkcji złożonej
y=f[g(x)]
y=f(u) ; u=g(x)
Jeżeli istnieje g'(x) i f'(u), gdzie u=g(x) to {f[g(x)]}'=f'(u)*u'=f'[g(x)]*g'(x)
Pochodne wyższych rzędów
Jeżeli istnieje pochodna funkcji pochodnej to mówimy, że mamy do czynienia z drugą pochodną:
y”=(y')'
y”'=(y”)'
yn=(yn-1)'
Tw. Rolle'a. Jeżeli funkcja f(x) spełnia następujące warunki:
1˚ jest ciągła w przedziale domkniętym <a,b>,
2˚ jest różniczkowalna w przedziale otwartym (a,b)
3˚ f(a)=f(b),
to istnieje taki punkt ![]()
, że: f '(c)=0.
Tw. Lagrange'a. Jeżeli funkcja f(x) spełnia następujące warunki:
1˚ jest ciągła w przedziale domkniętym <a,b>,
2˚ jest różniczkowalna w przedziale otwartym (a,b)
to istnieje taki punkt ![]()
, że: ![]()
W interpretacji geometrycznej tw. Lagrange'a oznacza, że istnieje taki punkt c (![]()
), w którym styczna do krzywej jest || do prostej łączącej końce krzywej.
Wnioski z tw. Lagrange'a:
Λx∈(a,b) f '(x)=0 funkcja f jest stała w przedziale <a,b>;
Λx∈(a,b) f '(x)>0 (<0) ⇒ funkcja f jest rosnąca (malejąca) w przedziale <a,b>;
Mówimy, że funkcja f w otoczeniu xo ma w punkcie xo maksimum lokalne (minimum lokalne), jeśli istnieje taka liczba δ>0, że dla x ![]()
(x0- δ, x0+ δ) :
f(x)≤f(xo) ,f(x) ≥ f(xo)
Jeżeli zachodzi nierówność : f(x)< f(xo) [f(x)> f(xo)] mamy do czynienia z ekstremum właściwym.
Warunek konieczny istnienia ekstremum ( tw. Fermata)
Jeżeli funkcja f jest różniczkowalna w otoczeniu x0 i w punkcie xo ma ekstremum to f'(xo)=0.
1. warunek wystarczający istnienia ekstremum.
Jeżeli funkcja jest różniczkowalna w otoczeniu x0, f'(x0) i :
I (x)<0 dla x-δ<x<x0
f”(x)>0 dla x0<x<x+δ
II x)>0 dla x- δ<x<x0
f'(x)<0 dla x0<x<x+δ
to w punkcie x0 występuje ekstremum i to dla przypadku I - minimum, II - maksimum.
W punkcie x0 występuje ekstremum ezeli pierwsza pochodna zmienia znak w tym punkcie,
Twierdzenie to można podać w wersji słabszej:
Wystarczy założyć, że funkcja w x0 jest ciągła, natomiast różniczkowalna w sąsiedztwie.
Tw. (wzór Taylora). Jeżeli funkcja f(x) ma ciągłe pochodne do rzędu (n-1) włącznie w przedziale domkniętym o końcach x0 i x i ma pochodną rzędu n wewnątrz tego przedziału, to istnieje taki punkt c leżący między x0 i x, że zachodzi wzór:
![]()
Twierdzenie jest uogólnionym tw. Lagrange'a.
Tn-1(x) - wielomian Taylora.
Jeżeli x0 = 0 to wzór przyjmuje postać Maclaurina:
![]()
2. warunek wystarczający istnienia ekstremum.
Jeżeli funkcja y=f(x) jest różniczkowalna n-krotnie w otoczeniu punktu x0, f'(x0 )=f”( x0 )= fn-1(x0 )=0 i
fn(x0)![]()
0, n jest liczbą parzystą to w x0 : jest maksimum, gdy fn(x0)<0; minimum, gdy fn(x0)>0.
Gdy n nieparzyste w x0 nie występuje ekstremum.
Dla n=0 WWE ma postać:
f'(x0)=0
f”(x0) >0 to w x0 maksimum
f”(x0) <0 to w x0 minimum
Wklęsłość, wypukłość, punkty przegięcia.
y=f(x) nazywamy wklęsłą w (a,b) jeżeli wykres tej funkcji leży nad styczną poprowadzoną w dowolnym punkcie x ![]()
(a,b).
analogicznie :
y=f(x) nazywamy wypukłą w (a,b) jeżeli wykres tej funkcji leży pod styczną poprowadzoną w dowolnym punkcie x ![]()
(a,b).
Punkt P0(x0, f(x0)) nazywamy punktem przegięcia funkcji jeżeli w lewostronnym otoczeniu f. wklęsła, a w prawostronnym wypukła lub odwrotnie.
Tw.
Jeżeli y=f(x) jest dwukrotnie różniczkowalna w (x0,x):
y”>0 dla x

(x0, x) to f(x)>y, czyli jest wklęsłay”<0 dla x

(x0, x) to f(x)<y, czyli jest wypukła
Zerowanie drugiej pochodnej w punkcie jest warunkiem koniecznym istnienia punktu przegięcia.
Warunek wystarczający istnienia punktu przegięcia jest zmiana znaku drugiej pochodnej przy przejściu przez x0 .
Tw. (reguła de L'Hospitala).
Jeżeli:
funkcje
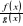
i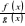
są określone w otoczeniu punktu x0,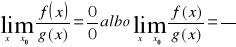
,istnieje
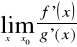
właściwa lub niewłaściwa to istnieje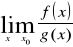
i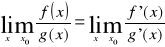
12
Wyszukiwarka
Podobne podstrony:
Ćwiczenie projektowe nr 1, Studia Budownictwo polsl, I semestr, Hydrologia i hydraulika, projekt
hydrologia-cw3, Studia Budownictwo polsl, I semestr, Hydrologia i hydraulika, Ćw. proj. nr 2
Funkcje wielu zmiennych, Studia Budownictwo UZ, 1 semestr, Matematyka, Wyklady matematyka
Zagadnienia na egzamin z matematyki dla kierunku Budownictwo, STUDIA, Budownictwo UZ, Semestr I, Mat
Sprawozdanie - Zaprawy 3, Studia Budownictwo polsl, II semestr, Materiały budowlane, Sprawko 7
Sprawozdanie nr 3 - zaprawa, Studia Budownictwo polsl, II semestr, Materiały budowlane, Sprawko 7
Sprawozdanie nr3 - zaprawa, Studia Budownictwo polsl, II semestr, Materiały budowlane, Sprawko 7
sciagafizykabudowli, Studia Budownictwo polsl, III semestr KBI, Fizyka budowli, Fizyka Budowli
Sprawozdanie - Zaprawy 1, Studia Budownictwo polsl, II semestr, Materiały budowlane, Sprawko 7
FB moja sciaga wlasciwa, Studia Budownictwo polsl, III semestr KBI, Fizyka budowli, Fizyka Budowli
basen, Studia Budownictwo polsl, III semestr KBI, Technologia robót budowlanych, Technologia Robót B
fizyk, Studia Budownictwo polsl, III semestr KBI, Fizyka budowli, Fizyka Budowli
Fizyka budowli, Studia Budownictwo polsl, III semestr KBI, Fizyka budowli, Fizyka Budowli
Tabelka do lab-cw1, Studia Budownictwo PB, 5 semestr, laborki metal
str. na teczkę, STUDIA, Budownictwo UZ, Semestr IV, Konstrukcje Betonowe - Podstawy [Korentz], Labol
fundamenty-sxzajna, STUDIA, Budownictwo UZ, Semestr IV, Fundamentowanie [Szajna], Egzamin
więcej podobnych podstron