TRANSFORMACJA LORENTZA
1887 r . doświadczenie Michelsona - Morley'a (M-M)
sprawdzanie natury eteru świetlnego i wyznaczenie prędkości światła
względem niego.
Wynik doświadczenia:
Prędkość światła c jest niezmiennicza; tzn. prędkość światła jest taka sama, niezależnie od tego czy jest ona mierzona przez obserwatora znajdującego się w układzie stacjonarnym , czy też przez obserwatora znajdującego się w układzie poruszającym się ze stałą prędkością względem źródła światła.
Wnioski te były podstawą teorii względności Einsteina.
Założenia prowadzące do Transformacji Lorentza (TL):
(patrz rys 1.1 Mechanika Klasyczna)
Układ S1 jest w spoczynku,
Układ S2 porusza się ruchem jednostajnym prostoliniowym wzdłuż osi x-ów z prędkością ![]()
,
W chwili początkowej ![]()
ze wspólnego początku obu układów
![]()
wysłany zostaje błysk światła. Światło jest falę kulistą, której czoło fali jest sferą o promieniu zwiększającym się z prędkością światła ![]()
w układzie ![]()
:
![]()
(2.1a)
w układzie ![]()
:
![]()
(2.1b)
Równanie czoła fali ma postać:
W układzie ![]()
:
![]()
(2.2a)
w układzie ![]()
:
![]()
(2.2b)
Korzystamy z TG , wyrażenia na współrzędne z równania (1.6a-c) wstawiamy do równania (2.2b), otrzymujemy wówczas:
![]()
(2.3)
Jak widać równanie (2.3) nie jest identyczne z równaniem (2.2a) czoła fali w układzie.
Wniosek
TG przestaje być słuszna, jeżeli prawdziwa jest zasada niezmienniczości prędkości światła
Szukamy transformacji, która spełnia następujące warunki:
Przechodzi w TG gdy
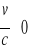
Zmienia wyrażenie (2.2b) w wyrażenie (2.2a)
Transformacja ta musi spełniać następujące założenia:
być prosta dla
i
, bo
oraz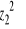
przechodzi odpowiednio w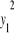
oraz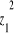
być liniowa względem
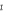
i
, ponieważ musimy otrzymać sferyczne czoło fali rozszerzające się ze stałą prędkością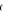
czas musi również podlegać transformacji, o ile wyrazy
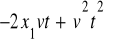
mają zniknąć w równaniu (2.3), czyli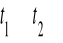
Zastosujmy transformację:
![]()
![]()
![]()
(2.4a-d)
![]()
Transformację (2.4a-d) wstawiamy do wzoru (2.2b) i otrzymujemy:
![]()
![]()
(2.5)
Żądamy spełnienia warunku:
![]()
(bo transformacja powinna być liniowa względem ![]()
oraz ![]()
), stad dostajemy wyrażenie na nieznaną wielkość ![]()
:
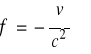
, wówczas transformacja czasu ma postać:
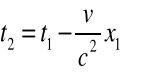
(2.6)
Wstawiamy (2.6) do (2.5) i otrzymujemy:
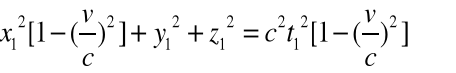
(2.7)
Równanie (2.2b) przejdzie w równanie czoła fali (2.2a) gdy przyjęta zastanie następująca transformacja:
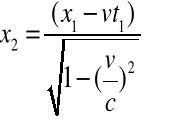
![]()
![]()
(2.8a-d)
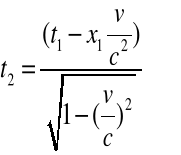
Równania (2.8a-d) stanowią Transformację Lorentza (TL). TL zachowuje niezmienniczość prędkości światła.
Dla ![]()
TL przechodzi w TG.
Standardowa forma zapisu TL:
Stosujemy podstawienia:
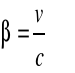
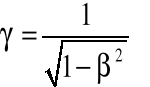
Wówczas TL jest zapisana w następującej postaci:
![]()
![]()
![]()
(2.9a-d)
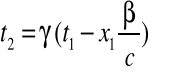
Transformacja odwrotna ma postać:
![]()
![]()
![]()
(2.10a-d)
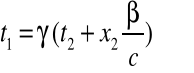
Zasada Korespondencji (odpowiedniości) Bohra sformułowana w 1932r.
Każda nowa teoria w fizyce musi sprowadzić się do dobrze ugruntowanej odpowiedniej teorii klasycznej, jeśli stosuje się ją w specjalnej sytuacji, gdy wiadomo, że mniej ogólna teoria jest słuszna. Innymi słowy TL ![]()
TG dla ![]()
Konsekwencje TL:
Kontrakcja przestrzeni: np. skrócenie długości
Przykład: oznaczmy przez ![]()
długość pręta mierzoną wzdłuż osi x-ów gdy pręt jest w spoczynku w układzie ![]()
przez ![]()
długość pręta mierzoną w układzie ![]()
, który porusza się względem ![]()
ruchem jednostajnym prostoliniowym wzdłuż osi x-ów z prędkością ![]()
W układzie ![]()
długość pręta wynosi:
![]()
(2.11)
natomiast w układzie ![]()
:
![]()
(2.12)
Górne wskaźniki odnoszą się do układów współrzędnych
Uwaga: pomiary wykonujemy w tym samym czasie,
We wzorze (2.11) wykorzystujemy TL przedstawioną równaniem
(2.10a-d) i wówczas otrzymujemy:
![]()
(2.13)
Podstawiając równanie (2.12) do (2.13) otrzymujemy:
![]()
(2.14a)
Lub w równoważnym zapisie:
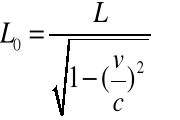
(2.14b)
Z równań (2.14a-b) wynika ,że ![]()
. Jest to tzw. skrócenie Lorentza- Fitzgeralda pręta poruszającego się równolegle do swojej długości.
2. Dylatacja czasu jest zjawiskiem polegającym na wydłużeniu odstępów czasu mierzonych przez zegar będący w ruchu
Przykład: Zegar znajduje się w układzie ![]()
w spoczynku w początku układu współrzędnych ![]()
(![]()
). Układ ![]()
jest układem własnym dla zegara, a wynik pomiaru odstępu czasu ![]()
nazywa się czasem własnym. Układ ![]()
porusza względem ![]()
wzdłuż osi x-ów z prędkością ![]()
.
Zgodnie ze wzorem (2.9d) mamy:
![]()
(2.15a)
Lub w równoważnym zapisie:
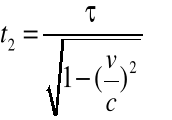
(2.15b)
Ze wzorów (2.15a,b) wynika, że ![]()
. Poruszające się zegary mierzą wydłużone przedziały czasowe w porównaniu z zegarami będącymi w spoczynku.
Lorentzowskie dodawanie prędkości -transformacja prędkości Lorentza
Przypomnienie:
Def. Prędkości:
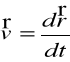
(2.16)
składowe prędkości
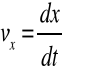
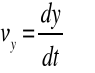
(2.17a-c)
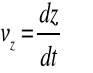
Korzystamy z TL wzór (2.8a-d) , następnie wyliczamy różniczki kolejnych współrzędnych a potem ich pochodne po czasie.
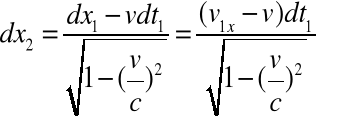
![]()
![]()
(2.18a-d)
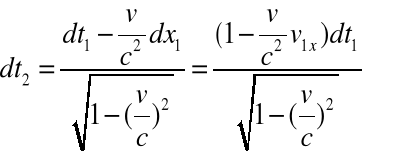
Szukamy: 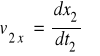
; 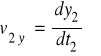
; 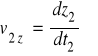
Dzieląc obustronnie równania (2.18a-c) przez (2.18d) otrzymujemy transformację prędkości Lorentza w następującej postaci:
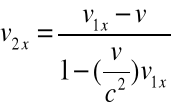
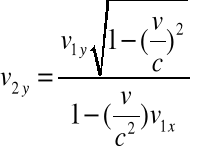
(2.19a-c)
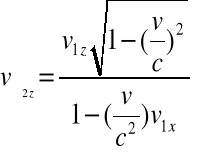
Ze związków (2.19a-c) wynika, że mimo iż ruch układu ![]()
względem ![]()
odbywa się wzdłuż osi x-ów to składowe prędkości ![]()
oraz ![]()
zależą również od ![]()
. Dla ![]()
transformacja prędkości Lorentza (2.19a-c). przechodzi w transformację prędkości Galileusza.
![]()
![]()
(2.20a-c)
![]()
Z równań (2.19a-c) można wyprowadzić odwrotną TL prędkości:
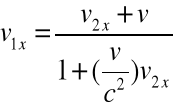
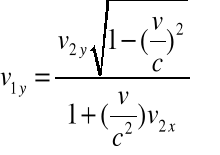
(2.21a-c)
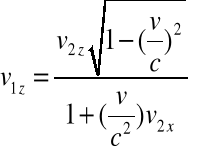
Przykład (R1):
Ciało ![]()
porusza się w układzie ![]()
wzdłuż osi ![]()
z prędkością ![]()
,
Układ ![]()
porusza się względem ![]()
wzdłuż osi ![]()
z prędkością ![]()
Wyliczamy prędkość ciała w układzie ![]()
Zgodnie z TG prędkość ta wynosi:
![]()
![]()
(R1.1a-c)
![]()
Zgodnie z TL prędkość ta wynosi:
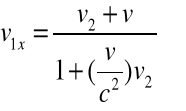
![]()
(R1.2a-c)
![]()
Rozważamy przypadek dużych prędkości ![]()
, wówczas zgodnie z równaniem (R1.1a-c) z TG otrzymujemy:
![]()
![]()
(R1.3a-c)
![]()
Wynik wskazuje, że TG nie spełnia zasady niezmienniczości prędkości światła
Natomiast zgodnie z równaniem (R1.2a-c) z TL otrzymujemy:
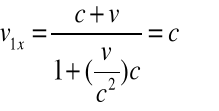
![]()
(R1.4a-c)
![]()
Wynik wskazuje, że TL spełnia zasadę niezmienniczości prędkości światła.
DYNAMIKA RELATYWISTYCZNA
Niezmienniczość praw fizyki względem transformacji Lorentza.
Pęd
Rozważając szczególny przypadek zderzeń można wykazać, że pęd newtonowski (nierelatywistyczny) ![]()
nie jest zachowany przy zderzeniach cząstek mających prędkości v duże, tzn, że ![]()
nie zmierza do zera.
Przykład:
Zderzenie dwóch kul o masach m1 oraz m2
(szczegóły są podane w aneksie A1, przygotowane zostały w oparciu o: „Mechanika” C. Kittel i współautorzy)
Wyrażenie na pęd musi ulec modyfikacji, żeby pęd był niezmienniczy względem TL. Korzystając się ze wzoru na dylatację czasu, otrzymuje się wyrażenie na pęd relatywistyczny w postaci:
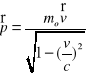
(2.22)
lub w postaci:
![]()
(2.23)
Została wprowadzona masa relatywistyczna:
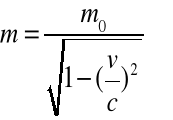
(2.24)
gdzie ![]()
jest masą bezwładną, która jest atrybutem ciała w mechanice klasycznej.
Zgodnie ze wzorem (2.24) masa relatywistyczna zależy od prędkości ciała.
Zależność ta została potwierdzona eksperymentalnie, stwierdzono również, że dla 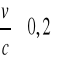
można przyjąć, że ![]()
.
Pęd relatywistyczny można zapisać w postaci:
![]()
(2.25)
Dla ![]()
, ![]()
i wyrażenie na pęd relatywistyczny przechodzi w wyrażenie na pęd klasyczny ![]()
Siła
Zgodnie z zasadami dynamiki Newtona siła jest zdefiniowana:
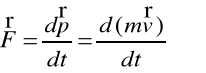
(2.26a)
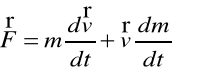
(2.26b)
Dla zjawisk relatywistycznych (![]()
) drugi składnik wyrażenia (2.26b): 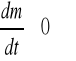
, gdyż masa ![]()
zależy od prędkości ![]()
. Ponieważ rozważamy przypadek, gdy na ciało działa siła ![]()
, to wówczas ![]()
nie jest stałe w czasie; ![]()
jest równe ![]()
. Tak więc 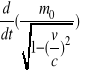
jest różne od zera. Przyjmujemy, że ciało o masie ![]()
jest związane z układem ![]()
, na ciało działa siła ![]()
wzdłuż osi x-ów: ![]()
, oznacza to, że układ ![]()
, a zarazem ciało porusza się względem ![]()
ze zmienną prędkością ![]()
. Wówczas zgodnie z zapisem (2.26b) oraz z uwzględnieniem masy relatywistycznej 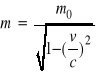
otrzymamy:
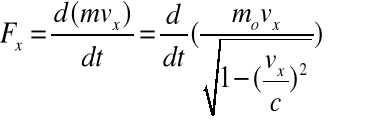
(2.27)
Po wyliczeniu pochodnej wyrażenie (2.27) przyjmuje postać:
![]()
(2.28)
Gdzie:
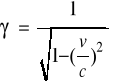
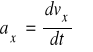
(przyspieszenie) obserwowane w układzie ![]()
, gdy przyjąć, ze układ ![]()
był związany z cząstką poruszająca się względem ![]()
z prędkością ![]()
Dla ![]()
, wówczas związek (2.28) przechodzi w znany z mechaniki klasycznej wzór na siłę: ![]()
3.Energia kinetyczna
Korzystamy z definicji energii kinetycznej ![]()
:
![]()
(2.29)
Zakładamy, ze siła ![]()
działająca na ciało o masie ![]()
jest równoległa do wektora wodzącego tego ciała ![]()
. Wówczas wyrażenie na energię kinetyczną będzie miało postać:
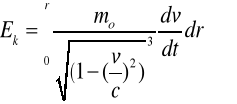
(2.30a)
Wykorzystując zależność: ![]()
, otrzymujemy:
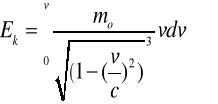
(2.30b)
Po scałkowaniu :
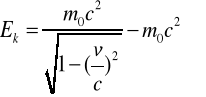
(2.31a)
Lub, korzystając z definicji masy relatywistycznej:
![]()
(2.31b)
Ażeby sprawdzić, czy spełniona jest zasada korespondencji, tzn. czy wzór na energię kinetyczną dla cząstki relatywistycznej przejdzie w znany związek mechaniki klasycznej ![]()
należy wyrażenie (2.31a) rozwinąć w szereg przyjmując, że ![]()
.
Przekształcamy równanie (2.31a):
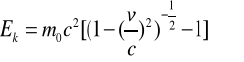
(2.32)
Zajmujemy się wyrażeniem 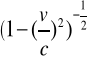
korzystamy z rozwinięcia dwumianu ![]()
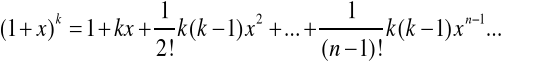
(2.33)
wprowadzamy następujące oznaczenia:
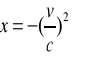
(2.34)
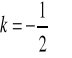
(2.35)
Wykorzystujemy oznaczenia (2.34) oraz (2.35) i wówczas z dokładnością do wyrazów pierwszego rzędu ze względu na x, wzór (2.33) przyjmuje postać:
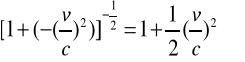
(2.36)
Podstawiamy wyrażenie (2.36) do wzoru (2.32) i otrzymujemy:
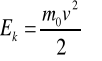
(2.37)
Wzór (2.37) stanowi wyrażenie na energię kinetyczną w mechanice klasycznej.
Energia całkowita
Praca potrzebna do zmiany prędkości ciała od ![]()
do ![]()
równa się zmianie energii kinetycznej tego ciała. Prędkości ![]()
odpowiada masa relatywistyczna ![]()
, natomiast prędkości ![]()
masa relatywistyczna ![]()
.
![]()
(2.38a)
![]()
(2.38b)
![]()
(2.38c)
gdzie ![]()
Związek (2.38c) oznacza, że zmiana energii kinetycznej jest równa zmianie masy relatywistycznej.
Zakładamy, że ciało porusza się w polu sił zachowawczych, którego energię potencjalną oznaczymy przez ![]()
, wówczas zgodnie z zasadą zachowania energii mamy:
![]()
(2.39)
Przekształcamy wzór (2.39) i korzystamy ze związku (2.38c), otrzymujemy :
![]()
(2.40)
Stąd mamy:
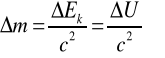
(2.41)
gdzie ![]()
Całkowitą energię relatywistyczną można również zapisać w postaci :
![]()
(2.42)
Gdzie ![]()
jest energię masy spoczynkowej:
![]()
(2.43)
Podstawiamy (2.43) do (2.42) i wówczas wzór (2.42) przyjmuje postać:
![]()
(2.44)
Wzór (2.44) oznacza równoważność masy i energii. Równoważność ta jest jedną z najważniejszych konsekwencji szczególnej teorii względności (teorii relatywistycznej). Oznacza to, że, zamiast zasady zachowania energii, należy stosować zasadę zachowania masy-energii :
Energia spoczynkowa + Energia kinetyczna + Energia potencjalna = const.
Korzysta się również z innego zapisu energii na energię całkowitą:
![]()
(2.45)
Gdzie ![]()
jest pędem relatywistycznym
Dla cząstki poruszającej się z prędkością ![]()
musi być spełniony warunek, że jej masa spoczynkowa ![]()
, gdyż inaczej, zgodnie ze wzorem (2.24) masa relatywistyczna takiej cząstki ![]()
W tym przypadku wyrażenie na energię całkowitą ma postać:
![]()
(2.46a)
![]()
(2.46b)
Energia całkowita jest równa energii kinetycznej:
![]()
(2.47)
Cząstki o tak dużych prędkościach (![]()
) noszą nazwę cząstek skrajnie relatywistycznych (ultrarelatywistyczne).
PODSUMOWANIE SZCZEGÓLNEJ TEORII WZGLĘDNOŚCI
Wyszukiwarka
Podobne podstrony:
3305
3305
3305
3305
3305
akumulator do daf f 3300 fa 3300 dkx 3305 dkx fac 3303 dkx f
więcej podobnych podstron