Powtórzenie z Algebry

1. Macierz

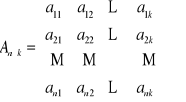
- macierz o n wierszach i k kolumnach

Macierz jest kwadratowa jeśli ma tyle samo wierszy co kolumn (n = k).

Macierz jest diagonalna jeśli jest kwadratowa i po za główną przekątną (diagonala) są elementy zerowe, np.: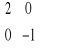
.

Macierz jednostkowa, to macierz diagonalna mająca same jedynki na głównej przekątnej, np.: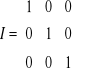
.

Powiemy, że dwie macierze A i B są równe, jeśli są tego samego wymiaru oraz
dla każdego i oraz j.

Macierz transponowaną do macierzy A (oznaczenie
) nazywamy macierz, która powstaje w wyniku zamiany kolumn z wierszami - i-tą kolumnę zapisujemy jako i-ty wiersz, np.: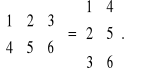

Macierz A jest symetryczna, jeśli jest macierzą kwadratową dla której zachodzi:
(lub równoważnie
dla każdego i oraz j).

Dodawanie macierzy jest zdefiniowane tylko dla macierzy, które są tego samego wymiaru. Dodając macierze sumujemy elementy stojące w tym samym wierszu i kolumnie:

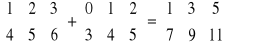
Mnożenie macierzy A przez macierz B (oznaczenie AB) jest wykonalne tylko wtedy, jeśli macierz A ma tyle kolumn co macierz B wierszy. Aby wyznaczyć element
stojący w i-tym wierszu i j-tej kolumnie macierzy wynikowej, należy pomnożyć i-ty wiersz macierzy A przez j-tą kolumnę macierzy B, np.:

Przydatne własności:

• 
  

• 
  

• 
  

• 
  

2. Wyznacznik macierzy

Wyznacznik macierzy jest zdefiniowany tylko dla macierzy kwadratowej. Wyznacznik macierzy A (oznaczenie
lub det(A)) definiujemy w sposób rekurencyjny:

,
oznacza macierz powstałą z macierzy A poprzez usunięcie i-tego wiersza oraz j-tej kolumny.

Warto pamiętać wzory na wyznacznik w przypadku macierzy 2x2 i 3x3:

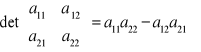
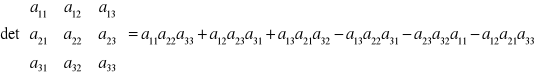
Własności wyznacznika:

3. Forma kwadratowa

Formę kwadratową definiuje się w następujący sposób:
, gdzie A jest macierzą symetryczną wymiaru nxn, natomiast x jest wektorem kolumnowym zawierającym n elementów. W wyniku przemnożenia
otrzymujemy skalar (liczbę):

Powiemy, że macierz A jest dodatnio (ujemnie) określona, jeżeli dla każdego niezerowego wektora x zachodzi:
. Powiemy, że macierz A jest nieujemnie (niedodatnio) określona, jeżeli dla każdego niezerowego wektora x zachodzi:
.

Jak sprawdzać określoność macierzy w praktyce?

Niech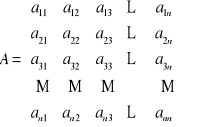
. Definiujemy następujące wyznaczniki: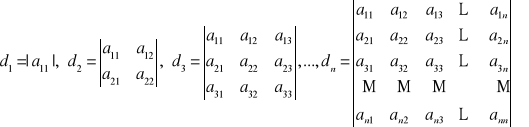
.

Macierz A jest dodatnio określona

Macierz A jest nieujemnie określona

Macierz A jest ujemnie określona

Macierz A jest niedodatnio określona

4. Ślad macierzy

Ślad macierzy definiujemy tylko dla macierzy kwadratowej:
- suma elementów stojących na głównej przekątnej (diagonali). Na przykład:

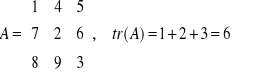
Niech c będzie liczbą, a wektorem kolumnowym, A macierzą kwadratową. Wówczas prawdą jest:

• 
  

• 
  

• 
  

• 
  

• 
  

• 
  

5. Macierz idempotenta

Macierz A jest macierzą idempotenta, jeśli

Kilka innych przydatnych pojęć

Liniowa niezależność wektorów

Wektory
są liniowo niezależne, jeśli jedynym rozwiązaniem równania:

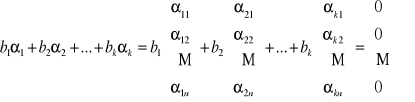
są:

Macierz odwrotna

Macierz B jest macierzą odwrotną do macierzy kwadratowej A (oznaczenie
), jeśli
Warto podkreślić, iż mnożenie macierzy przez macierz do niej odwrotną jest przemienne:
Macierz odwrotna nie zawsze istnieje. Warunkiem koniecznym
(i wystarczającym) na to, żeby istniała macierz odwrotna do macierzy A, jest to, żeby wiersze (kolumny) macierzy A były liniowo niezależne. Taką macierz nazywamy nieosobliwą.

Jak sprawdzać w praktyce czy macierz odwrotna istnieje? Wystarczy policzyć wyznacznik macierzy, jeśli jest różny od zera to macierz odwrotna istnieje!

Warto pamiętać wzór na macierz odwrotną wymiaru 2x2:

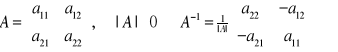
Niech A i B będą macierzami nieosobliwymi (istnieją macierze odwrotne). Wówczas:

• 
  

• 
  

• 
  

• 
  

Rząd macierzy

Rząd kolumnowy macierzy A to liczba liniowo niezależnych kolumn macierzy A.

Rząd wierszowy macierzy A to liczba liniowo niezależnych wierszy macierzy A.

Zawsze rząd kolumnowy i wierszowy macierzy A są sobie równe i będziemy je nazywać rzędem macierzy A (oznaczenie
).

6. Dowód twierdzenia, że symetryczna macierz idempotenta M ma wartości własne równe 0 lub 1 oraz
(szkic dowodu)

Z założenia wiemy, iż
Ponieważ M (również z założenia) jest macierzą symetryczną, to możemy ją przedstawić w następujący sposób:
(dekompozycja spektralna), gdzie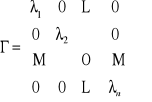
,
są wartościami własnymi macierzy M, natomiast w kolejnych kolumnach macierzy C, stoją wektory własne odpowiadające wartością własnym. Wektory własne są ortonormalne (tzn.
), więc
.

Podsumowując wszystkie dotychczasowe spostrzeżenia otrzymujemy: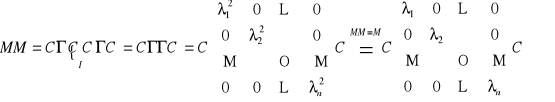

Przemnażamy ostatnią równość z prawej strony przez C i z lewej strony przez
i otrzymujemy:

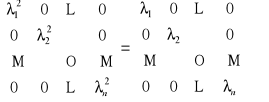
co oznacza, iż dla każdego i musi zachodzić:
. Na razie pokazaliśmy, że wartości własne macierzy są równe 0 lub 1.

W dalszej części będzie nam potrzebny następujący fakt: B i C są nieosobliwe, to
.

Wracając do naszego dowodu, macierze C i
są nieosobliwe (bo wektory własne są liniowo niezależne), więc:
Macierz
jest macierzą diagonalną, gdzie na diagonali stoi 0 lub 1, czyli jej rząd musi być równy liczbie jedynek na diagonali (w tym przypadku będzie to ślad macierzy), co oznacza:
.

Z drugiej strony mamy:
gdzie skorzystaliśmy z ostatniej własności śladu ze str. 3 oraz z
.

Ostatecznie otrzymujemy:

Powtórzenie z Analizy

1. Pochodna

Niech
(funkcja skalarna). Pochodną funkcji skalarnej względem wektora x definiujemy jako wektor pochodnych cząstkowych:

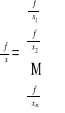
Niech
(funkcja wektorowa). Powyższy zapis możemy interpretować w następujący sposób:
gdzie
są funkcjami skalarnymi. Na przykład:

.

Pochodna funkcji wektorowej względem wektora x to macierz wymiaru nxm:

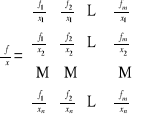
2.

Niech
Definiujemy funkcję skalarną:

. Dla każdego i
, więc zgodnie z definicją pochodnej funkcji skalarnej otrzymujemy:

(**)

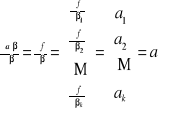
Pochodną funkcji skalarnej f względem
definiujemy jako:

Korzystając z powyższej definicji otrzymujemy:

(*)

3.

Niech A będzie macierzą wymiaru nxn natomiast
wektorem n-elementowym. Wówczas:

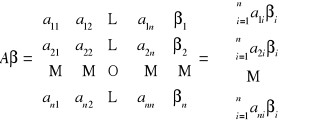
. Czyli: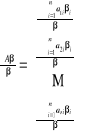
={Korzystamy z (*)}= A

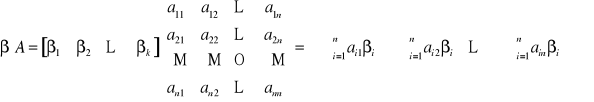
, czyli:
={Korzystamy z (**)}=A

4.

Przy oznaczeniach z podpunktu 3) mamy:
. Wówczas:

.

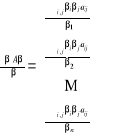
Rozwiniemy l-ty element powyższej macierzy:

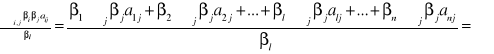
Teraz możemy zapisać:

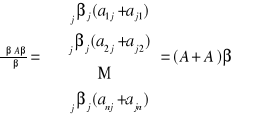
Jeśli macierz A jest symetryczna, to
, co upraszcza powyższy wzór do postaci:

5. Warunkiem koniecznym (ale nie wystarczającym!) na istnienie ekstremum funkcji f w punkcie
jest zerowanie się gradientu:

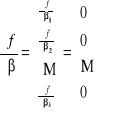
6. Macierz drugich pochodnych - Hessian

Niech
(funkcja skalarna). Macierz drugich pochodnych funkcji skalarnej definiujemy jako:

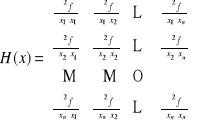
Jeżeli funkcja f jest ciągła oraz ma ciągłe pochodne cząstkowe pierwszego i drugiego rzędu, to Hessian jest macierzą symetryczną.

7. Warunek konieczny i wystarczający na istnienie ekstremum dla funkcji skalarnej

Funkcja f ma maksimum w punkcie
, jeśli:

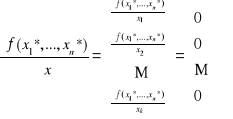
(zerowanie się gradientu)

oraz

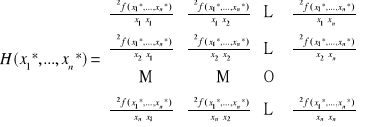
jest ujemnie określona.

W przypadku minimum, pierwszy warunek się nie zmienia, natomiast Hessian musi być dodatnio określony.

4

---