Def. Ciąg funkcyjny:

Ciąg funkcyjny w zbiorze A jest to przyporządkowanie każdej liczbie naturalnej dokł. jednej określonej na tym zbiorze. Funkcję przyporządkowaną liczbie naturalnej n ozn. f_n(x) natomiast cały ciąg będziemy oznaczać {f_n (x) } który po napisaniu daje: (f₁ (x) i f₂ (x), ...). Jeżeli ciąg funkcyjny {f_n(x)}jest określony w A, to dla każdego x₀∈A do funkcji granicznej z ciągu funkcyjnego, otrzymamy konkretny ciąg liczbowy {f_n(x₀)}, który jest zbieżny lub rozbieżny.

Def. Zbieżność ciągu funkcyjnego do funkcji granicznej:

Ciąg funkcyjny {f_n(x)} jest zbieżny w A do funkcji granicznej f(x), co zapisujemy lim_n→∞f_n(x)-f(x) lub f_n(x) _n^e_→∞→ f(x) ⇔ ^Λ_ε>0 ^Λ_x∈Α ^V_s ^Λ_n>s. f_n(x)- f(x)<ε oprócz zbieżności ciągu funkc. mówimy o jego zbieżności jednostronnej, którą ozn. symbolem: Λf_n(x) ^A⇒f(x) ⇔ ^Λ_ε>0 ^V_δ ^Λ_x∈A f_n(x)- f(x)<ε

Dla zb. zwykłej liczba δ ma istnieć dla każdego ε>0 i x∈A

Dla zb. jednostronnej ma mieć jednakową wartość dla całego zbioru A

Ze zbieżności jednostronnej wynika zbieżność zwykła

[f_n(x) ^A⇒ f(x)] ⇒ [f_n(x) ^e→ f(x)]

Tw. Granica jednostajnie zb. ciągu f. ciągłych jest f. ciągłą

Warunek Cauche'go:

Na to aby ciąg f_n(x) był zbieżny jednostajnie w zbiorze A potrzeba i wystarcza aby Λ_ε>0 V_r że Λ_n>r zachodzi [f_n(x) - f_r(x)]<ε

-Szereg geometryczny:

Saq^n-1 lub Saq^k

1. Jeżeli a=0 to szer. zb. & S= 0

2. Jeżeli a≠0 to szer. geom.

-dla q<1 szer. geom. zb. i S=a/1-q

-dla q≥1 szer. geom. rozb.

-Szereg Dirchleta: S1/n^a , a∈R, dla α>1 sz zbieżny; dla a ≤1 sz rozbieżny.

-Szereg naprzemienny: Szereg Σ(-1)ⁿ⁺¹a_n, gdzie a_n>0 dla n=1,2,3,… nazywamy szer naprzemiennym.

Def. Zbieżność szeregu liczbowego:

Szereg liczbowy nazywamy zbieżnym, jeżeli ciąg sum częściowych jest zbieżny do granicy właściwej lim S_n =S ; S- suma szeregu.

Def. Równość szeregów:

Z równości szeregów wynika równość ich sum, ale nie na odwrót.

Def. Iloczyn przez liczbę:

Def. N- reszta szeregu: jeżeli w szeregu Σa_k pominiemy n początkowych wyrazów to otrzymamy szereg:

który nazywamy n - resztą szeregu Σa_k .

Tw. Jeżeli szeregi Σa_n; Σb_n są zbieżne, a ich sumy wynoszą odpowiednio: S₁ i S₂ to Σ(a_n+ b_n ) i Σ(ka_n) wynoszą odpowiednio S₁+S₂ i kS₁ .

Tw Warunek konieczny zbieżności szeregu:

Jeżeli szereg Σa_n jest zbieżny, to lim a_n=0

Dowód:

a_n=S_n-S_n-1 ; lim a_n= lim (S_n-S_n-1) = lim S_n - lim S_n-1 = S-S=0

Tw. Zbieżność szeregu: Jeżeli ciąg sum częściowych szeregu o wyrazach nieujemnych jest ograniczony z góry, to szereg ten jest zbieżny.

Dowód:

S_n=a₁+ a₂+ a₃+…+ a_n Λ a_n≥0, ciąg S_n jest ciągiem niemalejącym, ciąg ograniczony z góry z założenia. Każdy ciąg monotoniczny i ograniczony jest zbieżny ⇒ S_n -jest zbieżny.

Kryterium porównawcze:

Jeżeli wyrazy szeregów Σ a_n i Σ b_n są nieujemne, a ponadto istnieje taka liczba naturalna n₀ , że n> n₀ i spełniona jest nierówność a_n≤ b_n, to:

- ze zbieżności szer b_n wynika zbieżność szeregu a_n

- z rozbieżności szeregu a_n wynika rozb szeregu b_n

Dowód:

S_n=Σ a_n - chcemy pokazać, że jest zbieżny.

S_n = S_n0+Σa_k ≤ S_n0 +Σb_k ≤ S_n0 + B;

k= n₀ +1 ciąg sum częściowych S_n =S_n0 + B jest ograniczony stąd wynika zbieżność Σb_k\n z założenia zbieżny i równy B.

Kryterium d'Alamberta:

Jeżeli istnieje granica właściwa lub niewłaściwa g=lim a_n+1/a_n, to szereg Σa_n o wyrazach dodatnich jest zbieżny, gdy g<1, natomiast rozb dla g>1.

Kryterium Cauchyego:

Jeżeli istnieje granica właściwa lub niewłaściwa g=lim n√a_n, to szereg o wyrazach nieujemnych jest zbieżny gdy g<1, natomiast rozb dla g>1.

Kryterium całkowe:

Niech funkcja f(x) będzie funkcją ciągłą, malejącą i dodatnią dla x≥ n₀∈N wówczas war koniecznym i dostatecznym zbieżności takiego szeregu jest zbieżność całki n₀∫^∞ f(x)dx

Kryterium Leibniza:

Jeżeli ciąg {a_n} jest nierosnący oraz lim a_n=0, to szereg naprzemienny jest zbieżny.

[Ciąg nierosnący Λa_n+1≤a_n ]

Kryterium Weierstrassa:

Jeżeli Σa_n liczb. jest zbież i jeżeli
spełniona jest nierówność f_n(x)≤a_n to Σ funkcyjny jest zbieżny jednostajnie i bezwzględnie w zbiorze A. Σa_n nazywamy majorantą Σ funkcyjnego.

Dowód:

Σa_n jako zbieżny musi spełniać warunek:

- war. konieczny i dostateczny zb Σ funkcyjnego.

Def: Bezwzględna zbieżność szeregu:

Σa_n nazywamy bezwzględnie zbieżnym jeżeli jest zbieżny Σ złożony z bezwzględnych wartości. Jeżeli Σa_n jest zbieżny bezwzględnie, to jest zbieżny. (Σa_n )=Σ (a_n). Jeżeli Σ jest zbieżny to nazywamy go warunkowo zbieżnym.

Def. Iloczyn Caychy'ego szeregów:

Szereg Σa_n, gdzie a_n = Σ a_k b_n-k+1; n=1,2...- nazywamy iloczynem Cauchy'ego szeregów Σa_n i Σb_n tzn:

(Σa_n ) (Σb_n ) = Σa_n

(Σa_n ) (Σb_n ) = Σa_n a_k =Σa_k b_n - _k

Twierdzenie: Jeżeli szeregi Σa_n i Σb_n s --> [Author:AS] ą zbieżne i chociaż jeden z nich jest bezwzględnie zbieżny, to ich iloczyn jest zbieżny.

Tw. Całkowanie szeregu funkcyjnego:

Jeżeli Σf_n(x) o wyrazach ciągłych w przedziale <a,b> jest w tym przedziale jednostajnie zbieżny to ₀∫^b[Σf_n(x)]dx=Σ₀∫^bf_n(x)dx.

Tw. Różniczkowanie szeregu funkcyjnego:

Jeżeli wyrazy sz. Funkcyjnego mają ciągłe pochodne f^'_n(x) w przedziale <a,b>, Σ funkcyjny Σf_n(x) jest zbieżny w przedziale <a,b> a ponadto sz.Σf'_n(x) jest jednostajnie zbieżny w przedziale <a,b> to:

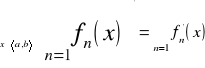
Def. Promień szeregu potęgowego:

Promieniem R zbieżności Σ potęgowego Σa_nxⁿ nazywamy kres górny zbioru bezwzględnych wartości x dla Σ ten jest Σ zbieżnym.

Tw. Promień szeregu potęgowego:

Jeżeli istnieje granica:

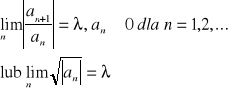
to promień zbieżności szeregu Σa_nxⁿ wynosi:

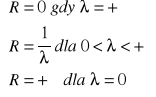
Tw. Całkowanie szeregu potęgowego:

Jeżeli x należy do wnętrza przedziału Σ pot. Σ a_nxⁿ tzn. x∈(-R,R) to całka: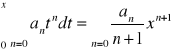
przy czym promień zbieżności tego szeregu jest taki jak szeregu wyjściowego.

Dowód: Założenia o całkowaniu szeregu są spełnione dla:

Tw. Różniczkowanie szeregu potęgowego:

Jeżeli x należy do wnętrza przedziału zb. Σ pot. Σ a_nxⁿ to pochodna:
- promień zb. tego Σ jest taki sam jak szeregu wyjściowego.

Uzasadnienie: zał. Tw. o różniczkowaniu Σ funkcyjnego są spełnione czyli możemy różniczkować wyraz po wyrazie:

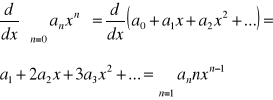
Szereg Taylora:

Niech f będzie funkcją, która ma w pewnym otoczeniu Q punktu x₀ wszystkie pochodne, tzn. jest klasy C^∞. Funkcję taką dla każdego x∈Q-{x₀} i każdego n∈N możemy rozwinąć w Σ Taylora:

Tw. o reszcie Taylora:

Jeżeli istnieje liczba M.>0, że
Spełniona jest nierówność:

czyli funkcja daje się rozwinąć w otoczeniu Q w Σ Taylora.

Dowód:

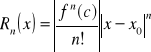
szacujemy moduł z reszty.

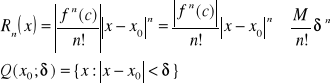
badamy zbieżność Σ z d'Alamberta:

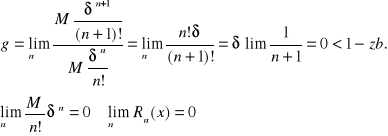
Rozwinięcie w szereg Taylora:

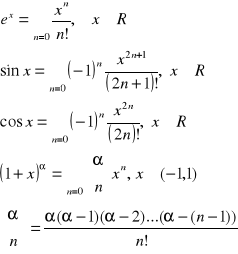
Szereg Fouriera:

Jeżeli dana jest funkcja f:<a,a+2l>→R, to szereg trygonometryczny

gdzie:

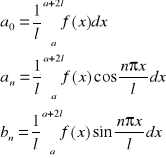
nazywamy trygonometrycznym szeregiem Fouriera funkcji f(x) i będziemy zapisywali:

,

Warunki Dirchleta:

Mówimy że funkcja f:<a,a+2l)→R ograniczona spełnia w przedziale <a;a+2l>Warunki Dirchleta jeżeli a) funkcja ta jest przedziałem monotoniczna: b) funkcja fest cuągła za wyjątkiem co najwyżej skończonej liczby punktów w których ma nieciągłość pierwszego rodzaju

Nieciągłość usuwalna Nieciągłość nieusuwalna

Lim f(x)= lim f(x)≠f(x₀) Lim f(x)= lim f(x)

^Χ→X₀^{- Χ→X}₀^{+ Χ→X}₀^{- Χ→X}₀⁺

Twierdzenie: Trygonometryczny szereg Fouriera dla funkcji f. która działa w przedziale f;<a;a+2l>→R spełniająca warunki Dirchleta, jest zbieżny w każdym punkcie przedziału <a; a+2l> przy czym w dowolnym punkcie x₀∈(a;a+2l) w którym f. f: fest ciągła suma szeregu wynosi f(x) natomiast w punktach x₀∈(a;a+2l) w któryvh funkcja f jest nieciągła suma szeregu wynosi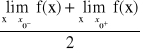
-śr. arytmet. granic jednostronnych

Na krańcach przedziału suma szer. wynosi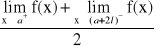

Macierze:

Def. Podobieństwo Macierzy:

Macierz kwadratową A nazywamy podobną do macierzy kw. B, jeżeli istnieje nieosobliwa macierz P (det≠0) taka, że B=P^-1AP, macierz P. nazywamy macierzą podobieństwa

Tw: Jeżeli macierz A jest podobna do macierzy b z macierzą podobieństwa P., to macierz B jest również podobna do macierzy A z macierzą podobieństwa P^-1

Dowód: B=P^-1AP *P.

PB=AP ⇒ PB*P^-1=A

Def. Macierz ortogonalna:

Macierz kwadratową i nieosobliwą A nazywamy ortogonalną ⇔

1. detA=±1

2. A*A^T =E

Dowód:

A - ortogonalna:

AA^T=E, AA^-1=E

AA^T=AA^-1|*A^-1

A^-1AA^T= A^-1AA^-1⇒ EA^T= EA^-1⇒ A^T= A^-1

Definicja Bazy:

Układ B{e₁,e₂} gdzie
są wektorami liniowo niezależnymi nazywamy bazą w przestrzeni V₂ (analogicznie dla B-{e₁,e₂,e₃} (Trzy wektory
liniowo niezależne jeżeli kombinacja

Bazę B nazywamy ortonormalną gdy wszystkie wektory bazowe mają dł. równą 1 i są wzajemnie do siebie prostopadłe

Macierz przejścia:

Dane są dwie bazy: B{e₁,e₂, e₃} oraz B'{e_1',e_2', e_3'} w prz.V₃. Z definicji bazy:

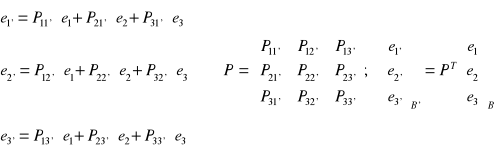
Tw. Macierz przejścia P od bazy ortonormalnej B do bazy B' jest zawsze macierzą ortogonalną: P^T=P^-1

Zmiana współrzędnych wektora przy zmianie bazy:

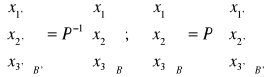
Def: Operacji liniowej:

Operacja A: V₃→V₃ (A: V₂→V₂) nazywamy liniową jeśli spełnia warunek:

1. 
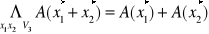
   - warunek addytywności (analogiczności dla V₂)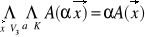

2. 
   -w jednorodności

Def: Operacji jednostkowej:

Operację A, która działa w V₃→V₃ (lub A: V₂→V₂ ) nazywamy jednostkową jeżeli: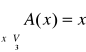
A=E - ozn. op. jednostkowej.

Macierz operacji jednostkowej:

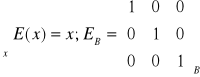
Macierz operacji jednostkowej nie zależy od bazy ( w każdej bazie jest taka sama) A_B'=P^-1A_BP; E_B'=P^-1E_BP=P^-1P=E_B.

Def: Operacji symetrycznej:

Operację A:V_n→V_n (n=2,3) nazywamy symetryczną⇔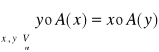

Def: Operacji antysymetrycznej:

Operację A:V_n→V_n (n=2,3) nazywamy antysymetryczną⇔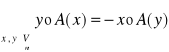

Def: Wartości własne i wektory własne:

Liczbę λ nazywamy wartością własną operacji liniowej A:V₃→V₃ (A: V₂→V₂) jeżeli istnieje niezerowy wektor

taki, że
.Wektor
nazywamy wektorem własnym odpowiadającym wart. własnej λ przy A.

Def. Tensor o walencji 1:

Dowolny obiekt nazywamy tensorem o welencji=1, nad przestrzenią V_n (n=2,3) jeżeli w każdej bazie B tej przestrzeni jest on określony jednoznacznie za pomocą n¹ liczb x_i zwanych współrzędnymi tensora w danej bazie, przy czym współrzędne te transformują się przy zmianie bazy według następującej zasady:

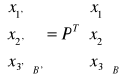
; (x_i')=p_ii'x_i

Def. Tensor o walencji 2:

Dowolny obiekt nazywamy tensorem o welencji=2, nad przestrzenią V_n (n=2,3) jeżeli w każdej bazie B tej przestrzeni jest on określony jednoznacznie za pomocą n² liczb α_ij zwanych współrzędnymi tensora w danej bazie, przy czym współrzędne te transformują się przy zmianie bazy według następującej zasady: α_i'j' =p_ii'p_jj'α_ij

Tensor bezwładności: Jest on reprezentowany w bazie B przez macież

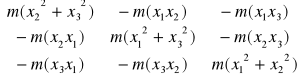
- Tensor bezwładnosci masy m Zaczepionej w punkcie M(x₁,x₂,x₃)

Jest to tensor symetryczny na przekątnej są to momenty bezwładności m. względem osi wyznaczonej przez wektory bazowe:
-moment względny x₁,x₂,x₃

Pozostałe momenty to momenty dewiacyjne.

Def. Kwadryka:

Zbiór wszystkich punktów M(x₁x₂x₃) o promieniach wodzących
i spełniających równanie

nazywamy kwadryką tensorową tensor T_B. Kwadryka tensorowa jest to pewna powierzchnia .

Równanie kwadryki i w postaci macierzowej:

Postać kanoniczna kwadryki tensorowej:

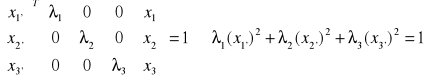
Rachunek operatorów:

Funkcja Heviside'a:

0 dla x<c

η(x-c)= 0,5 dla x=c

1 dla x>c

Def. Przekształcenie Laplace'a:

Przekształcenie Laplace'a funkcji f(x) zmiennej rzeczywistej x nazywamy funkcję F(s) zmiennej zespolonej s określoną wzorem:

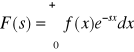
Jeżeli całka istnieje, to funkcję nazywamy transformatą Laplace'a funkcji f(x) i oznaczali będziemy symbolem:

F(s)=L[f(x)]

Def. Klasy oryginałów:

Mówimy, że funkcja f(x) przedziałami ciągła należy do klasy oryginałów gdy spełnia następujące warunki:

1. f(x)=0, dla x<0

2. f(x)=0,5(f(x⁺)+ f(x^-))

3. Istnieją stałe M i α takie, że f(x)≤Me^αx.

Twierdzenie o podobieństwie:

Twierdzenie o tłumieniu:

I. Twierdzenie o przesunięciu:

II. Twierdzenie o przesunięciu:

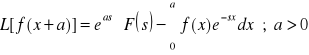
Tw. O Transformacji funkcji okresowej:

Jeżeli funkcja f(x) z klasy oryginałów jest funkcją okresową o okresie T dla wszystkich x∈R₊ , to:

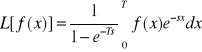
Najczęściej spotykane transformaty:

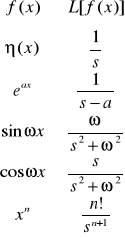
Liczby Zespolone:

Kryterium porównawcze:

Jeżeli
o wyrazach dodatnich jest zbieżny, to szereg Σz_n jest bezwzględnie zbieżny.

Kryterium d'Alamberta:

Jeżeli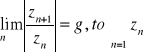
o wyrazach zespolonych jest bezwzględnie zbieżny gdy g<1, natomiast rozbieżny gdy g>1.

Kryterium Cauchy'ego:

Jeżeli
o wyrazach zespolonych jest bezwzględnie zbieżny gdy g<1, natomiast rozbieżny gdy g>1.

Tw. Warunek konieczny i dostateczny:

Warunkiem koniecznym i dostatecznym zbieżności Σz_n o wyrazach z_n=x_n+y_n do sumy S=S₁+S₂i jest jednoczesna zbieżność szeregów Σx_n i Σy_n odpowiedio do sum S₁ i S₂.

Def. Granicy według Heinego:

Def. Granicy według Cauchy`ego:

Def. Logarytm liczby zespolonej:

Liczbę zespoloną w=u+iv nazywamy logarytmem naturalnym z liczby zespolonej z=x+iy≠0 w =ln z, jeżeli e^w=z, ln z=lnz+i(ϕ+2kπ).

Def. Pochodna funkcji zesoplonej:

Pochodną funkcji w=f(z) w punkcie z₀ nazywamy granicę:

,jeżeli granica istnieje i jest skończona.

Def. Holomorficzność funkcji w punkcie:

Mówimy, że funkcja jest Holomorficzna, jeśli jest różniczkowalna w punkcie z₀ i pewnym jego otoczeniu.

Def. Holomorficzność funkcji w obszarze D:

Mówimy, że funkcja jest holomorficzna w obszerze D, jeśli jest różniczkowalna w każdym punkcie tego obszaru.

Tw. Cauchy'ego-Riemana:

Jeżeli funkcja f(z)=u(x,y)+iv(x,y) ma pochodną w punkcie z₀=x₀+ iy₀ ,to istnieją w tym punkcie pochodne cząstkowe części rzeczywistej u(x,y) i części urojonej v(x,y) oraz pochodne spełniają w tym punkcie równania:

Warunek konieczny, aby f(z) miała pochodną:

Jeżeli część rzeczywista u(x,y) i część urojona v(x,y) funkcji f(z)=u(x,y)+v(x,y) spełniają warunki Cauychego-Riemana w pewnym obszarze D i ponadto pochodne cząstkowe tych funkcji są ciągłe w tym obszarze, to funkcja f(z) w każdym punkcie a=x+iy tego obszaru pochodną f'(z) określoną wzorem:

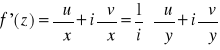
Rozwinięcia funkcji:

---