Termodynamika

Podejście mikroskopowe (~10²³) → termodynamika statystyczna

Podejście makroskopowe → termodynamika fenomenologiczna

Układ zamknięty (nie ma wymiany materii z otoczeniem) → układ otwarty (układy biologiczne)

Zmiana stanu układu → na sposób kwazistatyczny → przez ciąg stanów równowagi

Przykład rozpuszczanie kostki lodu w szklance soku

1. (sok + lód)→(sok)

2. (sok + lód)→→→→→→→......→→→→→→→→→→→→→ →→→→→→→→→→→......→→→→→→→→→→(sok)

Gaz doskonały (1 mol): 3 parametry do opisu - p, V, T

Układ zamknięty

pV = R*T - równanie stanu gazu doskonałego

Zmienne intensywne → T, p

Zmienna ekstensywna → V

Stała - R = 8.31 J/(mol*K)

Załóżmy, że T = const

Przejście między 2 stanami „A” i „B” (p_A > p_B)

p_AV_A = p_BV_B

Przejście od „A” do „B” w sposób kwazistatyczny

Zmieniam wartości parametrów (p, V) o bardzo niewielka ale skończoną wartość → (dp, dV)

Symbol dx → oznacza bardzo niewielką zmianę wartości x

Rzeczywistą zmianę funkcji przybliżam przez ciąg zmian liniowych → od stanu „A” do stanu „B” przechodzę przez wiele stanów pośrednich

dp = tgα dV = (
)dV

Stosunek
nazywamy pochodną funkcji p względem V → znając zależność p = f(V) mogę obliczyć pochodną (matematyka → rachunek różniczkowy) i dalej dla dowolnego dV obliczyć dp

Uogólnienie:

Dowolna funkcja y = f(x, z) → mogę obliczyć pochodną funkcji f względem x przy założeniu z = const → często stosowane oznaczenie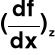
→ znając pochodną mogę dla każdego dx obliczyć dy jako

dy =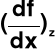
dx

Niewielka zmiana funkcji f = iloczynowi 2 wielkości f = pV

d(pV) =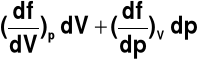
= pdV + Vdp

Funkcja f = sumie 2 wielkości

d(p + V) = dp + dV

Funkcja f = stałej

f = const → df = 0

Wielkości fizyczne wykorzystywane w termodynamice do opisu stanu układu → p, V, T

Praca → L

Praca objętościowa → L₀

dL_O = F*dx =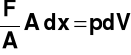

Praca przy skracaniu mięśnia o dl → dL_S

dL_S = F*dl

Praca dla przeniesienia ładunku dq przeciw różnicy potencjałów ψ → dL_Q

dL_Q = ψdq

Praca dostarczenie do układu dn moli substancji przeciw spadkowi stężenia → dL_C

dL_C = μdn

μ - potencjał chemiczny

Uwaga:

Interpretacja μ → gdy dn = 1 mol wtedy praca dL_C = μ

Można pokazać

μ_i =
+ RT ln(c_i)

→ standardowy potencjał chemiczny

c_i → stężenie substancji „i” w roztworze

Uogólnienie → dn₁, dn₂, ...,dn_N

dL_C =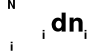

Ciepło → Q

Przykład:

Bilans cieplny

Kostka lodu (m_L, T_L < 273 K) umieszczam w naczyniu o temperaturze otoczenia T_O > 273 K. Ile ciepła (Q) zostanie pobranego z otoczenia ?

Uwaga:

Różnica między ciepłem i praca → pojęcie energii wewnętrznej

Energia wewnętrzna → U

Mikroskopowe ruchy cząsteczek (
kT dla gazu doskonałego) → wszystkie możliwe ruchy cząsteczek (drgania, rotacje, wzbudzenia)

I zasada termodynamiki

dU = dQ + dL

I zasada termodynamiki to zasada zachowania energii z uwzględnieniem równoważności ciepła i pracy

Ten sam efekt (dU) mogę wywołać dostarczając ciepło (dQ przy dL = 0) jak i wykonując pracę (dL przy dQ = 0)

Przejścia Q → L jak i L → Q zawsze odbywają się z udziałem energii wewnętrznej

Konwencja znaków

1. Q, L dostarczone do układu > 0

2. Q, L dostarczone do otoczenia < 0

Przykład:

Praca wykonana przy sprężaniu gazu

dL_O = - pdV = -p*(V_kon - V_poc)

Entropia - S

Procesy w przyrodzie są ukierunkowane i są nieodwracalne

1. przepływ ciepła → od cieplejszego do chłodniejszego

2. ruch klocka przesuwanego po stole → zamiana L → Q jest możliwa ale odwrotny proces nie jest obserwowany (Q → L)

Powstaje problem jak sprawdzić czy dany proces w przyrodzie będzie przebiegać samorzutnie

Wprowadzam nową wielkość fizyczną, której zmiany pozwolą określić możliwość samorzutnego przebiegu procesu

Rozważmy 2 naczynia zawierające 6 cząsteczek (mikroskopowo)

Na ile sposobów mogę zrealizować określony stan układu

A = 6, B = 0 W = 1

A = 5, B = 1 W = 6

A = 4, B = 2 W = 15

A = 3, B = 3 W = 20

A = 2, B = 4 W = 15

A = 1, B = 5 W = 6

A = 0, B = 6 W = 1

W sumie istnieją 64 możliwe stany

Zgodnie z naszą intuicją równy rozkład jest najbardziej prawdopodobny

Prawdopodobieństwo określonego stanu

Moneta → p = ½

Kostka → p = 1/6

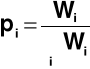
Stan 6 cząstek w naczyniu A

1 stan → p =

Podział 3 + 3

20 stanów → p =

Uwaga:

Układy makroskopowe składają się z bardzo dużej liczby cząstek (~10²³) → bardzo duża liczba możliwych stanów → dla 20 cząstek stan 10+10 mogę zrealizować na 184756 sposobów a stan 20+0 tylko na jeden → niektóre W mogą być bardzo dużymi liczbami inne bardzo małymi → bardzo duże różnice w wartościach p

Definiuje entropię

S = k ln(W)

k = 1.38*10^-23 J/K → stała Boltzmanna

Dwa stany → W₁ (początkowy) i W₂ (końcowy)

dS = S₂ - S₁ =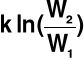
→ > 0, 0, <0

II zasada termodynamiki

Procesy w przyrodzie są ukierunkowane. Układ dąży od stanów mniej prawdopodobnych do bardziej prawdopodobnych. Procesy zachodzą w przyrodzie samorzutnie gdy towarzysząca im zmiana entropii (dS) jest dodatnia

dS > 0

Dla rozważanego układu → dążenie do stanu 3 cząstki w A i 3 cząstki w B

Definicja makroskopowa entropii

Można pokazać, że dla zamkniętego układu z kwazistatycznym przepływem ciepła dQ w procesie odwracalnym związana jest zmiana entropii dS

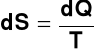
Idealizacja:

1) pojęcie procesu odwracalnego

2) kwazistatyczne przeniesienie dQ przy T₁ = T₂

Proces rzeczywisty

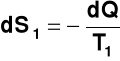
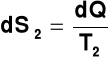
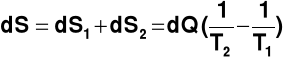
T₁ > T₂ → dS > 0 → proces samorzutny

Uwzględnieniu procesów odwracalnych i nieodwracalnych

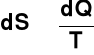
Ze względów praktycznych w termodynamice stosowane są także inne parametry do opisu układu

Entalpia → H

H = U + pV

Energia swobodna → F

F = U - TS

Entalpia swobodna (funkcja Gibbsa) → G

G = H - TS = U + pV - TS

Przykład:

Wykorzystanie entalpii swobodnej

Rozpatrzmy gaz w naczyniu z tłokiem w warunkach izobaryczno-izotermicznych

Warunki izobaryczne p = const (dp = 0)

Warunki izotermiczne T = const (dT = 0)

II zasada termodynamiki

TdS ≥ dQ → 0 ≥ dQ - TdS

• ≥ dQ - TdS = dU - dL - TdS = dU + pdV - TdS =

= dU + pdV + Vdp - TdS - SdT = dU + d(pV) - d(TS) =

= d(U + pV -TS) = dG

W samorzutnej przemianie izobaryczno-izotermicznej

• ≥ dG

Uwaga:

W żywych organizmach procesy przebiegają w warunkach izobaryczno-izotermicznych

Połączenie I i II zasady termodynamiki dla kwazistatycznego procesu odwracalnego (stanu równowagi)

I Zasada dU = dQ + dL

II Zasada TdS = dQ

Równanie Gibbsa

dU = TdS + dL = TdS + dL_O + dL_S + dL_Q + dL_C =

= TdS - pdV + Fdl + ψdq +

Uwaga:

Równanie Gibbsa jest spełnione w stanie równowagi

Przykład:

Opis termodynamiczny reakcji chemicznej w warunkach izobaryczno-izotermicznych → stosuje równanie Gibbsa (Dodatek 1)

αA + βB → γC + δD

dG =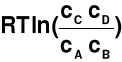
- RTln(K)

K = const → stała równowagi reakcji

Możemy obliczyć zmianę entalpii swobodnej przy dowolnym stężeniu składników → zastosowanie do opisu reakcji biochemicznych → reakcja powstawania kwasu mlekowego z glukozy

Glukoza → 2*(kwas mlekowy)

RTln(K) = 33 kcal/mol → wartość odczytana z tablic

Komórka

Glukoza → c = 0.005 mol/l

Kwas mlekowy → c = 0.001 mol/l

dG = [RT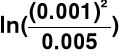
- 33 ] kcal/mol ≈ - 38 kcal/mol

1. Badana reakcja przebiega samorzutnie

2. Powstająca entalpia swobodna może być wykorzystana w innych reakcjach których samorzutny przebieg jest niemożliwy (glukoza + fruktoza → sacharozy + H₂O, dG = 5 kcal/mol)

Ciśnienie osmotyczne

Osmometr Pfeffera

Błona półprzepuszczalna → przepuszcza rozpuszczalnik a nie przepuszcza substancji rozpuszczonej

Rurkę wypełniam roztworem i zanurzam w naczyniu z czystym rozpuszczalniku → rozpuszczalnik wnika do rurki

Ciśnienie hydrostatyczne wewnątrz rurki będzie rosło aż do osiągnięcia stanu równowagi (Δp)

Przy podanych założeniach Δp = ciśnieniu osmotycznemu

Opis termodynamiczny w stanie równowagi

W opisanym zjawisku mam do czynienia z przepływem substancji elektrycznie obojętnej (dq = 0) w stałej temperaturze (dT = 0) i bez pracy skracania mięśnia (dl = 0)

Stosując rozważania jak dla reakcji chemicznej (Dodatek 1)

dG =

μ_i =
+ RT ln(c_i)

wyrażam c_i jako ułamek molowy x_i

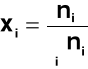
Dla czystego rozpuszczalnika x_i = 1

I → oznacza czysty rozpuszczalnik w naczyniu

II → oznacza roztwór rurce

Potencjały chemiczne rozpuszczalnika w „I” i „II”

μ_I =
+ RTln(x_I) = μ⁰

μ_II =
+ RTln(x_II) = μ⁰ + RT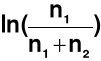

n₁ → liczba moli rozpuszczalnika

n₂ → liczba moli substancji

n₁ >> n₂

Przybliżenie matematyczne →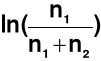
≈ -

μ_II = μ⁰ - RT

Przepływ rozpuszczalnika z I do II

dG =
= (Zmiana w I) + (Zmiana w II) =

= - μ⁰ dn + μ⁰ dn - RT
dn < 0

Taki proces zachodzi samorzutnie

Uwaga:

dn < 0 (wypływ z I) i dn > 0 (napływ do II)

Przepływ rozpuszczalnika z II do I

dG = μ⁰ dn - μ⁰ dn + RT
dn > 0

Taki proces NIE zachodzi samorzutnie

W wyniku napływu rozpuszczalnika μ_II wzrasta do momentu osiągnięcia stanu równowagi termodynamicznej gdy osiąga wartość
równą μ_I

Aby obliczyć zmianę μ korzystam z definicji potencjału chemicznego → praca na przeniesienie 1 mola substancji przeciw spadkowi stężenia równa się zmianie potencjału chemicznego

Praca objętościowa = pdV

p = Δp = π → ciśnienie w stanie równowagi (ciśnienie

osmotyczne)

dV = objętość 1 mola oznaczam V_m

W stanie równowagi

μ_I =
= μ_II + π*V_m

π =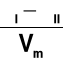
=
=
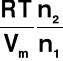
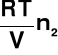
= cRT

c → stężenie molowe [mol/l]

Prawo van't Hoffa

π = cRT

Przykład:

1) c = 1 mol/l, T = 310 K, R = 8.31 J/mol*K

π ≈ 2.6*10⁶ Pa = 26 atm

2) 0.9% NaCl, c = 0.154 mol/l

π ≈ 4*10⁵ Pa = 4 atm

Uwaga:

NaCl 1 cząsteczka brak dysocjacji

Roztwory hiper-, izo- i hipo-toniczne → znaczenie fizjologiczne

Z reguły ciśnienie osmotyczne wyrażamy osmolach

Osmol jest to ciśnienie osmotyczne jakie wywiera w temperaturze 273 K idealny roztwór 1 molowy substancji niedysocjującej

Osmolarność → ciśnienie osmotyczne jednostki objętości

Osmolarność [osm/l] =

NaCl (0.9%) → 9 g/l

M_CZ = 23 + 35.5 = 58.5

Liczba jonów = 2

Osmolarność = 0.308 osm/l

Pomiar ciśnienia osmotycznego

1. metoda klasyczna → osmometr Pfeffera

2. krioskopowa

Temperatura krzepnięcia roztworu obniża się w stosunku do temperatury krzepnięcia czystego rozpuszczalnika proporcjonalnie do liczby osmotycznie czynnych cząsteczek

Stała krioskopowa H₂0 = 1.86⁰ C → 1 mol substancji rozpuszczony w H₂0 → roztwór zamarza w temperaturze
-1.86⁰ C

Stała krioskopowa surowicy = 0.547⁰ C

Termodynamicznie rozważam równowagę jonową - przepływ jonów

1. Błona półprzepuszczalna przepuszcza tylko jony A

2. Zaniedbuje zjawisko osmozy (wiele innych związków których stężenia nie zmieniają się)

3. T= const, p = const

Transport jonów A zgodnie z spadkiem stężenia będzie powodował powstanie różnicy potencjałów, która będzie przeciwdziałać przepływowi jonów

Badam stan równowagi (dG = 0) → nie występuje przepływ jonów

Przekształcam równanie Gibbsa

dU = TdS - pdV + Fdl + ψdq +

dq = Z*F*dn

F → stałą Faradaya (ładunek jednego mola jonów jednowartościowych) = 96500 C

Gdy mam wiele różnych jonów

dq =

dU = TdS - pdV + Fdl + ψF
+
=

= TdS - pdV + Fdl +
=

= TdS - pdV + Fdl +

Potencjał elektrochemiczny

= μ_i + ψFZ_i =
+ RT ln(c_i) + ψFZ_i

Uwaga:

ψ jest identyczne ponieważ zakładam, że wszystkie jony w jednym układzie

W stanie równowagi (dG = 0) dostaje zależność (Dodatek 2)

Uwaga:

Układ składa się z 2 podukładów charakteryzujących się różnymi wartościami ψ → ψ^I i ψ^II

+ RT ln(
) + Z F ψ^I =
+ RT ln(
) + Z F ψ^II

→ identyczne w obu podukładach

Równania Nernsta

Δψ = ψ^I - ψ^II =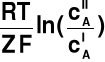

T = 310 K i Z = 1 oraz zmiana ln(x) = 2.303log(x)

Δψ = 0.061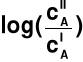

[Δψ] = V

= 10, Δψ = 61 mV

Przykład:

Zastosowanie równania Nernsta dla komórek mięśnia szkieletowego

Jon	Zewnątrz-komórkowe (mM)	Wewnątrz-komórkowe (mM)	Potencjał Nernsta (mV)
K^+	~5	140	-95
Na^+	145	~10	70
Cl^-	115	~5	-90

Uwaga:

Tabela podaje wartości orientacyjne stężeń

Δψ = ψ^I - ψ^II =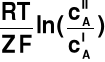
= ψ^W - ψ^Z =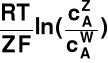

I → wewnątrz-komórkowy = „W”

II → zewnątrz-komórkowy = „Z”

Uwaga:

Równanie Nernsta nie ma zastosowania do żywych komórek

Uwaga:

Z reguły potencjał zewnątrz komórki przyjmuje jako zerowy

Dodatek 1

Reakcja chemiczna w warunkach izobaryczno-izotermicznych stosuje równanie Gibbsa bez zmian ładunku (dq = 0) i bez pracy na skracanie mięśnia (dl = 0)

αA + βB → γC + δD

dG = G_końcowe - G_wyjściowych = d(U + pV -TS) =

= dU+ pdV - TdS =

= TdS - pdV + Fdl + ψdq +
+ pdV - TdS =

=
= (γμ_C + δμ_D) - (αμ_A + βμ_B)

Korzystam z wyrażenia na potencjał chemiczny

μ_A =
+ RTln(c_A) i analogicznie dla B, C i D

dG = γ
+ δ
- α
- β
+

+ RT(γln(c_C)+ δln(c_D) - αln(c_A) - βln(c_B))

Wprowadzam oznaczenie

dG⁰ = γ
+ δ
- α
- β

Matematyka → własności funkcji ln

xln(y) = ln(y^x)

ln(x) + ln(y) = ln(xy)

ln(x) - ln(y) = ln

dG = dG⁰ +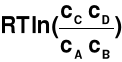

W stanie równowagi termodynamicznej dG = 0

dG⁰ = -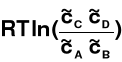
= const

→ stężenie w stanie równowagi sunctancji C i

odpowiednio dla A, B i D

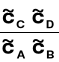
= K = const → stała równowagi reakcji

dG =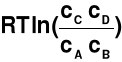
- RTln(K)

Dodatek 2

Równowaga jonowa przy przepływie jonów

Stosuje równanie Gibbsa bez pracy na skracanie mięśnia (dl = 0)

dG = G_końcowe - G_początkowe = d(U + pV -TS) =

= dU+ pdV - TdS =

= TdS - pdV +
+ pdV - TdS =

=
=
= 0

W rozważanej sytuacji

Otrzymujemy ostatecznie

1

14

W9

---