Teoria

Analiza regresji należy do analiz, które możemy wykorzystać wtedy, gdy interesuje nas analiza zróżnicowania zmiennej, zależności między zmiennymi i możliwość przewidywania wartości jeden zmiennej na podstawie drugiej. Dlatego zasadnicze dla analizy regresji jest pojęcie korelacji miedzy zmiennymi. Tak jak korelacja, analiza regresji wymaga ilościowego* poziomu pomiaru zmiennych. Podobnie też, jak korelacja, sama w sobie nie potwierdza zależności przyczynowej między badanymi zmiennymi.

Krótkie powtórzenie z korelacji

Korelację możemy policzyć dla dwóch pomiarów tej samej zmiennej, a także dla dwóch zmiennych, mierzonych u tych samych osób badanych - np. po to, aby odpowiedzieć na pytanie czy istnieje korelacja między wzrostem a wagą? (pomiary są zależne od siebie, wzorzec danych - jak dla grup zależnych). Odzwierciedla ona współzmienność dwóch zmiennych - czyli to, czy kiedy wartości jednej zmiennej zmieniają się, to wartości drugiej zmiennej także. Przyjmuje wartości od -1 (wartości małe jednej zmiennej współwystępują z dużymi wartościami drugiej zmiennej i odwrotnie) do +1 (wartości duże jednej zmiennej współwystępują z dużymi wartościami drugiej zmiennej i małe z małymi); skrajne wartości wskazują na korelację idealną, a zero na brak korelacji. Korelacja nie informuje o kierunku zależności przyczynowej między zmiennymi, a jedynie o tym, że jakaś zależność istnieje. Test istotności korelacji odpowiada na pytanie, czy w populacji, z której pochodzi próba, korelacja jest różna od 0. W SPSS wykonujemy ją: Analiza > Korelacje > Parami, do okienek wpisujemy parę zmiennych. Dla zmiennych, których korelację badamy, możemy także wykonać wykres rozrzutu (Wykresy >Rozrzutu > Prosty) i zaznaczyć na nim linię, odzwierciedlającą związek między zmiennymi (w oknie edycji wykresu: Ustawienia > Opcje).

Gdy istnieje liniowy związek między np. Ilorazem Inteligencji a wynikiem testu - czy mogę przewidzieć, jaki wynik testu będzie miała osoba o określonym II? Oczywiście jeśli nie ma zależności - to pytanie nie ma sensu. Linia z wykresu rozrzutu mogłaby służyć do przewidywania, gdybyśmy wiedzieli, jak ją opisać.

2. 
   gdzie się "zaczyna" - przecina środek układu współrzędnych

3. jak się zmienia przesuwając wzdłuż osi x.

Te wartości pomoże nam ustalić ANALIZA REGRESJI

Analiza regresji służy zatem do określenia równania pozwalającego wyliczyć przewidywane wyniki jednej zmiennej (zależnej, kryterium, y - np. liczba kwiatów) na podstawie wyników jednej lub kilku innych zmiennych (niezależnych, predyktorów, x - np. liczby nasion). W przypadku dwóch zmiennych połączonych zależnością liniową analiza regresji liniowej prowadzi do określenia równania linii prostej obrazującej korelację między jedną a drugą zmienną, wg wzoru y = a + bx.

Po wykonaniu analizy w wydruku znajduję współczynniki:

b dla stałej (stała regresji) = a, b dla predyktora (współczynnik regresji) = b

Y

[Jak wysoko

sięga Kryterium]

średnia

b

aa

X [Bazą jest Predyktor]

składowe błędu składowe wariancji

Równanie regresji dla wyników standardowych: pozwala przewidywać wystandaryzowaną wartość zmiennej zależnej (zy') na podstawie wystandaryzowanej wartości predyktora (zx);

w równaniu używamy także wystandaryzowanego współczynnika regresji, β (beta): zy' = β*zx

w regresji jednoczynnikowej: β = współczynnik korelacji r-Pearsona zmiennej zależnej i predyktora.

Wynik testu t (wartość i poziom istotności) podany w wydruku osobno dla każdego z predyktorów i dla stałej: hipoteza zerowa tego testu mówi, że współczynnik regresji dla danego predyktora jest w populacji równy 0. Jeżeli zatem wynik testu t jest nieistotny, dany współczynnik w równaniu regresji należy pominąć.

Czy przewidywania na podstawie wzoru regresji są dobre? Możemy sprawdzić to wyliczając przewidywaną wartość y dla obserwowanych wartości x i porównując te przewidywania z wartościami obserwowanymi w badaniu. Różnica między wynikiem wyliczonym a faktycznym składa się na błąd. Linia regresji jest bowiem wyznaczana tak, aby minimalizować łączny błąd (aby suma kwadratów wszystkich błędów była jak najmniejsza), więc dla któregoś z wyników może być on całkiem duży!

1 krok. wynik testu analizy wariancji F - jeśli istotność tego testu jest niska (jest on istotny) to znaczy, że sformułowane przez nas równanie wariancji dobrze wyjaśnia zmienną zależną.

2 krok. wartość R² - współczynnika determinacji, który wprost podaje jaki procent wariancji całkowitej wyjaśnia zbudowany przez nas model regresji [ w jednoczynnikowej = (r) ² ]

suma kwadratów całkowita (wariancji) - suma kwadratów błędu

R² [proporcjonalna redukcja błędu] =

suma kwadratów całkowita (wariancji)

Gdy chcemy sprawdzić wpływ więcej niż jednego predyktora:

w równaniu dla wyników surowych zamiast bx występuje wyrażenie b₁x₁+ b₂x₂ + ... dla każdego z predyktorów, gdzie b₁, b₂ - współczynniki regresji kolejnych predyktorów (w wydruku - w kolumnie "b" i wierszu z nazwą predyktora)

w równaniu dla wyników wystandaryzowanych zamiast β*zx występuje wyrażenie β₁*zx₁+ β₂*zx₂ + ... dla każdego z predyktorów, gdzie β₁, β₂ - współczynniki regresji kolejnych predyktorów (w wydruku - w kolumnie "beta" i wierszu z nazwą predyktora)

Czy dany predyktor jest silnie powiązany ze zmienną zależną? Współczynnik b obliczony jest na podstawie wyników surowych, więc bardzo trudno porównać dzięki niemu dwa współczynniki obliczone dla zmiennych o różnych zakresach wartości. Za to wystandaryzowany współczynnik regresji, β (beta) różnych zmiennych możemy wprost porównywać ze sobą.

Do oceny relatywnej wartości wyjaśniającej predyktorów warto też wykorzystać korelacje cząstkowe i semicząstkowe (w oknie regresji liniowej, pod klawiszem Statystyki). Korelacja rzędu zerowego to korelacja predyktora ze zmienną zależną, korelacją cząstkowa to ta sama korelacja po usunięciu wpływu pozostałych predyktorów z obu zmiennych, a korelacja semicząstkowa to korelacja między zmienną zależną a predyktorem po usunięciu tylko z niego wpływu pozostałych predyktorów. (ilustracja w zał.)

Przy więcej niż jednym predyktorze musimy zadecydować o wyborze metody łączenia predyktorów: wybór zależy od celów naszej analizy: jeśli chcemy poszukać najlepszego rozwiązania opisującego nasze dane, najlepiej wybrać metodę, która od razu spowoduje wygenerowanie kilku dobrych modeli. A wybór zwycięzcy będzie należał do nas.

1. Wprowadzanie - wszystkie predyktory wprowadzane są jednocześnie i analizowany jest unikalny wpływa każdego z nich na zmienną zależną

2. Selekcja postępująca - kolejno włączane są najsilniejsze predyktory, przy czym istotność każdego z nich nie może być mniejsza niż założona wartość (najczęściej 0.05)

3. Eliminacja wsteczna- po stworzeniu modelu ze wszystkimi predyktorami kolejno usuwane są najsłabsze, przy czym istotność każdego z nich nie może być większa niż założona wartość (najczęściej 0.10)

4. Krokowa - połączenie dwóch powyższych: kolejno włączane są najsilniejsze predyktory oraz usuwane są najsłabsze

5. Hierarchiczna - predyktory wprowadzane są w kolejności i w blokach ustalonych przez użytkownika.

Który z modeli wybrać? Ten, który ma największą moc wyjaśniającą, czyli przewidywania na podstawie jego wzoru regresji są najlepsze. Jeśli w modelu uwzględniliśmy więcej niż jeden predyktor, lepszą od R² miarą będzie tu skorygowane R² uwzględniające "karę" za zwiększoną liczbę predyktorów oraz liczebność próby. Najlepsze rozwiązanie ma maksymalne skorygowane R² przy minimalnej liczbie predyktorów.

* Zmienne nominalne możemy stosować w analizie regresji pod warunkiem przekodowania ich wartości w dychotomiczne kontrasty (np. -1 i 1).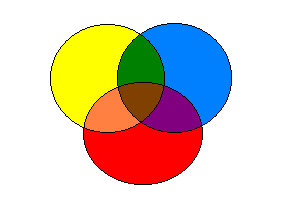
KORELACJĘ można przedstawić jako proporcję pomarańczowej części wspólnej zbiorów do żółtej części oznaczającej niewyjaśniony przez czerwony predyktor obszar zmienności zmiennej zależnej.

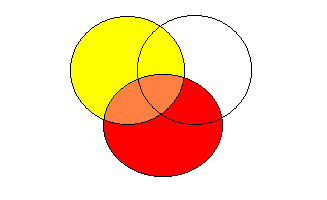
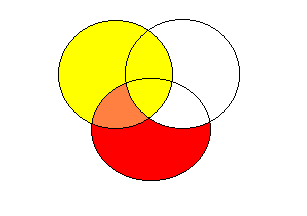
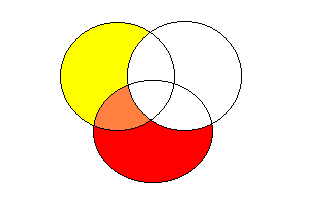
Praktyka

1. Aby sprawdzić, czy powodzenie w nauce można powiązać z ilorazem inteligencji uczniów, w klasie IVa przeprowadzono test na Iloraz Inteligencji oraz test wiedzy ogólnej. Oto wyniki uczniów w obu testach (odpowiednio):

II: 15, 18, 20, 21, 22, 25, 30, 16, 17, 19, 22, 23, 24, 29

test wiedzy:

19, 17, 15, 22, 24, 25, 27, 17, 18, 22, 25, 27, 28, 30

Zapisz równanie regresji (dla wyników surowych i wystandaryzowanych) dla przewidywania: (a) wyniku testu wiedzy z testu II oraz (b) wyniku II z wyniku testu wiedzy. Która analiza ma więcej sensu i dlaczego? Jaka jest moc wyjaśniająca uzyskanych równań?

2. kwiaty.sav

Na podstawie danych dostarczonych przez ogrodnika ustal, jak powinno wyglądać równanie regresji pozwalające przewidywać liczbę kwiatów uzyskanych z konkretnej liczby nasion (dla wyników surowych i wystandaryzowanych). Wykonaj także wykres pozwalający dokonywać takich przewidywań. Jaka jest moc wyjaśniająca tego równania?

3. bieganie.sav

Nauczyciel wychowania fizycznego chciał sprawdzić, czy pogoda ma wpływ na wyniki uczniów w biegach na 100 m. Sprawdził wyniki uczniów jednej klasy w dzień pochmurny i drugi raz w dzień słoneczny. Wyniki poszczególnych uczniów zapisał w tabeli w sekundach. Jakim równaniem można opisać zależność między wynikiem ucznia w dzień pochmurny a wynikiem w dzień słoneczny? Czy taka regresja dobrze wyjaśnia uzyskane wyniki? Zapisz równanie regresji dla wyników surowych i dla wyników wystandaryzowanych.

4. czytelnicy.sav

W klasie 1 Gimnazjum zauważono, że uczniowie którzy czytają dużo książek, mają lepsze oceny z języka polskiego niż uczniowie, którzy czytają mniej. W drugiej klasie wprowadzono program mający zachęcić uczniów do czytania, żeby sprawdzić, czy czytanie wielu książek wpłynie na polepszenie oceny z języka polskiego. Badacze zapisali oceny z języka polskiego w pierwszej i drugiej klasie, a także przeczytaną liczbę książek w obu latach. Dodatkowo kontrolowali również płeć uczniów.

Jakim równaniem regresji można opisać zależność między:

(a) liczbą książek przeczytanych w I klasie a przeczytanych w II klasie? (b) oceną w I klasie a oceną w II klasie? (c) liczbą książek i oceną w I klasie? (d) liczbą książek i oceną w II klasie?

(e) Jakim równaniem regresji można opisać zależność między: liczbą książek przeczytanych w I klasie, przeczytanych w II klasie, oceną w I klasie a oceną w II klasie?

w każdym z tych przypadków odpowiedz: czy regresja dobrze wyjaśnia zależność między zmiennymi?

oraz zapisz równanie regresji dla wyników surowych i dla wyników wystandaryzowanych.

5. pływanie.sav

Robiąc wiosenne porządki w swoich papierach z dokumentacją badań znajdujesz dane z badań pływaków na wyspie Ogao. Zainteresował Cię nowy aspekt tych danych - czy można opisać równaniem regresji zależność miedzy czasem pokonania wyznaczonego dystansu, pulsem spoczynkowym i konkurencją a pulsem wynikowym pływaka. Odpowiedz, czy regresja dobrze wyjaśnia zależność między zmiennymi oraz zapisz równanie regresji dla wyników surowych i dla wyników wystandaryzowanych.

5. pływanie.sav

Robiąc wiosenne porządki w swoich papierach z dokumentacją badań znajdujesz dane z badań pływaków na wyspie Ogao. Zainteresował Cię nowy aspekt tych danych - czy można opisać równaniem regresji zależność miedzy czasem pokonania wyznaczonego dystansu, pulsem spoczynkowym i konkurencją a pulsem wynikowym pływaka. Odpowiedz, czy regresja dobrze wyjaśnia zależność między zmiennymi oraz zapisz równanie regresji dla wyników surowych i dla wyników wystandaryzowanych.

6. All99.sav

Pamiętaj o sprawdzeniu skali odpowiedzi w testowanych zmiennych i zadeklarowaniu braków danych.

„Pieniądze dają szczęście, zdrowie, i nie tylko...” - przypominając sobie ludowe powiedzenie psycholog społeczny zastanawiał się, w jaki sposób wielkość dochodów osobistych (rincome) wpływa na poczucie dobrostanu psychicznego Polaków, a szczególnie na dwie ze składowych dobrostanu: poczucie chęci życia (deslive) i zadowolenie ze swojego zdrowia (sathealth).

Następnie rozbudowując swoją teorię ten sam psycholog zaczął zastanawiać się, czy być może większa liczba zmiennych determinuje poczucie dobrostanu psychicznego. Postanowił skoncentrować się wyłącznie na jednym jego aspekcie: poczuciu chęci życia (deslive). Postawił więc pytanie badawcze: w jaki sposób wiek (age), zarobki (rincome), liczba godzin pracy (hrs) oraz liczba dzieci (childs) wpływają na chęć do życia

7. zadowolenie.sav

Czy temperatura i/lub ilość światła słonecznego mają wpływ na zadowolenie odczuwane danego dnia?

8. truskawki.sav

Na dziesięciu plantacjach truskawek, podobnej wielkości, ale położonych w różnych regionach Polski, miłośnicy truskawek przeprowadzili badania, aby ustalić, czy temperatura powietrza i liczba dni słonecznych w maju mają wpływ na plon truskawek. A może raczej należy uwzględnić liczbę osób zatrudnionych przy pieleniu sadzonek? A może jeszcze inną kombinację tych zmiennych?

8. kawa.sav

Miłośnicy kawy postanowili stwierdzić, czy prawdą jest, ze wypicie kawy może być predyktorem poziomu koncentracji. W badaniu uwzględnili kilka dodatkowych zmiennych, które uznali za możliwe moderatory wpływu kawy. Sprawdź ich tezę. Sprawdź też, które z dodatkowych zmiennych mogą wpływać na wyniki.

1

2

Analiza regresji - z teorią w praktykę

mgr Ewa Lipiec Zastosowanie komputerów, semestr letni 2004/05

korelacja semicząstkowa

zmienna zależna

układ trzech zmiennych:

obszary oznaczają zmienność

części wspólne obszarów oznaczają wspólną zmienność

predyktor 2 (zakłócający)

predyktor 1 (badany)

korelacja rzędu zerowego

korelacja cząstkowa

---