Definicja zdania
Zdaniem w logice nazywamy wypowiedź zbudowaną zgodnie z zasadami ustalonego języka, której można przypisać jednoznacznie jedną z dwu ocen: prawdę lub fałsz -nazywane wartościami logicznymi danego zdania i oznaczane odpowiednio symbolami ![]()
, ![]()
.
Definicja formy zdaniowej
Formą zdaniową nazywamy wypowiedź, która może zawierać zmienne, zbudowaną według takich samych reguł gramatycznych jak zdanie. Fakt, że ![]()
jest zmienną formy zdaniowej![]()
oznaczamy pisząc ![]()
.
Uwaga 1. Każde zdanie jest formą zdaniową.
Uwaga 2. Istnieją formy zdaniowe nie będące zdaniami.
Zasada tworzenia zdań z form zdaniowych
Z formy zdaniowej można otrzymać zdanie na dwa sposoby:
Przez podstawienie w miejsce zmiennych, obiektów w stosunku do których będziemy mogli stosować oceny logiczne prawdziwości i fałszu.
Przez stosowanie kwantyfikatorów w odniesieniu do występujących w formie zdaniowej zmiennych. Stosowanie kwantyfikatora dużego do formy
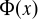
oznacza utworzenie zdania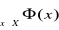
, które czytamy: „ dla każdego elementu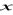
ze zbioru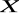
jest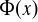
”. Stosowanie kwantyfikatora małego do formy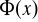
oznacza utworzenie zdania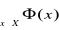
, które czytamy: „ istnieje element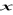
ze zbioru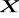
taki, że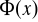
”.
Definicja
Jeśli zakresem zmienności zmiennej ![]()
w formie ![]()
jest zbiór ![]()
, to zbiór tych wszystkich elementów zbioru ![]()
, które podstawione w miejsce zmiennej ![]()
w formie ![]()
dają zdanie prawdziwe oznaczamy jako ![]()
.
Przykład. Przedział domknięty ![]()
gdzie ![]()
, ![]()
są liczbami rzeczywistymi takimi, że ![]()
można zapisać jako ![]()
.
Zasada weryfikacji prawdziwości zdań złożonych
Oceny prawdziwości zdań złożonych dokonujemy na podstawie informacji o prawdziwości ich składników zgodnie z następującymi ustaleniami:
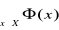
jest prawdą wtedy i tylko wtedy gdy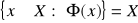
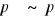
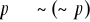
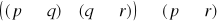
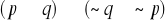




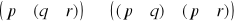
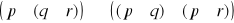



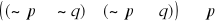

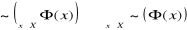
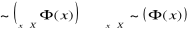
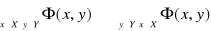
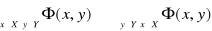
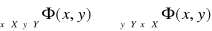
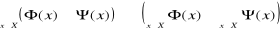
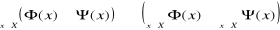
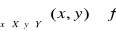
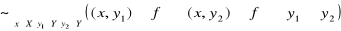
.Jeśli X ⊂ R i Y = R, to funkcję f nazywać będziemy funkcją rzeczywistą zmiennej rzeczywistej.
Jeśli X = N i Y = R, to funkcję f nazywać będziemy nieskończonym ciągiem liczbowym o wyrazach rzeczywistych.
Jeśli X = N i Y = N i f jest funkcją wzajemnie jednoznaczną, to f nazywać będziemy permutacją zbioru liczb naturalnych.
Jeśli X = {1, 2, ..., m}×{1, 2, ..., n} oraz Y = R, to funkcję f nazywać będziemy macierzą o m wierszach i n kolumnach.
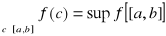
;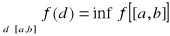
;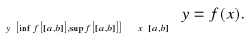
Jeśli
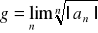
, to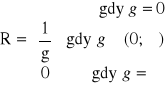
Jeśli
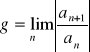
, to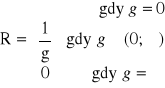
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
![]()
jest prawdą wtedy i tylko wtedy gdy ![]()
Definicja tautologii
Prawem logicznym albo tautologią nazywamy zdanie złożone, które jest prawdziwe niezależnie od wartości logicznych zdań składowych.
Wykaz ważniejszych tautologii
Zasada prowadzenia dowodu
Każdy element rozumowania zwanego dowodem w dowolnej teorii matematycznej daje się uzasadnić tautologią albo aksjomatem tej teorii.
Definicja iloczynu kartezjańskiego zbiorów
Iloczynem kartezjańskim zbiorów ![]()
i ![]()
nazywamy zbiór wszystkich par uporządkowanych ![]()
takich, że ![]()
i ![]()
. Iloczyn kartezjański zbiorów ![]()
i ![]()
oznaczamy jako ![]()
.
Definicja funkcji
Każdy podzbiór ![]()
iloczynu kartezjańskiego ![]()
zbiorów ![]()
i ![]()
nazywamy funkcją odwzorowującą zbiór ![]()
w zbiór ![]()
o ile spełnia on następujące dwa warunki:
Fakt, że ![]()
jest funkcją odwzorowującą zbiór ![]()
w zbiór ![]()
oznaczamy pisząc ![]()
. Zbiór funkcji odwzorowujących ![]()
w ![]()
oznaczamy jako ![]()
.
Definicja funkcji różnowartościowej
Jeśli ![]()
to mówimy, że ![]()
jest różnowartościowa jeśli spełnia następujący warunek:
![]()
Definicja funkcji odwzorowującej zbiór X na zbiór Y
Jeśli ![]()
to mówimy, że ![]()
odwzorowuje zbiór ![]()
na zbiór ![]()
jeśli spełnia następujący warunek:
![]()
.
Definicja funkcji wzajemnie jednoznacznej
Jeśli ![]()
to mówimy, że ![]()
jest funkcją wzajemnie jednoznaczną jeśli jest funkcją różnowartościową odwzorowującą zbiór ![]()
na zbiór ![]()
.
Definicja funkcji odwrotnej
Niech ![]()
będzie funkcją wzajemnie jednoznaczną. Wówczas zbiór ![]()
jest funkcją wzajemnie jednoznaczną odwzorowującą zbiór ![]()
na zbiór ![]()
. Nazywamy go funkcją odwrotną do funkcji ![]()
i oznaczamy jako ![]()
.
Definicja złożenia funkcji
Niech ![]()
, ![]()
przy czym ![]()
. Zbiór ![]()
jest funkcją odwzorowująca zbiór ![]()
w zbiór ![]()
. Nazywamy go złożeniem funkcji ![]()
i ![]()
i oznaczamy jako ![]()
.
Definicja obrazu zbioru przez funkcję
Niech ![]()
. Dla dowolnego zbioru ![]()
zbiór ![]()
nazywamy obrazem zbioru ![]()
przez funkcję ![]()
i oznaczamy jako ![]()
.
Definicja przeciwobrazu zbioru przez funkcję
Niech ![]()
. Dla dowolnego zbioru![]()
zbiór ![]()
nazywamy przeciwobrazem zbioru ![]()
przez funkcję ![]()
i oznaczamy jako ![]()
.
Definicja dziedziny i zbioru wartości funkcji
Niech f : X → Y. Wówczas zbiór X nazywamy dziedziną funkcji i oznaczamy jako Df natomiast f[X] nazywamy zbiorem wartości funkcji i oznaczamy jako Wf.
Przykłady rodzin funkcji
Niech f : X → Y.
Ciągłość. Niech x0 ∈ R.
Definicja otoczenia, sąsiedztwa i punktu skupienia
Niech a, b ∈ R i a < x0 < b. Otoczeniem (otoczeniem lewostronnym, prawostronnym) punktu x0 nazywamy przedział (a, b) ((a, x0], [x0 , b)). Rodzinę zbiorów będących otoczeniami (otoczeniami lewostronnymi, prawostronnymi) punktu x0 oznaczać będziemy symbolem O(x0) (O -(x0), O+(x0)). Każdy zbiór postaci U \ {x0}, gdzie U ∈ O(x0) (U ∈ O -(x0), U ∈ O+(x0)) nazywać będziemy sąsiedztwem (sąsiedztwem lewostronnym, prawostronnym) punktu x0. Rodzinę zbiorów będących sąsiedztwami (sąsiedztwami lewostronnymi, prawostronnymi) oznaczać będziemy symbolem S(x0) (S -(x0), S+(x0)).
Niech X ⊂ R. Mówimy, że x0 jest punktem skupienia (lewostronnym, prawostronnym punktem skupienia) zbioru X, jeśli
![]()
(![]()
, ![]()
).
Zbiór punktów skupienia (lewostronnych, prawostronnych punktów skupienia) zbioru X oznaczamy jako Xd (Xd-, Xd+).
Niech f będzie funkcją rzeczywistą zmiennej rzeczywistej.
Definicja granicy funkcji
Niech x0 ∈ (Df)d (x0 ∈ (Df)d-, x0 ∈ (Df)d+ ). Mówimy, że g ∈ R jest granicą (granicą lewostronną, prawostronną) funkcji f w punkcie x0, gdy
![]()
(![]()
, ![]()
).
Fakt, że g jest granicą (granicą lewostronną, prawostronną) zapisujemy symbolicznie
![]()
(![]()
, ![]()
).
Definicja ciągłości funkcji
Niech x0 ∈ Df.
f jest ciągła w x0 ⇔ x0 ∉ (Df)d ∨ ![]()
f jest lewostronnie ciągła w x0 ⇔ x0 ∉ (Df)d- ∨ ![]()
f jest prawostronnie ciągła w x0 ⇔ x0 ∉ (Df)d+ ∨ ![]()
Niech X ⊂ R. Mówimy, że f jest ciągła w zbiorze X, gdy jest ciągła w każdym punkcie tego zbioru. Zbiór punktów ciągłości funkcji f oznaczać będziemy przez Cf.
Uwaga. Funkcja jest ciągła w punkcie x0 wtedy i tylko wtedy, gdy jest ciągła lewostronnie i prawostronnie w tym punkcie.
Rodzaje nieciągłości - definicja
Niech x0 ∈ Df. Mówimy, że x0 jest punktem nieciągłości pierwszego rodzaju funkcji f, jeśli istnieją i są skończone granice ![]()
, ![]()
przy czym ![]()
lub ![]()
Mówimy, że x0 jest punktem nieciągłości drugiego rodzaju, jeśli x0 ∉ Cf i x0 nie jest punktem nieciągłości pierwszego rodzaju.
Twierdzenia o funkcjach ciągłych
Twierdzenie Weierstrassa-Darboux. Niech a, b ∈ R, a < b, [a, b] ⊂ Cf. Wówczas funkcja f jest ograniczona na [a, b]. Ponadto
Twierdzenie o klasie funkcji ciągłych
Funkcje elementarne są ciągłe. Działania algebraiczne wykonywane na funkcjach ciągłych dają funkcje ciągłe. Złożenia funkcji ciągłych są funkcjami ciągłymi. Funkcje odwrotne do funkcji ciągłych (o ile istnieją) też są funkcjami ciągłymi.
Uwaga. Jeśli x0 ∈ Cf i f(x0) > 0, to ![]()
Definicja ciągłości jednostajnej
Niech X ⊂ Df. Mówimy, że funkcja f jest jednostajnie ciągła na X, jeśli
![]()
Uwaga. Jeśli f jest jednostajnie ciągła na zbiorze X, to jest ciągła w każdym punkcie tego zbioru.
Uwaga. Istnieją funkcje ciągłe w każdym punkcie zbioru X lecz nie będące jednostajnie ciągłymi na tym zbiorze.
Uwaga. Funkcja ciągła na przedziale domkniętym i ograniczonym jest na tym przedziale jednostajnie ciągła.
SZEREGI LICZBOWE
Definicja szeregu
Niech ![]()
będzie ciągiem liczbowym. Szeregiem liczbowym nazywamy ciąg ![]()
gdzie 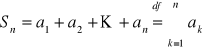
. Taki szereg liczbowy oznaczamy symbolem ![]()
. Liczbę ![]()
nazywamy n-tym wyrazem, a liczbę ![]()
- n-tą sumą tego szeregu.
Definicja szeregu zbieżnego, rozbieżnego i sumy szeregu
Mówimy, że szereg ![]()
jest zbieżny jeśli ciąg ![]()
jest zbieżny do granicy skończonej zwanej w tym przypadku sumą szeregu i oznaczanej symbolem identycznym z symbolem szeregu.
Mówimy, że szereg ![]()
jest rozbieżny gdy nie jest zbieżny.
Twierdzenie o kombinacji liniowej szeregów
Jeśli szeregi ![]()
, ![]()
są zbieżne odpowiednio do liczb ![]()
i ![]()
, to dla dowolnych liczb rzeczywistych ![]()
, ![]()
zbieżny jest również szereg 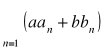
przy czym suma tego szeregu wynosi ![]()
.
Twierdzenie o zbieżności szeregu geometrycznego
Szereg ![]()
zwany szeregiem geometrycznym o podstawie ![]()
jest zbieżny wtedy i tylko wtedy gdy ![]()
.
Twierdzenie o zbieżności szeregu harmonicznego
Szereg ![]()
zwany szeregiem harmonicznym rzędu ![]()
jest zbieżny wtedy i tylko wtedy gdy ![]()
.
Warunek konieczny zbieżności szeregu
Jeśli szereg ![]()
jest zbieżny to ![]()
.
Niech ![]()
i ![]()
oznaczają szeregi liczbowe.
Uwaga. Jeśli ciągi ![]()
i ![]()
różnią się skończoną ilością wyrazów, to oba szeregi ![]()
i ![]()
są jednocześnie zbieżne lub rozbieżne.
KRYTERIA ZBIEŻNOŚCI SZEREGÓW
Kryterium porównawcze
Jeśli ![]()
to ze zbieżności szeregu ![]()
wynika zbieżność szeregu ![]()
i z rozbieżności szeregu ![]()
wynika rozbieżność szeregu ![]()
.
Kryterium ilorazowe
Jeśli ![]()
oraz ![]()
, to oba szeregi ![]()
i ![]()
są jednocześnie zbieżne lub rozbieżne.
Kryterium Cauchy'ego
Jeśli ![]()
to ![]()
jest zbieżny gdy ![]()
i rozbieżny gdy ![]()
.
Kryterium d'Alemberta
Jeśli ![]()
oraz 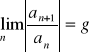
to szereg ![]()
jest zbieżny gdy ![]()
i rozbieżny gdy ![]()
.
Kryterium Raabego
Jeśli ![]()
oraz 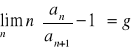
to szereg ![]()
jest zbieżny gdy ![]()
i rozbieżny gdy ![]()
.
Twierdzenie o zagęszczaniu
Jeśli ![]()
jest ciągiem nierosnącym o wyrazach nieujemnych to szeregi ![]()
i 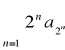
są jednocześnie zbieżne lub rozbieżne.
Kryterium Dirichleta
Jeśli ciąg sum częściowych szeregu ![]()
jest ograniczony oraz ![]()
jest ciągiem nierosnącym zbieżnym do zera to szereg 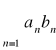
jest zbieżny.
Kryterium Abela
Jeśli szereg ![]()
jest zbieżny i ciąg ![]()
jest monotoniczny i ograniczony, to szereg 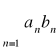
jest zbieżny.
Kryterium Leibniza
Jeśli ![]()
jest ciągiem nierosnącym zbieżnym do 0, to szereg 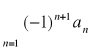
zwany szeregiem naprzemiennym jest zbieżny.
Definicja zbieżności bezwzględnej
Mówimy, że szereg ![]()
jest bezwzględnie zbieżny, gdy zbieżny jest szereg ![]()
.
Uwaga Każdy szereg zbieżny bezwzględnie jest zbieżny.
Uwaga Istnieją szeregi zbieżne lecz nie bezwzględnie zbieżne.
Definicja szeregu zbieżnego warunkowo
Szereg zbieżny lecz nie bezwzględnie zbieżny nazywamy szeregiem zbieżnym warunkowo.
Twierdzenie
Jeśli szereg ![]()
jest bezwzględnie zbieżny, to dla dowolnej permutacji ![]()
liczb naturalnych szereg 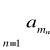
jest zbieżny i ma taką samą sumę jak szereg ![]()
.
Twierdzenie Cauchy'ego
Jeśli szeregi ![]()
i ![]()
są bezwzględnie zbieżne, to szereg 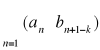
jest zbieżny przy czym suma tego szeregu wynosi ![]()
gdzie ![]()
oznacza sumę szeregu ![]()
, a ![]()
sumę szeregu ![]()
.
Twierdzenie Riemanna
Niech ![]()
będzie szeregiem warunkowo zbieżnym. Dla dowolnego ![]()
istnieje permutacja ![]()
zbioru liczb naturalnych taka, że ![]()
jest sumą szeregu 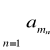
.
CIĄGI I SZEREGI FUNKCYJNE
Przyjmijmy, że ![]()
.
Definicja ciągu funkcyjnego
Ciągiem funkcyjnym określonym na zbiorze ![]()
nazywamy każdą funkcję odwzorowującą zbiór ![]()
w zbiór ![]()
. Załóżmy, że ![]()
. Wówczas dla oznaczenia ciągu funkcyjnego, którego n-tym wyrazem jest funkcja ![]()
używamy oznaczenie ![]()
.
Niech ![]()
oznacza ciąg funkcyjny taki, że ![]()
. Niech ![]()
.
Definicja zbieżności punktowej ciągu funkcyjnego
Mówimy, że ciąg ![]()
jest punktowo zbieżny na zbiorze ![]()
do funkcji ![]()
jeśli ![]()
.
Definicja zbieżności jednostajnej ciągu funkcyjnego
Mówimy, że ciąg ![]()
jest jednostajnie zbieżny na zbiorze ![]()
do funkcji ![]()
jeśli ![]()
.
Fakt, że ![]()
jest punktowo zbieżny do funkcji ![]()
na zbiorze ![]()
oznaczamy pisząc ![]()
.
Fakt, że ![]()
jest jednostajnie zbieżny do funkcji ![]()
na zbiorze ![]()
oznaczamy pisząc ![]()
![]()
![]()
.
Twierdzenie
Jeśli ![]()
![]()
![]()
to ![]()
.
Uwaga Twierdzenie odwrotne nie jest prawdziwe.
Twierdzenie Weierstrassa
Niech ![]()
dla ![]()
. Wówczas ![]()
Twierdzenie
Jeśli ![]()
i ![]()
jest ciągła na X, to również f jest ciągła na X.
Definicja funkcji przedziałami liniowej
Niech ![]()
, ![]()
i niech ![]()
. Funkcję f nazywamy przedziałami liniową na przedziale ![]()
jeśli f jest ciągła na ![]()
oraz jeśli istnieją układy liczb![]()
oraz ![]()
oraz ![]()
takie, że ![]()
Twierdzenie
Każda funkcja ciągła w przedziale domkniętym jest granicą jednostajnie zbieżnego ciągu funkcji przedziałami liniowych na tym przedziale.
Definicja szeregu funkcyjnego
Niech ![]()
będzie ciągiem funkcyjnym takim, że ![]()
. Szeregiem funkcyjnym nazywamy ciąg funkcyjny ![]()
gdzie ![]()
. Taki szereg funkcyjny oznaczamy symbolem ![]()
. Funkcję ![]()
nazywamy n-tym wyrazem a funkcję ![]()
nazywamy n-tą sumą tego szeregu.
Definicja zbieżności punktowej i jednostajnej szeregu funkcyjnego
Szereg funkcyjny ![]()
jest punktowo (jednostajnie) zbieżny na zbiorze X gdy ciąg funkcyjny ![]()
jest punktowo (jednostajnie) zbieżny na tym zbiorze.
Funkcję będącą granicą ciągu funkcyjnego ![]()
o ile ona istnieje nazywamy sumą szeregu ![]()
i oznaczamy tak jak sam szereg.
Wniosek. Szereg funkcyjny ![]()
jest punktowo zbieżny na zbiorze X wtedy i tylko wtedy gdy ![]()
jest zbieżny.
Wniosek. Jeśli szereg funkcyjny ![]()
jest jednostajnie zbieżny na zbiorze X, to jest punktowo zbieżny na tym zbiorze.
Twierdzenie Weierstrassa
Niech ![]()
będzie szeregiem funkcyjnym funkcji określonych na zbiorze X, a ![]()
szeregiem liczbowym zbieżnym takim, że ![]()
.
Wówczas szereg ![]()
jest jednostajnie zbieżny oraz ![]()
jest bezwzględnie zbieżny.
Definicja szeregu potęgowego
Niech ![]()
i niech ![]()
dla ![]()
. Załóżmy, że
![]()
jest funkcją taką, że ![]()
![]()
jest funkcją taką, że ![]()
dla ![]()
i ![]()
.
Szereg funkcyjny ![]()
nazywamy szeregiem potęgowym o środku w punkcie ![]()
i współczynnikach ![]()
. Oznaczamy go symbolicznie jako ![]()
.
Definicja promienia zbieżności szeregu potęgowego
Liczbę 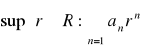
nazywamy promieniem zbieżności szeregu potęgowego ![]()
.
Uwaga. Promień zbieżności szeregu potęgowego nie zależy od jego środka ![]()
a jedynie od współczynników ![]()
dla ![]()
.
Uwaga. Promień zbieżności szeregu potęgowego jest zawsze liczbą nieujemną.
Niech R oznacza promień zbieżności szeregu potęgowego ![]()
.
Twierdzenie Cauchy'ego - Hadamarda
Twierdzenie o punktach zbieżności szeregu potęgowego
Jeśli R = 0, to szereg ![]()
jest zbieżny jedynie dla ![]()
.
Jeśli R = ∞, to szereg ![]()
jest zbieżny bezwzględnie dla dowolnego ![]()
.
Jeśli R ![]()
, to szereg ![]()
jest zbieżny bezwzględnie dla dowolnego ![]()
oraz rozbieżny dla ![]()
.
Definicja przedziału zbieżności szeregu potęgowego
Przedziałem zbieżności szeregu ![]()
nazywamy zbiór 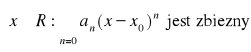
Twierdzenie
Szereg potęgowy ![]()
jest zbieżny jednostajnie w każdym przedziale domkniętym zawartym w przedziale zbieżności szeregu potęgowego.
8
Wyszukiwarka
Podobne podstrony:
Zadania dodatkowe z AM (5), Budownictwo studia pł, SEMESTR I, SEMESTR I, matematyka, Analiza matemat
materiały budowlane, Budownictwo studia pł, SEMESTR I, SEMESTR I, materiały budowlane, materiały lab
Materialy budowlane asfalt, Budownictwo studia pł, SEMESTR I, SEMESTR I, materiały budowlane, materi
ANALIZA MATEMATYCZNA, STUDIA, Polibuda - semestr I, Matematyka, Matematyka, Ściągi
matematyka, STUDIA, Polibuda - semestr I, Matematyka, Matematyka, Ściągi
twierdzenie rolla, STUDIA, Polibuda - semestr I, Matematyka
GEOMETRIA ANALITYCZNA, STUDIA, Polibuda - semestr I, Matematyka, Matematyka, Ściągi
dyskretna2, Studia, PWR, 2 semestr, Matematyka dyskretna
dyskretna-przyklad-zadania-na-pierwsze-kolokwium, Studia, PWR, 2 semestr, Matematyka dyskretna, kolo
dyskretna-egzamin-zaoczne-szablon, Studia, PWR, 2 semestr, Matematyka dyskretna, kolokwium
dyskretna-egzamin-zaoczne, Studia, PWR, 2 semestr, Matematyka dyskretna, kolokwium
równania różniczkowe I rzędu niejednorodne, Studia, EiT semestr-1, Matematyka (starsze roczniki), Ma
Sprawozdanie nr 1 CECHY TECHNICZNE MATERIAfLOW BUDOWLANYCH, Budownictwo studia pł, sprawka maater
fizyka - sprawko t1a, Budownictwo studia pł, Fizyka-sprawozdanie
sprawouuzdanie uunr 1.x, Budownictwo studia pł, sprawka maateriały budowlane
więcej podobnych podstron