KOSMOLOGICZNE ROZWIĄZANIA RÓWNAŃ EINSTEINA.

W rozdziale podstawy OTW stwierdzono, że einsteinowskie równania pola to w ogólnosci dość skomplikowany układ 10 równań różniczkowych, w których niewiadomymi są składowe g_ij tensora metrycznego. Układ ten udało się analitycznie rozwiązać dla kilku prostych sytuacji, w tym dla przypadku przestrzeni jednorodnie wypełnionej materią o stałej gęstości ρ . Przypadek ten odpowiada właśnie kosmologii czyli opisowi własności i ewolucji Wszechświata jako całości.

Prawa strona równań Einsteina opisująca rozkład masy (energii) w przestrzeni - tzw. tensor energii-pędu T_ij - brana jest z mechaniki ośrodków ciągłych i ma w tym przypadku następującą postać:

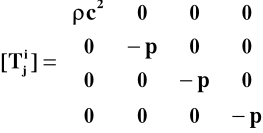
(1)

gdzie ρ to średnia gęstość materii we Wszechświecie zaś p to jej ciśnienie (obecnie praktycznie zaniedbywalne).

Dla określenia lewej strony równań Einsteina startuje się z interwału czasoprzestrzennego w postaci:

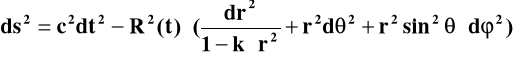
(2)

(patrz uzasadnienie w rozdziale o interwałach w przestrzeni o różnej krzywiźnie).

Przypominamy, że R to tzw. czynnik skalujący odległości przestrzenne zaś k charakteryzuje typ krzywizny przestrzeni: k = 0 odpowiada przestrzeni euklidesowej, k = +1 przestrzeni o geometrii typu sferycznego zaś k = -1 geometrii typu hiperbolicznego.

Z formuły (2) mamy więc składowe g_ij w postaci: g₀₀ = 1,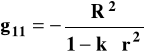
,

g₂₂ = - R²r², g₃₃ = -R²r²sin² Podstawową naszą niewiadomą jest jawna postać zależności R(t). Lewa strona równań Einsteina to dość skomplikowane funkcje pochodnych tensora g_ij. Wstawiając tam zapisane powyżej wielkości na g_oo, g₁₁, g₂₂ , g₃₃ otrzyma się po dość długich przekształceniach układ dwóch równań w postaci:

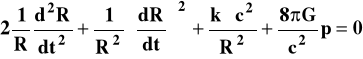
(3)

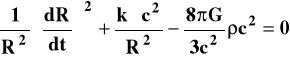
(4)

(w dalszym ciągu będziemy używali przyjętego powszechnie skrótowego oznaczenia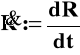
.

Równanie (4) można łatwo przekształcić do postaci:

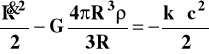
(4a)

Ponieważ jednak 4R³/3 =V to wielkość o wymiarze objętości zaś ρV = M ma wymiar masy więc (4a) można (po wymnożeniu stronami przez dowolną jednostkową masę m=1) zapisać:

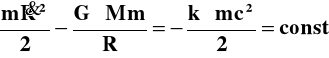
(4b)

Równanie to przypomina formalnie znany z mechaniki klasycznej bilans energii kinetycznej i potencjalnej cząstki m w polu grawitacyjnym masy M, gdyż pierwszy z lewej wyraz w (4b) to jakby energia kinetyczna zaś drugi to energia potencjalna.

Skorzystamy też z prawa zachowania masy w ekspandującym obszarze o promieniu R, (warunek ciągłości):

ρV = M = const lub ρR³ = const lub:

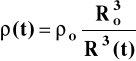
(5)

gdzie indeks “0” odnosi się do dowolnej (np. obecnej) chwili t_o .

Rozpatrzmy teraz poszczególne przypadki rozwiązania równania (4a).

I. k = 0. (przestrzeń globalnie euklidesowa).

Tutaj prawa strona w (4a) równa się zero, po lewe zaś stronie wielkość ρ zastępujemy zależnością (5). Otrzymujemy proste równanie różniczkowe:

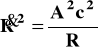
(6)

gdzie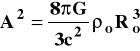
zawiera wszystkie wielkości stałe. Rozwiązanie równania (5) ma postać

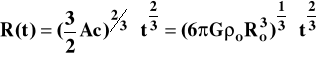
(7)

Zależność tempa ekspansji od czasu wyrazi się:

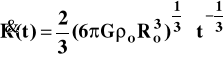
(8)

i zmierza do zera gdy
. Natomiast tzw. parametr Hubble'a:

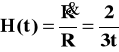
(9)

też zmierza z czasem do zera. Korzystając z otrzymanych powyżej rezultatów można też wyrazić zależność od czasu średniej gęstości materii :

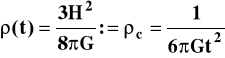
(10)

Jest to tzw. “gęstość krytyczna” charakterystyczna właśnie dla wszechświata o geometrii euklidesowej. Dla gęstości ρ>ρ_c mamy bowiem przestrzeń o geometrii typu sferycznego z k = +1 zaś dla ρρ_c przestrzeń ma geometrię hiperboliczną

z k = -1.

II. k = +1. (geometria typu sferycznego).

W tym przypadku równanie (4a) po podstawieniu (5) jest w postaci:

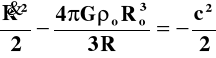
(11)

W postaci całkowej wygląda to następująco:

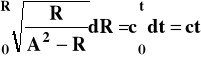
(12)

gdzie, jak poprzednio podstawiono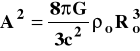
.

Dla rozwiązania (12) dokonuje się podstawienia:

(13)

gdzie  to bezwymiarowy parametr pomocniczy.

Wówczas zależność R(t) otrzymujemy w postaci parametrycznej:

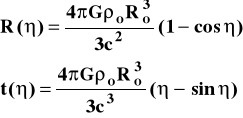
(14)

W chwili początkowej, dla  i t=0 mamy R(0) = 0. (początkowa osobliwość).

Wartości    odpowiada maksymalna wartość czynnika R = R_max:

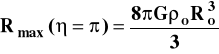
(15)

Odpowiada to czasowi t:

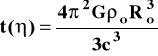
(16)

Następnie, dla 2>> wielkość R(t) maleje (Wszechświat kurczy się) i osiąga znów osobliwość R = 0 dla    (ilustruje to rysunek na końcu tego rozdziału).

III. k = -1. (geometria hiperboliczna).

W tym przypadku równanie (4) jest podobne do (11) z drobną (lecz istotną) zmianą znaku po prawej stronie:

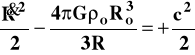
(17)

zaś równanie (12) też jest podobne z drobną różnicą znaku pod pierwiastkiem:

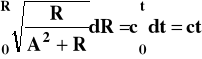
(18)

Tu także dokonuje się podstawienia (lecz z sinusem hiperbolicznym):

(19)

i otrzymuje się rozwiązania w postaci:

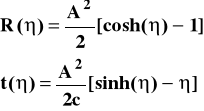
(20)

Tu także w chwili początkowej    (oraz t = 0 ) mamy osobliwość w postaci R = 0. Natomiast już dalsza ekspansja R(t) jest nieodwracalna (narastająca).

Graficznie zależność R(t) dla wszystkich trzech omówionych przypadków ilustruje poniższy rysunek.

Jak widać, wszystkie trzy rozwiązania zbiegają się w początkowej osobliwości R(t=0) = 0. W jej pobliżu nie można już zaniedbywać ciśnienia ośrodka, który przy tych gęstościach i temperaturach jest już ultra relatywistycznym gazem. Prześledzimy więc zachowanie się rozwiązań w tych warunkach.

Wychodzimy ze znanej postaci I-szej zasady termodynamiki (dla ekspansji adiabatycznej):

dE +p dV = 0 (21)

gdzie energia ośrodka E =  V = ρ c²R³ (zaś   ρ c² to gęstość energii). Równanie stanu gazu dla relatywistycznego przypadku ma postać

(22)

Wstawiając powyższe podstawienia do (21), różniczkując i porządkując otrzymamy:

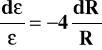
(23)

czyli  R⁴ = const. Zamiast równania (5) mamy więc teraz:

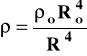
(24)

Taką właśnie postać na ρ musimy teraz wstawić do równania (4). Otrzymamy wówczas:

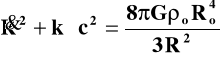
(25)

Dla przypadku k = 0 po prostym wycałkowaniu otrzymamy

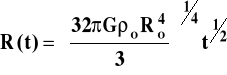
(26)

Dla pozostałych dwóch przypadków podobnie otrzymuje się w pobliżu osobliwości zależność typu:

(27)

Jest to bardzo ważna zależność, która przyda nam, się przy opisie wczesnych etapów ewolucji wszechświata. Odnotujmy tu jednak, że uwzględnienie ciśnienia gazu nie chroni rozwiązań kosmologicznych przed osobliwością w chwili t = 0.

RÓWNANIA KOSMOLOGICZNE WYPROWADZONE Z TEORII

NEWTONOWSKIEJ.

Otrzymane w poprzednim rozdziale (“Kosmologiczne rozwiązania równań Einsteina”) równania kosmologiczne Friedmanna (r-nie (3) i (4)) można także formalnie otrzymać na gruncie klasycznej teorii newtonowskiej. Rozważmy w tym celu pewien dowolny kulisty obszar wszechświata - kulę o promieniu r wypełnioną jednorodnie masą M o gęstości ρ.

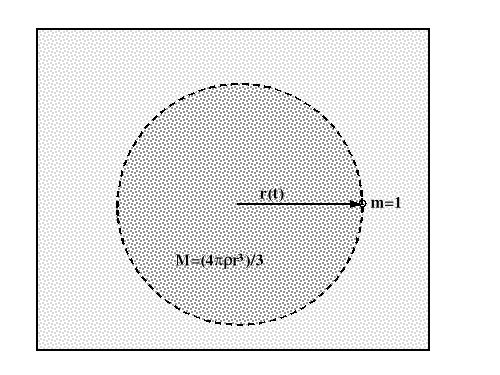
Ze względu na ogólną ekspansję wszechświata promień naszej sfery zmienia się w czasie:
(gdzie
jednostkowy wersor zaś R(t). to zmienny w czasie czynnik skali). Jednostkowa cząstka próbna m ma energię kinetyczną (wynikającą z udziału w ekspansji) oraz energię potencjalną w polu grawitacyjnym masy M:

(28)

co można przekształcić do postaci (przyjmując
)

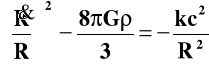
(28a)

gdzie -kc² = 2E zaś k = 0, +1, -1. Jest to odpowiednik równania (4) z poprzedniego rozdziału.

Przy ekspansji adiabatycznej mamy równanie (z I zasady termodynamiki)

dU +p dV =0. Energia wewnętrzna w naszej kuli to energia związana z masą M czyli
. Wówczas różniczkowania dają nam

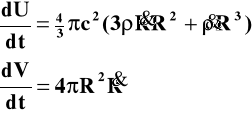
Po wstawieniu do I zasady termodynamiki i uporządkowaniu otrzymamy

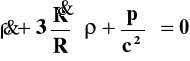
(29)

Jest to tzw. warunek zachowawczy (który w formalizmie OTW wynika z zerowania się kowariantnej dywergencji tensora energii-pędu
).

Zróżniczkujmy teraz r-nie (28a) po czasie:

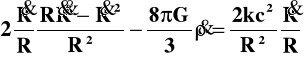
Wielkość
weźmiemy z r-nia (29) i otrzymamy:

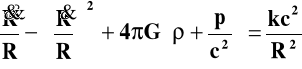
Za prawą stronę
wstawimy r-nie (28a) i uporządkujemy:

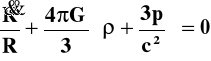
(30)

Jest to tzw. równanie na przyspieszenie.

Dodając stronami równania (28a) i (30) otrzymamy:

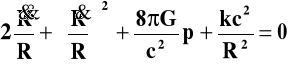
(31)

Jest to równanie identyczne jak równanie kosmologiczne (3) w poprzednim rozdziale. Jeśli ciśnienie jest zaniedbywalne (p = 0) to r-nie (31) przy zastosowaniu (30) jest identyczne z r-niem (28a).

Jak widać można formalnie otrzymać kosmologiczne równania Friedmanna bazując na mechanice newtonowskiej. Jednak mimo formalnej poprawności rachunków ideologia stojąca za nimi jest wątpliwej wartości. Trzeba bowiem pamiętać, że wszystko rozgrywa się tu w nieskończonej i euklidesowej przestrzeni a kosmologia newtonowska obarczona jest znanymi “paradoksami” (paradoks grawitacyjny oraz paradoks Olbersa). W pełni zadowalające uzasadnienie dla otrzymanych równań otrzymuje się na gruncie ogólnej teorii względności.

---