(cosϕ+isinϕ)n =cosnϕ+isinnϕ
zn=|z|n ( cosnϕ+isinnϕ)
![]()
k=0,1,2,...,n-1
![]()
=
T. Bezouta
Jeżeli z0 jest miejscem zerowym wielomianu p, to wielomian ten jest podzielny przez dwumian z- z0 i odwrotnie, czyli p(z)=0 ⇔ (z- z0)|p(z).
Macierze i wyznaczniki
Macierzą wymiaru m×n nazywamy wartość odwzorowania, którego dziedziną jest iloczyn kartezjański {1,2,...,m}×{1,2,...,n} a wartości są z pewnego zbioru (ciała) K : {1,2,...,m}×{1,2,...,n}→aij∈K
D. Minora :Minorem Mij elementu aij macierzy A nazywamy wyznacznik macierzy, którą otrzymamy usuwając z macierzy A i-ty wiersz i j-tą kolumnę.
Macierz A ma macierz odwrotną ⇔ gdy jest macierzą nieosobliwą
![]()
T. Cramera.Jeżeli macierz podstawowa A układu n równań z n niewiadomymi jest macierzą nieosobliwą, to istnieje dokładnie jedno rozwiązanie układu równań dane wzorami:
i=1,...,n lub x=A(-1)B
T. Kroneckera-Capelliego
Ukłąd równań liniowych Ax=B posiada co najmniej jedno rozwiązanie ⇔r(A)=r(Ab)
1.r(A)=r(Ab)=n-ilość niewiadomych-jedno rozwiązanie
2. r(A)=r(Ab)=k<n-nieskończenie wiele rozwiązań zależnych od n-k parametrów.
3. r(A)≠r(Ab)-układ sprzeczny-brak rozwiązań
D. Iloczynu skalarnego
Niech V będzie przestrzenią liniową nad ciałem R, odwzorowanie g: V2→R spełniające warunki:
1.∀x,y,z∈V g(x+y,z)=g(x,z)+g(y,z) g(x,y+z)=g(x,y)+g(x,z)
2.∀x,y,z∈V ∀λ∈R g(λx,y)=g(x,λy)=λg(x,y) - odwzorowanie jest liniowe
3.∀(x,y)∈V g(x,y)=g(y,x)
4.∀x≠0 g(x,x)>0 nazywamy mnożeniem skalarnym w przestrzeni V, a wartość tego odwzorowania na wektorach (x,y) nazywamy iloczynem skalarnym tych wektorów x°y=|x| |y| cosϕ
D. Iloczynu wektorowego
Mnożeniem wektorowym w R3 nazywamy odwzorowanie f:R3 ×R3 →R3 spełniające warunki:
1.∀a,b∈R3 a×b=--b×a
2.∀a,b,c∈R3 a×(b+c)=a×b+a×c (a+b)×c=a×c+b×c
3.∀λR∈ ∀a,b∈R3 (λa)×b=a×(λb)=λ(a×b)
4. i x j =k ,j x k = i , k x i = j
D. Iloczyn mieszany
Iloczynem mieszanym uporządkowanej trójki wektorów a,b,c nazywamy liczbę określoną wzorem: abc=a°(b×c).
![]()
1.
2.Trzy niezerowe wektory a,b,c są współpłaszczyznowe (komplementarne) jeśli abc=0
3. Jeśli a,b,c∈R3 a,b,c=det(a,b,c)
4.det(a,b,c) jest równy objętości równoległościanu rozpiętego na wektorach a,b,c
![]()
Kąt między płaszczyznami
![]()
Warunek prostopadłości
![]()
![]()
Warunek równoległości
Odległość punktu P0 od płaszczyzny:
![]()
Postać krawędziowa prostej
![]()
![]()
Pęk płaszczyzn :
![]()
![]()
Równanie prostej przechodzącej prze 2 punkty A i B:
Kąt między prostymi:
![]()
![]()
Odległość punktu od prostej
Odległość dwóch prostych skośnych:
![]()
![]()
Kąt między prostą i płaszczyzną:
![]()
Warunek przecinania się 2 prostych: ![]()
![]()
Jeżeli ![]()
to proste są skośne
Powierzchnie obrotowe:
![]()
v1(x-f1(t))+ v2(y-f2(t))+ v3(z-f3(t))=0
(x-a1)2+(y-a2)2 +(z-a3)2=( f1(t)- a1)2+( f2(t)- a2)2+( f3(t)- a3)2
![]()
walec:
![]()
![]()
stożek: wierzchołek F(a,b,c)
T. Bolzano Weierstrassa
Każdy ciąg ograniczony ma przynajmniej jeden punkt skupienia.
T. O trzech ciągach Jeżeli ciągi an i cn są zbieżne i lim an = lim cn =g oraz ![]()
n E N: an ![]()
bn![]()
cn to ciąg bn jest zbieżny i lim bn=g
T.Taylora Jeżeli f jest klasy Cn-1([a,b]) i f E Dn(a,b) to istnieje x0 należace do (a,b) takie, że ... f(b)=f(a)+...+1/(n-1)!fn-1(a)(b-a)n-1+Rn(x0) Rn(x0)=1/n! fn (b-a)n
T. Banacha
Jeżeli F jest odwzorowaniem zwężającym przestrzeni zupełnej (A,d) w siebie, to istnieje i jest tylko jeden punkt stały a E A tego odwzorowania.
D. Heinego granicy:
Odwzorowanie F ma w punkcie p0 E A granicę q E B jeżeli dla każdego ciągu pn elementów zbioru A\{ p0} zachodzi implikacja: lim pn= p0lim F(pn)=q
D. Cauchy'ego granicy:
![]()
Odwzorowanie F jest ciągłe w punkcie p0 należy do A jeżeli:
odwzorowaie jest określone w p0
istnieje granica lim F(p)
limp0 f(p)=f(p0)
T. O zachowaniu nierówności w granicy:
![]()
![]()
Jeżeli funkcjonały f: A->R i g: A->R maja granice w punkcie p0 E A i istnieje takie sąsiedztwo ![]()
punktu p0, że:
, to
T. O trzech funkcjonałach:
![]()
Jeżeli funkcjonały f: A->R i g: A->R spełniają w pewnym sąsiedztwie ![]()
punktu p0 warunki : to istnieje granica
![]()
T. O zachowaniu znaku przez f ciągłą
Jeżeli funkcja F->R jest ciągła w punkcie x0 E X to prawdziwe sa implikacje
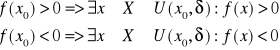
T. Bolzano Cauchy'ego
![]()
T. Weierstrassa
Jeżeli funkcja f:X->R jest ciągła na niepustym, domkniętym i ograniczonym zbiorze X zawarte w R, to osiąga w tym zbiorze swoje kresy.
Liniowość operatora pochodnej
Jeżeli funkcje f,g należą do D1(x) to ![]()
przy czym ![]()
T. Rolla
![]()
T.Cauchy'ego
![]()
T.Lagrange'a
![]()
T. de l'Hospitala
Jeżeli f,g spełniają założenia:
1. ![]()
![]()
![]()
2.![]()
lub ![]()
3.istnieje granica wtedy istnieje granica i zachodzi równość: ![]()
Ekstrema: warunek konieczny: jeżeli funkcja ma ekstremum w punkcie x0 E I i f E D1(I) to f'(x0)=0
1 wystarczający: Jeżeli funkcja f(a,b)->R jest ciągła w punkcie x0 E (a,b) oraz jest różniczkowalna w sąsiedztwie tego punktu i pochodna f' ma różne znaki w sąsiedztwach jednostronnych, to punkt x0 jest punktem ekstremum lokalnego funkci f
2 wystarczający: : Jeżeli funkcja f(a,b)->R jest klasy Cn w pewnym otoczeniu punktu x0 (n E N, n>2) i w punkcie x0 E (a,b) zachodzą związki: f'(x0)=f”(x0)=...=fn-1(x0)=0
i n jest liczbą parzystą to f osiąga ekstremum właściwe w punkcie x0
f2(x)<0 max, f2(x)>0 min
T. o całkowaniu przez podstawienie:
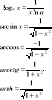
Oznaczona: Jeżeli funkcja f:[a,b]R jest ciągła a bijekcja φ:[α,β]>[a,b] jest klasy C1oraz φ' jest stałego znaku w przedziale [α,β] to: ![]()
![]()
Nieoznaczona: Jeżeli funkcja f:(a,b)->R jest całkowalna, a funkcja ![]()
jest klasy D1, to funkcja ![]()
Jest całkowalna i zachodzi równość
T. O całkowaniu przez części
Oznaczona: Jeżeli f,g są klasy C1na przedziale [a,b] to: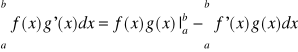
Nieoznaczona:
![]()
T. Riemanna
![]()
T. Główne rachunku całkowego
![]()
![]()
Jeżeli funkcja f jest całkowalna w sensie Riemanna na przedziale [a,b] jest ciągła w punkcie x E [a,b] to funkcja jest różniczkowalna w tym punkcie i ![]()
Podstawowy wzór rachunku całkowego
![]()
Jeżeli funkcja f jest ciągla w przedziale [a,b] to funkcja jest jedną z funkcji pierwotnych funkcji f ,wiec całka Riemanna z funkcji ciągłej na przedziale [a,b] jest równa całce oznaczonej z tej funkcji w granicach od a do b, czyli:
T. O wartości średniej rachunku całkowego
![]()
Jeżeli funkcje f i g są ciągłe w przedziale [a,b] i funkcja g ma stały znak w tym przedziale to istnieje w należące do (a,b) ze:
![]()
Całki niewłaściwe: I rodzaju: Jeżeli funkcja f:[a,8)R jest całkowalna w każdym przedziale [a,T] (T>0) i istnieje granica właściwa to granicę tę nazywamy całką niewłaściwą I rodzaju.
![]()
![]()
II rodzaju: Jeżeli funkcja f [a,b) jest całkowalna w każdym przedziale [a,b-s] (0<s<b-s) oraz a istnieje granica właściwa to granice tę nazywamy całką niewłaściwą II rodzaju
Kryterium Całkowe Zbieżności szeregu
Jeżeli funkcja f:[n0,+8)R jest dodatnia i nierosnąca w przedziale [n0,+8) gdzie n0 należy do N to całka 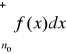
jest zbieżna wtw gdy szereg ![]()
jest zbieżny
Całki:
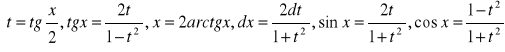
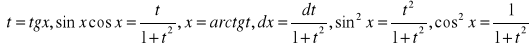
![]()
![]()
![]()
![]()
![]()
![]()
Postać parametryczna: x=φ(t); y=ψ(t)
![]()
![]()
Postać biegunowa: r=h(φ); y= h(φ)sin φ , x= h(φ)cosφ φ[α,β]:
![]()
![]()
![]()
Postać jawna y=f(x):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
rzut prostokątny wektora a na b:
![]()
![]()
![]()
![]()
![]()
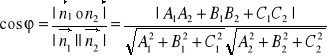
![]()
![]()
![]()

![]()
![]()
![]()
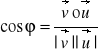
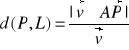
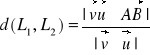
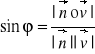
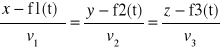
![]()
![]()
![]()
![]()
![]()
![]()
![]()
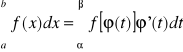
![]()
![]()
![]()
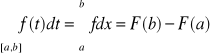
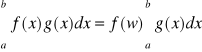
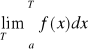
![]()
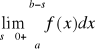
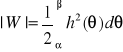
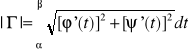
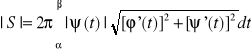
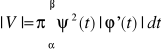
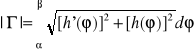
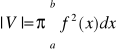

![]()
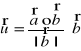
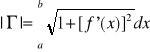
![]()
Wyszukiwarka