img042

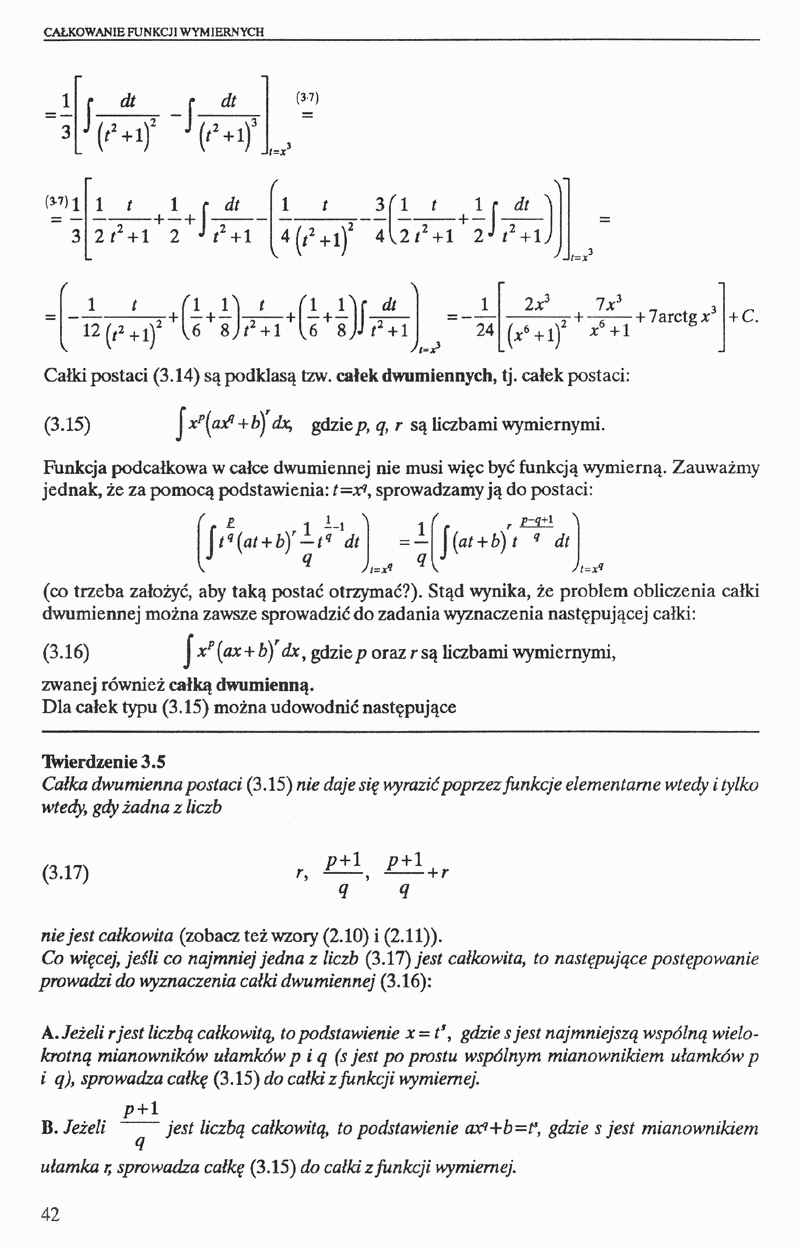
CAŁKOWANIE FUNKCJI WYMIERNYCH

CAŁKOWANIE FUNKCJI WYMIERNYCH

1 f di

ąw

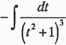
(3-7)

J.=x>

(3.15)

gdziep, q, r są liczbami wymiernymi.

(«)1		1 / 1 r dt	1 t	_3(! ' ą	hir	JL)
	3	2t^2 + l 2 J r^J+1	^4(/^2+iV	' 4v2/^2+1	2j	t^2+ij
			^ V /			*
	✓			\		-
		i ' ‘	A'		i	2Ć	lx^y _ , 3 .1. _L i n+s* i rr
	12 (r^a+!)^2 U 8J'^2 + 1 U 8.				~ 24	(x‘+l)^2 *‘+l

+ C.

Całki postaci (3.14) są podklasą tzw. całek dwumiennych, tj. całek postaci:

Funkcja podcałkowa w całce dwumiennej nie musi więc być funkcją wymierną. Zauważmy jednak, że za pomocą podstawienia: t=X>, sprowadzamy ją do postaci:

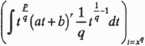
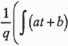
r

l “ dt

(co trzeba założyć, aby taką postać otrzymać?). Stąd wynika, że problem obliczenia całki dwumiennej można zawsze sprowadzić do zadania wyznaczenia następującej całki:

(3.16)    | x^p(ax+b)'dx, gdzie p oraz r są liczbami wymiernymi,

zwanej również całką dwumienną.

Dla całek typu (3.15) można udowodnić następujące

TVvierdzenie 3.5

Całka dwumienną postaci (3.15) nie daje się wyrazić poprzez funkcje elementarne wtedy i tylko wtedy, gdy żadna z liczb

(3.17)

Pźl

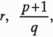
9

nie jest całkowita (zobacz też wzory (2.10) i (2.11)).

Co więcej, jeśli co najmniej jedna z liczb (3.17) jest całkowita, to następujące postępowanie prowadzi do wyznaczenia całki dwumiennej (3.16):

A.    Jeżeli r jest liczbą całkowitą, to podstawienie x = t’, gdzie s jest najmniejszą wspólną wielokrotną mianowników ułamków piq (s jest po prostu wspólnym mianownikiem ułamków p i q), sprowadza całkę (3.15) do całki z funkcji wymiernej.

p+l

B.    Jeżeli ^ jest liczbą całkowitą, to podstawienie axS+b=f, gdzie s jest mianownikiem ułamka r, sprowadza całkę (3.15) do całki z funkcji wymiernej.

42