113 2

224 X. Badanie przebiegu zmienności funkcji

zenie prądu w tych warunkach wyraża się wzorem

xe

(1)

Zbadać, przy jakiej wartości x (gdy n jest dane) natężenie prądu w obwodzie będzie _naj większe.

Rozwiązanie. Z sensu zadania wynika, że n i x są liczbami naturalnymi, przy czy_{m v} jest dzielnikiem liczby n. Załóżmy jednak, że x zmienia się w sposób ciągły i zbadajmy przebieg funkcji I=f(x) wyrażonej wzorem (1).

Obliczamy pochodną

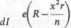
di 7 Pa³

(*⁺t)

Pochodna równa się zeru, gdy x=y/nR/r. Gdy x przechodzi przez tę wartość rosnąc od mniejszych wartości do większych, pochodna dl\dx zmienia znak z dodatniego na ujemny, a więc w punkcie x = \JnR/r funkcja I=f(x) osiąga maksimum.

W praktyce dobiera się daną ilość ogniw n w taki sposób, żeby obliczona wartość x=\lnRjr była bliska jednego z dzielników liczby n. Jeżeli x₁<x<x₂, gdzie x, i x₂ są dzielnikami liczby n, to podstawiamy wartości , x₂ do wzoru (1) i wybieramy tę z nich, która daje większe natężenie prądu.

Zadanie 10.55. Dane jest równanie ruchu drgającego tłumionego w postaci s=ae~^Xl sin cof,

gdzie a=2cm jest pierwotną amplitudą drgań, w=0,01 s'¹ jest pulsacją, a 2=0,01 s jest współczynnikiem tłumienia. Sporządzić wykres odchylenia s jako funkcji czasu '■

Rozwiązanie. Dana funkcja jest określona i ciągła przy wszystkich wartościach <• Obliczamy pochodną

ds

—=ae~^M (co cos cot-Asincot)-dt

Pochodna jest równa zeru, gdy tg cof=«a/A. Podstawiając co=0,01 i A=0,01 otrzy®^ui^en' równanie tg 0,01/= 1, skąd

f=100(Aji+/cii) gdzie k=0,l,2,...

Pisząc pierwszą pochodną w postaci

—=0,02e " °’⁰¹' (cos 0,011 - sin 0,011) dt

obliczmy drugą pochodną. W wyniku otrzymamy —0,0004e^0,01' cos 0,01/. Podstawiając vartości f = 100-(£71+kit), zauważmy, że przy parzystych wartościach k druga pochodna ji_sjdt² jest ujemna, a więc odchylenie s osiąga maksimum; natomiast przy nieparzystych k (jniga pochodna jest dodatnia i odchylenie s osiąga minimum.

Zbadajmy jeszcze punkty, w których wykres funkcji przecina oś Ot. Zachodzi to wtedy, sincof=0, czyli r=100fc'7t, gdzie k'=0, 1,2, ...

przebieg zmienności funkcji jest następujący. Przy t=0 jest s=0. Z biegiem czasu odchylenie s jest dodatnie i osiąga maksimum w punkcie f=25n; maksimum to wynosi Następnie wykres spada, przecina oś Ot w punkcie t= lOOrr i spadając dalej osiąga minimum przy t= 125n; minimum to wynosi -2 _s/2e~^snl*. Potem wykres wznosi się, przecina oś Ot w punkcie t = 200n i w punkcie /=

_225n osiąga maksimum równe 2y]2e~^9nl* i tak dalej. Będzie to gasnąca linia falista (rys. 10.40).

Wprowadźmy oznaczenia:

= b, e "=q, czyli b=0,645, q=0,0432.

Wtedy otrzymujemy s(0)=0, s(25n)=b, s(1007t) =

=0, j(1257c)= — bq, s(200ji) = 0, s(225n)=bq², r(300n)=0, s(325it) = —bq³.

Zauważmy, że tłumienie jest bardzo gwałtowne, gdyż 6=0,645 cm, 6<?=0,028 cm, a bq² =

=0,001 cm.

Zadanie 10.56. Tor pocisku wystrzelonego w punkcie (0,0) (rys. 10.41) jest określony równaniami parametrycznymi

fit

x=40000 (1 - e^-0-⁰²'),    y=45000(1 - e"⁰-⁰²¹) - 5001,

Idzie t jest to czas w sekundach, x — odległość pozioma pocisku w momencie t od punktu (0,0) wyrażona w metrach, a y jest to wysokość wzniesienia pocisku w momencie /. Obli-®yó pochodne dy/dx i d²yjdx². Następnie obliczyć, po jakim czasie i w jakiej odległości Pocisk osiągnie największą wysokość, i podać tę wysokość.

Rys. 10.41

Rozwiązanie. Obliczamy pierwszą pochodną; mamy d_;V    ,

d, = 40000 • 0,02e "¹°⁰²' = 800e ” °’⁰²',    — = 45000 • 0,02e " °-⁰²' - 500 = 900e ~ °-⁰²' - 500