231(1)

n

71 J

O

cos2«x

o

n

Podstawiając obliczone wartości współczynników do szeregu (1), otrzymamy

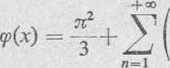
—, cos 2nx--sin

, nr    n

2nx

Rozwinięcie to jest słuszne w całym obszarze określoności funkcji, czyli na całej osi liczbowej, z wyjątkiem punktów x_k = kn (k — 0, ±1, +2,...), w których funkcja jest nieciągła (nieokreślona). W punktach nieciągłości funkcji otrzymany szereg też jest zbieżny i w myśl twierdzenia Dirichleta jego suma w tych punktach wynosi tĆ/2. Do wykresu funkcji nie wchodzą jednak punkty o odciętych x_k. Gdybyśmy sporządzili wykres sumy szeregu, to różniłby się on od wykresu funkcji tym, że występowałyby w nim punkty

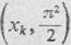
3) Funkcja u jest nieparzysta (rys. 211). Wobec tego a_n = 0. Współczynniki b_n obliczamy ze wzoru (4)

y

Rys. 211

_8n _

7i(2n — 1) (2/; +1)

1    \    21    ,    \ z/ _ _8n

i

7t    1    ¹    .t(2« — l)(2n+l)

n-\—-    n--

71

X

cos 2' =

nsinnx

Zatem

2 ⁼    (2n-l) (2n + l)

(2n —1)(2«4-1)

Otrzymane rozwinięcie jest słuszne w całym obszarze ciągłości funkcji, czyli dla wszystkich * oprócz x_k = 2nk (k = 0, ±1, ±2, ...). W punktach x_k funkcja jest nieciągła, a odpowiadające im sumy szeregu, na mocy twierdzenia Dirichleta, są równe zeru. Jest to oczywiste, ponieważ w punktach tych wszystkie wyrazy szeregu są równe zeru. Wykresy funkcji i sumy szeregu różnią się w punktach o odciętej x_k. Na wykresie funkcji rzędne tych punktów są równe —1, a na wykresie sumy szeregu są one równe zeru.

1042. W podanych przedziałach rozwinąć daną funkcję w niepełny szereg Fouriera, zawierający albo same cosinusy, albo same sinusy: f 0,3, dla 0 < x < 0,5

1)    <P(x) ⁼{_o,3, dla 0,5 <x< 1

2)    y — x cos x w przedziale od 0 do n. Na podstawie otrzymanego roz-

+ 00

...    ...    V¹ Ak*+^l

wimęcia znalezc sumę szeregu

Rozwiązanie: l)a. Aby otrzymać rozwinięcie danej funkcji w szereg Fouriera zawierający tylko cosinusy, przedłużamy ją na sąsiadujący z lewa przedział (—1, 0] parzyście (rys. 212a).

a) y	1
-1 zBŚ.	\0,5 1 _
LJ ■	X
b) </
n	^g 1 l j 05 1 _
1 0,5 I 0 1 m	! i *
Rys.	212

Wtedy b„ = 0 i ze wzoru (3), podstawiając / = 1 oraz ę?(x) = 0,3 dla przedziału (0; 0,5) i <p(x) = —0,3 dla przedziału (0,5; 1), znajdujemy

I    0,5    i

a_n — ~J <p(x) cosrmxdx = 2 ( j 0,3cosrmxdx— j 0,3cosmtxdx^ —

= 0,6

r • no: sinrcjw: '

tlTZ

-Jo

-0,6

o

sinmi*

rm

0.5

1,2 . nn

= -^-sin—;    nź 0

Jo ₅ nn 2

30 Metody rozwiązywania zadań 465