FIZYKA WZORY 1

MECHANIKA

KINEMATYKA

Ar

Prędkość średnia v_łr= —

chwilowa v_ch= *'^m    = :r

^ch jt.odt dt

Ruch jednostajny Ar-As Ar-przesunięcie, As-droga dla lvl = const.: ds = vdt,v_Ch = V|_r

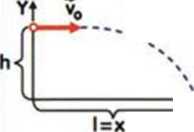
Rzut poziomy

^Ruch 2_m_„_mdv_dv(t| zmienny ^{a( 1} JJlidt" dt

dla lal = const.: v_k = ^2±^₌^|

ds = v_edt+^y^    vk = VFat

a>0 : ruch jedn. przyśpieszony a<0 : ruch jedn. opóźniony

_m0, ,

qx^z

Równanie toru ruchu y=h- —z x=v©t    2v₀

^{1 =} M ^vk=V^vo+Vy'⁼V^vo+2hg

!ly

m

Rzut ukośny v_0y = v₀sincc „ v_ox=v₀cosa

Spadek swobodny _Vk=9t=V2h? t=# h = ⁹i-²

v_e = 0

Rzut pionowy -w górę : a=-g    ^vk=^vo^-9^ł

gt²

Vo²

h = v₀t- ^ h_mox-2g -w dół: a = g, v_k=v₀+gt =Vv₀²+2gh

Ruch po torze kołowym , , _,_imda_da

U)_rh = lim = -rr

^ch óuo** dt

MECHANIKA 3
DYNAMIKA Ruch postępowy i-_0 Izas. dynamiki EF=0 =>|y-có^t U zasada dynamiki £Fj*0=>a = j^ mzasada dynamiki FAb=-FbA	Zasada zachowjnomentu pędu moment pędu b=rxp, b=I0u> M=37 M=0 to b=const. dt
	Ruch drgajgcy Fd = mu> ^2A v=u>A ct-wt -
Siła tarcia Ft=>jN p - współczynnik tarcia, N - nacisk
	x=Asina "\* 1 Vh,„=wAcos<X
Ruch po torze kołowym -przyśpieszenie liniowe a,=£R - przyśp. dośrodkowe ad = u>^2R -przyśp.w ruchu postępowym a=Vaf+ad Fd=mad
	Siła zwracajęca Fx(x)^w vdrfl Fz(x)=-kx Fz(x) = -mcu^2Asina Równanie drgań liniowych md^2x_ . __d^2x * dt^2~’^k a“ dt^2 xOkres drgań własnych ^v k v-częstotliwość Całkowita energia drgań kinetyczna potencjalna r mv^2 kx^2 kA^2 mvmox ^c~ 2 2 “ 2 “ 2
Ruch obrotowy bryły M = r*F dla rlF:M=rF,£=^=^ a n^dt ło ~^7 Io=m1r1^2+...mnr^2 = Zm,r^2 a; !Q . ^1=1 *i^ro \ ^1 a*^a=m r°^A+I ° r0A-odległość środka Af ,0 masy 0 od osi A-A I0- moment bezwładności bryły względem osi0-0,M-moment siły
	Zjawisko Dopplera uv V»— uv v = — l-y l+y u - prędkość źródła, v- pręd.foli
Zasada zachowania pędu p=mv _ Brok sił zewnętrznych: p=const. ^ęd masy=popęd siły^ _ d£ Fdt=pk-p0 Fdt = d(mv) F = — m0 ^aT gdy v~c: m= --- m0-mosa spoczynkowa V^" Ć2
	Okres drgań wahadła « -matematycznego T = 271^— -fizycznego T=27T-^^ 1-długość wahadła, r-odległość środka masy od osi obrotu

MECHANICZNE I TERMODYNAMICZNE WŁASNOŚCI CIAŁA 5

Ciśnienie

ść

Gaz doskonały _ _2n_P ^p’3V^E|r

V-ol.

n-liczba cząstek, E_łr-średnia energia kinetyczna czgstki

Równanie Clapeyrona

_PV=!3rt

E„=|^kT k=5_A

Ciecze

Gęstość 6=^ Ciśnienie P = ^

Parcie F = *hS,p=*h y-ciężar właściwy y=g9 r p₁=p₂ Warunek równowagi

m- masa gazu, p - masa 1 kilomola R = 8,3M0³J/kmol-K-stoła gazowa k=l,38-10'²³J/K-stała Bołtzmanna N_A= 6,02-10²⁶kmor-liczba Avogadra

Siła wyporu _{Fw = Qc}

Q_c-ciężar wypartej cieczy V_C>V => cioło pływa, y_e< y => tonie tf,łf_c " ^c'ęż^Qr właściwy ciała,cieczy

Napięcie powierzchniowe 6 = j- W=Fa = 6al dE_P=6dS

Siła prostopadła do krawędzi błony cieczy, a-przesunięcie Zmiana pola powierzchni dS = la I-długość krawędzi

Mieszanina gazów pV=(n₁₊n_J+...n_k|RT_{T temperofuro}

nj - liczby kilomoli składników

^voy_

= tgct ₌!^_X';_9__X2 ^V- 2Vo²x = §sin2a

QT •    y 2

y=v₀tsincx- h=y_max=^|sin²a

T

I

Równ. toru ruchu Y

x=v₀tcosa l=x gt²

mox

Vox

Prędkości kosmiczne

-iK-«

9 = 9.8)*

R_x = 6,37110⁴m, M_x= 5,96-10²⁴kg

G=6,67-10‘ⁿ_n!L kg-s²

Ri/M_x-promień, masa Ziemi g - przyśpieszenie ziemskie a - przyśpieszenie, T-czas 1 obrotu, G - stoki grawitacyjna u>-prędkość kgtowa; v₀,Y|< - prędkość początkową, końcowa

OTT

dla lu>l = const.: cj = —=2TTv v = uiR u> = 27Tn _{v =} i

n - ilość obrotów w 1 sek.

Współczynnik rozszerzalności objętościowej gazu

a ^v'^v° a-J-K*¹

V₀(T-T₀)^/ "273 p = const.

Współczynnik prężności termicznej gazu

8 =    8=—^ v= const.

Po(^T-'o)

Współczynnik rozszerzalności objętościowej cieczy

^a=G^T> ^va^=v'(l^+a,T*'^T'l)

Vi(T₂-Ti)

273

3 N

T_o=273K,p_o=l,01310 ^

Wilgotność powietrza

-bezwzględna -względna

w.-2    _w -™-L

^b~V    ^Ww-m_n“p_n

m_n,p_n-masa, ciśnienie pory

nasyconej przy V,T= const.

Współczynnik rozszerzalności liniowej ciała stałego

*⁼M&'^l,=l,(W,VT'^l)a=3*

Zasada zachowania ilości, cieczy nieściśliwej _/T-f^7>f²

^si^vi = ^s2^vi

Prawo Hooke'a

dl = k^2

P-if

•o

\— - naprężenie p wewnętrzne P ⁼ jj - moduł Younga _{E =} 1 FT k-współczynnik k

W*